Cox回归分析
cox回归多分类变量结果解读

cox回归多分类变量结果解读Cox回归是一种常用的生存分析方法,用于研究事件发生时间与多个预测变量之间的关系。
在Cox回归中,我们可以使用多分类变量作为预测变量,以探究其对事件发生时间的影响。
本文将介绍如何解读Cox回归多分类变量的结果。
首先,我们需要了解Cox回归的基本原理。
Cox回归基于半参数模型,它假设预测变量对事件发生时间的影响是通过一个风险比例函数来描述的。
这个风险比例函数可以解释为某一组别相对于参考组别的风险。
因此,Cox回归的结果通常以风险比例(Hazard Ratio,HR)的形式呈现。
在Cox回归中,多分类变量的结果解读与二分类变量类似。
我们可以通过HR来衡量不同组别之间的风险差异。
如果HR大于1,表示该组别的风险高于参考组别;如果HR小于1,表示该组别的风险低于参考组别。
同时,HR的置信区间也是解读结果的重要指标,它可以帮助我们评估结果的可靠性。
除了HR,Cox回归还提供了其他一些重要的统计指标,如p值和95%置信区间。
p值可以用来判断预测变量是否对事件发生时间有显著影响。
通常,如果p值小于0.05,我们认为结果是显著的,即预测变量与事件发生时间存在关联。
而95%置信区间可以帮助我们评估HR 的精确程度,如果置信区间较窄,说明结果较为可靠。
在解读Cox回归多分类变量的结果时,我们还需要考虑一些其他因素。
首先,我们需要注意样本的选择和数据的质量。
如果样本具有代表性,并且数据质量良好,那么结果的可靠性会更高。
其次,我们需要考虑调整变量的影响。
Cox回归可以同时考虑多个预测变量,但我们需要确保这些变量之间不存在共线性。
如果存在共线性,结果的解释可能会出现偏差。
此外,我们还可以通过绘制Kaplan-Meier曲线来进一步解读Cox回归的结果。
Kaplan-Meier曲线可以帮助我们观察不同组别之间的生存曲线差异。
如果曲线之间存在明显的分离,说明预测变量对事件发生时间有显著影响。
最后,我们需要注意Cox回归的局限性。
cox回归分析

生存分析之COX回归分析1、生存分析,就是将终点事件出现与否与对应时间结合起来分析得一种统计方法;2、生存时间,就是从规定得观察起点到某一特定终点事件出现得时间,如膀胱癌术后5年存活率研究,及膀胱癌手术为观测起点,死亡为事件终点,两点为生存时间;3、完全数据,观测起点到终点事件所经历得时间,上述例子即膀胱癌手术到因膀胱癌死亡得时间;4、删失数据,因失访、研究结束终点事件未发生或患者死于规定得终点事件以外得原因而终止观察,不能确定具体生存时间得一类数据;5、生存概率,表示某时段开始存活得个体到该时段结束仍存活得概率,p=活满某时段得人数/该时段期初有效人口数;6、生存率,为观察起点起到研究时间点内各个时段得生存概率得累积概率,S(tk)=p1、p2、pk=S(tk-1)、pk;7、生存曲线,以生存时间为横轴,将各个时间点得生存率连在一起得曲线图;8、中位生存期,又称半数生存期,表示50%得个体存活得时间;9、PH假定(等比例风险假定),某研究因素对生存得影响不随时间得改变而改变,就是COX回归模型建立得前提条件。
Cox回归分析及其SPSS操作方法概述前面我们已经讲过生存分析及KM法得内容,详细可以回复数字26-28查瞧。
但有对统计不太熟悉得“微粉”还不太明白生存分析与一般统计得区别,不知道如何区别Cox回归与Logistic回归。
在我们做研究时,有时我们不仅关心某种结局就是否出现,还会关心结局出现得时间,例如肺部手术后观察五年生存率,一个有在1年之后死亡,另外一个人在在4、5后死亡,如果只瞧第5年时得结局,两者就是一样得(均死亡),但就是实际我们认为后者得治疗效果可能优于前者,即生存分析同时考虑结局与结局出现得时间,而一般分析只考虑结局。
另外在队列随访时,可能有人在没有到5年时就失访了,如迁徙或者电话更改,我们不了解其结局如何,在一般得分析中这种病例无法使用,而中间失访得病例结局可能更差,如果直接扔掉,可能会产生偏倚;而用生存分析,这种病例可以给我们提供部分资料,即我们记录最后一次随访时病例得状态,失访前得资料可以用于分析。
Cox回归分析—非常详细的SPSS操作介绍

患者生存状态的影响因素分析——生存资料的COX回归分析1、问题与数据某研究者拟观察某新药的抗肿瘤效果,将70名肺癌患者随机分为两组,分别采用该新药和常规药物进行治疗,观察两组肺癌患者的生存情况,共随访2年。
研究以死亡为结局,两种治疗方式为主要研究因素,同时考虑调整年龄和性别的影响,比较两种疗法对肺癌患者生存的影响是否有差异。
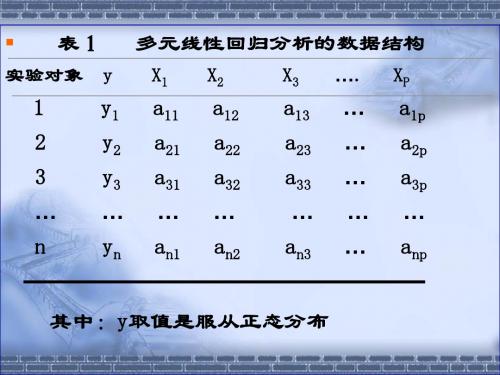
变量的赋值和部分原始数据见表1和表2。
表1. 某恶性肿瘤的影响因素与赋值表2. 两组患者的生存情况group gender age time survival0 1 0 22 10 1 1 10 10 1 1 64 10 1 1 12 10 1 0 17 11 0 0 19 11 1 1 4 11 0 1 12 01 0 0 5 01 1 1 27 02、对数据结构的分析该研究以死亡为结局,治疗方式为主要研究因素,每个研究对象都有生存时间(随访开始到死亡、失访或随访结束的时间),同时考虑调整年龄和性别的影响。
欲了解两种疗法对肺癌患者生存的影响是否有差异,可以用Cox比例风险模型(Cox proportional-hazards model,也称为Cox回归)进行分析。
实际上,Cox回归的结局不一定是死亡,也可以是发病、妊娠、再入院等。
其共同特点是,不仅考察结局是否发生,还考察结局发生的时间。
在进行Cox回归分析前,如果样本不多而变量较多,建议先通过单变量分析(KM法绘制生存曲线、Logrank检验等)考察所有自变量与因变量之间的关系,筛掉一些可能无意义的变量,再进行多因素分析,这样可以保证结果更加可靠。
即使样本足够大,也不建议把所有的变量放入方程直接分析,一定要先弄清楚各个变量之间的相互关系,确定自变量进入方程的形式,这样才能有效的进行分析。
单因素分析后,应当考虑应该将哪些自变量纳入Cox回归模型。
一般情况下,建议纳入的变量有:1)单因素分析差异有统计学意义的变量(此时,最好将P值放宽一些,比如0.1或0.15等,避免漏掉一些重要因素);2)单因素分析时,没有发现差异有统计学意义,但是临床上认为与因变量关系密切的自变量。
COX回归分析
Total a. Dependent Variable: DAY
Omnibus Tests of Model Coefficientsa,b Overall (score) -2 Log Likelihood Chi-square df 45.145 14.783 6 Change From Previous Step Change From Previous Block Sig. Chi-square df Sig. Chi-square df Sig. .022 16.199 6 .013 16.199 6 .013
Enter和Remove的确定同前
调试法:P从大到小取值0.5,0.1, 0.05,一般实际用时, Enter , Remove应多次选取调整。
例.某医师对1988年收治的16例鼻腔 淋巴瘤患者随访了13年,数据见表7, 试作COX回归。
1 2 3
… 16
表2
1 0 0
… 0
鼻腔淋巴瘤患者随访资料
(6)Cox模型中回归系数的检验
假设为 H0: k 0 ,其它参数β固定; H1: k 0 ,其它参数β固定。 H0成立时,统计量 Z =bk/SE(bk) 服 从标准正态分布。SE(bk)是回归系数bk的标准 误。
3、Cox回归模型的作用 (1) 可以分析各因素的作用 (2)可以计算各因素的相对危险度 (relative risk,RR)
logit( p) ln[p /(1 p)]
为Logistic变换,即:
Logit( p) 0 1 X 1 p X p
SPSS操作步骤:
Analyze-----Regression-----Binary Logistic -----Dependent框(y)-----Covariates框 (x1,x2,…)------ok
cox回归分析

生存分析之COX回归分析1.生存分析,是将终点事件出现与否与对应时间结合起来分析的一种统计方法;2.生存时间,是从规定的观察起点到某一特定终点事件出现的时间,如膀胱癌术后5年存活率研究,及膀胱癌手术为观测起点,死亡为事件终点,两点为生存时间;3.完全数据,观测起点到终点事件所经历的时间,上述例子即膀胱癌手术到因膀胱癌死亡的时间;4.删失数据,因失访、研究结束终点事件未发生或患者死于规定的终点事件以外的原因而终止观察,不能确定具体生存时间的一类数据;5.生存概率,表示某时段开始存活的个体到该时段结束仍存活的概率,p=活满某时段的人数/该时段期初有效人口数;6.生存率,为观察起点起到研究时间点内各个时段的生存概率的累积概率,S(tk)=p1.p2.pk=S(tk-1).pk;7.生存曲线,以生存时间为横轴,将各个时间点的生存率连在一起的曲线图;8.中位生存期,又称半数生存期,表示50%的个体存活的时间;9.PH假定(等比例风险假定),某研究因素对生存的影响不随时间的改变而改变,是COX回归模型建立的前提条件。
1.Cox回归分析及其SPSS操作方法概述前面我们已经讲过生存分析及KM法的内容,详细可以回复数字26-28查看。
但有对统计不太熟悉的“微粉”还不太明白生存分析与一般统计的区别,不知道如何区别Cox回归与Logistic回归。
在我们做研究时,有时我们不仅关心某种结局是否出现,还会关心结局出现的时间,例如肺部手术后观察五年生存率,一个有在1年之后死亡,另外一个人在在4.5后死亡,如果只看第5年时的结局,两者是一样的(均死亡),但是实际我们认为后者的治疗效果可能优于前者,即生存分析同时考虑结局和结局出现的时间,而一般分析只考虑结局。
另外在队列随访时,可能有人在没有到5年时就失访了,如迁徙或者电话更改,我们不了解其结局如何,在一般的分析中这种病例无法使用,而中间失访的病例结局可能更差,如果直接扔掉,可能会产生偏倚;而用生存分析,这种病例可以给我们提供部分资料,即我们记录最后一次随访时病例的状态,失访前的资料可以用于分析。
univariate cox regression analysis

univariate cox regression analysis【原创版】目录1.单变量 Cox 回归分析简介2.单变量 Cox 回归分析的步骤3.单变量 Cox 回归分析的优缺点正文一、单变量 Cox 回归分析简介单变量 Cox 回归分析是一种用于研究生存时间数据和事件发生风险的统计分析方法,由英国统计学家 Richard Cox 于 1972 年首次提出。
该方法主要通过建立一个数学模型,以预测某个事件在特定时间内发生的概率,同时评估不同变量对事件发生风险的影响。
在实际应用中,单变量Cox 回归分析被广泛应用于医学、生物统计学、金融等领域。
二、单变量 Cox 回归分析的步骤1.数据收集:首先需要收集一组生存时间数据,包括事件发生时间、事件类型、个体特征等。
2.数据整理:对收集到的数据进行清洗、整理,确保数据的准确性和完整性。
3.变量筛选:根据研究目的和数据特点,筛选出可能影响事件发生风险的自变量。
4.建立数学模型:根据所选自变量,构建单变量 Cox 回归模型,包括风险函数和生存函数。
5.模型估计:利用最大似然估计法或贝叶斯方法,估计模型中的参数。
6.模型检验:检验模型的有效性和假设是否成立,通常采用 log-rank检验或 Schmidt-Norman 检验。
7.结果解释:根据模型估计结果,解释自变量对事件发生风险的影响程度。
三、单变量 Cox 回归分析的优缺点优点:1.可以处理生存时间数据,适用于研究长时间内事件发生的风险。
2.能够评估多个自变量对事件发生风险的相对影响。
3.具有较强的统计学性质,可以进行模型检验和参数估计。
缺点:1.对模型的假设较强,如线性关系、恒定风险比等,可能不适用于所有情况。
2.参数估计的精确性受样本量和数据分布的影响较大。
cox比例风险回归模型结果解读

COX比例风险回归模型是一种常用的生存分析方法,它能够对生存时间或事件发生时间进行建模,并且能够考虑到不同个体的观测时长不同这一特点。
在研究中,COX比例风险回归模型通常被用来探究某种因素对于生存时间或事件发生时间的影响程度。
本文将以COX比例风险回归模型为主题,深入探讨其原理、应用、结果解读和个人理解。
一、COX比例风险回归模型原理COX比例风险回归模型是由David R. Cox于1972年提出的,它是一种半参数模型,既考虑了危险比的比例关系,又不需要对基本风险函数作出严格的假设。
模型的基本形式为:$$ h(t|x) =h_0(t)exp(\beta_1x_1+\beta_2x_2+...+\beta_px_p) $$ 其中,h(t|x)为在给定协变量x情况下,观测到时间t的瞬时事件发生率;h0(t)为基础风险函数,与协变量无关;β1, β2,…, βp为协变量的回归系数;x1, x2,…, xp为对应的协变量。
二、COX比例风险回归模型应用COX比例风险回归模型主要适用于生存分析领域,例如医学、流行病学和生态学等研究中。
研究者可以利用COX比例风险回归模型来探究不同因素对于生存时间或事件发生时间的影响情况。
这种模型在临床试验中也得到了广泛的应用,可以用来评估治疗效果、预测疾病风险等。
三、COX比例风险回归模型结果解读在进行COX比例风险回归模型分析后,我们通常会得到各个协变量的回归系数、危险比和相应的置信区间。
这些结果对于理解不同因素对生存时间或事件发生时间的影响至关重要。
如果某个协变量的危险比为2.0,且置信区间不包含1.0,就说明该因素对事件发生的影响是显著的。
还需要考虑模型的比例风险假设是否成立,以及是否存在共线性等问题。
个人理解与观点:COX比例风险回归模型是一种非常有用的统计方法,它能够帮助研究者从更深层次理解不同因素对生存能力的影响程度。
然而,在进行模型分析时,我们还需要注意模型的适用性和准确性,避免结果的误导性。
lasso cox regression analysis

Lasso Cox回归分析是一种结合了Lasso回归和Cox回归分析的统计方法。
这种方法在生物信息学、医学和其他领域中被广泛应用,用于研究多个变量对生存时间的影响,尤其是在存在多重共线性和变量个数大于样本量的情况下。
Lasso回归是一种线性模型,通过添加一个惩罚项来压缩模型系数,从而实现变量选择和降低模型复杂度。
这个惩罚项是一个绝对值之和的函数,使得一些系数被压缩为零,从而达到变量选择的目的。
在Lasso回归分析中,通过调整惩罚项的系数λ,可以控制变量选择的严格程度。
Cox回归是一种生存分析方法,用于研究多个变量对生存时间的影响。
Cox回归模型是一种半参数模型,不需要对生存时间分布做出假设,因此在实际应用中比较灵活。
Cox回归模型通过最大化部分似然函数来估计模型系数,从而得到每个变量对生存时间的影响。
将Lasso回归和Cox回归结合起来,可以形成一种新的分析方法——Lasso Cox回归分析。
这种方法首先利用Lasso回归进行变量选择,将不重要的变量压缩为零,然后利用Cox回归模型分析筛选后的变量对生存时间的影响。
这种方法可以克服传统Cox回归在变量个数大于样本量或存在多重共线性时的局限性,提高模型的稳定性和预测能力。
在进行Lasso Cox回归分析时,需要注意选择合适的λ值,以便在变量选择和模型复杂度之间取得平衡。
常用的方法是通过交叉验证等方式来评估不同λ值下模型的性能,选择最优的λ值进行建模。
此外,还需要注意模型的假设条件和适用范围,以确保分析结果的准确性和可靠性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
◦ 当其它协变量相同,变量Xi改变一个单位时,引起的死亡 风险改变倍数的自然对数值
从本质上讲,Cox模型无法准确估计出具体风险状 况和计算生存率
研究癌细胞是否有转移(x1:x1=0 无转移,x1=1 有转移)和是否 手术(x2:x2=0 无手术,x2=1 有手术)这两个协变量对癌症患者 生存时间的影响,建立了如下Cox回归模型:
(proportional hazard model) S (t) = S0 (t)exp( Xβ ')
Xβ'=β1x1+β2x2+…+βmxm
h0(t)称为基础风险函数(Baseline Hazard Function)
◦ 表示个体在时点t的基线死亡风险,也就是说 所有协变量为0,即风险因素为基线值时的死 亡风险率
4
3-
30
30
0.30
0.65
5
4-
10
10
0.10
0.75
6
5-
5
5
0.05
0.80
7
6-
4
4
0.04
0.84
8
7-
3
3
0.03
0.87
9
8-
2
2
0.02
0.89
10
9-
2
2
0.02
0.91
11
10-
1
1
0.01
0.91
12 11-21
8
0.8
0.008
1.00
半参数法
◦ 规定了影响因素和生存结局间的关系,对时间 (和风险函数)的分布没有加以限定
RR=exp(β)
表示协变量每增加一个单位,危险度改变多少倍。
treat的β= -1.617,RRtreat=0.199,表示治疗方 案2与1比较,其危险度是治疗方案1的0.199倍,提 示治疗方案2优于治疗方案1。
age的β=0.119,RRage=1.127,表明年龄每增加 一岁,死亡的可能性增加到1.127倍
◦ 假定这个个体存活时间大于等于t。 ◦ 这个函数为发病或死亡密度(ID或MD)
= λ(t) lim 1 P[T ∈(t,t + ∆t) / T ≥ t] ∆t→0 ∆t
λ(t) = f (t) S (t )
累积风险函数(cumulative hazard function)
◦ 风险函数的右侧积分面积
Number of obs =
LR chi2(2)
=
Prob > chi2 =
Pseudo R2
=
34 18.16 0.0001 0.1320
------------------------------------------------------------------------------
time |
4
2017/4/13
在Stata命令中加入hr,可以直接给出RR值。 cox time treat age , dead(dead) hr
time | dead | Haz. Ratio Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------treat | .1985735 .0982651 -3.27 0.001 .0752835 .5237726 age | 1.126916 .0458782 2.93 0.003 1.040491 1.220521
┆
┆
23
1
2
52
32
0
2
57
Stata命令 gen ta=treat*age 生成age和treat的交互项ta cox time treat age ta, dead(dead) 拟合含有
交互项的Cox模型 cox命令的语句格式为:cox 生存时间变量 协变量,
dead(结局变量)
2017/4/13
2017/4/13
5例癌患者随访记录
序号
1 2 3 4 5
姓名
马** 李** 张** 吴** 王**
性别 (男=1)
1 0 1 0 1
处理组
0 1 1 0 1
开始日期 终止日期
98-07-12 98-07-01 98-07-14 98-08-22 98-10-20
98-11-29 98-12-08 98-12-31 98-11-29 98-11-25
age | .119485 .0407113 2.93 0.003 .0396924 .1992776
------------------------------------------------------------------------------
Cox回归方程 h(t, X ) = h0 (t) ⋅ e(−1.617⋅treat+0.119⋅age)
treat | -3.005587 5.033301 -0.60 0.550 -12.87068 6.859502
age | .0891689 .116237 0.77 0.443 -.1386514 .3169892
ta | .0220285 .0792198 0.28 0.781 -.1332394 .1772965
0.84
3
3
0.03
0.87
9
8-
2
10
9-
2
11
10-
1
12 11-21
8
2
0.02
0.89
2
0.02
0.91
1
0.01
0.92
8
0.08
1.00
11
估计该病患者生存时间不超过2年的概率: F(2)=0.15
该病患者在时点2(年)死亡的危险性:
f(2)=0.20
估计该病患者生存时间超过2 (年)的概率: S(2)=1-F(2)=1-0.15=0.85
i 确诊后(年) 死于本病例数 频数/年 频率/年 累计频率/年
ti
fi
fi/年
f(ti)
F(ti+1)
1
0-
2
1-
3
2-
4
3-
5
4-
6
5-
7
6-
8
7-
5
5
0.05
0.05
10
10
0.10
0.15
20
20
0.20
0.35
30
30
0.30
0.65
10
10
0.10
0.75
5
5
0.05
0.80
4
4
0.04
dead |
Coef. Std. Err.
z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
treat | -1.616596 .4948552 -3.27 0.001 -2.586495 -.6466978
◦ 一般来说指的是Cox比例风险模型,属多因素 分析方法,主要用于分析影响生存率的因素
◦ 是目前医学中应用最广的生存分析方法之一
生存函数S(t) (survival function)
◦ 个体存活时间超过t的概率,随时间t的增大而减小 S(t) = P[T > t]
概率密度函数f(t) (probability density function)
------------------------------------------------------------------------------
time |
dead |
Coef. Std. Err.
z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
◦ 个体在单位时间内死亡的概率极限,一般为一右侧长尾曲线, 其右侧积分面积即为S(t)
= f (t) lim 1 P[t ∈(t,t + ∆t)] ∆t→0 ∆t
1
2017/4/13
累积死亡函数F(t ) (cumulative distribution function) F(t) = 1− S(t) = P[T ≤ t]
结局 (死=1)
0 1 0 1 1
生存天数
140 160 170 99 36
生存时间
◦ 完全数据(complete data) ◦ 截尾数据(censored data),亦称为删失数据
非参数法
◦ 随访资料的常用分析方法
参数法
◦ 要求观察的生存时间t服从某一特定的分布,根据 特定的分布估计参数,从而得到生存率的估计值。
RH (t) = h(t, X )
+Λ
+ βmXm
h0 (t)
RH(t)表示在时间t,协变量X下,个体风险率相对于
基础风险率的比
= RH (t) ex= p(X β ′) exp(β1x1 + ...+ β p xp )
可见, RH(t)不随时间变化 因此,COX回归模型又称为比例风险模型
