相似多边形 导学案
4.6《相似多边形》导学案
4.6 相似多边形
学习目标:
了解相似多边形的概念和性质;在简单情形下,能根据定义判断两个多边形相似;会用相似多边形的性质解决简单的几何问题.
学习重难点:
重点是相似多边形的定义和性质;难点是判断两个多边形是否相似.
导学过程:
一、合作学习
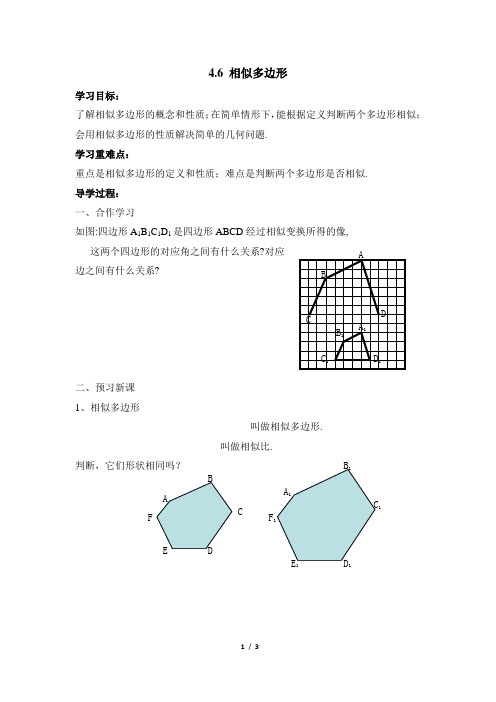
如图:四边形A1B1C1D1是四边形ABCD经过相似变换所得的像,
这两个四边形的对应角之间有什么关系?对应
边之间有什么关系?
二、预习新课
1、相似多边形
___________________________________叫做相似多边形. _____________________________叫做相似比.
判断,它们形状相同吗?A
B
C
D
A
1
B
1
C
1
D
1
C 1
1
1
F
1 / 3
2 / 3
2、练习
(1)它们相似吗? (2)它们呢?
3、相似多边形的性质
问题:如果两个多边形相似,那么它们的对应角有什么关系?对应边呢? 相似多边形的性质:
相似多边形的________相等,_________成比例.
相似多边形的__________等于相似比;__________等于相似比的平方. 4、例题学习
矩形纸张的长与宽的比为 2 ,对开后所得的矩形纸张是否与原来的矩形纸相似?请说明理由.
5、课内练习
(1)右面两个矩形相似,求它们对应边的比.
8
A
B
C
D
E
F
2
3。
北师大九年级数学上4.3相似多边形导学案教案

DEF4.3相似多边形班级 姓名 月 日一、课前热身1. 已知a=3cm ,b=4cm ,c=6cm ,d=8cm 能否组成比例线段?2.如图△ABC 和△DEF 全等,那么对应边有 ,对应角有 ,对应边的比是 3.下面形状相同的图形有( ) 二、做一做,填一填:1.从08奥运会游泳馆水立方和自由体操场地中抽象出的两个正方形形状相同吗? 两个正方形边、角之间的关系如下:(1) 在这两个正方形中,是否有对应相等的内角?(2) 在这两个正方形中,夹相等内角的两边是否成比例? 2.自学书上P 86-P 87内容,完成下列问题:形状相同的多边形对应角________对应边__________相似多边形: . 相似符号为 . 练一练:1)△ABC 相似于△HMN 记作:____________;若21HM AB ,则相似比为_____ _。
2)六边形ABCDEF 相似于六边形GHIJKL 记作:_________________总结:两个相似多边形对应角有什么关系?对应边有什么的关系? 3、独立思考探究,然后说说你的想法:1)如果两多边形对应角相等,那么这两个多边形是相似多边形,对吗? 2)如果两多边形对应边成比例,那么这两个多边形是相似多边形,对吗?三、课堂练习:1.如果两个多边形形相似,则对应边 , 对应角 ,对应边的比就是它们的 。
2、两个相似多边形的对应边的比是32,则这两个多边形的相似比是________. 3.如果六边形ABCDEF ∽六边形A ′B ′C ′D ′E ′F ′,∠B=62°,那么∠B ′等于( ) A. 28° B. 118° C. 62° D. 54°4.等边三角形ABC 和三角形A ′B ′C ′相似,相似比为5:2,若AB=10,B ′C ′等于 5、判断下列每组中的两个图形是相似多边形吗?并说明理由.(1)两个大小不等的矩形;( ) (2)两个大小不等的正五边形;( ) (3)一个正方形与一个平行四边形;( ) (4)两个大小不等的菱形( ) 四.自我检测: 1、如图,EF AD ∽ABCD ,则∠A 的对应角是________,A B CA BC DABCDA DB CNM∠B 的对应角是________,ABAF )() (.2、△ABC ∽△'''C B A ,若对应边AB 与''B A 的长分别为50厘米和40厘米,则△'''C B A 与△ABC 的相似比是( )A.5∶4B.4∶5C.5∶25D.25∶5A.有一个角相等的两个平行四边形B.有一个角相等的两个等腰梯形 五.思考题:1、如果一个矩形对折后所得矩形与原矩形相似,则此矩形的长边与短边的比是( ) A.2∶1B.4∶1C.2∶1D.1∶23、如图,把矩形ABCD 对折,折痕为MN,矩形DMNC 与矩形ABCD 相似,已知AB=4 (1) 求AD 的长:(2)求矩形DMNC 与矩形ABCD 的相似比。
相似多边形导学案1

《4.5相似多边形》导学案学习目标:探索相似多边形的性质并会运用性质解决有关问题。
课中导学【一】自学新知:阅读教材118-119页例题之前,完成下列填空。
1、的两个多边形叫做相似多边形。
如图六边形ABCDEF与六边形A1B1C1D1E1F1相似记为_____________________2、相似多边形的________________________比叫做它们的相似比。
3、在记两个多边形相似时,要注意___________________________。
4、如图,四边形ABCD∽四边形A1B1C1D1,且11BAAB=k(1)由定义可知,相似多边形的对应角对应边。
(2)的周长四边形的周长四边形1111DCBAABCD=(3)将两个四边形对应的分割为两个三角形①△ABC与△A1B1C1相似吗?为什么?②S△ABC与S△A1B1C1有什么关系?S△ACD与S△A1C1D1呢?③S四边形ABCD︰S四边形A1B1C1D1=___5、对于一般的相似多边形也有相同的结论吗?小结:相似多边形的对应角,对应边,周长比等于它们的,面积比等于它们的。
【三】新知应用:1、如果四边形ABCD∽四边形EFGH相似,且∠A=68°,则∠E= ________ 。
2、一个多边形的边长分别是2、3、4、5、6,另一个和它相似的多边形的最短边长为6,则这个多边形的最长边为____________ 。
3、下列说法中正确的是()A、所有的矩形都相似B、所有的正方形都相似C、所有的菱形都相似D、所有的等腰梯形都相似E、所有的正多边形都相似F、所有的直角三角形都相似G、所有的等腰直角三角形都相似【四】例题解析:例.矩形纸张的长与宽的比为2,对开后所得的矩形纸张是否与原来的矩形纸相似?请说明理由.思考:某种纸张有以下特征:每次对折后,所得到的长方形均与原长方形相似。
这种纸张的长与宽满足什么条件?达标测评1、两个多边形相似的条件是()A 对应角相等B 对应边成比例C 对应角相等或对应边成比例D 对应角相等且对应边成比例2、两个相似六边形的周长分别是l1,l2,面积分别是S1,S2,若 l1:l2=2︰3,S2-S1=30,则S1=_________,S2=___________.3、在一张比例尺为1︰3000的地图上,一块多边形区域的周长是4㎝,面积是1㎝2,这个区域的实际周长为__________,面积为__________。
《相似多边形》导学案1

A B C D EF 相似多边形教师寄语:相信自己,一定能行.加油!一、自主探究:根据课前预习,并类比相似三角形的性质,可以得出相似多边形的性质:相似多边形的性质:.思考:你还有哪些拓展性发现或困惑二、深化应用:1、“打桩式”练习:(1)一个五边形的边长扩大为原来的3倍,则面积扩大为原来的____倍,周长扩大为原来的 倍.(2)把一个六边形的面积扩大为原来的49倍,形状不变,那么对应对角线扩大为原来的 倍.2、“魔方式”练习:(3)已知正五边形ABCDE ∽正五边形11111A B C D E ,且相似比为4:3,如果正五边形ABCDE 的周长是20cm ,则11A B ______,它们的面积比为 .(4)两个相似多边形的一组对应边的边长分别是15cm 和12cm ,①若它们的周长相差24cm ,则这两个多边形的周长分别为 ;②若它们的面积相差2702cm ,则较大的多边形面积为 2cm .3、“蹦极式”练习:(5)在比例尺为1:100000的地图上,某开发区的图上周长为25cm ,图上面积为252cm ,那么该开发区的实际周长为 km ;实际面积是 2km .回思:此题最易犯什么错误(6)如右图,在梯形ABCD 中,AD ∥BC ,EF ∥BC ,EF 与AB ,CD 分别相交于点E ,F ,且梯形AEFD ∽梯形EBCF .①若AD=4,AB=6,BC=9,求AE 的长;②AEFD EBCFS S 梯形梯形与AD BC 相等吗请说明理由. 友情提示:如果想不出来,可以与同组同学共同研究;若还有困难的话,请翻到反面,将有小提示,相信你一定能解决这问题.三、自我检测:(7)五边形ABCDE 边的各边长分别是1,2、3、4、5,面积是20,与它相似的另一个五边形1111A B C D 1E 的最长边是8,则这个五边形1111A B C D 1E 的周长为 ,面积为 .四、学后记:(1)本节你学到的知识点是 ;(2)本节所涉及的思想方法是: ;(3)本节你独特的感受或存在的困惑是: .五、作业超市:A 层:(必作题)伴你学:57P 页1~6.B 层:(选作题)1、如右图,把一个矩形纸片ABCD 沿AD 和BC 的中点连线EF 对折,要使矩形AEFB 与原矩形相似,则原矩形长与宽的比为( )∶1B.3∶1C.2∶1 ∶12、某生活小区开辟了一块矩形绿草地,并画了甲、乙两张规划图,其比例尺分别为1∶200和1∶500,求这块矩形草地在甲、乙两张图纸上的面积比.3、一条河的两岸有一段是平行的,在河的这一岸每隔5米有一棵树,在河的对岸每隔50米有一根电线杆,在这岸离开岸边25米看对岸,看到对岸相邻的两根电线杆恰好被这岸的两棵树遮住,并且在这两棵树之间还有三棵树,求河宽.4、学生张敏利用树影测松树的高度.他在某一时刻测得1.5米长的竹竿影长是0.9米,但当他马上测松树的高度时,因松树靠近一幢高楼,影子不是全部落在地面上,有一部分影子落在墙上.他测得留在地面部分的影长是2.4米,留在墙壁部分的影高是1.5米,求松树的高度.友情提示:可利用相似多边形的性质先求出线段EF的长.。
北师大版初中八年级数学4.4相似多边形导学案

AC B(2) (1)(3)AC B ADE CBFE DH GFA 1E 1D 1北师大版初中八年级数学《 相似多边形》导学案一、 学习目标: 1.经历探索相似多边形概念的进程,明白相似多边形的对应角相等,对应边成比例。
2.在探索相似多边形的进程中,进一步进展归纳、类比、反思、交流等方面的能力,提高数学思维水平,体会反例的作用。
二、教学重难点:重点: “相似多边形概念”的理解与应用.难点:“对应边成比例”的理解与正确运用.三、教学进程 (一)、温习引入 一、全等图形的概念?二、全等三角形的边、角各有什么特点? (二)、初步探讨一、你能发觉每一对图形中有什么一路特征吗?二、观察下列三组图形有什么一路特征?CFD E BA3、下面两个图形之间,角有什么关系?边有什么联系?4、在小组合作、班内交流的基础上,类比全等给出: ①相似多边形的概念 ②表示法 ③相似比的概念(三)、议一议:它们是相似多边形吗? 一、任意两个等边三角形; 二、任意两个正方形;的两个正多边形必然相似。
3、任意两个菱形;的两个菱形必然相似。
4、任意两个矩形;的两个矩形必然相似。
五、如图,点E 、F 别离是等腰梯形ABCD 两腰的中点, 梯形AEFD 和梯形EBCF 相似吗? (四)、想一想一、只知足各角对应相等的两个多边形必然相似吗? 二、只知足各边对应成比例的两个多边形必然相似吗? 3、若是两个多边形要相似,需要知足哪些条件? 反过来会如何?1、若是两个多边形相似,那么它们的对应角有什么关系? 对应边呢?A 1D 111DEAD C2、若是两个多边形不相似,那么它们的角有可能对应相等吗? 它们的各边可能对应成比例吗?3、多边形相似和多边形全等有什么关系? (五)、应用与延伸一、如图,五边形ABCDE ∽五边形A ´B ´C ´D ´E ´。
则∠ E = ,∠ A ´= ,C ´D ´= ;五边形A ´B ´C ´D ´E ´与五边形ABCDE 的相似比为 。
北师大版-数学-八年级下册--4.4相似多边形 导学案

4.4相似多边形学习目标、重点、难点【学习目标】1、 相似多边形的定义;2、 相似多边形的特征;【重点难点】相似多边形的定义和特征.知识概览图相似多边形⎩⎨⎧相似多边形的特征相似多边形的定义 新课导引观察下图所示的图形.【问题探究】观察上述三组图形,每组图形的对应角和对应边之间有什么关系?【点拨】每组图形的对应角相等,对应边的比相等.教材精华知识点 相似多边形各角对应相等、各边对应成比例的两个多边形叫做相似多边形.拓展 这个定义跟其他定义一样,有两个功能:一方面,如果两个多边形的角都对应相等,且边都对应成比例,那么我们就可以判定这两个多边形是相似的;另一方面,如果已知两个多边形相似,那么它们的对应角一定相等,对应边一定成比例,这是相似多边形的本质特征,用它可以解决有关的问题.相似多边形的表示方法:若五边形ABCDE 与五边形E D C B A '''''相似,记作:五边形ABCDE ∽五边形E D C B A '''''.相似多边形对应边的比叫做相似比.拓展 (1)“多边形”的“多”字包含3或3以上的所有自然数,所以有了相似多边形的定义,就不必再重新定义“相似三角形”“相似四边形”…….(2)前面我们学过图形的全等,全等其实是相似的一个特例,全等图形是相似比为l 的相似图形.多边形相似的判定:(1)边数相同;(2)对应角相等;(3)对应边成比例.拓展 (1)判定两个多边形相似,这三个条件缺一不可.(2)两个边数不相同的多边形一定不相似.相似多边形的特征:如果两个边数相同的多边形相似,那么这两个多边形的对应角相等,对应边成比例.相似多边形特征的应用:应用相似多边形的特征,可以证明角相等、线段成比例. 课堂检测基础知识应用题1、(1)正三角形ABC 与正三角形DEF 相似吗?(2)正方形ABCD 与正方形EFGH 相似吗?综合应用题2、如图4-33所示,梯形ABCD 与梯形D C B A ''''相似,求未知边x ,y ,z 的长度和角α,β的度数.探索创新题3、小强将一张报纸对折后,发现对折后的半张报纸与整张报纸相似,则整张报纸的长和宽的比是 ( )A .2∶lB .4∶1C .2∶1D .1.5∶l体验中考1、如图4-35所示,若△ABC ∽△DEF ,则∠D 的度数为 .学后反思附: 课堂检测及体验中考答案课堂检测1、分析 根据相似多边形的定义和等边三角形、正方形的性质来判定.解:(1)由于正三角形的每个内角都等于60°, 所以∠A =∠D =60°,∠B =∠E =60°,∠C =∠F =60°.由于正三角形的三条边都相等,所以FDCA EF BC DE AB ==.所以正三角形ABC 与正三角形DEF 相似. (2)由于正方形的每个内角都是直角,所以∠A =∠E =90°,∠B =∠F =90°,∠C =∠G =90°,∠D =∠H =90°.由于正方形的四条边都相等,所以EHAD GH CD FG BC EF AB ===, 所以正方形ABCD 与正方形EFGH 相似.【解题策略】 根据相似多边形的定义来确定.2、分析 解题中要充分利用相似多边形的特征和梯形的性质.解:由于梯形ABCD 与梯形D C B A ''''相似,所以对应边成比例,所以 4.5 4.8324 3.22x y z ====, 所以x =3,y =6,z =3.由于对应角相等,所以α=∠D =180°-∠A =180°-62°=118°,β=∠B =180°-∠C =180°- 110°=70°.【解题策略】 准确掌握相似多边形的特征及梯形上、下底平行这一条件是解决此题的关键.3、分析 抓住题中的关键:整张报纸和半张报纸相似,设原报纸的长为x ,宽为y ,则对折后得到的半张报纸的长为y ,宽为x 21,如图4-34所示,由相似多边形的定义知AB AD AE AB =,所以y 2=x ·x 21,所以2122=x y ,所以2x y=.故选A.体验中考1、分析 本题考查相似三角形的性质.∵△ABC ∽△DEF ,∴∠A =∠D .又∵∠A =30°,∴∠D =30°.故填30°.【解题策略】 相似多边形(包括三角形)的对应角相等.。
(完整word版)相似多边形导学案
(完整word版)相似多边形导学案
花装饰,这种蝴蝶花的边框宽为20cm,边框内外边缘所围成的两个矩形相似吗?
4。
如图中,有三个矩形,其中相似的是( )
A .甲和乙
B .甲和丙
C .乙和丙
D .没有相似的矩形
5。
已知四边形ABCD ∽四边形A ,B ,C ,D ,
,426AB A B BC ''===,,,70B '∠=. (1)求B ∠的度数; (2)求B C ''的长.
五、拓展延伸:(组内试着完成)
1.将一个矩形纸片ABCD 沿边AD 和BC 的中点连线EF 对折,要使矩形AEFB 与原矩形相似,则原矩形的长与宽的比应为( ) A 。
2:1 B 1:3 C .
1:2 D.1:1
2。
两个相似多边形的相似比为7:4,已知期中一个多边形的最小边长为28,则另一个多边形的最小边长为
3。
在 ΔABC 中,AB=10厘米,另一个与它相似的ΔA ´B ´C ´中, A ´B ´=5厘米,B ´C ´=4厘米,A ´C ´=6厘米;求这两三角形的相似比.。
人教版九年级下册数学第2课时 相似多边形(导学案)
27.1图形的相似物以类聚,人以群分。
《易经》如海学校陈泽学漂市一中钱少锋第2课时相似多边形一、新课导入1.课题导入问题1:形状相同的两个多边形相似吗?问题2:怎样从数学的角度刻画“形状相同”呢?这节课我们一起来探究相似多边形.2.学习目标(1)知道相似多边形的性质,并能判定两个多边形是否是相似的.(2)知道相似比,能根据相似多边形的性质进行相关的计算.3.学习重、难点重点:相似多边形的性质.难点:相关的计算.二、分层学习1.自学指导(1)自学内容:教材P26相似多边形.(2)自学时间:6分钟.(3)自学方法:阅读教材并完成自学参考提纲,然后同桌之间交流.(4)自学参考提纲:①相似多边形的定义:两个边数相同的多边形,如果它们的角相等,边成比例,那么这两个多边形相似.②相似比:相似多边形对应边的比叫做相似比,全等的两个图形的相似比为1.③如图,△ABC与△DEF中,∠ACB=∠DFE=90°,∠A=∠D,则△ABC与△DEF相似吗?为什么?相似.2222=-=-=,534AC AB BC2222=+=+=.2 1.5 2.5DE DF EF∵AB BC AC==,∠A=∠D,∠B=∠E,∠C=∠F=90°, DE EF DF∴△ABC与△DEF相似.④如图所示的两个三角形相似吗?为什么?不一定相似.理由:第三条边数量关系未知.2.自学:学生参考自学指导进行自学.3.助学(1)师助生:①明了学情:了解学生对相似多边形定义的理解.②差异指导:根据学情进行指导.(2)生助生:小组间相互合作,共同研讨.4.强化:(1)相似多边形的定义.(2)点两名学生口答自学参考提纲中第③、④题,并点评.1.自学指导(1)自学内容:教材P26例题.(2)自学时间:6分钟.(3)自学方法:自主探究后合作交流,完成自学参考提纲.(4)自学参考提纲:①相似多边形的性质:相似多边形的对应角相等,对应边成比例.②如图,四边形ABCD和EFGH相似,求角α,β的大小和EH 的长度x.由已知四边形ABCD和EFGH相似,结合图形可确定:α与∠C是对应角,直接求α,∠A与∠E是对应角,再据四边形的内角和求得β=81°.由AB 和EF 是对边,AD 和EH 是对应边,根据对应边成比例,可得方程242118x =,解方程得x=28. ③如图所示的两个五边形相似,求a,b,c,d 的值.根据相似多边形的性质:697.5235a b c d ====, 可求得a=3,b=4.5,c=4,d=6.2.自学:学生参考自学指导进行自学.3.助学(1)师助生:①明了学情:观察学生能否利用相似多边形的性质解决问题.②差异指导:指导学生寻找对应元素.(2)生助生:小组合作交流..强化(1)多边形相似的性质.(2)最大边(角)与最大边(角)是对应边(角);最小边(角)与最小边(角)是对应边(角).(3)方程思想的运用.三、评价1.学生学习的自我评价:这节课你有哪些收获?还有哪些方面的不足?2.教师对学生的评价:(1)表现性评价:从学习态度、注意力状况和小组合作等方面评价.(2)纸笔评价:课堂评价检测.3.教师的自我评价(教学反思).本课时以探究方式引入,使学生通过操作、观察、猜想、探究、交流和发现等学习方式掌握似多边形的性质及判别方法,并且能够运用这些知解决具体问题.课堂上安排出一定的时间让学生画图,并予以指导.在画图的过程中,学生会有意无意地应用相似多边形的性质,为今后的学习做铺垫.相似多边形在实际生活中有广泛的运用,为了让学生学以致用,可以在课后布置图案设计,增加生的学习兴趣.、基础巩固(70分)1.(10分)下列说正确的是(D )A.所有的平行四边形都相似B.所有的矩形都相似C.所有的菱形都相似D.所有的正方形都相似2.(10分)如图,四边形ABCD 与EFGH 相似,AB=3,BC=4,∠D=∠H ,则34EF FG ,∠A=∠E.3.(10分)如图所示,四边形ABCD 和EFG 相似,求角α,β的大小和EH 的长度x.解:根据相似多边形的性质得α=∠C=85°,∴β=360°-80°-85°-120°=75°. 又∵EH EF AD AB =,即202410x =,∴x=48(cm). 4.(10分)如图,DE ∥BC ,证明:△ADE 与△ABC 相似. 证明:∵DE ∥BC,∴∠ADE=∠B,∠AED=∠C.又∵ADAB=AEAC=DEBC=13,∠A=∠A,∴△ADE 与△ABC 相似.5.(10分)如图,△AOB 和△DOC 相似,OA ∶OD=OB ∶OC=1∶2,OB=3,求BC 的长.解:∵12OB OC=,OB=3, ∴OC=6,∴BC=BO+OC=9.6.(20分)如图,△ABC 与△DEF 相似,求DF 的长度x 和DE 的长度y.解:∵△ABC与△DEF相似,二、综合应用(20分)7.(20分)如图,矩形草坪长30 m,宽20 m,沿草坪内部四周有1 m宽的环形小路,小路内外边缘所形成的两个矩形相似吗?说出你的理由.解:不相似.小矩形的长为28 m,宽为18 m.∵3020,2818∴小路内外边缘所形成的两个矩形不相似.三、拓展延伸(10分)8.(10分) 如图,将一张矩形纸片沿较长边的中点对折,如果得到的两个矩形都和原来的矩形相似,那么原来矩形的长宽比是多少?将这张纸再如此对折下去,得到的矩形都相似吗?解:设原矩形的长为2y,宽为x.将这张纸再如此对折下去,得到的矩形都相似.【素材积累】1、人生只有创造才能前进;只有适应才能生存。
九年级数学上册 3.3 相似多边形导学案
3.3 相似多边形【学习目标】课标要求:一、 相似多边形概念,了解相似多边形的含义二、相似多边形本质特点目标达到:一、 相似多边形概念二、 相似多边形本质特点学习流程:【课前展现】如图,在△ABC 中,E 、F 别离是AB 和AC 上的点,且 EF ∥BC,(1).若是AE = 7, F C = 4 ,那么AF 的长是多少?(2).若是AB = 10, AE=6,AF = 5 ,那么FC 的长是多少?【创境激趣】学生展现搜集生活中各类相似图形【自学导航】一、 对相似图形的特点有了全面的熟悉,通过问题一、二、3的回答,进一步完善相似多边形的概念和内涵。
【合作探讨】 一、展现和播放两个五边形的对应内角相等及图形的放大缩小动画,提出问题:(1)在上图两个多边形中,你以为有相等的内角吗?若是有,请你把他一一表示出来? (2)在上图两个多边形中, 你以为相等内角的两边是不是成比例? 若是有,请你把他一一表示出来?【展现提升】典例分析 知识迁移一、 例:以下每组图形形状相同,它们的对应角有如何的关系?对应边呢? A B CE F(1)正三角形ABC 与正三角形DE F(2)正方形ABCD 与正方形EFGH【强化训练】一、解:(1)由于正三角形每一个内角都等于600,因此∠A =∠D=600,∠B =∠E =600, ∠C =∠F=600; 由于正三角形三边相等,因此(2)由于正方形的每一个角度是直角,因此∠A =∠E=900, ∠B =∠F=900,∠C =∠G=900, , ∠D =∠H=900; 由于正方形四边相等,因此HE DA GH CD FG BC EF AB ===. 【归纳总结 】一、相似多边形的概念。
二、 相似比。
154.北师大版九年级数学上册4.3 相似多边形-导学案
4.3 相似多边形学习目标:1、认识相似图形,理解相似多边形及相似比等有关概念.2、经历观察、操作相似图形的过程,进一步体会相似图形的本质特征和相似图形在现实生活中的应用.学习重点:认识生活中相似的图形,学会画简单相似图形的方法.预设难点:判断两个多边形是否是相似形.【预习案】一、链接1、能够的两个图形是全等形,全等形中互相重合的边叫做,它们相等;互相重合的角叫,它们相等.2、若△ABC和△DEF全等,则可以记作:△ABC≌△DEF,读作“△ABC全等于△DEF”,可得:AB = ,BC = ,AC = ,∠A = ∠,∠B = ∠,∠C = ∠ .二、导读阅读课本解决下列问题1、观察下面两幅图说说它与全等图形有哪些区别?2、通过阅读课本,你能说说相似多边形及相似比的概念吗,相似多边形有哪些性质?【探究案】1、如图,下面右边的四个图形中,与左边的图形相似的是()2、如图,矩形ABCD和矩形EBFG中,E是AB的中点,F是BC的中点,这两个矩形相似吗?若相似请求出它们的相似比,若不相似请说明理由.【训练案】1、下面每组图形中的两个图形是相似图形的是().2、下列图形中不一定是相似图形的是()A、两个等边三角形B、两个等腰直角三角形C、两个长方形D、两个正方形3、把下列菱形缩小为原来的一半.初中数学公式大全1 过两点有且只有一条直线2 两点之间线段最短3 同角或等角的补角相等4 同角或等角的余角相等5 过一点有且只有一条直线和已知直线垂直6 直线外一点与直线上各点连接的所有线段中,垂线段最短7 平行公理经过直线外一点,有且只有一条直线与这条直线平行8 如果两条直线都和第三条直线平行,这两条直线也互相平行9 同位角相等,两直线平行10 内错角相等,两直线平行11 同旁内角互补,两直线平行12 两直线平行,同位角相等13 两直线平行,内错角相等14 两直线平行,同旁内角互补15 定理三角形两边的和大于第三边16 推论三角形两边的差小于第三边17 三角形内角和定理三角形三个内角的和等于180 °18 推论1 直角三角形的两个锐角互余19 推论2 三角形的一个外角等于和它不相邻的两个内角的和20 平行四边形判定定理 1 两组对角分别相等的四边形是平行四边形21 平行四边形判定定理 2 两组对边分别相等的四边形是平行四边形22 平行四边形判定定理 3 对角线互相平分的四边形是平行四边形23 平行四边形判定定理 4 一组对边平行相等的四边形是平行四边形24 矩形性质定理 1 矩形的四个角都是直角25 矩形性质定理 2 矩形的对角线相等26 矩形判定定理 1 有三个角是直角的四边形是矩形27 矩形判定定理 2 对角线相等的平行四边形是矩形28 菱形性质定理 1 菱形的四条边都相等29 菱形性质定理 2 菱形的对角线互相垂直,并且每一条对角线平分一组对角30 菱形面积= 对角线乘积的一半,即S= (a×b )÷231 菱形判定定理1 四边都相等的四边形是菱形32 菱形判定定理2 对角线互相垂直的平行四边形是菱形33 正方形性质定理1 正方形的四个角都是直角,四条边都相等34 正方形性质定理2 正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角35 定理1 关于中心对称的两个图形是全等的36 定理2 关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分37 逆定理如果两个图形的对应点连线都经过某一点,并且被这一点平分,那么这两个图形关于这一点对称38 等腰梯形性质定理等腰梯形在同一底上的两个角相等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课题:《相似多边形》导学设计
学校:海阳市新英杰学校备课人:史俊杰
授课班级:___________ 姓名:_____________ 授课时间:___________
1.经历相似多边形概念的形成过程,了解相似多边形的含义;
2.在探索相似多边形本质特征的过程中,进一步发展归纳、类比、反思、交流等能力,提高数学思维水平,体会反例的作用;
3.由相似三角形的性质推导演绎出相似多边形的性质,并能进行综合运用来解决实际问题。
由相似三角形性质演绎出相似多边形的性质,并培养学生数学学习能力。
一.想一想(课前复习)——开启学习之门!
1.知识放影:
(1)定义:相似三角形,对应边_____________,对应角_____________。
(2)
_________________
_________________
_________________
⎧
⎪
⎨
⎪
⎩
的两个三角形相似;判定定理的两个三角形相似;
的两个三角形相似.
(3)
(1)_________________________;
(2)_________________________.
⎧
⎨
⎩
相似三角形的性质
2.已知△ABC∽△A1B1C1,AB:A1B1=1:2,则△ABC与的△A1B1C1周长比为_________;面积比为______________。
3.课前预习:(1)什么是相似多边形?(2)相似多边形又有哪些性质?
[我的得与失]:
二.学一学(自学探究)——展示你的身手!
1.如图,四边形ABCD∽四边形A1B1C1D1,∠A=750,∠B=850,∠D1=1180,AD=18,A1D1=8,A1B1=12。
求:∠C1的度数及AB的长度。
2.如左图,四边形ABCD∽四边形A1B1C1D1,AB:A1B1=2:1.求它们的周长的比及面积的比。
[我学会了]:
三.练一练(巩固练习)——小荷崭露尖尖角!
1.课本P52《随堂练习》:2及习题2.12:1-3;
2.课本P56《随堂练习》:1-2及习题2.13:1-2。
3.有一张长方形的纸,折成一半后的形状与原来的形状相似,请问该长方形边长的比是多少?
4.两个相似多边形最长边分别为10cm和25cm,它们的周长之差为60cm,则这两个多边形的周长分别为________________.
5.如图,正方形ABCD的面积是1002
cm,△ADE与△CEF的面积差等于302
cm,求CF 的长。
四.试一试(当堂诊断)——牛刀小试我最棒!
1.下列多边形一定相似的是()
A.两个矩形
B.两个菱形
C.两个正方形
D.两个平行四边形
2.林老师在投影片上画了一个六边形,上课时,发现投影大屏幕上原图上的一条5cm的边变成了15cm,那么投影仪的放大比例是__________,这个六边形的面积扩大为原来的________倍。
3.如图,在梯形ABCD中,AB∥CD,AB=60,
CD=15,EF∥AB,若梯形DCFE∽梯形EABF,那么
EF=__________________。
[我学会了]:
五.思一思(课堂小结)——我的课堂我做主!
[我学会了]:
[我的不足之处]:
[今后我努力的方向]:
六.学后反思:
1 1
B
F。
