高二数学必修5双向细目表
最新推荐高中数学基础知识双向细目表(定稿)
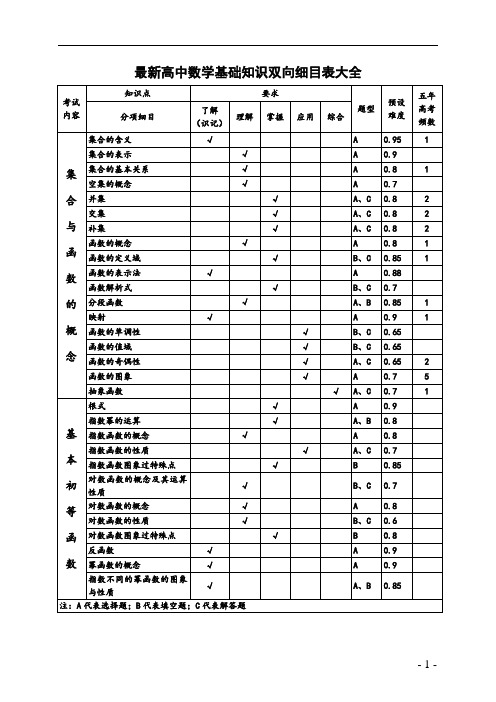
了解
（识记）
理解
掌握
应用
综合
空
间
几
何
体
公理1
√
A
0.95
公理2
√
A
0.9
公理3
√
A
0.85
公理4
√
A
0.85
等角定理
√
A
0.8
线面平行的判定定理
√
A、B、C
0.8
3
面面平行的判定定理
√
A、B、C
0.8
线面平行的性质定理
√
A、B、C
0.8
面面平行的性质定理
√
A、B、C
0.8
1
线面垂直的判定定理
秦九韶算法
√
B
0.8
进位制
√
B
0.65
统
计
简单随机抽样
√
A
0.95
抽签法
√
A
0.95
随机数法
√
A
0.9
系统抽样
√
AC
0.7
1
分层抽样
√
B
0.88
频率分布
√
BC
0.7
总体密度曲线
√
A
0.95
茎叶图
√
BC
0.8
1
众数、中位数、平均数
√
B
0.8
标准差与方差
√
AC
0.75
1
频率分布直方图的应用
√
A
0.8
1
两个变量的线性相关
分项细目
了解
（识记）
理解
掌握
应用
全国数学双向细目表
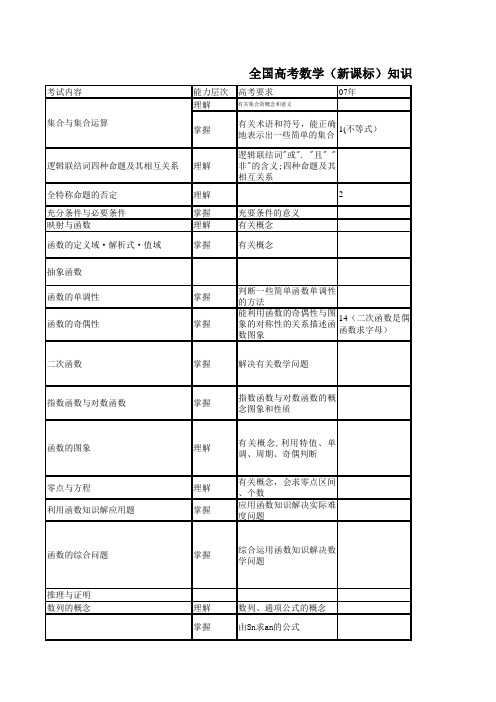
考试内容能力层次高考要求07年理解有关集合的概念和意义逻辑联结词四种命题及其相互关系理解逻辑联结词"或"."且""非"的含义;四种命题及其相互关系全特称命题的否定理解2充分条件与必要条件掌握充要条件的意义映射与函数理解有关概念抽象函数函数的单调性掌握判断一些简单函数单调性的方法二次函数掌握解决有关数学问题指数函数与对数函数掌握指数函数与对数函数的概念图象和性质函数的图象理解有关概念,利用特值、单调、周期、奇偶判断零点与方程理解有关概念，会求零点区间、个数利用函数知识解应用题掌握应用函数知识解决实际难度问题函数的综合问题掌握综合运用函数知识解决数学问题推理与证明数列的概念理解数列、通项公式的概念全国高考数学（新课标）知识双掌握由Sn求an的公式掌握能利用函数的奇偶性与图象的对称性的关系描述函数图象14（二次函数是偶函数求字母）函数的定义域·解析式·值域掌握有关概念集合与集合运算掌握有关术语和符号，能正确地表示出一些简单的集合1(不等式）函数的奇偶性等比数列掌握等比数列的通项公式，前n 项和公式6（等比性质）掌握差比裂项求和三角函数概念公式掌握任意角的正弦、余弦、正切的定义，用三角函数线表示正弦、余弦和正切;同角三角函数的基本关系式;正弦、余弦的诱导公式和差倍公式掌握通过公式的推导，了解它们的内在联系，从而培养逻辑推理能力9（二倍角、和差公式约分，含π/4的）求值图象与性质掌握会用三角函数线画正弦函数，正切函数的图象，由诱导公式画余弦函数的图象;理解它们的性质;会用"五点法"3(一个半周期闭区间上图象）用"五点法"画函数y=Asin(ωx+Φ)的简图图象变换掌握利用三角知识求范围最值掌握运用所学三角知识解决实际问题A 、ω、Φ的物理意义y=Asin(ωx+Φ)的图象三角最值及综合应用掌握数列的综合应用理解掌握有关概念及解决实际问题等差数列掌握等差数列的通项公式，前n 项和公式16（基本量求d ）了解共线向量，平面向量基本定理理解向量，向量共线的充要条件，平面向量的坐标掌握向量的几何表示，实数与向量的积，向量加法与减法，平面向量的坐标运算4（线性运算的坐标表示）了解用平面向量的数量积可以处理有关长度、角度和垂直等问题掌握平面向量的数量积及其几何意义;向量垂直的条件向量综合掌握综合不等式的概念性质理解不等式的性质不等式证明分析法、综合法、比较法证明简单的不等式均值不等式掌握并会简单的应用;解不等式掌握二次不等式、简单的分式不等式的解法掌握简单的绝对值不等式的解法直线方程及位置关系理解直线的倾斜角和斜率掌握两点斜率公式:一点和斜率求出直线方程的方法;点斜式、两点式和一般式，熟练求出直线方程.两条直线平行与垂直的条件，两条直线成的角、点到直线的距离公式，两条直线的位直关系了解简单的线性规划问题，线性规划的意义掌握二元一次不等式表示平面区域，简单线性规划问题向量、向量的加法与减法、实数与向量的积数量积正余弦定理掌握正弦定理、余弦定理，并能运用它们解斜三角形17（实际测量，用字母表示）线性规化不等式的应用灵活运用有关概念绝对值不等式理解不等式|a+b|≤|a|+|b|圆与圆理解16（外切）直线与圆掌握直线与圆的位置关系21（交点个数，结合向量共线类似椭圆问题）掌握椭圆的标准方程及其几何性质理解椭圆的定义、概念双曲线了解双曲线的标准方程及其几何性质13（几何性质应用求离心率）抛物线了解抛物线的标准方程及其几何性质7（从坐标考抛物线定义)轨迹方程了解直线与圆锥曲线掌握综合综合应用熟练掌握综合线面、面面平行线面、面面垂直18（面面垂直化为线面垂直，存在问题）三视图掌握三视图8（体积）体积计算了解会求几何体的表面积、体积，会处理几何体的侧面展开图问题8,11了解球的概念11（球内接三棱锥）掌握球的性质、表面积、体积公式，球面距离综合圆的方程球椭圆掌握圆的标准方程和一般方程算法初步掌握程序框图5（求和）古典概型掌握计算等可能性事件的概率，会用互斥事件的概率加法公式和相互独立事件的概率乘法公式计算一些事件的概率20（1）几何概型了解计算几何概型概率20（2）了解独立性检验了解线性回归的方法简单应用了解茎叶图掌握频率分布直方图抽样导数概念运算掌握函数在一点处的导数的定义和导数的几何意义；基本导数公式；和、差、积、商的求导法则；会求某些简单函数的导数；掌握导数求切线10导数应用了解可导函数的单调性与其导数的关系；可导函数在某点取得极值的必要条件和充分条件19掌握平均数与方差计算12统计掌握会求一些实际问题的最大值和最小值19掌握导数证明不等式、恒成立了解复数的有关概念及复数的代数表示和几何意义掌握运算法则，能进行复数代数形式的加法、减法、乘法、除法运算15说明21题必考有选修选考复数08年09年10年11年12年备注4(全特称命题的真假）321（2）（二次函数最值及解含参二次不等式）11（指对都有的不等式）12（画图象求最值）12（综合周期、奇偶绝对值画图求交点个数）11（指对都有的不等式）10（求零点区间）18（1）9（奇偶与指数不等式结合）12（图象与对数运算结合）知识双向细目表（文史类）1(绝对值不等式与有限集）1(有限集）316（奇偶性求和）1(不等式）1(有限集）1(不等式）8（和与项的比）1517（1）14（由和求公比）7（用到定义）11（二倍角化为二次函数求最值）17（1）107、11（用到）17（1）6（由定义得解析式并判断图象）11（单调区间、对称轴）16（由图象求ω、Φ进而求值）9（由图象求ω、Φ）12（求和）8（性质应用）17（求完通项、和后求和最值）17（2）13（通项应用）9（共线条件）2（用数量积坐标运算求夹角）5（由垂直求字母）7（由垂直求字母）13（由垂直求字母，非坐标）7（二次不等式解法，三个范围公共解）21（2）（讨论解含参二次不等式）20（斜率取值范围，化为不等式问题）10（线段点到原点距离）61114520（1）（1次比2次型不等式求范围）17（2）17（实际测量求值）16（解三角形求线段长）15（解三角形后求面积）17（2）20（2）（分成弧的比）20（2）（结合OA、OB垂直类似椭圆问题）20（1）由定义性质求方程20（1）椭圆定义4(离心率）42(直接求焦距）5（渐近线求离心率）1014（弦中点求抛物线方程）4（知切点求切线）9（定义应用求距离）10(用到）20（2）（切线方程）20（2）代入法求轨迹并讨论什么曲线16（求交点与原点组成三角形面积）20（2）（弦长问题）12（平行垂直判断）1812（平行垂直判断）18（线线垂直与线面垂直、面面垂直转化，求体积）18（1）1819（1）1811（三视图求全面积）1587（三视图求体积）1818（2）19（2）14（球内接正六棱柱求球的体积）7（知内接长方体求表面积）16（球中直角三角形）18（由直观图得三视图计算体积，证线面平行）9（平行、垂直，体积计算）5（求关于直线对称的圆）13（求圆的方程）20（1）（由三点定方程）20（1）（结合抛物线条件求圆的方6（三数输出最大）10（条件结构）56（图的含义）19（2）14（估计古典概型）618（2）19（2）3（散点图观察正负相关）3(相关系数的理解）16（说明直观含义）19（2）（画图并由图估计平均数）19（1）（分层抽样人数）19（1）（估计比例）（3）（用分层更好）421（切线求字母，切线与定直线围成面积）1321（1）（切线求字母）13（知切点求切线）21（1）（2）（恒成立求字母范围）21（1）（求极值）21（1）（单调区间）19（1）。
2021年高考数学备考双向细目表
√ √ √
√ √
√
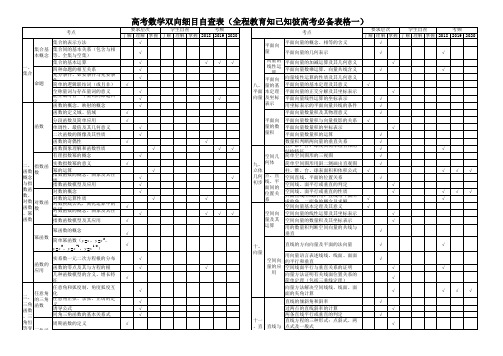
解三 解三角 角形 形
简单的三角恒等变换 正弦定理、余弦定理
√ √
√ √√
数列
数列表示法 数列与函数的关系（特殊函
等差等 比数列
数 等）差数列、等比数列与函数关 系 等差数列通项公式与前n 项和公
√ √
四、
式
√
√
√√ √√√
数列
等比数列通项公式与前n 项和公 式
√
√√
等差、等比数列解决相应问题
古典概型及其计算公式
几何概型，随机数的意义，运 用模拟方法估计概率
√
√ √
√ √
√
√
√ √
√√
√√√ √
十五
回归分析的思想方法及应用
√
、统 计案
例
案例分 析
独立性检验思想方法及应用（2*2列 联表）
√
正态分布曲线及其应用
√
有限值离散型随机变量及其分布列
√
十六
超几何分布
√
、概 率与
概率
n次独立重复试验与二项分布
函数 单调性、最值及其几何意义
二次函数的图像及其性质
函数的奇偶性
函数图象理解和函数性质
有理指数幂的概念
二、 指数函 函数 数 概念 与指 数函 数、 对数 对数函 函数 数 、幂 函数
实数指数幂的意义
幂的运算 指数函数的概念、图象及其性 质 指数函数模型及应用
对数的概念
对数的运算性质 对数换底公式，简化运算中的 作 对用数函数的概念、图象及其性 质 指数函数模型及其应用
等式 (ab )1/2(a,b ≥0)及其应用求最
√
值问题
导数概 念及其
双向细目表的编制及其他
双向细目表的编制及其他泉州市教科所纪荣海一、双向细目表的定义双向细目表是命题过程中所应用的一种表格工具。
一般包括两个维度：内容维度，要求列出考试内容细目；认知能力层次维度，要求列出认知能力层次细目，并确定每一细目应占的比重。
更细致的双向细目表还包括难度和题型。
编制双向细目表的目的是为了恰当地把内容范围和目标层次的考核要求较好地结合起来，是考试中命题规范化的重要步骤之一。
（《中国考试大辞典》，上海辞书出版社，2006年12月第1版）附：布卢姆认知目标分类（《学习、教学和评估的分类学》，华东师大出版社，2008年1月第1版）例1：反映考试内容与测量目标关系的双向细目表例2：反映考试内容与测量目标、题型、难度关系的双向细目表二、编制双向细目表的意义1．有利于在命题前全面把握测量目标。
2．有利于在命题前明确考试内容。
3．有利于提高命题的规范化和科学性。
4．有利于进行科学有效的教学评价。
三、编制双向细目表的依据1．《课程标准》培养目标。
2．《考试大纲》测量目标和行为目标。
3．教材。
4．学生。
四、编制双向细目表的步骤1．列出考试测量的行为目标。
（表格最终呈现的是测量目标）2．列出具体的考试内容。
（表格最终呈现的不一定是具体内容）3．确定每一考试内容与测量行为目标的对应关系。
4．编制以考试内容和测量目标为两维的表格。
5．确定题量（赋分）和题型，预估难度值。
五、双向细目表的编制（一）考试类型1．标准参照考试、常模参照考试。
2．阶段性考试、终结性考试。
附：标准参照考试和常模参照考试的比较（二）单元考试例1：必修1第1单元——中国现代诗歌说明：全卷20题左右。
例2：必修1第1单元——中国现代诗歌说明：全卷20题左右。
例3：必修1第2单元——古代叙事散文说明：全卷20题左右。
例4：必修1第2单元——古代叙事散文说明：全卷20题左右。
（三）模块考试例1：泉州市2006－2007学年度高一年第一学段水平测试语文必修模块1双向细目表能力层级：A－识记，B－理解，C－分析综合，D－鉴赏评价，E－表达应用，F－探究。
什么是双向细目表
什么是双向细目表？双向细目表一、试卷编制的具体步骤1、进行总体构思，确定试卷的目标要求明确考试的目的（为什么考）和性质：是期前预备性（摸底、预测、分组）的，或者是期中形成性（评定）的；根据考试目的确定考试的内容、范围和要求（合格标准）。
2、拟订命题计划，设计多项细目表命题计划包括两项内容：一是编制试题的原则和要求，说明试题类型、编制试题和组配试卷的要求体考试内容中各部分试题的数量分布和所占比例。
根据《课程标准》、《考试大纲》、教材、考试目的、性质与要求，设计好试卷多项细目表，这是3、选择题型，实施编制4、编选和审查试题，组编试卷5、检查、修改、试做、复核、调整、编制标准答案和评分标准二、试卷命题双向细目表（一）为什么在编制试卷时需要制定双向细目表原因之一：命题双向细目表是设计试卷的蓝图。
它使题工作避免盲目性而具有计划性，使命题者明量，提高命题的效率和质量。
原因之二：它对于审查试题的效度也有重要的指导意义。
命题双向细目表包括两个维度（双向）的型与难度之间的关系。
（二）什么是双向细目表所谓“双向细目表”，实际上就是教材内容和学习结果两个维度，其中一维反映教学的内容，另一维水平”这一维，普遍采用布卢姆等人关于认知领域教育目标的分类，即把学习结果或认知水平分为价”六种水平。
教材内容这一维则根据具体学科内容加以确定。
双向细目表是在命题中根据考试的目的和要求制定的测试内容和目标的具体计划，并以图表形式详用以规范、指导编题和制卷。
案例1：高考文综Ⅱ卷政治试题双向细目表案例2：高三月考数学试题双向细目表马鞍山市二十二中学2010届高中教学质量第一次月考数学试卷双向细目表（理科）高三数学第一次月考目的：检查前一阶段复习效果考试范围：第一次月考前已复习完成的内容，必修3和选修2－3中的概率和统计、排列组合、二程。
命题计划：按照2009年安徽省高考理科试卷的试题类型、试卷结构组配试卷；试卷中试题为第一建议：为了把握好试题方向，所命试题要以近两年的高考原题为参考依据，但是，为了考试公平，过四分之一，可以适当改编，或从各地模拟题中选择，还可以从教材中选择或改编题目。
高考数学双向细目表模板
高考数学双向细目表模板江西高考数学自主命题知识双向细目表(理工农医类)备考试内容能力层次高考要求 05年 06年 07年 08年注有关集合的概念和理解意义集合与集合运算有关术语和符号，1 1 6 2掌握能正确地表示出一些简单的-集合逻辑联结词"或". " 逻辑联结词与四且" "非"的含义;理解种命题四种命题及其相互关系充分条件与必要掌握充要条件的意义条件映射与函数理解有关概念函数的定义17(1) 17(1) 3,12 域?解析式?值掌握有关概念域判断一些简单函数函数的单调性掌握单调性的方法能利用函数的奇13偶性与图象的对函数的奇偶性掌握称性的关系描述函数图象反函数的概念及了解互为反函数图象间的关系反函数会求一些简单函 14 13 理解数的反函数解决有关数学问 6 二次函数掌握题指数函数与对数10 指数函数与对掌握函数的概念图象数函数和性质函数的图象理解有关概念 12 利用函数知识应用函数知识解掌握解应用题决实际难度问题函数的综合问综合运用函数知 22 掌握题识解决数学问题数列、通项公式的理解概念数列的概念 Sa掌握由求的公式 nnwhen the Terminal level when installed on the line number (Word) should be arranged from top to bottom. 6.4.4 cable core must be completely loose and straight, but not damage the insulation and core. Core bundle of the same plate vertically or horizontally arranged 等差数列的通项公掌握式，前n项和公式等差数列等差数列的性质解熟练应用题等比数列的通项公掌握式，前n项和公式等比数列等比数列的性质解 21 19 熟练应用题有关概念及解决实21 22 22 5 数列的综合应用掌握际问题任意角的正弦、余弦、正切的定义，用三角函数线表三角函数概念示正弦、余弦和正掌握公式切;同角三角函数的基本关系式;正弦、余弦的诱导公式通过公式的推导， 3了解它们的内在和差倍公式掌握联系，从而培养逻辑推理能力会用三角函数线5 19(2) 5 6画正弦函数，正切函数的图象，由诱图象与性质掌握导公式画余弦函数的图象;理解它们的性质; 会用"五点法"A,、、的物,理解yAx,，sin(),, 理意义的图象用"五点法"画函数yAx,，sin(),,掌握的简图三角最值及综利用三角知识求11 掌握合应用最值运用所学二角知18 18 应用掌握识解决实际问题向量、向量的加共线向量，平面向 15 了解法与减法、实数量基本定理when the Terminal level when installed on the line number (Word) should be arranged from top to bottom. 6.4.4 cable core must be completely loose and straight, but not damage the insulation and core. Core bundle of the same plate vertically or horizontally arranged 与向量的积向量，向量共线的 7理解充要条件，平面向量的坐标向量的几何表示，实数与向量的积，掌握向量加法与减法，乎面向量的坐标运算用平面向量的数量积可以处理有了解关长度、角度和垂数量积直等问题平面向量的数量6 13掌握积及其几何意义;向量垂直的条件平面两点间的距离公式，线段的定掌握距离公式、定比比分点和中点坐分点标公式，灵活运平移公式用正弦定理、余弦 19(1) 17 正余弦定理掌握定理，并能运用它们解斜三角形不等式的概念理解不等式的性质性质两个(不扩展到三 11个)正数的算术平均数不小于它们的几何平均数的均值不等式掌握定理.并会简单的应用; 分析法、综合法、比较法证明简单的不等式二次不等式、简单17(2) 17(2) 17(2) 14 解不等式掌握的分式不等式的解法不等式理解 ||||||||||ababab,,,,，绝对值不等式简单的绝对值不掌握等式的解法不等式的应用灵活运用有关概念 22直线的倾斜角和直线方程及位理解斜率置关系掌握两点斜率公式:一when the Terminal level when installed on the line number (Word) should be arranged from top to bottom. 6.4.4 cable core must be completely loose and straight, but not damage the insulation and core. Core bundle of the same plate vertically or horizontally arranged点和斜率求出直线方程的方法;点斜式、两点式和一般式，熟练求出直线方程.两条直线平行与垂直的条件，两条直线成的角、点到直线的距离公式，两条直线的位直关系简单的线性规划了解问题，线性规划的意义线性规化二元一次不等式掌握表示平面区域，简单线性规划问题了解参数方程的概念理解圆的参数方程圆的方程圆的标准方程和 16 掌握一般方程直线与圆掌握相关概念 3 16椭圆的标准方程16 21 9 掌握椭圆及其几何性质了解椭圆的参数方程双曲线的标准方 9 21 21 双曲线掌握程及其几何性质抛物线的标准方22 4 15 抛物线掌握程及其几何性质直线与圆锥曲线掌握综合 16 21 21 21轨迹方程掌握综合 22 21 21 21综合应用熟练掌握综合 22 21 21 21平面的基本性质，斜二侧的画法;画出空间两条直线的各种位置关系的图空间直线理解形，根据图形想象它们的位置关系;直线与直线所成角、距离when the Terminal level when installed on the line number (Word) should be arranged from top to bottom. 6.4.4 cable core must be completely loose and straight, but not damage the insulation and core. Core bundle of the same plate vertically or horizontally arranged 画出空间直线和平面的各种位置关系的图形，根据图形想象它们的位置关直线与平面掌握系;直线和平面平行、垂直的判定定理和性质定理，线面角和距离，三垂线定理及其逆定理平面与平面所成的角、距离，掌握两平面与平面掌握个平面平行和垂直的判定定理和性质定理(多面体、凸多面体、棱柱棱锥的概念、了解正多面体、欧拉公式棱柱的性质，会画11，15 15 7 16 出直棱柱的直观简单多面体图，正棱锥的性质，会画正棱锥的直观掌握图，会求几何体的表面积、体积，会处理几何体的侧面展开图问题了解球的概念球的性质、表面积、9 8 10 球掌握体积公式，球面距离通过空间图形的20 20 20 20 各种位置关系间的教学，培养空间综合应用掌握想像能力，发展逻辑思维能力，并培养辩证唯物主义观点理解排列、组合的意义分类、分步计数原理，排列数计算公排列组合式，组合数计算公掌握式和组合数的性质，并能用它们解决一些简单的应用when the Terminal level when installed on the line number (Word) should be arranged from top to bottom. 6.4.4 cable core must be completely loose and straight, but not damage the insulation and core. Core bundle of the same plate vertically or horizontally arranged 问题(二项式展开式的性4 8 4 8质，并能用它们计二项式掌握算和证明一些简单的问题等可能性事件的概率，互斥事件的意了解义，相互独立事件的意义，随机事件计算等可能性事件12 10 10的概率，会用互斥事件的概率加法公概率式和相互独立事件的概率乘法公式计掌握算一些事件的概率，会计算事件在n次独立重复试验中恰好发生k次的概率离散型随机变量的了解意义及其期望值和方差的意义会求出某些简单的19 18 19 18随机变量离散型随机变量的分布列;会根据离掌握散型随机变量的分布列求出期望值、方差正态分布的意义及主要性质;线性回了解归的方法和简单应用会用随机抽样、系统计统抽样、分层抽样等常用的抽样方法掌握从总体中抽取样本;会用样本频率分布去估计总体分布数学归纳法的原理解理数学归纳法能用数学归纳法证掌握明一些简单的数学命题when the Terminal level when installed on the line number (Word) should be arranged from top to bottom. 6.4.4 cable core must be completely loose and straight, but not damage the insulation and core. Core bundle of the same plate vertically or horizontally arranged 从数列和函数的变化趋势了解数了解列和函数的极限的概念;连续的意义借助数学直观理17(1) 极限解闭区间上连续理解函数有最值的性质极限的四则运算法8 13 2 4 掌握则(会求某些数列与函数的极限导数的概念;复合了解函数求导法则理解导函数的概念函数在一点处的导 5 11数的定义和导数的导数几何意义;基本导掌握数公式;和、差、积、商的求导法则;会求某些简单函数的导数;可导函数的单调性17(1) 7 12与其导数的关系;了解可导函数在某点取导数应用得极值的必要条件和充分条件会求一些实际问题掌握的最大值和最小值复数的有关概念及了解复数的代数表示和几何意义复数运算法则，能进行2 2 1 1复数代数形式的加掌握法、减法、乘法、除法运算when the Terminal level when installed on the line number (Word) should be arranged from top to bottom. 6.4.4 cable core must be completely loose and straight, but not damage the insulation and core. Core bundle of the same plate vertically or horizontally arranged。
2023年考点统计打印版双向细目表
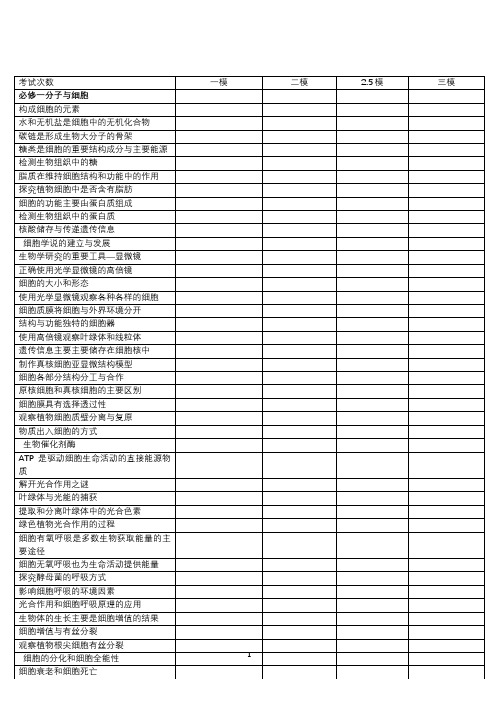
神经系统的分级调节
人脑的高级功能
激素与内分泌系统
激素调节的过程
体液调节与神经调节的关系
免疫系统的组成与功能
免疫失调
免疫学的应用
植物生长素
其他植物激素
植物生长调节剂的应用
环境因素参与调节植物的生命活动
选择性必修二 生物与环境
种群的特征
调查种群的其他方法
培养液中种群数量的变化
影响种群数量变化的因素
基因重组
人类遗传病的类型
人类遗传病的监测和预防
调查常见的人类遗传病
生物进化理论
生物进化的证据
模拟用DNA分子杂交方法分析人员间亲缘关系
生物进化导致生物的多样性和适应性
生物进化与生物多样性的形成
选择性物体维持PH的稳定
神经调节的结构基础
神经调节的基本方式
(7) 探究影响酶活性的因素
(8) 叶绿体色素的提取和分离
(9) 探究酵母菌的呼吸方式
(10) 观察细胞的有丝分裂
(11) 模拟探究细胞表面积与体积的关系
必修二遗传与进化
(1) 观察细胞的减数分裂
(2) 低温诱导染色体加倍
(3) 调查常见的人类遗传病
选择性必修一稳态与调节
模拟生物体维持PH的稳定
探索生长素类调节剂促进插条生根的最适浓度
生物体的生长主要是细胞增值的结果
细胞增值与有丝分裂
观察植物根尖细胞有丝分裂
细胞的分化和细胞全能性
细胞衰老和细胞死亡
必修二遗传与进化
减数分裂产生精子或卵细胞
观察植物细胞的减数分裂
模拟哺乳动物精子和卵细胞的形成过程
(4) 癌细胞的主要特征及防治
受精作用孕育新生命
数学必修五目录
数学必修五目录
第一章正弦余弦定理
第一节正弦定理
正弦定理的推导正弦定理的应用三角形中的边角关系第二节余弦定理
余弦定理的推导余弦定理的应用三角形的形状判定第二章解三角形应用
第一节三角形的面积
三角形面积公式面积公式的应用
第二节三角形的角度与边长关系
角度与边长的求解应用问题
第三章数列基本概念
第一节数列的定义与分类
数列的定义数列的分类（等差数列、等比数列等）第二节数列的通项公式与前n项和
通项公式的求法前n项和的求法
第四章等差数列性质
第一节等差数列的定义与通项公式
等差数列的定义等差数列的通项公式
第二节等差数列的前n项和
等差数列前n项和的公式等差数列求和的应用
第五章等比数列性质
第一节等比数列的定义与通项公式
等比数列的定义等比数列的通项公式
第二节等比数列的前n项和
等比数列前n项和的公式等比数列求和的应用
第六章不等关系与不等式
第一节不等关系与不等式的概念
不等关系的理解不等式的定义与性质
第二节不等式的解法
一元一次不等式的解法一元二次不等式的解法
第七章一元二次不等式
第一节一元二次不等式的解法
求解一元二次不等式的方法实际应用问题
第八章线性规划问题
第一节线性规划的基本概念
线性规划的定义线性规划的图解法
第二节线性规划的实际应用
线性规划问题的建模线性规划的应用案例
此目录结构仅作为参考，实际内容可以根据具体教学需求和学生情况进行适当的调整和优化。
高二数学理 试卷命制双向细目表
19 解答题 正、余弦定理在解三角形中的综合运用问题 20 70分 用递推关系求数列通项公式及特殊数列求和
21
空间向量证明平行垂直、计算夹角和距离
22
曲线方程的求法及直线与圆锥曲线的综合
合
5√
5√
5√
5
√
5
√
5
√
5
√
5
√√
5
√√
5√
5
√
5
√
5
√
10 √ √
12 √ √
8
等比数列通项及前n项和
9
抛物线的定义及性质
10
空间向量基本定理
11
判断三角形形状
12
求椭圆、双曲线离心率的范围
13
含有一个量词的命题的否定
14 填空题 分式不等式的解法 15 20分 求异面直线所成的角
16
不等式恒成立、基本不等式求最值
17
结合命题真假，充分、必要条件求参数范围
18
一元二次不等式解法、在区间上的恒成立
12 √ √
12 √ √
12
√√
12
√√
150
及格率
备课组长
命 题 人
教研组 长
高二学业水平质量检测理科数学试卷命制双向细目表
50 分
综合
√ √ √
2019—2020学年第一学期期末高二学业水平质量检测理科数学试卷命制双向细目表
考试用时： 120 分钟；分值： 150 分 考试范围： 必修5 选修2-1
题号 题型
考查知识点
1
不等式的基本性质
2
等差数列的通项及性质
3
用正弦、余弦定理解三角形
高考文科数学双向细目表
证明过程 解决最值问题
√ √
命题的概念
√
命题及其关系
常用基本逻辑用语
命题及其关系 四种命题及其关系
√
常用基本逻辑用语
简单的逻辑连接 词
全称量词与 存在量词
充分、必要、充要条件 或、且、非 全称量词 存在量词
含有量词的命题的否定
√ √
√ √
实际背景
√
椭圆定义、几何图形、标准方程、
简单性质
圆锥曲线与方程
√
代数方法处理几何问题的思想
√
空间直角坐标系 空间直角坐标表示点的位置
√
空间两点间的距离公式
√
算法的含义、 算法的含义与思想
√
算法初步
程序框图 基本算法语句
随机抽样
顺 输序 入、 、条 输件 出分 、支 赋、 值循 、环 条逻 件辑 、结 循构 环语
句 简单随机抽样
√
分层抽样和系统抽样
√
√ √
样本频率分布表、频率分布直方图 、折线图
√
三角恒等变换
积化和差、和差化积 半角公式
√ √
解三角形
正余弦定理
正弦定理 余弦定理
应用
三角形度量问题
数列的概念 与简单的表示法
数列的概念 列表、图像、通项公式表示法 数列是自变量为正整数的函数
√ √ √
等差数列的概念
√
数列
等差数列通项公式和求和公式
等差数列、 等比数列概念
√
等比数列 等比数列通项公式和求和公式
生活中的优化问 题
合情推理与 演绎推理
函数的最值 实际问题 归纳和类比推理 演绎推理的基本模式
√ √ √
推理与证明
高考数学知识点双向细目表
高考数学知识点双向细目表在高中阶段，数学是学生们的重要学科之一，也是高考必考科目之一。
为了顺利备战高考，了解数学知识点是非常重要的。
本文将为大家提供一份高考数学知识点双向细目表，以帮助同学们更好地了解数学知识体系和复习规划。
首先，我们来了解一下高考数学知识点的分类。
数学高考知识点主要包括代数、几何、三角学、概率与统计以及数学思维能力等五个方面。
每个方面又包含了具体的知识点。
下面将以这五个方面进行详细介绍。
代数部分是数学中的基础内容，主要包括函数、方程与不等式、数列与数学归纳法、概率与统计等几个知识点。
其中函数是代数部分的核心，包括一次函数、二次函数、指数函数、对数函数等。
函数的性质、图像与应用都是需要掌握的内容。
方程与不等式也是非常重要的知识点，包括一元一次方程、二元一次方程、二次方程、绝对值不等式以及分式方程等。
此外，数列与数学归纳法是代数部分的另一重点，需要了解等差数列与等比数列的概念与性质，以及如何利用数学归纳法证明数学命题。
最后，概率与统计是数学中的实际应用部分，需要了解基本的概率与统计方法，如频率、概率、条件概率、正态分布等。
几何部分是数学中的空间内容，主要包括平面几何、立体几何和空间解析几何。
平面几何包括了直线、曲线、多边形、圆等基本图形的性质与应用。
立体几何则需要了解体积、表面积等概念，要掌握球、圆锥、棱柱、棱台等几何体的性质。
空间解析几何是几何部分的进阶内容，需要掌握平面与直线的表示方法、位置关系与求交点的方法。
三角学是数学中的三角函数部分，主要包括三角函数的定义与性质、三角函数的图像与变换、三角恒等式与解三角方程等。
在此部分，还涉及到向量的概念与性质，包括向量的表示方法、运算法则、点积与叉积等。
概率与统计部分是数学中的实际应用部分，需要了解概率的基本概念与性质，条件概率、事件独立性的判定与计算方法等。
统计部分则包括数据的收集与整理、频数分析与频率分析、正态分布与抽样调查等内容。
-高考数学双向细目表(精)
2020届理科数学双向细目表模块知识点考查内容知识要求2015 分值2016 分值2017 分值备注了解理解掌握集合集合的含义与表示集合的含义、元素与集合的属于关系√列举法、描述法√集合间的基本关系包含与相等的含义√识别给定集合子集√全集与空集√集合的基本运算并集与交集含义与运算√补集含义与运算√韦恩图表达集合的关系与运算√函数概念与基本初等函数I 函数简单定义域值域，了解映射√图像法、列表法、解析法表示函数√分段函数√函数单调性、最值及几何意义√函数奇偶性√函数图像研究函数性质√指数函数指数函数模型背景√有理、实数指数幂、幂的运算√指数函数概念、单调性√指数函数图像过定点√对数函数对数的概念及其运算√换底公式、自然对数、常用对数√对数函数的概念、单调性√对数函数图像过定点√指数函数与对数函数互为反函数√幂函数幂函数概念√幂函数图像√函数与方程二次函数、零点与方程根√一元二次方程根的存在性及根的个数√结合图像，用二分法求近似解√函数模型及应用指、对、幂的增长特征√函数模型的应用√立体几何初步空间几何体柱锥台的结构特征√三视图√斜二测画出直观图√平行、中心投影√会画视图和直观图√球柱锥台的表面积和体积公式√点线面位置关系线面位置关系定义√线面平行判定√面面平行判定√线面垂直判定√面面垂直判定√线面平行性质√面面平行性质√线面垂直性质√面面垂直性质√用已获结论证明空间图形的位置关系√平面解析几何初步直线与方程结合图形，确定直线位置的几何要素√直线倾斜角和斜率√过两点的直线斜率计算公式√判定直线平行或垂直√点斜式、两点式、一般式√斜截式与一次函数的关系√两条相交直线的交点坐标√两点间距离公式√点到直线距离公式√两条平行直线间距离√圆与方程圆的几何要素，标准方程和一般方程√判断直线与圆的位置关系√判断两圆的位置关系√应用直线与圆的方程√代数方法处理几何问题的思想√空间直角坐标系空间直角坐标表示点的位置√空间两点间距离公式√算法初步算法的含义、程序框图算法的含义和思想√顺序、条件分支、循环逻辑结构√基本算法语句输入、输出、赋值、条件、循环语句√统计随机抽样会用简单随机抽样从总体中抽取样本√分层抽样和系统抽样√用样本估计总体频率分布表、频率分布直方图、折线图√茎叶图√数据标准差意义和作用√平均数和标准差√用样本估计总体思想√变量的相关性会画散点图，并认识变量间的相关关系√最小二乘法，线性回归方程√概率事件与概率频率与概率的意义√互斥事件的概率加法公式√古典概型古典概型计算公式√随机事件所含的基本事件数及发生概率√几何概型随机数的意义，运用模拟方法估计概率√几何概型的意义√基本初等函数II 任意角的概念、弧度制任意角的概念√弧度制的概念、弧度与角度的互化√三角函数理解正弦、余弦、正切的定义√单位圆的三角函数线√诱导公式√会画三角函数图像√三角函数周期性√正余弦单调性、最值与X轴交点等性质√正切函数性质√同角三角函数的基本关系式√正弦型函数参数对图像变化的影响√平面向量平面向量的实际背景及基本概念向量的实际背景√平面向量的概念√两个向量相等√向量的几何表示√向量的线性运算加法、减法、几何意义√数乘的运算、几何意义√两个向量共线的含义√线性运算的性质和几何意义√平面向量基本定理和坐标表示平面向量基本定理及意义√正交分解及坐标表示√加法、减法、数乘坐标运算√用坐标表示平面向量共线的条件√平面向量的数量积平面向量的数量积含义与物理意义√平面向量的数量积与向量投影关系√数量积坐标表达式与运算√用数量积表示夹角√用数量积判断两个向量的垂直关系√向量的应用解决平面几何问题√解决实际问题√三角恒等变换和与差的三角函数公式两角和与差的余弦、正弦、正切公式√二倍角公式√三角恒等变换积化和差、和差化积√半角公式√解三角形正弦定理余弦定理正弦定理√余弦定理√应用三角形度量问题√数列数列的概念与简单表示法数列的概念√列表、图像、通项公式表示方法√数列是自变量为正整数的函数√等差数列、等比数列等差数列概念√等差数列通项公式和求和公式√等比数列概念√等比数列通项公式和求和公式√等差数列与一次函数√等比数列与指数函数√不等式不等关系实际背景√一元二次不等式实际情景中抽象√与二次函数、一元二次方程联系√会解一元二次不等式，设计程序框图√二元一次不等式组与简单的线性规划问题实际情景抽象出二元一次不等式组√二元一次不等式组表示平面区域√二元线性规划问题√基本不等式了解证明过程√解决最值问题√常用基本逻辑用语命题及其关系命题的概念√四种命题及其关系√充分、必要、充要条件√简单的逻辑联结词或、且、非√全称量词与存在量词全称量词√存在量词√含有量词命题的否定√圆锥曲线与方程圆锥曲线实际背景√椭圆定义几何图形标准方程、简单性质√抛物线定义几何图形标准方程简单性质√双曲线定义几何图形标准方程简单性质√简单应用、数形结合思想√曲线与方程方程的曲线与曲线的方程√空间向量与立体几何空间向量及其运算空间向量概念、基本定理、坐标√空间向量线性运算√空间向量数量积√用空间向量数量积表示共线与垂直√空间向量的应用直线方向向量与平面的法向量√线线、线面、面面平行关系√线线、线面、面面垂直关系√三垂线定理√线线、线面、面面夹角计算√导数及其应用导数概念及几何意义导数概念实际背景√导数的几何意义√导数的运算求导运算法则√基本初等函数导数公式√在研究函数中应用单调性与导数关系√函数取极值的必要条件和充分条件√会求函数的极值√会求闭区间上的最值√生活中的优化问题实际问题√定积分与微积分定积分概念、实际背景、思想√微积分基本定理√推理与证明合情推理与演绎推理归纳和类比推理√演绎推理的基本模式√联系和差异√直接证明与间接证明分析法与综合法√反证法√数学归纳法数学归纳法√数系的扩充与复数的引入复数的概念复数的概念√复数相等的充要条件√复数代数表示法与几何意义√复数的四则运算四则运算√加减法运算的几何意义√计数原理分类加法、分步乘法分类加法√分步乘法√排列与组合排列概念与公式√组合概念与公式√二项式定理证明二项式定理√展开式有关问题√概率与统计概率离散型随机变量与分布列√超几何分布√条件概率√两个事件相互独立√N次独立重复试验与二项分布√均值、方差√正态分布曲线特点及意义√统计案例独立性检验√回归分析√坐标系与参数方程坐标系用极坐标表示点的位置√极坐标与直角坐标互化√简单图形的方程√柱坐标系、球坐标系表示空间中点位置√参数方程参数方程和参数的意义√直线、圆、圆锥曲线的参数方程√平摆线与渐开线√不等式选讲含绝对值不等式几何意义√绝对值三角不等式√柯西不等式不同形式√几何意义√柯西不等式一般情参数配方法√排序不等式向量递归法√伯努利不等式数学归纳法√均值不等式求极值√证明不等式方法比较、综合、分析、反证、放缩√。
高中数学基础知识双向细目表(定稿)
√
ABC
0.65
会求平行线间的距离
√
ABC
0.8
圆的方程
圆的方程
圆的标准方程与一般方程
√
AC
0.85
直线与圆的位置关系
能根据给定直线、圆的方程，判断直线与圆、圆与圆的位置关系
√
ABC
0.6
直线与圆的方程应用
能用直线和圆的方程解决一些简单的问题
√
BC
0.7
2
空间直角坐标系
高中数学必修基础知识双向细目表
考试
内容
知识点
要求
题型
预设
难度
五年
高考频数
分项细目
了解
（识记）
理解
掌握
应用
综合
空
间
几
何
体
棱柱的结构特征
√
B
0.95
1
棱锥的结构特征
√
A
0.9
1
棱台的结构特征
√
A
0.8
圆柱的结构特征
√
A
0.7
1
圆锥的结构特征
√
A、B
0.8
圆台的结构特征
√
A、C
0.8
球的结构特征
√
A
0.8
分项细目
了解
（识记）
理解
掌握
应用
综合
三
角
函
数
任意角
√
A
0.95
象限角的表示
√
AB
0.8
扇形的弧长与扇形面积
√
AB
0.85
三角函数的定义
√
全国新课标(理科)数学高考双向细目表
题
题 、 填√ 空 题 、 解 答 题
选 择 题 、
√ √
填
角 形
正弦定理、余弦定理 选 解决三角形的边角问 择
恒等变换
题
题
、
三角恒等变换
解三角形
正弦定理、余弦 面积公式
填选 择
等差数列、等比 学生了解数列的概 选 等差数列 数列的概念． 念，会求数列的通项 择
√
、等比数 列
数 列
通项公式与前n 项和公式 综合应用 错位相减
公式，以及求数列的 前n项和；理解并应用
通项与前n项和的关 系；掌握等差、等比 数列的通项及求和公
题 、 填 空 题
数列求和
裂项相消 并项求和
式；会结合函数不等 、 式处理数列的综合问 解
分组求和
题。
答
数学归纳 法
数学归纳法
了解合情推理的含 义，能利用归纳和类 选√
空
题
任意角三角函数
√
同角三角函数的
选
基本关系式、诱
择√
导公式
学生理解并应用同角
三 角 函
三角函数 的图像与
性质
三角函数的周期 性
三角函数的图像
数
三角函数的单调
与
性、最值、对称
解
性
三
图像变换
角
三角函数模型
形
两角和与差的三
恒等变换
角函数 二倍角公式
三角函数的基本关 系；理解并应用函数 图象基本性质，图象 的伸缩、翻折、平移
√ √
试卷命题双向细目表
试卷命题双向细目表（一）为什么在编制试卷时需要制定双向细目表原因之一：命题双向细目表是设计试卷的蓝图。
它使题工作避免盲目性而具有计划性，使命题者明确测验的目标，把握试题的比例与分量，提高命题的效率和质量。
原因之二：它对于审查试题的效度也有重要的指导意义。
命题双向细目表包括两个维度（双向）的表格，反映测验内容、测验目标、题型与难度之间的关系。
（二）什么是双向细目表所谓“双向细目表”，实际上就是教材内容和学习结果两个维度，其中一维反映教学的内容，另一维反映学生的学习水平。
目前在“学习水平”这一维，普遍采用布卢姆等人关于认知领域教育目标的分类，即把学习结果或认知水平分为“知识、理解、应用、分析、综合、评价”六种水平。
教材内容这一维则根据具体学科内容加以确定。
双向细目表是在命题中根据考试的目的和要求制定的测试内容和目标的具体计划，并以图表形式详细、明确地列出各项内容的量化指标，用以规范、指导编题和制卷。
案例1：高考文综Ⅱ卷政治试题双向细目表表格1：试题内容与考查范围、考点双向细目表表格2：知识与能力考核双向细目表案例2：高三月考数学试题双向细目表马鞍山市二十二中学2010届高中教学质量第一次月考数学试卷双向细目表（理科）高三数学第一次月考目的：检查前一阶段复习效果考试范围：第一次月考前已复习完成的内容，必修3和选修2－3中的概率和统计、排列组合、二项式定理、选修4－1极坐标和参数方程。
命题计划：按照2009年安徽省高考理科试卷的试题类型、试卷结构组配试卷；试卷中试题为第一次月考前已复习完成的内容。
（编写前将下表填好，以利选题）建议：为了把握好试题方向，所命试题要以近两年的高考原题为参考依据，但是，为了考试公平，所选试题为近年的高考原题的不能超过四分之一，可以适当改编，或从各地模拟题中选择，还可以从教材中选择或改编题目。
（三）双向细目表的突出特点在于：1、反映题型与难度、测验内容之间关系2、反映测验内容与测验目标关系3、反映测验内容与测验目标、题型之间关系（四）制作双向细目表的程序如下：1、列出课标或考纲的细目表2、列出各部分内容的权重3、列出各种认知能力(学习水平)目标的权重4、审查各考查点的分配是否合理案例3：常用的各类试题双向细目表表1：年级学科测试题双向细目表表2：试题命题双向细目表试题用途：使用时间：表3：试题命题双向细目表。
高中数学必修5目录
高中数学必修5目录第一章三角函数1.1 弧度制和角度制 1.2 三角函数的定义 1.3 三角函数的基本性质 1.4 三角函数的图像与性质 1.5 三角函数的应用第二章数列与数学归纳法2.1 数列的概念和表示方法 2.2 等差数列 2.3 等比数列 2.4 通项公式与求和公式2.5 数列的应用与推广第三章空间解析几何3.1 空间直角坐标系 3.2 点、线、面方程 3.3 空间几何问题的解法 3.4 空间几何问题的应用第四章二次函数4.1 二次函数的定义 4.2 二次函数的图像与性质 4.3 二次函数的最值与应用 4.4 二次函数与一次函数的关系第五章指数函数与对数函数5.1 指数函数的定义与性质 5.2 对数函数的定义与性质 5.3 指数函数与对数函数的图像与性质 5.4 指数方程与对数方程的解法与应用第六章三角恒等变换6.1 三角恒等变换的基本公式 6.2 三角恒等变换的证明方法 6.3 三角函数方程的解法与应用第七章三角函数图像与性质7.1 正弦函数和余弦函数的图像与性质 7.2 正切函数、余切函数和割函数的图像与性质 7.3 诱导公式和和差化积公式 7.4 三角函数的应用第八章排列、组合和概率8.1 排列与组合的基本概念 8.2 排列与组合的计数原理 8.3 排列与组合的运算法则 8.4 概率的基本概念与计算第九章统计与数据分析9.1 调查与统计的基本概念 9.2 统计数据的整理与处理 9.3 统计指标的计算与应用 9.4 数据分析与解决问题第十章平面向量10.1 平面向量的概念与表示 10.2 平面向量的运算 10.3 平面向量与几何计算10.4 平面向量的线性相关与线性独立第十一章空间向量11.1 空间向量的概念与表示 11.2 空间向量的运算 11.3 点与向量的关系 11.4 空间向量的线性相关与线性独立以上是高中数学必修5的目录，包括了各个章节的名称和主要内容概述。
通过学习这本教材，学生将掌握三角函数、数列与数学归纳法、空间解析几何、二次函数、指数函数与对数函数、三角恒等变换、排列、组合和概率、统计与数据分析、平面向量和空间向量等内容，为进一步深入学习数学打下坚实的基础。
必修5双向细目表(高一第二学期第一次月考)
单元 知识点 正弦定理推导 余弦定理推导 正弦定理 余弦定理 正、余 解三角形的概念 弦定理 已知两角与一边解三角形 已知两边与其中一边对角解三角形 已知两边及其夹角解三角形 已知三边解三角形 能解决简单的三角形度量问题 应用 解决与测量与几何计算有关的实际问题 举例 在恒等变形上的应用 数列的概念 数列的表示方法 等差数列的概念 等差数列的通项公式 等差数列与一次函数的关系 等差 数列 等差数列通项公式的推导方法累加法 等差数列项的性质 等差数列前n项和的公式 倒序相加法求和 等差数列前n项和的性质 裂项相消法求和 等比数列的概念 等比数列的通项公式 等比数列与指数函数的关系 等比 数列 累乘法求通项公式 等比数列项的性质 等比数列的前n项和公式 专题 数列通项公式求法 数列前n项和求法 1.通过具体情境，感受在现实世界和日常生活中存在着大量的 不等关系 不等关系及 2.用不等式（组）来表示不等关系 不等式的性质 3.作差法 4.不等式的性质的应用 1.了解一元二次不等式的概念 2.会解一元二次不等式 3.通过函数图象了解一元二次不等式与相应函数、方程的联系 不等式 的解法 4.含参的一元二次不等式的解法 5.分式不等式 6.简单的一元高次不等式 1.了解二元一次不等式（组）的几何意义 2.会用表示二元一次不等式（组）表示平面区域 线性规划 3.会求简单的二元线性规划问题 4.从实际情境中抽象出一些简单的二元线性规划问题，并能加 以解决 1.探索并了解基本不等式的证明过程，并了解基本不等式的代 数、几何背景 基本不等式 2.会用基本不等式解决简单的最大（小）值问题 要求 了解（识 理解 掌握 应用 综合 记） √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
0.8 0.6 0.6
0.55
要求
了解（识 记）
理解 掌握 应用
综 合
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√ √
√ √
√ √
√ √ √ √
√ √
√
√
2.会用基本不等式解决简单的最大（小）值问题
√
注：A代表选择题，B代表填空题，C代表解答题。
题型
C C A A、B A、B A、B A、B C A、B C A A A、C C A C A、B C C A、B C A C A C A、B C C C
A、B A
A、B A、B
A、B ALeabharlann BA、B A、BC
A、B 、C
预设 难度
0.88 0.88 0.88 0.88 0.7 0.7
0.95 0.9 0.9
0.85 0.7
0.85 0.81
0.9 0.85
0.8 0.8 0.8 0.8 0.7 0.75 0.8 0.8 0.7 0.7
0.9 0.85
高中数学第五模块教学内容与检测双向细目表
单元 解三 角形
数列
不等 式
正、 余弦 定理
应用 举例
等差 数列
等比 数列
专题 不等 关系 及不 等式 的性
质
不等 式的 解法
线性 规划
基本 不等
式
知识点 正弦定理推导 余弦定理推导 正弦定理 余弦定理 解三角形的概念 已知两角与一边解三角形 已知两边与其中一边对角解三角形 已知两边及其夹角解三角形 已知三边解三角形 能解决简单的三角形度量问题 解决与测量与几何计算有关的实际问题 在恒等变形上的应用 数列的概念 数列的表示方法 等差数列的概念 等差数列的通项公式 等差数列与一次函数的关系 等差数列通项公式的推导方法累加法 等差数列项的性质 等差数列前n项和的公式 倒序相加法求和 等差数列前n项和的性质 裂项相消法求和 等比数列的概念 等比数列的通项公式 等比数列与指数函数的关系 累乘法求通项公式 等比数列项的性质 等比数列的前n项和公式 数列通项公式求法 数列前n项和求法 1.通过具体情境，感受在现实世界和日常生活中存在着大量的 不等关系 2.用不等式（组）来表示不等关系 3.作差法 4.不等式的性质的应用 1.了解一元二次不等式的概念 2.会解一元二次不等式 3.通过函数图象了解一元二次不等式与相应函数、方程的联系 4.含参的一元二次不等式的解法 5.分式不等式 6.简单的一元高次不等式 1.了解二元一次不等式（组）的几何意义 2.会用表示二元一次不等式（组）表示平面区域 3.会求简单的二元线性规划问题 4.从实际情境中抽象出一些简单的二元线性规划问题，并能加 以解决 1.探索并了解基本不等式的证明过程，并了解基本不等式的代 数、几何背景