4.1空间图形基本关系的认识1209
4.1空间图形基本关系的认识
c
b
B
记作: P
β
3. 空间两条直线的位置关系有三种:A
①平行直线—— 在同一个平面内,没有公 共点的两条直线。 ②相交直线—— 在同一个平面内,有且只有 一个公共点的两条直线。
α α
a
c
b
B
b 记作:a//b
a
β
a O b
记作: b O a
③异面直线— 不在任何一个平面内,没有公共点的两条直线。 —
b
α
b
a
a β b
α
γ
a
A (1)直线在平面内— 直线与平面有无数个 — 公共点。 (2)直线与平面相交— 直线与平面只 α 有一个公共点。 —
4. 空间直线与平面的位置关系有三种:
b
a
β
F
E
(3)直线与平面平行—— 直线与平面没有公共点。
5. 空间平面与平面的位置关系有两种:
(1)平行平面—— 没有公共点的两个平面。 (2)相交平面—— 两个平面不重合, 并且有公共点。 α
E
β
F
练习
1.思考题:
(1)没有公共点的两条直线叫做平行直线,对吗? (2)空间两条没有公共点的直线叫做异面直线,对吗?
(3)分别在两个平面内的两条直线一定是异面直线吗?
(4)平面内一直线与这个平面外的一条直线一定是异面直线吗?
2.说出正方体中各对线段、线段与平面的位置关系: (1)AB和CC1; D1 (2)A1 C和BD1 ; B1 A1 (3)A1 A和CB1; (4)AC和A1 C1; (5)BC与平面A1 C1; (6)B1 C与平面AC; D (7)AB与平面AC。 A B
§4
实例分析
空间图形基本关系的认识教学课件

江西师大附中 郑永盛
4.1空间图形的基 本关系的认识
一、情景创设
1.空间图形包括平面图形和立体图形, 都看作点集。
平面图形是指各点都在同一个平面内的图形。
立体图形是指各点不都在同一个平面内的图形。
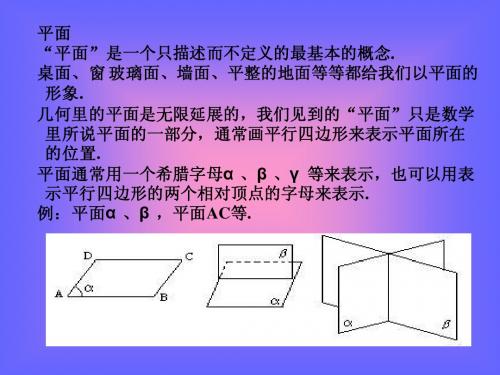
二、新课讲授 2.平面的概念、特征及表示:
(1)平面的概念 象这些桌面、平静的湖面、 镜面、黑板面等都给我们以平面 ____的印象 光滑的桌面、平静的湖面等都是我们很熟悉.
(1)水平放置的平面:(2)垂直放置的平面:
ß
a
一般用水平放置的正方形的直观图作为水平放 置的平面的直观图
3.用数学符号来表示点、线、面之间的位置关系(以
点作为元素,直线,平面作为点集)
(1)空间点与直线的位置关系: 点A在直线a上: 记为:A∈a
点B在直线a外: 记为:B∈a
A
a
B
(2)空间点与平面的位置关系: 点A在平面α内: 记为:A∈α 点B在平面α外:记为:B∈ α
(A)最多4条最少3条 (B)最多3条最少1条 (C)最多3条最少2条 (D)最多2条最少1条
例3. 将下列文字语言转化为符号语言:
(1)点A在平面 内,但不在平面 内 (2)直线a经过平面 外一点M (3)直线 l 在平面 内,又在平面 内 (即平面和平面相交于直线)
解:(1)A , A (2) M , M a
五. 思考交流:
两个平面能将空间分成几部分? 3或4 1 2 3 两个平面相交
两个平面平行
1
2
3
4
三个平面能将空间分成几部分?
1
4
3 4
2
高中数学第一章立体几何初步4空间图形的基本关系与公理4.1空间图形基本关系的认识4.2空间图形的公理

[小组合作型]
空间点、线、面的位置(wèi zhi)关系
(1)如果 a α,b α,l∩a=A,l∩b=B,l β,那么 α 与 β 的位置关系是________.
(2)如图 1-4-1,在正方体 ABCD-A′B′C′D′中, 哪几条棱所在的直线与直线 BC′是异面直线?
图 1-4-1
第十页,共42页。
两个平面若有三个公共点,则这两个平面( )
A.相交
B.重合
C.相交或重合
D.以上都不对
【解析】 若三个点在同一条直线上,则两平面可能相交;若这三个点不 在同一直线上,则这两个平面重合.
【答案】 C
第十一页,共42页。
[质疑·手记] 预习完成后,请将你的疑问记录,并与“小伙伴们”探讨交流: 疑问 1: _____________________________________________________ 解惑: _______________________________________________________ 疑问 2: _____________________________________________________ 解惑: _______________________________________________________ 疑问 3: ______________________________________________________ 解惑: _______________________________________________________
平面与平面 的位置关系
面面平行 面面相交
α∥β α∩β=a
第五页,共42页。
4.1空间图形基本关系的认识

符号 语言
a∥α
首页
X 新知导学 INZHIDAOXUEຫໍສະໝຸດ D答疑解惑 AYIJIEHUO
D当堂检测 ANGTANGJIANCE
做一做1 如图点、直线、平面的关系如下:
则O
α;AB
α;AB∩α=
.
答案:∈ ⊈ O
首页
X 新知导学 INZHIDAOXUE
D答疑解惑 AYIJIEHUO
D当堂检测 ANGTANGJIANCE
直线
公 理
平行于同一条直线 的两条直线平行
4
给定点 P 以及平面 α,β, 若点 P∈α,且 P∈β,则 存在直线 l,使得 α∩β=l,且 P∈l
已知直线 a,b,c,且 a∥ b,b∥c⇒a∥c
首页
X 新知导学 INZHIDAOXUE
D答疑解惑 AYIJIEHUO
D当堂检测 ANGTANGJIANCE
图形语言
符号语言 A,B,C 三点不共线⇒ 有且只有一个平面 α,使 A∈α,B∈α,C∈ α
若 A∈l,B∈l,且 A∈ α,B∈α,则 l⫋α
首页
X 新知导学 INZHIDAOXUE
D答疑解惑 AYIJIEHUO
D当堂检测 ANGTANGJIANCE
如果两个不重合的 公 平面有一个公共点, 理 那么它们有且只有 3 一条过该点的公共
图形语言
如果平面 α 与平面 β 没有公 共点,我们称平面 α 与平面 β 是平行平面
两个平 如果平面 α 和平面 β 不重合,
面
但有公共点,我们称平面 α
相交 与平面 β 是相交平面
符号语 言 α∥β
α∩β=l
首页
X 新知导学 INZHIDAOXUE
第一章第四节空间图形基本关系的认识

§4.1空间图形基本关系的认识【教材分析】1.知识内容与结构分析本节课的教学内容是《数学必修2》第一章§4.1节空间图形基本关系的认识,教学课时为1课时.教材借助长方体模型,在直观认识和理解空间点、线、面的位置关系的基础上,抽象出空间点、线、面位置关系的定义.具体说来,教材通过展示长方体的顶点、对角线、棱和面的位置关系,并能用数学语言来表述这些关系.教材也隐藏从具体的模型、实物出发,逐步建立图形语言、文字语言、符号语言的联系.2.知识学习意义分析通过这节课的学习,建立空间点、线、面三者的位置关系的概念,学会用图形语言和自然语言表述,了解符号语言,从微观角度体会点、线、面之间的关系,进一步体会几何学习中,语言的简洁精确,初步建立几何直观的能力,为后面的公理学习奠定基础.3.教学建议与学法指导空间点、线、面的位置关系是立体几何的重点,这是这部分内容的第一节.“立体几何初步”要求借助长方体模型,在直观认识和理解空间点、线、面的位置关系的基础上,抽象出空间线、面位置关系的定义.教师要努力帮助学生构建概念.一可以通过具体的模型、实物来帮助我们理解抽象的定义.二、在“立体几何初步”的教学过程中,不论是在教师的教学中,还是在学生的学习中,都要养成画图的习惯.图形不仅可以培养学生的几何直观能力,而且运用图形语言来描述几何问题可以更加清晰和自然.三、通过自然语言、图形语言和符号语言的转换,要让学生尽快熟悉立体几何中的各种语言的表述方法.要从图形出发,有序地建立图形、文字、符号这三种数学语言的联系.“立体几何初步”的教学重点的培养和发展学生的几何直观能力和空间想象能力.在立体几何初步的教学过程中,要树立“动起来”的观念,“动”意味着:动手操作、动眼观察、动脑想像、动口表达.如动手搭一搭.空间两条直线位置关系片段:师:请同学们拿出两支笔,动手搭搭看,如果不考虑两支笔重叠在一起,在空间,这两支笔的位置关系有哪几种(从公共点个数考虑)?生:有一个公共点;没有公共点.师:在没有公共点的情况下,你能摆出几种?生:两种(学生动手搭).师:如果把两支笔抽象成空间的两条不重合的直线,那么在空间,这两条直线的位置关系有哪几种?“笔是线,书是面,摆摆搭搭真方便.”培养空间感觉的第一步,是动手去搭一搭.在空间两条直线的位置关系、直线和平面的位置关系、平面和平面的位置关系的教学过程中,都可以让学生用自己手中的笔与书本摆摆搭搭.【学情分析】学生已经通过实物模型等认识空间几何体,已经能够从整体上把握空间几何体的主要元素点、线、面.同时长方体是学生再熟悉不过的一个几何体了.义务教育阶段,学生都能体会几何中“相交”、“公共点”、“平行”的概念.在这一节课,以长方体为载体,直观认识和理解空间点、线、面的位置关系,不是很难的问题.但是,用符号语言去描述这些关系,是学生觉得困难的地方.【教学目标】1.知识与技能(1)认识和理解空间点、线、面的位置关系,能抽象出空间线、面位置关系的定义.(2)初步了解三种数学语言的转化2.过程与方法借助长方体模型,在直观认识和理解空间点、线、面的位置关系的基础上,抽象出空间线、面位置关系的定义.3.情感态度价值观通过直观感知和操作确认容易建立空间想像能力,利用实物培养学生的空间相像和几何直观能力是很有帮助的.【重点难点】1.教学重点:空间点、线、面位置关系的定义.2.教学难点:异面直线的理解.【教学环境】多媒体和普通课堂相结合【教学过程】一、导入新课生:观看图片,相像空间中的各种图形,并列举一些立体图形.师:空间图形是丰富的,它由一些基本的图型:点、线、面所组成.认识清楚它们的位置关系,对于我们认识空间图形是很重要的.师评:点、线、面都是只描述而不定义的原始概念.(1)几何中的点是没有大小,没有面积的.点一般用大写字母A、B、C、D等表示.l a b c等(2)几何中的直线是没有面积的,向两端无限延长.直线一般用小写字母,,,表示,也可以用直线上的两点表示.如直线AB等.(3)桌面、窗玻璃面、墙面、平整的地面等等都给我们以平面的形象.几何中的平面是无限延展的.我们见到的“平面”只是数学里所说的平面的一部分,通、、等来表示,也常画平行四边形来表示平面所在的位置.平面通常用一个希腊字母αβγ、,平面AC等等.可以用表示平行四边形的两个相对顶点的字母表示.例如:平面αβ图1二、新知探究实例1:长方体是我们最常见的空间图形,如图2所示.为了直观地了解点、线、面的位置关系,我们先观察以下这个长方体.回答三个问题:(1)长方体有几个点?(2)长方体有几条棱?(3)长方体有几个面?这些直线、平面及顶点的位置关系有哪些呢?我们把这些位置关系抽象出来,就得到点、线、面三者位置关系的定义.1、抽象概括(1)、空间点与直线的位置关系有两种①点在直线上 记作A a ∈(如图3)②点在直线外 记作B b ∉(如图4)图3 图4(2)、空间点与平面的位置关系有两种①点在平面内 记作O β∈②点在平面外 记作P β∉(如图5)图52、动手操作1师:请同学们拿出两支笔,动手搭搭看,如果不考虑两支笔重叠在一起,在空间,这两支笔的位置关系有哪几种(从公共点个数考虑)?生:有一个公共点;没有公共点.师:在没有公共点的情况下,你能摆出几种?图2生:两种(学生动手搭).师:如果把两支笔抽象成空间的两条不重合的直线,那么在空间,这两条直线的位置关系有哪几种?师评:通过动手搭一搭,引导学生理解空间两条直线的三种位置关系,尤其是异面直线,让学生搭一搭,两条不相交的直线,可能平行,也可能异面.抽象概括:空间两条直线的位置关系有三种①平行直线:在同一个平面内,没有公共点的两点直线.(如图6)②相交直线:在同一个平面内,有且只有一个公共点的两条直线(如图7)图6 图7③异面直线:不在任何一个平面,没有公共点的两条直线.(如图8)异面直线的三种画法:b图8板书如下:表13、动手操作2师:请同学们拿出一支笔和一张纸,动手搭一搭,在空间,这支笔所成的线和这张纸所在的平面可能有哪些位置关系(从有多少个交点这个角度看,笔在纸上也可以考虑成为一种)?生:三种师:同学们自己搭一下.抽象概括:空间直线与平面的位置关系有三种①直线在平面内:直线与平面有无数个交点.②直线与平面相交:直线与平面只有一个交点.③直线与平面平行:直线与平面没有交点.板书如下:表24、动手操作3师:请同学们拿两张纸来,动手搭搭,在空间中,这两张纸所在的平面可能有哪些位置关系(从有没有公共点,多少个公共点来看)?生:两个师:有公共点的情况下,会有多少个公共点?请同学们拿出三本书,把它们的模型搭一下.师评:让学生用三本书搭一下,可以非常直观地观察到,两个平面相交时,会有一条交线.抽象概括:空间平面与平面的位置关系有两种:①平行平面:没有公共点的平面②相交平面:两个平面不重合,并且有公共点.三、课堂练习1、思考题(1)没有公共点的两条直线叫做平行线,对吗?(2)空间两条没有公共点的两条直线是异面直线,对吗?(3)分别在两个平面内的两条直线,一定是异面直线?(4)平面内一直线与这个平面外的一条直线一定是异面直线吗?2、说出正方体中各对线段,线段与平面的关系:(如图9)(1)AB 1和CC ;(2) 1A 1C 和BD (3) 1A 1A 和CB ;(4) 1C 1AC 和A(5)1C 1BC 与平面A ;(6) C 1B C 与平面A ;(7) C AB 与平面A图9四、布置作业P26习题1—4A 组第4题【专家点评】空间图形由点、线、面基本图形所组成,学习立体几何首先应从点、线、面之间的位置关系研究开始。
高中数学北师大版必修二 §4.1 空间图形基本关系的认识 课件(38张)

自学导引 1.空间点与直线的位置关系 空间点与直线的位置关系有两种: (1)如果点 P 在直线 a 上 ,记作 P∈a,如图①所示. (2)如果点 P 在直线 a 外 ,记作 P∉a,如图②所示.
2.空间点与平面的位置关系 空间点与平面的位置关系有两种: (1)如果点 P 在平面 α 内 ,记作 P∈α,如图①所示. (2)如果点 P 在平面 α 外 ,记作 P∉α,如图②所示.
8.公理 3 文字语言:如果两个不重合的平面有一个 公共点 ,那么它们 有且只有一条通过这个点的公共直线. 图形语言:如图所示. 符号语言:P∈α∩β⇒α∩β=l 且 P∈l. 作用:它是判定两个平面是否相交的依据,是证明点共线和线 共点的依据.
名师点睛 1.三个公理的作用: 公理 1——判定直线在平面内的依据. 公理 2——判定点共面、线共面的依据. 公理 3——判定点共线、线共点的依据.
(3)异面直线:如果直线 a 和 b 不同在 任何一个 平面内,这样 的两条直线叫作异面直线,如图①②③所示.
画两条异面直线时,为了充分显示出它们既不平行又不相交的 特点,即不共面的特点,通常采用平面衬托法,以加强立体感, 常见的画法如图①②③所示.
4.空间直线与平面的位置关系 空间直线与平面的位置关系有三种: (1)直线在平面内:如果直线 a 与平面 α 有 无数 个公共点,我 们称直线 a 在平面 α 内,记作 a α,如图①所示.
想一想:如何从集合的角度理解点、线、面之间的关系? 提示 (1)直线可以看成无数个点组成的集合,故点与直线的关 系是元素与集合的关系;用“∈”或“∉”表示. (2)平面也可以看成点集,故点与平面的关系也是元素与集合的 关系,用“∈”或“∉”表示. (3)直线和平面都是点集,它们之间的关系可看成集合与集合的 关系,故用“ ”或“ ”表示.
4.1空间图形的基本关系的认识

记作: 平面α 平面β 直线a
a
理论迁移
知识点一 空间图形基本关系及语言转换 例 1 用符号表示下列语句,并作出图形.
(1)直线 l 经过平面 α 内两点 A、B; (2)直线 l 在平面 α 外,且过平面 α 内一点 P; (3)直线 l 是平面 α 与 β 的交线,平面 α 内有一条直线 m 与 l 平行.
解析
A、B 都不能保证 α、β 无公共点,如图 1
所示;C 中当 a∥α,a∥β 时 α 与 β 可能相交,如 图 2 所示;只有 D 说明 α、β 一定无公共点.
答案
D
2.两平面 α、β 平行,a α,下列四个命题: ①a 与 β 内的所有直线平行;②a 与 β 内无数条 直线平行;③直线 a 与 β 内任何一条直线都不垂 直;④a 与 β 无公共点. 其中正确命题的个数有 A.1 个 C.3 个 B. 2 个 D.4 个 ( B )
在平行四边形 B1BDD1 中,B1D1∥BD, B1D1 与 BD 无公共点, ∴B1D1 与平面 AC 无公共点,∴B1D1∥平面 AC.
分析 可先转换成符号语言,再作图.
解 (1)A∈α,B∈α,A∈l,B∈l
α,P∈l,P∈α. (2)l
(3)α∩β=l,m α,m∥l.
变式训练 1 将下面用符号语言表示的关系改用文 字语言予以叙述,并且用图形语言予以表示.
解 文字语言叙述为: 点 A 在平面 α 与平面 β 的交线 l 上,AB、AC 分 别在 α、β 内. 图形语言表示为如图所示.
4.下列命题中正确的是
( D )
A.若直线 l 上有无数个点不在平面α内,则 l∥α B.若直线 l 与平面α平行,则 l 与平面α内的任 意一条直线都平行 C.如果两条平行直线中的一条与一个平面平行, 那么另一条也与这个平面平行 D.若直线 l 与平面α平行,则 l 与平面α没有公 共点
高中数学第一章立体几何初步4空间图形的基本关系与公理4.1空间图形基本关系的认识4.2空间图形的公理第2课时

1.下列结论中正确的是( )
①在空间中,若两条直线不相交,则它们一定平行;②平行于同一条直线
的两条直线平行;③一条直线和两条平行直线的一条相交,那么它也和另一条
相交;④空间四条直线 a,b,c,d,如果 a∥b,c∥d,且 a∥d,那么 b∥c.
A.①②③
B.②④
C.③④
D.②③
我还有这些不足: (1) ________________________________________________________ (2) ________________________________________________________ 我的课下提升方案: (1) ________________________________________________________ (2) ________________________________________________________
过空间任意一点 P 分别引两条异面直线 a,b 的平行线 l1,l2(a∥l1, 定义 b∥l2),这两条相交直线所成的 锐角(或直角) ,就是异面直线 a、
b 所成的角
取值 范围
异面直线所成的角 θ 的取值范围: 0,π2
特例
π
当 θ= 2 时,a 与 b 互相垂直,记作 a⊥b
[小组合作型] 公理4的应用
2.结论:这两条直线平行.
3.符号表述:
a∥b
b∥c
⇒
a∥c
.
教材整理 2 等角定理
阅读教材 P26“等角定理”部分内容,完成下列问题. 1.条件:空间中,如果两个角的两条边分别对应 平行. 2.结论:这两个角 相等或互补.
教材整理 3 异面直线所成的角
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
•直线与平面相交 直线AB与平面 相交
•直线与平面平行 直线AB与平面 平行 请问直线CG在哪些平面内?与哪些平面相交? 与哪些平面平行?
5、空间平面与平面的位置关系有二种:
•平行平面 —两个平面没有公共点 平面 与平面 平行
•相交平面 —两个平面有公共点 平面 与平面 相交 请问平面 与哪些平面平行?与哪些平面相交?
练习题
3、判断对错
(1)没有公共点的两条直线叫做平行直线; (2)直线在平面外则直线与平面没有公共点;
内,则l // . (3)若直线l上有无数个点不在平面
(4)空间两条直线的位置关系可以分为共面和不共面两种.
4、说出长方体中下列各对线段所在的直线以及线 段 D1 所在的直线与平面的位置关系:
2、空间点与平面的位置关系有两种:
•点在平面上
点D在平面 上
•点在平面外
点D在平面 外
请大家说出点A、B、C分别在哪些平面上? 分别在哪些平面外?
3、空间两条直线的位置关系有三种:
Hale Waihona Puke •平行直线直线AB与CD平行 •相交直线 直线AB与BC相交 •异面直线 直线AB与GF异面 你还能说出哪些直线是平行直线?相交直线? 异面直线?
1、异面直线是指( D ) A、空间中两条不相交的直线 B、分别位于两个不同平面内的两条直线 C、平面内的一条直线与平面外的一条直线 D、不同在任何一个平面内的两条直线 2、想一想:正方体的12条棱以及 标出的面对角线所在的直线那
A' D' C' B'
些与直线BD是异面直线?
D A B C
4、空间直线与平面的位置关系有三种: •直线在平面内 直线AB在平面 内
(1)AB和CC1; (2)A1C和BD1 ; (3)A1A和CB1; (4)AC和A1C1;
异面
相交 异面 平行
C1
A1
B1
(5)BC与平面A1C1; 平行
D A B
C
(6)B1C与平面AC; 相交
(7)AB与平面AC。在平面内
空间图形的组成:
点
线 点
面
线
面
点和线,线和面,点和面之间具有怎样的位置关系?
8 个顶点、____ 12 条棱、___ 6 个表面. 长方体有____ 观察图形,讨论这些直线、平面及顶点的位置关系.
1、空间点与直线的位置关系有两种:
•点在直线上
点D在直线AD上
•点在直线外 点D在直线CG外 请大家说出点A、B、C分别在哪些直线上? 分别在哪些直线外?
