第八章差错控制编码要点
差错控制编码
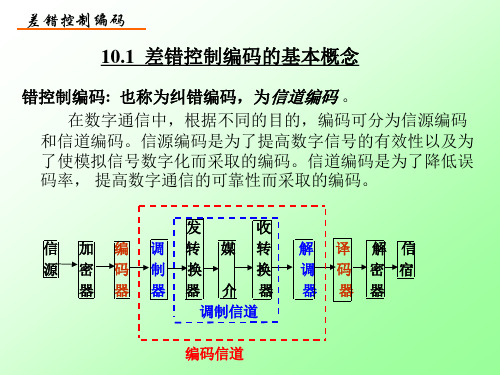
0110101 1 1101100 1 1001010 0 0011011 1 1000101 0 1000101 0
特点:适合突发信道。
差错控制编码
3 .恒比码
码字中 1 的数目与 0 的数目保持恒定比例的码称为恒比 码。接收端只要检测接收到的码组“1”的数目是否对,就可 以知道有无错误。 例:“5中取3”恒比码,有C53 =10种不同组合,表示10个阿 拉伯数字。如表 10.2 所示。 “7中取3”恒比码,有C73 =35种不同组合,表示26个英文字 母和其他符号。 而每个汉字又是以四位十进制数来代表的。。
源密码 制 换
换
器器 器器 介 器
调制信道
解 译 解信 调 码 密宿 器 器器
编码信道
差错控制编码
由于数字信号传输过程中受到加性干扰和乘性干扰的影
响,会产生误码。由加性干扰引起的码间干扰,通常可以采 用信道均衡、匹配滤波器、升余弦系统特性、增加发射功率、 合理选择调制/解调方法等措施,减少误码。由于乘性干扰 影响,或采用了上述方法后,仍不能有效地抑制加性干扰的 影响时, 就要采用差错控制技术。
5. 重复码
监督码元是信息码元的简单重复。
接收端将接收到的码组的前一半(信息位)与后一半(监 督位)作模2加(“同或”),结果全为0则无错码。 特点:能够纠正错码。但效率低。(1/2)
差错控制编码
10.1.4 差错控制编码的基本概念
1. 分组码 分组码一般可用(n,k)表示。其中,k是每组二进制信息 码元的数目,n是编码码组的码元总位数,又称为码组长度, 简称码长。n-k = r 为每个码组中的监督码元数目。 分组码的结构如下:
差错控制编码
10.2 线 性 分 组 码
差错控制编码要点

2024/2/9
2
第3页/共67页
10.1 差错控制编码的基本原理
常用的差错控制方式
1. ARQ(Automatic Repeat Request)方式 (自动请求重发或检错重发)
发端发送出可以发现错误的码字。经过传输到接 收端译码后,如果没有发现错误,则输出。如果发现 错误,则自动请求发端重发,直到正确接收到码字为 止。
2024/2/9
11
第12页/共67页
10.1 差错控制编码的基本原理
码间距离d 及检错纠错能力 码字:由信息位和监督位组成的一组码元。
用C = ( cn-1 cn-2 … c0 )表示。
(许用码、禁用码) 码元: 组成码字的元素,用Ci表示。 码长:码字中码元的个数,用n表示。
码组:由多个许用码组成的一组码字。
2024/2/9
7
第8页/共67页
10.1 差错控制编码的基本原理
香农有扰信道编码定理:
在有扰信道中只要信息的传输速率R小于信道容 量C,总可以找一种编码方法,使信息以任意小的差 错概率通过信道传送到接收端,即误码率Pe可以任意 小,而且传输速率R可以接近信道容量C。但若R > C, 在传输过程中必定带来不可纠正错误,不存在使差错 概率任意小的编码。
9
第10页/共67页
10.1 差错控制编码的基本原理
减小误码率Pe的两种途径:
(1)n 及 R一定时,增加信道容量C。由图可见,E(R) 随C的增加而增大。由信道容量公式知, 增加C, 可通过增加S和B来实现;
(2)在C及 R一定的情况下,增加n可以使Pe指数减小。
2024/2/9
10
第11页/共67页
我国电传机传输汉字采用的是“5中取3” 恒比码,其码长 为5,码字中“1”的个数为3。这种码我国称为保护电码。码长 为5的二进制数共有32种组合,选择其中含有3个“1”的组合作 为许用码,为10个。
差错控制编码

2.差错控制编码2.1. 引言什么是差错控制编码(纠错编码、信道编码)?为什么要引入差错控制编码?差错控制编码的3种方式?本章主要讲述:前向纠错编码(FEC)、常用的简单编码、线性分组码(汉明码、循环码)、简单介绍RS码*、BCH码*、FIRE码*、交织码,卷积码极其译码、TCM编码*。
一、什么是差错控制编码及为什么引入差错控制编码?在实际信道上传输数字信号时,由于信道传输特性不理想及加性噪声的影响,接收端所收到的数字信号不可避免地会发生错误。
为了在已知信噪比情况下达到一定的误比特率指标,首先应该合理设计基带信号,选择调制解调方式,采用时域、频域均衡,使误比特率尽可能降低。
但若误比特率仍不能满足要求,则必须采用信道编码(即差错控制编码),将误比特率进一步降低,以满足系统指标要求。
随着差错控制编码理论的完善和数字电路技术的发展,信道编码已经成功地应用于各种通信系统中,并且在计算机、磁记录与存储中也得到日益广泛的应用。
差错控制编码的基本思路:在发送端将被传输的信息附上一些监督码元,这些多余的码元与信息码元之间以某种确定的规则相互关联(约束)。
接收端按照既定的规则校验信息码元与监督码元之间的关系,一旦传输发生差错,则信息码元与监督码元的关系就受到破坏,从而接收端可以发现错误乃至纠正错误。
研究各种编码和译码方法是差错控制编码所要解决的问题。
二、差错控制的三种方式1、检错重发(ARQ)检错重发:在接收端根据编码规则进行检查,如果发现规则被破坏,则通过反向信道要求发送端重新发送,直到接收端检查无误为止。
ARQ系统具有各种不同的重发机制:如可以停发等候重发、X.25协议的滑动窗口选择重发等。
ARQ系统需要反馈信道,效率较低,但是能达到很好的性能。
2、前向纠错前向纠错(FEC):发送端发送能纠正错误的编码,在接收端根据接收到的码和编码规则,能自动纠正传输中的错误。
不需要反馈信道,实时性好,但是随着纠错能力的提高,编译码设备复杂。
第八章差错控制编码要点

❖ 定理3.3若一种码的最小距离为d0,则它的检错能 力和纠错能力应满足: d0 >=e+t+1 (e>=t)
❖ 例3.1 求码集合{(000),(011),(101),(110)}和
{(000),(111)}最小距离d0及纠(检)错的能
C 使E(Rb ) 或 n 使e-nE(Rb )
香农信道编码定理
❖ 可见根据定理,减小Pe 的方法: 一是增加信道容量C,从而使E(Rb ) 增加(通信硬件系统设计人员通常采 用的方法);
另一种方法是只要Rb<=C增加码长n 可使Pe随n的增加而指数下降,如果n↑ 则Pe ↓香农信道编码定理是差错控制 编码的理论基础,通过编译码过程来 降低误码率。
矛盾! tradeof
f!
二 差错控制编码的特性和能力
1.海明(hamming)距离 2.最小距离 3.海明距离(码距) 4.最小距离与抗干扰能力的关系
1.海明(hamming)距离
❖ 1.海明(hamming)距离:指两个不同的码
组其对应码位(二进制位)的码元不同的个
数,简称码距 ;用d表示:
误无能为力;
水平奇偶校验
❖ 避免简单奇偶校验不能检测突发错误的缺点。 ❖ 编码规则:经过奇偶监督编码的码元序列按
行排成方阵,每一行为一组奇偶监督码(见 实例)。 ❖ 发送端在发送时则按列的顺序传输;而接收 端仍将码元恢复成发送时方阵形式,然后按 行进行奇偶校验水平奇偶监督码。
实例
信息码元 11 1 0 0 1 11 0 1 0 0 10 0 0 0 1 00 0 1 0 0 11 0 0 1 1
差错控制编码教学课件

循环冗余校验码(CRC)
总结词
广泛应用、可靠性高
详细描述
循环冗余校验码是一种广泛应用于数据传输和存储的差错控制编码方法。它通过将数据视为一段二进制数,计算 出一个冗余码附加在数据末尾,使得整个数据(包括冗余码)的模2除法结果为0。CRC能够检测出多位错误,具 有较高的可靠性。
海明 码
总结词
高效、可纠正多位错误
详细描述
海明码是一种高效的差错控制编码方法,能够纠正多位错误。它通过将数据分成多个分组,在每个分 组之间插入一些校验位,使得每个分组和校验位之间存在一定的关系。海明码能够检测和纠正多个错 误,但编码效率相对较低。
里德-所罗门码
总结词
纠错能力强、适用于通信和存储领域
VS
详细描述
里德-所罗门码是一种纠错能力较强的差 错控制编码方法,适用于通信和存储领域。 它通过将数据分成多个块,并使用多个校 验方程来检测和纠正多个错误。里德-所 罗门码具有较高的纠错能力和较低的错误 概率,但实现较为复杂。
联合信源信道编码
总结词
联合信源信道编码是一种新型的编码方式,它将信源编码和信道编码相结合,以提高通 信系统的整体性能。
详细描述
传统的信源信道编码通常分开进行,但在某些场景下,这种分离的方式可能无法充分利 用数据的信息。联合信源信道编码通过将信源编码和信道编码相结合,能够更好地利用
数据的信息,提高通信系统的性能。
差错控制编码教学课 件
• 差错控制编码概述 • 常见差错控制编码方法 • 差错控制编码原理
01
差错控制编码概述
差错控制编码的定义
差错控制编码是一种通过增加冗余信 息来检测和纠正数据传输过程中发生 的错误的编码方式。
它通过在数据中加入额外的信息,使 得接收方可以检测到数据是否发生错 误,并在必要时进行纠正。
通信系统中的差错控制编码技术培训课件

式中a0为监督位,其他位为信息位。
这种编码能够检测奇数个错码。在接收端,按照上式求 “模2和”,若计算结果为“1”就说明存在错码,结果为 “0”就认为无错码。
奇数监督码与偶数监督码相似,只不过其码组中“1”的 数目为奇数:an1 an2 a0 1
19
2 二维奇偶监督码(方阵码)
二维奇偶监督码的构成
不同的编码方法,有不同的检错或纠错能力。
多余度:就是指增加的监督码元多少。例如,若编 码序列中平均每两个信息码元就添加一个监督码元, 则这种编码的多余度为1/3。
编码效率(简称码率) :设编码序列中信息码元数量 为k,总码元数量为n,则比值k/n 就是码率。
冗余度:监督码元数(n-k) 和信息码元数 k 之比。
11
4. 码重、码距和编码效率 分组码的码重和码距
码重:把码组中“1”的个数目称为码组的重量,简称码重。 码距:把两个码组中对应位上数字不同的位数称为码组的
距离,简称码距。码距又称汉明距离。 例如,“000”=晴,“011”=云,“101”=阴,“110”=
雨,4个码组之间,任意两个的距离均为2。 最小码距:把某种编码中各个码组之间距离的最小值称为
23
4 恒比码
在恒比码中,每个码组均含有相同数目的“1”(和 “0”)。由于“1”的数目与“0”的数目之比保持恒定, 故得此名。
这种码在检测时,只要计算接收码组中“1”的数目是 否对,就知道有无错码。
恒比码的主要优点是简单和适于用来传输电传机或其 他键盘设备产生的字母和符号。对于信源来的二进制 随机数字序列,这种码就不适合使用了。
其中任一码组在传输中若发生一个或多个错码,则将变 成另一个信息码组。这时,接收端将无法发现错误。
7
差错控制编码II
Output equation:
ci.0 ai ci.1 ai ai 1 ci.2 ai ai 2 The input information blocks are kept by the registers, they are called register state.
Convolution operation
第8章 差错控制编码
The output and input of a convolutional coder follow a linear relationship, which is can be investigated by its impulse response.
k n
Example:
3,1,3
Convolutional code
第8章 差错控制编码
3,1,3 n 3, k 1, L 3
For each k 1 bit input, the coder output n 3 -bi t codeword. Coder structure
第8章 差错控制编码
The generator polynomial based on the impulse response can be defined. Example: (3,1,3) code. Its generator polynomial is defined as:
g g g
000 000 g 2,0 g 2,1 g 2,2 ...
.... ... .... ...
The Generator matrix is defined as:
g 0,0 g 0,1 g 0,2 000 G 000 ... g1,0 g1,1 g1,2 g 0,0 g 0,1 g 02 000 ... g 2,0 g 2,1 g 2,2 g1,0 g1,1 g1,2 g 0,0 g 0,1 g 02 ... 000 g 2,0 g 2,1 g 2,2 g1,0 g1,1 g1,2 ... 000 000 g 2,0 g 2,1 g 2,2 ... .... ... .... ...
信息论基础-第八章差错控制编码2
f Z Z 2 X 7Z X 0 的根。
注意:在上面的方程中,未知数是 Z 。
有限域上的方程并无一般解,因为方程的解是定义在有限域上 的,所有可能的解只有有限多个,所以可用试探法求解;
根据上一示例的元素表,可得
f X 6 X 6 2 X 7 X 6 X X 12 X 13 X X 3 X 2 X 1 X 3 X 2 1 X 0
多项式关于模 nX 的加法和乘法运算
加法 u X v X u X v X nX 乘法 u X v X u X v X nX
若 nX 为 n 次的多项式,则余式具有如下的一般 形式 p X cn1X n1 cn2 X n2 ... c1X c0 , ci 0,1
性质1 若要线性分组码能够检测出任一码字中的小于等于 e 位的误码,则应满足
dmin e 1
e
1
dmin
wi
wj
禁禁 禁用禁码禁 字 许禁用禁 禁码禁字
性质2 若要线性分组码能够检出并纠正任一码字中的小于等 于t位的误码,则应满足
dmin 2t 1
t wi
dmin 1 wj
t wj
禁禁用禁 禁码禁字 许禁用禁 禁码禁字
... m0,n1
... m1,n1
..ቤተ መጻሕፍቲ ባይዱ ...
mk
...
1,
n
1
系统码的特点
a0a1...ak2ak1 编码 a0a1...ak2ak1ck 2cn1 c0c1...ck2ck1ck 2cn1
系统码的编码输出结构
信息位部份 监督位部份
c0c1...ck2ck1 a0a1...ak2ak1 ck 2cn1
差错控制编码(纠错码)
三、误码的类型 随机误码
•错码出现是随机的、错码之间统计独立。 •由随机噪声引起 •存在随机误码的信道称为随机信道
突发误码
•错码成串集中出现,在很短的时间出现大量错码,而 过后又存在较大的无错码位,且差错之间是相关的 •例如:脉冲噪声,信道中衰落 •存在这种差错的信道称为突发信道
6
四、差错控制方法
即满足: vn-1+ vn-2+…+ v1+ v0=0
(8-1)与(8-2)叫做监督方程或监督关系式
(8-2)
24
在接收端,按上式计算各码元,若结果为1认为有错; 否则,无错。如: 11010 1
注意:只能检测奇数个错误,当错码为奇数个时,由于 打乱了码字中”1”个数的奇偶性,故能发现差错。但当 错码为偶数个时,因码字中1个数奇偶性保持不变,则 无法发现错码。
12
这种方法只能检测错误,但不能纠正错误 比如:当接收端收到禁用码组100时,无法判决哪一位码 发生了错误 000(晴) 101(云) 110(雨) 错一位 100
要想纠正错误,需要增加多余度,比如,只准使用两 个码组
13
000(晴)
111(阴)
其他均为禁用码组,则它可检测两个错码或能纠正一 个错码。 如:接收端接收到禁用码组100,若认为只有一个错码, 可纠正,若错码数不超过2个,只能检测错误 4种信息完全可以由2位二进制数字来表示,即前两位。 可见,第三位完全是多余的,这第三位就作为附加的 监督码
mn (3) 编码效率 (m 1)(n 1) 信息码元共m行n列
28
4、恒比码(等比码或等重码)
每个码组中含“1”和“0”的个数的比例恒定 在检测时,计算接收码组中“1”的数目是否正确,能检测
出所有奇数个错误,并能部分检测出偶数个错误(成对交 换错误检测不出)
第八章 差错控制编码
一般地,若码组有纠t个差错的能力,则应能指出无 错、单错到t个差错所有可能情况,此时校验位数m应 满足:2 m
j 0
t
Cnj
上式称为汉明界。它给出了纠t个错的必要条件。
8.3 循环码 8.3.1 循环码的特点及表达式
循环码是一种系统分组码,前k位是信息码,后r位
是监督码。不仅具有封闭性,还具有循环性,即一 许用码组经循环移位后得到另一个许用码组。
000、011、101、110用来传递信息可以检一位错,
但无法纠错;
000、111用来传递信息可以检一位或两位错码,还
可以纠一位错码。
可见,码组间的差异与纠检错能力十分重要。
定义1:码组中非零码元的数目称为码组的重量,简
称码重。
定义2:两码组中对应码位上具有不同码元的数目称
为两码组的距离,简称码距,又叫汉明距。
n ( x 1) 进行因式分 ( x 1) 的n–k次多项式,所以对
n
解,便可得到相应的g(x)。 通常,由信息码组D和生成多项式求出的码组不是 系统码。根据系统码的定义,码组的前k位是信息码, 后m位是校验码。
n k 用多项式表示为: c( x) x d ( x) R( x)
又因为 c( x) d1 ( x) g ( x) ,所以,有:
T CH 0 。 ,则有
任何码组都应该满足上述关系,或者说,信息码 与监督码间的校验关系完全取决于H,因此,H矩阵
称为校验矩阵或监督矩阵。
设接收码组为R,它可分解为 R=C+E 。 其中,C为正确码组,E为错误码组。 当无错接收时,E为0,当有错接收时,E为非零。
S RH T , 再设伴随矩阵为:
则有: S CH T EH T EH T
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
矩阵/子矩阵的4个顶点上的差错
失效!!!
信息码元 11 1 0 0 1 11 0 1 0 0 10 0 0 0 1 00 0 1 0 0 11 0 0 1 1 01 1 0 1 1
监督码元(偶)
0
0
1
0
1
1
0
1
1
1
1
1
恒比码(定比码)
式中⊕表示模2加 n表示码组长度
aki和aji表示第k个码组和第j个码组的第i位码元 min表示最小值
最小距离实例
❖ 举例:
❖ 码 组 集 合 { ( 000 ) ( 001 ) ( 010 ) ( 011 ) ( 100 ) ( 101 ) ( 110 ) (111)} d0=1 没有检错能力。
差错控制实例
❖ 总结:(信息码+监督码=码组)构成的 信息序列通过降低信息传输效率来提高 传输的可靠性。
6. 编码效率
❖ 编码效率:指信息码在码组中所占的比重。 ❖ 假定n=k(信息码长)+r(监督码长),用R
表示编码效率 η=k/n=k/(k+r) ❖ 当n ↑ ❖ η↓ ❖ Pe ↓ 可靠性↑
❖ 几何表示:用3位码元构成的8个码组表示立 方体中各个顶点;
海明距离(码距):就是从一个顶点移动到另一个顶点所经 历立方体的最少边数;
2.最小距离
❖ 2.最小距离:一个码组集合中,任何两个码组 间海明距离(即码距)的最小值称为码组集合的最 小距离。用d0或dmin表示:
n
d0/dminmin{(ajiak)i}表示 i1
差错控制的基本概念
❖ 所谓差错即为误码;差错控制的核心是抗 干扰编码,简称差错编码。
❖ 基本思想:是通过对信息序列作某种变换, 使原来彼此独立、互不相关的信息码元产 生某种规律性(相关性),从而在接收端 根据这种规律性来检查,进而纠正传输信 号序列中的差错。
❖ 变换的方法不同就构成了不同的编码,即 信道编码
信号在交到用户之前应当去掉监督码元。
❖插入监督码元的目的是使原来彼此独 立、互不相关的信息码元产生某种规 律性(相关性)从而使接收端能够根 据这种规律性来检测传输过程是否有 误。
7
2.差错控制的基本特点
❖ ①引入差错编码控制后,实际传输的 信息序列W=(hy信? 息码元+监督码元),称为码 组。
(an-1,an-2……,a1,c0)其中前n-1位为信息 位,第n位c0为监督位
① 奇 校 验 : an-1⊕an-2⊕……⊕a1⊕c0=1 即 c0= an-1⊕an-2⊕……⊕a1⊕1
② 偶 校 验 : an-1⊕an-2⊕……⊕a1⊕c0=0 即 c0= an-1⊕an-2⊕……⊕a1
实例
第八章-差错控制编码要点
❖ 必要性:
数据通信要求信息传输过程具有高度的可靠性 即误码率足够低;
然而信号在传输过程中由于传输损耗(噪声, 衰损,失真)不可避免要产生一些差错即出现 误码。
大体上分为:
❖随机差错:由信道的加性随机噪声引起的差 错
❖突发差错:某一段时间内出现一连串的差错 ❖混合差错:既有随机差错又有突发差错
数字
1 2 3 4 5
编码
01011 11001 10110 11010 00111
数字
6 7 8 9 0
编码
10101 11100 01110 10011 01101
正反码
❖ 多用于10单位电码的前向自动纠错设备中, 能纠正一位差错,发现大部分两位错。
n=k+r 且 k=r=5
❖ 1.编码规则:
Pe满足:
Pe<=A
e-n
E(R ) b
式中
香农信道编码定理
n—码字长度(码长) E(Rb)—误差指数(当Rb<=C时E(Rb )
>0) A—正系数 Pe=Ne/N误码率是指二进制码元在数据
传输系统中被传错的概率 ;N为传输的二 进制码元总数, Ne为被传错的码元数。
E(Rb)与Rb的关系如图所示:
方阵校验码
❖ 又称行列监督码,矩阵码,纵向冗余校验码 (LRC,Lognitudinal Redundancy Check),它的码元受到行和列两个方向奇 偶监督,又称二维奇偶校验码。
❖ 编码规则:使的每个码元受到纵向(列)和 横向两次监督;将欲发送的信息码按行排成 一个矩阵,每行的最后加上一个奇偶监督码 元;在每列最后也加上一个监督码元,进行 奇偶校验;最后按行或列码组的顺序发送。
1
督 码
11 0 0 1 1 1
1
元 01 1 0 1 1 1
1
发送端在发送时则按列(或行)的顺序传输:111010 110011 100001 010100 ……001111
接收端仍将码元恢复成发送时方阵形式,然后按行、 列进行奇偶校验
方阵校验码
❖ 特点:
可以检测出某行某列上的奇数个错误和长度不 大于行(列)数的突发错误。
❖ 写出下列二进制序列的偶校验码: ①1001110 10011100 ②0101111 01011111
写出下列二进制序列的奇校验码: ①1100101 11001011 ②0110010 01100100
奇偶校验编码
❖ 特点:
无论信息位为多少位,监督位只有一位。 只能检测信息码组中奇数个错误,对偶数个错
如果2种码组作为许用码组(000 111), 任两个码距间的最小距离为3,记dmin =3;
所以码组集合中最小距离越大,其抗干扰 能力(包括检错和纠错能力)越强。
4.最小距离与抗干扰能力的关系
❖ 定理3.1若一种码的最小距离为d0 ,则它能检查传 输错误个数(检错能力)e应满足:d0>=e+1
❖ 码 组 集 合 { ( 000 ) ( 011 ) ( 101 ) (110)} d0=2 能检测出1位码位出错。
❖ 码组集合{(000)(111)} d0=3 能 检测出2位出错并能纠正1位错误。
如果8种码组都作为许用码组,任两个 码距间的最小距离为1,记dmin =1;
如果4种码组(000 011 101 110)作为 许用码组,任两个码距间的最小距离为 2,记dmin =2;
方阵校验码结构
XX X X X X X X XX X X X X X X X X X X X XX X X X X X X X X X X X X X X X X X
实例
信息码元
行监督码元(偶)
11 1 0 0 1 0
0
11 0 1 0 0 1
0
10 0 0 0 1 1
1
列 监
00 0 1 0 0 0
4.差错控制编码的基本原理
❖ 从而差错控制编码的基本原理就是:在保 持信息位数不变(信息码元)情况下,采 用增加码长的方法来降低误码率。
5.差错控制实例
❖ 信源发出的任何消息通过信源编码表达成二进制信 号“0”和“1”的形式。
Source
Channel
Destination
❖ Source→Destination传输A和B两个消息。
三 常用差错控制编码方法
❖ 1 奇偶校验编码 ❖ 2 方阵校验码 ❖ 3 恒比码 ❖ 4 正反码 ❖ 5 循环冗余校验编码(CRC) ❖ 6 卷积码
❖ 差错控制的核心就是抗干扰编码,为了 提高通信系统的检错和纠错能力,人们创造 出许多差错控制编码,比较常用的有奇偶校 验编码、循环冗余校验编码、卷积码等。
差错控制的基本概念
❖ 通俗地讲,差错控制方法:对要传送的二 进制数字信息中增加一些附加的信息,通 过增加冗余度使得原来的信息可以检错或 纠错。
❖ 一般来讲,加入的冗余度越多,检错纠错 能力(即差错控制能力)越强,传输效率 越低。
1.信息码和监督码
❖ 信息码(元):发送用户端欲发送的信 息序列。
❖ 监督码(元):为了使信息码元产生某种 规律性,可按照某种规则在用户信息序 列中插入一定数量的新码元,这种新码 元叫监督码(元)。
奇偶校验编码
❖ 编码规则:
发送端,将所要传输的数据码元分组,在分 组数据后面加一位监督码(校验位),使得 该组码连同监督码在内的码组中“1”的个数 为奇数(奇校验)或偶数(偶校验)。
接收端,按照编码规则检查如果发现不符, 就说明产生差错,但不能明确差错的具体位 置即不能纠错。
奇偶校验编码
❖公式表示:设码组长度为n,表示为
矛盾! tradeof
f!
二 差错控制编码的特性和能力
1.海明(hamming)距离 2.最小距离 3.海明距离(码距) 4.最小距离与抗干扰能力的关系
1.海明(hamming)距离
❖ 1.海明(hamming)距离:指两个不同的码
组其对应码位(二进制位)的码元不同的个
数,简称码距 ;用d表示:
(1)当信息码中“1”的个数为奇数时,监督码与 信息码相同(正码)10101 10101
(2)当信息码中“1”的个数为偶数时,监督码与 信息码相反(反码)10100 01011
正反码
❖ 2.解码方法:
(1)将接收到信息码与监督码按相应的 码位模2加(异或),得到一个新的5 位码组。
力。
实例(P58)
解:最小距离
实例
❖ 检错和纠错能力 第一组:d0=2,e<=d0 –1=1,可检测出一个错,
(定理1) 第二组: d0 =3
e<=d0 –1=2 ,可检测出二个错,(定理1) t<=(d0-1)/2=1,可纠正一个错,(定理2) e+t<=d0-1=2 ,令(t<=e) e=1,t=1, 纠错、检错各1,(定理3)
❖ ②在信道容量既定的情况下,信息传输效率 有所降低,但信息传输的可靠性有所提高, 既差错控制编码用降低传输效率的代价来提 高传输的可靠性。
