信号与系统第2章 习题
信号与系统课后题解第二章

⑺
对⑺式求一阶导,有:
de(t ) d 2 i 2 (t ) di (t ) du (t ) =2 +2 2 + c 2 dt dt dt dt de(t ) d 2 i2 (t ) di (t ) =2 + 2 2 + 2i1 (t ) + 2i 2 (t ) 2 dt dt dt
⑻
将⑸式代入⑻式中,有:
λ 2 + 2λ + 1 = 0
可解得特征根为 微分方程齐次解为
λ1, 2 = −1
y h (t ) = C1e −t + C2 te− t
由初始状态为 y (0 ) = 1, y ' (0 ) = 0 ,则有:
C1 = 1 − C 1 + C 2 = 0
由联立方程可得 故系统的零输入响应为:
由联立方程可得 故系统的零输入响应为:
A1 = 2, A2 = −1
y zi (t ) = 2e − t − e −2 t
(2)由原微分方程可得其特征方程为
λ 2 + 2λ + 2 = 0
可解得特征根为 微分方程齐次解为
λ1, 2 = −1 ± i
y h (t ) = e −t (C1 cos t + C2 sin t )
(− 3C1 + 3C2 )δ (t ) + (C1 + C2 )δ ' (t ) − (− 2C1 + C 2 )δ (t ) = δ (t )
(
(
( + C e )δ (t ) + (C e
2 1
)
−2 t
+ C2 e t δ ' (t )
信号与系统(习题课)

∴ y(t) = e-3t + t e-3t = (1+ t) e-3t
by wky
习题 3-6 (1)
已知系统的微分方程为 y’’(t) +5 y’(t) + 4 y(t) =2 f ’(t) + 5f(t), t >0; 初始状态y(0-) =1,y’(0-) =5, 求系统的零输入响应yx(t)。 解:系统特征方程为 s2+5s+4=0 , 解得特征根 s1=-1, s2=-4
特解 (强迫响应)
比较:完全响应=零输入响应 + 零状态响应 = e-t + (1 - 1/2e-t -1/2e-3t)
by wky
习题 3-4
已知微分方程为 y’(t) + 3 y (t) = f(t),t >0; y(0) =1,
求系统的固有响应(齐次解) yh(t)、强迫响应 (特解) yp(t)和完全响应(全解) y(t) 解:系统特征方程为 s+3=0,
f(t)
f(-t)
2
2
1
1
-3 -2 -1 0 1 2 3 t -3 -2 -1 0 1 2 3 t
2 f(t+2)
f(-3t)
2
1
1
-3 -2 -1 0 1 2 3 t -3 -2 -1 0 1 2 3 t by wky
2-10 已知信号波形, 绘出下列信号波形
f(t)
f(-t)
2
2
1
1
-3 -2 -1 0 1 2 3 t -3 -2 -1 0 1 2 3 t
信号与系统习题给学生
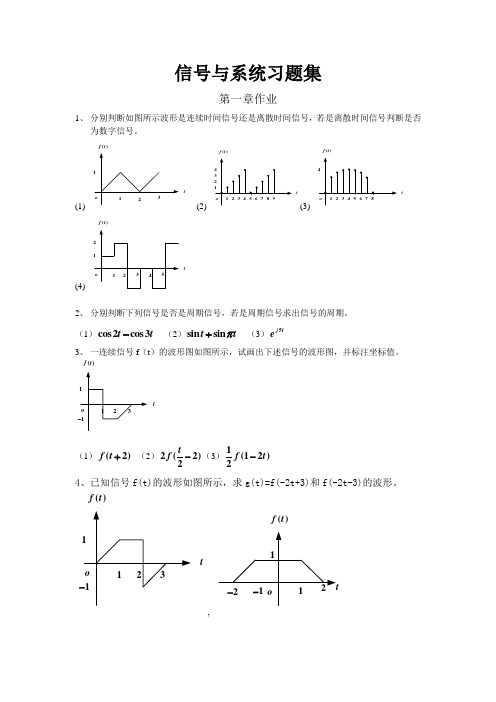
信号与系统习题集第一章作业1、 分别判断如图所示波形是连续时间信号还是离散时间信号,若是离散时间信号判断是否为数字信号。
(1)t()f t (2) t()f t(3) t()f t(4) t()f t2、 分别判断下列信号是否是周期信号,若是周期信号求出信号的周期。
(1)cos 2cos 3t t - (2)sin sin t t π+ (3)5j te3、 一连续信号f (t )的波形图如图所示,试画出下述信号的波形图,并标注坐标值。
t()f t(1)(2)f t + (2)2(2)2t f -(3)1(12)2f t- 4、已知信号f(t)的波形如图所示,求g(t)=f(-2t+3)和f(-2t-3)的波形。
t()f t,()f t5、写出如图所示的各波形的函数式。
(1)t()f t(2)t()f t-6、画出下列各时间函数的波形。
(1)[](1)(2)t u t u t ---,(2)[](1)(2)(2)t u t u t u t ---+- (3)[](3)()(2)t u t u t --- 7、求下列函数值。
(1)2()()td r te u t dt-⎡⎤=⎣⎦,(2)3()()t r t e t δ-= (3)()cos ()4r t t t dt πδ∞-∞=-⎰,(4)2()()(1)tr t t e t dt δ∞--∞=+-⎰, ( 5 ) 3'()()t r t e t δ=8、画出下列系统的仿真框图。
()()3()2()dr t de t r t e t dt dt+=+ 9、判断下列系统是否为线性的,时不变的,因果的? (1)()(2)r t e t =- (2)()(3)r t e t = (3)()()(1)r t e t u t =- (4)()()r t te t =第二章作业1、已知系统的电路图如图所示,写出电压()o v t 的微分方程。
()e tR +-()o v t2、已知系统的微分方程和起始状态如下,求齐次解。
信号与系统第2章习题

信号与系统第2章习题一、选择题1、下列信号不能用复指数信号stAe t x =)(表示的是( )A.冲激信号B.直流信号C.指数信号D.正弦信号 2、)22(4t e t--δ等于( )A. te4- B. )22(t -δ C.)1(214--t e δ D. )1(214δ-e 3、积分⎰--+642)8(dt t e t δ等于( )A.0B.16e C.1 D.)8(+t δ 4、已知信号)(t x 如下图所示,其表达式是( )A.)3()2(2)(---+t u t u t uB. )3(2)2()1(---+-t u t u t uC. )3()2()(---+t u t u t uD. )3()2()1(---+-t u t u t u 5、已知信号)(t x 如下图所示,其反转右移的信号)(1t x 是( )A. B.C. D.6、如下图所示:)(t x 为原始信号,)(1t x 为变换信号,则)(1t x 的表达式是( )A. )1(+-t xB. )1(+t xC. )12(+-t xD. )121(+-t x 7、若)(t x 是已录制声音的磁带,则下列表述错误的是( )A.)(t x -表示将磁带倒转播放产生的信号B.)2(t x 表示将磁带以二倍速度加快播放C.)2(t x 表示原磁带放音速度降低一半播放D.2)(t x 表示将磁带的音量放大一倍播放8、设)(t x 表示你在山谷喊话的声音,则你耳朵听到的声音可表示为( ) A.∑∞=0)(n nt x a,0>n a B. ∑∞=+0)(n n nT t x a,0,0>>n n T aC.∑∞=-0)(n n nT t x a,0,0>>n n T a D.∑∞=-0)(n nTt x ,0>n T9、如下图所示周期信号)(~t x ,其直流分量等于( )A.0B.2C.4D.6二、判断题1、两个奇信号的和还是奇信号( )2、任何信号可分解为直流分量与交流分量之和( )3、任何信号可分解为偶分量与奇分量之和( )4、)cos(t 是功率信号,)]()()[cos(T t u t u t --是能量信号( )5、积分1)(=⎰∞-td ττδ( )6、对连续周期信号进行抽样所得离散序列一定还是周期的( )7、设)2()(1k x k x =,则)2/()(1k x k x =( )三、简答题1、单位冲激信号和单位脉冲序列各有什么特性?2、正弦信号)sin(0t ω和正弦序列)sin(0k Ω有什么区别与联系?3、信号的时域分解有哪几种方法?4、连续时间信号分解为冲激信号的线性组合有何实际意义?四、计算题教材P66习题:2-9、2-10、2-12、2-14。
考研专业课郑君里版《信号与系统》第二章补充习题——附带答案详解
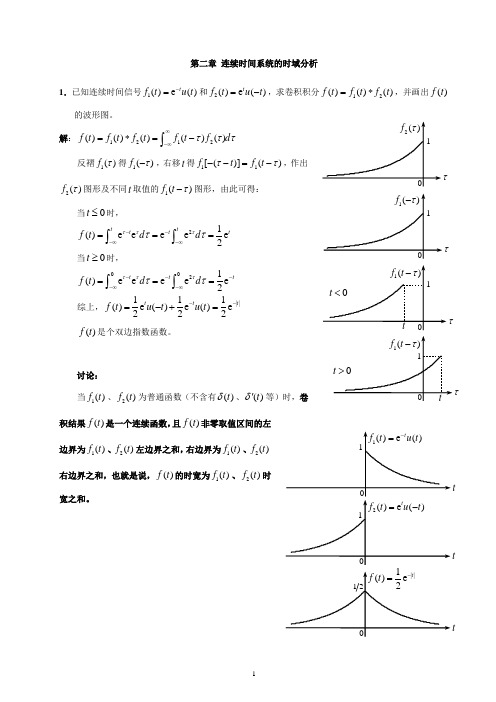
第二章 连续时间系统的时域分析1.已知连续时间信号1()e ()t f t u t -=和2()e ()t f t u t =-,求卷积积分12()()()f t f t f t =*,并画出()f t 的波形图。
解:1212()()()()()f t f t f t f t f d τττ∞-∞=*=-⎰反褶1()f τ得1()f τ-,右移t 得11[()]()f t f t ττ--=-,作出2()f τ图形及不同t 取值的1()f t τ-图形,由此可得:当0t ≤时,21()e e ee e 2ttt tt f t d d τττττ---∞-∞===⎰⎰当0t ≥时,0021()e e e e e 2t t t f t d d τττττ----∞-∞===⎰⎰综上,||111()e ()e ()e 222t t t f t u t u t --=-+=()f t 是个双边指数函数。
讨论:当1()f t 、2()f t 为普通函数(不含有()t δ、()t δ'等)时,卷积结果()f t 是一个连续函数,且()f t 非零取值区间的左边界为1()f t 、2()f t 左边界之和,右边界为1()f t 、2()f t 右边界之和,也就是说,()f t 的时宽为1()f t 、2()f t 时宽之和。
τttt2.计算题图2(a )所示函数)(1t f 和)(2t f 的卷积积分)()()(21t f t f t f *=,并画出)(t f 的图形。
解法一:图解法1212()()()()()f t f t f t f t f d τττ∞-∞=*=-⎰其中1()f t τ-的波形见题图2(b),由此可得: 当10t +≤,即1t ≤-时,()0f t = 当011t ≤+≤,即10t -≤≤时,120()2(1)t f t d t ττ+==+⎰当11t +≥但10t -≤,即01t ≤≤时,1()21f t d ττ==⎰当011t ≤-≤,即12t ≤≤时,121()21(1)t f t d t ττ-==--⎰当11t -≥,即2t ≥时,()0f t =综上,220,1,2(1),10()1,011(1),12t t t t f t t t t ≤-≥⎧⎪+-≤≤⎪=⎨≤≤⎪⎪--≤≤⎩ ()f t 波形见题图2(c)。
信号与系统课后答案(第二版)+曾禹村+第二章作业参考答案

i1(t) = i2 (t) + i3 (t) , i2 (t) R2 − L 有 8i2 `(t) + 3i2 (t) = 2e`(t) ˆ ˆ 由 h`(t) + 3h(t) = 2δ (t)
0
h
(−1) t 3
T
t
t 3E − τ E (t) = ∫ δ (τ )dτ − ∫ e 8 u(τ )dτ −∞ 4 −∞ 32
x(t)
1
2 t
yx(t)
1 2 3 4 t
0
1
0
Qh(0) = 0, t ≤ 0, 有 0 ≤ t <1 , h(t) + h(t −1) + h(t − 2) = h(t) = t 时 1≤ t < 2时 h(t) + h(t −1) + h(t − 2) = h(t) + h(t −1) =1 , h(t) =1− h(t −1) =1− (t −1) = 2 −t 2 ≤ t < 3 , h(t) + h(t −1) + h(t − 2) =1 时 h(t) =1− h(t −1) − h(t − 2) =1− (2 − (t −1)) − (t − 2) = 0 3 ≤ t < 4时 h(t) = 4 − t − h(t −1) − h(t − 2) =4 −t − 0 − (2 − (t − 2)) = 0 , t, 0 ≤ t < 1 ∴h(t) = 2 − t, 1 ≤ t ≤ 2 0, t < 0,2 < t
解: (e) 特征方程为 λ2+4λ+4=0 得 λ1=-2, λ2=-2。 则 h(t)= (c1eλ1 t+ c2eλ2t)u(t)=( c1e- 3 t+ c2e-2 t)u(t) h`(t)= (c1+ c2)δ(t)+(-3c1e- 3 t-2c2e- 2t)u(t) h``(t)= (c1+ c2)δ`(t)+(-3c1-2c2) δ(t)+ (9c1e- 3 t+4c2e- 2t)u(t) 将x(t)= δ(t), y(t)=h(t)代入原方程得:
信号与系统 第二章习题 王老师经典解法(青岛大学)小白发布
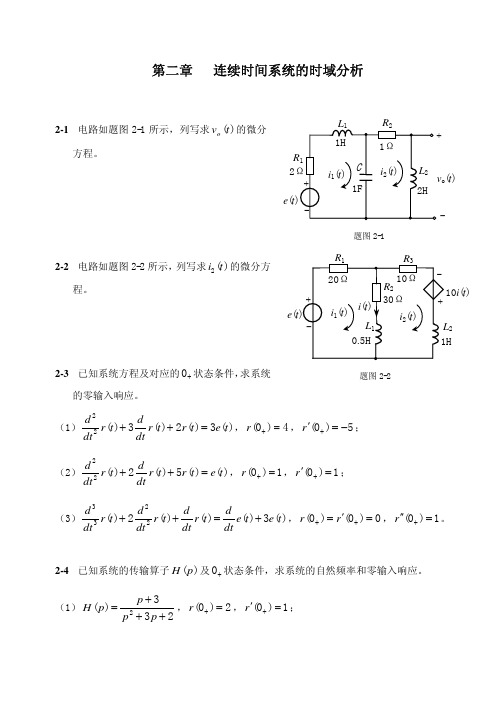
2-16 已知 f1 (t ) =
画出下列各卷积的波形。 (1) s1 (t ) = f1 (t ) ∗ f 2 (t ) ; (2) s2 (t ) = f1 (t ) ∗ f 2 (t ) ∗ f 2 (t ) ; (3) s3 (t ) = f1 (t ) ∗ f 3 (t ) 。
2-17 求题图 2-17 所示电路在 e(t ) = (1 + 2e
第二章
连续时间系统的时域分析
2-1 电路如题图 2-1 所示,列写求 vo (t ) 的微分 方程。
L1 1H R1 2Ω + e(t) i 1 (t )
R2 1Ω + L2 2H 题图 2-1
C
1F
i 2 (t )
vo(t)
2-2 电路如题图 2-2 所示, 列写求 i2 (t ) 的微分方 程。
题图 2-18
−2 t
− 1)U (t ) , 试利用卷积的性质求题
1 0 -1
e2(t)=tU(t) 1 t 0
e3(t)
t 0 1
2-19 一线性时不变的连续时间系统,其初始状态一定,当输入 e1 (t ) = δ (t ) 时,其全响应
r1 (t ) = −3e − tU (t ) ; 当 输 入 e2 (t ) = U (t ) 时 , 其 全 响 应 r2 (t ) = (1 − 5e − t )U (t ) 。 求 当 输 入 e(t ) = tU (t ) 时的全响应。
2-14 计算卷积 f (t ) = f 1 (t ) ∗ f 2 (t ) ,其中 f1 (t ) = sgn(t − 1) , f 2 (t ) = e 2-15 求下列卷积 (1) f1 (t ) = e
《信号与系统分析基础》第二章部分习题参考答案

第二章部分习题参考答案2-6 试求下列各函数1()f t 与2()f t 之卷积。
121212(-)01(1) ()() ()() (0) ()()()(-) ()(-)11(1) 0(2) ()t tt t tt t f t u t f t e u t f t f t f f t d u eu t d e e d e e e t f t ααταατααταατττττττααδ-+∞-∞+∞---∞--==>*===⋅=⋅=-≥=⎰⎰⎰,解:,2121212() ()cos(45)()()()cos[()45] cos(45)(3) ()(1)[()(1)] ()(1)(2) ()()t f t t f t f t t d t f t t u t u t f t u t u t f t f t ωδτωττω+∞-∞=+*=-+=+=+--=---*⎰,解:,解:ττ222221211211()(-1)(-1)-2(-2)(-2)(-1)(-1)-(-2)(-2)2211-(-2)(-2)(-3)(-3)-(-2)(-2)(-3)(-3)22()*()()1,()0123, (1-)(1)21(1)--(12ttf t t u t t u t t u t t u t t u t t u t t u t t u t f t f t f t t f t t t dt t ft t t t τττ=+++=<=<<+=+-=++⎰222-112222212111)-222123, (1-)(1)-221()2(1)-2(1-)(-1)211121---152223, ()*()0.t t t t t t d t f t t t t t t t t t t t f t f t ττττ-+=<<+=+=+++=+++=++>=⎰121221--(4) cos , (1)-(-1)()*()()(-) [(1)-(-1)][cos(-)] cos[(1)]-cos[(-1)]f t t f t t t f t f t f f t d t t t d t t ωδδτττδδωττωω+∞∞+∞∞==+==+⋅=+⎰⎰ -212-212--2-220(5) ()(), ()sin ()()()*()()sin(-)(-) sin(-)sin t t ttt tf t e u t f t t u t f t f t f t e u t u t d e t d ee d τττττττττ+∞∞==⋅==⋅⋅⋅=⋅=⋅⎰⎰⎰-12-(-)--0022-(-)-33-2-3(6) ()2[()-(-3)], ()4()-(-2)0, ()0.02,()2488-825, 88()8(-)5, ()0.t tt t t tt t t t t f t e u t u t f t u t u t t f t t f t e d e e e t ft ed ef t e e e t f t ττττττ-==<=<<==⋅=<<===>=⎰⎰2-8 求阶跃响应为32()(21)()t t s t e e u t --=-+的LTI (线性时不变)系统对输入()()t x t e u t =的响应。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
卷积运算性质: 卷积积分满足微分、积分及时移特性: ①若 x(t)h(t),则y(t) x(t)h(t)x(t)h (t)y(t)
[ t x()d ]h (t)x(t)[ t h()d ][ t y()d ]
②若 x(t)h(t),则y(t)
x ( t t 0 ) h ( t ) x ( t ) h ( t t 0 ) y ( t t 0 )
1δ 4 n 1δ 2 n 1 9 δ n 2 5 δ n 3
结果如图(a)所示。
(a)
sn
说明
•
6
1•
15 • 10•
3• 6 •
•14•12 •
9
•5
o
4
•
•
n
这种方法虽然计算比较简单,但表达式较长,因而只适应于较短的
时限序列。另外,用这种方法求得的卷积结果有时不容易写出其函
数表达式的闭式形式。
(2 )y t x t
在某个正的时刻t0的输出y(t0)=x(-t0) ,仅仅决定于 输入在时刻(-t0)的值,(-t0)是负的,因此属于t0的过去 时刻,这时可能要得出该系统是因果的结论。然而,
我们总是要检查在全部时间上的输入-输出关系,对于
t<0,如
t 4 ,y 4 x 4
所以在这一时间上输出就与输入的将来有关。因此, 该系统不是因果系统。
1f1nsinn 1π6sinn 3
sinnπ虽 然 是 周 期 序 期列 是 N, 3, 2其但 周 sinn是 非
16
3
周 期 序 列 , 所 乘以 积二 序 f1者 n列 实的际 是 非 周 期
2 f2 n 2 s in 1 n π 6 c o n 8 π s 6 s in 2 n π π 6
是因果系统。
( 1 )y t x tct o 1 s (2 )y tx t
在检验一个系统的因果性时,重要的是要考查系 统的输入-输出关系,同时要把输入信号的影响仔细 地从在系统定义中所用到的其他函数的的影响区分开 来。
( 1 )y t x tct o 1 s
在这个系统中,任何时刻t的输出等于在同一时刻 的输入再乘以一个随时间变化的函数,因此仅仅是输 入的当前值影响了输出的当前值,可以得出该系统是 因果系统。
设 x3(t)ax1tbx2t x3 t y3 t x32 t ax1tbx2 t2 a2x12 tb2x22 t2abx1tx2 t
a2y1tb2y2 t2abx1tx2 t ay1tby2 t
所以系统是非线性的。
例7
系统的输入为x(t),输出为y(t),系统关系如下,判断系统是否
[x(n ) x(n 1 )] h (n )x(n ) h (n ) h (n 1 )
y(n )y(n 1 )
n
n
n
[ x(k)]h (n )x(n ) [ h (k)] y(k)
k
k
k
② 若 x(n)h(n),则y(n)
x ( n n 0 ) h ( n ) x ( n ) h ( n n 0 ) y ( n n 0 )
O
1 2 3t
d f 6 2 t
dt
1
(1) (1)
3
O
12
t
(2)
对信号的波形进行微分变换时, 应注意在函数的跳变点处会出 现冲激信号。
例5 判断下列离散信号是周期序列还是非周期
序列。若是周期序列试确定其基波周期N。
1f1nsinn 1π6sinn 3 2 f2 n 2 s in 1 n π 6 c o n 8 π s 6 s in 2 n π π 6
则
y2n -2, 0,0,01, 0 ,, 0 0,n 2 ,00 ,0,,0 ,-1
如图(c)所示
x
n
3
•2
•
1
9
•
•
•
•
•
•
3
•o
• •3 n
1
•
•
2
(c)
第三步将 y2n右移2位即得
yn -2, 0,0,01, ,n0 0 0,0, ,20 ,,0, ,0 ,-1
如图(d)所示。
g t f1 tf2 t 0
-1 t 1
f2t向右f2移 t
1 f1
t 3 1 O t 1
t 1时两波形有公共部分,积分开始不为0,
积分下限-1,上限t ,t 为移动时间;
g (t) t1f1 ()f2 (t )d t11 2 t d
2
2
4
t 1
t2 t 1
4 24
1 t 2
例8
f1 t
1 t 1 f1(t) 0 t 1
t f2(t)2 (0t3 )
f 1
1 1 O 1 t
t
1 1 O 1
f 2 t
f2
3
3
2
t t
2
O
3t
3
O
f2t
3
2
t 3 O t
t -1
f2t
1 f1
t 3
t 1 O
1
t 1
两波形没有公共处,二者乘积为0,即积分为0
f1 f2 t 0
方法二:ft d e tδ t d e t t d te t
d t
d t
d t
et tet t
t t t
t
方法二没有注意利用冲激函数的性质,求解过
程较繁。另外,对冲激偶信号的性质 f t t f 0 t f 0 t
往往被错误写成
ftt f0 t
1
3
4
O
7
t
4
1
例2
已知序列 xn如图(a)所示,
x n
试求序列
2•
1•
ynxn2,并作图。
3 3
1 o
•
12
3
• 1
n
2
•
(a)
本例是关于离散信号运算的例题,离散信号的移位、 反褶、标度运算与连续信号的运算相同。但需注意, 序列的尺度倍乘将波形压缩或扩展,这时要按规律去 除某些点或补足相应的零值。
f1 (t )
O
t
(2) f2td dtetcotu st
此题应注意冲激信号的性质
d u t t
ftt f0 t
d t
f2
t
d dt
et
costu
t
et cost et sint ut et cost t
et cost sintut t
波形如下图
2
et
cos
t
π 4
u
t
t
f2(t)
卷积结果
f 2 t
3 2 t
O
3t
t2 t 1
g(t
)
4 t
t
2
2
4
t 2
1 t 1 1t 2 2 t 4
g(t) 2
4 2
0
其 他t
1 O 1 2
4t
例9 已知离散信号
x 1 n n u n u n 6
x 2 n u n 6 u n 1 求卷积, sn x 1 n x 2 n
把 yn 改写为 ynx13n2
第一步设
y1n xn 3
0
n3,0,3,6,9 其他
则
y1n -1, 0, 0, n 2 0,0,0,,10,,00, ,00,-2
如图(b)所示。 x n
3
2•
1
•
3 •
• •1 o
• 1
1
• 2
3
•
•
•
•
•9
n
2
•
(b)
第二步设 y2n y1n
2
1
(2) d f(62t)
dt
O 12
t
在描绘某些信号的波形时,有时不必求出函数的表达 式,而可直接利用信号运算及相应的波形变换图解。 画(2)的波形时,应先画出(1)的波形。 需要注意,对信号的基本运算都是对独立的、单一的 变量t而言的,而不是对变量at或at+b进行变换。
f 6 2t
2
1
x 2 n δ n 6 δ n 5 δ n 4 δ n 3 δ n 2
利用单位样值信号的卷积性质
δ n n 1 δ n n 2 δ n n 1 n 2
sn x 1 n x 2 n δ n 5 3 δ n 4 6 δ n 3 1δ 0 n 2 1δ 5 n 1
f2t
1
f1
t 3 1 O
1t
t 3 1
t1
即1 t 2
g(t)1112tdt
2t4
1 f1 f2t
1 O t 31
t
t 3 1
t
3
1
即2 t 4
1
g(t)
1(t)dt2t2
t32
42
t4
1 f1
f2t
t
1 O 1 t 3
t-31
即t 4
gt0
f1 t
1
1 O 1
求离散信号的卷积有多种方法,本例只介绍其中的几种 方法一:利用单位脉冲序列求卷积 方法二:借助图解,分区间求卷积 方法三:利用对位相乘法求卷积
方法一:利用单位样值信号求卷积
任何一个离散信号可以用单位样值信号表示为
m
xnxmδnm
对于本例
m
m
x1n m um um 6 δnm m
δn 1 2δn23 δn34δn45δn5
例6 判 断 方 yt程 x2t 描 述 的 系 性统 系是
