第一章 习题解析.
高中数学,必修一,《第一章,集合与函数概念》习题解析

目录第一章集合与函数概念 (1)1.1.1、集合的含义与表示 ............................................................................................................................. 1 1.1.2、集合间的基本关系 ............................................................................................................................. 2 1.1.3、集合的基本运算 (3)习题1.1 集合 ....................................................................................................................................... 4 1.2.1 函数的概念 ........................................................................................................................................... 7 1.2.2、函数的表示法 . (8)习题1.2 函数及其表示 ....................................................................................................................... 9 1.3.1 单调性与最大(小)值 ................................................................................................................... 13 1.3.2、奇偶性 .. (14)习题1.3 函数的基本性质 ................................................................................................................. 16 复习参考题 . (18)第一章集合与函数概念 1.1.1、集合的含义与表示1.用符号“∈”或“∉”填空:(1)设A 为所有亚洲国家组成的集合,则: 中国∈A,美国∉A,印度∈A,英国∉A.【解析】美国∈北美洲,英国∈欧洲.(2)若2{|A x x x ==},则1-∉A ;【解析1】2{|}{0,1}A x x x === ,1A ∴-∉; 【解析2】因为2(1)1-=-不成立,所以1A -∉.(3)若2{|60}B x x x =+-=,则3∉B ;【解析1】2{|60}{|(2)(3)0}{3,2}B x x x x x x =+-==-+==- ,3B ∴∉; 【解析2】因为23360+-=不成立,所以3B ∉;(4)若{|110}C x N x =∈≤≤,则8∈C ,9.1∉C.【解析1】{|110}{1,2,3,4,5,6,7,8,9,10}C x N x =∈≤≤=,9.1C ∴∉.【解析2】9.1N ∉ ,9.1C ∴∉.注1:判断一个元素是否属于某个集合,方法有二:(1)如果集合是用列举法表示的,就看元素有没有在集合中.如果元素在集合中,则元素属于集合;如果元素不在集合中,则元素不属于集合.如果集合是用描述法给出的,且集合中元素的个数有限,则往往先将集合改用列举法表示. (2)检验元素是否符合特征.如果元素符合特征,则元素属于集合;如果元素不符合特征,则元素不属于集合.注2:熟练掌握集合的三种表示方法,必要时将集合从一种形式转换为另一种形式。
复变函数论第三版课后习题答案解析

第一章习题解答(一)1.设z ,求z 及Arcz 。
解:由于3i z e π-== 所以1z =,2,0,1,3Arcz k k ππ=-+=±。
2.设121z z =,试用指数形式表示12z z 及12z z 。
解:由于6412,2i i z e z i e ππ-==== 所以()64641212222i i iiz z e eee πππππ--===54()146122611222ii i i z e e e z e πππππ+-===。
3.解二项方程440,(0)z a a +=>。
:解:12444(),0,1,2,3k ii za e aek πππ+====。
4.证明2221212122()z z z z z z ++-=+,并说明其几何意义。
证明:由于2221212122Re()z z z z z z +=++2221212122Re()z z z z z z -=+-所以2221212122()z z z z z z ++-=+其几何意义是:平行四边形对角线长平方和等于于两边长的和的平方。
5.设z 1,z 2,z 3三点适合条件:0321=++z z z ,1321===z z z 。
证明z 1,z 2,z 3是内接于单位圆1=z 的一个正三角形的顶点。
证 由于1321===z z z,知321z z z ∆的三个顶点均在单位圆上。
因为33331z z z ==()[]()[]212322112121z z z z z z z z z z z z +++=+-+-=]21212z z z z ++=所以, 12121-=+z z z z ,又)())((122122112121221z z z z z z z z z z z z z z +-+=--=-()322121=+-=z z z z故 321=-z z ,同理33231=-=-z z z z ,知321z z z ∆是内接于单位圆1=z 的一个正三角形。
化工原理课后习题解析(第一章)

第1章 流体流动1-1.容器A 中气体的表压力为60kPa ,容器B 中的气体的真空度为Pa 102.14⨯。
试分别求出A 、B 二容器中气体的绝对压力为若干Pa 。
该处环境大气压等于标准大气压。
(答:A,160kPa ;B,88kPa )解:取标准大气压为kPa 100,所以得到:kPa 16010060=+=A P ;kPa 8812100=-=B P 。
1-2.某设备进、出口的表压分别为 12kPa -和157kPa ,当地大气压为101.3kPa ,试求此设备进、出口的压力差为多少Pa 。
(答:169kPa -) 解:kPa 16915712-=--=-=∆出进P P P 。
1-3.为了排除煤气管中的少量积水,用如图示水封设备,水由煤气管道上的垂直支管排出,已知煤气压力为10kPa (表压)。
问水封管插入液面下的深度h 最小应为若干? (答:m 02.1)解:m 02.18.910101033=⨯⨯=∆=g P H ρ习题1-3 附图1-4.某一套管换热器,其内管为mm,25.3mm 5.33⨯φ外管为mm 5.3mm 60⨯φ。
内管流过密度为3m 1150kg -⋅,流量为1h 5000kg -⋅的冷冻盐水。
管隙间流着压力(绝压)为MPa 5.0,平均温度为C 00,流量为1h 160kg -⋅的气体。
标准状态下气体密度为3m 1.2kg -⋅,试求气体和液体的流速分别为若干1s m -⋅?( 答:1L s m 11.2U -⋅=;1g s 5.69m U -⋅= )习题1-4 附图解:mm 27225.35.33=⨯-=内d ,m m 5325.360=⨯-=外d ;对液体:122s m 11.2027.011503600/500044/-⋅=⨯⨯⨯===ππρ内d m A V u l l l l l ; 对气体:0101P P =ρρ⇒3560101m kg 92.51001325.1105.02.1-⋅=⨯⨯⨯==P P ρρ,()224内外内外D d A A A g -=-=π()2322m 1032.10335.0053.04⨯=-=π,13s m 69.592.51032.13600/160/--⋅=⨯⨯===ggg gg g A m A V u ρ。
《高等数学一》第一章-函数--课后习题(含答案解析)

第一章函数历年试题模拟试题课后习题(含答案解析)[单选题]1、设函数,则f(x)=()A、x(x+1)B、x(x-1)C、(x+1)(x-2)D、(x-1)(x+2)【正确答案】B【答案解析】本题考察函数解析式求解.,故[单选题]2、已知函数f(x)的定义域为[0,4],函数g(x)=f(x+1)+f(x-1)的定义域是().A、[1,3]B、[-1,5]C、[-1,3]D、[1,5]【正确答案】A【答案解析】x是函数g(x)中的定义域中的点,当且仅当x满足0≤x+1≤4且0≤x-1≤4即-1≤x≤3且1≤x≤5也即1≤x≤3,由此可知函数g(x)的定义域D(g)={x|1≤x≤3}=[1,3]. [单选题]3、设函数f(x)的定义域为[0,4],则函数f(x2)的定义域为().A、[0,2]B、[0,16]C、[-16,16]D、[-2,2]【正确答案】D【答案解析】根据f(x)的定义域,可知中应该满足:[单选题]4、函数的定义域为().A、[-1,1]B、[-1,3]C、(-1,1)D、(-1,3)【正确答案】B【答案解析】根据根号函数的性质,应该满足:即[单选题]写出函数的定义域及函数值().A、B、C、D、【正确答案】C【答案解析】分段函数的定义域为各个分段区间定义域的并集,故D=(-∞,-1]∪(-1,+∞).[单选题]6、设函数,则对所有的x,则f(-x)=().A、B、C、D、【正确答案】A【答案解析】本题考察三角函数公式。
.[单选题]7、设则=().A、B、C、D、【正确答案】B【答案解析】令则,故[单选题]8、则().A、B、C、D、【正确答案】D【答案解析】[单选题]9、在R上,下列函数中为有界函数的是().xA、eB、1+sin xC、ln x【正确答案】B【答案解析】由函数图像不难看出在R上e x,lnx,tanx都是无界的,只有1+sinx可能有界,由于|sinx|≤1,|1+sinx|≤1+|sinx|≤2所以有界.[单选题]10、不等式的解集为().A、B、C、D、【正确答案】D【答案解析】[单选题]11、().A、B、C、D、【正确答案】A【答案解析】根据二角和公式,[单选题]12、函数的反函数是().A、B、C、D、【正确答案】A【答案解析】由所以,故.[单选题]13、已知则().A、B、C、D、【正确答案】C【答案解析】[单选题]14、已知为等差数列,,则().A、-2B、1C、3D、7【正确答案】A因为同理可得:故d=a4-a3=-2.[单选题]15、计算().A、B、C、D、【正确答案】A【答案解析】根据偶次根式函数的意义,可知,故[单选题]16、计算().A、0B、1C、2D、4【正确答案】C【答案解析】原式=[单选题]将函数|表示为分段函数时,=().A、B、C、D、【正确答案】B【答案解析】由条件[单选题]18、函数f(x)=是().A、奇函数B、偶函数C、有界函数D、周期函数【正确答案】C【答案解析】易知不是周期函数,,即不等于,也不等于,故为非奇、非偶函数.,故为有界函数.[单选题]19、函数,则的定义域为().A、[1,5]C、(1,5]D、[1,5)【正确答案】A【答案解析】由反正切函数的定义域知:,故定义域为[1,5].[单选题]20、下列等式成立的是()A、B、C、D、【正确答案】B【答案解析】A中(e x)2=,C中,D中[单选题]21、下列函数为偶函数的是()A、y=xsinxB、y=xcosxC、y=sinx+cosxD、y=x(sinx+cosx)【正确答案】A【答案解析】sinx是奇函数,cosx是偶函数。
微观经济学习题解析

微观经济学习题第一章导论一. 选择题:1.“资源是稀缺的”是()A.指资源是不可再生的B.存在于人类社会的任何阶段的C.指生产力不发达造成了物品供给不足D.指可用的经济资源与人类的欲望相比总是显得不足解析:资源的稀缺性是任何社会和任何时代都存在的基本问题。
它是指与人们的需要相比较,资源的供给量相对不足。
事实上有些资源是可再生的,并且用之不竭,但我们对其用途进行选择,这仍然是稀缺资源如何配置的问题。
答案:B D2.下列哪项会导致一国生产可能性曲线的外移()A.资本存量增加B.技术进步C.失业减少D.劳动力增加解析:生产可能性曲线(边界)表示一个经济社会在一定的技术条件下,充分利用现有的社会资源所能生产的不同的商品组合。
生产可能性曲线的形状和位置,将随着生产技术的进步而发生变化。
技术进步将使生产可能性边界外移。
而技术进步对各种商品生产的不同影响,决定改变以后的生产可能性曲线的形状。
资本存量、劳动力增加都增加了可用资源。
答案:A B D3.某先生辞去月薪1000元的工作,取出自有存款100 000元(月息1%),办一家独资企业,如果不考虑商业风险,则该先生自办企业按月计算的机会成本是()元A.2000B.10 000C.1 000D.101 000解析:机会成本:把一定量的具有多种用途的资源用于生产某种商品后,放弃该资源用于其它用途所能获得的最大收益,即为这种商品的生产中使用该资源的机会成本。
月薪1000+利息100 000*1%=2000元答案:A4.一个经济体系必须作出的基本选择是()A.生产什么B.生产多少C.如何生产D.为谁生产解析:一个社会经济系统必须解决以下问题:1、决定产出的水平和构成——生产什么,生产多少;2、生产过程中的资源配置——怎么生产;3、产品在社会成员间的分配——为谁生产. 一个好的经济制度,是在解决上述问题的同时,还要保证社会资源的充分利用和产出的稳步增长。
答案:A B C D5.以下属于规范分析命题的是()A.“让一部分人先富起来”的政策,拉开了中国居民收入的贫富差距B.美国经济比俄罗斯经济增长得快C.应当继续实施适度从紧的货币政策D.在市场经济的汪洋大海中,企业的规模越大越好解析:实证分析解释各种经济变量之间的关系。
电路分析课后习题答案解析第一章
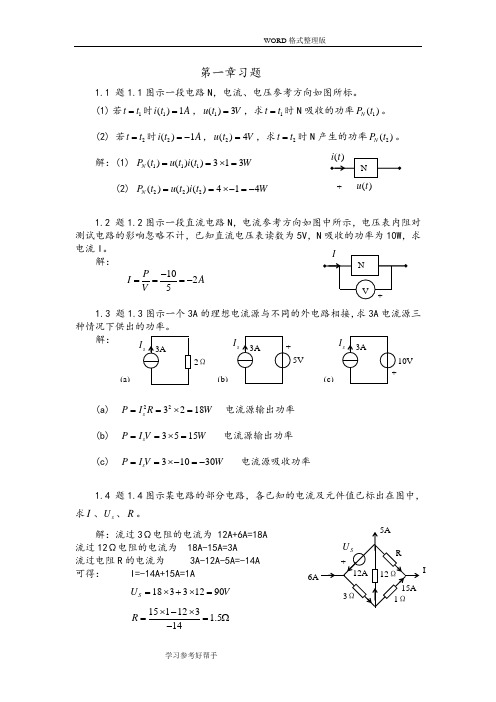
第一章习题1.1 题1.1图示一段电路N ,电流、电压参考方向如图所标。
(1) 若1t t =时1()1i t A =,1()3u t V =,求1t t =时N 吸收的功率1()N P t 。
(2) 若2t t =时2()1i t A =-,2()4u t V =,求2t t =时N()P t 解:(1) 111()()()313N P t u t i t W ==⨯= (2) 222()()()414N P t u t i t W ==⨯-=-1.2 题1.2图示一段直流电路N ,电流参考方向如图中所示,电压表内阻对测试电路的影响忽略不计,已知直流电压表读数为5V,电流I 。
解: 1025P I A V -===-1.3 题1.3图示一个3A 的理想电流源与不同的外电路相接,求3A 电流源三解:(a) 223218s P I R W ==⨯= 电流源输出功率 (b) 3515s P I V W ==⨯= 电流源输出功率 (c) 31030s P I V W ==⨯-=-电流源吸收功率1.4 题1.4图示某电路的部分电路,各已知的电流及元件值已标出在图中,求I 、s U 、R 。
解:流过3Ω电阻的电流为 12A+6A=18A 流过12Ω电阻的电流为 18A-15A=3A流过电阻R 的电流为 3A-12A-5A=-14A 可得: I=-14A+15A=1A 18331290S U V =⨯+⨯= 1511231.514R ⨯-⨯==Ω-'28I R --1.6 求题1.6图示各电路的开路电压。
解:(a) 2010530OC U V A V =-⨯Ω=-(b) 开路时,流过8Ω电阻的电流为 931189A ⨯=+ 流过6Ω电阻的电流为 1832189A ⨯=+可得: 26184OC U V =⨯-⨯=(c) 开路时,8Ω电阻的电压为 8208128V ⨯=+ 2Ω电阻的电压为 5210A V ⨯Ω= 可得:82100OC U V V V V =+-=解:(a) 6242I A +== (b) 201610221I A --==-+(c) 将电压源等效为电流源,如右图示 显然 0I = (d) 电压源供出的总电流为: 2121313//612//6124I A ===++++根据分流关系,流过3Ω电阻的电流为 63236A ⨯=+流过12Ω电阻的电流为 631126A ⨯=+可得: 211I A A A =-=1.8求题1.8图示各电路的电压U 。
第一章习题解析
1-3 在图1-3所示电路中,试求: (1)若元件A吸收10W功率,求其电压UA; (2)若元件B吸收-10W功率,求其电流IB; (3)若元件C发出10W功率,求其电流IC; (4)若元件D发出10mW功率,求其电流ID。
+
4A
UA
A
-
+
IB
10V B
-
IC
P3 U3I 60 (10) 600w P4 U4I (80) (10) 800w
电路发出的功率为
P发出=1000 +400=1400
电路吸收的功率为
P吸收=600+800=1400
1-8 在图1-9(a)所示电路中,已知I1=0.2A,I2=0.3A, I6=1 A。试求电流I3、I4和I5。
I2
I6
I4
I2
I6
I4
I1
I3
I5
I1
I3
I5
(a)
(b)
图1-9
解 应用KCL对图1-9(a)电路中各结点列写电流方程,得
I3 I1 I2 0.2 0.3 0.5A
I4 I6 I2 1 0.3 0.7 A
由KVL,得
Ubc 5v
Uac Uab Ubc (20) 5 15v
Ucd 10I 10 (2) 20v
由KVL,得
Ude 3v
U ae U ac U cd U de (15) (20) (3) 38V
1-6 在图1-6所示电路中, 已知U1=10 V,Us1=4V,Us2=2V,R1=4Ω,R2=2Ω,R3=5Ω。 试计算端子1、2开路时流过电阻R2的电流I2和电压U2。
U x 6.3 V
电阻Rx的电流应为
【VIP专享】第一章习题解析
h
0
h0
1 2
c02
3120 52.32
/
2000
3121.3kj/
kg
由级后压力查得h2t 3063kj/ kg
h
t
3121.3 3063
58.3kj/
kg
喷管的滞止理想比焓降为h
n
(1
-
m)
h
t
(1- 0.12) 58.3
51.3kj/
kg
动叶的滞止理想比焓降
为h b
m
h
t
0.12
解:(1)u dmn 3.14 1 3000 157 m / s
60
60
(2)w2 c22 u 2 2uc2 cos 2 1002 1572 186.1 m / s
2
arctan
c2 u
arctan 100 157
32.5
解:由级前压力和温度,查h s图可得h0 3120kj/ kg
58.3
7kj
/ kg
喷管的出口速度为c1 2hn 0.97 251.31000 310.7m / s
圆周速度 u x c1 0.54 310 .7 167.8m / s
动叶进口速度w1 c12 u12 2c1ucos1 310.72 167.82 2 310.7167.8cos11.1 149.6m/ s
487.4m / s
(3)临界速度ccr
2k k 1
p0v0
2 1.3 8.6 106 0.038 607.8(m / s) 1.3 1
2.已知:某级的动叶片出口速度c2 100m / s,2 90,其平均直径dm 1m,
工作转速n 3000r / min, 求: (1)动叶的圆周速度; (2)动叶出口相对速度的大小和方向
大学物理第一章习题解析
3. 推广至一般平面曲线运动
r v2 r dv r a = n+ t ρ dt
2011学年秋季学期
ρ:曲率半径。
大学物理(1)
15
2. 掌握质点圆周运动的角量描述。 角位移: Δθ Δ θ dθ 角速度: ω = lim = Δt → 0 Δ t dt Δω dω d 2θ = = 2 α 角加速度: = lim
r r r r = r ′ + r0 r r r rPS = rP S ′ + rS ′S r r r v PS = v P S ′ + v S ′S r r r a PS = a P S ′ + a S ′S
2011学年秋季学期
参考系S′
r r r P ( r ′, v ′, a ′, t )
选择参考系,确定变换关系
解:
建立如图所示坐标系, 由题意可知
r v船水
r v风地
大学物理(1)
30o
r v水地
x 东
24
O
2011学年秋季学期
r v 船水
北 y
30 o
r v 风地
r v 水地
x 东
O
r r r r 根据相对速度公式,v PS = v P S ′ + v S ′S ′′ + v S ′′S r r r r r v烟船 = v风船 = v风地 + v地水 + v水船 r r r ( ) = v风地 − v船水 + v水地 r r r r o o = (−10)i − (−20 sin 30 i + 20 cos 30 j ) − 10i r r −1 = −10i − 17.3 j (km ⋅ h )
第1章绪论习题解析(答)
《数据结构》第一章绪论部分习题一、选择题1. 下面说法错误的是。
(1)算法原地工作的含义是指不需要任何额外的辅助空间。
(2)在相同的规模n下,复杂度O(n)的撒在时间上总是优于复杂度O(2n)的算法。
(3)所谓时间复杂度是指最坏情况下,估算算法执行时间的一个上界。
(4)同一个算法,实现语言的级别越高,执行效率越低。
A、(1)B、(1)(2)C、(1)(4)D、(3)2. 一个递归算法必须包括。
A、递归部分B、终止条件和递归部分C、迭代部分D、终止条件和迭代部分3. 数据的包括查找、插入、删除、更新、排序等操作类型。
A、存储结构B、逻辑结构C、基本运算D、算法描述4. 在数据结构中,从逻辑上可以把数据结构分成。
A、动态结构和静态结构B、紧凑结构和非紧凑结构C、线性结构和非线性结构D、内部结构和外部结构5. 与数据元素本身的形式、内容、相对位置、个数无关的是数据的。
A、存储结构B、存储实现C、逻辑结构D、运算实现6. 通常要求同一逻辑结构中的所有数据元素具有相同的特性,这意味着。
A、数据具有同一特点B、不仅数据元素所包含的数据项的个数要相同,而且对应数据项的类型要一致C、每个数据元素都一样D、数据元素所包含的数据项的个数要相等7. 以下说法正确的是。
A、数据元素是数据的最小单位B、数据项是数据的基本单位C、数据结构是带有结构的各数据项的集合D、一些表面上很不相同的数据可以有相同的逻辑结构8. 以下说法错误的是。
A、程序设计的实质是数据处理B、数据的逻辑结构是数据的组织形式,基本运算规定了数据的基本操作方式C、运算实现是完成运算功能的算法或这些算法的设计D、数据处理方式总是与数据的某种相应表示形式相联系,反之亦然9. 下列程序段的时间复杂度为。
x=n;y=0;while (x>=(y+1)*(y+1))y=y+1;A、O(n)B、O(n1/2 )C、O(1)D、O(n2)10. 下列叙述中有关好的编程风格的正确描述是。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
15. 将有 3 名优秀生的 15 名课外活动小组成员随机地 人小组, 分成三个科目不同的 5 人小组,每个小组有 1 名优秀生的 概率是多少? 概率是多少 ? 3 名优秀生同时分到一个小组的概率是多 少?
15! 种分法. 总的可能情况为 C C C = 种分法 5!5!5!
12.
10 把钥匙中有 3 把能打开门,现任取 2 把,求能 把能打开门,
2 0 1 1 C 3 C 7 + C 3 C 7 3 + 21 8 P= = = ≈ 0.533 2 C10 45 15
打开门的概率. 打开门的概率
解
13. 5 双不同的手套, 双不同的手套, 任取 4 只, 4 只都不配对的概 求 率.
解 只都不配对},则事件 设 A={4 只都不配对 则事件 A 发生就是从 5 双手
再从每双中取一只, 套中取 4 双 ,再从每双中取一只,而这种取法每双都有 2 种可能性, 种可能性,因此
4 1 C 5 (C 2 ) 4 8 P ( A) = = 4 C10 21
14. 任意将 10 本书放在书架上,其中有两套书,一套 本书放在书架上,其中有两套书, 含三卷,另一套含四卷,求下列事件的概率. 含三卷,另一套含四卷,求下列事件的概率
分别表示一等品、二等品、 解 设 Ai ( i = 1,2,3) 分别表示一等品、二等品、次品三事 为非次品事件, 件, A 为非次品事件,则所求概率为
P ( A1 | A) = P ( A1 A) P ( A1 ) = P ( A) P ( A1 ) + P ( A2 ) 0.85 85 17 = = = 0.85 + 0.10 95 19
第一章 习题解析 7.证明下列关于事件的等式 证明下列关于事件 证明下列关于事件的等式.
(1) A U B = A U ( BA ) ) 证
A U B = ( A U B ) S = ( A U B )( A U A )
(2) 证
= A U AA U AB U BA = A U AB U BA = A U BA ( A − B ) U ( B − A) = ( AB ) U ( A )( B )
18.
50 只电子管随机地取来,用在 10 个电路板上,其 只电子管随机地取来, 个电路板上,
只电子管是次品, 只电子管, 中有 3 只电子管是次品,每个电路板用 3 只电子管,若将 3 只 次品都安装在一个电路板上,则这个电路板就是废品, 次品都安装在一个电路板上,则这个电路板就是废品,问发生 电路板是废品的概率是多少? 电路板是废品的概率是多少?
16. 甲盒中有红、黑、白皮笔记本各 3 本,乙盒中有 甲盒中有红、 今从两盒中各取一本, 黄、黑、白皮笔记本各 2 本,今从两盒中各取一本,求所 本是相同颜色的概率. 取 2 本是相同颜色的概率
由于取到相同颜色的情形只能是黑、 白两种, 解 由于取到相同颜色的情形只能是黑、白两种, 因此 所求概率
(1)三卷一套放在一起; )三卷一套放在一起; (2)四卷一套放在一起; )四卷一套放在一起; 3)两套各自放在一起. (3)两套各自放在一起.
解
10 本书的摆放顺序共有 10!种,这是样本空间 本书的摆放顺序 顺序共有 ! 这是样本空间 样本空间.
)三卷一套放在一起, (1)三卷一套放在一起,应首先将这套书看作一本与 本一起, 其余 7 本一起,则应有 8!种方法,另外一套三本书又有 3! !种方法, ! 种方法, 种方法, 因此
求酒杯落下三次而未被打碎的概率. 求酒杯落下三次而未被打碎的概率
解 设 A 为 “未被打碎事件” Ai 为 “第 i 次未被打碎 未被打碎事件” ; 事件” , 事件” i = 1,2,3 , 则 A = A1 A2 A3 , 于是
P ( A) = P ( A1 A2 A3 ) = P ( A1 ) P ( A2 | A1 ) P ( A3 | A1 A2 ) 1 7 9 3 = (1 − )(1 − )(1 − ) = 2 10 10 200
( AB )( A B ) = ( A U B )( A B )
= AB U BAB = AB = B− A
8.设 A, B 为 两个 事件 , 且 P ( A) = 0.5, P ( B ) = 0.6 , 问 两个事件 事件, 设
条件下 取到最大值 求出最大值 最大值? 最大值; (1)在什么条件下,P ( AB ) 取到最大值?求出最大值; ) 什么条件 条件下 取到最小 最小值 求出最小 最小值 (2)在什么条件下, P ( AB ) 取到最小值?求出最小值. ) 什么条件 情形. 解 由 P ( A) = 0.5, P ( B ) = 0.6 ,知必不会有 AB = φ 情形
21. 盒中有 5 个水果,其中有 3 个梨,2 个桃,从中任 个水果, 个梨, 个桃, 取两次,每次取一个不放回, 表示“第一次取到梨” 取两次,每次取一个不放回,设 A 表示“第一次取到梨” ,
B 表示 “第二次取到的还是梨” 求条件概率 P ( B | A) . 表示“第二次取到的还是梨” ,
( AB ) U ( A B ) = ( AB ) A B
= ( A U B )( A U B ) = A A U AB U B A U B B = AB U BA = ( B − A) U ( A − B ) = ( A − B ) U ( B − A)
(3) 证
B − A = ( AB )( A B )
1 9. 设 A, B , C ,为三个事件,且 P ( A) = P ( B ) = P (C ) = , 三个事件, 4 1 至少有 P ( AB ) = P ( BC ) = 0 ,P ( AC ) = ,求 A, B , C 至少有一个发生的 8
概率. 概率 解
P( A U B U C )解 Nhomakorabea根据实际意义计算
P ( B | A) = 2 1 = 4 2
22. 某玻璃器皿厂生产制造酒杯,第一次酒杯落下打碎 某玻璃器皿厂生产制造酒杯,
1 的概率是 ;若第一次未打碎而第二次落下打碎的概率是 2 7 9 若前两次均未被打碎, ;若前两次均未被打碎,第三次落下打碎的概率为 .试 试 10 10
解:所求概率为
3 47 27! 3 27 3!3!3!3!3!3!3!3!3! 1 p = = 1960 30! 50 30 3!3!3!3!3!3!3!3!3!3!
19 甲、 乙两艘轮船驶向一个不能同时停泊两艘轮船的 乙两艘轮船驶向一个不能同时停泊两艘轮船的 码头停泊, 它们在一昼夜内到达的时刻是等可能的, 码头停泊, 它们在一昼夜内到达的时刻是等可能的, 如果甲 船的停泊时间是一小时, 乙船停泊的时间是两小时, 求它们 船的停泊时间是一小时, 乙船停泊的时间是两小时, 中任何一艘船都不需要等候码头空出的概率. 中任何一艘船都不需要等候码头空出的概率 设甲、 解 设甲、乙两船到达码头的时刻分别为 x, y ,由题
为最大值. (1)当 B ⊃ A 时, P ( AB ) = P ( A) = 0.5 为最大值 )
(2)当 A U B = S 时, )
P ( S ) = P ( A U B ) = P ( A) + P ( B ) − P ( AB ) ⇒ 1 = 0.5 + 0.6 − P ( AB )
为最小值. 有 P ( AB ) = 1.1 − 1 = 0.1,为最小值
1 1 2C 3 C 2 12 2 P= 1 1 = = C9C6 54 9
17. 袋中有 12 个球,其中 2 个球有号码 1;4 个球有 个球, ; 个球, 号码 5;6 个球有号码 10,今从袋中取 6 个球,求这 6 个球 ; , 的概率. 的号码之和至少为 50 的概率
6 种方法, 解 从 12 个球中取 6 个,共有C12 种方法,其中 6 个球
P ( AB ) .
解 所以
P ( A − B ) = P ( A) − P ( AB ) ⇒ P ( AB ) = 0.7 − 0.3 = 0.4
P ( AB ) = 1 − P ( AB ) = 0.6
11. 电话号码由 8 位数字组成,每个数字可以是 0,1, 位数字组成, ,
L , 9 中的任一数字 求电话号码是由完全不同的数字组成的 中的任一数字.求电话号码是由完全不同的数字组成的
8!3! 1 P1 = = 10! 15
2) ( 2)同理
7!4! 1 P2 = = 10! 30
各自放在一起也 如此考虑 考虑, 先将二套 二套书 (3)两套各自放在一起也是如此考虑,即先将二套书 )两套各自放在一起 看成二本与 一起应有 ! 方法, 看成二本与其余 3 本一起应有 5!种方法,因此有 二本
1 1 1 23. 已知 P ( A) = , P ( B | A) = , P ( A | B ) = ,试求 3 3 4
P ( AB ), P ( AB ), P ( A | B ) .
1 1 1 解 P ( AB ) = P ( A) P ( B | A) = ⋅ = 3 4 12 1 11 P ( AB ) = 1 − P ( AB ) = 1 − = 12 12 1 P ( AB ) 12 1 P( B) = = = 1 4 P( A | B) 3 P( A B ) 1 − P( A U B) 则 P( A | B ) = = P( B ) 1 − P( B)
设所求事件为 A , 则导致 A 发生的集合应由图形中阴 影部分组成, 影部分组成, 由几何概率知
1 1 2 ( 24 − 1) + ( 24 − 2) 2 1013 2 P ( A) = 2 = 2 ( 24) 1152
20. 在 100 件同类型产品中有 85 件一等品,10 件二 同类型 一等品, 等品和 次品, 任取一件 非次品的条件下 一件为 等品和 5 件次品,求在从中任取一件为非次品的条件下, 等品的概率 的概率. 为一等品的概率
