4根轨迹绘制的基本规则
合集下载
自动控制原理4根轨迹
4.1 控制系统的根轨迹
根轨迹定义
[根轨迹]：控制系统的某一参数由零变化到无穷大时， 闭环系统的特征根（闭环极点）在[s]平面上形成的轨 迹。
[例]：如图所示二阶系统， R(s)
+
E ( s)
开环传递函数： K k G( s) , k 2 K s0.5s 1 ss 2 开环极点： p1 0， p2 2
nm
k
（ 3）
与横轴的交角： 2l 1 s a l 0,1,2,, n m 1 （4） nm 即，根轨迹渐近线是n-m条直线，它们有一个公共点 a，j0 ，与横轴有不同的交角。
渐近线与实轴的交点为 a 利用多项式除法和乘法，由（1）、（2）、（3）式， n m 得： pi z j i 1 j 1 （ 5） a nm 若开环传递函数无零点，取 z j 0 规则四 如果控制系统的开环零点数目m小于开环极点 数目n，当k→∞时，伸向无穷远处根轨迹的渐近线共 有（n-m）条。这些渐近线在实轴上交于坐标为 a，j 0 的一点，而渐近线与实轴正向的夹角为（4）式。
渐近线与实轴的交点：
a
pi z j
i 1
3
nm
1 5 2 30
5
2 1
0
渐近线与实轴倾角：
5 l 0， ； l 1， ； l 2， 3 3 3
零极点分布和渐近线 （红线）如图所示。
5
j
180
”
z1
p3
再看s2点： 不满足根轨迹相角条件， 所以不是根轨迹上的点。
s s
p2
2
1
p1
四章线系统的根轨迹法
pi
)
K
*
m
(s
z
j
)
0
i 1
j 1
n
(s pi ) 0
i 1
s pi
又从
1 K*
n
(s
i 1
m
pi ) (s
j 1
z
j)
0
K*
m
(s z j ) 0
j 1
s zj
在实际系统通常是 n m ，则还有 (n m) 条根轨迹终 止于s平面的无穷远处，这意味着在无穷远处有 (n m)
j 1
3 2.3 1 0
n
(s
pi
)
K
*
m
(s
z
j
)
n
(s
pl
)
i 1
j 1
l 1
sn
n
(
pi
)s n1
(1) n
n
pi
K
*[s m
(
z
j
)s m1
(1) m
n
z
j
]
i 1
i 1
l 1
sn
(
pl
)s
n1
(1) n
n
pl
l 1
nm 2
n
n
pi pl
i 1
l 1
(1)
n
n
pi
K * (1) m
s(s 4)(s 2 2s 2)
（1） p1 0, p2 4 , p3 1 j
p4 1 j, z1 1
（2）有4条根轨迹的分支，对称于实轴
（3）有n-m=4-1=3条根轨迹渐近线
与实轴夹角
第2讲 绘制根轨迹的基本规则
证明：（2）对称性
因为特征方程的根或为实数，或为共轭复数，所以根轨迹对 称于实轴。
规则2：根轨迹的分支数及其起点和终点
闭环特征方程：
n
m
s pl K0 s zi 0 (1 GH 0)
l 1
i 1
当K0 由0 变化时，方程中任一根由始点连续地向终点变化
的轨迹称为根轨迹的一条分支；
例1 绘制下图所示系统的根轨迹
解： 1） 有三条根轨迹分支,它们的始点为开环极点(0,-1,-2） 2） 三条根轨迹分支的终点均在无限远
3） 渐近线与正实轴的夹角
2k 1 , , 5 ,
3
33
j j1.414 [s]
k 0,1,2
渐近线与正实轴的交点为
- A
1 3
2
1
4）实轴上的-1 至0和-2至-∞间 的线段为根轨迹
3） 渐近线与正实轴的夹角
2k 1 , , 5 ,
3
33
Im j1.414 [s]
k 0,1,2
渐近线与正实轴的交点为
- A
1 3
2
1
4）实轴上的-1 至0和-2至-∞间 的线段为根轨迹
180
60
2
1 60
0
Re
控制系统方框图
j1.414
❖ n=[1]; ! 分子 1 各项系数 ❖ d1=[1 0]; ! 分母第一项 (s+0) 各项系数 ❖ d2=[1 3 2]; ! 分母第二项( s^2+3s+2) 各项系数 ❖ d=conv(d1,d2); ! 分母二项相乘 ❖ rlocus(n,d); ! 绘制根轨迹 ❖ sgrid; !绘制出阻尼系数和自然频率栅格
例3 已知一单位反馈控制系统的开环传递函数为
自动控制原理 第四章 根轨迹法
第4章 根 轨 迹 法根轨迹法是分析和设计线性控制系统的图解方法，使用简便，在控制工程上得到了广泛应用。
本章首先介绍根轨迹的基本概念，然后重点介绍根轨迹绘制的基本法则，在此基础上，进一步讨论广义根轨迹的问题，最后介绍控制系统的根轨迹分析方法。
4.1 根轨迹的基本概念4.1.1 根轨迹概念所谓根轨迹，就是系统开环传递函数的某一参数从零变化到无穷时，闭环特征根在s 平面上变化的轨迹。
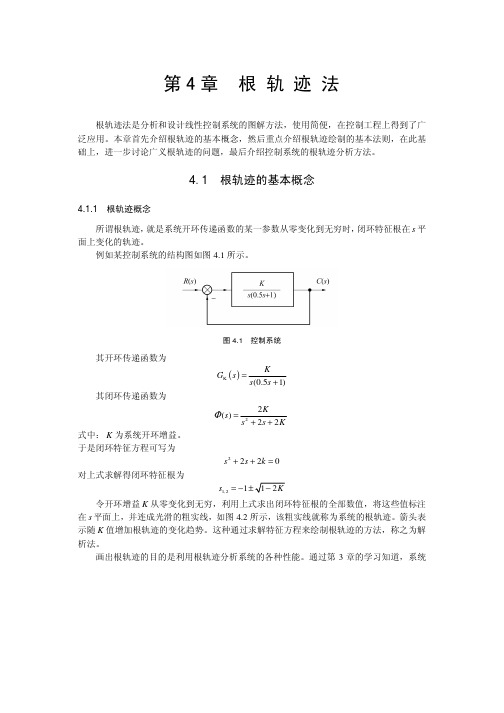
例如某控制系统的结构图如图4.1所示。
图4.1 控制系统其开环传递函数为()K (0.51)KG s s s =+其闭环传递函数为22()22Ks s s KΦ=++式中：K 为系统开环增益。
于是闭环特征方程可写为2220s s k ++=对上式求解得闭环特征根为1,21s =−令开环增益K 从零变化到无穷，利用上式求出闭环特征根的全部数值，将这些值标注在s 平面上，并连成光滑的粗实线，如图4.2所示，该粗实线就称为系统的根轨迹。
箭头表示随K 值增加根轨迹的变化趋势。
这种通过求解特征方程来绘制根轨迹的方法，称之为解析法。
画出根轨迹的目的是利用根轨迹分析系统的各种性能。
通过第3章的学习知道，系统第4章 根轨迹法·101··101·特征根的分布与系统的稳定性、暂态性能密切相关，而根轨迹正是直观反应了特征根在复平面的位置以及变化情况，所以利用根轨迹很容易了解系统的稳定性和暂态性能。
又因为根轨迹上的任何一点都有与之对应的开环增益值，而开环增益与稳态误差成反比，因而通过根轨迹也可以确定出系统的稳态精度。
可以看出，根轨迹与系统性能之间有着比较密切的联系。
图4.2 控制系统根轨迹4.1.2 根轨迹方程对于高阶系统，求解特征方程是很困难的，因此采用解析法绘制根轨迹只适用于较简单的低阶系统。
而高阶系统根轨迹的绘制是根据已知的开环零、极点位置，采用图解的方法来实现的。
下面给出图解法绘制根轨迹的根轨迹方程。
绘制根轨迹图的规则
K *的表达式为
K*
j 1 m
(s zi )
iห้องสมุดไป่ตู้1
则在分离点处有
dK* 0 ds
分离点坐标d是以下方程的解。
m 1
n1
i1 d zi j1 d p j
在一般情况下，绘制多回路系统的根轨迹时，首先根据内反馈回路的开环传递 函数，绘制内反馈回路的根轨迹，并确定内反馈回路的极点分布；然后由内反馈回 路的零、极点和内反馈回路外的零、极点构成整个多回路系统的开环零、极点；再 按照单回路根轨迹的基本规则，绘制出系统总的根轨迹。但这样绘制出来的根轨迹 只能确定多回路系统极点的分布，而多回路系统的零点还需要根据系统的闭环传递 函数来确定。
(z j
zi )
l 1
( zi
pl
)
，为开环零点（除
zi 外）和开环极
(i j)
点往零点 引zi 出向量的相角净值。
规则9 根轨迹的分离点。两条或两条以上的根轨迹分支，在s平 面上某处相遇后又分开的点，称为根轨迹的分离点（或会合点）。 可见，分离点就是特征方程出现重根之处。重根的重数就是会合到 （或离开）该分离点的根轨迹分支的数目。
坐标及相应的 K值* 可由劳斯判据求得，也可在特征方程中令 s j，然
后使特征方程的实部和虚部分别等于零而求得。根轨迹与虚轴相交，表明系 统在相应 K值* 下处于临界稳定状态。此处的根轨迹增益 K*称为临界根轨 迹增益。
【例 3-2】
设系统的开环传递函数为
Gk
(s)
s(s
K* 1)(s
2)
，求根轨迹与
时的根轨迹方程则有
m
K* (s zi )
i 1
≈
K*
n
绘制根轨迹的一般规则
1
p
第三节
绘制根轨迹的一般规则
七.（规则7）根轨迹的起始角和终止角
当开环传递函数中有复数极点或零点时，根轨迹是 沿着什么方向离开开环复数极点或进入开环复数零 点的呢？这就是所谓的起始角和终止角问题 , 先给 出定义如下： ⑴起始角 根轨迹离开开环复数极点处在 切线方向与实轴正方向的夹角。参看图4-8（a）中 的 和 。θp θ p2 1 ⑵终止角 根轨迹进入开环复数零点处的 切线方向与实轴正方向的夹角。参看图4-8（b）中 的 θ z1 和 θ z 2 。
第三节
绘制根轨迹的一般规则
纯粹用试验点的办法手工作图，工作量
是十分巨大的，而且对全貌的把握也很困难，
于是人们研究根轨迹图的基本规则，以便使
根轨迹绘图更快更准。概括起来， 以开环
增益K为参变量的根轨迹图主要有下列基本
规则：
第三节
绘制根轨迹的一般规则
如果以系统的其他参量为参变量时，经 过适当变换，以下规则仍能适用。 一.（规则1）根轨迹分支数 根轨迹在s平面的分支数等于闭环特征 方程的阶数n，也就是总分支数等于开环传 递函数的极点数。
1
第三节
绘制根轨迹的一般规则
d 1 D s d D s d 1 0 2 ds G s H s ds k N s ds N s Ds 的阶次高于N s ，因此用2 式计算简单。
第三节
绘制根轨迹的一般规则
三（规则3）根轨迹的起点和终点 根轨迹起始于开环极点，终止于开环零点。 如果n≠m ，则有（n-m）条根轨迹终止于无 穷远处。
第三节
m
绘制根轨迹的一般规则
s z 1 证明： k s p
p
第三节
绘制根轨迹的一般规则
七.（规则7）根轨迹的起始角和终止角
当开环传递函数中有复数极点或零点时，根轨迹是 沿着什么方向离开开环复数极点或进入开环复数零 点的呢？这就是所谓的起始角和终止角问题 , 先给 出定义如下： ⑴起始角 根轨迹离开开环复数极点处在 切线方向与实轴正方向的夹角。参看图4-8（a）中 的 和 。θp θ p2 1 ⑵终止角 根轨迹进入开环复数零点处的 切线方向与实轴正方向的夹角。参看图4-8（b）中 的 θ z1 和 θ z 2 。
第三节
绘制根轨迹的一般规则
纯粹用试验点的办法手工作图，工作量
是十分巨大的，而且对全貌的把握也很困难，
于是人们研究根轨迹图的基本规则，以便使
根轨迹绘图更快更准。概括起来， 以开环
增益K为参变量的根轨迹图主要有下列基本
规则：
第三节
绘制根轨迹的一般规则
如果以系统的其他参量为参变量时，经 过适当变换，以下规则仍能适用。 一.（规则1）根轨迹分支数 根轨迹在s平面的分支数等于闭环特征 方程的阶数n，也就是总分支数等于开环传 递函数的极点数。
1
第三节
绘制根轨迹的一般规则
d 1 D s d D s d 1 0 2 ds G s H s ds k N s ds N s Ds 的阶次高于N s ，因此用2 式计算简单。
第三节
绘制根轨迹的一般规则
三（规则3）根轨迹的起点和终点 根轨迹起始于开环极点，终止于开环零点。 如果n≠m ，则有（n-m）条根轨迹终止于无 穷远处。
第三节
m
绘制根轨迹的一般规则
s z 1 证明： k s p
第4章 根轨迹法
，即系统的开环极点。
时，由根轨迹方程知根轨迹的终点为
，即系统的开环零点。
但是，当
时，
条根轨迹趋向于开环零点（称为有限零点），还有
条根轨迹将趋于无穷远处（称为无限零点）。
如果出现
的情况，必有
条根轨迹的起点在无穷远处。
规则2 根轨迹的分支数、对称性和连续性根轨迹的分支 数等于 ， 根轨迹对称于实轴并且连续变化。
由根轨迹的对称性和连续性，根轨迹只需作出上半部分，对称画出另一部分，且根轨迹连续变化。
规则3 根轨迹的渐近线 当开环极点数大于开环零点数时，有n-m条根轨迹 趋于无穷远处，无穷远处的渐近线与实轴的交点为 ， 渐近线与实轴正方向的夹角(倾角)为
例4-1单位负反馈系统的开环传递函数为
规则10 根之积 根据特征方程根和系数的关系，得
第1章 引 论
例：系统的开环传递函数为
开环极点为
渐近线于实轴的交点为
渐近线的倾角为
与虚轴的交点为
第1章 引 论
根轨迹的分会点：
第1章 引 论
第1章 引 论
第1章 引 论
例：系统的开环传递函数为
开环极点为
渐近线于实轴的交点为
4.6 MATLAB绘制系统的根轨迹 对于比较复杂的系统，人工绘制根轨迹十分复杂和困难，MATLAB绘制系统根轨迹是十分方便的。 通常将系统的开环传递函数写成如下形式
分别为分子和分母多项式。
采用MATLAB命令： pzmap(num,den)可以绘制系统的零、极点图； rlocus(num,den)可以绘制系统的根轨迹图； rlocfind(num,den)可以确定系统根轨迹上某些点的增益。
渐近线的倾角为
与虚轴的交点为
时，由根轨迹方程知根轨迹的终点为
，即系统的开环零点。
但是，当
时，
条根轨迹趋向于开环零点（称为有限零点），还有
条根轨迹将趋于无穷远处（称为无限零点）。
如果出现
的情况，必有
条根轨迹的起点在无穷远处。
规则2 根轨迹的分支数、对称性和连续性根轨迹的分支 数等于 ， 根轨迹对称于实轴并且连续变化。
由根轨迹的对称性和连续性，根轨迹只需作出上半部分，对称画出另一部分，且根轨迹连续变化。
规则3 根轨迹的渐近线 当开环极点数大于开环零点数时，有n-m条根轨迹 趋于无穷远处，无穷远处的渐近线与实轴的交点为 ， 渐近线与实轴正方向的夹角(倾角)为
例4-1单位负反馈系统的开环传递函数为
规则10 根之积 根据特征方程根和系数的关系，得
第1章 引 论
例：系统的开环传递函数为
开环极点为
渐近线于实轴的交点为
渐近线的倾角为
与虚轴的交点为
第1章 引 论
根轨迹的分会点：
第1章 引 论
第1章 引 论
第1章 引 论
例：系统的开环传递函数为
开环极点为
渐近线于实轴的交点为
4.6 MATLAB绘制系统的根轨迹 对于比较复杂的系统，人工绘制根轨迹十分复杂和困难，MATLAB绘制系统根轨迹是十分方便的。 通常将系统的开环传递函数写成如下形式
分别为分子和分母多项式。
采用MATLAB命令： pzmap(num,den)可以绘制系统的零、极点图； rlocus(num,den)可以绘制系统的根轨迹图； rlocfind(num,den)可以确定系统根轨迹上某些点的增益。
渐近线的倾角为
与虚轴的交点为
自动控制原理4 根轨迹法的基本概念
K*
K* 8.16
1.1
pi 71.6
例子4-5 P150
解:1) m=1,n=3,
z1=-20,p1=0,p2=p3=-12, 2）实轴上0--12 ,-12--20 必为根轨迹。 3）渐近线。n-m=2 故有2条渐近线.
G(s) K * (s 20) s(s2 24s 144)
m
n
pi ( pl zi ) ( pl pi )
izl zi )
j 1
jl
p2 1800 56.50 190 590 (108.50 900 370 )
790
z2 1800 1530 1990 1210 63.50 1170 900
（2）闭环极点与开环零点、开环极点以及根轨迹增益均有关。 （需专门研究）
j1
（3）
m
K*
(s z j )
m
(zj)
K limsνG(s) H(s) limsν
（4）根轨迹法 s0
s0
sν
j1 nν
(s
pi )
K*
j1 nν
( pi )
根轨迹图
闭环极点
闭环传递函数
性i 1能指标
i 1
3.根轨迹方程
4-2 根轨迹绘制的基本法则
法则1 根轨迹的起点和终点。 法则2 根轨迹的分支数、对称性和连续性。 法则3 根轨迹的渐近线 法则4 实轴上的根轨迹 法则5 根轨迹的分离点和分离角 法则6 根轨迹的起始角与终止角 法则7 根轨迹与虚轴的交点 法则8 根之和
法则一、根轨迹的对称性、分支数和分布性
1．根轨迹连续且对称于实轴。 2. 根轨迹的分支数与开环有限零点数m与有 限个极点数n中的最大者相等。
绘制根轨迹的基本法则
4.2 绘制根轨迹的基本法则本节讨论根轨迹增益*K （或开环增益K ）变化时绘制根轨迹的法则。
熟练地掌握这些法则，可以帮助我们方便快速地绘制系统的根轨迹，这对于分析和设计系统是非常有益的。
法则1 根轨迹的起点和终点：根轨迹起始于开环极点，终止于开环零点；如果开环零点个数m 少于开环极点个数n ，则有)(m n -条根轨迹终止于无穷远处。
根轨迹的起点、终点分别是指根轨迹增益0=*K 和∞→时的根轨迹点。
将幅值条件式（4-9）改写为∏∏∏∏==-==--=--=mi inj j mn m i i nj jsz sp sz s ps K 1111*|1||1||)(||)(|(4-11)可见当s=j p 时，0*=K ；当s=i z 时，∞→*K ；当|s|∞→且m n ≥时，∞→*K 。
法则2 根轨迹的分支数，对称性和连续性：根轨迹的分支数与开环零点数m 、开环极点数n 中的大者相等，根轨迹连续并且对称于实轴。
根轨迹是开环系统某一参数从零变到无穷时，闭环极点在s 平面上的变化轨迹。
因此，根轨迹的分支数必与闭环特征方程根的数目一致，即根轨迹分支数等于系统的阶数。
实际系统都存在惯性，反映在传递函数上必有m n ≥。
所以一般讲，根轨迹分支数就等于开环极点数。
实际系统的特征方程都是实系数方程，依代数定理特征根必为实数或共轭复数。
因此根轨迹必然对称于实轴。
由对称性，只须画出s 平面上半部和实轴上的根轨迹，下半部的根轨迹即可对称画出。
特征方程中的某些系数是根轨迹增益*K 的函数，*K 从零连续变到无穷时，特征方程的系数是连续变化的，因而特征根的变化也必然是连续的，故根轨迹具有连续性。
法则3 实轴上的根轨迹：实轴上的某一区域，若其右边开环实数零、极点个数之和为奇数，则该区域必是根轨迹。
设系统开环零、极点分布如图4-5 所示。
图中，0s 是实轴上的点，)3,2,1(=i i ϕ是各开环零点到0s 点向量的相角，)4,3,2,1(=j j θ是各开环极点到0s 点向量的相角。
自动控制原理第四章 根 轨 迹 法
K=2.5
-2
＞0.5时，特征根为共轭复根，欠阻尼系 统，响应为衰减振荡；可根据性能要求
K
设置闭环极点。
当特征方程>2阶时无法求解，如何绘制根轨迹图？
4-2. 绘制根轨迹的基本依据和条件
特征方程为： 1+G(s)H(s)=0
即： G(s)H(s)= -1
R(s)
Y(s)
G(s)
-
H(s)
G( s )H( s ) 1
4-1. 根轨迹基本概念
根轨迹的定义：
开环传递函数的某一参数从0变到∞时，闭环系 统特征方程式的根在s平面上的变化轨迹。
R(s)
-
E(s) G1(s)
D1(s) G 2(s)
H(s)
Y(s) D2(s)
如
G1( s )G2 ( s )H ( s )
Kg s( s 1 )( s 2 )
常规根轨迹
求解：设 Gk ( s ) KgG1( s )，则对于1 KgG1( s ) 0，有
dK g ds
d [G11( s )] ds
0 （Kg在根轨迹的分离点上取极值）
或 dG1( s ) 0 （特征式满足 d( s ) 0）
ds
ds
注：只须用其中之一，且只是必要条件
续前例：求分离点上的坐标。
幅值条件
G( s )H( s ) 180( 2k 1 ), k 0，1，2，
相角条件
零极点表达形式下的幅值条件和相角条件：
m
n
K g (s zi )
(s pi )
G(s)H(s)
i1 n
1 ,或
Kg
i1 m
,
(s pi )
(s zi )
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2 1 0
60
11/24/2020
13
实轴上的根轨迹
6、实轴上的根轨迹：
实轴上具有根轨迹的区间是：其右方开
环系统的零点数和极点数的总和为奇数。
[证明]：例如在实轴上有两个开环极点p1、 p2，复平面上有一对共轭极点p3、 p4和一对 共轭零点z1、 z2 。
先看试验点s1点：
①成对出现的共轭极点p3、 p4对实轴上任意 试探点构成的两个向量的相角之和为0°；
t
g(2k1)
nm
nm
11/24/2020
8
根轨迹的渐近线
y t( g 2 k 1 ) x a n 1 b m 1 t( g 2 k 1 )x n m n m n m
n
m
n
m
a n 1 b m 1j 1pji 1zi j 1pji 1zi
nm
的交点和倾角。
[解]：根轨迹有3支。起点为开环极点 p 1 0 , p 2 1 , p 3 5 , 无有限值零点，所以三支根轨迹都趋向无穷远。
渐近线与实轴的交点： pizi 152
nm 30
渐近线与实轴的倾角： q(2k1)60 ,180
nm
零极点分布和渐近线（红线） 如图所示。
5
180
60
nm
nm
这是与实轴交点为－，斜率为 tg (2k 1) 的直线方程。也就
nm
是渐近线方程。渐近线与实轴的夹角(称为渐近线的倾斜角为
q (2 k 1 ) k0 , 1 , 2
nm
180 0
nm1
90
90 0
nm2
11/24/2020
180 60
0
60
nm3
180
45
45 0
nm4
9
[例4-2]系统开环传递函数为：Gk(s)s(sK 1)g(s5) ，试确定根 轨迹支数，起点和终点。若终点在无穷远处，求渐近线与实轴
轨迹的性质。
1、根轨迹的连续性：
闭环系统特征方程的某些系数是增益Kg的函数。当Kg从0到
无穷变化时，这些系数是连续变化的。故特征方程的根是连续 变化的，即根轨迹曲线是连续曲线。
2、根轨迹的对称性：
一般物理系统特征方程的系数是实数，其根必为实根或共轭 复根。即特征根位于复平面的实轴上或对称于实轴。
11/24/2020
4根轨迹绘制的基本规则
第二节 根轨迹绘制的基本规则
11/24/2020
2
根轨迹的连续性和对称性
一、根轨迹绘图的基本规则
用解析法或试探法绘制根轨迹很烦琐。下面讨论的内容通 过研究根轨迹和开环零极点的关系，根轨迹的特殊点，渐近线 和其他性质将有助于减少绘图工作量，能够较迅速地画出根轨
迹的大致形状和变化趋势。以下的讨论是针对参数Kg的180度根
3
根轨迹的支数和起始点
3、根轨迹的支数：
n阶特征方程有n个根。当Kg 从0到无穷大变化时， n个根在复平
面内连续变化组成n支根轨迹终点：
根轨迹起始于开环极点，终止于开环零点。
Kg= 0时为起点， Kg= ∞时为终点。
由根轨迹方程
m
n
K g ( s zi )
11/24/2020
5
根轨迹的渐近线
5.根轨迹的渐近线：
若开环零点数m小于开环极点数n，则当系统的开环增益 Kg→∞时趋向无穷远处的根轨迹共有n-m条。这n-m条根轨迹 趋向无穷远的方位可由渐近线决定。
由根轨迹方程可得： n
(s p j)
j 1 m
Kg
(s zi)
n
i 1
(spj)
j1
m
sn m (a n 1 b m 1 )sn m 1 K g
snm(1an1 sbm 1)Kg
两边开n-m次方
s(1an 1 sbm 1)n 1m(K g)n 1m
利用二项式定理
( 1 x ) K 1 K K ( K x 1 ) x 2 K ( K 1 ) ( K I 1 ) x I ( 1 x 1 )
(s p j)
i 1 n
1 得 j1 m
Kg
(s p j) j 1
(s zi)
i1
当Kg= 0时，只有s = －pj (j = 1~n) 时，上式才能成立。而－pj是 开环传递函数的极点，所以根轨迹起始于开环极点。n阶系统有
n个开环极点，分别是n支根轨迹的起点。
11/24/2020
4
根轨迹的起点和终点
m
m
由根轨迹方程
K g ( s zi )
i 1 n
1
(s p j)
得
(s
i 1
n
(s
zi ) p j)
1 Kg
j 1
j 1
当Kg= ∞时，① s = －zi (i = 1~m) ，上式成立。 －zi是开环传递函
数有限值的零点，有m个。故n阶系统有m支根轨迹的终点在m个
(szi)
ssm n a bm n11ssnm 11 ab11ssab00
Kg
i1
n
m
式中 an1 p j ，bm1 zi
j 1
i 1
11/24/2020
6
根轨迹的渐近线
s n m ( a n 1 b m 1 ) s n m 1 K g
当Kg→∞，由于m<n，故s→∞满足根轨迹方程，上式近似为
有限零点处。②若n>m，那么剩余的n-m个终点在无穷远处。
由根轨迹方程知：当s→∞时
m
根轨迹方 ls i 程 min1((s左 s p zij))边 ls i m ssm n ls i m sn1m0 j1
根轨迹方程 li右 m边 1 0 Kg Kg
我们称系统有n－m个无限远零点。有限值零点加无穷远零 点的个数等于极点数。
2 !
I !
当 x1时，(1x)K 1Kx，令 xan1bm1 ， K 1
s
nm
s(1n 1m an 1 sbm 1)(K g)n 1m
11/24/2020
7
根轨迹的渐近线
san n1 m bm1(Kg)n 1m
设s=x+jy, 利用－1=cos(2k+1)π+jsin(2k+1)π，并根据德莫弗(De Moive)代数定理(cosq +jsinq )n= cos(nq )+jsin(nq )，上式可写为
x j y a n n 1 m b m 1 K g n 1 m c( o 2 n k s m 1 ) js( i 2 n k n m 1 )
xan n 1 m bm 1K g n 1mco (2 n k s m 1 )
1
yKgnmsi
n(2k1)
nm
y xan1bm1