《医学物理学教学资料》第十五章 量子力学基础
第15章 量子物理基础 PPT课件

行
“但是在物理晴朗天空的远处,还有两朵小小令人不安的乌 云”,即运用当时的物理学理论所无法正确解释的两个实验
现象。
厚
其一是否定绝对时空观的迈克尔逊—莫雷实验;
德
其二是热辐射现象中的紫外灾难。 正是这两朵小小的乌云,冲破了经典物理学的束缚,打
弘 消了当时绝大多数物理学家的盲目乐观情绪,为后来建立近
毅
代物理学的理论基础作出了贡献。事实上还有第三朵小小的 乌云,这就是放射性现象的发现,它有力地表明了原子不是
并且应用越来越广泛。
由安培、法拉第和麦克斯韦等人对电磁现象进行的深入
厚 而系统的研究,为电动力学奠定了坚实的基础,特别是由麦
德
克斯韦的电磁场方程组预言了电磁波的存在,随即被赫兹的 实验所证实。后来又把牛顿、惠更斯和菲涅耳所建立的光学
弘 也纳入了电动力学的范畴,更是一项辉煌的成就。因此当时
毅
许多著名的物理学家都认为物理学的基本规律都已被发现, 今后的任务只是把物理学的基本规律应用到各种具体问题上,
笃 和透射的物体。
行
煤烟
厚
约99%
德
弘 黑体辐射的特点 :
毅 • 温度
黑体模型
黑体热辐射
材料性质
• 与同温度其它物体的热辐射相比,黑体热辐射本领最强
11
实验表明 辐射能力越强的物体,其吸收能力也越强.
博 学 黑体 能完全吸收照射到它上面的各种频率的电磁辐射的 笃物体称为黑体 .(黑体是理想模型) 行
学 1.热辐射现象
笃
一切物质中的原子、分子因
行
热激发而向外辐射电磁波的现象。 实验证明不同温度下物体能发出
不同的电磁波,这种能量按频率
厚
的分布随温度而不同的电磁辐射 叫做热辐射。
医学物理学(第7版)教学大纲

前言《医学物理学》是国家教育部规定的高等医学院校临床医学、预防医学等专业的一门必修基础课,是为这些专业的学生提供较系统的物理学知识,使他们在中学物理学教育基础上,进一步学习医学专业所必需的物理学的基本概念、基本规律、基本方法,为后继课程的学习以及将来从事专业工作打下一个良好的基础。
我校《医学物理学》教材选用人民卫生出版社出版普通高等教育“十一五”国家级规划教材《医学物理学》第7版(胡新珉主编)。
依据学校的教学计划,本课程共96学时,其中理论课68学时,实验课28学时。
因此制定本“教学大纲”。
因为教材是按72~108学时编写。
所以,“教学大纲”既参照卫生部1982年“高等医学院校《医用物理学》教学大纲(试用本)”和医药类大学物理课程教学的基本要求,也结合当前教育改革倡导素质教育,针对临床医学、预防医学、影像学、法医学、护理学、药学等专业的特点编写。
“大纲”内容分为掌握、熟悉、了解和自学。
自学内容课堂上教师原则上不讲授,属自学内容,结业考试中一般不作要求。
第一章力学的基本定律(自学)第二章物体的弹性一、学习要求本章要求熟悉描述物体弹性的基本概念,对人体骨骼和肌肉组织的力学特性要有一定的了解。
二、讲授内容和要求等级章节次序内容等级第一节线应变与正应力一线应变熟悉二正应力熟悉三正应力与线应变的关系熟悉四弯曲自学第二节切应变与切应力一切应变熟悉二切应力熟悉三切应力与切熟应变的关系悉四扭转自学第三节体应变与体应力一体应变熟悉二体应力熟悉三体应力与体应变的关系熟悉第四节生物材料的黏弹性自学三、授课学时:2学时。
四、练习:第27~28页,2-6、2-9。
第三章流体的运动一、学习要求本章要求掌握理想流体作稳定流动时的基本规律,即连续性方程和伯努利方程以及它们的应用;熟悉实际流体的流动规律和泊肃叶定律;了解斯托克司定律和血液在循环系统中的流动规律。
二、讲授内容和要求等级章节次序内容等级第一节理想流体的稳定流动一理想流体熟悉二稳定流动熟悉三连续性方程掌握第二节伯努利方程一伯努利方程掌握二伯努利方程的应用掌握第三节黏性流体的流动一层流和湍流熟悉二牛顿黏滞定律熟悉三雷诺数了解第四节黏性流体的运动规律一黏性流体的伯努利方程了解二泊肃叶定律熟悉三斯托克司定律了解第五节血液在循环系统中的流动一血液的组成及特性自学二心脏做功了解三血流速度分布自学四血流过程中的血压分布自学三、授课学时:4学时。
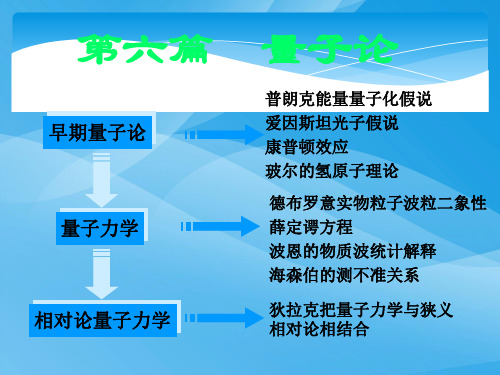
大学物理讲稿(第15章量子力学基础)

第15章 量子力学基础人们用经典物理解释黑体辐射、光电效应、氢原子光谱等实验规律时,遇到了不可克服的困难.经过不断的探索和研究,终于突破了经典物理的传统观念,建立起量子理论.量子理论和相对论是现代物理学的两大支柱.量子理论的诞生,对研究原子、电子、质子、光子等微观粒子的运动规律提供了正确的导向.从此使物理学发生了一次历史性的飞跃,促进了原子能、激光、超导、半导体等众多新技术的生产和发展.本章前部分,分别介绍黑体辐射、光电效应、氢原子光谱等实验规律以及为解释这些实验规律而提出的量子假设,即早期的量子论.本章的后部分简要介绍量子力学的基本概念及原理,并通过几个具体事例的讨论说明量子力学处理问题的一般方法.§15.1 黑体辐射与普朗克的量子假设一、黑体辐射的基本规律1 热辐射组成物体的分子中都包含着带电粒子,当分子作热运动时物体将会向外辐射电磁波,由于这种电磁波辐射与物体的温度有关,故称其为热辐射.实验表明,热辐射能谱是连续谱,发射的能量及其按波长的分布是随物体的温度而变化的.随着温度的升高,不仅辐射能在增大,而且辐射能的波长范围向短波区移动.物体在辐射电磁波的同时,也吸收投射到物体表面的电磁波.理论和实验表明,物体的辐射本领越大,其吸收本领也越大,反之亦然.当辐射和吸收达到平衡时,物体的温度不再变化而处于热平衡状态,这时的热辐射称为平衡热辐射.为描述物体热辐射能按波长的分布规律,引入单色辐射出射度(简称单色辐出度)这一物理量,其定义为:物体单位表面积在单位时间内发射的、波长在λ+λ→λd 范围内的辐射能dM λ与波长间隔d λ的比值,用M λ(T)表示,即λ=λλd dM T M )( (15.1) 而辐出度定义为⎰∞λλ=0d T M T M )()( (15.2) 2 黑体辐射的基本规律投射到物体表面的电磁波,可能被物体吸收,也可能被物体反射和透射.能够全部吸收各种波长的辐射能而完全不发生反射和透射的物体称为绝对黑体,简称黑体.绝对黑体是一种理想模型,实验室中用不透明材料制成带有小孔的空腔物体可近似看作黑体.图15.1为用实验方法测得的黑体单色辐出度M B λ (T)按波长和温度分布的曲线.关于黑体辐射,有两个基本定律:一个是斯特藩—玻耳兹曼定律(M B (T )=σT 4 ,即黑体的辐出度与其热力学温度的四次方成正比 ,其中σ=5.6705×10-8 W•m -2 • K -4 称为斯特藩—玻耳兹曼常数);另一个是维恩位移定律(λm T=b,即黑体单色辐出度的最大值对应的波长λm 与其绝对温度T 成反比,其中b=2.8978×10-3m •K 为与温度无关的常数).这两个定律在现代科学技术中有广泛的应用.通常用于测量高温物体(如冶炼炉、钢水、太阳或其他发光体等)温度的光测高温法就是在这两个定律的基础上建立起来的,同时,这两个定律也是遥感技术和红外跟踪技术的理论依据.从理论上导出绝对黑体单色辐出度与波长和温度的函数关系,即M Bλ=f(λ, T) ,是19世纪末期理论物理学面临的重大课题.维恩(W.Wien,1864—1928年)假定带电谐振子的能量按频率的分布类似于麦克斯韦速率分布率,然后用经典统计物理学方法导出了黑体辐射的下述公式T c B e c T M λ-λλ=/)(251 (15.3) 其中 和 是两个由实验确定的参数.上式称为维恩公式.维恩公式只是在短波波段与实验曲线相符,而在长波波段明显偏离实验曲线,如图15.2所示.瑞利(J.W.S.Rayleigh,1842—1919年)和金斯(J.H.Jeans,1877—1946年)根据经典电动力学和经典统计物理学导出了另一个力图反映绝对黑体单色辐出度与波长和温度关系的函数 42λπ=λckT T M B )( (15.4) 式中c 是真空中的光速,k 是玻耳兹曼常数.上式称为瑞利—金斯公式.该公式在长波波段与实验相符,但在短波波段与实验曲线有明显差异,如图15.2所示.这在物理学史上曾称为“紫外灾难”.234167895οοοοοοοοοοοοοο瑞利—金斯线 维恩线 普朗克线 能量密度 m/μ波长图15.2二、普朗克的量子假设1900年普朗克(M.Planck,1858—1947年)在综合了维恩公式和瑞利—金斯公式各自的成功之处以后,得到黑体的单色辐出度为)()(/11252-λπ=λλkT hc B e hc T M (15.5) 这就是普朗克公式,式中h 为普朗克常数,1986年的推荐值为 h=6.6260755×10-34 J ·s.普朗克公式与实验结果的惊人符合预示了其中包含着深刻的物理思想.普朗克指出,如果作下述假定,就可以从理论上导出他的黑体辐射公式:物体若发射或吸收频率为ν的电磁辐射,只能以ε=hν为单位进行,这个最小能量单位就是能量子,物体所发射或吸收的电磁辐射能量总是这个能量子的整数倍,即),,,(Λ321=ν=ε=n nh n E (15.6)普朗克的能量子思想是与经典物理学理论不相容的,也正是这一新思想,使物理学发生了划时代的变化,宣告了量子物理的诞生.普朗克也因此荣获1918年的诺贝尔物理学奖.作业(P224):23§15.2 光电效应与爱因斯坦的光量子假设普朗克的量子假设提出后的最初几年中,并未受到人们的重视,甚至普朗克本人也总是试图回到经典物理的轨道上去.最早认识普朗克假设重要意义的是爱因斯坦,他在1905年发展了普朗克的思想,提出了光子假设,成功的解释了光电效应的实验规律.一、光电效应的实验规律金属在光的照射下,有电子从表面逸出,这种现象称为光电效应.光电效应中逸出金属表面的电子称为光电子.光电子在电场的作用下所形成的电流叫光电流.研究光电效应的实验装置如图15.3所示.在一个抽空的玻璃泡内装有金属电极K(阴极)和A(阳极),当用适当频率的光从石英窗口射入照在阴极K 上时,便有光电子自其表面逸出,经电场加速后为阳极A 所吸收,形成光电流.改变电位差U AK ,测得光电流 i ,可得光电效应的伏安特性曲线,如图15.4所示.实验研究表明,光电效应有如下规律:1)阴极K 在单位时间内所发射的光电子数与照射光的强度成正比.从图15.4可以看出,光电流i 开始时随 增大而增大,而后就趋于一个饱和值 ,它与单位时间内从阴极K 发射的光子数成正比.所以单位时间内从阴极K 发射的光电子数与照射光强成正比.2)存在截止频率.实验表明,对一定的金属阴极,当照射光频率小于某个最小值i s 时,不管光强多大,都没有光电子逸出,这个最小频率v 0称为该种金属的光电效应截止频率,也叫红限,对应的波长0λ称为截止波长.每一种金属都有自己的红限.3)光电子的初动能与照射光的强度无关,而与其频率成线性关系.在保持光照射不变的情况下,改变电位差U AK ,发现当U AK =0时,仍有光电流.这显然是因为光电子逸出时就具有一定的初动能.改变电位差极性,使U AK <0 ,当反向电位差增大到一定值时,光电流才降为零,如图15.4所示.此时反向电位差的绝对值称为遏止电压,用U a 表示.不难看出,遏止电压与光电子的初动能间有如下关系a eU m =υ2021 (15.7) 式中m 和e 分别是电子的静质量和电量, 0υ是光电子逸出金属表面的最大速率. 实验还表明,遏止电压U a 与光强I 无关,而与照射光的频率v 成线性关系,即 0V K U a -ν= (15.8)式中K 和V 0都是正值,其中K 为普适恒量,对一切金属材料都是相同的,而V 0=Kv 0对同一种金属为一恒量,但对于不同的金属具有不同的数值.将式(15.8)代入式(15.7)得 )(002021ν-ν=-ν=υeK eV eK m (15.9) 上式表明,光电子的初动能与入射光的频率成线性关系,与入射光强无关.4)光电子是即时发射的,滞后时间不超过10-9s.实验表明,只要入射光的频率大于该金属的红限,当光照射这种金属表面时,几乎立即产生光电子,而无论光强多大.二、爱因斯坦光子假设和光电效应方程对于上述实验事实,经典物理学理论无法解释.按照光的波动理论,光波的能量由光强决定,在光照射下,束缚在金属内的“自由电子”将从入射光波中吸收能量而逸出表面,因而逸出光电子的初动能应由光强决定,但光电效应中光电子的初动能与光强无关;另外,如果光波供给金属中“自由电子”逸出表面所需的足够能量,光电效应对各种频率的光都能发生,不应该存在红限,而且,光电子从光波中吸收能量应有一个积累过程,光强越弱,发射光子所需要的时间就越长,这都与光电效应的实验事实相矛盾.由此可见,光的波动理论无法解释光电效应的实验规律.为了克服光的波动理论所遇到的困难,从理论上解释光电效应,爱因斯坦发展了普朗克能量子的假设,于1905年提出了如下的光子假设:一束光就是一束以光速运动的粒子流,这些粒子称为光量子(简称光子);频率为v 的光子所具有的能量为hv ,它不能再分割,而只能整个的被吸收或产生出来.按照光子理论,当频率为v 的光照射金属表面时,金属中的电子将吸收光子,获得 的能量,此能量的一部分用于电子逸出金属表面所需要的功(此功称为逸出功A);另一部分则转变为逸出电子的初动能.据能量守恒定律有(15.10) 这就是爱因斯坦的光电效应方程.)(002021ν-ν=-ν=υ↓eK eV eK m 比较 00eK νeV A eK,h === (15.11)由实验可测量K 和V 0,算出普朗克常数h 和逸出功A,进而还可求出金属的红限v 0.按照光子理论,照射光的光强就是单位时间到达被照物单位垂直表面积的能量,它是由单位时间到达单位垂直面积的光子数N 决定的.因此光强越大,光子数越多,逸出的光电子数就越多.所以饱和光电流与光强成正比;由于每一个电子从光波中得到的能量只与单个光子的能量hv 有关,所以光电子的初动能与入射光的频率成线性关系,与光强无关.当光子的能量hv 小于逸出功A,即入射光的频率v 小于红限v 0时,电子就不能从金属表面逸出;另外,光子与电子作用时,光子一次性将能量 全部传给电子,因而不需要时间积累,即光电效应是瞬时的.这样光子理论便成功地解释了光电效应的实验规律,爱因斯坦也因此获得1921年的诺贝尔物理学奖.例题15.1 用波长为400nm 的紫光去照射某种金属,观察到光电效应,同时测得遏止电压为1.24V ,试求该金属的红限和逸出功.解:由光电效应方程得逸出功为1.87eV J 102.9919=⨯=-=-=-020eU λc h m υ21h νA 根据红限与逸出功的关系,得红限为Hz 1051410626610992143419⨯=⨯⨯==--...h A ν0 三、光(电磁波)的波粒二象性一个理论若被实验证实,它必定具有一定的正确性.光子论被黑体辐射、光电效应以及其他实验所证实,说明它具有一定的正确性.而早已被大量实验证实了的光的波动论以及其他经典物理理论的正确性,也是无可非议的.因此,在对光的本性的解释上,不应该在光子论和波动论之间进行取舍,而应该把它们同样地看作是光的本性的不同侧面的描述.这就是说,光具有波和粒子这两方面的特性,这称为光的波粒二象性.既是粒子,也是波,这在人们的经典观念中是很难接受的.实际上,光已不是经典意义下的波,也不是经典意义下的粒子,而是波和粒子的统一.光是由具有一定能量、动量和质量的粒子组成的,在它们运动的过程中,在空间某处发现它们的几率却遵从波动的规律.描述光的粒子特征的能量与描述其波动特征的频率之间的关系为(15.12)由狭义相对论能量—动量关系并考虑光子的静质量为零得光子动量与波长的关系为====Ph Pc/h c E/h c νc λ (15.13) 它们通过普朗克常数紧密联系起来.通过质能关系还可得光子的质量为c P ch c E m 22=ν==作业(P224):26§15.3 氢原子光谱与玻尔的量子论经典物理学不仅在说明电磁辐射与物质相互作用方面遇到了如前所述的困难,而且在说明原子光谱的线状结构及原子本身的稳定性方面也遇到了不可克服的困难.丹麦物理学家玻尔发展了普朗克的量子假设和爱因斯坦的光子假设等,创立了关于氢原子结构的半经典量子理论,相当成功的说明了氢原子光谱的实验规律.一、氢原子光谱的实验规律实验发现,各种元素的原子光谱都由分立的谱线所组成,并且谱线的分布具有确定的规律.氢原子是最简单的原子,其光谱也是最简单的.对氢原子光谱的研究是进一步学习原子、分子光谱的基础,而后者在研究原子、分子结构及物质分析等方面有重要的意义.在可见光范围内容易观察到氢原子光谱的四条谱线,这四条谱线分别用H α、H β、H γ和H δ表示,如图15.5所示.1885年巴耳末(J.JBalmer,1825—1898)发现可以用简单的整数关系表示这四条谱线的波长6543,,,=-=n ,2n n B λ222(15.14) 式中B 是常数,其值等于364.57nm.后来实验上还观察到相当于n 为其他正整数的谱线,这些谱线连同上面的四条谱线,统称为氢原子的巴耳末系.光谱学上经常用波数 表示光谱线,它被定义为波长的倒数,即λ=ν1~(15.15) 引入波数后,式(15.14)可改写为Λ,,,),(~54312122=-=n n R ν (15.16) 式中172m 100967761B 2R -⨯==./,称为里德伯(J.R.Rydberg,1854—1919)常数.在氢原子光谱中,除了可见光范围的巴耳末线系以外,在紫外区、红外区和远红外区分别有赖曼(T.Lyman)系、帕邢(F.Paschen)系、布拉开(F.S.Brackett)系和普丰德(A.H.Pfund)系.这些线系中谱线的波数也都可以用与式(15.16)相似的形式表示.将其综合起来可表为)(~2211n k R T(n)T(k)νkn -=-= (15.17) 式中k 和n 取一系列有顺序的正整数,k 取1、2、3、4、5分别对应于赖曼线系、巴耳末线系、帕邢线系、布拉开线系和普丰德线系;一旦k 值取定后,n 将从k+1 开始取k+1, k+2, k+3等分别代表同一线系中的不同谱线. T(n)=R/n 2称为氢的光谱项.式(15.17)称为里德伯—里兹并合原理.实验表明,并合原理不仅适用于氢原子光谱,也适用于其他元素的原子光谱,只是光谱项的表示式要复杂一些.并合原理所表示的原子光谱的规律性,是原子结构性质的反映,但经典物理学理论无法予以解释.按照原子的有核模型,根据经典电磁理论,绕核运动的电子将辐射与其运动频率相同的电磁波,因而原子系统的能量将逐渐减少.随着能量的减少,电子运动轨道半径将不断减小;与此同时,电子运动的频率(因而辐射频率)将连续增大.因此原子光谱应是连续的带状光谱,并且最终电子将落到原子核上,因此不可能存在稳定的原子.这些结论显然与实验事实相矛盾,从而表明依据经典理论无法说明原子光谱规律等.二、玻尔的量子论玻尔(N.H.D.Bohr,1885—1962)把卢瑟福关于原子的有核模型、普朗克量子假设、里德伯—里兹并合原理等结合起来,于1913年创立了氢原子结构的半经典量子理论,使人们对于原子结构的认识向前推进了一大步.玻尔理论的基本假设是1)原子只能处在一系列具有不连续能量的稳定状态,简称定态,相应于定态,核外电子在一系列不连续的稳定圆轨道上运动,但并不辐射电磁波;2)作定态轨道运动的电子的角动量L 的数值只能是)/(π2h η的整数倍,即(15.18)这称为角动量量子化条件,n 称为主量子数,m 是电子的质量;3)当原子从一个能量为E k 的定态跃迁到另一个能量为E n 的定态时,会发射或吸收一个频率为v kn 的光子(15.19) 上式称为辐射频率公式, v kn >0表示向外辐射光子, v kn <0表示吸收光子.玻尔还认为,电子在半径为r 的定态圆轨道上以速率υ绕核作圆周运动时,向心力就是库仑力,因而有2202re πεr υm ⋅=41 (15.20) 由式(15.18)和式(15.20)消去υ,即可得原子处于第n 个定态时电子轨道半径为),,,()Λ321(1===n r n πme h εn r 22202n (15.21)对应于n=1的轨道半径r 1是氢原子的最小轨道半径,称为玻尔半径,常用a 0表示,其值为m 10291772495111-⨯===.2200πme h εr a (15.22) 这个数值与用其他方法得到的数值相符合.氢原子的能量应等于电子的动能与势能之和,即re πεr e πεm υE 20202⋅-=⋅-=814121 处在量子数为n 的定态时,能量为),,,()(Λ321n 81812n n =-=⋅-=220420h εme n r e πεE (15.23)由此可见,由于电子轨道角动量不能连续变化,氢原子的能量也只能取一系列不连续的值,这称为能量量子化,这种量子化的能量值称为原子的能级.式(15.23)是氢原子能级公式.通常氢原子处于能量最低的状态,这个状态称为基态,对应于主量子数n=1, E 1=-13.6 eV . n>1的各个稳定状态的能量均大于基态的能量,称为激发态,或受激态.处于激发态的原子会自动地跃迁到能量较低的激发态或基态,同时释放出一个能量等于两个状态能量差的光子,这就是原子发光的原理.随着量子数n 的增大,能量E n 也增大,能量间隔减小. 当n →∞时,rn →∞, E n →0 ,能级趋于连续,原子趋于电离. E > 0时,原子处于电离状态,能量可连续变化.图15.6和图15.7分别是氢原子处于各定态的电子轨道图和氢原子的能级图.使原子或分子电离所需要的能量称为电离能.根据玻尔理论算出的氢原子基态能量值与实验测得的氢原子基态电离能值13.6eV 相符.下面用玻尔理论来研究氢原子光谱的规律.按照玻尔假设,当原子从较高能态E n 向较低能态E k (n>k)跃迁时,发射一个光子,其频率和波数为1n =2n =3n =4n =1r r =14r r =19r r =116r r =赖曼系巴耳末系帕邢系 图15.6 氢原子定态的轨道图hE E νk n nk -= (15.24) )~k n nk nk nk E E hcc νλν-===(11 (15.25) 将能量表示式(15.23)代入即可得氢原子光谱的波数公式)()(~k n nk c h εme ν0nk >-=22324118 (15.26) 显然式(15.26)与氢原子光谱的经验公式(15.17)是一致的,同时可得里德伯常数的理论值为173204m 10097373118-⨯=ε=.ch me R H 理论 (15.27) 这也与实验值符合得很好.这表示玻尔理论在解释氢原子光谱的规律性方面是十分成功的,同时也说明这个理论在一定程度上反映了原子内部的运动规律.三、玻尔理论的缺陷和意义玻尔的半经典量子理论在说明光谱线规律方面取得了前所未有的成功.但是它也有很大的局限性,如只能计算氢原子和类氢离子的光谱线,对其他稍微复杂的原子就无能为力了;另外,它完全没有涉及谱线强度、宽度及偏振性等.从理论体系上讲,这个理论的根本问题在于它以经典理论为基础,但又生硬的加上与经典理论不相容的若干重要假设,如定态不辐射和量子化条件等,因此它远不是一个完善的理论.但是玻尔的理论第一次使光谱实验得到了理论上的说明,第一次指出经典理论不能完全适用于原子内部运动过程,揭示出微观体系特有的量子化规律.因此它是原子物理发展史上一个重要的里程碑,对于以后建立量子力学理论起到了巨大的推动作用.另外,玻尔理论在一些基本概念上,如“定态”、“能级”、“能级跃迁决定辐射频率”等在量子力学中仍是非常重要的基本概念,虽然另有一些概念,如轨道等已被证实对微观粒子不再适用.作业(P224):27§15.4 微观粒子的波—粒二象性 不确定关系一、微观粒子的波—粒二象性1923~1924年间,德布罗意仔细地分析了光的微粒说和波动说的历史,深入的研究了光子假设.他认为,19世纪以来,在光的研究中人们只重视了光的波动性,而忽视了它的粒子性.但在实物粒子的研究中却又发生了相反的情况,只重视实物粒子的粒子性,而忽略了它的波动性.在这种思想的支配下,德布罗意大胆的提出了物质的波—粒二象性假设.他认为,质量为m,速度为υ的自由粒子,一方面可用能量E 和动量p 来描述它的粒子性;另一方面还可用频率v 和波长λ来描述它的波动性.它们之间的关系与光的波—粒二相性所描述的关系一样,即h/p λE/h,ν== (15.28)式(15.28)叫德布罗意公式.这种和实物粒子相联系的波称为德布罗意波,或叫物质波.德布罗意因这一开创性工作而获得了1929年的诺贝尔物理学奖.由于自由粒子的能量和动量均为常量,所以与自由粒子相联系的波的频率和波长均不变,这说明与自由粒子相联系的德布罗意波可用平面波描述.对于静质量为m 0,速度为υ的实物粒子,其德布罗意波长为220/c υυm h p h λ-==1 (15.30) 德布罗意关于物质波的假设,1927年首先由戴维孙(C.J.Davisson,1881—1958)和革末(L.H.Germer,1896—1971)通过电子衍射实验所证实.戴维孙和革末作电子束在晶体表面散射实验时,观察到了和X 射线在晶体表面衍射相似的电子衍射现象,从而证实了电子具有波动性.当时的实验中,采用50KV 的电压加速电子,波长约为0.005nm.由于波长非常短,实验难度很高,因此这一实验是极其卓越的.后来证实了不仅电子具有波动性,其他微观粒子,如原子、质子和中子等也都具有波动性.微观粒子的波动性在现代科学技术上已得到广泛的应用,利用电子的波动性,已制造出了高分辨率的电子显微镜;利用中子的波动性,制成了中子摄谱仪.既然微观粒子具有波动性,原子中绕核运动的电子无疑也具有波动性.不过处于原子定态中的电子的波动形式,与戴维孙和革末实验中由小孔衍射的电子束的波动形式是不同的,后者可认为是行波,而前者则应看为驻波.处于定态中的电子形成驻波的情形,与端点固定的振动弦线形成驻波的情形是相似的.原子中电子驻波可如图15.8形象地表示.由图可见,当电子波在离开原子核为r 的圆周上形成驻波时,圆周长必定等于电子波长的整数倍,即),,,(Λ3212==n n λπr (15.31)利用德布罗意关系便可得电子的轨道角动量应满足下面的关系),,,(Λη3212====n n λh πλn rP L (15.32) 这正是玻尔作为假设引入的量子化条件,在这里,考虑了微观粒子的波动性就自然的得出了量子化条件.例题15.2 计算经过电势差U=150V 和U=104V 加速的电子的德布罗意波长(在U<104V 时,可不考虑相对论效应).解:忽略相对论效应,经过电势差U 加速后,电子的动能和速率分别为202,21m eU eU υm =υ= 式中m 0为电子的静止质量.利用德布罗意关系可得德布罗意波长nm 11.225m 1102512121000UU U e m h υm h λ=⨯=⋅==-. 式中U 的单位是伏特. 1nm 0150V U 11.=λ→=,0.0123nm V 10U 242=λ→=由此可见,在这样的电压下,电子的德布罗意波长与X 射线的波长相近。
大学物理讲义(第15章量子力学基础)第五节

§15.5 量子力学的基本概念和基本原理描述微观粒子运动的系统理论是量子力学,它是薛定谔、海森伯等人在1925~1926年期间初步建立起来的.本节介绍量子力学的基本概念和基本方程.一、波函数极其统计解释在经典力学中我们已经知道,一个被看作为质点的宏观物体的运动状态,是用它的位置矢量和动量来描述的.但是,对于微观粒子,由于它具有波动性,根据不确定关系,其位置和动量是不同时具有确定值的,所以我们就不可能仍然用位置、动量及轨道这样一些经典概念来描述它的运动状态.微观粒子的运动状态称为量子态,是用波函数来描述的,这个波函数所反映的微观粒子的波动性,就是德布罗意波.这是量子力学的一个基本假设.例如一个沿X 轴正方向运动的不受外力作用的自由粒子,由于能量E 和动量p都是恒量,由德布罗意关系式可知,其物质波的频率ν和波长λ也都不随时间变化,因此自由粒子的德布罗意波是一个单色平面波.对机械波和电磁波来说,一个单色平面波的波函数可用复数形式表示为)(2)x/λνt πi Ae t y(x,--=但实质是其实部.类似地,在量子力学中,自由粒子的德布罗意波的波函数可表示为η)/(0)(Px Et i e t x,--ψ=ψ式中0ψ是一个待定常数, η/0iPx e ψ相当于x 处波函数的复振幅,而ηiEt/e -则反映波函数随时间的变化.对于在各种外力场中运动的粒子,它们的波函数要随着外场的变化而变化.力场中粒子的波函数可通过下面要讲的薛定谔方程来求解.经典力学中的波函数总代表某一个物理量在空间的波动,然而量子力学中的波函数又代表着什么呢?对此,历史上提出了各种不同的看法,但都未能完善的解释微观粒子的波—粒二象性,直到1926年玻恩(M.Born,1882—1970)提出波函数的统计解释才完善的解释了微观粒子的波—粒二象性.玻恩认为:实物粒子的德布罗意波是一种几率波;t 时刻,粒子在空间 r 附近的体积元dV 中出现的几率dW与该处波函数的模方成正比,即V t r,Ψt r,ΨV t r,ΨW *d d d 2)()()(== (15.35)由式(15.35)可知,波函数的模方2)(t r,Ψ代表t 时刻粒子在空间r 处的单位体积中出现的几率,称为几率密度.这就是波函数的物理意义,波函数本身没有直接的物理意义.波函数的这种统计解释将量子概念下的波和粒子统一起来了.其量子概念中的粒子性表现为它们具有一定的能量、动量和质量等粒子的属性,同时某时刻,一个粒子总是作为整体出现在某处的,但粒子的运动不具有确定的轨道;量子概念中的波动性是指用波函数的模方表示在空间某处出现的几率密度,而波函数并不代表某个实在的物理量在空间的波动.由于用波函数的模方表示粒子在空间出现的几率密度分布,所以波函数允许包含一个任意常数因子,如)(t r,ΨA 和)(t r,Ψ表示相对几率密度相同的同一个量子态.既然波函数与粒子在空间出现的几率相联系,所以波函数必定是单值的、连续的和有限的.这是波函数的标准条件.又因为粒子必定要在空间中的某一点出现,因此粒子在空间各点出现的几率的总和应等于1,即应有1d 2=⎰⎰⎰V t r,Ψ)( (15.36)此式称为波函数的归一化条件,其中积分区域遍及粒子可能达到的所有空间.在经典力学中,曾经讨论过波动遵从的叠加原理,即各列波共同在某质点引起的振动,是各列波单独在该质点所引起的振动的合成.在量子力学中也有一个类似的原理,这个原理称为态叠加原理,是量子力学原理的又一个基本假设,适用于一切微观粒子的量子态.态叠加原理可以表述为:如果波函数, )(t r,Ψ1 ,)(t r,Ψ2,… ,都是描述系统的可能的量子态,那么它们的线性叠加Λϖϖϖ+ψ+ψ=ψ),(),(),(t r c t r c t r 2211 (15.37)也是这个系统的一个可能的量子态.式中c 1,c 2是任意的复数.二、薛定谔方程1薛定谔方程和算符薛定谔建立了适用于低速情况下的、描述微观粒子在力场中运动的波函数)(t r,Ψ所满足的微分方程,也就是物质波波函数所满足的方程,称为薛定谔方程.质量为m 的粒子在外力场中运动时,一般情况下,其势能V 可能是空间坐标和时间的函数,即),(t r V V ϖ=,而薛定谔方程为tt r i t r H ∂ψ∂=ψ),(),(ˆϖηϖ (15.38)式中 )],()([ˆt r V zy x m H ϖη+∂∂+∂∂+∂∂-=22222222 (15.39) 称为哈密顿算符.在量子力学中,一切力学量都要用算符来表示,这是量子力学的一个基本假设.算符代表对波函数的某种运算(即操作),如微分运算( d/dt)称为微分算符.一般情况下,一算符对某一量子态波函数的运算结果将得到另一个量子态波函数.若一算符作用在某波函数Ψ上的效果和Ψ与某一常数的乘积相当,即ψ=ψF Fˆ (15.40) 则F 称为Fˆ的本征值,Ψ称为算符F ˆ对应于本征值F 的本征函数,它所描述的状态称为F 的本征态,而上式称为本征值方程.对自由粒子波函数Ψ,由于r ˆϖΨ=r ϖΨ,所以坐标算符r r ϖϖ=ˆ (15.41)而 ψ=ψ∇-P i η ,所以动量算符为∇-=ηi Pˆ (15.42) 一般地说,在量子力学中,某力学量若在经典力学中有相应的力学量 ,则只需将力学量F(r ,P )中的r , P 换成其算符就得到该力学量的算符 ,即),(),(ˆ∇-=ηϖϖϖi r F P r F (15.43)在经典力学中,哈密顿量V mP H +=22,所以有式(15.39)所表示的哈密顿算符.在哈密顿算符中,前项是动能算符,后项是势能算符.薛定谔方程式(15.38)是一个关于r 和t 的线性偏微分方程,具有波动方程的形式.可以证明,自由粒子的波函数满足上述方程.它实际上是量子力学的一个基本假设,而不是由更基本的原理经过逻辑推理得到的.但将这个方程应用于分子、原子等微观体系所得到的大量结果和实验符合,这就说明了它的正确性.薛定谔因在创立量子理论方面的贡献而荣获1933年诺贝尔物理学奖.2 定态薛定谔方程在一般情况下,势能函数是空间和时间的函数,但在有些情况下,势能函数只与空间坐标有关,即V=V(r).在这种情况下,波函数可表示为)()(),(r t f t r ϖϖψ=ψ (15.44)将其代入薛定谔方程式 (15.38)可得如下两常微分方程ηη/)(iEt Ce t f Ef dtdf i -=−−→−=解得 (15.45) )()(ˆr E r Hϖϖψ=ψ (15.46) 其中C 为常数.这时波函数为ηϖϖ/)(),(iEt r t r -ψ=ψe (15.48)这种状态下,粒子的能量具有确定的值,把具有这种形式的波函数所描述的状态称为定态,这样的波函数称为定态波函数.显然定态下,几率密度分布22)()(),(r t ,r Ψt r ϖϖϖψ==ρ与时间无关,这是定态的一个重要特征.从这个意义上讲,可将Ψ(r )直接称为定态波函数或波函数.定态波函数Ψ(r )所满足的方程式 (15.46)称为定态薛定谔方程(或不含时薛定谔方程).在本课程中我们只处理定态问题.在关于微观粒子的各种定态问题中,把势能函数V(r)的具体形式))(,)((2202214x m r V r e r V ω=πε=对一维线性谐振子如对氢原子中的电子代入定态薛定谔方程(15.46)中即可求得定态波函数,同时也就确定了几率密度的分布以及能量和角动量等.我们将看到,如果粒子处于束缚态,即只能在有限区域中运动时,由于波函数必须满足单值、有限、连续的条件,解出微观粒子的能量、角动量等必定不连续,即它们是量子化的.三、一维无限深势阱作为量子力学一些概念和原理的具体应用,我们本节介绍最简单的一种情形——一维无限深势阱.在金属中自由电子、原子核中的质子等,它们的运动都被限制在一个很小的空间内,作为近似和简化,我们抽象出一维无限深势阱模型.它是解释金属物理性质等的基础.通过对这一模型的量子力学处理的学习,可以大致了解量子力学的基本概念和基本原理.一维无限深势阱的势能函数为⎪⎩⎪⎨⎧≥≤∞<<=),()()(a x x a x r V 000 (15.49) 其曲线形如深井,如图15.10所示,故称为一维无限深势阱.因为势能V (x )与时间无关,所以属定态问题.在势阱内V (x ) =0,其定态薛定谔方程可写作02222=ψ+ψηmE dx d (15.50) 其中m 是势阱中粒子的质量,令ηmE k 2= 方程(15.50)变为0222=ψ+ψk dxd (15.52) 其通解为kx B kx A x cos sin )(+=ψ (15.53)式中A 和B 是积分常数,应通过边界条件和归一化条件确定.由于是无限深势阱,粒子不能穿越阱壁而到达阱外去,它只能限制在阱内的平底深谷中运动.所以在阱壁和阱外波函数应为零.据波函数的连续条件应有000=ψ==ψ)()(a ,将代入通解(15.53)式得00000=⇒=ψ=⇒=ψka A a B sin )(,)(此时不能取A=0 ,否则只能得到零解,那么只有),,,(sin Λ3210=π=⇒=n n ka ka (15.54)由式(15.51)和式(15.54)得粒子的能量为),,,(Ληη32122222222=π==n ma n m k E n (15.55) 由此可见,一维无限深势阱中粒子的能量是量子化的,n 称为量子数.当n=1时,粒子处于能量最低的基态,基态能量为022221≠π=maE η (15.56) 这一能量也称为零点能,零点能01≠E 表明束缚在势阱中的粒子不会静止,这也是不确定关系所要求的,因为x ∆有限, x P ∆不能为零,从而粒子动能也不可能为零.相应于量子数为n 的定态波函数为);,,,(sin )(a x n x an A x <<=π=ψ0321n n Λ (15.57)而归一化波函数为);,,,(sin )(a x n x an x <<=π=ψ0321a 2n Λ (15.58) 如图15.11所示画出了对应于能量本征值4321E E E E 和、、的波函数以及相应的几率密度.由图15.11(a)可以看出,波函数在阱内区域的分布与在弦线上形成的驻波情形很相似,这一结论与德布罗意关于粒子定态对应于驻波的概念是一致的.对基态波函数,整个阱区相当于半波长的驻波.显然,随着量子数n 的增大,波长在缩短,频率在增加,所以相应状态的能量在提高.图15.11(b)画出了对应于四个能级的粒子几率密度分布.可以看出,在不同的能级上粒子出现的几率密度是不同的.随着量子数n 的增大,几率密度起伏的越来越频繁.这与经典中粒子在阱内出现的几率相等的结论不一致,只有当量子数n 很大时,粒子在阱区内各处的几率才趋于均匀.例题15.4 一有限方势垒的势能函数为⎪⎩⎪⎨⎧≥≤<<=),()()(a x x a x U r V 0000 试讨论粒子能量E<U 0情况下通过方势垒的透射问题.解:为方便,令 ηη)(,E U m k mE k -==02122 则在不同区域中,定态薛定谔方程分别为)(),(a x k dx d a x x k dxd <<=ψ+ψ≥≤=ψ+ψ000022222122解上述方程,得⎪⎪⎩⎪⎪⎨⎧>+<<+<+=ψ---)(')(')(')(a x e C Ce a x e B Be x e A Ae x x ik x ik x k x k x ik x ik 11221100假定粒子由左方( x < 0)入射,由于势垒的存在,因而在x < 0的区域内,既有入射波,又有反射波;在x > a 的区域内,由于无势场作用,因而只有透射波 ,而无反射波,所以C' = 0 .容易理解,入射的粒子数与入射粒子的几率密度成正比,透射的粒子数与透射粒子的几率密度成正比.由波函数及其导数在x = 0和x= a 处连续的条件,可得四个方程,将它们联立求解则可求得透射系数.22212222212221224k k a k sh k k k k A C D ++===)(入射的粒子数透射的粒子数 2e :222/)(a k a k e a shk -+=其中按经典力学的观点,若E<U 0,则粒子不能穿透势垒,将全部被反弹(散射)回去.上述计算表明,在一般情况下,透射系数0D ≠ ,这说明粒子能够穿过比其能量更高的势垒,这种现象称为势垒贯穿,也叫隧道效应.它是一种量子效应,类似于光波在非均匀介质中的传播情况.我们知道,光波入射到不同介质界面时,既有反射的可能,也有折射透过第二种介质的可能.所以隧道效应被认为是微观粒子波动性的表现.作业(P225):32、34。
医学物理学课程教学大纲

《医用物理学》大纲一、课程简介要求:掌握流体、液体表面现象、声波、磁场、电场、电流、几何光学、波动光学、X射线、核医学成像技术的物理原理;理解物理现象的基本过程;了解物理因子与生物体的相互作用规律等。
二、内容和要求【要求】通过对物理学研究对象的了解,弄清物理学与现代医学的内在联系。
【内容】物理学的研究对象,物理学与医学的关系。
第一章力学基本定律【要求】在中学力学知识的基础上总结提高,对医学上需要的力学基础知识作进一步的讨论,掌握物体弹性的一般规律,为了解生物组织的力学性质打基础。
【内容】刚体的转动角量与线量的关系转动动能与转动惯量力矩与转动定律动量矩守恒定律,物体的弹性,应力与应变,杨氏弹性模量,骨骼与肌肉的力学性质。
第二章流体的运动【要求】掌握理想流体和稳定流动的概念、连续性方程、伯努力方程与泊肃叶定律及其应用;理解层流与湍流、雷诺数的概念、粘性流体的伯努力方程的物理意义;了解心脏作功、血液的粘度及其影响因素、人体循环系统中的血流特点。
【内容】1.理想流体的流动理想流体,稳定流动,液流连续原理。
2.伯努利方程伯努利方程及应用。
3.实际流体的流动流体的粘滞性,层流、湍流、雷诺数,泊肃叶方程,流量与流阻、压强差的关系,粘性流体的伯努力方程。
4.斯托克斯定律斯托克斯定律,沉降速度。
5.血液在循环系统中的流动心脏作功,血流速度分布,血流过程中的血压分布。
重点:1.稳定流动的概念,流体连续原理的应用。
2.伯努利方程的意义及其应用(计算和解释现象)。
难点:伯肃叶公式推导。
第三章振动、波动和声波【要求】深入掌握振动与波动的基本规律。
了解声学的基本概念和超声的特点及医学应用。
【内容】简谐振动谐振动方程相位相位差旋转矢量法谐振动能量振动的合成同方向同频率谐振动的合成垂直方向同频率谐振动的合成受迫振动阻尼振动共振波的产生和传播简谐波的波动方程波的强度波的衰减惠更斯原理波的叠加原理波的干涉和衍射声波声压声阻声强声强级和响度级超声的产生与接收超声的性质超声诊断与治疗多普勒效应超声血流计第四章分子动理论【要求】掌握液体表面张力的基本规律。
大学物理量子物理基础(stone)

金属来说,只有当入射光的
频率大于某一频率υo时,电 子才能从金属表面逸出,电 路中才有光电流,这个频率 υo叫做截止频率——红限.
0
Ua
红限频率
(3).线性关系:用不同频率的光照射金属K的表面时, 只要入射光的频率大于截止频率,遏止电势差与入射 光频率具有线性关系,即最大初动能与入射光的频率 成正比而与入射光的光强无关.
普朗克(Max Karl Ernst Ludwig Planck, 1858―1947)
德国物理学家,量子物理学的开创者 和奠基人。 普朗克的伟大成就,就是创立了量子理论, 1900年12月14日他在德国物理学会上,宣 读了以《关于正常光谱中能量分布定律的 理论》为题的论文,提出了能量的量子化 假设,并导出了黑体辐射的能量分布公式。 这是物理学史上的一次巨大变革。从此结 束了经典物理学一统天下的局面。劳厄称 这一天为“量子论的诞生日”。
1918年普朗克由于创立了量子理论而获 得了诺贝尔奖金。
1.普朗克公式
2hc2 1
M (T) 5
hc
e kT 1
2.普朗克假说
•谐振子的能量可取值只能是某一最小能量单元ε 的整 数倍,即:E=nε , n=1,2,3,....ε叫能量子,n为量子数, 它只取正整数—能量量子化. •对于频率为υ的谐振子,最小能量为:ε=hυ 其中h=6.62610-34 J·s为普朗克常数 结论:谐振子吸收或辐射的能量只能是ε=hυ的整数倍.
里兹组合原理:任一条谱线的波数都等于该元素所固有 的许多光谱项中的两项之差,这是里兹在1908年发现的.
~ 1 T( k ) T( n )
T(k) R k2
T (n)
R n2
R=1.096776 107m1
2020年高中物理竞赛辅导课件★★第15章 量子力学基础(PPT)
15-2 光的量子性电效应
一、光电效应 爱因斯坦方程的实验规律
光电效应 光照射到金属表面时, 有电子从金属表面逸出的现象。
光电子 逸出的电子。
光电子由K飞向A,回路中 形成光电流。
AK
OO
OO
OO
G
V R
OO
实验规律
光电效应伏安特性曲线
1、单位时间内从阴极逸出 的光电子数与入射光的强
饱 和
Is2
量按波长的分布随温度而不同的电磁辐射
单色辐射本领(单色辐出度)
波长为的单色辐射本领是指单位时间内从物 体的单位面积上发出的波长在附近单位波长间隔
所辐射的能量。
M (T ) W / m3
如果一个物体能全部吸收投射在 它上面的辐射而无反射,这种物 体称为绝对黑体,简称黑体。
BB ( T )
(μm) 0 1 2 3 4 5 6
m
峰值波长
射度最大值向短波方向移动。
二、普朗克量子假设
MB ( T )
实验值
紫
外 灾
难
维恩
MB ( T ) C34T
瑞利--金斯
M B
(T
)
C e 5
C2 T
1
01 2 3 4 5
67
89
( m )
普朗克得到了黑体辐射公式:
M B ( T ) 2hc 2 5
1
hc
e kT 1
c ——光速 k ——玻尔兹曼恒量
1、若光子和外层电子相碰撞,光子有一部分能量 传给电子, 光子的能量减少,因此波长变长,频率 变低。
2、若光子和内层电子相碰撞时,碰撞前后光子能 量几乎不变,故波长有不变的成分。
3、因为碰撞中交换的能量和碰撞的角度有关,所以 波长改变和散射角有关。
大学物理量子力学的基础

大学物理量子力学的基础量子力学是一门研究微观世界的物理学科,它是对自然界最基本的物质粒子行为进行描述的理论。
在大学物理学课程中,量子力学作为重要的一部分,对于学生来说是一门具有挑战性的学科。
本文将介绍大学物理中量子力学的基础知识,包括量子力学的起源、基本理论、波粒二象性等内容。
一、量子力学的起源量子力学最早起源于20世纪初的实验观察,其中包括普朗克黑体辐射定律和爱因斯坦光电效应等重要实验结果。
这些实验现象无法被经典物理学所解释,迫使科学家们提出一种新的理论来描述微观尺度的物理现象。
1918年,德国物理学家玻恩提出了量子假设,为后来的量子力学奠定了基础。
二、量子力学的基本理论量子力学的基本理论由薛定谔方程和量子力学算符理论构成。
薛定谔方程是描述量子系统演化的基本方程,它描述了系统波函数随时间的演化规律。
而量子力学算符则用来描述物理量的测量和运算,它们对应于物理量的观测值和运动方程。
三、波粒二象性波粒二象性是量子力学的核心概念之一。
根据量子力学的理论,微观粒子在不同的实验条件下既可以呈现出波动性质,又可以表现出粒子性质。
具体而言,光的行为表现为波动性,在双缝实验中呈现出干涉和衍射现象;而电子、中子等微观粒子也可以表现出波动性质,例如在杨氏实验中呈现出干涉条纹。
四、量子力学中的基本概念为了更好地理解量子力学,我们需要掌握其基本概念。
首先是波函数,它描述了量子系统的状态,并且可以用来计算物理量的平均值。
其次是量子态,量子系统所处的状态可以用量子态来描述,量子力学中的态叠加原理也是量子力学与经典物理学的一个重要差异。
最后是测量,量子力学中的测量与经典物理学有很大的不同,测量结果会塌缩波函数,并且存在不确定性原理。
五、量子力学在实际应用中的意义量子力学不仅是基础物理学的重要学科,还被广泛应用于许多领域。
在材料科学中,量子力学的理论模型可以用来解释材料的电子结构和性质。
在计算机科学中,量子计算的概念正在成为未来计算机技术的重要方向。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
普朗克公式
如何给出与实验曲线完全的符合的黑体辐射公式(即M与 T、λ的关系)?
1、瑞利—金斯公式
1900-1905年间,瑞利和金斯根据经典电动力学和 统计物理学导出: Mλ(T)=C1λ- 4 T 此公式在长波区域与曲线符合,短波时Mλ(T)趋于 无穷大,不符合曲线。历史上称其为“紫外区灾 难”。
单色吸收比 aλ(T) : 物体对某一单色波长吸收的能量与入射能量之比。 单色反射比 rλ(T) : 物体对某一单色波长反射的能量与入射能量之比。
对于不透明的物体,单色吸收比和单色反射比的总和等于1 黑体的单色吸收比等于1
实验发现:孤立系统中几个物体,在同样的温度下,各种不同物体 对相同波长的单色辐出度与单色吸收比之比值都相等,并且都等于 黑体对同一波长的单色辐出度。-基尔霍夫辐射定律
固体在温度升高时颜色的变化
800K
1000K
1200K
1400K
2、热平衡辐射
一个物体若辐射电磁波的能量(称为辐射能)等于 它在相同时间内吸收的辐射能时,物体的温度保持 不变,此即热平衡辐射。
一个物体辐射能小于它同时间内吸收的辐射能,物 体的温度将升高;否则,温度降低。
3、辐出度
物体单位时间在单位表面积上辐射的能量称为辐出 度,用M (T)表示;(T 表示辐出度与温度有关) 物体对某一单色光的辐出度称为单色辐出度, 单色辐出度用M λ(T)表示,单位为:W·m -2 某一温度下物体对所有波长的总辐出度为:
由左图可看出温度T升 高,各波长的能量增
Mλ (T)
加,实验确定:黑体
总辐射能量
1700K 1500K 1300K 1100K
M(T)=∫Mλ(T)dλ 与绝对温度T的四次方
成正比,即
1 2 3 4 λ(μm)
斯特藩—玻尔兹曼定律
实验证明:总辐射能量M(T)=∫Mλ(T)dλ与 绝对温度T的四次方成正比,即
海森堡的矩阵力学,薛定鄂的波动力学建立起了量子力 学的理论基础
物体为什么有颜色?
1.物体自身发光 2.对色光的反射、吸收和透射不同,产生了物体的颜色
红黄蓝三种基本颜料(也称三原色)可以调配出各种色 彩的颜料,颜料的颜色是反射光的颜色。 三原色光(红绿蓝)可以组合出各种色彩;
色光 红
混合
黄 品红
白
绿 青蓝
一、量子力学的产生
二、量子力学的发展过程
黑体辐射实验—1900年普朗克提出电磁辐射的能量交换 只能是量子化的。 光电效应实验-1905年爱因斯坦提出光子假设 1911年卢瑟福α粒子轰击原子核散射试验,提出了原子 的核式模型
1913年波耳理论解释了氢光谱证实原子中量子态的存在
1923年德布罗意提出所有的物质粒子都具有波粒二向性 假设,1925电子在晶体中的衍射证明了该结论的正确性
颜料
红 混合
橙紫
黑
黄 绿蓝
第一节 黑体辐射
1、热辐射(Thermal radiation) :
一切物体或固体,在任何温度下都向空间发射各种波 长的电磁波 由原子分子热运动引起的辐射现象称为热辐射。 低温物体的辐射远红外线,不易觉察; 高温物体的辐射可见光、紫外线,易被感知、感觉, 如太阳发光、火炉发热等。 所辐射电磁波的特征仅与温度有关。
M (T)=σT 4
σ= 5.67×10-8 w/m2k4 ,称5—1893)建立了黑体面辐射强 度与绝对温度之间关系的经验公式,制成辐射高温 计,测得太阳表面温度约为6000℃; 1884年玻尔兹曼同时也从热力学理论上证明了此公 式成立,故此定律称为斯特藩-玻尔兹曼定律。
此式与实验曲线完全符合,称为普朗克公式。
黑体辐射实验是物理学晴朗天空中
作用;在已知物体表面温度时,我们可以求出物 体因辐射损失的能量。
维恩位移定律
Mλ
每一曲线都对应 (T) 一个辐射能量最大 的波长(峰值波长) λm,λm随温度升 高向短波方向位移。
1700K 1500K 1300K 1100K
1 2 3 4 λ(μm)
维恩根据热力学理论指出:
λm
λm = b/T
常数b=2.898×10-3 m·k,
《医学物理学教学资料》第十 五章 量子力学基础
对于许多人来说,也许量子力学比相对论更为 有用。后者一般用于研究基本粒子的产生和相互转 化以及大尺度的时空结构,但对于20世纪人类的生 产生活,原子层次的世界显得更为重要。在量子力 学基础上,材料科学、激光技术、超导物理等学科 蓬勃发展,为深刻影响20世纪人们生活方式的计算 机技术、信息技术、能源技术的发展打下了基础。
M a( 11(T T))M a( 22(T T))... ..M ..0(T)
M (0 T)表示黑体的单色辐出度。
5、黑体辐射能谱曲线
给黑体模型加热,由小孔处发出的辐射就是黑体 辐射。
用分光技术把从空腔发出的辐射拍摄成光谱,再 测量各种波长的功率,可得出黑体辐射的能量分 布曲线,如图。
此曲线给出两个重要的定律:
M( 0 T dλ ) ( M T 0 M ) λ (d Tλ )
4、黑体 (black body)
如果一个物体对入射的电磁波能全部吸收,即称为黑体(black body) 。
用一个耐高温不透明材料做成一个大空腔,外面开一个小 孔,入射光线不会被反射,此空腔可看作是黑体模型。
补充:基尔霍夫辐射定律
此结果称为维恩位移定律。铁块被加热
维恩位移定律的作用:
①、已知λm求发光体的温度
如太阳的λm=490nm (蓝绿色光),太阳的温度约
为多少?
T = b/λm =5918k
②、已知温度,确定物体辐射电磁波的波长范围 如人体温度为35℃(308k),其辐射电磁波的峰值 波长λm约为多少?
λm =b/308=93×10-7m =93000A 在远红外线范围
2、维恩辐射公式
1896年,维恩把热力学和多普勒原理结合起来并由
此得出:Mλ(T)=C1λ-5e – C2/λT
此公式在短波区与曲线相符,长波时误差大。
3、普朗克公式
1900年,马克思·普朗克,根据能量量子化的假 设拟合实验曲线得出一个经验公式:
e Mλ (T) 2π 2 λ h 5 λ c h1ck T 1
