二叉排序树
二叉排序树

9
第9章
第三节
二、二叉排序树(插入)
查找
动态查找表
二叉排序树是一种动态查找表
当树中不存在查找的结点时,作插入操作
新插入的结点一定是叶子结点(只需改动一个 结点的指针) 该叶子结点是查找不成功时路径上访问的最后 一个结点的左孩子或右孩子(新结点值小于或 大于该结点值) 10
第9章
第三节
查找
19
在二叉排序树中查找关 键字值等于37,88,94
3
第9章
第三节
查找
动态查找表
二、二叉排序树(查找函数)中结点结构定义 二叉排序树通常采用二叉链表的形式进行存 储,其结点结构定义如下:
typedef struct BiNode { int data; BiNode *lChild, *rChild; }BiNode,*BitTree;
4
第9章
第三节
查找
动态查找表
2、二叉排序树的定义 定义二叉排序树所有用到的变量 BitTree root; int
//查找是否成功(1--成功,0--不成功) //查找位置(表示在BisCount层中的第几个位置
BisSuccess;
int
int
BisPos;
BisCount;
//查找次数(相当于树的层数)
7
第9章
第三节
查找
动态查找表
二、二叉排序树(查找函数)
else { BisSuccess = 0; root=GetNode(k);//查找不成功,插入新的结点}
} BiNode * GetNode(int k) { BiNode *s; s = new BiNode; s->data = k; s->lChild = NULL; s->rChild = NULL; return(s);}
二叉排序树

②若*p结点只有左子树,或只有右子树,则可将*p的左子 树或右子树直接改为其双亲结点*f的左子树,即: f->1child=p->1child(或f->1child=p->rchild); free(p); *f
F *p P P1
*f
F
*f
F *p P
*f
F
Pr
P1
Pr
③若*p既有左子树,又有右子树。则:
-1 0
47
-1
47
47
0
31 69
69
25
0
47
0
25
0
47
-1 0
31
0
69
0
40
69
40
69
0
25 76
40
76
(a)
AL、BL、BR 都是空树
(b) AL、BL、BR 都是非空树
LR型调整操作示意图
2
A
-1
0
C
AR C BL CL CR AR
0 0
B BL CL S
B
A
CR
(a) 插入结点*s后失去平衡
31
0 0 -1
31
0 1
28
0
25
0 0
47
0
25
-1
47
0
25
0
31
0
16 0
28
16
28
0
16 30
30
47
(c) LR(R)型调整
RL型调整操作示意图
A B C A BR CR B BR
AL
C
AL
CL CR
数据结构 二叉排序树

9.6.2 哈希函数的构造方法
构造哈希函数的目标:
哈希地址尽可能均匀分布在表空间上——均 匀性好; 哈希地址计算尽量简单。
考虑因素:
函数的复杂度; 关键字长度与表长的关系; 关键字分布情况; 元素的查找频率。
一、直接地址法 取关键字或关键字的某个线性函数值为哈希地址 即: H(key) = key 或: H(key) = a* key + b 其中,a, b为常数。 例:1949年后出生的人口调查表,关键字是年份 年份 1949 1950 1951 … 人数 … … … …
9.4 二叉排序树
1.定义:
二叉排序树(二叉搜索树或二叉查找树) 或者是一棵空树;或者是具有如下特性的二叉树
(1) 若它的左子树不空,则左子树上所有结点的 值均小于根结点的值;
(2) 若它的右子树不空,则右子树上所有结点 的值均大于等于根结点的值; (3) 它的左、右子树也都分别是二叉排序树。
例如:
H(key)
通常设定一个一维数组空间存储记录集合,则 H(key)指示数组中的下标。
称这个一维数组为哈希(Hash)表或散列表。 称映射函数 H 为哈希函数。 H(key)为哈希地址
例:假定一个线性表为: A = (18,75,60,43,54,90,46) 假定选取的哈希函数为
hash3(key) = key % 13
H(key) = key + (-1948) 此法仅适合于: 地址集合的大小 = = 关键字集合的大小
二、数字分析法
假设关键字集合中的每个关键字都是由 s 位数 字组成 (u1, u2, …, us),分析关键字集中的全体, 并从中提取分布均匀的若干位或它们的组合作为 地址。 例如:有若干记录,关键字为 8 位十进制数, 假设哈希表的表长为100, 对关键字进行分析, 取随机性较好的两位十进制数作为哈希地址。
二叉排序树

二叉排序树1.二叉排序树定义二叉排序树(Binary Sort Tree)或者是一棵空树;或者是具有下列性质的二叉树:(1)若左子树不空,则左子树上所有结点的值均小于根结点的值;若右子树不空,则右子树上所有结点的值均大于根结点的值。
(2)左右子树也都是二叉排序树,如图6-2所示。
2.二叉排序树的查找过程由其定义可见,二叉排序树的查找过程为:(1)若查找树为空,查找失败。
(2)查找树非空,将给定值key与查找树的根结点关键码比较。
(3)若相等,查找成功,结束查找过程,否则:①当给值key小于根结点关键码,查找将在以左孩子为根的子树上继续进行,转(1)。
②当给值key大于根结点关键码,查找将在以右孩子为根的子树上继续进行,转(1)。
3.二叉排序树插入操作和构造一棵二叉排序树向二叉排序树中插入一个结点的过程:设待插入结点的关键码为key,为将其插入,先要在二叉排序树中进行查找,若查找成功,按二叉排序树定义,该插入结点已存在,不用插入;查找不成功时,则插入之。
因此,新插入结点一定是作为叶子结点添加上去的。
构造一棵二叉排序树则是逐个插入结点的过程。
对于关键码序列为:{63,90,70,55,67,42,98,83,10,45,58},则构造一棵二叉排序树的过程如图6-3所示。
4.二叉排序树删除操作从二叉排序树中删除一个结点之后,要求其仍能保持二叉排序树的特性。
设待删结点为*p(p为指向待删结点的指针),其双亲结点为*f,删除可以分三种情况,如图6-4所示。
(1)*p结点为叶结点,由于删去叶结点后不影响整棵树的特性,所以,只需将被删结点的双亲结点相应指针域改为空指针,如图6-4(a)所示。
(2)*p结点只有右子树或只有左子树,此时,只需将或替换*f结点的*p子树即可,如图6-4(b)、(c)所示。
(3)*p结点既有左子树又有右子树,可按中序遍历保持有序地进行调整,如图6-4(d)、(e)所示。
设删除*p结点前,中序遍历序列为:① P为F的左子女时有:…,Pi子树,P,Pj,S子树,Pk,Sk子树,…,P2,S2子树,P1,S1子树,F,…。
详解平衡二叉树
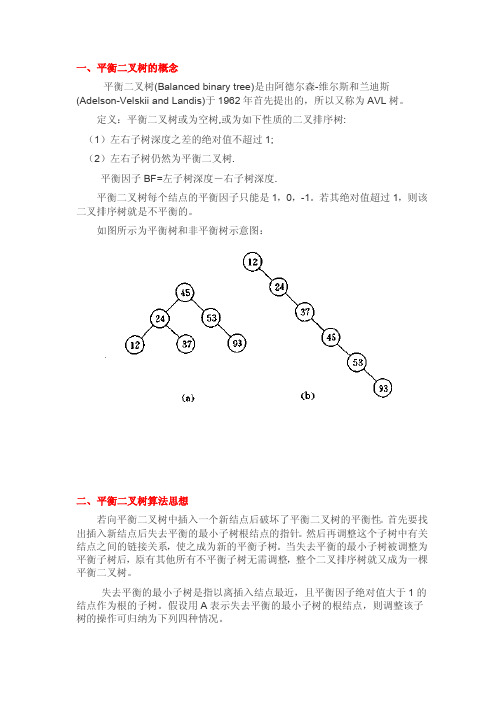
一、平衡二叉树的概念平衡二叉树(Balanced binary tree)是由阿德尔森-维尔斯和兰迪斯(Adelson-Velskii and Landis)于1962年首先提出的,所以又称为AVL树。
定义:平衡二叉树或为空树,或为如下性质的二叉排序树:(1)左右子树深度之差的绝对值不超过1;(2)左右子树仍然为平衡二叉树.平衡因子BF=左子树深度-右子树深度.平衡二叉树每个结点的平衡因子只能是1,0,-1。
若其绝对值超过1,则该二叉排序树就是不平衡的。
如图所示为平衡树和非平衡树示意图:二、平衡二叉树算法思想若向平衡二叉树中插入一个新结点后破坏了平衡二叉树的平衡性。
首先要找出插入新结点后失去平衡的最小子树根结点的指针。
然后再调整这个子树中有关结点之间的链接关系,使之成为新的平衡子树。
当失去平衡的最小子树被调整为平衡子树后,原有其他所有不平衡子树无需调整,整个二叉排序树就又成为一棵平衡二叉树。
失去平衡的最小子树是指以离插入结点最近,且平衡因子绝对值大于1的结点作为根的子树。
假设用A表示失去平衡的最小子树的根结点,则调整该子树的操作可归纳为下列四种情况。
1)LL型平衡旋转法由于在A的左孩子B的左子树上插入结点F,使A的平衡因子由1增至2而失去平衡。
故需进行一次顺时针旋转操作。
即将A的左孩子B向右上旋转代替A作为根结点,A向右下旋转成为B的右子树的根结点。
而原来B的右子树则变成A的左子树。
(2)RR型平衡旋转法由于在A的右孩子C 的右子树上插入结点F,使A的平衡因子由-1减至-2而失去平衡。
故需进行一次逆时针旋转操作。
即将A的右孩子C向左上旋转代替A作为根结点,A向左下旋转成为C的左子树的根结点。
而原来C的左子树则变成A的右子树。
(3)LR型平衡旋转法由于在A的左孩子B的右子数上插入结点F,使A的平衡因子由1增至2而失去平衡。
故需进行两次旋转操作(先逆时针,后顺时针)。
即先将A结点的左孩子B的右子树的根结点D向左上旋转提升到B结点的位置,然后再把该D结点向右上旋转提升到A结点的位置。
数据结构之二叉树(BinaryTree)

数据结构之⼆叉树(BinaryTree)⽬录导读 ⼆叉树是⼀种很常见的数据结构,但要注意的是,⼆叉树并不是树的特殊情况,⼆叉树与树是两种不⼀样的数据结构。
⽬录 ⼀、⼆叉树的定义 ⼆、⼆叉树为何不是特殊的树 三、⼆叉树的五种基本形态 四、⼆叉树相关术语 五、⼆叉树的主要性质(6个) 六、⼆叉树的存储结构(2种) 七、⼆叉树的遍历算法(4种) ⼋、⼆叉树的基本应⽤:⼆叉排序树、平衡⼆叉树、赫夫曼树及赫夫曼编码⼀、⼆叉树的定义 如果你知道树的定义(有限个结点组成的具有层次关系的集合),那么就很好理解⼆叉树了。
定义:⼆叉树是n(n≥0)个结点的有限集,⼆叉树是每个结点最多有两个⼦树的树结构,它由⼀个根结点及左⼦树和右⼦树组成。
(这⾥的左⼦树和右⼦树也是⼆叉树)。
值得注意的是,⼆叉树和“度⾄多为2的有序树”⼏乎⼀样,但,⼆叉树不是树的特殊情形。
具体分析如下⼆、⼆叉树为何不是特殊的树 1、⼆叉树与⽆序树不同 ⼆叉树的⼦树有左右之分,不能颠倒。
⽆序树的⼦树⽆左右之分。
2、⼆叉树与有序树也不同(关键) 当有序树有两个⼦树时,确实可以看做⼀颗⼆叉树,但当只有⼀个⼦树时,就没有了左右之分,如图所⽰:三、⼆叉树的五种基本状态四、⼆叉树相关术语是满⼆叉树;⽽国际定义为,不存在度为1的结点,即结点的度要么为2要么为0,这样的⼆叉树就称为满⼆叉树。
这两种概念完全不同,既然在国内,我们就默认第⼀种定义就好)。
完全⼆叉树:如果将⼀颗深度为K的⼆叉树按从上到下、从左到右的顺序进⾏编号,如果各结点的编号与深度为K的满⼆叉树相同位置的编号完全对应,那么这就是⼀颗完全⼆叉树。
如图所⽰:五、⼆叉树的主要性质 ⼆叉树的性质是基于它的结构⽽得来的,这些性质不必死记,使⽤到再查询或者⾃⼰根据⼆叉树结构进⾏推理即可。
性质1:⾮空⼆叉树的叶⼦结点数等于双分⽀结点数加1。
证明:设⼆叉树的叶⼦结点数为X,单分⽀结点数为Y,双分⽀结点数为Z。
不能构成二叉排序树的一条查找路径

不能构成二叉排序树的一条查找路径在这个充满算法和代码的世界里,咱们聊聊二叉排序树吧,听起来是不是有点高深?二叉排序树就是一个神奇的家族,大家各自有各自的地方。
想象一下,咱们把一群人放在一个大房子里,每个人都有自己的房间,按大小来排列。
大一点的在右边,小一点的在左边。
这个家族的规矩就是,左边的小于自己,右边的大于自己,大家齐心协力让这个家变得有序,谁都不能打乱这个秩序。
不过,有时候啊,这个秩序就会被打破。
你想啊,假如有一天,一个家伙来了,他在外面嚷嚷着:“我可是最厉害的,我不想按照规矩来!”这可麻烦了,大家心里一紧,这条查找路径就会变得曲曲折折,甚至有点让人头疼。
二叉排序树可不是随便什么都能进来的,要有良好的家庭背景,懂规矩才能有位置。
想象一下,如果那个家伙的数字比家里最大的都要大,硬是往右边挤,那可真是让人哭笑不得。
再说说查找路径,简直就像寻宝一样。
想要找到宝藏,就得沿着正确的路线走。
可是,如果你走了一条“二叉排序树”的弯路,嘿,那可是个大问题。
比如说,有个数字在树的左边,结果你非要往右走,真是太离谱了。
你说这查找路径就像迷路,完全走偏了。
可是,偏偏这条错路就成了你的终点,简直让人感到无奈啊。
哎呀,咱们再想想,如果这个家族里出现了很多不合规矩的人,他们在这儿混乱得不可开交,二叉排序树就会失去意义。
你想啊,所有的数字都乱七八糟地挤在一起,左边也不再小于右边,树就变成了一堆杂乱无章的东西。
那种感觉就像大扫除时,家里突然变得乱七八糟,让人想要大喊:“我的天啊,快来帮忙!”二叉排序树是个追求秩序的地方,想要在里面生存,得遵循规矩。
如果你想插入一个新成员,得确保他是合适的。
否则,不仅你自己找不到路,连别人也会跟着懵圈。
那种情况下,别说“查找路径”了,连“家”都找不到了。
在这个二叉排序树的大家庭中,大家都有自己的位置,没位置的人可得想办法来适应。
像极了生活中的很多场景,有时候为了融入一个圈子,你可能得调整自己,找对路径,不然就会被排除在外。
数据结构二叉排序树

05
13
19
21
37
56
64
75
80
88
92
low mid high 因为r[mid].key<k,所以向右找,令low:=mid+1=4 (3) low=4;high=5;mid=(4+5) div 2=4
05
13
19
low
21
37
56
64
75
80
88
92
mid high
因为r[mid].key=k,查找成功,所查元素在表中的序号为mid 的值
平均查找长度:为确定某元素在表中某位置所进行的比 较次数的期望值。 在长度为n的表中找某一元素,查找成功的平均查找长度:
ASL=∑PiCi
Pi :为查找表中第i个元素的概率 Ci :为查到表中第i个元素时已经进行的比较次数
在顺序查找时, Ci取决于所查元素在表中的位置, Ci =i,设每个元素的查找概率相等,即Pi=1/n,则:
RL型的第一次旋转(顺时针) 以 53 为轴心,把 37 从 53 的左上转到 53 的左下,使得 53 的左 是 37 ;右是 90 ,原 53 的左变成了 37 的右。 RL型的第二次旋转(逆时针)
一般情况下,假设由于二叉排序树上插入结点而失去 平衡的最小子树的根结点指针为a(即a是离插入结点最 近,且平衡因子绝对值超过1的祖先结点),则失去平衡 后进行调整的规律可归纳为下列四种情况: ⒈RR型平衡旋转: a -2 b -1 h-1 a1
2.查找关键字k=85 的情况 (1) low=1;high=11;mid=(1+11) / 2=6
05
13
19
21
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
就维护表的有序性而言,二叉排序树无须移 动结点,只需修改指针即可完成插入和删 除操作,且其平均的执行时间均为O(lgn), 因此更有效。二分查找所涉及的有序表是 一个向量,若有插入和删除结点的操作, 则维护表的有序性所花的代价是O(n)。当 有序表是静态查找表时,宜用向量作为其 存储结构,而采用二分查找实现其查找操 作;若有序表里动态查找表,则应选择二 叉排序树作为其存储结构。
if(q->lchild) //*q的左子树非空,找*q的左子 树的最右节点r. {for(q=q->lchild;q->rchild;q=q->rchild); q->rchild=p->rchild; } if(parent->lchild==p)parent->lchild=p>lchild; else parent->rchild=p->lchild; free(p); /释放*p占用的空间 } //DelBSTNode
下图(a)所示的树,是按如下插入次序构成的: 45,24,55,12,37,53,60,28,40,70 下图(b)所示的树,是按如下插入次序构成的: 12,24,28,37,40,45,53,55,60,70
在二叉排序树上进行查找时的平均查找长度和二叉树的形态 有关: ①在最坏情况下,二叉排序树是通过把一个有序表的n 个结点依次插入而生成的,此时所得的二叉排序树蜕化为 棵深度为n的单支树,它的平均查找长度和单链表上的顺 序查找相同,亦是(n+1)/2。 ②在最好情况下,二叉排序树在生成的过程中,树的形 态比较匀称,最终得到的是一棵形态与二分查找的判定树 相似的二叉排序树,此时它的平均查找长度大约是lgn。 ③插入、删除和查找算法的时间复杂度均为O(lgn)。 (3)二叉排序树和二分查找的比较 就平均时间性能而言,二叉排序树上的查找和二分查找 差不多。
二叉排序树的生成,是从空的二叉排序树开始,每输入一个结点数据, 就调用一次插入算法将它插入到当前已生成的二叉排序树中。生成二 叉排序树的算法如下: BSTree CreateBST(void) { //输入一个结点序列,建立一棵二叉排序树,将根结点指针返回 BSTree T=NULL; //初始时T为空树 KeyType key; scanf("%d",&key); //读人一个关键字 while(key){ //假设key=0是输人结束标志 InsertBST(&T,key); //将key插入二叉排序树T scanf("%d",&key);//读人下一关键字 } return T; //返回建立的二叉排序树的根指针 } //BSTree
二叉排序树插入新结点的递归算法 InsertBST(BSTNode *Tree,KeyType key) { if(*Tree==NULL) { BSTNode *p= new BSTNode; p->key=key; p->lchild=NULL; p->rchild=NULL; Tree=p; } else { if(tree->key>key) insert(tree->lchild,key); else insert(tree->rchild,key); } }
二叉排序树插入新结点的非递归算法 void InsertBST(BSTNode *Tptr,KeyType key) { //若二叉排序树 *Tptr中没有关键字为key,则插入,否则直接返回 BSTNode *f,*p=TPtr; //p的初值指向根结点 while(p){ //查找插入位置 if(p->key==key) return;//树中已有key,无须插入 f=p; //f保存当前查找的结点 p=(key<p->key)?p->lchild:p->rchild; //若key<p->key,则在左子树中查找,否则在右子树中查找 } //endwhile p=(BSTNode *)malloc(sizeof(BSTNode)); p->key=key; p->lchild=p->rchild=NULL; //生成新结点 if(TPtr==NULL) //原树为空 Tptr=p; //新插入的结点为新的根 else //原树非空时将新结点关p作为关f的左孩子或右孩子插入 if(key<f->key) f->lchild=p; else f->rchild=p; } //InsertBST
与二分查找类似,和关键字比较的次数不超过树的深度。 (2)在二叉排序树上进行查找时的平均查找长度和二叉树的形 态有关 二分查找法查找长度为n的有序表,其判定树是惟一的。 含有n个结点的二叉排序树却不惟一。对于含有同样一组 结点的表,由于结点插入的先后次序不同,所构成的二叉 排序树的形态和深度也可能不同 【例】下图(a)所示的树,是按如下插入次序构成的: 45,24,55,12,37,53,60,28,40,70 下图(b)所示的树,是按如下插入次序构成的: 12,24,28,37,40,45,53,55,60,70
二叉排序树上的查找 ①查找递归算法 在二叉排序树上进行查找,和二分查找类似,也是一个逐步缩小查 找范围的过程。 递归的查找算法: BSTNode *SearchBST(BSTree T,KeyType key) { //在二叉排序树T上查找关键字为key的结点,成功时返回该结点位置, 否则返回NUll if(T==NULL||key==T->key) //递归的终结条件 return T; //T为空,查找失败;否则成功,返回找到的结点位置 if(key<T->key) return SearchBST(T->lchild,key); else return SearchBST(T->rchild,key);//继续在右子树中查找 } //SearchBST
• (2)二叉排序树的删除 • 从二叉排序树中删除一个结点,不能 把以该结点为根的子树都删去,并且还要 保证删除后所得的二叉树仍然满足BST性质。
• 删除*p结点的过程如下: (1)首先查找p节点,如找不到则返回。 (2)若节点p没有左子树,则用右子树 的根代替被删除的节点。 (3)若节点p有左子树,则在其左子树 中找到最右节点r,将p的右子树置为r的右 子树,再用p的左子树的根节点代替被删除 的节点p.
算法分析 在二叉排序树上进行查找时,若查找成功,则是从根结 点出发走了一条从根到待查结点的路径。若查找不成功, 则是从根结点出发走了一条从根到某个叶子的路径。
(1) 二叉排序树查找成功的平均查找长度 在等概率假设下,下面(a)图中二叉排序树查找成功的平 均查找长度为 ASLa=(1+2*2+3*4+4*3)/10=3 在等概率假设下,(b)图所示的树在查找成功时的平均查 找长度为: ASLb=(1+2+3+4+5+6+7+8+9+10)/10=5.5
二叉排序树的特点 由BST性质可得: (1) 二叉排序树中任一结点x,其左(右)子树中任一结 点y(若存在)的关键字必小(大)于x的关键字。 (2) 二叉排序树中,各结点关键字是惟一的。 注意: 实际应用中,不能保证被查找的数据集中各元素的关键 字互不相同,所以可将二叉排序树定义中BST性质(1)里的 "小于"改为"大于等于",或将BST性质(2)里的"大于"改为" 小于等于",甚至可同时修改这两个性质。 (3) 按中序遍历该树所得到的中序序列是一个递增有 序序列。
void DelBSTNode(BSTNode *Tptr,KeyType key) {//在二叉排序树*Tptr中删去关键字为key的结点 BSTNode *parent=NUll,*p=Tptr,*q; while(p){ //从根开始查找关键字为key的待删结点 if(p->key==key) break;//已找到,跳出查找循环 parent=p; //parent指向*p的双亲 p=(key<p->key)?p->lchild:p->rchild; //在关p的左或右 子树中继续找 } if(!p) return; //找不到被删结点则返回 q=p; //q记住被删结点*p
• 下图所示的两棵树均是二叉排序树,它们 的中序序列均为有序序列:2,3,4,5,7, 8。
2 5 3
3
7
7
2
4
8
5
8
4
typedef int KeyType; //假定关键字类型为整数 Typedef struct nodห้องสมุดไป่ตู้ { //结点类型 KeyType key; //关键字项 InfoType otherinfo; //其它数据域,InfoType视应 用情况而定,下面不处理它 struct node *lchild,*rchild; //左右孩子指针 } BSTNode; typedef BSTNode * BSTree; //BSTree是二叉排 序树的类型
完成二叉排序树。
• 二叉排序树上的运算 • (1) 二叉排序树的插入和生成 • ①二叉排序树插入新结点的过程 • 在二叉排序树中插入新结点,要保证插入后仍满足 BST性质。其插入过程是: • (a)若二叉排序树T为空,则为待插入的关键字key申 请一个新结点,并令其为根; • (b)若二叉排序树T不为空,则将key和根的关键字比 较: • (i)若二者相等,则说明树中已有此关键字key, 无须插入。 • (ii)若key<T→key,则将key插入根的左子树中。 • (iii)若key>T→key,则将它插入根的右子树中。 • 子树中的插入过程与上述的树中插入过程相同。如此 进行下去,直到将key作为一个新的叶结点的关键字插入 到二叉排序树中,或者直到发现树中已有此关键字为止。
