UG7.5表达式应用
UG草图和表达式功能在参数化模型创建中的应用

UG草图和表达式功能在参数化模型创建中的应用一.引言UG是CAID/CAD/CAM/CAE一体化的三维参数化高端软件,自从它1990年进入中国市场以来,发展迅速,现已广泛应用于中国的航空,航天,汽车,造船和电子等工业领域,且其中尤CAD功能应用较广。
因为无论是UG在CAM、CAE还是其它方面的应用,它们总需要模型做为处理对象,这就使得高效,快速,准确地建立起可编辑性强的三维模型作为一个重要问题摆在了我们面前。
二.UG的草图和表达式功能UG的建模功能是很强大的,其主要的建模方法有:UG/实体建模(UG/Solid Modeling);UG/特征建模(UG/Features Modeling);UG/自由曲面建模(UG/Freedom Modeling);UG/用户自定义特征(UG/User-Defined Features)等。
其中,相对于其它CAD软件,UG的特征建模是其比较大的亮点,对于不太复杂的模型,特征建模完全可以胜任,且可以达到很高的建模效率,但对于形状、位置复杂或要求实现参数化的模型,单纯的特征建模就显得麻烦或者很难,这时就需要考虑采用其它的方法,草图(Sketch)和表达式(Expression)功能就是最常用的处理此方面问题的简洁高效的方法。
UG中的草图(Sketch)是指与实体模型相关联的二维图形。
它可以通过对近似的曲线轮廓进行尺寸和几何约束来准确地表达设计师们的设计意图,再辅以拉伸(Extruded Body),旋转(Revolved Body)和扫描(Sweep along Guide)等实体建模方法来创建模型。
利用草图功能创建的模型有以下两个突出优点:易于编辑和修改;易于实现参数化和系列化设计。
UG的表达式功能则可以很方便的将尺寸关联起来以实现参数化。
下面就通过在UG NX环境下,充分利用草图和表达式功能来创建一个足球模型的实例,来认识一下怎样利用草图和表达式的尺寸关联来实现模型的参数化。
UGNX7.5高级应用教程课程设计 (2)

UGNX7.5高级应用教程课程设计介绍UGNX是一款三维计算机辅助设计(CAD)软件,由美国公司Siemens PLM Software开发。
UGNX软件是一款使用广泛的CAD工具,它提供了强大的功能,可用于设计、建模、分析和生产工艺。
本课程将对UGNX7.5高级应用进行教学,使学生们更好地掌握UGNX软件技术,提升其技能水平。
目标通过本课程的学习,学生应当掌握以下技能:•了解UGNX软件的基本功能和界面•掌握UGNX7.5高级应用技巧•能够使用UGNX进行模型设计、分析和生产工艺•能够应用UGNX进行模型转换和转化内容第一章 UGNX7.5基础知识回顾本章将对UGNX7.5基础知识进行回顾,包括软件安装和基本功能介绍。
第二章 UGNX7.5高级建模技巧本章将介绍UGNX7.5高级建模技巧,包括参数化设计、草图和曲面建模等。
第三章 UGNX7.5高级分析技巧本章将介绍UGNX7.5高级分析技巧,包括模型应力分析、振动分析和变形分析等。
第四章 UGNX7.5CAM工艺制造本章将介绍UGNX7.5CAM工艺制造,包括模型加工、数控编程和生产工艺设计等。
第五章 UGNX7.5转化技巧本章将介绍UGNX7.5转化技巧,包括模型转换和导出等。
实验学生应当进行以下实验:1.UGNX7.5软件的基本操作:创建、打开、保存、关闭、撤销、重做、移动、旋转、缩放等2.UGNX7.5草图设计技巧:圆、矩形、直线、多边形、椭圆、双曲线等3.UGNX7.5曲面建模技巧:Revolve、Sweep、Loft等4.UGNX7.5模型分析和生产工艺设计:模型分析、工艺规划、加工参数等5.UGNX7.5模型转换和导出:转换格式、导出模型、数据转换等总结通过本课程的学习,学生们能够掌握UGNX7.5高级应用技能,提高其CAD设计和分析的能力。
同时,学生们也能够应用所学技能,满足工业制造领域的需求,为未来的工作奠定坚实的基础。
表达式在UGII工程图中的应用

表达式在UGII工程图中的应用在UGII系统中建立工程图时,使用表达式常常会达到事半功倍的效果,下面就是笔者的一些心得。
一、表达式在工程图模块中变得可用UG系统的缺省设置是在进入工程图模块后,表达式变成不可用,也就意味着,在工程图模块中不能通过更改表达式的值的方法来改变零件的模型参数。
如果需要在工程图模块中使用表达式,则只要在UGII_ENV.DAT文件中将环境变量UGII_DRAFT_EXPRESSIONS_OK的值设置成1。
表达式对话框在制图模块中将可使用。
二、表达式用于视图比例当有些零部件的尺寸变化较大,无法固定其工程图图幅时,可通过表达式控制视图比例,确保其工程图图幅不变。
具体步骤如下:(1)在表达式中建立如下变量:p0=200view_scale=1/(ceil(p0/100))其中p0为该零件尺寸变化幅度最大的尺寸之一,view_scale为用户自定义变量,将用于控制视图比例。
(2)在工程图模块中添加视图时,将图1所示scale文本框的值设置成view_scale。
这样,当p0尺寸变化时,view_scale也跟着变化,结果是视图的大小变化不大,故其图幅也就不需变化。
图1添加视图对话框三、表达式用于特殊标注图2所示的模型中,尺寸标注随凹槽的数量、凹槽间间距的变化而变化。
该模型在建模时,两端的凹槽通过slot特征建立,中间的凹槽通过instance特征建立,并在表达式中生成相应变量: n=3jz=20其中n为阵列特征数量,jz为阵列特征间距。
图2 特殊标注在建立图2所示尺寸标注时,需在图3尺寸标注对话框中做如下事情:(1)在附加文本方式组合框中选择simple append选项,在Place Text组合框中选择before/after选项;(2)在before text文本框中加入“<X@n>X<X@jz>=(”,在after text文本框中加入“)”;(3)标注尺寸。
UG方程式应用实例1
在UG软件中,对于曲线的生成有多种生成工具,可生成直线、圆弧、椭圆、样条、抛物线、双曲线等等,特别值得一提的是,在UG软件中,具有生成以方程式表达的曲线的功能,且该曲线还具有相关性,即如果方程式变化时,曲线也会跟着变化,这特别适合某些特定的需要,如凸轮的建模等。
在UG软件中方程式曲线在UG软件中,对于曲线的生成有多种生成工具,可生成直线、圆弧、椭圆、样条、抛物线、双曲线等等,特别值得一提的在UG软件中,具有生成以方程式表达的曲线的功能,且该曲线还具有相关性,即如果方程式变化时,曲线也会跟着变化,特别适合某些特定的需要,如凸轮的建模等。
在UG软件中方程式曲线的建模步骤主要由两步构成:第一步是建立表达式,第二步是建立该方程式曲线,下面以一实例为例,说明其建立步骤。
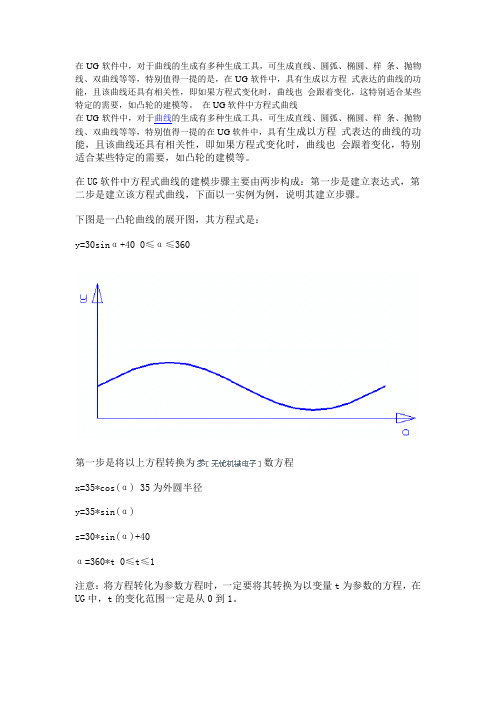
下图是一凸轮曲线的展开图,其方程式是:y=30sinα+40 0≤α≤360第一步是将以上方程转换为数方程x=35*cos(α) 35为外圆半径y=35*sin(α)z=30*sin(α)+40α=360*t 0≤t≤1注意:将方程转化为参数方程时,一定要将其转换为以变量t为参数的方程,在UG中,t的变化范围一定是从0到1。
第二步,将参数方程输入为UG软件中的表达式,对应以上参数方程,请输入以下表达式:t=1α=360*tx=35*cos(α)y=35*sin(α)z=30*sin(α)+40第三步建立曲线:Toolbox->Curve…->Law Curve->提示定义X轴->选By Equation->提示定义X 轴,输入参数表达式->输入t->提示定义X轴,输入方程表达式->输入 x->接着提示定义Y轴,同样按照步骤定义Y轴和Z轴->选择OK,生成所需曲线。
第四步建立实体模型,用UG软件的其他功能,完成最终模型。
ug7.5实用教程14

自由形状建立的基本过程
注意∶ 基于点生成的片体为非参数化特征;基于曲线生成的片体为参数化特征( 全息片体) ;基于片体生成的片体大部分为参数化特征。
自由形状建模过程∶ 1、建立样条。 2、构建”主要(primary)”片体_利用过曲线、直纹、过曲线网格、扫掠 选项。
3、构建”过渡(Transition)”片体_ 利用挢接面、剖切截面、软倒圆、面 倒圆、N-边曲面、过渡选项。
再点击section命令,将type切换到parallel planes
截面对象依然选择先前的solid body Base plane换成yc-zc plane 平面位置进行如下设置
点击OK
在部件导航器中将前两部所创建的特征删除掉
继续执行section命令 将类型切换成radial planes
Fit 用最小两乘方误差拟合样条。该方法减小定义样条所需 的点数,并确保样条的光顺 Perpendicular to plans 样条线正交与选择的平面和通过选择的点。
练习1-1-1 样条 SPLINE.prt
打开 1-01-
insert →curve→spline 分别用By poles、Through points、Fit的方式构造曲线
控制定义点:在定义点上按右键→选择specify constraint
所创建的样条与定义点,定义切矢和曲 率的几何体保持全相关;默认的curve degree=5;可用同一个窗口创建和编辑 全相关的样条
样条编辑
studio spline 的编辑 •edit →feature → editparameters •双击曲线 •在模型导航器中右键(如图)
全息片体
所谓全息片体(Smart Sheet)就是指全参数化、全相关曲面。 在UG系统中,大多数命令所构造的曲面都是具有参数化的特征,在 Freefrom Features中称为Smart Sheet。这类曲面的共同特点是都是 由曲线生成,曲面与曲线具有关联性,即当构造曲面的曲线编辑修改 后,曲面会自动更新。 为了保证所构造的曲面的参数化特性,即关联性、宜于编辑的性 能,构造曲面时应该注意以下几点: 避免使用非参数化命令构造曲面(through points,from poles, from point cloud,foreign四种方法为非参数化方法,尽可能不要用)。 构造的曲线尽可能采用草图方法生成。 编辑面采用Edit →Feature →Edit Parameters 尽可能采用修剪体(trim body)、抽壳(shell)方法建模。
UG 深度解析-表达式在参数化建模中的应用

深度解析-表达式在参数化建模中的应用在参数化方面,有意愿交流的加qq 59562466,,,加的时候注明参数化,,,如何用表达式处理参数关联的问题什么是参数关联。
if 参数A=100,then 参数B=300;if 参数A=200,then 参数B=700;if 参数A=300,then 参数B=900;if 参数A=400,then 参数B=500;这样一一对应,而没有其他函数关系的一组参数。
以GB-T5781-2000 螺栓模型为例子。
如何将“公称直径”和型号,两个独立的参数关联起来。
1.定义一个“直径”参数,直径=11,2.定义一个公称直径参数,作用是防止修改参数“直径”时,输入和标准值不符的值,当然这么做只是提供一个思路,处理防错的思路,,具体怎么设置界限值,根据具体需求而定。
MAJOR_DIAMETER= If ( 直径<=5 )Then ( 5 )Else If ( 直径>5&&直径<=6 )Then ( 6 )Else If ( 直径>6&&直径<=8 )Then ( 8 )Else If ( 直径>8&&直径<=10 )Then ( 10 )Else If ( 直径>10&&直径<=12 )Then ( 12 )Else If ( 直径>12&&直径<=16 )Then ( 16 )Else If ( 直径>16&&直径<=20 )Then ( 20 )Else If ( 直径>20&&直径<=24 )Then ( 24 )Else If ( 直径>24&&直径<=30 )Then ( 30 )Else If ( 直径>30&&直径<=64 )Then ( 64 )Else ( 64 )3.定义个公称直径的列表,将所有值“依次!!!!”列表出来LB_MAJOR_DIAMETER= {"5","6","8","10","12","16","20","24","30","64"}4.定义一个整数N,N= ug_findNumberInList( MAJOR_DIAMETER, LB_MAJOR_DIAMETER )+1,获取输入的直径参数在“直径列表”参数中的位置,是第几个。
UG用表达式的方式测量几何数据

用表达式的方式测量几何数据下面我们想通过表达式测量数据线A,是一条假想的线,总是以下图的长方体的对角线的顶点为起始点线B,是孔的中心线,总保持与线A垂直且通过线C孔的深度总等于F值的80%线A和线B的交点总是线A的中点第一步:打开measure .第二步:进入建模第三步:按默认方向拉伸草图250mm,并适合窗口Fit第四步:将21和61层改为不可见第五步:为孔特征创建一个参考几何体选择基准轴(Datum Axis).选用两个点(Two Points)的方式,选图示的两个点单击确定选择基准面(Datum Plane).选择图示的两条边并应用(Apply).选择刚建的基准面和基准轴,键入角度值90然后应用(Apply)选择下图中新建的基准面和端点并确定再建一个基准面第六步:选择工具→表达式(Tools→Expression),打开更多选项选择测量距离(Measure Distance).选择下图的点并确定OK将捕捉点的对话框打开,将选定端点选项选中将列出的表达式(Listed Expressions)设为测量(Measurements.)注意现在列表中表达式的值约为282.2清单中公式栏显示(Measure),相应的名字在名称栏显示,可能是P12(如果你之前没有删除一些东西的话,这个关系不大)现在公式编辑窗口出现了测量表达式的名字,当你在表达式对话框中选择一个测量图标时,你实际上是调用了浮动的分析工具栏来创建测量特征,当你在浮动的分析工具栏选择确定,又将回到表达式对话框,系统假定你现在想用深入表达式为另一个测量特征创建一个新的表达式如果你键入一个新的名字并同意编辑它,选择拒绝编辑(Reject Edit).现在新的表达式还未命名但测量特征仍在列表中,只为你刚刚离开浮致动工具条时已经完成了测量将测量的表达式重命名为diagonal.将列出的表达式(Listed Expressions)设为全部(All)下面是创建一个深入表达式来控制孔的深度第七步:创建一个孔开头就有要求孔的深度是F值的80%选择孔Hole选择简单的Simple选择最后创建的基准面为孔的放置平面如果需要,将图形翻转过来,确保工具体打穿了长方体接受默认的直径值Diameter25mm和顶角值Tip Angle是118度创建一个深入的测量,在深度窗口中选择Parameter Entry Options选择Measure.测量选择通过基准轴的基准面和下图所示的端点并确定OK可以看到现在深度的键入参数区域是灰色的,不可变的键入参数的图标被换成了测量的图标,说明现在是测量尺寸控制着深度选择测量图标中的键入参数选项选择公式Formula.在表达式对话框中,新的深度参数添加上*0.8附加条件(“distance”后面所附带的数字可能与图示的不同)选择接受编辑Accept Edit.注意尚未确定的深度的表达式现在的显示是distance18*0.8.(“distance”后面所附带的数字可能不同)因为现在孔还没有被完全创建好,所以系统参数(p#)也没有确定,名称栏暂时显示为Depth. 单击确定,回到创建孔的对话框注意现在深度的参数键入值旁边显示的是公式选择确定创建该孔选择点在线上Point onto Line的定位方式,选择基准轴选择水平Horizontal.在图形窗口选择基准轴作为水平参考选择图中所示的基准轴的一个端点作为目标点在定位对话框中选择参数键入选项公式(Formula)作为目前的尺寸用键入或复制的方式编辑CurrentParm的值为diagonal/2.选择确定退出表达式对话框如果选择应用的话你将会又返回到定位对话框,因为现在孔已经完全定位,该对话框将被关闭第八步:编辑拉伸特征以检验是否达到设计意图在图形窗口,将指针放在拉伸出的实体上直到其呈高亮显示,然后MB3→Edit Parameters.编辑参数在浮动工具条中结束End键入125并Enter.选择确定更新模型将结束值改为500完成再次更新孔仍然位于对角线的中点处在表达式对话框中检验表达式用组合键Ctrl+E打开表达式对话框将列出的表达式(Listed Expressions)设为测量(Measurements.)将列出的表达式(Listed Expressions)设为对象参数(Object Parameters.)选择孔特征注意对孔的深入的测量现在有了一个系统名称P13(“distance”后面所附带的数字可能不同),并且公式栏现在显示distance11*.8(“distance”后面所附带的数字可能不同)关闭表达式对话框在部件导航器中查看表达式将部件导航器设为模型视图(时间)选择SIMPLE_HOLE特征如果需要将细节栏Details打开。
最新UG表达式应用说明分析

U G表达式应用说明分析精品好资料-如有侵权请联系网站删除●表达式左侧必须是一个简单变量,等式右侧是一个数学语句或一条件语句。
●所有表达式均有一个值(实数或整数),该值被赋给表达式的左侧变量。
●表达式等式的右侧可认是含有变量、数字、运算符和符号的组合或常数。
●用于表达式等式右侧中的每一个变量,必须作为一个表达式名字出现在某处。
Length=.5+2*Cos(60)图2-1 表达式格式2.1.2 表达式的方法1.手工创建表达式●选择下拉菜单Tool→Expression或按快捷键Ctrl+E●改变一个已存在的表达式的名字,可选择下拉菜单Tool→Expression,选取已存在的表达式,然后单击Rename。
●将文本文件中存在的表达式引入到UG中,可选择下拉菜单Tool→Expression→Import。
精品好资料-如有侵权请联系网站删除精品好资料-如有侵权请联系网站删除2. 系统自动建立表达式当用户作下列操作时,系统自动地建立表达式,其名字用一个小写字母p开始。
●建立一个特征(Create a Feature)时,系统对特征的每个参数建立一个表达式。
●建立一个草图(Create a Sketch)时,系统对定义草图基准的XC和YC坐标建立两个表达式。
例如:p1_YDATUM_V1=0●标注草图尺寸(Dimension a Sketch)后,系统对草图的每一个尺寸都建立一个相应的表达式。
●定位一个特征或一个草图(Position a feature or sketch)时,系统对每一个定位尺寸都建立一个相应的表达式。
●生成一个匹配条件(Create a mating)时,系统会自动建立相应的表达式。
表达式可应用于多个方面,它可以用来控制草图和特征尺寸和约束;可用来定义一个常量,如pi=3.1415926;也可被其它表达式调用,如expression1=expression2+expression3,这对于缩短一个很长的数字表达式十分有效,并且能表达它们之间的关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
UG7.5 表达式及应用1、表达式输入:工具----表达式2、执行:插入----曲线----规律曲线----根据方程。
如果没有“规律曲线”命令,用:帮助----命令查找器;查找。
3、“表达式”对话框如下:将方程转换为参数方程时注意:将方程转化为参数方程时,一定要将其转换为以变量t为参数的方程,在UG中,t的变化范围一定是从0到1。
4、规律曲线命令如下:恒定允许您给整个规律函数定义一个常数值。
系统会提示您只输入一个规律值(即该常数)。
线性用于定义一个从起点到终点的线性变化率。
三次用于定义一个从起点到终点的三次变化率。
沿着样条的值- 线性使用沿着脊线的两个或多个点来定义线性规律函数。
在选择脊线曲线后,可以沿着这条曲线指出多个点。
系统会提示您在每个点处输入一个值。
沿着样条的值- 三次的使用沿着脊线的两个或多个点来定义一个三次规律函数。
在选择脊线曲线后,可以沿着该脊线指出多个点。
系统会提示您在每个点处输入一个值。
根据等式使用一个现有表达式及“参数表达式变量”来定义一个规律。
根据规律曲线允许您选择一条由光顺连接的曲线组成的线串来定义一个规律函数。
5、UG常用内置函数在UG中利用【规律曲线】|【根据方程】绘制各种方程曲线:1、极坐标(或柱坐标r,θ,z)与直角坐标系(x,y,z)的转换关系:x=r*cos(θ);y=r*sin(θ);z=z2、球坐标系(r,θ,φ)与直角坐标系(x,y,z)的转换关系:x=rsinθcosφ;y=rsinθsinφ;z=rcosθ在UG表达式中输入的theta=θ;phi=φ;r=rho【注:所有UG表达式中,必须先在名称栏输入t,公式栏输入0,类型为恒定的,即无单位。
t是UG自带的系统变量,其取值为0~1之间的连续数】1.直线直线的数学方程为y-y0=tan(θ)*(x-x0),若直线经过点(10,20),倾角θ为30°,长度L为40,即UG 表达式为:theta=30L=40xt=10+L*cos(theta)*tyt=20+L*sin(theta)*tzt=0效果如图1图1 图22.圆和圆弧圆的数学方程为(x-x0)^2+(y-y0)^2=r^2,若圆心坐标为(50,40),半径r为30,即UG表达式为:r=30theta=t*360xt=50+r*cos(theta)yt=40+r*sin(theta)zt=0效果如图23.椭圆和椭圆弧椭圆的数学方程为(x-x0)^2/a^2+(y-y0)^2/b^2=1,若椭圆中心坐标为(50,40),长半轴a为30(在X轴上),短半轴b为20,即UG表达式为:a=30b=20theta=t*360xt=50+a*cos(theta)yt=40+b*sin(theta)zt=0效果如图3图3 图44.双曲线双曲线的数学方程为x2/a2-y2/b2=1,若中心坐标为(0,0),实长半轴a为4(在x轴上),虚半轴b为3,y的取值范围为-5~+5内的一段,即UG表达式为:a=4b=3yt=10*t-5xt=a/b*sqrt(b^2+yt^2)或xt=-a/b*sqrt(b^2+yt^2)zt=0做出一半后进行镜像复制,效果如图45.抛物线抛物线I的数学方程为y2=2px,若抛物线的顶点为(30,20)焦点到准线的距离p=8,y的取值范围为-25~+25,即UG表达式为:p=8yt=50*t-25+20xt=(yt-20)^2/(2*p)+30zt=0效果如图5-1抛物线II数学参数方程:x=2pt2,y=2pt(其中t为参数)。
UG表达式为:p=8tt=t*4-2xt=2*p*tt^2yt=2*p*ttzt=0效果如图5-2图5-1图5-26.正弦曲线若正弦曲线一个周期X方向长度为50,振幅为10,即UG表达式为:theta=t*360xt=50*tyt=10*sin(theta)zt=0效果如图67.余弦曲线若余弦曲线一个周期X方向长度为50,振幅为10,即UG表达式为:theta=t*360xt=50*tyt=10*cos(theta)zt=0效果如图7图6图78.圆柱螺旋线若圆柱螺旋线半径r为20,螺距p为10,圈数n为5,即UG表达式为:r=20p=10n=5theta=t*360xt=r*cos(theta*n)yt=r*sin(theta*n)zt=p*n*t或zt=cos(theta*n)+p*n*t效果如图8图8图99.碟形弹簧若碟形弹簧半径r为20,螺距p为10,圈数n为5,即UG表达式为:r=20p=10n=5theta=t*360xt=r*cos(theta*n)yt=r*sin(theta*n)zt=cos(theta*n^2)+p*n*t或zt=cos(theta*n^2.4)+p*n*t效果如图910.圆锥螺旋线和圆台螺旋线若圆锥螺旋线底圆半径r为20,螺距p为5,圈数n为10,即UG表达式为:r=20*(1-t),若圆台上端半径为5,则r=20*(1-t*0.75)p=5n=10theta=t*360xt=r*cos(theta*n)yt=r*sin(theta*n)zt=p*n*t效果如图10-1、10-2图10-1 图10-211.三尖瓣线三尖瓣线数学方程:x=r(2cosθ+cos2θ);y=r(2sinθ-sin2θ)若将2变为n即扩展为n+1尖瓣线。
若r=20,即UG表达式为:r=20n=2theta=t*360xt=r*(n*cos(theta)+cos(n*theta))yt=r*(n*sin(theta)-sin(n*theta))zt=0效果如图11图11图1212.星形线【四尖瓣线】星形线的数学方程:x=r*cos3θ;y=r*sin3θ。
【由n+1尖瓣线通式:x=r(n*cosθ+cos(n*θ));y=r(n*sinθ-sin(n*θ))当n=3时的情况。
三角函数公式:sin3θ=3sinθ-4sin3θ;cos3θ=4cos3θ-3cosθ】若r=20,即UG表达式为:r=20theta=t*360xt=r*(cos(theta))^3yt=r*(sin(theta))^3zt=0效果如图1213.渐开线渐开线的数学方程:x=r(cosθ+θ*sinθ);y=r(sinθ-θ*cosθ)。
假设渐开线的基圆半径r为10,展开角度θ为360*2,即UG表达式为:r=10theta=360*2*ts=r*rad(theta)=r*(2*pi()/360)*theta=2*pi()*r*t*2xt=r*cos(theta)+s*sin(theta)yt=r*sin(theta)-s*cos(theta)zt=0效果如图13图13 图1414.阿基米德螺线(等径螺线)阿基米德螺线(等径螺线)数学方程:r=a*θ(极坐标),假设a=10,θ=360*2,即UG表达式为:a=10theta=t*360*2r=a*thetaxt=r*cos(theta)yt=r*sin(theta)zt=0效果如图1415.对数螺线(等角螺线)对数螺线(等角螺线)数学方程:r=aemθ。
对数螺线的定义和性质:运动方向始终与极径保持定角λ的动点轨迹称为对数螺线。
假设a=0.005,即UG表达式为:a=0.005theta=t*360*2r=exp(a*theta)xt=r*cos(theta)yt=r*sin(theta)zt=0效果如图1516.双曲螺线数学方程:r=a/θ。
若a=10,即UG表达式为:a=100theta=t*360*2+1r=a/thetaxt=r*cos(theta)yt=r*sin(theta)zt=0效果如图16图15图1617.连锁螺线数学方程:r2=a2/θ。
若a=10,即UG表达式为:a=10theta=t*360*2+1r=a/sqrt(theta)xt=r*cos(theta)yt=r*sin(theta)zt=0效果如图17图17图1818.心脏线(肾形线)心脏线数学方程:r=2a(1+cosθ);肾形线数学方程:r=a(1+2sin(θ/2))。
若a=10,θ=360°,即UG表达式为:a=10theta=360*tr=2*a*(1+cos(theta))【或r=a*(1+sin(theta))】【或r=a*(1+2*sin(theta/2))】xt=r*cos(theta)yt=r*sin(theta)zt=0效果如图1819.双弧外摆线双弧外摆线的数学方程:x=3b*cosθ+a*cos3θ,y=3b*sinθ+a*sin3θ。
即UG表达式为:a=10b=10theta=t*360xt=3*b*cos(theta)+a*cos(3* theta)yt=3*b*sin(theta)+a*sin(3* theta)zt=0效果如图19图19 图2020.肾脏线数学方程:x=a(3cost-cos3t);y=a(3sint-sin3t)a=10theta=360*txt=a*(3*cos(theta)-cos(3*theta))yt=a*(3*sin(theta)-sin(3*theta))zt=0效果如图2021.Talbot曲线【?x=(a2+f2+sin2t)cost/a,y=(a2+f2sin2t-2f2)sint/b】Talbot曲线数学方程:x=(a2+f2sin2θ)cosθ/a,y=(a2+f2sin2θ-2f)sinθ/b。
若a=1.1,b=0.666,θ=360°,f=1,即UG表达式为:theta=360*ta=1.1b=0.666c=sin(theta)f=1xt=(a^2+f^2*c^2)*cos(theta)/ayt=(a^2-2*f+f^2*c^2)*sin(theta)/bzt=0效果如图21图21 图2222.四叶线四叶线数学方程:r=a*cos2θ,若a=10,θ=360°,即UG表达式为:a=10theta=t*360r=a*cos(2*theta)xt=r*cos(theta)yt=r*sin(theta)zt=0效果如图2223.三叶线三叶线数学方程:r=a*cos3θ=a*cosθ*(4sin2θ-1),若a=10,θ=180°,即UG表达式为:a=10theta=t*180r=a*cos(3*theta)xt=r*cos(theta)yt=r*sin(theta)zt=0效果如图23图23 图2424.双叶线双叶线数学方程:r=4a*cosθ*sin2θ,若a=10,θ=89.999°,即UG表达式为:a=10theta=t*89.999r=4*a*cos(theta)*sin(2*theta)xt=r*cos(theta)yt=r*sin(theta)zt=0绘制一半后利用y轴镜像,效果如图2425.Rhodonea曲线Rhodonea曲线数学方程:r=a*sin(kθ),若UG表达式为:theta=t*360*3xt=(10-6)*cos(theta)+10*cos((10/6-1)*theta)yt=(10-6)*sin(theta)-6*sin((10/6-1)*theta)zt=0则效果如图25-1若UG表达式为:theta=t*360*5xt=4*cos(theta)+10*cos(0.8*theta)yt=4*sin(theta)-10*sin(0.8*theta)zt=0则效果如图25-2图25-1 图25-226.外摆线外摆线数学方程:x=(a+b)cosθ-r cos((a+b)/bθ);y=(a+b)sinθ-r sin((a+b)/bθ)【其中a、b、r分别是基圆、滚圆、摆点半径,θ为公转角】。
