第七章 空间问题的基本理论
《马克思主义哲学原理》第七章-社会发展和人的发展精选全文完整版

可编辑修改精选全文完整版《马克思主义哲学原理》第七章社会发展和人的发展第七章社会发展和人的发展(一)社会发展的历史进程1.社会形态及其活动构成人类社会发展的主要内容和阶段。
(1)五种社会形态社会形态是一定生产力基础之上的经济基础和上层建筑的统一体,是社会的经济形态、政治形态和观念形态的统一体。
到目前为止,人类历史已经形成了五种社会形态,即原始社会形态、奴隶社会形态、封建社会形态、资本主义社会和社会主义社会(共产主义的第一阶段)。
(2)社会形态的发展是一种自然历史过程把人类社会看做是一种自然历史过程,是历史唯物主义对社会历史的唯物辩证本性的揭示。
这一思想表明,人类社会虽然有着与自然迥然不同的特点,但本质上同自然界一样,是一种物质体系,其发展是一个不以人的意志为转移的自然历史过程。
社会发展是一个自然历史过程的主要含义是:第一,从人类社会的起源和存在的基础看,人类社会同自然界一样,在本质上是一个客观的物质体系。
人类社会是自然界长期发展的产物;人类社会的存在离不开自然界,其存在与发展的基础就是每日每时都必须进行的人与自然之间的“物质交换”活动,即采取一定的生产方式进行的物质生产活动。
第二,从人类社会的发展来看,人类社会同自然界一样,本质上是一个不以人的意志为转移的、合乎规律的辩证发展过程。
生产力与生产关系、经济基础与上层建筑的矛盾是社会的基本矛盾,人类社会正是在这两对矛盾的推动下,依次经历了原始社会、奴隶社会、封建社会、资本主义社会、社会主义社会五种社会形态,这是一个不依任何个人、任何阶级以至整个人类的意志为转移的发展过程。
第三,社会现象尽管是不可逆的,但在不可逆的社会现象背后,历史规律却有着“重复性”。
只要具备一定的条件,某种合乎规律的现象就必然重复出现。
确认社会发展是一种自然历史过程,只有把社会关系归结于生产关系,把生产关系归结于生产力的高度,才有可靠的根据把社会发展看做是自然历史过程。
这是因为:①生产力是整个社会发展的最终决定力量和根源。
弹性力学-第7章 空间问题
zx
z
dz
zy
zy
z
dz
z 0
y
y
yx yz
xy
x
yz
yz
y
dy
fz
fy fx
xz
yx
y yx dy
y
y y
dy
zx zy
x
x
x x
dx
z
根椐平衡条件: Fx 0
xz
xzx
x
dx
x
x
x
dx dydz
xdydz
(
yx
yx
x
dy)dxdz
yxdxdz
( zx
zx
z
dz)dxdy
zxdxdy
Xdxdydz
0
§7-1平衡微分方程
x x
yx y
zx
z
fx
0
xy
y
x
y
zy
z
f y
0
xz yz
x
y
z z fz 0
(7-1)
平面应力问题:
1、平面应力问题z方向应力为零:
0
xz
yz
0
z
2、所有的应力、应变和位移分量均与z无关,仅是x,y的函数。 以上方程可以直接转化为平面应力的平衡方程。
在计算任一平面上的应力时,方向余弦l,m,n可变化,但 均为有限值,故必存在某个平面,其上正应力取得极值。
主平面:正应力取得极值的平面。 主应力:主平面上的正应力。 主方向:主应力的方向,也称应力主向。 在主平面上,正应力取极值、剪应力为零。
二、主应力的确定:
设主平面存在,其外法线为n,
空间问题的基本理论

e
dz
yz P
e'
xz
dy zx
y
y y
dy
yx
yx y
dy
B
dx zy
中心的直线 e e ' 为矩轴,列出力矩 o A
z
的平衡方程 Mee' 0
xz
xz x
dx
x
x x
dx
xy
xy x
y
dx
x
y z y y zd y d x d z d 2 y y z d x d z d 2 y z y z z y d z d x d y d 2 z z y d x d y d 2 z 0
现 §在3-推6 导按第位四移在个求方解平程空式间面。问题问题里,通过研究oxy平面内平行于x、y轴两微元线
式第中四素章[D空]的—间问弹变题性的矩形基阵本或得理应论力到应变几关系何转换方矩阵程,用同样方法研究另外两平面线素的变
第第四四形章 章 空空可间间问问得题题的的到基基本本类理理论论似的方程。综合起来,得到空间问题的几何方程。
y
及
z e 2 G z
xy G xy
yz G yz
zx G zx
其中 、G — 拉密常数
ü各种弹性常数之间的关系
G 2 1 E , 1 E 1 2 ,K 3 1 E 2
D
式中 [D] — 弹性矩阵或应力应变关系转换矩阵
1
1 1
0
0
0
1
1
1
0
0
0
D
1
E 1 1
2
1
0
1 0
1 0
0
1 2
2 1
弹性力学复习思考题

其中: 为曲梁圆周边界上的分布载荷。 其中: q 为曲梁圆周边界上的分布载荷。 M, Q分别为梁截面上弯矩与剪力。 分别为梁截面上弯矩与剪力。 分别为梁截面上弯矩与剪力 应力函数: 结合应力分量与应力函数的关系确定 应力函数:
2 σθ = 2 r
= f (r)
= f (r) sin θ
= f (r) cosθ
力偶、 (9)半无限平面体在边界上作用力偶、集中力、分布力下,应力函数 )半无限平面体在边界上作用力偶 集中力、分布力下 、应力分量、位移分量的确定? 应力分量、位移分量的确定? 应力分量、位移分量的确定? (10)圆孔附近应力集中问题应力函数 、应力分量、位移分量的确定? ) (11)叠加法的应用。 )叠加法的应用。
X = l(1+ )αT,
Y = m(1+ )αT
(5)温度应力问题求解的基本思路与方法: )温度应力问题求解的基本思路与方法: (a)求出满足位移平衡方程(6-18)的一组特解(此时,无需满足 )求出满足位移平衡方程( )的一组特解(此时, 边界条件;用位移势函数求解)。 边界条件;用位移势函数求解)。 (b)不计变温,求出满足平衡方程(6-18)的一组补充解(常由应 )不计变温,求出满足平衡方程( )的一组补充解( 力函数求解,其边界条件为特解给出的面力)。 力函数求解,其边界条件为特解给出的面力)。 的概念; 与位移分量的关系; (6)位移势函数 ψ 的概念;位移势函数 ψ 与位移分量的关系;温 ) 度应力问题中, 满足的方程; 度应力问题中,位移势函数 ψ 满足的方程;应力分量的位移势 的表示。 函数 ψ 的表示。
王俊民 编 徐秉业 编
《弹性力学学习方法及解题指导》 弹性力学学习方法及解题指导》
同济大学出版社 机械工业出版社
初中数学空间理论教案

初中数学空间理论教案1. 让学生掌握空间中点、线、面的基本概念和性质。
2. 培养学生识别和运用点、线、面解决实际问题的能力。
3. 培养学生空间想象能力和抽象思维能力。
二、教学内容1. 空间中点、线、面的定义及性质。
2. 点、线、面的位置关系。
3. 点、线、面在实际问题中的应用。
三、教学重点与难点1. 重点:空间中点、线、面的基本概念和性质,点、线、面的位置关系。
2. 难点:点、线、面的位置关系的运用,解决实际问题。
四、教学方法1. 采用讲授法,讲解点、线、面的定义及性质。
2. 采用案例分析法,分析点、线、面的位置关系。
3. 采用实践法,让学生通过实际问题运用点、线、面的知识。
五、教学过程1. 导入:通过生活中的实例,引导学生认识空间中的点、线、面,激发学生的学习兴趣。
2. 讲解:详细讲解点、线、面的定义及性质,让学生理解并掌握基本概念。
3. 分析:分析点、线、面的位置关系,引导学生运用所学知识分析实际问题。
4. 实践:布置练习题,让学生通过实际问题运用点、线、面的知识,巩固所学内容。
5. 总结:对本节课的内容进行总结,强调重点知识点,布置课后作业。
六、教学评价1. 课后作业:检查学生对点、线、面知识的掌握程度。
2. 课堂练习:评估学生在实际问题中运用点、线、面的能力。
3. 学生反馈:了解学生对教学内容的满意度和建议,不断改进教学方法。
七、教学反思在教学过程中,要注意引导学生从生活中的实例认识点、线、面,培养学生的空间想象力。
同时,通过实际问题,让学生学会运用点、线、面的知识解决实际问题,提高学生的抽象思维能力。
在教学方法上,要注重启发式教学,激发学生的学习兴趣,提高学生的参与度。
空间问题的基本理论

§7-1 平衡微分方程
工程实际中,除经常碰到一些平面问题外,还会 碰到大量的空间问题,对空间问题,必须考虑三个方 向的尺度
分析空间问题,仍然要从三个方面考虑:a、静力 学方面 b、几何学方面 c、物理学方面
空间问题中未知量为: x、y、z、xy、xz、yz x、y、z、xy、xz、yz u、v、w
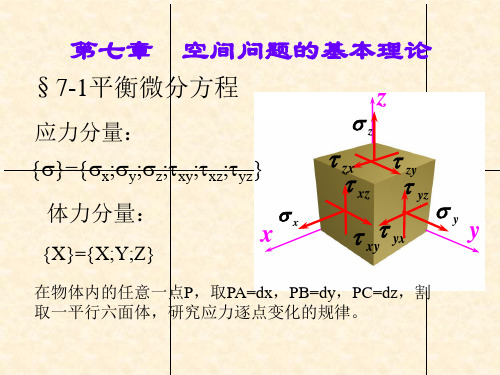
先从静力学方面考虑,导出空间问题的平衡微分方程 从物体内任一点P,取微小的平行六面体,它的六个面 垂直于坐标轴,棱边长分别为:
PA=dx, PB=dy, PC=dz
各面上的应力分量如图所示,体积力为fx、fy、fz
建立微单元的平衡微分方程:
Fx 0
x
x
yx
y
zx
z
fx
0
Fy 0
y
y
xy
r
E
1
[
1 2
r ]
j
E
1
[
1 2
j ]
z
E
1
[ 1 2
z]
zr
2(1 E
)
zr
(7-20)
小结:
空间轴对称问题的基本未知量为: 应力分量:r、j、z、zr 应变分量:r、j、z、zr 位移分量:ur、uz 这10个未知量应满足2个平衡微分方程;4个几何 方程;4个物理方程;在边界上还要满足边界条件
§ 7-4 几何方程及物理方程
一、几何方程(参照平面问题几何方程):
x
u x
y
v y
z
w z
xy
u y
v x
xz
u z
w x
yz
v z
w y
位移在边界上满足位移边界条件:
弹性力学课件-弹性力学简明教程电子教案简介与目录
2021/3/18
11
第六章 用有限元法解平面问题 第七章 空间问题的基本理论 第八章 空间问题的解答 第九章 薄板弯曲问题 附录:关于提高课堂教学质量的文章
2021/3/18
12
《弹性力学简明教程》立体化教材体系
—列入高等教育出版社百门精品课程项目
一、《弹性力学简明教程》(第三版,徐芝编) —主教材。
编者
2021/3/18
二零零六年六月16
相信梦想是价值的源泉,相信眼光决定未来的一 切,相信成功的信念比成功本身更重要,相信人 生有挫折没有失败,相信生命的质量来自决不妥
协的信念。
谢谢观看
2021/3/18
17
142021318关于弹性力学简明教程电子教案使用指南本教案是以徐芝纶教授编著的弹性力学简明教程为主教材编写的为便于用户的使用教案分为powerpoint教案弹性力学简明教程电子教案正本和打包后的教案弹性力学简明教程电子教案副本两种形式
20XX年复习资料
大学复习资料
专 业: 班 级: 科目老师: 日 期:
七、《Applied Elasticity》(徐芝纶编),
—供参考和深入学习使用。
八、《弹性力学的问题的有限单元法》(陈国荣
编),—供参考和深入学习使用。
2021/3/18
14
关于《弹性力学简明教程电子教案》使用指南
本教案是以徐芝纶教授编著的《弹性力学简明教程》为主
教材编写的,为便于用户的使用,教案分为powerpoint教案(弹
《弹性力学简明教程》电子教案(光盘), 是《弹性力学简明教程》立体化教材体 系的内容之一,是配合《弹性力学简明教 程》的教学,为教师编写的电子教案。其 中提供了示范的电子板书,及有关教学素 材,以帮助教师备课和形成自己的讲稿。
7-5 相对论时空观与牛顿力学的局限性 (教学课件)-高中物理人教版(2019)必修第二册
(钟慢效应)。
这一现象可以通过实验来验证:我们
能够在地面上探测到大气层上层产生的μ
子(曾被称为μ介子),如果没有钟慢效
应,那些μ子在到达地面之前就已经衰变
了。
钟慢效应(相对时间): ∆ =
∆
− ( )
思考1:有一种基本粒子叫μ子,当它低速运动时,它的平均寿命是3.0μs,
绕地球一周,回到原处后,分别比静止在地面上
的钟慢59纳秒和快273纳秒。
实验结果与理论预言符合的很好,
这是相对论的第一次宏观验证。
相对论的思想实验:双生子佯谬
有一对双生兄弟,其中一人跨上一宇
宙飞船作接近光速的长程太空旅行,而另
一个则留在地球。结果当旅行者回到地球
后,我们发现他比留在地球上的兄弟更年
思考2:事实上到达地面的μ子,大多产生于距地面8km的高空,科学家
们根据经典理论,可以计算出每秒到达地面的μ子个数,但这个理论数值
小于实际观察到μ子个数,这是为什么呢?
由于钟慢效应,对于地面观察者
看来,μ子的平均寿命,已不是3.0μs
了,而是约为21μs,在这段时间内,
μ子可以飞行更远的距离,更多的μ子
的结果应该是:闪光先到达后壁,后到达前壁。
闪光先到达后方侧壁
时间不再是绝对的,而是相对的——同时性是相对的
相对时空观
(1)同时是相对的
在经典物理学家的头脑中,如果两个事件在一
个参考系中看来是同时的,在另一个参考系中看来
也一定是同时的,但是如果接受爱因斯坦的两个假
设,我们会得出“同时是相对的”这样一个结论。
是一样的。
迈克尔逊-莫雷实验(Michelson-Morley Experiment),是
「第七章空间问题的基本理论」
第七章 空间问题的基本理论§7-1 平衡微分方程图7-1在物体内的任意一点P ,割取一个微小的平行六面体,它的六面垂直于从标轴,而棱边的长度为dz PC dy PBdx PA ===,,,图7-1。
一般而论,应力分量是位置坐标的函数。
因此,作用在这六面体两对面上的应力分量不完全相同,而具有微小的差量。
例如,作用在后面的正应力是x σ,由于坐标x 改变了dx 作用在前面的正应力应当是dx xx x ∂∂+σσ,余类推。
由于所取的六面体是微小的,因而可以认为体力是均匀分布的。
首先,以连接六面体前后两中心的直线ab 为矩轴,列出力矩的平衡方程0∑=abM :略去微量以后,得zy yz ττ=。
同样可以得出yx xy xz zx ττττ==,只是又一次证明了切应力的互等性。
其次,以x 轴为投影轴,列出投影的平衡方程∑=0x F ,得.0d d d d d d d )(d d d d )d (d d d d )d (=+-∂∂++-∂∂++-∂∂+z y x f y x y x dz zx z x z y y z y z y x x x zx zxzx yx yx yz x xx ττττττσσσ由其余2个平衡方程,∑=0yF 和∑=0z F ,可以得出与此相似的2个方程。
将这3个方程约简以后,除以z y x d d d ,得⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫=+∂∂+∂∂+∂∂=+∂∂+∂∂+∂∂=+∂∂+∂∂+∂∂.0,0,0z yzxz z y xy zy y x zxyz x f y x z f x z y f z y x ττσττσττσ (7-1)这就是空间问题的平衡微分方程。
§7-2 物体内任一点的应力状态现在,假定物体在任一点P 的6个直角坐标面上的应力分量,,,z y x σσσyx xy xy zx zy yz ττττττ===,,为已知,试求经过P 点的任一斜面上的应力。
6 第七章 岛屿生物地理学理论
Dr.zengzhiyong Guizhou University 4/28
Dr.zengzhiyong@
S= CAZ
式中:S——物种数 C——常数(其变化反映地理位臵的变化对种 丰富度的影响 ) Z——物种数与面积之间的系数 A——岛屿面积 对上式两边取对数,则得: log S = log C + Zlog A
Dr.zengzhiyong Guizhou University 9/28
Dr.zengzhiyong@
Dr.zengzhiyong Guizhou University 19/28
Dr.zengzhiyong@
可以设想如果岛上拥有临近大陆上所有的物种时,就 不存在新种的迁入。实际上这种情况是不可能出现的,因 为当岛上的物种越来越多时,灭绝率也越来越高。 假定在某一陆地的边缘最新形成一排大小不相同,但 距离陆地又相等的岛屿。从陆地迁入这些岛屿的物种的速 率将是一样。但是,这些岛屿上物种的灭绝率则不相同。 小岛屿上物种灭绝率要比大岛屿快,这是因为小岛屿有限 的空间使得物种之间对资源的竞争加剧,允许容纳的物种 数就相对较少,并且每个物种的种群数量也小,当迁入率 与灭绝率相等时,总的物种数也小。
达林顿(Darlington,1957)关于岛屿面积增加10倍, 岛上的动物的种数加倍的结论,即是z=0.3时的特殊 情况。设S1=CAz,那么,当岛屿的面积增加10倍, S2=C(10A)z,所以,
正常情况下,空间面积每增加10倍,物种数目平均增 ,即如果原始生态系统只有10%的面积 加 1 倍,反之亦然。 保存下来,那么,该生态系统有50%的物种丢失;如果1% 的面积保存下来,则该生态系统中有75%的物种丢失。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第七章 空间问题的基本理论§7-1 平衡微分方程图7-1在物体内的任意一点P ,割取一个微小的平行六面体,它的六面垂直于从标轴,而棱边的长度为dz PC dy PB dx PA ===,,,图7-1。
一般而论,应力分量是位置坐标的函数。
因此,作用在这六面体两对面上的应力分量不完全相同,而具有微小的差量。
例如,作用在后面的正应力是x σ,由于坐标x 改变了dx 作用在前面的正应力应当是dx xxx ∂∂+σσ,余类推。
由于所取的六面体是微小的,因而可以认为体力是均匀分布的。
首先,以连接六面体前后两中心的直线ab 为矩轴,列出力矩的平衡方程0∑=ab M :略去微量以后,得zyyzττ=。
同样可以得出yx xy xz zx ττττ==,只是又一次证明了切应力的互等性。
其次,以x 轴为投影轴,列出投影的平衡方程∑=0xF ,得.0d d d d d d d )(d d d d )d (d d d d )d (=+-∂∂++-∂∂++-∂∂+z y x f yx y x dz zxz x z y yz y z y x x x zx zxzxyx yxyzx xxττττττσσσ由其余2个平衡方程,∑=0y F 和∑=0z F ,可以得出与此相似的2个方程。
将这3个方程约简以后,除以z y x d d d ,得⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫=+∂∂+∂∂+∂∂=+∂∂+∂∂+∂∂=+∂∂+∂∂+∂∂.0,0,0zyzxzzy xyzyyx zxyzxf yxzf x z y f zy x ττσττσττσ (7-1)这就是空间问题的平衡微分方程。
§7-2 物体内任一点的应力状态现在,假定物体在任一点P 的6个直角坐标面上的应力分量,,,z y x σσσyx xy xy zx zy yz ττττττ===,,为已知,试求经过P 点的任一斜面上的应力。
为此,在P 点附近取一个平面ABC ,图7-2。
当四面体PABC 无限减小而趋于P 点,平面ABC 上的应力就成为该斜面上的应力。
n命平面ABC 的外法线为n ',其方向余弦为n z n m y n l x n ='='='),cos(,),cos(,),cos(。
设三角形ABC 面积为S d ,则三角形BPC ,CPA ,APB 的面积分别为S l d ,S m d ,S n d 。
四面体PABC 的体积用V d 代表。
三角形ABC 上的全应力p 在坐标轴上的投影用z y x p p p ,,代表。
根据四面体的平衡条件∑=0x F ,得:xyzx yzzyxn lm nl mn n m l τττσσσσ222222+++++=。
(7-3)22222n z y x n p p p στ-++=。
(7-4)如果在S 面上作用面力,则面力和应力的关系式为:⎪⎭⎪⎬⎫=++=++=++.)(,)(,)(z s yz xz z y s xy zy y x s zxyxxf m l n f l n m f n m l ττσττσττσ(在σs 上) (7-5)其中s yz s x )(,,)(τσ 是应力分量的边界值。
这就是空间问题的应力边界条件,它表明应力分量的边界值与面力分量之间的关系 。
§7-3 主应力 最大与最小的应力设经过一点P 的某一斜面上的切应力等于零,则该斜面上的正应力称为在P 点的一个主应力,该斜面称为在P 点的一个应力主面,而该斜面的法线方向称为P 点的一个应力主向。
假设在P 点有一个应力主面存在。
这样,由于该面上的切应力等于零,所以该面上的全应力就等于该面上的正应力,也就等于主应力σ。
于是该面上的全应力在坐标轴上的投影成为σσσn p m p l p z y x ===,,。
将式(7-2)代入,即得⎪⎭⎪⎬⎫=++=++=++.,σττσσττσσττσn m l n m l n m l n m l yzxzzxy zyyzx yx x(a )此外还有方向余弦的关系式1222=++n m l。
(b )如果将式(a )与(b )联立求解,能够得出n m l ,,,σ的一组解答,就得到P 点的一个主应力以及与之对应的应力主面和应力主向。
用下述方法求解,比较方便。
将式(a )改写为⎪⎭⎪⎬⎫=-++=+-+=++-.0)(,0)(,0)(n m l n m l n m l z yz xz zy y xy zxyxxσστττσστττσσ(c)这是n m l ,,的3个齐次线性方程。
因为由式(b )可见n m l ,,不能全等于零,所以这三个方程的系数的行列式式等于零,即.0=---σστττσστττσσzyzxzzy y xy zxyxx用式xy zx yz τττ,,代替yx xz zy τττ,,,将行列式展开,得σ的三次方程.0)2()()(222223=+-----+++++-xyzx yz xy y yzx zy x xyyzyx xz zy z yx ττττστσσσσσττσσσσσσσσσσσ(7-6)证明:在受力物体内的任意一点,一定存在三个互相垂直的应力主面以及对应的三个主应力。
0))()((321=---σσσσσσ。
z yxσσσσσσ++=++321。
1、体内的任意一点,三个互相垂直的面上的正应力之和是不变量(不随坐标系而变的量),并且等于该点的三个主应力之和。
2、三个主应力中最大的一个就是该点的最大正应力,而三个主应力中最小的一个就是该点的最小正应力。
3、又可见,在三个主应力相等的特殊情况下,所有各截面上的正应力都相同(也就等于主应力),而切应力都等于零。
4、最大与最小的切应力,在数值上等于最大主应力与最小主应力之差的一半,作用在通过中间主应力并且“平分最大主应力与最小主误码力的夹角”的平面上。
§7-4 几何方程及物理方程1 几何方程现在来考虑空间问题的几何学方面。
在空间问题中,形变分量与位移分量应当满足下列六个方程,即空间问题的几何方程:⎪⎪⎭⎪⎪⎬⎫∂∂+∂∂=∂∂+∂∂=∂∂+∂∂=∂∂=∂∂=∂∂=y u x x z u z y z y x u xy zx yz z y x υγωγυωγωευεε,,,,(7-8)其中的第一式、第二式和第六式已在§2-4中导出,其余三式可用同样的方法导出。
此外,在物体的给定约束位移的边界u s 上,位移分量还应当满足下列三个位移边界条件,即空间问题的位移边界条件:.)(,)(,)(ωωυυ===s s s u u (在u s 上) (7-9)此三式的等号左边是位移分量的边界值,等号右边是该边界上的约束位移分量的已知值。
2、几个重要概念。
设有微小的正平行六面体,其棱边的长度为z y x d ,d ,d 。
在变形之前,它的体积是x y x d d d ;在变形之后,它的体积将成为)d d )(d d )(d d (z z y y x x z y x εεε+++。
其公式为.1)1)(1)(1(d d d d d d )d d )(d d )(d d (z y x yx z z z y z yx z y x z y x zy x zy x z z y y x x εεεεεεεεεεεεεεεεεεθ++++++=-+++=-+++=由位移和形变量是微小的假定,可略去线应变的乘积项(更高阶的微量),则上式简化为z y x εεεθ++=。
(7-10)将几何方程(7-8)中的前三式代入,得zyxu ∂∂+∂∂+∂∂=ωυθ。
(7-11)它表明体应变与位移分量之间的简单微分关系。
物理方程:⎪⎪⎪⎪⎪⎪⎪⎭⎪⎪⎪⎪⎪⎪⎪⎬⎫+=+=+=+-=+-=+-=.)1(2,)1(2,)1(2)],([1)],([1)],([1xy xy zx zx yz yz y x z z x z y y z y x x EE E E EEγμγτμγτμγσσμσεσσμσεσσμσε (7-14)将上式的三个应变分量相加得:)(21z yx z y x Eσσσμεεε++-=++设 )(z yx σσσ++=Θ 为一个不变量得空间问题的虎克定律: Θ-=Eμθ21上式的Θ就称为 μ21-E 称为第五节 轴对称问题的基本方程在空间问题中,如果弹性体的几何形状、约束情况,以及所受的外力作用,都是对称于某一轴(通过这个轴的任一平面都是对称面),则所有的应力、形变和位移也对称于一轴。
这就问题称为空间轴对称问题。
首先来导出对称问题的平衡微分方程。
用相距ρd 的两个圆柱,互成ϕd 角的两个沿直面及相距z d 的两个水平面,从弹性全割取一个微小六面体PABC ,图7-4。
沿ρ方向的正应力,称为径向正向应力,用ρσ代表;沿ϕ方各听正应力,称为环向正应力,用ϕσ代表;沿z 方向的正应力,称为轴向正应力,代然用z σ代表;作用在圆柱面上而沿z 方向作用的切应力用z ρτ代表,作用在水平面上而沿ρ方向作用的切应力用ρτz 代表。
根据切应力的互等性,z z ρρττ=。
由于对称性,ϕρρϕττ=及ϕϕττz z =都不存在。
这样,总共只有四个应力分量:z z z ρρϕρττσσσ=,,,,一般都是ρ和z的函数。
ρd图7-4将六面体所受的各力投影到六面体中心的径向轴上,取2d sin ϕ及2d cos ϕ分别近似地等于2d ϕ及1,得平衡方程.0d d d d d d d )(2d d d 2d d d d )d )(d (=+-∂∂++--+∂∂+z f zzz z z z z ρϕρρϕρτρϕρττϕρσϕρσϕρρρρσσρρρρϕρρρZx中得空间轴对称问题的平衡微分方程如下:⎪⎪⎭⎪⎪⎬⎫=++∂∂+∂∂=+-+∂∂+∂∂.0,0zzz zz f zf z ρτρτσρσστρσρρρϕρρρ (7-15) 现在来导出轴对称问题的几何方程。
沿ρ方向的线应变,称为径向线应变,用ρε代表;沿ϕ方向的线应变,称为环向线应,用ϕε代表;沿z方向的线应变,称为轴向线应变,仍然用z ε代表;ρ方向与z 方向之间的直角的改变用ργz 代表。
由于对称,ρϕγ及ϕργ都等于零。
沿ρ方向的位移分量称为径向位移,用ρu 代表;沿z 方向的位移分量称为轴向位移,用z u 代表。
由于对称,环向位移0=ϕu 。
通过与§2-4及§4-2中同样的分析,可见,由于径向位移ρu 引起的形变是ργρερερρρϕρρ∂∂==∂∂=u u u z ,,。
将以上两组形变相叠加,得空间轴对称问题的几何方程ργερερερρρϕρρ∂∂+∂∂=∂∂==∂∂=z z z z u zu zu u u ,.,。
