06自回归条件异方差(ARCH)模型
使用ARCH模型进行金融计算
使用ARCH模型进行金融计算ARCH模型是金融领域中常用的一种计量经济学方法，用于分析和预测金融时间序列数据的波动性。
ARCH模型的全称是自回归条件异方差模型（Autoregressive Conditional Heteroskedasticity Model），它能够捕捉到金融市场中的波动性聚集现象，帮助投资者更好地理解和应对市场风险。
首先，ARCH模型的基本思想是，金融市场中的价格和收益率并不是随机波动的，而是存在一定的波动性聚集现象。
也就是说，市场的波动性在某个时期内可能会比其他时期更高或更低。
ARCH模型通过引入条件异方差的概念，能够对这种波动性聚集进行建模。
ARCH模型的核心是条件异方差，即波动性的方差是与过去的波动性有关的。
在ARCH模型中，通过引入滞后期的平方误差项来捕捉波动性的变化。
具体来说，ARCH模型可以表示为：σt^2 = α0 + α1ε(t-1)^2 + α2ε(t-2)^2 + ... + αpε(t-p)^2其中，σt^2表示第t期的条件异方差，ε(t-i)表示第t-i期的误差项，α0、α1、α2...αp是模型的参数，p是滞后期数。
ARCH模型的核心思想是，过去的波动性会对当前的波动性产生影响，通过对过去波动性的建模，可以更好地预测未来的波动性。
ARCH模型的应用范围非常广泛，包括股票、债券、汇率、商品等金融市场中的各种时间序列数据。
例如，在股票市场中，投资者可以利用ARCH模型对股票的波动性进行建模，从而制定更合理的投资策略。
在外汇市场中，投资者可以利用ARCH模型对汇率的波动性进行预测，从而进行有效的风险管理。
此外，ARCH模型还可以与其他模型相结合，进行更复杂的金融计算。
例如，可以将ARCH模型与随机游走模型相结合，构建GARCH模型（GeneralizedARCH Model），从而更准确地描述金融市场中的波动性聚集现象。
GARCH模型在金融风险管理、期权定价等领域有着广泛的应用。
自回归条件异方差模型在经济统计学中的应用
自回归条件异方差模型在经济统计学中的应用自回归条件异方差模型（ARCH）是一种经济统计学中常用的时间序列模型，用于分析和预测金融市场波动性。
本文将探讨ARCH模型的应用，以及其在经济统计学中的重要性。
首先，我们来了解一下ARCH模型的基本原理。
ARCH模型是由罗伯特·恩格尔于1982年提出的，用于描述时间序列数据中的异方差性。
在传统的线性回归模型中，假设误差项的方差是恒定的，但实际上，金融市场的波动性往往是不稳定的。
ARCH模型通过引入滞后期的方差来捕捉时间序列数据中的异方差性，从而更准确地描述和预测金融市场的波动性。
ARCH模型的核心思想是，当前时刻的波动性受到过去一段时间内波动性的影响。
具体而言，ARCH模型假设波动性的变化是由过去一段时间内的波动性决定的，而不是由其他因素决定的。
这种模型的优势在于能够捕捉到金融市场中的波动性聚集效应，即波动性在一段时间内呈现出明显的聚集或离散的特征。
ARCH模型的应用非常广泛，尤其在金融领域中发挥着重要的作用。
首先，ARCH模型可以用于金融市场的风险度量和风险管理。
通过对金融资产的波动性进行建模，可以更准确地估计风险水平，为投资者提供更可靠的风险评估指标。
其次，ARCH模型可以用于金融市场的波动性预测。
通过对过去一段时间内的波动性进行建模，可以预测未来的波动性水平，为投资者提供投资决策的参考依据。
此外，ARCH模型还可以用于金融市场的高频交易策略。
通过对短期波动性的建模，可以捕捉到市场中的短期交易机会，实现高频交易的盈利。
除了金融领域，ARCH模型在宏观经济学中也有着重要的应用。
例如，ARCH模型可以用于对宏观经济数据中的波动性进行建模和预测。
通过对经济数据的波动性进行分析，可以更好地理解经济的周期性波动和结构性变化，为宏观经济政策的制定提供参考。
此外，ARCH模型还可以用于对宏观经济风险的度量和管理，为国家和地区的宏观经济政策提供支持。
总之，自回归条件异方差模型在经济统计学中具有重要的应用价值。
arch模型的原理 -回复
arch模型的原理-回复ARCH模型，即自回归条件异方差模型（Autoregressive Conditional Heteroskedasticity Model），是为了捕捉时间序列数据中异方差（heteroskedasticity）现象而生的一种经济计量模型。
在本文中，将一步一步回答“ARCH模型的原理”。
第一步，我们先了解什么是异方差。
异方差是指时间序列数据中，随着时间的推移，序列的方差出现明显变化的情况。
在金融市场，股票价格或金融资产的收益率常常呈现出异方差现象，即在某些时期波动较小，而在其他时期波动较大。
这种异方差现象对于风险度量和预测模型的构建都有很大的影响。
第二步，ARCH模型的基本思想是通过引入时间序列自己的过去序列的方差来解释序列的异方差现象。
也就是说，ARCH模型假设时间序列数据的方差是由过去的误差平方项决定的。
如果过去的方差较大，那么未来的方差也会较大；反之，如果过去的方差较小，那么未来的方差也会较小。
第三步，ARCH模型的具体形式是通过引入一个滞后期数的误差项平方的线性组合来表示方差的变化。
以ARCH(p)模型为例，其表达式为：σ^2_t = α_0 + α_1 * ε^2_(t-1) + α_2 * ε^2_(t-2) + ... + α_p * ε^2_(t-p)其中，σ^2_t表示时间t的方差，α_0为常数项，α_i（i=1,2,...,p）为参数，ε_t（t=1,2,...,p）为误差项。
在ARCH(p)模型中，根据过去p期的误差项平方的线性组合来估计当前时间的方差。
第四步，ARCH模型的参数估计可以使用最大似然估计法（Maximum Likelihood Estimation，简称MLE）进行。
MLE的思想是找到一组参数值，使得模型产生的数据的概率最大化。
对于ARCH模型，我们需要对误差项的平方进行参数估计，然后利用MLE来求解最优的参数。
第五步，ARCH模型的估计和预测过程需要进行模型检验。
arch模型
ARCH 模型不确定性是现代经济和金融理论经常涉及到的一个焦点问题。
例如，宏观经济波动的不确定性、金融市场上收益的不确定性以及外汇市场上各国汇率的不确定性等。
在模型分析中，经济或金融变量的不确定性一般用方差来进行描述和度量。
而且为了分析简洁，通常对模型作出一些假定，例如在回归模型中假定随机扰动项满足零均值、同方差和互不相关。
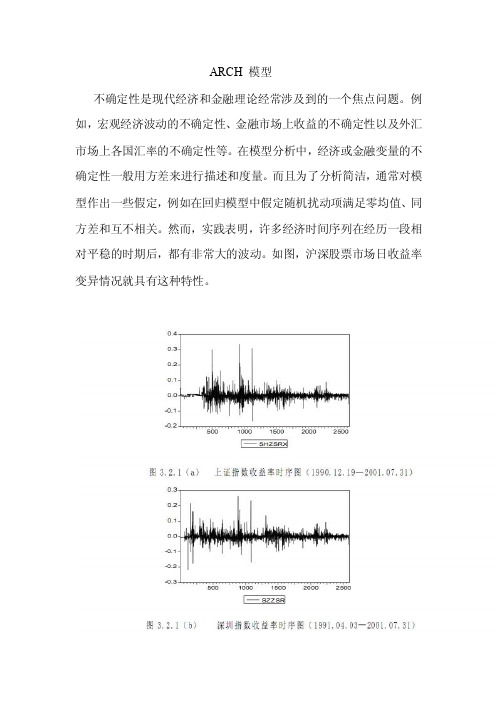
然而，实践表明，许多经济时间序列在经历一段相对平稳的时期后，都有非常大的波动。
如图，沪深股票市场日收益率变异情况就具有这种特性。
在这种情况下，同方差假定是不恰当的。
在这种情况下，人们关心的是如何预测序列的条件方差。
例如，作为资产持有者，他既关心收益率的预测值，同时也关心持有期内方差的大小。
如果一位投资者计划在第 t 时期买入某项资产，在第 t+1 时期售出，则无条件方差（即方差的长期预测值）对他来讲就不重要了。
对于这一类问题，可以使用自回归条件异方差模型 （autoregressive conditiona heteroskedastic model ，简称 ARCH 模型）来进行分析。
最早的 ARCH 模型是由 Robert Engle 于 1982 年建立的，因此它的发展历史不长。
但是，这种模型及其各种推广形式已被广泛应用于经济和金融数据序列的分析，ARCH 模型族已成为研究经济变量变异聚类特性的有效工具。
第一节 ARCH 模型的概念与性质 1、ARCH 过程ARCH 模型的一般性定义如下。
假设时间序列{}t y 服从如下回归模型：'t t ty x u ξ=+(8.1.1)其中 t x 是外生变量向量，它可以包含被解释变量的滞后项，ξ是回归参数向量。
如果扰动项序列{}t u 满足：11|~(0,)(,,)t t t t t t q u N h h h u u ---Ω= (8.1.2)其中：11122{,',,'}t t t t t y x y x -----Ω= 为t 时期以前的信息集。
时间序列计量经济学模型概述
时间序列计量经济学模型概述时间序列计量经济学模型是在经济学研究中广泛使用的一种方法，用于分析经济变量随时间的变化。
该模型基于时间序列数据，即经济变量在一段时间内的观测值。
时间序列计量经济学模型的核心是建立经济变量之间的关系，以解释和预测经济现象的变化。
其中最常用的模型是自回归移动平均模型（ARMA）、自回归条件异方差模型（ARCH）和季节性时间序列模型。
自回归移动平均模型（ARMA）是一个包含自回归项和移动平均项的线性模型。
该模型以过去的观测值和随机项为输入，预测当前观测值。
ARMA模型基于假设，即经济变量的行为受到历史观测值的影响。
自回归条件异方差模型（ARCH）是一种考虑了随时间变化方差的模型。
该模型通过引入一个条件异方差项，模拟经济变量中的波动性。
ARCH模型的应用范围广泛，特别是在金融市场波动性分析中。
季节性时间序列模型用于分析具有明显季节性特征的经济变量，如销售额、就业人数等。
这些模型通常基于季节、趋势和随机成分的组合，以预测未来观测值。
在建立时间序列计量经济学模型时，常常需要进行模型识别、参数估计和模型诊断等步骤。
识别模型的目标是确定适当的模型结构，参数估计则是利用历史数据估计模型的参数值。
模型诊断用于检验模型的拟合程度和误差分布是否符合模型假设。
时间序列计量经济学模型在经济研究中有广泛的应用，例如预测未来经济指标、分析经济周期和波动性、评估政策效果等。
它提供了一种量化的方法，使经济学家可以更好地理解和解释经济变量的演变。
时间序列计量经济学模型是经济学研究中一种重要的统计工具，广泛应用于宏观经济、金融市场和企业经营等领域。
它可以帮助我们理解和解释经济变量随时间的变化规律，进行预测和政策分析。
本文将进一步探讨时间序列计量经济学模型的相关概念和应用。
在构建时间序列计量经济学模型之前，首先需要了解时间序列数据的特点。
时间序列数据是按照时间顺序排列的一系列观测值，通常具有趋势性、季节性、周期性和随机性等特征。
GARCH模型
二、ARCH过程
Engle(1982)提出的ARCH模型，正是在不使用特定变量 xt 或数据转 换的情况下，同时对序列的均值和方差进行建模。要理解Engle的方 法，首先我们要估计平稳ARCH模型 yt a0 a1 yt 1 t 并预测 yt 1 ， 则 yt 1 的条件均值为 Et yt 1 a0 a1 yt ，若我们用这个条件均值去预 测 yt 1 ，则预测误差方差为 Et [( yt 1 a0 a1 yt )2 ] Ett21 2。 ˆt 表示模型 yt a0 a1 yt 1 t 的残差估计值，那么 yt 1的条件方 若用 差为： var( y y ) E [( y a a y )2 ] E ( )2
GRACH模型
三、GRACH模型
Bollerslev广义自回归条件异方差(Generalized ARCH,GARCH)模型。 GARCH类模型最早是Engle提出的ARCH模型，即自回归条件异方差 模型。设标的资产时间序列为{ yt } , Engle年建立了回归模型ARCH(q)，
y t 是因变量，x t 是解释变量的向量， 其中， 是未知参数的向量, 假设 t 的在给定 (t 1) 时间内的信息 t 1 满足正态分布， t | t 1 ~ N ( 0, ht ) ， 但其条件方差为：
ARCH模型
一、金融时间序列的异方差性特征
现实金融市场上，许多金融时间序列并没有恒定的均值，大多数 序列在呈现出阶段性的相对平稳的同时，往往伴随着出现剧烈的 波动性。 金融市场中，波动率（volatility）是金融时间序列最重要的特征 之一，因而模拟和预测股票市场的波动性已经成为众多理论和实 证研究的重要领域。然而，金融市场时间序列存在非平稳性，样 本均值并不恒定，有明显的异方差性特征。因此，传统线性结构 模型（以及时间序列模型）并不能很好地解释金融数据的重要特 征。
ARCH模型介绍
ARCH模型介绍σ_t^2=α_0+α_1*ε_(t-1)^2+α_2*ε_(t-2)^2+...+α_p*ε_(t-p)^2其中，σ_t^2表示在t时刻的波动性，α_0表示常数项，α_1,α_2,...,α_p是ARCH模型的参数，ε_t-1,ε_t-2,...,ε_t-p是t时刻的残差。
ARCH模型最重要的特点是它能够捕捉到波动性的聚集，即高波动性的时期往往会持续一段时间，而低波动性的时期也会持续一段时间。
这是因为ARCH模型中的参数可以控制波动性的趋势和持续性。
当参数值较大时，波动性的变化会更加剧烈；当参数值较小时，波动性的变化会更加平缓。
ARCH模型在金融领域特别受到关注，因为金融市场的波动性非常重要。
通过使用ARCH模型，我们可以对金融市场的波动性进行建模和预测。
例如，可以利用ARCH模型来估计股票价格的波动性，进而对股票的风险进行评估。
此外，ARCH模型还可以用于进行对冲策略的设计，以便在市场波动性较高时降低风险。
除了ARCH模型，还有一种更广义的模型叫做GARCH模型，即广义自回归条件异方差模型。
GARCH模型在ARCH模型的基础上增加了过去时刻波动性的指数加权平均项。
这允许GARCH模型能够更好地捕捉到波动性的长期记忆特性。
GARCH模型的一般形式可以表示为：σ_t^2=α_0+α_1*ε_(t-1)^2+α_2*ε_(t-2)^2+...+α_p*ε_(t-p)^2+β_1*σ_(t-1)^2+β_2*σ_(t-2)^2+...+β_q*σ_(t-q)^2其中，σ_t^2表示在t时刻的波动性，α_0表示常数项，α_1,α_2,...,α_p是ARCH模型的参数，β_1,β_2,...,β_q是GARCH 模型的参数，ε_t-1,ε_t-2,...,ε_t-p是t时刻的残差，σ_t-1,σ_t-2,...,σ_t-q是t时刻的波动性。
GARCH模型在金融领域的应用更为广泛，因为它可以更准确地描述金融市场中的波动性。
条件异方差模型
条件异方差模型条件异方差模型是一种用于描述时间序列数据的统计模型，它考虑到了不同时间点上的方差可能是不同的。
这种模型可以用来分析股票价格、汇率等金融数据，也可以用来分析环境变量、气象数据等自然科学数据。
在条件异方差模型中，方差是一个随时间变化的函数，通常被称为条件方差。
这意味着，在给定一些先前观察到的数据之后，我们可以预测未来观测值的方差。
这种方法比传统的线性回归模型更加准确，因为它能够捕捉到随着时间推移而发生变化的不确定性。
条件异方差模型最常见的形式是ARCH（自回归条件异方差）和GARCH（广义自回归条件异方差）模型。
ARCH模型是一种基于过去观测值的平方误差来预测未来观测值误差方差的模型。
GARCH模型则扩展了ARCH模型，并允许过去多个时间点上的平方误差对当前观测值误差方差产生影响。
在实际应用中，我们通常使用最小二乘法或极大似然估计法来拟合条件异方差模型。
最小二乘法是一种通过最小化残差平方和来确定模型参数的方法，而极大似然估计法则是一种基于观测到的数据来估计未知参数的方法。
需要注意的是，条件异方差模型并不适用于所有类型的时间序列数据。
例如，在具有周期性变化或季节性变化的数据中，方差通常是稳定的，因此不需要使用条件异方差模型。
此外，在具有明显趋势或趋势突变的数据中，也可能需要使用其他类型的时间序列模型。
总之，条件异方差模型是一种强大而灵活的统计工具，可以用于分析各种类型的时间序列数据。
它能够捕捉到随着时间推移而发生变化的不确定性，并且可以通过最小二乘法或极大似然估计法来拟合模型参数。
但需要注意，它并不适用于所有类型的时间序列数据，并且在实际应用中需要谨慎选择合适的模型。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
④ 用第3步得到的可决系数R2构造统计量LM = TR2。其中T表示辅 助回归式的样本容量。 在原假设成立条件下，LM统计量服从自由度为p的2分布，计算 的LM统计量小于临界值，接受原假设；否则，拒绝原假设。
6
一、ARCH过程
检验方法2：ARCH的F检验
① 建立原假设 H0：a1 = a2 = … = ap = 0 （不存在ARCH） H1：a1, a2 , …, ap 不全为零 ˆt2 ② 估计均值方程，求出残差的平方序列 ③ 分别估计有约束模型和无约束模型
ht a0 a
2 1 t 1d 源自2 1 t 1 t 1 1ht 1
1, t 1 0 dt 1 0, t 1 0
14
四、模型扩展
2. 非对称模型：TARCH和EGARCH EGARCH模型
ln(ht ) a0 a1 (t 1 / h ) 1 | t 1 / h | 1 ln(ht 1 )
yt 0 1 yt 1 t
均值方程
ARCH方程
t t a0 a
2 1 t 1
其中t是均值为0，方差为1的白噪声过程，且与t-1 相互独立。 t序列特征
零均值，无自相关 2 E ( 无条件方差： t ) a0 / (1 a1 ) 条件方差： t2 E( t2 | t 1 , t 2 ,) a0 a1 t2 1
ht a0 a1 (0.4 t21 0.3 t22 0.2 t23 0.1 t24 )
8
二、GARCH模型
ARCH模型中条件方差是自回归过程，Bollerslev （1986）将其扩展到ARMA过程 假定误差过程为： t t ht p q 且 2
qt 2.767 pte 0.521ht 4.325 pfeedt 1 1.887hatcht 1 0.603qt 4 1t
10
三、EViews应用举例（波动缓和）
问题提出
宏观经济变量特征：1984年后波动出现衰减 Stock和Watson（2002）指出1984~2002年的美国真实 GDP增长的标准差相对于1960~1983年减少了61%. Romer（1999）也谈到，良好的货币政策可以使中央银 行更好地促进经济稳定
15
① 建立原假设 H0：a1 = a2 = … = ap = 0 （不存在ARCH） H1：a1, a2 , …, ap 不全为零 ˆt2 ② 估计均值方程，求出残差的平方序列 ③ 估计辅助回归式
ˆt2 a0 a1 ˆt21 ap ˆt2 p t
第六讲 自回归条件异方差(ARCH)模型
一、ARCH过程 二、GARCH模型 三、EViews应用举例 四、模型扩展
一、ARCH过程
传统计量经济学都假设干扰项的方差为常数，但 很多经济时间序列具有非常大的波动，持续一段 时间后又会相对稳定一段时间，并且这种现象是 循环往复的。
400 300 200 100 0 -100 -200 -300 -400
研究目的：1984年第1季度是否有波动性突变 合理的均值模型：
yt 0.006 0.331yt 1 t (7.14) (5.47)
11
三、EViews应用举例（波动缓和）
异方差检验：
2 5 2 2 ˆ ˆ ˆ t 5.48 10 0.099 t 1 0.131 t 2
(1 0.511L 0.129L2 0.130L3 0.138L4 )Pt 1.632 2t (0.092) (0.098) (0.094) (0.175) (0.073) (1.347)
2 ht 1.353 0.163 2 t 1 0.591ht 1
(0.747) (0.80)
ht a0 a1 t i i ht i
i 1 i 1
上式称为GARCH(p,q)模型 GARCH模型的优点在于：一个高阶的ARCH模型 可能有一个更为简洁且更易识别和估算的GARCH 表达式。
9
二、GARCH模型
例：风险的GARCH模型（Holt和Aradhyula，1990） 研究目的：测算美国烤鸡业生产者的风险厌恶程度 烤鸡的供给函数
ˆt23 0.140 t24 0.015
可以证明序列yt表现了条件性波动 引入虚拟变量Dt，ARCH(1)模型重新估计
yt 0.005 0.321yt 1 t (8.23) (5.10) ˆt21 9.54 105 Dt ht 1.16 104 0.086 (7.55) (1.08) (6.24)
考虑如下模型
yt 1 t 1xt
var( yt 1 | xt ) xt2 2
如果xt = xt-1 = … = 常数，则yt就是方差恒定的白噪 声过程；如果xt变化，则yt就是异方差；如果xt呈 现出正序列相关，则yt的条件方差也呈现出序列正 相关。
3
一、ARCH过程
简单ARCH(1)模型（Engle，1982）
一般ARCH(p)模型
t t a0 i 1 ai t2i
p
a0 a
2 t
2 1 t 1
a
2 2 t 2
a
2 p t p
5
一、ARCH过程
均值方程的误差项是否存在自回归条件异方差应该进行假 设检验 检验方法1：ARCH的LM检验
12
四、模型扩展
1. ARCH-M模型
允许序列的均值依赖于它的条件方差 适用于资产市场的研究，其基本观点是风险厌恶的投资者 会在持有风险资产时要求相应的风险补偿。由于一项资产 的风险可以用收益的方差来衡量，风险溢价就是收益的条 件方差的增函数。 如：持有一项风险资产所带来的超额收益可描述为
ˆt2 a0 t ˆt2 a0 a1 ˆt21 a p ˆt2 p t
④ 利用两个模型的残差平方和构造F统计量
( SSRr SSRu ) / p F ~ F ( p, T p 1) SSRu / (T p 1)
检验方法3：模型残差平方的Q检验
qt a0 a1 pte a2ht a3 pfeedt 1 a4 hatcht 1 at qt 4 1t
注意：这里衡量了价格的条件方差对烤鸡供给的负面影响 2 3 4 (1 L L L L )P 价格模型： 1 2 3 4 t 0 2t 经检验价格存在异方差，GARCH(1,1)估计结果
4
一、ARCH过程
yt序列特征
条件均值和方差
Et 1 ( yt ) 0 1 yt 1 var( yt | yt 1 , yt 2 ,) Et 1 ( yt 0 1 yt 1 ) 2 Et 1 ( t ) 2 a0 a1 t21
7
一、ARCH过程
例：Engle的英国通货膨胀模型 pt：英国消费者物价指数的对数；wt：名义工资率 指数的对数，则通货膨胀率为t = pt – pt-1，实际 工资为rt = wt – pt t=0.0257+0.334t-1+0.408t-4–0.404t-5+0.0559rt-1+t (0.006) (0.103) (0.110) (0.114) (0.014) ht = 8.910-5 ARCH检验：ARCH(1)不显著，但ARCH(4)=15.2， 大于临界值13.28，因此，存在ARCH误差
0.5 t 1 0.5 t 1
特点
(1)条件方差为线性对数形式，ht不会为负，所以允许系 数为负 (2)EGARCH使用标准化的t-1的值，这种标准化的值能 够更准确地解释冲击的大小和持续性，因为标准化的 值没有度量单位 (3)EGARCH模型考虑了杠杆效应。如果t-1为正，冲击 对条件方差的对数的影响是a1+1，否则为-a1+1
2
波动集群 (volatility clustering)
-500 2000 2001 2002 2003 2004 2005 2006 2007 2008
一、ARCH过程
有时，我们可能需要预测序列的条件方差
对于资产持有者，往往对该资产在持有期间的回报率 及其方差感兴趣。 如果投资者打算在t期买进该资产，在t+1期卖出，无条 件方差（即对方差的长期预测）就不重要了
yt t t
t ht 0
ht a0 a
i 1 p 2 i t i
13
四、模型扩展
2. 非对称模型：TARCH和EGARCH
“坏”消息对资产价格波动性的影响远大于“好”消息的 影响 对许多股票而言，当前收益和未来波动之间呈很强的负相 关，收益增加时波动减小，收益减少时，波动增加，这一 趋势通常被称为杠杆效应（leverage effect） TARCH模型