Hough变换实例 很清晰的
利用Hough变换实现直线的快速精确检测

第13卷 第2期2008年2月中国图象图形学报Journal of I m age and GraphicsVol .13,No .2Feb .,2008收稿日期:2006204225;改回日期:2006210217第一作者简介:滕今朝(1970~ ),男,讲师。
2007年于海军航空工程学院获测试计量仪器与科学专业硕士学位。
主要从事电气自动化、检测技术方面的教学和研究。
E 2mail:t w rite@利用Hough 变换实现直线的快速精确检测滕今朝1) 邱 杰2)1)(威海职业学院机电工程系,威海 264210) 2)(海军航空工程学院,烟台 264000)摘 要 利用Hough 变换对直线进行检测,通常存在“速度缓慢、结果不够精确”的问题,本文提出了“分式查表法”,能在大幅度减少Hough 变换的总计算量的情况下,检测精度保持最高,从而使超大型图像中,直线的实时、精确检测成为可能。
关键词 Hough 变换 参数空间 精度 分式查表法中图法分类号:TP391.41 文献标识码:A 文章编号:100628961(2008)022*******Fa st and Prec ise D etecti on of Stra i ght L i n e w ith Hough Tran sformTE NG J in 2zhao 1),Q I U J ie2)1)(E lectro m echanical Engineering D epart m ent,W eihai V ocational College,W eihai 264210)2)(College of N avy A viation Engineering,Yantai 264000)Abstract Pr oble m s as l ow s peed or inaccurate results in the p r ocess of line detecti on with Hough Transf or m re main unsatisfact orily s olved .This paper puts f or ward a ne w l ook 2up table t o decrease the computati on distinctly and keep ing the highest p recisi on .It offers the possibility in real 2ti m e app licati ons es pecially in large i m age .Keywords Hough Transf or m,para meter s pace,p recisi on,table l ook 2up1 引 言Hough 变换具有优异的鲁棒性和极佳的抗干扰能力,利用Hough 变换进行直线检测,是图像分析和计算机视觉的一个重要内容。
Python下opencv使用hough变换检测直线与圆
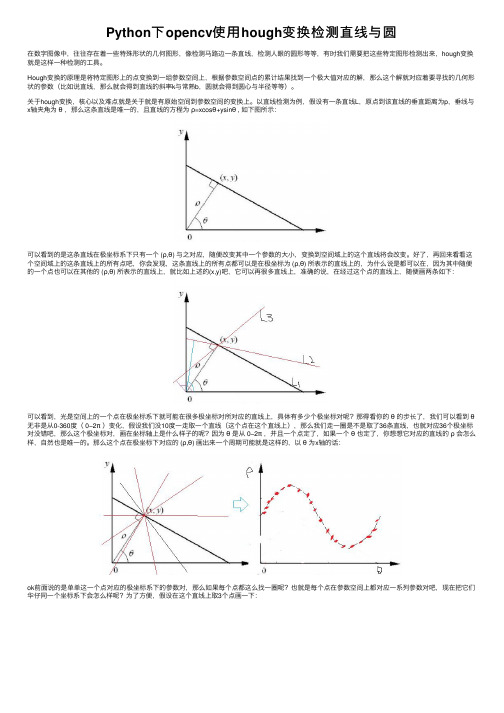
Python下opencv使⽤hough变换检测直线与圆在数字图像中,往往存在着⼀些特殊形状的⼏何图形,像检测马路边⼀条直线,检测⼈眼的圆形等等,有时我们需要把这些特定图形检测出来,hough变换就是这样⼀种检测的⼯具。
Hough变换的原理是将特定图形上的点变换到⼀组参数空间上,根据参数空间点的累计结果找到⼀个极⼤值对应的解,那么这个解就对应着要寻找的⼏何形状的参数(⽐如说直线,那么就会得到直线的斜率k与常熟b,圆就会得到圆⼼与半径等等)。
关于hough变换,核⼼以及难点就是关于就是有原始空间到参数空间的变换上。
以直线检测为例,假设有⼀条直线L,原点到该直线的垂直距离为p,垂线与x轴夹⾓为θ,那么这条直线是唯⼀的,且直线的⽅程为ρ=xcosθ+ysinθ , 如下图所⽰:可以看到的是这条直线在极坐标系下只有⼀个 (ρ,θ) 与之对应,随便改变其中⼀个参数的⼤⼩,变换到空间域上的这个直线将会改变。
好了,再回来看看这个空间域上的这条直线上的所有点吧,你会发现,这条直线上的所有点都可以是在极坐标为 (ρ,θ) 所表⽰的直线上的,为什么说是都可以在,因为其中随便的⼀个点也可以在其他的 (ρ,θ) 所表⽰的直线上,就⽐如上述的(x,y)吧,它可以再很多直线上,准确的说,在经过这个点的直线上,随便画两条如下:可以看到,光是空间上的⼀个点在极坐标系下就可能在很多极坐标对所对应的直线上,具体有多少个极坐标对呢?那得看你的θ的步长了,我们可以看到θ⽆⾮是从0-360度( 0−2π)变化,假设我们没10度⼀⾛取⼀个直线(这个点在这个直线上),那么我们⾛⼀圈是不是取了36条直线,也就对应36个极坐标对没错吧,那么这个极坐标对,画在坐标轴上是什么样⼦的呢?因为θ是从 0−2π,并且⼀个点定了,如果⼀个θ也定了,你想想它对应的直线的ρ会怎么样,⾃然也是唯⼀的。
那么这个点在极坐标下对应的 (ρ,θ) 画出来⼀个周期可能就是这样的,以θ为x轴的话:ok前⾯说的是单单这⼀个点对应的极坐标系下的参数对,那么如果每个点都这么找⼀圈呢?也就是每个点在参数空间上都对应⼀系列参数对吧,现在把它们华仔同⼀个坐标系下会怎么样呢?为了⽅便,假设在这个直线上取3个点画⼀下:那么可以看到,⾸先对于每⼀个点,在极坐标下,会存在⼀个周期的曲线来表⽰通过这个点,其次,这三个极坐标曲线同时经过⼀个点,要搞清楚的是,极坐标上每⼀个点对 (ρ,θ) 在空间坐标上都是对应⼀条直线的。
Hough变换

3)将全部(xi,yi)处理后,分析M(,),如果 M(,)T,就认为存在一条有意义的线段,是该线段
的拟合参数。T是一个非负整数,由图像中景物的先 验知识决定。
y
(xi,yi)
图8-14 点的Houghx变换的极坐标形式
y
0=xcos0+ysin0 (xi,yi)
(0,0)
图8-15 共线点Houxgh变换的极坐标形式
数字图像处理与分析基础
算法
1)将(,)空间量化,得到二维矩阵M(,), M(,)是一个累加器,初始值为0,M(,)=0。
直线。对于(x,y)空间的任意一点(xi,yi),采用
极坐标(,)作为变换空间,其变换方程为:
=xicos+y间的一点(xi,yi)对应于(,)空
间的一条正弦曲线,其相位和幅值由xi、yi决定。
数字图像处理与分析基础
(x,y)空间的同一条直线上的点在(,)空间的正弦 曲线都会相交于点(0, 0),0为这条直线到原点的 距离, 0为直线的法线与轴的夹角,
边缘连接——Hough变换
Hough变换[Hough,1962]是一种基于图像全局分割 结果的边缘连接技术,它抗干扰能力强,能检测出 任意形状的曲线,即使线上有许多的断裂,因此在 图像分析的预处理中获得广泛应用。下面只介绍检 测直线的经典方法。
设图像空间(x,y)中的一条直线的方程为:
y=u0x+v0 式中u0为斜率,v0为截距。那么对于直线上的任意 一点pi(xi,yi),它在由斜率和截距组成的变换空间
(u,v)中将满足方程式:
Hough变换检测直线

Hough 变换检测直线实验报告一,实验要求用hough 算法检测图像中的直线算法。
使用这一算法来求一幅图像中的所有大于规定长度的直线段,设规定的长度为20点。
二,Hough 变换简介Hough 变换是图像处理中从图像中识别几何形状的基本方法之一。
Hough 变换的基本原理在于利用点与线的对偶性,将原始图像空间的给定的曲线通过曲线表达形式变为参数空间的一个点。
这样就把原始图像中给定曲线的检测问题转化为寻找参数空间中的峰值问题。
图1 Hough 变换)sin(sin cos 00θαθθρ+=+=A y x如上图所示,在图像空间,直线上一点),(00y x 转换到参数空间就是一条曲线,而且,图像空间同一直线上的点转换到参数空间的曲线一定相交于一点,即参数空间各曲线的交点对应着图像空间的一条直线,这样,检测参数空间曲线交点就检测出了图像空间的直线。
三,实验过程和结果分析用Hough 变换之前, 首先要对图像进行边缘检测的处理,也即霍夫线变换的直接输入只能是边缘二值图像。
本实验基于VS2008和OPENCV 来实现。
实验的步骤如下:(1)读入图像,转换成灰度图像OPENCV 中用cvLoadImage 函数来读取图像,函数原型:IplImage* cvLoadImage( const char* filename, int flags=CV_LOAD_IMAGE_COLOR );filename :要被读入的文件的文件名(包括后缀);flags :指定读入图像的颜色和深度;例如:cvLoadImage( fileame, -n1 ); //默认读取图像的原通道数cvLoadImage( filename, 0 ); //强制转化读取图像为灰度图 cvLoadImage( filename, 1 ); //读取彩色图(2)进行边缘检测本实验选择Canny算子的边缘检测,OPENCV中用Canny函数来进行Canny 算子的边缘检测,函数原型为:void cvCanny( const CvArr* image, CvArr* edges, double threshold1, double threshold2, int aperture_size=3 );image:单通道输入图像edges:单通道存储边缘的输出图像threshold1 :第一个阈值threshold2 :第二个阈值aperture_size :算子内核大小3,对检测出的二值图像进行Hough变换OPENCV中用cvHoughLines2函数来进行Hough变换,函数原型为:CvSeq* cvHonghLines2(CvArr* image,void* line_storage,int mehtod,double rho,double theta,int threshold,double param1 =0,double param2 =0);Image:输入8-比特、单通道(二值)图像line_storage:检测到的线段存储仓Method:Hough 变换变量,是下面变量的其中之一CV_HOUGH_STANDARD ——传统或标准Hough 变换CV_HOUGH_PROBABILISTIC——概率Hough 变换CV_HOUGH_MULTI_SCALE ——传统Hough 变换多尺度变种Rho:以象素为单位的距离精度,一般取1Theta:以弧度为单位角度精度,一般取CV_PI/180Threshold:阈值参数,当在一条直线上的像素点数大于threshold时,才将该直线作为检测结果显示出来,该值越大,得到直线越少。
霍夫变换(hough transform)

霍夫变换(hough transform)霍夫变换(Hough Transform)霍夫变换是一种图像处理技术,用于在图像中检测直线、圆形等几何形状。
它最早由Paul Hough在1962年提出。
霍夫变换在计算机视觉和模式识别领域得到广泛应用,特别在边缘检测和形状分析中表现出色。
一、霍夫变换原理1. 直线检测霍夫变换的直线检测基于极坐标下的直线方程:ρ = xcosθ + ysinθ。
其中,ρ表示直线与原点的距离,θ为直线与x轴的夹角。
霍夫变换通过在ρ-θ空间中进行投票,找到出现频率最高的ρ和θ组合,即可以确定一条直线。
2. 圆形检测霍夫变换的圆形检测考虑到圆心坐标和半径。
以圆心坐标(xc, yc)和半径r为变量,对每个像素点进行投票。
根据累加器中出现频率最高的圆心和半径组合,即可确定一个圆。
二、霍夫变换的步骤1. 边缘检测霍夫变换需要基于边缘图像进行处理,因此首先需要对原始图像进行边缘检测。
常用的边缘检测算法有Canny边缘检测和Sobel算子等。
2. 构建累加器对于直线检测,构建一个二维累加器数组,用于记录直线参数的出现频率。
对于圆形检测,构建一个三维累加器数组,用于记录圆心和半径的出现频率。
3. 参数空间搜索遍历边缘图像上的每个像素点,对于每个边缘像素,计算对应的ρ和θ(直线检测)或圆心坐标和半径(圆形检测)。
在累加器中相应位置加1。
4. 参数估计根据累加器中出现频率最高的位置,估计出最佳直线或圆形的参数。
可以设定一个阈值,只接受出现频率高于该阈值的参数。
5. 绘制检测结果根据参数估计的结果,在原始图像上绘制检测出的直线或圆形。
三、霍夫变换的应用1. 直线检测霍夫变换的直线检测广泛应用于计算机视觉领域。
例如,道路标线检测、物体边缘检测、图像中的几何形状检测等。
通过直线检测,可以提取出图像中的重要几何特征,为后续的图像处理和分析提供基础。
2. 圆形检测霍夫变换的圆形检测可以应用于许多领域,例如医学图像处理、目标跟踪、光学字符识别等。
图像中的线检测——hough变换

图像中的线检测——hough变换
对于图像中的线检测问题,诸如直线检测或者椭圆检测,有⼀种⼗分经典的⽅法是霍夫变换。
霍夫变换的基本思想史:点——线的对偶关系,即原空间的像素对应霍夫空间的线。
如果原图中存在直线(即很多像素在⼀条直线上,那么在霍夫空间中,原空间直线映射到霍夫空间中的点)。
因此,检测原空间的直线,变成了检测霍夫空间中的点。
关于霍夫变换,下⾯两篇⽂章讲解的⾮常好:
霍夫变换运⽤两个坐标空间之间的变换,将在⼀个(图像)空间中具有相同形状(数学模型+参数)的曲线或直线,映射到另⼀个(参数)坐标空间的⼀个点上形成峰值,从⽽把检测任意形状的问题转化为统计峰值问题。
Hough变换

%Hough变换 clc;clear;close all f=imread('D:\dj.jpg');%若是彩色图片转灰度化 if length(size(f))>2 f=rgb2gray(f); end %figure(1)subplot(121);imshow(f);%利用edge函数进行边缘检测 j=edge(f,'Sobel');subplot(122);imshow(j); [row,col]=size(j); pinfang=round((row*row+col*col)^0.5); A=zeros(2*pi nfang,180);for m=1:row for n=1:col if j(m,n)>0for thera=1:180r=thera/180*pi; %角度转弧度rho=round(m*cos(r)+n*sin(r));%ρ=cosθ+sinθ rho=rho+pinfang+1;%-l:l转换到1:2l+1 A(rho,thera)=A(rho,thera)+1; end end end end[rho,thera]=find(A>40);%交点超过60条线的点,ma,na为参数空间的坐标点 nma=length(rho); for i=1:nma hold onm=1:row; %rho=ma(i)-1; r=thera(i)/180*pi;n=(rho(i)-pinfang-m*cos(r))/(0.00001+sin(r)); plot(n,m,'r'); end%Hough变换 clc;clear;close all f=imread('D:\dj.jpg');%若是彩色图片转灰度化 if length(size(f))>2 f=rgb2gray(f); end %figure(1)subplot(121);imshow(f);%利用edge函数进行边缘检测 j=edge(f,'Sobel');subplot(122);imshow(j); [row,col]=size(j); pinfang=round((row*row+col*col)^0.5); A=zeros(2*pi nfang,180);for m=1:row for n=1:col if j(m,n)>0for thera=1:180r=thera/180*pi; %角度转弧度rho=round(m*cos(r)+n*sin(r));%ρ=cosθ+sinθ rho=rho+pinfang+1;%-l:l转换到1:2l+1 A(rho,thera)=A(rho,thera)+1; end end end end[rho,thera]=find(A>40);%交点超过60条线的点,ma,na为参数空间的坐标点 nma=length(rho); for i=1:nma hold onm=1:row; %rho=ma(i)-1; r=thera(i)/180*pi;n=(rho(i)-pinfang-m*cos(r))/(0.00001+sin(r)); plot(n,m,'r'); endclc;clear; %% 录入图像并显示f=imread('D:\dj2.jpg');%读入彩色图像,注意不能使用灰度图像f=rgb2gray(f);%将彩色图像转换为灰度图像, f=im2double(f); figure();subplot(2,2,1);imshow(f);title('原图'); %% 提取图像边缘 [m,n]=size(f);%得到图像矩阵行数m,列数n for i=3:m-2for j=3:n-2%处理领域较大,所以从图像(3,3)开始,在(m-2,n-2)结束 l(i,j)=-f(i-2,j)-f(i-1,j-1)-2*f(i-1,j)-f(i-1,j+1)-f(i,j-2)-2*f(i,j-1)+16*f(i,j)-2*f(i,j+1)-f(i,j+2)-f(i+1,j -1)-2*f(i+1,j)-f(i+1,j+1)-f(i+2,j);%LoG算子 end endsubplot(2,2,2);imshow(l);title('LoG算子提取图像边缘'); %% 滤波 [m,n]=size(l); for i=2:m-1 for j=2:n-1y(i,j)=l(i-1,j-1)+l(i-1,j)+l(i-1,j+1)+l(i,j-1)+l(i,j)+l(i,j+1)+l(i+1, j-1)+l(i+1,j)+l(i+1,j+1);y(i,j)=y(i,j)/9; %LoG算子提取边缘后,对结果进行均值滤波以去除噪声,为下一步hough变换提取直线作准备 end endsubplot(2,2,3);imshow(y);title('均值滤波器处理后') %% 二值化 q=im2uint8(y); [m,n]=size(q); for i=1:m for j=1:nif q(i,j)>80; %设置二值化的阈值为80q(i,j)=255; %对图像进行二值化处理,使图像边缘更加突出清晰 else q(i,j)=0; end end subplot(2,2,4);imshow(q);title('二值化处理后'); %% 检测直线%Hough变换检测直线,使用(a,p)参数空间,a∈[0,180],p∈[0,2d] a=180; %角度的值为0到180度d=round(sqrt(m^2+n^2)); %图像对角线长度为p的最大值 s=zeros(a,2*d); %存储每个(a,p)个数z=cell(a,2*d); %用元胞存储每个被检测的点的坐标 for i=1:mfor j=1:n%遍历图像每个点if(q(i,j)==255)%只检测图像边缘的白点,其余点不检测 for k=1:ap = round(i*cos(pi*k/180)+j*sin(pi*k/180));%对每个点1到180度遍历一遍,取得经过该点的所有直线的p值(取整)if(p > 0)%若p大于0,则将点存储在(d,2d)空间s(k,d+p)=s(k,d+p)+1;%(a,p)相应的累加器单元加一 z{k,d+p}=[z{k,d+p},[i,j]'];%存储点坐标 elseap=abs(p)+1;%若p小于0,则将点存储在(0,d)空间 s(k,ap)=s(k,ap)+1;%(a,p)相应的累加器单元加一 z{k,ap}=[z{k,ap},[i,j]'];%存储点坐标 end end end end end for i=1:afor j=1:d*2 %检查每个累加器单元中存储数量 if(s(i,j) >70) %将提取直线的阈值设为70 lp=z{i,j};%提取对应点坐标for k=1:s(i,j)%对满足阈值条件的累加器单元中(a,p)对应的所有点进行操作 o(lp(1,k),lp(2,k),1)=255; %每个点R分量=255,G分量=0,B分量=0 o(lp(1,k),lp(2,k),2)=0; o(lp(1,k),lp(2,k),3)=0; %结果为在原图上对满足阈值要求的直线上的点赋红色 end end end endfigure,imshow(o);title('hough变换提取直线'); rotf = imrotate(f,33,'crop');%ͼÏñÌ«´ó£¬²Ã¼ô BW = edge(rotf,'canny'); [H,T,R] = hough(BW); imshow(H,[],'XData',T,'YData',R,'InitialMagnification','fit'); xlabel('\theta'), ylabel('\rho'); axis on, axis normal, hold on;P = houghpeaks(H,7,'threshold',ceil(0.3*max(H(:)))); x = T(P(:,2)); y = R(P(:,1));plot(x,y,'s','color','white');% Find lines and plot themlines = houghlines(BW,T,R,P,'FillGap',5,'MinLength',7); figure, imshow(rotf), hold on max_len = 0;for k = 1:length(lines)xy = [lines(k).point1; lines(k).point2];plot(xy(:,1),xy(:,2),'LineWidth',2,'Color','green'); % plot beginnings and ends of linesplot(xy(1,1),xy(1,2),'x','LineWidth',2,'Color','yellow'); plot(xy(2,1),xy(2,2),'x','LineWidth',2,' Color','red'); % determine the endpoints of the longest line segment len = norm(lines(k).point1 - lines(k).point2); if ( len > max_len) max_len = len; xy_long = xy; end end% highlight the longest line segmentplot(xy_long(:,1),xy_long(:,2),'LineWidth',2,'Color','cyan');f=imread('D:\dj.jpg');%读入彩色图像,注意不能使用灰度图像 o=f; %保留彩色原图f=rgb2gray(f);%将彩色图像转换为灰度图像, f=im2double(f); figure();subplot(2,2,1);imshow(o);title('原图');[m,n]=size(f);%得到图像矩阵行数m,列数n for i=3:m-2 for j=3:n-2%处理领域较大,所以从图像(3,3)开始,在(m-2,n-2)结束l(i,j)=-f(i-2,j)-f(i-1,j-1)-2*f(i-1,j)-f(i-1,j+1)-f(i,j-2)-2*f(i,j-1)+16*f(i,j)-2*f(i,j+1)-f(i,j+2)-f(i+1,j-1) -2*f(i+1,j)-f(i+1,j+1)-f(i+2,j);%LoG算子end endsubplot(2,2,2);imshow(l);title('LoG算子提取图像边缘');[m,n]=size(l); for i=2:m-1 for j=2:n-1y(i,j)=l(i-1,j-1)+l(i-1,j)+l(i-1,j+1)+l(i,j-1)+l(i,j)+l(i,j+1)+l(i+1,j-1)+l(i+1,j)+l(i+1,j+1);y(i,j)=y(i,j)/9; %LoG算子提取边缘后,对结果进行均值滤波以去除噪声,为下一步hough变换提取直线作准备 end endsubplot(2,2,3);imshow(y);title('均值滤波器处理后')q=im2uint8(y); [m,n]=size(q); for i=1:m for j=1:nif q(i,j)>80; %设置二值化的阈值为80q(i,j)=255; %对图像进行二值化处理,使图像边缘更加突出清晰 elseq(i,j)=0; end end endsubplot(2,2,4);imshow(q);title('二值化处理后'); %Hough变换检测直线,使用(a,p)参数空间,a∈[0,180],p∈[0,2d] a=180; %角度的值为0到180度d=round(sqrt(m^2+n^2)); %图像对角线长度为p的最大值 s=zeros(a,2*d); %存储每个(a,p)个数z=cell(a,2*d); %用元胞存储每个被检测的点的坐标 for i=1:mfor j=1:n%遍历图像每个点if(q(i,j)==255)%只检测图像边缘的白点,其余点不检测 for k=1:a p = round(i*cos(pi*k/180)+j*sin(pi*k/180));%对每个点从1到180度遍历一遍,取得经过该点的所有直线的p值(取整)if(p > 0)%若p大于0,则将点存储在(d,2d)空间s(k,d+p)=s(k,d+p)+1;%(a,p)相应的累加器单元加一 z{k,d+p}=[z{k,d+p},[i,j]'];%存储点坐标 elseap=abs(p)+1;%若p小于0,则将点存储在(0,d)空间 s(k,ap)=s(k,ap)+1;%(a,p)相应的累加器单元加一 z{k,ap}=[z{k,ap},[i,j]'];%存储点坐标 end end end end endfor i=1:afor j=1:d*2 %检查每个累加器单元中存储数量 if(s(i,j) >70) %将提取直线的阈值设为70 lp=z{i,j};%提取对应点坐标for k=1:s(i,j)%对满足阈值条件的累加器单元中(a,p)对应的所有点进行操作o(lp(1,k),lp(2,k),1)=255; %每个点R分量=255,G分量=0,B分量=0o(lp(1,k),lp(2,k),2)=0;o(lp(1,k),lp(2,k),3)=0; %结果为在原图上对满足阈值要求的直线上的点赋红色end end end endfigure,imshow(o);title('hough变换提取直线');clc;clear;i=imread('D:\dj.jpg');imshow(i)figurei=rgb2gray(i);i_hight=size(i,1);i_width=size(i,2);% i_edge=edge(i,'robert');i_hough=zeros(600,360);for y=1:i_hightfor x=1:i_widthif i(y,x)==0 %坐标系转换for l=1:360r=x*cos(l*pi/180)+y*sin(l*pi/180);w=fix(r)+300; %修正为正整数i_hough(w,l)=i_hough(w,l)+1;endendendendm=max(max(i_hough));i_hough=(i_hough./m); %亮度调整threshold=0.75; %设置直线亮度阈值ih_hight=size(i_hough,1);ih_width=size(i_hough,2);temp=zeros(20,20);count=0;for y=1:ih_hight %找那些亮度高的直线for x=1:ih_width/2if i_hough(y,x)>thresholdcount = count+1;temp(count,1) = x;temp(count,2) = y;endendendimshow(i)hold onfor i=1:count %画呀话% y=kx+bk = tan(temp(i,1)*pi/180);b = (temp(i,2)-300)/sin(temp(i,1)*pi/180);for j=1:360x(j)=j;y(j)=-x(j)/k+b;endplot(x,y)hold onendaxis equalfigureimshow(i_hough)clc;clear;img=imread('D:\dj.jpg');% imshow(img)% figureimg=rgb2gray(img);i_hight=size(img,1);i_width=size(img,2);% i_edge=edge(img,'robert');% figure% imshow(img)i_hough=zeros(800,360);for y=1:i_hightfor x=1:i_widthif img(y,x)==0 %坐标系转换for l=1:360r=x*cos(l*pi/180)+y*sin(l*pi/180);w=fix(r)+400; %修正为正整数i_hough(w,l)=i_hough(w,l)+1;endendendendm=max(max(i_hough));i_hough=(i_hough./m); %亮度调整figureimshow(i_hough)threshold=0.50; %---------------------------设置直线亮度阈值ih_hight=size(i_hough,1);ih_width=size(i_hough,2);temp=zeros(100,2);count=0;for y=1:ih_hight %找那些亮度高的直线for x=1:ih_width/2if i_hough(y,x)>thresholdcount = count+1;temp(count,1) = x;temp(count,2) = y;endendend% 调和高亮点while(1)flag = 0;for i=1:countif flag==0for j=i+1:countdis = sqrt((temp(i,1)-temp(j,1))^2 + (temp(i,2)-temp(j,2))^2);if dis<50 %---------------------------调和半径flag = 1;temp(i,1)=(temp(i,1)+temp(j,1))/2;temp(i,2)=(temp(i,2)+temp(j,2))/2;temp(j,:)=[];count = count-1;break;endendendendif flag == 0break;endendfigureimshow(img)hold onfor i=1:count %画呀话% y=kx+bk = tan(temp(i,1)*pi/180);b = (temp(i,2)-400)/sin(temp(i,1)*pi/180); %-400是为了反修正for j=1:360x(j)=j;y(j)=-x(j)/k+b;endplot(x,y)hold onendaxis equalaxis([0,400,0,400]);function Img_hough = hough_s(‘D:\Img, jpg’)%该函数实现hough变换提取直线的功能。
霍夫变换(hough transform)

一、概述霍夫变换是一种常用的图像处理技术,它可以用于检测图像中的直线、圆或者其他形状。
它具有很好的鲁棒性,可以应对图像中存在的噪声和其他干扰。
霍夫变换在计算机视觉、图像处理和模式识别领域有着广泛的应用,成为了处理图像中几何形状的重要工具。
二、霍夫变换的原理霍夫变换最初是由美国科学家保罗·霍夫在1962年提出的,用于检测图像中的直线。
后来,霍夫变换被扩展到检测圆或者其他形状。
霍夫变换的基本原理是将空间域中的坐标转换到参数域中,在参数域中对应的曲线经过的点在空间域中具有共线的特点。
通过累加空间域中的点的参数,可以找到曲线或者形状的参数方程,从而实现对图像中形状的检测。
具体来说,对于检测直线来说,可以通过霍夫变换将直线表示为参数空间中的斜率和截距,从而可以在参数空间中进行累加,最终找到直线的参数方程。
三、霍夫变换在直线检测中的应用1. 边缘检测在使用霍夫变换检测直线之前,通常需要对图像进行边缘检测。
边缘检测可以帮助找到图像中明显的过渡区域,这些过渡区域通常对应着直线的轮廓。
常用的边缘检测算法包括Sobel算子、Canny算子等。
2. 参数空间的设置为了使用霍夫变换来检测直线,需要设定参数空间的范围。
对于直线检测来说,一般可以设定直线的斜率和截距的取值范围。
3. 累加过程在设定好参数空间后,需要对图像中的边缘点进行霍夫变换的累加过程。
对于每一个边缘点,都可以在参数空间中找到对应的直线,通过对参数空间的累加,可以找到参数空间中的峰值,这些峰值对应着图像中的直线。
4. 直线检测可以根据参数空间中的峰值来确定图像中的直线。
通常可以设定一个阈值来筛选参数空间中的峰值,从而得到最终的直线检测结果。
四、霍夫变换在圆检测中的应用除了直线检测,霍夫变换也可以用于检测图像中的圆。
与直线检测类似,圆检测也需要进行边缘检测和参数空间的设定。
不同的是,在圆检测中,需要设定圆心和半径的参数空间范围。
五、霍夫变换的改进和应用1. 累加数组的优化在传统的霍夫变换中,需要对参数空间进行离散化,这会导致计算量较大。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数字图像处理第八次作业实验内容1、拍摄一张包含硬币、橡皮等物品的照片,通过Hough 变换检测出圆形的硬币个数并区分不同半径的硬币。
最终计算出照片中的总钱数。
解:Hough 变换的实质是对图像进行坐标的变换,将图像空间的线条变为参数空间的聚集点,从而将原始图像中检测给定形状的曲线问题,变成寻找参数空间中的峰点的问题。
它不仅可以检测直线,而且可以很方便地检测圆、椭圆和抛物线等形状。
由于这里需要检测圆形的硬币,所以下面给出检测圆的具体方法:因为圆的图像空间方程为:222()()x a y b r -+-=,我们需要通过Hough 变换,将图像空间(,)x y 对应到参数空间(,,)a b r ,然后对其进行累加完成检测。
但是显然这种方法的计算量是非常大的,所以一般都是先对灰度图像进行边缘提取,利用边界像素的灰度梯度信息估计出下式中的角度θ,以此来降低计算量:cos cos a x r b y r θθ=-*⎧⎨=-*⎩ (1)一般在检测过程中需要对图像进行预处理,使得检测更加准确和容易。
检测过程如下所示:○1真彩色图像转为灰度图像; ○2去除噪声,进行中值滤波; ○3转为二值图像,利用边缘算子进行图像边缘提取; ○4最后进行图像的平滑和填充。
这里处理的图像并没有太多噪声,所以处理的时候略去了中值滤波的步骤,直接对边缘提取后的图像进行Hough 变换检测圆形。
根据式(1),我们需要对半径r 和角度θ进行搜索,所以这里应该首先设置半径和角度方向的搜索步长step_r 和step_angle ,接着给出半径搜索的最大和最小值,当然这两个数值需要根据经验来自己确定。
最后就可以根据这些确定半径和角度的最大搜索次数。
由于Hough变换需要用到稀疏矩阵,也即首先得找到图像矩阵中的非零量,针对这些非零量进行进一步的处理。
这个操作可以直接通过Matlab中的find语句来实现:>> [rows, cols] = find(BW); %找出矩阵中的非零值接着只需要根据式(1)计算出对应参数空间的参数a b和,根据,a b的范围确定hough空间累加器hough_adder是否自增。
由于这里的图像中不止一个圆形,所以不能直接利用hough_adder中的最大值来确定半径,需要设置一定的阈值thre来确定一定半径的圆,当阈值设置合理后才可以找出图像中的圆。
接着对阈值范围内的点进行搜索,当满足圆周内外各5个像素点时,该点可以认为是我们搜寻的圆上的点。
对其相应的坐标赋1即可。
经过上述的步骤,便通过hough变换的思想将图像的中的圆给检测出来了。
并且可以将圆心坐标和圆的半径都显示出来。
那接下来按照题目的意思是需要我们计算总的钱数,所以首先需要区分一元和五角的硬币,也就是区分圆的半径。
由于这里我们设置搜索出来的圆的半径是逐渐递增的,所以只需要判断在两个相邻点之间圆的半径是否存在跳变即可。
因为如果是不同的一元硬币,那么他们的半径即使相差一点也不会很多。
这样我们便可以得出首先将圆分成两类(这里只考虑一元和五角的两种情况),然后在每一类中再寻找半径相似的圆位于不同坐标的个数,也就是同样面值的硬币的个数了。
可以通过如下代码实现:从以上代码我们可以看出,这里只要当相邻两个半径相差超过5即可认定为是不同的硬币了。
接着在相同的硬币中,通过循环搜索当前半径和之前像素点的半径,当横纵坐标相差都小于10的时候可以认为是同一个点,也即是同一个硬币,否则将硬币数加一。
最后通过统计得到的总硬币数计算出总钱数。
下面先给出具体代码:clc,clear allImage = imread('final.bmp');imshow(Image),title('原始图像');Gray = rgb2gray(Image);bw = im2bw(Gray); % 先转为二值图像BW = edge(bw); % 然后提取边缘figureimshow(BW),title('图像边缘);step_r = 1; % 设定半径搜索步长step_angle = 0.1; % 设定角度搜索步长r_min = 50; % 最小半径和最大半径,确定搜索范围r_max = 100;thre = 0.8; % 设定阈值%***************hough变换*********************************[m, n] = size(BW);Count_r = round((r_max-r_min)/step_r)+1; % °半径最大搜索次数hough_adder = zeros(m, n, Count_r);Count_angle = round(2*pi/step_angle); % 角度最大搜索次数[rows, cols] = find(BW); % 找出矩阵中的非零值count = size(rows); % 计算非零值的个数for Count_Num = 1 : countfor Count_R = 1 : Count_rfor Count_Angle = 1 : Count_anglea =round(rows(Count_Num)-(r_min+(Count_R-1)*step_r)*cos(Count_Angle*step_angle ));b =round(cols(Count_Num)-(r_min+(Count_R-1)*step_r)*sin(Count_Angle*step_angle) );isTrue = (a>0 && a<=m && b>0 && b<=n);if(isTrue)hough_adder(a,b,Count_R) = hough_adder(a,b,Count_R) + 1;% 参数空间累加器加1endendendendmax_hough_adder = max(max(max(hough_adder))); % 计算最大值index = find(hough_adder >= max_hough_adder * thre); % 设定阈值length = size(index);hough_circle=zeros(m,n);for Count_Num = 1 : countfor Count_Length = 1 : lengthpar3 = floor(index(Count_Length)/(m*n));par2 = floor((index(Count_Length)-par3*(m*n))/m);par1 = index(Count_Length)-par3*(m*n)-par2*m;isTrue =(rows(Count_Num)-par1)^2+(cols(Count_Num)-par2-1)^2<(r_min+par3*step_r)^2+5 &&(rows(Count_Num)-par1)^2+(cols(Count_Num)-par2-1)^2>(r_min+par3*step_r)^2-5 ;if(isTrue)hough_circle(rows(Count_Num),cols(Count_Num)) = 1;endendendfigureimshow(hough_circle),title('圆形检测结果');for Count_Length = 1 : lengthpar3 = floor(index(Count_Length)/(m*n));par2 = floor((index(Count_Length)-par3*(m*n))/m);par1 = index(Count_Length)-par3*(m*n)-par2*m;par3 = r_min+par3*step_r;para(:,Count_Length) = [par1,par2,par3]; % 存储符合条件的圆坐标以及半径end%***************计算总钱数*********************************total_wu = 0;for idx = 1 : length-1total_wu = total_wu + para(3,idx);if (para(3,idx+1) - para(3,idx) > 5)break;endendtotal_yi = sum(para(3,:)) - total_wu;Ave_wu = total_wu / idx;Ave_yi = total_yi / (length(1,1)-idx);% 计算五角硬币的个数count_wu = 1;j = 1;for i = 2 : idxif j<= i-1if abs(para(1,i) - para(1,j)) < 10 && abs(para(2,i) - para(2,j)) < 10 count_wu = count_wu;elsecount_wu = count_wu + 1;break;endendend% 计算一元硬币的个数count_yi = 1;j = idx+1;for i = (idx+2) : lengthif j <= i-1if abs(para(1,i) - para(1,j)) < 10 && abs(para(2,i) - para(2,j)) < 10 count_yi = count_yi;elsecount_yi = count_yi + 1;break;endendendtotal_money = count_wu * 0.5 + count_yi * 1 % 计算总钱数下面给出处理的图像:原始图像图1 原始图像图像边缘图2 提取的图像边缘最后给出检测出的图像如下:检测结果图3 检测出圆轮廓从图3可以看出此时检测结果还是很准确的,当然这个和我们所选取的阈值thre有关,如果thre选择偏大,则无法将三个圆都检测出来,相反,如果thre 偏小,那么可能检测出来图形中其他的圆(比如该图像中的U盘上的圆圈)。
所以说这里的关键就是阈值的选择,我是通过不断调试得出这个比较理想的结果的。
最后,在屏幕上打印总的钱数为:>> total_money =2.5000一、实验小结由于老师上课只讲述了直线的hough变换,所以在一开始做这题的时候感觉有点无从下手。
后来查阅了冈萨雷斯的图像处理书对hough变换有了一个更深刻的了解。
