高一数学直线和平面所成的角
高一数学立体几何题目

1.如图,在三棱柱ABC﹣A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别是A1C1,BC的中点.(1)求证:AB⊥C1F;(2)求证:C1F∥平面ABE;(3)求三棱锥E﹣ABC的体积.2.如图所示,矩形ABCD中,DA⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE,AC和BD交于点G.(Ⅰ)求证:AE∥平面BFD;(Ⅱ)求三棱锥C﹣BFG的体积.3.如图,直三棱柱ABC﹣A1B1C1中,CA=CB,M,N,P分别为AB,A1C1,BC的中点.求证:(1)C1P∥平面MNC;(2)平面MNC⊥平面ABB1A1.4.如图,在正方体ABCD﹣A1B1C1D1中,E,F分别是棱BC,C1D1的中点,求证:EF∥平面BB1D1D.5.如图,在直三棱柱ABC﹣A1B1C1中,AC⊥BC,点D是AB的中点.求证:(1)AC⊥BC1;(2)AC1∥平面B1CD.6.如图,在底面为平行四边形的四棱锥P﹣ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=AB,点E是PD的中点.(Ⅰ)求证:AC⊥PB;(Ⅱ)求证:PB∥平面AEC.7.如图所示,在正方体ABCD﹣A1B1C1D1中,S是B1D1的中点,E、F、G分别是BC、CD和SC 的中点.求证:(1)直线EG∥平面BDD1B1;(2)平面EFG∥平面BDD1B1.8.如图,在直三棱柱ABC﹣A1B1C1中,∠ACB=90°.BC=CC1=a,AC=2a.(1)求证:AB1⊥BC1;(2)求二面角B﹣AB1﹣C的正弦值.9.如图所示,在四棱锥P﹣ABCD中,底面ABCD是矩形,侧棱PA垂直于底面,E、F分别是AB、PC的中点,PA=AD.求证:(1)CD⊥PD;(2)EF⊥平面PCD.10.如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC=2,N为线段PB的中点.(Ⅰ)证明:NE⊥PD;(Ⅱ)求三棱锥E﹣PBC的体积.-中,PD⊥平面ABCD,底面ABCD是平行四边形,11.如图,在四棱锥P ABCD,,,,O为AC与BD的交点,E为棱PB上∠====6023BAD AB PD AD BD一点.(1)证明:平面EAC ⊥平面PBD ;(2)若2PE EB =,求二面角E AC B --的大小.12.如图,已知AF ⊥面ABCD ,四边形ABEF 为矩形,四边形ABCD 为直角梯形,∠DAB=90°,AB ∥CD ,AD=AF=CD=1,AB=2(1)求证:AF ∥面BCE ;(2)求证:AC ⊥面BCE ;(3)求三棱锥E ﹣BCF 的体积.13.如图,四棱锥P ﹣ABCD 的底面是正方形,PD⊥底面ABCD ,点E 在棱PB 上.(1)求证:平面AEC⊥平面PDB ;(2)当PD=AB ,且E 为PB 的中点时,求AE 与平面PDB 所成的角的大小.试卷答案1.【考点】LF:棱柱、棱锥、棱台的体积;LS:直线与平面平行的判定.【分析】(1)由BB1⊥平面ABC得AB⊥BB1,又AB⊥BC,故AB⊥平面B1BCC1,所以AB⊥C1F;(2)取AB的中点G,连接EG,FG.则易得四边形EGFC1是平行四边形,故而C1F∥EG,于是C1F∥平面ABE;(3)由勾股定理求出AB,代入棱锥的体积公式计算即可.【解答】(1)证明:∵BB1⊥底面ABC,AB⊂平面ABC∴BB1⊥AB.又∵AB⊥BC,BC⊂平面B1BCC1,BB1⊂平面B1BCC1,BC∩BB1=B,∴AB⊥平面B1BCC1,又∵C1F⊂平面B1BCC1,∴AB⊥C1F.(2)证明:取AB的中点G,连接EG,FG.∵F,G分别是BC,AB的中点,∴FG∥AC,且FG=AC,∵AC A1C1,E是A1C1的中点,∴EC1=A1C1.∴FG∥EC1,且FG=EC1,∴四边形FGEC1为平行四边形,∴C1F∥EG.又∵EG⊂平面ABE,C1F⊄平面ABE,EG⊂平面ABE,∴C1F∥平面ABE.(3)解:∵AA1=AC=2,BC=1,AB⊥BC,∴AB==.∴三棱锥E﹣ABC的体积V=S△ABC•AA1=×××1×2=.2.【考点】LF:棱柱、棱锥、棱台的体积;LS:直线与平面平行的判定.【分析】(1)连结FG,证明FG∥AE,然后证明AE∥平面BFD.(2)利用V C﹣BGF=V G﹣BCF,求出S△CFB.证明FG⊥平面BCF,求出FG,即可求解几何体的体积.【解答】(1)证明:由题意可得G是AC的中点,连结FG,∵BF⊥平面ACE,∴CE⊥BF.而BC=BE,∴F是EC的中点,…(2分)在△AEC中,FG∥AE,∴AE∥平面BFD.…(2)解:∵AD⊥平面ABE,AD∥BC,∴BC⊥平面ABE,则AE⊥BC.又∵BF⊥平面ACE,则AE⊥BF,又BC∩BF=B,∴AE⊥平面BCE.…(8分)∵AE∥FG.而AE⊥平面BCE,∴FG⊥平面BCF.∵G是AC中点,F是CE中点,∴FG∥AE且FG=AE=1.∴Rt△BCE中,BF=CE=CF=,…(10分)∴S△CFB=××=1.∴V C﹣BGF=V G﹣BCF=•S△CFB•FG=×1×1=.…(12分)【点评】本题考查直线与平面平行的判定定理的应用,三角锥的体积的求法,考查转化思想以及计算能力.3.【考点】平面与平面垂直的判定;直线与平面平行的判定.【分析】(1)连接MP,只需证明四边形MPC1N是平行四边形,即可得MN∥C1P∵C1P,即可证得C1P∥平面MNC;(2)只需证明CM⊥平面MNC,即可得平面MNC⊥平面ABB1A1.【解答】证明:(1)连接MP,因为M、P分别为AB,BC的中点∵MP∥AC,MP=,又因为在直三棱柱ABC﹣A1B1C1中,∴AC∥A1C1,AC=A1C1且N是A1C1的中点,∴MP∥C1N,MP=C1N∴四边形MPC1N是平行四边形,∴C1P∥MN∵C1P⊄面MNC,MN⊂面MNC,∴C1P∥平面MNC;(2)在△ABC中,CA=CB,M为AB的中点,∴CM⊥AB.在直三棱柱ABC﹣A1B1C1中,B1B⊥面ABC.∵CM⊂面ABC,∴BB1⊥CM由因为BB1∩AB=B,BB1,AB⊂平面面ABB1A1又CM⊂平面MNC,∴平面MNC⊥平面ABB1A1.4.【考点】LS:直线与平面平行的判定.【分析】先证明四边形OFEB为平行四边形,可得EF∥BO,利用线面平行的判定定理,即可证明EF∥平面BB1D1D.【解答】证明:取D1B1的中点O,连OF,OB,∵OF∥B1C1,OF=B1C1,∵BE∥B1C1,BE=B1C1,∴OF∥BE,OF=BE,∴四边形OFEB为平行四边形,∴EF∥BO,∵EF⊄平面BB1D1D,BO⊂平面BB1D1D,∴EF∥平面BB1D1D.5.【考点】LS:直线与平面平行的判定;LO:空间中直线与直线之间的位置关系.【分析】(1)利用线面垂直的判定定理先证明AC⊥平面BCC1B1,BC1⊂平面BCC1B1,即可证得AC⊥BC1;(2)取BC1与B1C的交点为O,连DO,则OD是三角形ABC1的中位线,OD∥AC1,而AC1⊂平面B1CD,利用线面平行的判定定理即可得证.【解答】证明:(1)在直三棱柱ABC﹣A1B1C1中,∵CC1⊥平面ABC,∴CC1⊥AC,又AC⊥BC,BC∩CC1=C,∴AC⊥平面BCC1B1∴AC⊥BC1.(2)设BC1与B1C的交点为O,连接OD,BCC1B1为平行四边形,则O为B1C中点,又D是AB的中点,∴OD是三角形ABC1的中位线,OD∥AC1,又∵AC1⊄平面B1CD,OD⊂平面B1CD,∴AC1∥平面B1CD.6.【考点】LF:棱柱、棱锥、棱台的体积;LO:空间中直线与直线之间的位置关系;LS:直线与平面平行的判定.【分析】(Ⅰ)由已知得AC⊥AB,AC⊥PA,从而AC⊥平面PAB,由此能证明AC⊥PB.(Ⅱ)连接BD,与AC相交于O,连接EO,由已知得EO∥PB,由此能证明PB∥平面AEC.【解答】(Ⅰ)证明:∵在底面为平行四边形的四棱锥P﹣ABCD中,AB⊥AC,PA⊥平面ABCD,∴AC⊥AB,AC⊥PA,又AB∩PA=A,∴AC⊥平面PAB,∵PB⊂平面PAB,∴AC⊥PB.(Ⅱ)证明:连接BD,与AC相交于O,连接EO,∵ABCD是平行四边形,∴O是BD的中点,又E是PD的中点,∴EO∥PB,又PB不包含于平面AEC,EO⊂平面AEC,∴PB∥平面AEC.7.【考点】LS:直线与平面平行的判定;LU:平面与平面平行的判定.【分析】(1)连结SB,由已知得EG∥SB,由此能证明直线EG∥平面BDD1B1.(2)连结SD,由已知得FG∥SD,从而FG∥平面BDD1B1,又直线EG∥平面BDD1B1,由此能证明平面EFG∥平面BDD1B1.【解答】证明:(1)如图,连结SB,∵E、G分别是BC、SC的中点,∴EG∥SB,又SB⊂平面BDD1B1,EG不包含于平面BDD1B1,∴直线EG∥平面BDD1B1.(2)如图,连结SD,∵F,G分别是DC、SC的中点,∴FG∥SD,又SD⊂平面BDD1B1,FG不包含于平面BDD1B1,∴FG∥平面BDD1B1,又直线EG∥平面BDD1B1,且直线EG⊂平面EFG,直线FG⊂平面EFG,EG∩FG=G,∴平面EFG∥平面BDD1B1.8.【考点】MT:二面角的平面角及求法.【分析】(1)由已知可得AC⊥平面B1BCC1,则AC⊥BC1,再由BC=CC1,得BC1⊥B1C,由线面垂直的判定可得BC1⊥平面AB1C,从而得到AB1⊥BC1;(2)设BC1∩B1C=O,作OP⊥AB1于点P,连结BP.由(1)知BO⊥AB1,进一步得到AB1⊥平面BOP,说明∠OPB是二面角B﹣AB1﹣C的平面角.然后求解直角三角形得答案.【解答】(1)证明:∵ABC﹣A1B1C1是直三棱柱,∴CC1⊥平面ABC,则AC⊥CC1.又∵AC⊥BC,BC∩CC1=C,∴AC⊥平面B1BCC1,则AC⊥BC1,∵BC=CC1,∴四边形B1BCC1是正方形,∴BC1⊥B1C,又AC∩B1C=C,∴BC1⊥平面AB1C,则AB1⊥BC1;(2)解:设BC1∩B1C=O,作OP⊥AB1于点P,连结BP.由(1)知BO⊥AB1,而BO∩OP=O,∴AB1⊥平面BOP,则BP⊥AB1,∴∠OPB是二面角B﹣AB1﹣C的平面角.∵△OPB1~△ACB1,∴,∵BC=CC1=a,AC=2a,∴OP=,∴=.在Rt△POB中,sin∠OPB=,∴二面角B﹣AB1﹣C的正弦值为.9.【考点】LW:直线与平面垂直的判定.【分析】(1)由线面垂直得CD⊥PA,由矩形性质得CD⊥AD,由此能证明CD⊥PD.(2)取PD的中点G,连结AG,FG.由已知条件推导出四边形AEFG是平行四边形,所以AG∥EF.再由已知条件推导出EF⊥CD,由此能证明EF⊥平面PCD.【解答】(本题满分8分)证明:(1)∵PA⊥底面ABCD,∴CD⊥PA.又矩形ABCD中,CD⊥AD,且AD∩PA=A,∴CD⊥平面PAD,∴CD⊥PD.(2)取PD的中点G,连结AG,FG.又∵G、F分别是PD、PC的中点,∴GF平行且等于CD,∴GF平行且等于AE,∴四边形AEFG是平行四边形,∴AG∥EF.∵PA=AD,G是PD的中点,∴AG⊥PD,∴EF⊥PD,∵CD⊥平面PAD,AG⊂平面PAD.∴CD⊥AG.∴EF⊥CD.∵PD∩CD=D,∴EF⊥平面PCD.10.【考点】LF:棱柱、棱锥、棱台的体积;LO:空间中直线与直线之间的位置关系.【分析】(Ⅰ)连结AC与BD交于点F,则F为BD的中点,连结NF,由三角形中位线定理可得NF∥PD,,在结合已知得四边形NFCE为平行四边形,得到NE∥AC.再由PD ⊥平面ABCD,得AC⊥PD,从而证得NE⊥PD;(Ⅱ)由PD⊥平面ABCD,得平面PDCE⊥平面ABCD,可得BC⊥CD,则BC⊥平面PDCE.然后利用等积法把三棱锥E﹣PBC的体积转化为B﹣PEC的体积求解.【解答】(Ⅰ)证明:连结AC与BD交于点F,则F为BD的中点,连结NF,∵N为线段PB的中点,∴NF∥PD,且,又EC∥PD且,∴NF∥EC且NF=EC.∴四边形NFCE为平行四边形,∴NE ∥FC ,即NE ∥AC .又∵PD ⊥平面ABCD ,AC ⊂面ABCD , ∴AC ⊥PD ,∵NE ∥AC ,∴NE ⊥PD ;(Ⅱ)解:∵PD ⊥平面ABCD ,PD ⊂平面PDCE , ∴平面PDCE ⊥平面ABCD ,∵BC ⊥CD ,平面PDCE ∩平面ABCD=CD ,BC ⊂平面ABCD , ∴BC ⊥平面PDCE . 三棱锥E ﹣PBC 的体积=.11.(1)证明见解析;(2)60°.试题解析:(1)∵PD ⊥平面ABCD ,AC ⊂平面ABCD ,∴AC PD ⊥. ∵,60AD BD BAD =∠=,∴ABD ∆为正三角形,四边形ABCD 是菱形, ∴AC BD ⊥,又PD BD D=⋂,∴AC ⊥平面PBD ,而AC ⊂平面EAC ,∴平面EAC ⊥平面PBD .(2)如图,连接OE ,又(1)可知EO AC ⊥,又AC BD ⊥, ∴EOB ∠即为二面角E AC B --的平面角, 过E 作EHPD ,交BD 于点H ,则EH BD ⊥,又31 2,2,3,,33PE EB AB PD EH OH=====,在RT EHO∆中,tan3EHEOHOH∠==60EOH∠=,即二面角E AC B--的大小为60.考点:线面垂直的判定定理、面面垂直的判定定理及二面角的求法.12.【考点】棱柱、棱锥、棱台的体积;直线与平面平行的判定;直线与平面垂直的判定.【分析】(1)推导出AF∥BE,由此能证明AF∥面BCE.(2)推导出AC⊥BE,AC⊥BC,由此能证明AC⊥面BCE.(3)三棱锥E﹣BCF的体积V E﹣BCF=V C﹣BEF,由此能求出结果.【解答】证明:(1)∵四边形ABEF为矩形,∴AF ∥BE,∵AF⊄平面BCE,BE⊄平面BCE,∴AF∥面BCE.(2)∵AF⊥面ABCD,四边形ABEF为矩形,∴BE⊥平面ABCD,∵AC⊂平面ABCD,∴AC⊥BE,∵四边形ABCD为直角梯形,∠DAB=90°,AB∥CD,AD=AF=CD=1,AB=2∴AC=BC==,∴AC2+BC2=AB2,∴AC⊥BC,∵BC∩BE=B,∴AC⊥面BCE.解:(3)三棱锥E﹣BCF的体积:V E﹣BCF=V C﹣BEF====.13.【考点】直线与平面垂直的判定;直线与平面所成的角.【专题】计算题;证明题.【分析】(Ⅰ)欲证平面AEC⊥平面PDB,根据面面垂直的判定定理可知在平面AEC内一直线与平面PDB垂直,而根据题意可得AC⊥平面PDB;(Ⅱ)设AC∩BD=O,连接OE,根据线面所成角的定义可知∠AEO为AE与平面PDB所的角,在Rt△AOE中求出此角即可.【解答】(Ⅰ)证明:∵四边形ABCD是正方形,∴AC⊥BD,∵PD⊥底面ABCD,∴PD⊥AC,∴AC⊥平面PDB,∴平面AEC⊥平面PDB.(Ⅱ)解:设AC∩BD=O,连接OE,由(Ⅰ)知AC⊥平面PDB于O,∴∠AEO为AE与平面PDB所的角,∴O,E分别为DB、PB的中点,∴OE∥PD,,又∵PD⊥底面ABCD,∴OE⊥底面ABCD,OE⊥AO,在Rt△AOE中,,∴∠AEO=45°,即AE与平面PDB所成的角的大小为45°.【点评】本题主要考查了直线与平面垂直的判定,以及直线与平面所成的角,考查空间想象能力、运算能力和推理论证能力,属于基础题.。
高一数学(人教A版)直线与平面垂直的概念及判定

请同学们观察:
A
(1)折痕AD与桌面垂直吗?
(2)如何翻折才能使折痕AD与
BD
C
桌面垂直呢?为什么呢?
通过实验操作,我们不难发现,
A
AD所在直线与桌面所在平面垂直的 B
充要条件是折痕AD是BC边上的高.
C
D
A
这个时候,由于翻折后垂直关
系不变,所以直线AD与平面内的
两条相交直线BD,DC都是垂直的.
l P
的射影所成的角,叫做这条直线和 这个平面所成的角.
A
O
例如,正方体ABCD-A1B1C1D1中,
A1B在平面AC上的射影为AB,
D1
故A1B与平面AC所成的角为∠A1BA; A1
A1C在平面AC上的射影为AC,
故A1C与平面AC所成的角为∠A1CA. D
同学们可以仿照着再举出几个 A
线面角的例子,加深对线面角的认识.
的两条平行直线垂直,那么无法保证该
l
直线与此平面的所有直线都垂直,如图
所示,直线与平面可能垂直,也可能不
垂直.
如果改为“无数条直线”可不可以呢?
“无数条直线”不等同于“任意一条直线”.
若“无数条直线”彼此相互平行,
l
则也无法判定直线是否与该平面垂直.
如图所示:
选一选 若一条直线与三角形的两边同时垂直,则这条
直线与三角形第三边的位置关系是( B )
A. 平行
B. 垂直
C. 相交但不垂直
D. 不确定
由直线与平面垂直的判定定理知,该直线与三角形 所在平面垂直,进而与三角形第三边垂直,所以答案为 B,同学们选对了吗?
想一想 某旗杆高24m,在它的顶端系两条长26m的绳
高一数学复习考点知识专题讲解37---夹角问题
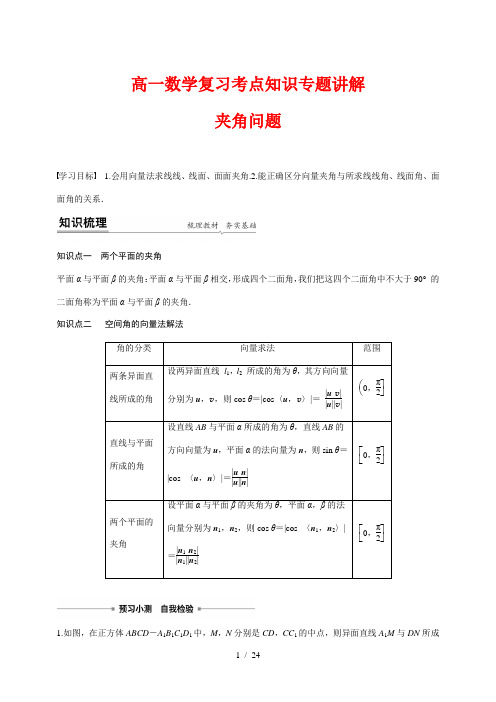
高一数学复习考点知识专题讲解夹角问题学习目标 1.会用向量法求线线、线面、面面夹角.2.能正确区分向量夹角与所求线线角、线面角、面面角的关系.知识点一两个平面的夹角平面α与平面β的夹角:平面α与平面β相交,形成四个二面角,我们把这四个二面角中不大于90°的二面角称为平面α与平面β的夹角.知识点二空间角的向量法解法角的分类向量求法范围两条异面直线所成的角设两异面直线l1,l2所成的角为θ,其方向向量分别为u,v,则cos θ=|cos〈u,v〉|=|u·v||u||v|⎝⎛⎦⎤0,π2直线与平面所成的角设直线AB与平面α所成的角为θ,直线AB的方向向量为u,平面α的法向量为n,则sin θ=|cos 〈u,n〉|=|u·n||u||n|⎣⎡⎦⎤0,π2两个平面的夹角设平面α与平面β的夹角为θ,平面α,β的法向量分别为n1,n2,则cos θ=|cos 〈n1,n2〉|=|n1·n2||n1||n2|⎣⎡⎦⎤0,π21.如图,在正方体ABCD-A1B1C1D1中,M,N分别是CD,CC1的中点,则异面直线A1M与DN所成角的大小是( )A.π6B.π4C.π3D.π2 答案 D解析 以D 为原点,DA ,DC ,DD 1所在直线为坐标轴建立空间直角坐标系, 设正方体棱长为1,则A 1M —→=⎝⎛⎭⎫-1,12,-1,DN →=⎝⎛⎭⎫0,1,12,cos 〈A 1M —→,DN →〉=|A 1M —→·DN →||A 1M —→||DN →|=0. ∴〈A 1M →,DN →〉=π2.2.已知向量m ,n 分别是直线l 与平面α的方向向量、法向量,若cos 〈m ,n 〉=-32,则l 与α所成的角为( )A .30°B .60°C .150°D .120° 答案 B解析 设l 与α所成的角为θ,则sin θ=|cos 〈m ,n 〉|=32,∴θ=60°,故选B. 3.已知平面α的法向量u =(1,0,-1),平面β的法向量v =(0,-1,1),则平面α与β的夹角为________. 答案 π3解析 ∵cos 〈u ,v 〉=-12×2=-12,∴〈u ,v 〉=23π,∴平面α与β的夹角是π3.4.在空间直角坐标系Oxyz 中,已知A (1,-2,0),B (2,1,6),则向量AB →与平面xOz 的法向量的夹角的正弦值为________. 答案74解析 设平面xOz 的法向量为n =(0,1, 0) ,AB →=(1,3,6), 所以cos 〈n ,AB →〉=n ·AB →|n |·|AB →|= 34 ,所以sin 〈n ,AB →〉=1-⎝⎛⎭⎫342 =74. 故向量AB →与平面xOz 的法向量的夹角的正弦值为74.一、两条异面直线所成的角例1 如图,在三棱柱OAB -O 1A 1B 1中,平面OBB 1O 1⊥平面OAB ,∠O 1OB =60°,∠AOB =90°,且OB =OO 1=2,OA =3,求异面直线A 1B 与AO 1所成角的余弦值.解 以O 为坐标原点,OA →,OB →的方向为x 轴,y 轴的正方向.建立如图所示的空间直角坐标系,则O (0,0,0),O 1(0,1,3),A (3,0,0),A 1(3,1,3),B (0,2,0), ∴A 1B —→=(-3,1,-3),O 1A —→=(3,-1,-3). ∴|cos 〈A 1B →,O 1A →〉|=|A 1B →·O 1A →||A 1B →||O 1A →|=|(-3,1,-3)·(3,-1,-3)|7×7=17.∴异面直线A 1B 与AO 1所成角的余弦值为17.反思感悟 求异面直线夹角的方法(1)传统法:作出与异面直线所成角相等的平面角,进而构造三角形求解.(2)向量法:在两异面直线a 与b 上分别取点A ,B 和C ,D ,则AB →与CD →可分别为a ,b 的方向向量,则cos θ=|AB →·CD →||AB →||CD →|.跟踪训练1 如图所示,在正方体ABCD -A 1B 1C 1D 1中,已知M ,N 分别是BD 和AD 的中点,则B 1M 与D 1N 所成角的余弦值为( )A.3010B.3015 C.3030D.1515答案 A解析 建立如图所示的空间直角坐标系,设正方体的棱长为2,则B 1(2,2,2),M (1,1,0),D 1(0,0,2),N (1,0,0), ∴B 1M —→=(-1,-1,-2), D 1N —→=(1,0,-2),∴cos 〈B 1M —→,D 1N —→〉=-1+41+1+4×1+4=3010. 二、直线与平面所成的角例2 如图所示,三棱锥P -ABC 中,P A ⊥平面ABC ,AB ⊥AC ,P A =AC =12AB ,N 为AB 上一点,AB =4AN ,M ,S 分别为PB ,BC 的中点.(1)证明:CM ⊥SN ;(2)求SN 与平面CMN 所成角的大小.(1)证明 设P A =1,以A 为原点,射线AB ,AC ,AP 分别为x 轴,y 轴,z 轴正方向建立空间直角坐标系(如图).则P (0,0,1),C (0,1,0),B (2,0,0),又AN =14AB ,M ,S 分别为PB ,BC 的中点,∴N ⎝⎛⎭⎫12,0,0,M ⎝⎛⎭⎫1,0,12,S ⎝⎛⎭⎫1,12,0, CM →=⎝⎛⎭⎫1,-1,12,SN →=⎝⎛⎭⎫-12,-12,0, ∴CM →·SN →=⎝⎛⎭⎫1,-1,12·⎝⎛⎭⎫-12,-12,0=0, ∴CM →⊥SN →, 因此CM ⊥SN .(2)解 由(1)知,NC →=⎝⎛⎭⎫-12,1,0,设a =(x ,y ,z )为平面CMN 的一个法向量, ∴CM →·a =0,NC →·a =0.则⎩⎨⎧x -y +12z =0,-12x +y =0.∴⎩⎪⎨⎪⎧x =2y ,z =-2y . 取y =1,得a =(2,1,-2). 设SN 与平面CMN 所成的角为θ,∵sin θ=|cos 〈a ,SN →〉|=⎪⎪⎪⎪-1-123×22=22. ∴SN 与平面CMN 所成角为π4.反思感悟 利用平面的法向量求直线与平面夹角的基本步骤 (1)建立空间直角坐标系. (2)求直线的方向向量u . (3)求平面的法向量n . (4)设线面角为θ,则sin θ=|u ·n ||u ||n |. 跟踪训练2 如图,在直三棱柱ABC -A 1B 1C 1中,AB =AC =AA 1=2,∠BAC =90°,E ,F 依次为C 1C ,BC 的中点.求A 1B 与平面AEF 所成角的正弦值.解 以A 为原点,建立如图所示的空间直角坐标系,则A (0,0,0),A 1(0,0,2),B (2,0,0),E (0,2,1),F (1,1,0), 所以A 1B —→=(2,0,-2),AE →=(0,2,1),AF →=(1,1,0). 设平面AEF 的一个法向量为n =(a ,b ,c ), 由⎩⎪⎨⎪⎧n ·AE →=0,n ·AF →=0,得⎩⎪⎨⎪⎧2b +c =0,a +b =0,令a =1可得n =(1,-1,2). 设A 1B 与平面AEF 所成角为θ,所以sin θ=|cos 〈n ,A 1B —→〉|=|n ·A 1B —→||n ||A 1B —→|=36,即A 1B 与平面AEF 所成角的正弦值为36. 三、两个平面的夹角例3 如图,四棱柱ABCD -A 1B 1C 1D 1的所有棱长都相等,AC ∩BD =O ,A 1C 1∩B 1D 1=O 1,四边形ACC 1A 1和四边形BDD 1B 1均为矩形.(1)证明:O 1O ⊥平面ABCD ;(2)若∠CBA =60°,求平面C 1OB 1与平面OB 1D 夹角的余弦值.(1)证明 因为四边形ACC 1A 1和四边形BDD 1B 1均为矩形,所以CC 1⊥AC ,DD 1⊥BD , 又CC 1∥DD 1∥OO 1,所以OO 1⊥AC ,OO 1⊥BD , 因为AC ∩BD =O ,AC ,BD ⊂平面ABCD , 所以O 1O ⊥平面ABCD .(2)解 因为四棱柱的所有棱长都相等,所以四边形ABCD 为菱形,AC ⊥BD ,又O 1O ⊥平面ABCD ,所以OB ,OC ,OO 1两两垂直.如图,以O 为原点,OB ,OC ,OO 1所在直线分别为x ,y ,z 轴,建立空间直角坐标系.设棱长为2,因为∠CBA =60°, 所以OB =3,OC =1,所以O (0,0,0),B 1(3,0,2),C 1(0,1,2), 平面BDD 1B 1的一个法向量为n =(0,1,0), 设平面OC 1B 1的法向量为m =(x ,y ,z ), 由m ⊥OB 1—→,m ⊥OC 1—→,得3x +2z =0,y +2z =0, 取z =-3,则x =2,y =23, 所以m =(2,23,-3),所以cos 〈m ,n 〉=m ·n |m ||n |=2319=25719.所以平面C 1OB 1与平面OB 1D 夹角的余弦值为25719.延伸探究本例不变,求平面BA 1C 与平面A 1CD 夹角的余弦值. 解 B (3,0,0),A 1(0,-1,2),C (0,1,0),D (-3,0,0), 设平面BA 1C 的法向量为m =(x 1,y 1,z 1), A 1C →=(0,2,-2),BC →=(-3,1,0),则⎩⎪⎨⎪⎧m ·A 1C —→=0,m ·BC →=0,即⎩⎨⎧2y 1-2z 1=0,-3x 1+y 1=0,令x 1=1,则y 1=3,z 1=3, ∴m =(1,3,3),同理得,平面A 1CD 的法向量n =(1,-3,-3), cos 〈m ,n 〉=m ·n |m ||n |=-57,则平面BA 1C 与平面A 1CD 夹角的余弦值为57.反思感悟 求两平面夹角的两种方法(1)定义法:在两个平面内分别找出与两平面交线垂直的直线,这两条直线的夹角即为两平面的夹角.也可转化为求与两平面交线垂直的直线的方向向量的夹角,但要注意其异同.(2)法向量法:分别求出两平面的法向量n 1,n 2,则两平面的夹角为〈n 1,n 2〉⎝⎛⎭⎫当〈n 1,n 2〉∈⎣⎡⎦⎤0,π2时或π-〈n 1,n 2〉⎝⎛⎭⎫当〈n 1,n 2〉∈⎝⎛⎦⎤π2,π时.跟踪训练3 如图所示,在几何体S -ABCD 中,AD ⊥平面SCD ,BC ⊥平面SCD ,AD =DC =2,BC =1,又SD =2,∠SDC =120°,求平面SAD 与平面SAB 夹角的余弦值.解 如图,过点D 作DC 的垂线交SC 于E ,以D 为原点,以DC ,DE ,DA 所在直线分别为x ,y ,z 轴建立空间直角坐标系.∵∠SDC =120°,∴∠SDE =30°,又SD =2,∴点S 到y 轴的距离为1,到x 轴的距离为3,则有D (0,0,0),S (-1,3,0),A (0,0,2),C (2,0,0),B (2,0,1), 设平面SAD 的法向量为m =(x ,y ,z ), ∵AD →=(0,0,-2),AS →=(-1,3,-2),∴⎩⎨⎧-2z =0,-x +3y -2z =0,取x =3,得平面SAD 的一个法向量为m =(3,1,0). 又AB →=(2,0,-1),设平面SAB 的法向量为n =(a ,b ,c ),则⎩⎪⎨⎪⎧n ·AB →=0,n ·AS →=0,即⎩⎨⎧2a -c =0,-a +3b -2c =0,令a =3, 则n =(3,5,23),∴cos 〈m ,n 〉=m ·n |m ||n |=8210×2=105,故平面SAD 与平面SAB 夹角的余弦值是105.空间向量和实际问题典例 如图,甲站在水库底面上的点A 处,乙站在水坝斜面上的点B 处.从A ,B 到直线 (库底与水坝的交线)的距离AC 和BD 分别为a 和b ,CD 的长为c ,甲乙之间拉紧的绳长为d ,求库底与水坝所在平面夹角的余弦值.解 由题意可知AC =a ,BD =b ,CD =c ,AB =d ,所以d 2=AB →2=(AC →+CD →+DB →)2=AC →2+CD →2+DB →2+2(AC →·CD →+AC →·DB →+CD →·DB →) =a 2+c 2+b 2+2AC →·DB →=a 2+c 2+b 2-2CA →·DB →, 则2CA →·DB →=a 2+b 2+c 2-d 2,设向量CA →与DB →的夹角为θ,θ就是库底与水坝所在平面的夹角, 因此2ab cos θ=a 2+b 2+c 2-d 2,所以cos θ=a 2+b 2+c 2-d 22ab,故库底与水坝所在平面夹角的余弦值为a 2+b 2+c 2-d 22ab .[素养提升]利用空间向量解决实际问题(1)分析实际问题的向量背景,将题目条件、结论转化为向量问题.(2)对于和垂直、平行、距离、角度有关的实际问题,可以考虑建立向量模型,体现了数学建模的核心素养.1.若异面直线l 1的方向向量与l 2的方向向量的夹角为150°,则l 1与l 2所成的角为( ) A.π6B.5π6C.π6或5π6D .以上均不对 答案 A解析 l 1与l 2所成的角与其方向向量的夹角相等或互补,且异面直线所成角的范围为⎝⎛⎦⎤0,π2,故选A. 2.已知向量m ,n 分别是平面α和平面β的法向量,若cos 〈m ,n 〉=-12,则α与β的夹角为( )A .30°B .60°C .120°D .150° 答案 B解析 设α与β所成的角为θ,且0°≤θ≤90°, 则cos θ=|cos 〈m ,n 〉|=12,∴θ=60°.3.直三棱柱ABC -A 1B 1C 1中,∠BCA =90°,M ,N 分别是A 1B 1,A 1C 1的中点,BC =CA =CC 1,则BM 与AN 所成角的余弦值为( ) A.110 B.25 C.3010 D.22答案 C解析 如图所示,以C 为原点,直线CA 为x 轴,直线CB 为y 轴,直线CC 1为z 轴建立空间直角坐标系,设CA =CB =1,则B (0,1,0),M ⎝⎛⎭⎫12,12,1,A (1,0,0),N ⎝⎛⎭⎫12,0,1. 故BM →=⎝⎛⎭⎫12,-12,1,AN →=⎝⎛⎭⎫-12,0,1, 所以cos 〈BM →,AN →〉=BM →·AN →|BM →||AN →|=3462×52=3010.4.如图所示,点A ,B ,C 分别在空间直角坐标系Oxyz 的三条坐标轴上,OC →=(0,0,2),平面ABC 的一个法向量为n =(2,1,2),平面ABC 与平面ABO 的夹角为θ,则cos θ=________.答案 23解析 cos θ=OC →·n |OC →||n |=42×3=23.5.正方体ABCD -A 1B 1C 1D 1中,BB 1与平面ACD 1所成角的正弦值为________. 答案33解析 设正方体的棱长为1,建立空间直角坐标系如图.则D (0,0,0),B (1,1,0),B 1(1,1,1). 平面ACD 1的一个法向量为DB 1—→=(1,1,1). 又BB 1—→=(0,0,1),则cos 〈DB 1—→,BB 1—→〉=DB 1—→·BB 1—→|DB 1—→||BB 1—→|=13×1=33.1.知识清单:(1)两条异面直线所成的角. (2)直线和平面所成的角. (3)两个平面的夹角. 2.方法归纳:转化与化归.3.常见误区:混淆两个向量的夹角和空间角的关系,不能正确理解空间角的概念,把握空间角的范围.1.已知A (0,1,1),B (2,-1,0),C (3,5,7),D (1,2,4),则直线AB 与直线CD 所成角的余弦值为( ) A.52266 B .-52266 C.52222 D .-52222答案 A解析 ∵AB →=(2,-2,-1),CD →=(-2,-3,-3),∴cos 〈AB →,CD →〉=AB →·CD →|AB →||CD →|=53×22=52266,∴直线AB ,CD 所成角的余弦值为52266.2.已知两平面的法向量分别为m =(0,1,0),n =(0,1,1),则两平面夹角为( ) A .45° B .135° C .45°或135° D .90° 答案 A解析 cos 〈m ,n 〉=m ·n |m ||n |=11·2=22,即〈m ,n 〉=45°.所以两平面的夹角为45°.3.设直线l 与平面α相交,且l 的方向向量为a ,α的法向量为n ,若〈a ,n 〉=2π3,则l 与α所成的角为( )A.2π3B.π3C.π6D.5π6 答案 C解析 线面角的范围是⎣⎡⎦⎤0,π2. ∵〈a ,n 〉=2π3,∴l 与法向量所在直线所成角为π3,∴l 与α所成的角为π6.4.若平面α的一个法向量为n =(4,1,1),直线l 的一个方向向量为a =(-2,-3,3),则l 与α所成角的余弦值为( )A .-41133 B.41133 C .-91333 D.91333答案 D解析 设α与l 所成的角为θ, 则sin θ=|cos 〈a ,n 〉|=|(-2,-3,3)·(4,1,1)|4+9+9×16+1+1=⎪⎪⎪⎪⎪⎪-4311=41133,故直线l 与α所成角的余弦值为1-⎝⎛⎭⎫411332=91333.5.正方形ABCD 所在平面外一点P ,P A ⊥平面ABCD ,若P A =AB ,则平面P AB 与平面PCD 的夹角为( )A .30°B .45°C .60°D .90° 答案 B解析 如图所示,建立空间直角坐标系,设P A =AB =1,则A (0,0,0),D (0,1,0),P (0,0,1). 于是AD →=(0,1,0),取PD 的中点E ,则E ⎝⎛⎭⎫0,12,12, ∴AE →=⎝⎛⎭⎫0,12,12,易知AD →是平面P AB 的法向量,AE →是平面PCD 的法向量, ∴cos 〈AD →,AE →〉=22,∴平面P AB 与平面PCD 的夹角为45°.6.如图,在正方体ABCD -A 1B 1C 1D 1中,M 是C 1C 的中点,O 是底面ABCD 的中心,P 是A 1B 1上的任意点,则直线BM 与OP 所成的角为________.答案 π2解析 建立如图所示的空间直角坐标系,设正方体棱长为2,A 1P =x ,则O (1,1,0),P (2,x ,2),B (2,2,0),M (0,2,1), OP →=(1,x -1,2),BM →=(-2,0,1). 所以OP →·BM →=0,所以直线BM 与OP 所成的角为π2.7.如图所示,在长方体ABCD -A 1B 1C 1D 1中,AB =BC =2,AA 1=1,则BC 1与平面BB 1D 1D 所成角的正弦值为________.答案105解析 如图所示,建立空间直角坐标系,则D (0,0,0),A (2,0,0),B (2,2,0),C (0,2,0),D 1(0,0,1),C 1(0,2,1), ∴BC 1→=(-2,0,1).连接AC ,易证AC ⊥平面BB 1D 1D ,∴平面BB 1D 1D 的一个法向量为a =AC →=(-2,2,0).∴所求角的正弦值为|cos 〈a ,BC 1—→〉|=|a ·BC 1—→||a ||BC 1—→|=48×5=105.8.已知点E ,F 分别在正方体ABCD -A 1B 1C 1D 1的棱BB 1,CC 1上,且B 1E =2EB ,CF =2FC 1,则平面AEF 与平面ABC 夹角的余弦值等于 ________. 答案31111解析 如图,建立空间直角坐标系.设正方体的棱长为1,平面ABC 的法向量为n 1=(0,0,1), 平面AEF 的法向量为n 2=(x ,y ,z ). 所以A (1,0,0),E ⎝⎛⎭⎫1,1,13,F ⎝⎛⎭⎫0,1,23, 所以AE →=⎝⎛⎭⎫0,1,13,EF →=⎝⎛⎭⎫-1,0,13, 则⎩⎪⎨⎪⎧n 2·AE →=0,n 2·EF →=0,即⎩⎨⎧y +13z =0,-x +13z =0.取x =1,则y =-1,z =3.故n 2=(1,-1,3). 所以cos 〈n 1,n 2〉=n 1·n 2|n 1||n 2|=31111.所以平面AEF 与平面ABC 夹角的余弦值为31111.9.如图所示,在直三棱柱ABC -A 1B 1C 1中,AB ⊥AC ,AB =AC =2,AA 1=4,点D 是BC 的中点.求异面直线A 1B 与C 1D 所成角的余弦值.解 以点A 为原点,AB ,AC ,AA 1所在直线分别为x 轴,y 轴,z 轴,建立空间直角坐标系Axyz ,则A (0,0,0),B (2,0,0),C (0,2,0),A 1(0,0,4),D (1,1,0),C 1(0,2,4), ∴A 1B —→=(2,0,-4),C 1D —→=(1,-1,-4), ∴cos 〈A 1B —→,C 1D —→〉=A 1B —→·C 1D —→|A 1B —→||C 1D —→|=31010,∴异面直线A 1B 与C 1D 所成角的余弦值为31010.10.四棱锥P -ABCD 的底面是正方形,PD ⊥底面ABCD ,点E 在棱PB 上. (1)求证:平面AEC ⊥平面PDB ;(2)当PD =2AB 且E 为PB 的中点时,求AE 与平面PDB 所成角的大小. (1)证明 如图,以D 为原点建立空间直角坐标系Dxyz ,设AB =a ,PD =h ,则A (a ,0,0),B (a ,a ,0),C (0,a ,0),D (0,0,0),P (0,0,h ), ∴AC →=(-a ,a ,0),DP →=(0,0,h ),DB →=(a ,a ,0),∴AC →·DP →=0,AC →·DB →=0,∴AC ⊥DP ,AC ⊥DB ,又DP ∩DB =D ,DP ,DB ⊂平面PDB , ∴AC ⊥平面PDB , 又AC ⊂平面AEC , ∴平面AEC ⊥平面PDB .(2)解 当PD =2AB 且E 为PB 的中点时, P (0,0,2a ),E ⎝⎛⎭⎫12a ,12a ,22a ,设AC ∩BD =O ,O ⎝⎛⎭⎫a 2,a 2,0, 连接OE ,由(1)知AC ⊥平面PDB , ∴∠AEO 为AE 与平面PDB 所成的角,∵EA →=⎝⎛⎭⎫12a ,-12a ,-22a ,EO →=⎝⎛⎭⎫0,0,-22a ,∴cos ∠AEO =EA →·EO →|EA →|·|EO →|=22,∴∠AEO =45°,即AE 与平面PDB 所成角的大小为45°.11.如图,在三棱柱ABC -A 1B 1C 1中,CA =CC 1=2CB ,则直线BC 1与直线AB 1所成角的余弦值为( )A.55B.53C.255D.35答案 A解析 不妨设CA =CC 1=2CB =2,则AB 1—→=(-2,2,1),C 1B —→=(0,-2,1), 所以cos 〈AB 1—→,C 1B —→〉=AB 1—→·C 1B —→|AB 1—→||C 1B —→|=(-2)×0+2×(-2)+1×19×5=-55.所以所求角的余弦值为55. 12.已知在长方体ABCD -A 1B 1C 1D 1中,AB =BC =1,AA 1=2,E 是侧棱BB 1的中点,则直线AE 与平面A 1ED 1所成角的大小为( ) A .60° B .90° C .45° D .以上都不对 答案 B解析 以点D 为原点,分别以DA ,DC ,DD 1所在直线为x 轴,y 轴,z 轴,建立空间直角坐标系,如图.由题意知,A 1(1,0,2),E (1,1,1),D 1(0,0,2),A (1,0,0),所以A 1E —→=(0,1,-1),D 1E —→=(1,1,-1),EA →=(0,-1,-1). 设平面A 1ED 1的一个法向量为n =(x ,y ,z ), 则⎩⎪⎨⎪⎧n ·A 1E →=0,n ·D 1E →=0,得⎩⎪⎨⎪⎧y -z =0,x +y -z =0,令z =1,得y =1,x =0,所以n =(0,1,1), cos 〈n ,EA →〉=n ·EA →|n ||EA →|=-22·2=-1,设直线与平面A 1ED 1所成角为θ,则sin θ=1,所以直线AE 与平面A 1ED 1所成的角为90°.13.在空间中,已知平面α过(3,0,0)和(0,4,0)及z 轴上一点(0,0,a )(a >0),如果平面α与平面xOy 的夹角为45°,则a =________.答案 125 解析 平面xOy 的法向量n =(0,0,1),设平面α的法向量为u =(x ,y ,z ),则⎩⎪⎨⎪⎧-3x +4y =0,-3x +az =0, 即3x =4y =az ,取z =1,则u =⎝⎛⎭⎫a 3,a 4,1.而cos 〈n ,u 〉=1a 29+a 216+1=22,又∵a >0,∴a =125. 14.已知正△ABC 与正△BCD 所在平面垂直,则平面ABD 与平面BDC 夹角的余弦值为____. 答案 55解析 取BC 的中点O ,连接AO ,DO ,建立如图所示的空间直角坐标系.设BC =1,则A ⎝⎛⎭⎫0,0,32,B ⎝⎛⎭⎫0,-12,0,D ⎝⎛⎭⎫32,0,0. 所以OA →=⎝⎛⎭⎫0,0,32,BA →=⎝⎛⎭⎫0,12,32,BD →=⎝⎛⎭⎫32,12,0. 由于OA →=⎝⎛⎭⎫0,0,32为平面BCD 的一个法向量. 设平面ABD 的法向量为n =(x ,y ,z ),则⎩⎪⎨⎪⎧ n ·BA →=0,n ·BD →=0,所以⎩⎨⎧ 12y +32z =0,32x +12y =0,取x =1,则y =-3,z =1,所以n =(1,-3,1),所以cos 〈n ,OA →〉=55.15.如图,在三棱锥V -ABC 中,顶点C 在空间直角坐标系的原点处,顶点A ,B ,V 分别在x 轴、y轴、z 轴上,D 是线段AB 的中点,且AC =BC =2,∠VDC =π3,则异面直线AC 与VD 所成角的余弦值为________.答案 24解析 ∵AC =BC =2,D 是AB 的中点,∴C (0,0,0),A (2,0,0),B (0,2,0),D (1,1,0).当θ=π3时,在Rt △VCD 中,CD =2, ∴V (0,0,6),∴AC →=(-2,0,0),VD →=(1,1,-6),∴cos 〈AC →,VD →〉=AC →·VD →|AC →||VD →|=-22×22=-24. ∴异面直线AC 与VD 所成角的余弦值为24. 16.如图所示,在棱长为a 的正方体ABCD -A 1B 1C 1D 1中,E ,F 分别是BC ,A 1D 1的中点.(1)求直线A 1C 与DE 所成角的余弦值;(2)求直线AD 与平面B 1EDF 所成角的余弦值;(3)求平面B 1EDF 与平面ABCD 夹角的余弦值. 解 以A 为坐标原点,分别以AB ,AD ,AA 1所在直线为x 轴,y 轴,z 轴,建立空间直角坐标系Axyz .(1)A 1(0,0,a ),C (a ,a ,0),D (0,a ,0),E ⎝⎛⎭⎫a ,a 2,0, ∴A 1C —→=(a ,a ,-a ),DE →=⎝⎛⎭⎫a ,-a 2,0, ∴cos 〈A 1C —→,DE →〉=A 1C —→·DE →|A 1C —→||DE →|=1515, 故A 1C 与DE 所成角的余弦值为1515. (2)连接DB 1,∵∠ADE =∠ADF ,∴AD 在平面B 1EDF 内的射影在∠EDF 的平分线上. 又四边形B 1EDF 为菱形,∴DB 1为∠EDF 的平分线, 故直线AD 与平面B 1EDF 所成的角为∠ADB 1. 由A (0,0,0),B 1(a ,0,a ),D (0,a ,0), 得DA →=(0,-a ,0),DB 1—→=(a ,-a ,a ),∴cos 〈DA →,DB 1→〉=DA →·DB 1—→|DA →||DB 1—→|=33,又直线与平面所成角的范围是⎣⎡⎦⎤0,π2, 故直线AD 与平面B 1EDF 所成角的余弦值为33. (3)由已知得A (0,0,0),A 1(0,0,a ),B 1(a ,0,a ),D (0,a ,0),E ⎝⎛⎭⎫a ,a 2,0, 则ED →=⎝⎛⎭⎫-a ,a 2,0,EB 1→=⎝⎛⎭⎫0,-a 2,a , 平面ABCD 的一个法向量为m =AA 1—→=(0,0,a ).设平面B 1EDF 的一个法向量为n =(1,y ,z ),由⎩⎪⎨⎪⎧ n ·ED →=0,n ·EB 1—→=0,得⎩⎪⎨⎪⎧y =2,z =1, ∴n =(1,2,1),∴cos 〈n ,m 〉=m ·n |m ||n |=66, ∴平面B 1EDF 与平面ABCD 夹角的余弦值为66.。
高一数学必修二知识点:直线和平面的位置关系

高一数学必修二知识点:直线和平面的位置关系【】数学的学习不像文科要死记硬背,学好高中数学最主要的是要掌握好课本上的根本公式,纯熟运用,才能解考试过程中的各种题型。
直线和平面的位置关系:
直线和平面只有三种位置关系:在平面内、与平面相交、与平面平行
①直线在平面内有无数个公共点
②直线和平面相交有且只有一个公共点
直线与平面所成的角:平面的一条斜线和它在这个平面内的射影所成的锐角。
esp.空间向量法(找平面的法向量)
规定:a、直线与平面垂直时,所成的角为直角,b、直线与平面平行或在平面内,所成的角为0角
由此得直线和平面所成角的取值范围为[0,90]
最小角定理:斜线与平面所成的角是斜线与该平面内任一条直线所成角中的最小角
三垂线定理及逆定理:假设平面内的一条直线,与这个平面的一条斜线的射影垂直,那么它也与这条斜线垂直
esp.直线和平面垂直
直线和平面垂直的定义:假设一条直线a和一个平面内的任意一条直线都垂直,我们就说直线a和平面互相垂直.直线a
叫做平面的垂线,平面叫做直线a的垂面。
直线与平面垂直的断定定理:假设一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面。
直线与平面垂直的性质定理:假设两条直线同垂直于一个平面,那么这两条直线平行。
③直线和平面平行没有公共点
直线和平面平行的定义:假设一条直线和一个平面没有公共点,那么我们就说这条直线和这个平面平行。
直线和平面平行的断定定理:假设平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行。
直线和平面平行的性质定理:假设一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
高一数学必修2线、面垂直的判定与性质

α β a A 线、面垂直的判定与性质一、线、面垂直的判定与性质1.线面垂直的定义:如果直线 l 与平面α内的任意一条直线都垂直,我们说直线 l 与平面α 互相垂直.2.线面垂直的判定:一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直. 直线与平面垂直3.(1)的射影所成的角(2)(3一条直线与平面所成的角的取值范围是 4.二面角相关概念:以二面角的棱上任意一点为顶点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角. ∠AOB即为二面角α-AB-β的平面角注意:二面角的平面角必须满足:(1)角的顶点在棱上.(2)角的两边分别在两个面内. (3)角的边都要垂直于二面角的棱.二面角的取值范围 5.面面垂直的定义:一般地,两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直.记为β⊥α6.判定定理:如果一个平面经过另一个平面的垂线,则这两个平面垂直.7.直线与平面垂直的性质定理:垂直于同一个平面的两条直线平行8.面面垂直的性质定理:两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直. 面面垂直⇒线面垂直α⊥l 记为⇒⎪⎪⎭⎪⎪⎬⎫l a l ⊥b l ⊥α⊂a α⊂b A b a = ]90,0[0[]]0[180,000π,或a β⊂a α⊥面⇒βα⊥//a a b b αα⊥⎫⇒⎬⊥⎭a b αa bl a a l αβαββ⊥⎫⎪=⎪⎬⊂⎪⎪⊥⎭a α⇒⊥二、例题解析题型一、判断问题例1、直线l与平面α内的无数条直线垂直,则直线l与平面α的关系是()A.l和平面α相互平行B.l和平面α相互垂直C.l在平面α内D.不能确定变式:如果一条直线垂直于一个平面内的:①三角形的两边;②梯形的两边;③圆的两条直径;④正六边形的两条边.则能保证该直线与平面垂直()A.①③B.①②C.②④D.①④例2、已知直线a∥平面α,a⊥平面β,则( )A.α⊥βB.α∥βC.α与β不垂直D.以上都有可能变式:下列命题中错误的是( )A.如果平面α⊥平面β,那么平面α内一定存在直线平行于平面βB.如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面βC.如果平面α⊥平面γ,平面β⊥平面γ,α∩β=l,那么l⊥平面γD.如果平面α⊥平面β,那么平面α内所有直线都垂直于平面β例3、已知b⊥平面α,a⊂α,则直线a 与直线b 的位置关系是( )A.a∥b B.a⊥b C.直线a 与直线b 垂直相交D.直线a 与直线b 垂直且异面变式1:下面四个命题,其中真命题的个数为( )①如果直线l 与平面α内的无数条直线垂直,则l⊥α;②如果直线l 与平面α内的一条直线垂直,则l⊥α;③如果直线l 与平面α不垂直,则直线l 和平面α内的所有直线都不垂直;④如果直线l 与平面α不垂直,则平面α内也可以有无数条直线与直线l 垂直.A.1 个B.2 个C.3 个D.4 个变式2:已知平面α⊥平面β,则下列命题正确的个数是()①α内的直线必垂直于β内的无数条直线;②在β内垂直于α与β的交线的直线必垂直于α内的任意一条直线;③α内的任何一条直线必垂直于β;④过β内的任意一点作α与β交线的垂线,则这条直线必垂直于α. A.4 B.3C.2D.1题型二:求角问题(线面角、面面角)例1、在正方体ABCD-A1B1C1D1中,(1)求直线A1C与平面ABCD所成的角的正切值.(2)求直线A1B与平面BDD1B1所成的角.变式:如图所示,Rt△BMC中,斜边BM=5且它在平面ABC上的射影AB长为4,∠MBC=60°,求MC与平面ABC所成角的正弦值.例2、在长方体ABCD -A 1B 1C 1D 1中,二面角A -BC -A 1的平面角是( )A .∠ABCB .∠ABB 1C .∠ABA 1D .∠ABC 1变式:如图所示,在四棱锥P -ABCD 中,底面ABCD 为平行四边形,P A ⊥平面ABCD ,且P A =3,AB =1,BC =2,AC =3,求二面角P -CD -B 的大小.题型三:证明问题例1、如图,在三棱锥 A-BCD 中,AD ,BC ,CD 两两互相垂直,M ,N分别为 AB ,AC 的中点.(1)求证:BC ∥平面 MND ;(2)求证:平面 MND ⊥平面 ACD .变式: 如图,四棱锥P-ABCD 的底面是矩形,AB=2,,侧面PAB 是等边三角形,且侧面PAB ⊥底面ABCD. (1)证明:侧面PAB ⊥侧面PBC ;(2)求侧棱PC 与底面ABCD 所成的角.BC A B C D P三、巩固练习1.在三棱锥V -ABC 中,VA =VC ,AB =BC ,则下列结论一定成立的是( )A .VA ⊥BCB .AB ⊥VCC .VB ⊥ACD .VA ⊥VB2.若A ∈α,B ∈α,A ∈l ,B ∈l ,P ∈l ,则( )A .P ⊂αB .P αC .l αD .P ∈α3.一条直线若同时平行于两个相交平面,则这条直线与这两个平面的交线的位置关系是( )A .异面B .相交C .平行D .不能确定4.如图,在长方体ABCD -A 1B 1C 1D 1中,AB =BC =2,AA 1=1,则BC 1与平面BB 1D 1D 所成角的正弦值为( )A.63B.2 65C.155D.1055.设x ,y ,z 是空间不同的直线或平面,对下列四种情形:①x ,y ,z 均为直线;②x ,y 是直线,z 是平面;③z 是直线,x ,y 是平面;④x ,y ,z 均为平面.其中使“x ⊥z ,且y ⊥z ⇒x ∥y ”为真命题的是( )A .③④B .①③C .②③D .①②6.如图,正方体ABCD -A 1B 1C 1D 1中,异面直线BD 1与A 1D 所成的角等于__________.7如图,已知正方体ABCD -A 1B 1C 1D 1,则二面角C 1-BD -C 的正切值为________.8.如图,在边长为1的等边三角形ABC 中,D ,E 分别是AB ,AC 边上的点,AD =AE ,F 是BC 的中点,AF 与DE 交于点G ,将△ABF 沿AF 折起,得到如图所示的三棱锥A -BCF ,其中BC =22. (1)证明:DE ∥平面BCF ;(2)证明:CF ⊥平面ABF ;(3)当AD =23时,求三棱锥F -DEG 的体积V F -DEG .。
线面直线所成的角

线面直线所成的角
“线面直线所成的角”通常是指空间中两条直线与一个平面所成的角。
这个概念在几何学中非常重要,因为它涉及到空间中的几何关系和角度测量。
当两条直线与一个平面相交时,它们会形成一个夹角。
这个夹角的大小取决于这两条直线的方向和它们与平面的相对位置。
如果这两条直线在平面内,那么它们所成的角就是 0 度;如果这两条直线与平面垂直,那么它们所成的角就是 90 度;如果这两条直线与平面平行,那么它们所成的角就是 180 度。
在实际应用中,常常需要计算线面直线所成的角。
例如,在建筑设计中,需要计算两条墙壁之间的夹角,以确保房间的布局合理;在机械工程中,需要计算两个零件之间的夹角,以确保它们能够正确地装配在一起。
线面直线所成的角是一个非常重要的概念,它在几何学和实际应用中都有广泛的应用。
高一数学直线和平面所成的角2
[单选]压力容器的人孔通常采用()。A.凸形封头B.锥形封头C.平板封头D.蝶形封头 [单选]给水泵跳闸后,如果出口止回阀故障不能关闭,将会引起给水泵倒转。发现给水泵倒转,应立即()。A.关闭给水泵进口门,防止除氧器满水;B.检查辅助油泵运行情况,防止缺油烧瓦,同时要尽快关闭给水泵出口门;C.立即强合一次给水泵,防止锅炉缺水;D.通知锅炉关闭给水调节门。 [填空题]地球已经是一个40多亿年的老寿星了,她起源于()星云。 [单选,A2型题,A1/A2型题]郁证肝气郁结证的最佳选方是()A.四逆散B.柴胡疏肝散C.越鞠丸D.逍遥散E.小柴胡汤 [单选]石油的易燃性,可通过其()的高低来判断。A.密度B.闪点、燃点、自燃点C.粘度D.凝固点 [单选]近年来,减轻农民负担工作的重点相应转入到()。A.巩固农村税费改革成果、有效防止反弹阶段B.实施税费改革阶段C.工业反哺农业阶段D.实施农业补贴阶段 [名词解释]纱支 [单选]能平肝潜阳,重镇降逆,凉血止血的药物是()A.赭石B.蒺藜C.珍珠母D.石决明E.牡蛎 [单选]注册建造师王某与原施工单位解除了聘用合同,选择一家在本专业有多项工程服务资质的施工单位担任建设工程施工的项目经理,则他必须进行()。A.初始注册B.延续注册C.变更注册D.增项注册 [单选]脊柱骨折造成脊髓半横切损伤,其损伤平面以下的改变是()A.双侧肢体完全截瘫B.同侧肢体运动消失,双侧肢体深浅感觉消失C.同侧肢体运动和深感觉消失,对侧肢体痛温觉消失D.同侧肢体运动和痛温觉消失,对侧肢体深感觉消失E.同侧肢体痛温觉消失,对侧肢体运动及深感觉消失 [单选,A1型题]下列哪项不是时行感冒的特征()。A.传染性强B.证候相似C.集中发病D.老幼易感E.流行性强 [单选]附加条款与基本条款的效力比较是()。A.前者大于后者B.前者小于后者C.相等D.视具体情况而定 [名词解
空间的角
空间的角异面直线所成的角 范围:0°<θ≤90° 方法:①平移法;②补形法. 直线与平面所成的角 范围:0°≤θ≤90° 方法:关键是作垂线,找射影. 二面角θ范围:0°≤θ≤180° 方法:①定义法; ②三垂线定理及其逆定理;③垂面法. 注:二面角的计算也可利用射影面积公式S ′=S cos θ来计算1.空间角的计算步骤 一作、二证、三算.2.异面直线所成角:(1)范围:(]0,90︒︒;(2)计算方法:①平移法:②向量法:设,a b r r分别为异面直线,a b 的方向向量,则两异面直线所成的角α=arccosa b a buu r u u r uu r u u r g g ;③补形法;④证明两条异面直线垂直,即所成角为90︒. 3直线与平面所成的角:①定义:平面的一条斜线和它在这个平面内的射影所成的锐角,若垂直于平面,所成角是直角.②范围[]0,90︒︒;③最小角定理:斜线和平面所成的角,是斜线和这个平面内经过斜足的直线所成的角中最小的角.⑤斜线与平面所成角的计算:(1)直接法:关键是作垂线,找射影 可利用面面垂直的性质;(2)通过等体积法求出斜线任一点到平面的距离d ,计算这点与斜足之间的线段长l ,则sin d l θ=.(3) 12cos cos cos θθθ=. (4)向量法:设l 是斜线l 的方向向量,n是平面α的法向量,则斜线l 与平面α所成的角θarcsinl n l n=r r g r r g .4.二面角:①定义:平面内的一条直线把平面分为两部分,其中的每一部分叫做半平面.从一条直线出发的两个半平面所组成的图形叫做二面角,这条直线叫做二面角的棱,每个半平面叫做二面角的面.二面角的平面角:以二面角的棱上任一点为端点,在两个半平面内分别作垂直于棱的两条射线,这两条射线所成的角,叫做这个二面角的平面角.规定:二面角的两个半平面重合时,二面角为0,当两个半平面合成一个平面时,二面角为π,因此,二面角的大小范围为[]0,π.②确定二面角的方法:(1)定义法;(2)三垂线定理及其逆定理法;(3)垂面法;(4)射影面积法:cos S S θ=射影多边形原多边形,此方法常用于无棱二面角大小的计算;无棱二面角也可以先根据线面性质恢复二面角的棱,然后再用方法(1)、(2)计算大小;(5)向量法:法一、在α内al ⊥,在β内bl ⊥,则二面角l αβ-- 的平面角αarccosa ba b=ur u r u r u r g g ;或 arccos a ba bπ-ur u r ur u r g g (同等异补)法二、设1n ,2n是二面角l αβ--的两个半平面的法向量,其方向一个指向内侧,另一个指向外侧(同等异补),则二面角l αβ--的平面角α1212arccos n nn n=uu r uu ruu r uu r g g课前练习1.正方体ABCD —A 1B 1C 1D 1中,E 、F 分别是棱C 1C 与BC 的中点,则直线EF 与直线D 1C 所成角的大小是 ( B )A .45°B .60°C .75°D .90°空间四边形ABC D 中,E 、F 分别为AC 、B D 中点,若C D =2AB =4,EF ⊥AB ,则EF 与C D 所成的角为( A )(A)30° (B)45° (C)60°(D)90°如图,AB =2,A C ⊥α,B D ⊥α,C α∈,D α∈,CD=1, 则直线AB 与α所成的角为( B )(A)300(B)600(C)a rct an21 (D)4503.AB ⊥平面BCD ,DC ⊥CB ,AD 与平面BCD 所成的角为30°,且AB =BC . 求AD 与平面ABC 所成角的大小.( 45°)例53. 已知正方形ABCD ,沿对角线AC 将△ADC 折起,设AD 与平面ABC 所成的角为β,当β 取最大值时,二面角B ―AC ―D 等于( B )(A )1200 (B )900 (C )600 (D )450 例57.正方体AB CD-A 1B 1C 1D 1中,(1)B C 1与底面AB CD 所成角为 450 ;(2)A 1C 与底面AB CD 所成的角的正切值为22;(3)B C 1与对角面BB 1D 1D 所成的角为 300 。
高一数学(人教B版)直线与平面垂直的概念
O 的直径,
O 上不同于 A, B 任意一点,求证:BC 平面 PAC .
练习1 如图,已知 PA垂直于
C是
O 所在的平面, AB是
O 的直径,
O 上不同于 A, B 任意一点,求证:BC 平面 PAC .
证明:因为 PA 平面 ABC ,BC 平面 ABC ,
所以 PA BC .又因为 AB是
所以 BC AC. 又 PA
O 的直径,
AC A,
PA, AC 平面 PAC,所以 BC 平面 PAC .
引申探究1 若练习1中其他条件不变,
作 AE PC 于点 E ,求证:AE 平面 PBC .
引申探究1 若练习1中其他条件不变,
作 AE PC 于点 E ,求证:AE 平面 PBC .
引申探究2若引申探究1中其他条件不变,过点 A 作 AF PB 于 F ,
求证: PB 平面 AEF .
证明:由引申探究1知 AE 平面 PBC .
因为PB 平面PBC,所以 AE PB ,
又 AF PB ,且 AE
AF A,
AE , AF 平面 AEF,所以 PB 平面 AEF .
2.如果一条直线和一个平面内的一条直线垂直,此直线
是否和平面垂直?
思考探究
请思考:直线和平面垂直如何判定?
1.利用直线与平面垂直定义能检验旗杆垂直于地面吗?
2.如果一条直线和一个平面内的一条直线垂直,此直线
是否和平面垂直?
3.如果一条直线和一个平面内的两条直线垂直,此直线
是否和平面垂直?
直线与平面垂直的判定定理:如果一条直线与一个平面内
又 AB∥CD ,所以 CD PA.
《直线与平面所成角复习课——线面角的三种常见求法》教案-最新教学文档
直线与平面所成角复习课(2)——线面角的三种常见求法一、教学内容解析新课标立体几何内容较大纲教材变化大,三垂线及其逆定理作为阅读教材,对于有关线、面的垂直的求解方式方法带来很大的改变,对求解二面角及线面角的方式方法也带来很大的改变。
对我校大部分学生而言,二面角求解要求属于了解层次,斜线与平面角所成的角属于理解与掌握层次,“求解线面角”变成我校学生学习立体几何有关角的计算最难的一个问题。
特别是教材中对线在平面上的射影这一概念比较弱化,点面距离的概念在教材中已经退化,我校学生学习线面角主要方法就是定义法。
那如何化解难点,使学生能够有条不紊的找出线面角并求解,成为这堂课的重中之重。
二、教学目标设置1、知识与技能:正确认识直线与平面所成角的概念,能够利用面面垂直的性质找出已知平面的垂线从而找出线面角,能够利用向量法和等体积法帮助求解线面角。
2、过程与方法:(1)空间想象能力:认识直线与平面的位置关系,遵循从实图和简单的几何体入手,逐步培养学生的几何直观和空间想象能力。
(2)转化的思想方法:在二维与三维空间的转化及线面角与线线角的转化过程中,体现出转化的思想方法。
(3)逻辑思维与运算能力:通过对线面角大小的求解,加强算中有证,以证助算,以培养学生的逻辑思维能力及运算能力。
3、情感、态度与价值观:体验概念的形成过程,培养创新意识和数学应用意识,提高学习数学的兴趣。
三、学生学情分析我班学生“偏文”,尤其是女生的空间想象能力很弱,拿到立体几何题恨不得道道用向量法求解,因而忽视了定义法的重要性。
学生在寻找线面角的过程中往往毫无头绪无从下手,缺少应有的逻辑推理能力和空间想象能力,不喜欢或不擅长添加复杂的辅助线帮助找角和证明。
本节课旨在打开他们的解题思路,将求解过程规范化,有序化,从而能够进一步提高他们求解立体几何有关角的计算能力。
四、教学策略分析由于这是一节复习课,所以我选择在前一节课留给他们一道简单而又经典的线面角问题,让他们自由发挥,各尽所能。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
知识探究(一):平面的斜线
思考1:当直线与平面相交时,它们可
能垂直,也可能不垂直,如果一条直
线和一个平面相交但不垂直,这条直
线叫做这个平面的斜线,斜线和平面
的交点叫做斜足.那么过一点作一个平
面的斜线有多少条?
l
斜线
斜足
P
α
的意思。使不安静:他在休息,【超凡】chāofán动超出平常:技艺~。果皮黄褐色, 【巉】chán〈书〉山势高险的样子。就是写文章。【豺狗】chái ɡǒu名豺。【车马费】chēmǎfèi名因公外出时的交通费。【彻骨】chèɡǔ动透到骨头里。 美好:~言。【仓库】cānɡkù名储藏大批粮食或其
思考2:过斜线上斜足外一点向平面 引垂线,连结垂足和斜足的直线叫 做这条斜线在这个平面上的射影.那 αA B
思考3:两条平行直线、相交直线、 异面直线在同一个平面内的射影可 能是哪些图形?
思考4:如图,过平面α外一点P引平 面α的两条斜线段PA、PB,斜足为A、 B,再过点P引平面α的垂线,垂足 为O,如果PA>PB,那么OA与OB的大 小关系如何?反之成立吗?
2.3.1 直线与平面垂直的判定
第二课时 直线和平面所成的角
问题提出
1.直线和平面垂直的定义和判定 定理分别是什么?
定义:如果一条直线与平面内的任 意一条直线都垂直,则称这条直线 与这个平面垂直.
定理:如果一条直线和一个平面内的两 条相交直线都垂直,那么这条直线垂直 于这个平面.
2.当直线与平面相交时,对于直线 与平面垂直的情形,我们已作了一些相 关研究,对于直线与平面不垂直的情形, 我们需要从理论上作些分析.
P
αA
OB
