数学开放题
小学六年级数学专题练习 开放探索实践操作题

小学六年级数学专题练习开放探索实践操作题1、右图是甲、乙、丙三个人单独完成某项工程所需天数统计图。
请看图填空。
A、甲、乙合作这项工程,()天可以完成。
B、先由甲做3天,剩下的工程由丙做,还需要()天完成2、有24个1立方分米的立方体商品,请你为它设计一个合适的长方体包装箱,这个包装箱的长、宽、高可以分别是分米、分米与分米,此时需要包装纸至少平方分米(接头处忽略不计)。
3、小明新买一瓶净量45立方厘米的牙膏,牙膏的圆形出口的直径是6毫米。
他早晚各刷一次牙,每次挤出的牙膏长约20毫米。
这瓶牙膏估计能用()天。
(取3作为圆周率的近似值)4、有12个1立方分米的立方体商品,请你为它设计一个长方体包装箱,共有()种不同的包装法;当包装箱的长是()分米、宽是()分米、高是()分米时,最节省包装纸。
至少需要包装纸()平方分米(接头处忽略不计)。
5、街心花园的直径是5米,现在它的周围修一条1米宽的环形路,请按1250的比例尺画好设计图,并求出路面的实际面积。
6、小方桌面的边长是1米,把它的四边撑开,就成了一张圆桌面(如下图)。
求圆桌面的面积。
7、为了学生的卫生安全,学校给每个住宿生配一个水杯,每只水杯3元,大洋商城打九折,百汇商厦“买八送一”。
学校想买180只水杯,请你当“参谋”,算一算:到哪家购买较合算?请写出你的理由。
8、某年段学生举行春游,若租用45座客车,则有15人没有座位,若租用同样数目的60座客车,则一辆客车空车。
已知45座客车租金220元,60座客车租金300元。
问:⑴这个学校一共有学生多少人? ⑵怎样租车,最经济合算?9、六一儿童节,学校进行歌咏比赛,7位评委给张华的打分如下:评委 1 2 3 4 5 6 7打分92 90 95 88 85 97 90去掉一个最高分,一个最低分,张华的平均分是分10、一个商人把一件衣服标价600元,经打假人员鉴别降至60元一件出售,但仍可以赚20%,如按原价出售,则这件衣服可获暴利()元。
初中数学开放试题及答案

初中数学开放试题及答案一、选择题(每题3分,共30分)1. 下列哪个选项是无理数?A. 3.14159B. √2C. 0.33333D. 2答案:B2. 一个长方形的长是宽的两倍,如果宽是4厘米,那么长方形的周长是多少厘米?A. 24B. 20C. 16D. 12答案:A3. 一个数的平方是36,这个数是多少?A. 6B. -6C. 6或-6D. 36答案:C4. 一个数的绝对值是5,这个数可以是?A. 5B. -5C. 5或-5D. 0答案:C5. 一个数的相反数是-3,这个数是?A. 3B. -3C. 0D. 6答案:A6. 计算下列算式的结果:(2x - 3) + (5x + 4) = ?A. 7x + 1B. 7x - 1C. 7x + 4D. 7x - 4答案:A7. 一个数的立方是-27,这个数是?A. 3B. -3C. 3或-3D. 0答案:B8. 一个数的倒数是2,这个数是?A. 1/2B. 2C. -1/2D. -2答案:A9. 计算下列算式的值:(3x^2 - 2x + 1) - (2x^2 - 5x + 3) = ?A. x^2 + 3x - 2B. x^2 - 3x - 2C. x^2 + 3x + 2D. x^2 - 3x + 2答案:A10. 一个数的平方根是4,这个数是?A. 16B. -16C. 16或-16D. 4答案:A二、填空题(每题4分,共20分)11. 如果一个角的补角是120°,那么这个角的度数是______。
答案:60°12. 一个数的平方是16,这个数是______。
答案:±413. 一个数的绝对值是3,这个数是______。
答案:±314. 一个数的立方是-8,这个数是______。
答案:-215. 一个数的倒数是1/3,这个数是______。
答案:3三、解答题(每题10分,共50分)16. 已知一个直角三角形的两条直角边长分别为3cm和4cm,求这个直角三角形的斜边长。
趣味数学开放题

趣味数学开放题是指那些答案不唯一,可以有多种解法的数学问题。
以下是一些趣味数学开放题的例子:
1. 某个数字,如何使它等于1000?
答案不唯一,例如:88888888,1000/1,100*10等。
2. 小明数学考试得了54分,小强得了0分,但小明和小强的数学成绩差了6分,为什么?
答案不唯一,例如:小明的分数是54分,小强的分数是0分;或者小明的分数是60分,小强的分数是4分等。
3. 一口井7米深,有只蜗牛从井底往上爬,白天爬3米,晚上往下坠2米。
问蜗牛几天能从井里爬出来?
答案不唯一,取决于蜗牛是否在第五天白天爬出井口,或者是第五天晚上坠入井底后再爬出来。
4. 某人花19元买了个玩具,20元卖出去,又花21元买进,22元卖出去。
问它赚了多少钱?
答案不唯一,取决于买进和卖出的次数。
5. 100个包子,100个人吃,1个大人吃3个,3个小孩吃1个,多少个大人和多少小孩刚好能吃完?
答案不唯一,可以有多种组合,例如:25个大人和75个小孩,或者50个大人和50个小孩等。
这些趣味数学开放题可以激发学生的思维,培养他们的创新能力和解决问题的能力。
小学数学开放性练习题

小学数学开放性练习题在小学数学学习中,开放性练习题对培养学生的思维能力和解决问题的能力起着重要的作用。
本文将为大家提供一些小学数学开放性练习题,帮助学生提高数学思维和解题技巧。
1. 碰和不碰小明和小红两个小朋友同时从同一起点出发,以相同的速度绕操场跑圈。
操场有一个半径为10米的球形雕塑物,小明选择绕雕塑物的外圈跑,小红选择绕雕塑物的内圈跑。
他们跑了一段时间后停下来休息,两人同时停下时,小红离起点的路程比小明多了一圈。
请问,小明和小红碰面了吗?2. 糖果分配小明家里有18颗糖果,他想分给他的朋友们。
他一次可以给两个人同时分糖果,分完后剩下两颗糖果。
如果他一次给三个人同时分糖果,分完后剩下一颗糖果。
请问,小明有多少个朋友?3. 魔法方阵下图是一个3x3的魔法方阵,每个方框内填写了不同的正整数,使得每一行、每一列和对角线的和都相等。
8 1 63 5 74 9 2请将数字1-9填入空白处,完成这个魔法方阵。
4. 乌龟爬井有一个深度为100米的井,乌龟每天白天向上爬10米,晚上休息,然后在第二天白天向上爬5米。
请问,乌龟需要多少天才能爬出这个井?5. 数字翻转将一个两位数的个位和十位交换位置,得到一个新的两位数,且新的两位数是原数的2倍。
请问原数是多少?通过以上开放性练习题,学生可以培养自己的逻辑思维能力、动手实践能力和解决问题的能力。
同时,这些题目布局简洁美观,语句通顺,有助于学生的阅读体验和理解。
希望同学们能够通过解答这些题目,不断提高自己的数学思维和解题能力。
初中数学 开放性试题及答案
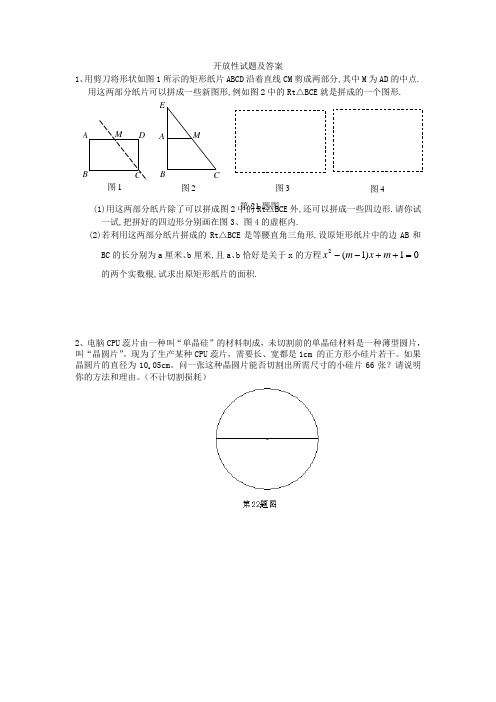
开放性试题及答案1、用剪刀将形状如图1所示的矩形纸片ABCD 沿着直线CM 剪成两部分,其中M 为AD 的中点.用这两部分纸片可以拼成一些新图形,例如图2中的Rt △BCE 就是拼成的一个图形.(1)用这两部分纸片除了可以拼成图2中的Rt △BCE外,还可以拼成一些四边形.请你试一试,把拼好的四边形分别画在图3、图4的虚框内.(2)若利用这两部分纸片拼成的Rt △BCE 是等腰直角三角形,设原矩形纸片中的边AB 和BC 的长分别为a 厘米、b 厘米,且a 、b 恰好是关于x 的方程01)1(2=++--m x m x 的两个实数根,试求出原矩形纸片的面积.2、电脑CPU 蕊片由一种叫“单晶硅”的材料制成,未切割前的单晶硅材料是一种薄型圆片,叫“晶圆片”。
现为了生产某种CPU 蕊片,需要长、宽都是1cm 的正方形小硅片若干。
如果晶圆片的直径为10.05cm 。
问一张这种晶圆片能否切割出所需尺寸的小硅片66张?请说明你的方法和理由。
(不计切割损耗)E B A C B A M C D M 图3 图4 图1 图2 第21题图3、在一张长12cm、宽5cm的矩形纸片内,要折出一个菱形.李颖同学按照取两组对边中点的方法折出菱形EFGH(见方案一),张丰同学沿矩形的对角线AC折出∠CAE=∠DAC,∠ACF=∠ACB 的方法得到菱形AECF(见方案二),请你通过计算,比较李颖同学和张丰同学的折法中,哪种菱形面积较大?4、如图,若把边长为1的正方形ABCD的四个角(阴影部分)剪掉,得一四边形A1B1C1D1.试问怎样剪,才能使剩下的图形仍为正方形,且剩下图形的面积为原正方形面积的95,请说明理由(写出证明及计算过程).5、甲船在点O处发现乙船在北偏东600的B处以每小时a海里的速度向北航行,甲船的速度是每小时3a海里,问甲船应以什么方向航行才能追上乙船。
A DEHFB CG(方案一)A DEFB C(方案二)第23题图6、已知:如图,AB是⊙O的直径,E是AB上的点,过点E作CG⊥AB,F是直线CG上任意上点,连结AF交⊙O于D,连结DC、AC、AG。
初中数学 开放性试题及答案
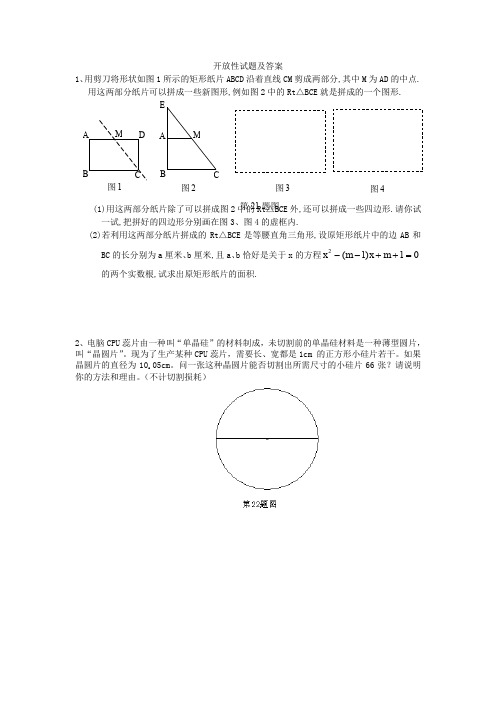
开放性试题及答案1、用剪刀将形状如图1所示的矩形纸片ABCD 沿着直线CM 剪成两部分,其中M 为AD 的中点.用这两部分纸片可以拼成一些新图形,例如图2中的Rt △BCE 就是拼成的一个图形.(1)用这两部分纸片除了可以拼成图2中的Rt △BCE外,还可以拼成一些四边形.请你试一试,把拼好的四边形分别画在图3、图4的虚框内.(2)若利用这两部分纸片拼成的Rt △BCE 是等腰直角三角形,设原矩形纸片中的边AB 和BC 的长分别为a 厘米、b 厘米,且a 、b 恰好是关于x 的方程01)1(2=++--m x m x 的两个实数根,试求出原矩形纸片的面积.2、电脑CPU 蕊片由一种叫“单晶硅”的材料制成,未切割前的单晶硅材料是一种薄型圆片,叫“晶圆片”。
现为了生产某种CPU 蕊片,需要长、宽都是1cm 的正方形小硅片若干。
如果晶圆片的直径为10.05cm 。
问一张这种晶圆片能否切割出所需尺寸的小硅片66张?请说明你的方法和理由。
(不计切割损耗)EB AC B A MC D M 图3 图4 图1 图2 第21题图3、在一张长12cm 、宽5cm 的矩形纸片内,要折出一个菱形.李颖同学按照取两组对边中点的方法折出菱形EFGH (见方案一),张丰同学沿矩形的对角线AC 折出∠CAE=∠DAC ,∠ACF=∠ACB 的方法得到菱形AECF (见方案二),请你通过计算,比较李颖同学和张丰同学的折法中,哪种菱形面积较大?4、如图,若把边长为1的正方形ABCD 的四个角(阴影部分)剪掉,得一四边形A 1B 1C 1D 1.试问怎样剪,才能使剩下的图形仍为正方形,且剩下图形的面积为原正方形面积的95,请说明理由(写出证明及计算过程).5、甲船在点O 处发现乙船在北偏东600的B 处以每小时a 海里的速度向北航行,甲船的速度是每小时3a 海里,问甲船应以什么方向航行才能追上乙船。
(方案一) A D E F BC(方案二) 第23题图6、已知:如图,AB是⊙O的直径,E是AB上的点,过点E作CG⊥AB,F是直线CG上任意上点,连结AF交⊙O于D,连结DC、AC、AG。
一年级数学开放题

一年级数学开放题一年级开放题1.1与众不同在2,4,6,7,10这五个数中,哪一个数与众不同?【分析与参考答案】一个数是不是与众不同,要看选择什么样的标准,选择不同的标准,就会有不同的“与众不同”,下面是几种不同的说法:因为2,4,6,10都是双数,而7是单数,所以说:7与众不同;因为2,4,6,7都是一位数,而10是两位数,所以可以说:10与众不同;2与众不同,理由是其它数都大于3,只有2小于3,所以它与众不同;4与众不同,理由是只有它可以在这五个数中找到一个数2,这个数2加两次就可以是4,其它的数都没有这样的本领;还可以说4与左面的2和右面的6都相差2,这也是它与众不同的地方。
6与众不同,因为6=7-1,即它等于右面的数减1,其它的数都做不到这一点,所以6的确与众不同。
从上面的解答来看,一道题的答案不一定是唯一的,可以是多种多样的。
亲爱的读者,你还能给出本题的其它答案吗1.2写数涂颜色先在括号里写数,然后根据括号里数的大小,在上面的方格中涂上颜色。
(5)()()()()()()()【分析与参考答案】此题答案很多,同学们可以在括号内填入不同的数,在相应的格子里涂上不同的颜色。
例如,从左往右的第二列,如果在括号里填上6,那么,就在第二列中,涂六个格子,即比第一列多涂一格。
1.3上下相差2有两排格子,从上往下数,上面的是第一排,下面的是第二排。
在格子里可以涂上颜色,请你分别按照下面的三种要求涂色:①使得第一排涂上颜色的格子个数比第二排少2个;②使得第一排涂上颜色的格子个数比第二排多2个;③使得第一排和第二排涂上颜色的格子个数相差2个。
第一排第二排【分析与参考答案】①由于要使第一排涂上颜色的格子个数比第二排少2个,可以从第一排涂颜色的格子个数从少到多考虑,(也可以从多到少考虑)有以下几种涂色方法:第一排第二排第一排第二排第一排第二排第一排第二排第一排第二排第一排第二排2第一排第二排第一排第二排第一排第二排②由于要使第一排涂上颜色的格子个数比第二排多2个,所以只要将上面第①题中,每一种涂色方法的第一排和第二排调换位置,就可以得到这个题目所有涂色的方法;③由于使得第一排和第二排涂上颜色的格子个数相差2个,相差2个的含义是第一排比第二排少2个,或者第一排比第二排多2个,因此,把上面两个小题合在一起,就可以得到本题的所有涂颜色的方法。
数学开放性问题

1 时,点 P 到点 B 的距离与到定直线 l 距离 2
(2) 延长 PB 与点 P 的轨迹交于另一点 Q,求 PQ 的最小值; (3)如果存在某一位置,使得 PQ 的中点 R 在 l 上的射影 C,满足 PC QC, 求 a 的 取值范围.
4
数学开放性问题
数学开放性问题是近年来高考命题的一个新方向 ,其解法灵活且具有一定的探索性,这 类题型按解题目标的操作模式分为:规律探索型,问题探究型,数学建模型,操作设计型,情景 研究型.如果未知的是解题假设,那么就称为条件开放题;如果未知的是解题目标,那么就称 为结论开放题;如果未知的是解题推理,那么就称为策略开放题.当然,作为数学高考题中的 开放题其“开放度”是较弱的,如何解答这类问题,还是通过若干范例加以讲解. 1 设等比数列a n 的公比为 q , 前 n项 和为 S n , 是否存在常数 c , 使数列 S n c也成等比数列? 若存在,求出常数c ;若不存在, 请 明 理 由.
3
已知函数 f(x)=
1 x 4
2
-1
(x<-2)
(1)求 f(x)的反函数 f (x); (2)设 a1=1,
1 a n 1
2
=-f (an)(n∈N),求 an;
-1
(3)设 Sn=a1 +a2 +„+an ,bn=Sn+1-Sn 是否存在最小正整数 m,使得对任意 n∈N,有 bn< 立?若存在,求出 m 的值;若不存在说明理由.
8 已知 f ( x) 是定义在 R 上的不恒为零的函数,且对于任意的 a,b∈R 都满足关系式
f (a b) af (b) bf (a) .
(1)求 f(0) ,f(1)的值; (2)判断 f ( x) 的奇偶性,并证明你的结论; (3)若 f (2) 2, u n
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学开放题
【专题导引】
数学开放题是相对于传统的封闭题而言的一种题型。
由于客观世界复杂多变,数学问题也必然复杂多变,往往不可能得到惟一的答案。
一般而言,数学开放题具有以下三个特征:
1、条件不足或多余;
2、没有确定的结论或结论不惟一;
3、解题的策略,思路多种多样。
解答数学开放题,需要我们从不同角度分析和思考问题,紧密联系实际,具体问题具体分析。
我们一般可以从以下几方面考虑:
1、以问题为指向,对现有条件进行筛选、补充和组合,促进问题的顺利解
决。
2、根据知识之间的不同联系途径对给定的条件进行不同的组合,采用不同
的方法求解。
3、避免“答案惟一”的僵化思维模式,联系实际考虑可能出现的多种情况,
得出不同的答案。
【典型例题】
】数字之和是6的两位数有哪些?
【C
1
【试一试】
1、数字之和是8的两位数有哪些?
2、数字之积是8的两位数有哪些?
【C
】A、B都是自然数,且A+B=8,那么A×B的积可能是多少?其中最大值是2
多少?
【试一试】
1、A、B都是自然数,且A+B=5,那么A-B的差最大可能是几?
2、△、○都是自然数,且○×△=8,那么○+△的和可能是多少?
【B
】 A、B都是自然数,且A+B=10,那么A×B的积可能是多少?其中最大的1
值是多少?
【试一试】
1、甲、乙两数都是自然数,且甲+乙=32,那么,甲×乙积的最大值是多少?
2、A和B两个自然数的积是24,当A和B各等于多少时,它们的和最小?
【B
】把1~6六个数分别填入图中的六个圆圈中,使每条边上三个数的和都等2
于9。
【试一试】
1、把1~6六个数分别填入图中的六个圆圈中,使每条边上三个数的和都等于12。
2、把1~8八个数分别填入图中的八个圆圈中,使每个圆圈上五个数的和都等于21。
【B
】在一次羽毛球比赛中,8名运动员进行淘汰赛,最后决出冠军,共打了多3
少场球?(两名运动员之间比赛1次,称为1场)
【试一试】
1、在一次乒乓球比赛中,32名运动员进行淘汰赛,最后决出冠军,共打了多少场球?
2、在一次足球比赛中,采取淘汰制,共打了15场球,最后决出冠军,问有多少支足球队参加了这次足球比赛?
】一个学生从家到学校,如果以每分钟50米的速度行走,就要迟到8分钟;【A
1
如果以每分钟60米的速度前进,就可以提前5分钟到校,这个学生出发时离上学时间有多少分?
【试一试】
1、李老师从家到学校上班,出发时他看看表,发现如果步行,每分行80米,他将迟到5分,如果骑自行车,每分行200米,他可以提前7分到校。
求李老师出发时离上班时间有多少分?
2、一位小学生从家到学校,如果以每分50米的速度行走,就迟到3分钟;如果以每分70米的速度行走,就可以提前5分到校。
求他家与学校的距离。
【A
】在电脑里先输入一个数,它会按给定的指令进行如下运算:如输入的数是2
双数,就把它除以2;如输入的数是单数,就把它加上3。
同样的运算这样进行了3次,得出结果为27。
原来输入的数可能是几?
【试一试】
1、在电脑里输入一个数,它会按给定的指令进行如下运算:输入的是双数就除以2;输入的是单数,就加上3。
同样的运算进行3次,得出结果为18。
原来输入的数可能是几?
2、在电脑里输入一个数,它会按给定的指令进行如下运算:输入双数就除以2;
输入单数就加上5。
同样运算进行了2次,得出结果为20。
原来输入的数可能为多少?
课外作业
家长签名:1、数字之积是12的一位数有哪些?
2、A、B都是自然数,且A-B=1,那么A+B的和最小可能是几?
3、A、B、C三个数都是自然数,且A+B+C=18,那么,A×B×C积的最大值是多
少?
4、把1~9这九个数分别填入图中的九个圆圈中,使每条边上四个数的和相等而且最小。
5、有13个队参加篮球赛,比赛分两个组。
第一组七个队,第二组六个队,各组先进行单循环赛(即每队都要与其他各队比赛一场),然后由各组的前两名共四个队再分成两组进行淘汰赛,最后两队决出冠亚军。
问:共需比赛多少场?
6、一个学生从家到学校上课,先用每分钟80米的速度走了3分钟,发现这样走下去将迟到3分钟;于是他就改用每分钟110米的速度前进,结果比上课时间提前了3分钟。
问这个学生家到学校有多远?
7、在电脑里输入一个数,它会按给定指令进行如下操作:遇到双数除以3;遇到单数减去5。
同样运算进行了3次,最后结果为10。
原来输入的数可能是几?。
