10 信号与系统(2)
信号与系统课件:第二章 LTI系统

2.1 离散时间LTI系统: 卷积和
(1)用移位单位抽样信号表示离散时间信号 (2)卷积和在离散时间信号LTI系统中的表征 (3)卷积和的计算 (4) 离散时间信号LTI系统的性质
(1)用单位抽样信号表示离散时间信号
x[n] ... x[1] n 1 x[0] n x[1] n 1... x[n][0] x[n 1][1]
(1)初始条件为n<0时,y(n)=0,求其单位抽样响应;
(2)初始条件为n≥0时,y(n)=0,求其单位抽样响应。
解:(1)设x(n) (n),且 y(1) h(1) 0 ,必有
y(n) h(n) 0, n 0
依次迭代
y(0) h(0) (0) 1 y(1) 1 0 1
2
当系统的初始状态为零,单位抽样响应h(n)就 能完全代表系统,那么对于线性时不变系统,任意 输入下的系统输出就可以利用卷积和求得。
差分方程在给定输入和边界条件下,可用迭代 的方法求系统的响应,当输入为δ(n)时,输出 (响应)就是单位抽样响应h(n)。
例:常系数差分方程
y(n) x(n) 1 y(n 1) 2
x[n]u[n] x[k]u[n k] x[k]
k
k
(ii)交换律:
yn xnhn hn xn
例子: 线性时不变系统中的阶跃响应 sn
sn unhn hnun
阶跃输入
输 单位抽样信号 入 响应的累加
n
sn hk
k
(iii)分配律:
xnh1n h2 n xnh1n xnh2 n
y(1) h(1) (1) 1 y(0) 0 1 1
2
22
y(2) h(2) (2) 1 y(1) 0 1 1 (1)2
信号与系统(第二版)电子工业出版社【参考答案】

第一章1.8 系统的数学模型如下,试判断其线性、时不变性和因果性。
其中X (0-)为系统的初始状态。
(2)()()2f t y t e = (5)()()cos2y t f t t = (8)()()2y t f t = 解:(2)()()2f t y t e = ① 线性: 设 ()()()()1122,f t y t f t y t →→,则 ()()()()122212,f t f t y t ey t e==那么 ()()()()()()()112211222221122a f t a f t a f t a f t a f t a f t y t ee e +⎡⎤⎣⎦+→==,显然,()()()1122y t a y t a y t ≠+,所以是非线性的。
② 时不变性设()()11,f t y t →则 ()()()()10122110,f t t f t y t e y t t e-=-=设()()102,f t t y t -→则()()()102210f t t y t e y t t -==-,所以是时不变的。
③ 因果性因为对任意时刻 t 1,()()121f t y t e =,即输出由当前时刻的输入决定,所以系统是因果的。
(5)()()cos2y t f t t = ① 线性: 设 ()()()()1122,f t y t f t y t →→,则 ()()()()1122cos2,cos2y t f t t y t f t t ==那么()()()()()()()112211221122cos 2cos 2cos 2a f t a f t y t a f t a f t t a f t t a f t t +→=+=+⎡⎤⎣⎦, 显然()()()1122y t a y t a y t =+,所以系统是线性的。
② 时不变性设()()11,f t y t →则 ()()()()()1110100cos2,cos2y t f t t y t t f t t t t =-=--设()()102,f t t y t -→则()()()21010cos2y t f t t t y t t =-≠-,所以是时变的。
考研专业课郑君里版《信号与系统》第二章补充习题——附带答案详解
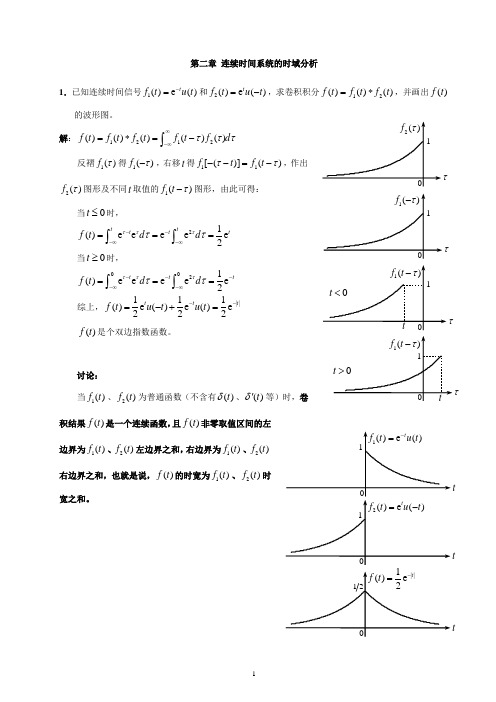
第二章 连续时间系统的时域分析1.已知连续时间信号1()e ()t f t u t -=和2()e ()t f t u t =-,求卷积积分12()()()f t f t f t =*,并画出()f t 的波形图。
解:1212()()()()()f t f t f t f t f d τττ∞-∞=*=-⎰反褶1()f τ得1()f τ-,右移t 得11[()]()f t f t ττ--=-,作出2()f τ图形及不同t 取值的1()f t τ-图形,由此可得:当0t ≤时,21()e e ee e 2ttt tt f t d d τττττ---∞-∞===⎰⎰当0t ≥时,0021()e e e e e 2t t t f t d d τττττ----∞-∞===⎰⎰综上,||111()e ()e ()e 222t t t f t u t u t --=-+=()f t 是个双边指数函数。
讨论:当1()f t 、2()f t 为普通函数(不含有()t δ、()t δ'等)时,卷积结果()f t 是一个连续函数,且()f t 非零取值区间的左边界为1()f t 、2()f t 左边界之和,右边界为1()f t 、2()f t 右边界之和,也就是说,()f t 的时宽为1()f t 、2()f t 时宽之和。
τttt2.计算题图2(a )所示函数)(1t f 和)(2t f 的卷积积分)()()(21t f t f t f *=,并画出)(t f 的图形。
解法一:图解法1212()()()()()f t f t f t f t f d τττ∞-∞=*=-⎰其中1()f t τ-的波形见题图2(b),由此可得: 当10t +≤,即1t ≤-时,()0f t = 当011t ≤+≤,即10t -≤≤时,120()2(1)t f t d t ττ+==+⎰当11t +≥但10t -≤,即01t ≤≤时,1()21f t d ττ==⎰当011t ≤-≤,即12t ≤≤时,121()21(1)t f t d t ττ-==--⎰当11t -≥,即2t ≥时,()0f t =综上,220,1,2(1),10()1,011(1),12t t t t f t t t t ≤-≥⎧⎪+-≤≤⎪=⎨≤≤⎪⎪--≤≤⎩ ()f t 波形见题图2(c)。
第一章 信号与系统概论(2)

+∞
∫ (1 − x )δ (x )dx = ∫ δ (x )dx = u (t )
t t −∞ −∞
( t ∈ [t , t ]) ( t ∉ [t , t ])
1 2 1 2
6. 符号函数
定义
1 sgn(t) = 0 −1
(t > 0) (t = 0) (t < 0)
sgn(t) 1 0 -1
可用阶跃信号表示
sg ( t) = 2u(t) −1 n
信号的因果和反因果分解
任意信号 f (t ) 有因果反因果分解
at
1.指数信号
实际上,经常遇到的是因果指数衰减信号 因果指数衰减信号
2.正弦信号
正弦信号和余弦信号统称为正弦信号,一 般可表示为: f t = K sin ωt + φ 其中 K 为振幅, 是角频率,φ 称为初 2π 1 = 相位。正弦信号的周期 T = , ω f 其中 f 是频率。 与指数信号相似,正弦信号对时间的微分 或积分仍是正弦信号
∫
t
−∞
δ (τ ) d τ = u ( t )
d dt
u (t ) = δ (t )
∫
+∞ −∞
δ ( t − t 0 ) f ( t ) dt =
∞ −∞
=
∫
f ( t 0 )δ ( t − t 0 ) dt = f ( t 0 )
相乘
f (t )δ (t − t0 ) = f (t0 )δ (t − t0 )
冲激函数的检零性质
当冲激函数应用于非线性函数时,具有 应用于非线性函数时, 应用于非线性函数时 检测其零点,并反映其导数的性质。 检测其零点,并反映其导数的性质 由于函数在其零点 t i ,i=1, 2, …, n 有 f t i = 0 ,使得在其零点领域,有
奥本海姆《信号与系统》(第2版)(下册)课后习题-Z变换(圣才出品)

第10章Z变换习题10.1 试对下列和式,为保证收敛确定在r=|z|上的限制:解:(a)为了保证收敛,需满足即使和式收敛的z均满足,亦即有又因在和式中含有一个正幂项z,故z≠∞。
综上所述,使和式收敛的z的模需满足为了保证收敛,需,即满足|2z|<1,从而知使和式收敛的z的模需满足为了保证收敛,需,即|z|>1;为了保证收敛,需,即|z|>1综上所述,使和式收敛的z的模需满足r>1。
对于上式右端第二项,要保证其收敛,需,即|z|<2。
对于上式右端第三项,要保证其收敛,需,即|z|<2。
对于上式右端第四项,要保证其收敛,需,即。
对于上式右端第五项,要保证其收敛,需,即。
综上所述,要使和式收敛,z的模需满足。
10.2 设信号x[n]为利用式(10-3)求该信号的z变换,并标出对应的收敛域。
解:为使该级数收敛,需,即,于是可得10.3 设信号x[n]为已知它的z变换x(z)的收敛域是试确定在复数α和整数n0上的限制。
解:令x[n]=x1[n]+x2[n],其中x1[n]=(-1)n u[n],x2=αn u[-n-n0]于是有则X(z)=X1(z)+X2(z),1<|z|<|α|由于已知X(z)的收敛域为1<|z|<2,所以α应满足|α|=2,而n0可为任意整数。
10.4 考虑下面信号:对x(z)确定它的极点和收敛域。
解:因为,要使x(z)收敛,显然应有及,即X(z)的ROC为由于故X(z)的两个极点分别为,它们是互为共轭自两个复数极点。
10.5 对下列信号z变换的每个代数表示式,确定在有限z平面内的零点个数和在无限远点的零点个数。
解:(a)由于X(z)的分母多项式的阶数比分子多项式的阶数高1阶,所以X(z)在有限z平面上零点的个数为1(即X(z)的有限零点个数为1),同样在无穷远处的零点个数也为1。
由于x(z)的分母多项式与分子多项式有相同的阶数,所以X(z)仅有2个有限零点,而在无穷远处无零点。
由于X(z)的分母多项式的阶数比分子多项式的阶数高2阶,所以X(z)有1个有限零点,而在无穷远处有2个零点。
信号与系统讲义-2

f (t) u 3 10
p
u pf (t) 2p 10
u(t) (Ae5t B)U(t)
2 du(t) 10u(t) df (t)
dt
dt
u(t) 5Ae5t U(t) (A B)(t)
2(A B) 1 B0
u(t) 1 e5tU(t)V 2
H
(
p)
2p2 8p 3 ( p 1)( p 3)2
求系统的响应 y(t)。
解: D(p) (p 1)(p 3)2 0 p1 1 p2 p3 3
y0 (t) K1e t K 2e3t K 3te3t
y0 (0 ) K1 K2 =2 y0 (0 ) K1 3K 2 K3=1
3、共轭复根:(欠阻尼) 即 R 2 L C
uc Aet cos(dt ) Us
R 2L
,
d
02 2 , 0
1 LC
4
三、 RLC串联电路全响应
d 2uc dt 2
R L
duc dt
1 LC
uc
1 LC Us
(二阶常系数线性非齐次微分方程)
t<0 , K在2,有 uc (0 ) U0
C
uc Aep1t Be p2t Us
2、重根:(临界阻尼) 即
R2
L C
(自然频率、固有频率)
uc (A Bt)ept Us
3、共轭复根:(欠阻尼) 即 R 2 L C
uc Aet cos(dt ) Us
R 2L
d 02 2
信号与系统课后答案 第2章 习题解
第2章 习 题2-1 求下列齐次微分方程在给定起始状态条件下的零输入响应(1)0)(2)(3)(22=++t y t y dt d t y dt d ;给定:2)0(,3)0(==--y dt dy ; (2)0)(4)(22=+t y t y dt d ;给定:1)0(,1)0(==--y dtd y ;(3)0)(2)(2)(22=++t y t y dt d t y dt d ;给定:2)0(,1)0(==--y dt dy ; (4)0)()(2)(22=++t y t y dt d t y dt d ;给定:2)0(,1)0(==--y dtdy ; (5)0)()(2)(2233=++t y dt d t y dt d t y dt d ;给定:2)0(,1)0(,1)0(22===---y dt d y dt d y 。
(6)0)(4)(22=+t y dt d t y dt d ;给定:2)0(,1)0(==--y dtdy 。
解:(1)微分方程的特征方程为:2320λλ++=,解得特征根:121, 2.λλ=-=- 因此该方程的齐次解为:2()t th y t Ae Be --=+.由(0)3,(0)2dy y dt--==得:3,2 2.A B A B +=--=解得:8, 5.A B ==- 所以此齐次方程的零输入响应为:2()85tty t e e--=-.(2)微分方程的特征方程为:240λ+=,解得特征根:1,22i λ=±.因此该方程的齐次解为:()cos(2)sin(2)h y t A t B t =+.由(0)1,(0)1d y y dx --==得:1A =,21B =,解得:11,2A B ==. 所以此齐次方程的零输入响应为:1()cos(2)sin(2)2y t t t =+.(3)微分方程的特征方程为:2220λλ++=,解得特征根:1,21i λ=-± 因此该方程的齐次解为:()(cos()sin())th y t e A t B t -=+.由(0)1,(0)2dy y dx--==得:1,2,A B A =-= 解得:1,3A B ==.所以齐次方程的零输入响应为:()(cos()3sin())ty t e t t -=+.(4)微分方程的特征方程为:2210λλ++=,解得二重根:1,21λ=-.因此该方程的齐次解为:()()th y t At B e -=+. 由(0)1,(0)2dy y dx--==得:1,2,B A B =-=解得:3, 1.A B == 所以该方程的零输入响应为:()(31)ty t t e -=+.(5)微分方程的特征方程为:3220λλλ++=,解得特征根: 1,21λ=-,30λ=. 因此该方程的齐次解为:()()th y t A Bt C e -=++.由22(0)1,(0)1,(0)2d d y y y dx dt---===得:1,1,22A C B C C B +=-=-=. 解得:5,3,4A B C ==-=-.所以方程的零输入响应为:()5(34)ty t t e -=-+.(6)微分方程的特征方程为:240λλ+=,解得特征根:120,4λλ==-. 因此该方程的齐次解为:4()th y t A Be -=+.由(0)1,(0)2d y y dx --==得:1,42A B B +=-=.解得:31,22A B ==-. 所以此齐次方程的零输入响应为:431()22ty t e -=-.2-2 已知系统的微分方程和激励信号,求系统的零状态响应。
《信号与系统(第2版》【附录+习题答案】
附 录 A 常 用 数 学 公 式A.1 三角函数公式j e cos jsin t t t ωωω=+ j e e (cos jsin )t t t σωσωω+=+j j 1cos (e e )2t t t ωωω-=+j j 1sin (e e )2jt t t ωωω-=-sin()sin cos cos sin αβαβαβ±=± cos()cos cos sin sin αβαβαβ±=sin22sin cos ααα=2222cos2cos sin 12sin 2cos 1ααααα=-=-=-1sin sin [cos()cos()]2αβαβαβ=--+1cos cos [cos()cos()]2αβαβαβ=-++1sin cos [sin()sin()]2αβαβαβ=-++双曲正弦:e e sh 2x xx --=双曲余弦:e e ch 2x xx -+=A.2 微积分公式d()d Cu C u =,C 为常数(下同)d()d d u v u v ±=±,u 、v 为t 的函数(下同) d()d d uv v u u v =+ 2d d d u v u u v v v -⎛⎫= ⎪⎝⎭d d Cu t C u t =⎰⎰()d d d u v t u t v t ±=±⎰⎰⎰信号与系统288d d u v uv v u =-⎰⎰()d ()()()()d ()bb baaau t v t u t v t v t u t =-⎰⎰A.3 数列求和公式(1)等比数列123,,,,N a a a a 的通项为11n n a a q -=,q 为公比,前n 项的和为 111(1)11NN N N n n a a q a q S a q q =--===--∑(2)等差数列123,,,,N a a a a 的通项为1(1)n a a n d =+-,d 为公差,前n 项的和为111()(1)22NN N n n N a a N N dS a Na =+-===+∑附 录 B 常 用 信 号 与 系 统 公 式B.1 连续时间信号的卷积121221()()()()d ()()d x t x t x x t x x t ττττττ∞∞-∞-∞*=-=-⎰⎰B.2 离散时间信号的卷积121221()()()()()()m m x n x n x m x n m x m x n m ∞∞=-∞=-∞*=-=-∑∑B.3 连续时间三角形式的傅里叶级数0000011()[cos()sin()]cos()kk kkk k x t a ak t b k t A A k t ωωωϕ∞∞===++=++∑∑0000001()d t T t a A x t t T +==⎰000002()cos()d 1,2,t T k t a x t k t t k T ω+==⎰, 000002()sin()d 1,2,t T k t b x t k t t k T ω+==⎰,1,2,k A k = arctan 1,2,k k k b k a ϕ⎛⎫=-=⎪⎝⎭,B.4 连续时间指数形式的傅里叶级数FS000j 01()e d t T k t k t X x t t T ω+-=⎰0j 0()()ek tk x t X k ωω∞=-∞=∑信号与系统290B.5 连续时间傅里叶变换FTj (j )()e d t X x t t ωω∞--∞=⎰j 1()(j )e d 2πt x t X ωωω∞-∞=⎰B.6 双边拉普拉斯变换()()e d st X s x t t ∞--∞=⎰j j 1()()e d 2πjst x t X s s σσ+∞-∞=⎰B.7 单边拉普拉斯变换0()()e d st X s x t t ∞--=⎰j j 1()()e d 2πjst x t X s s σσ+∞-∞=⎰,0t ≥B.8 离散时间傅里叶级数DFS2πj 1()()ekn NN N n N X k x n N -=<>=∑,0,1,2,k =±±2πj()()ekn NN N k N x n X k =<>=∑,0,1,2,n =±±B.9 离散时间傅里叶变换DTFTj j (e )()enn X x n ΩΩ∞-=-∞=∑j j 2π1()(e )e d 2πn x n X ΩΩΩ=⎰B.10 离散傅里叶变换DFT1()()01N knNn X k x n Wk N -==-∑≤≤,附 录 B 常 用 信 号 与 系 统 公 式29111()()01N kn Nk x n X k Wn N N--==-∑≤≤,B.11 双边Z 变换b ()()nn X z x n z∞-=-∞=∑11()()2n cx n X z z dzj π-=⎰B.12 单边Z 变换s 0()()nn X z x n z∞-==∑11()()2n cx n X z z dzj π-=⎰习题参考答案第1章1.1(a)确定信号、连续时间信号、非周期信号、能量信号、非因果信号。
信号与系统第二版课后答案_西安交大_奥本海姆(汉语)
第一章1.3 解:(a). 2401lim(),04Tt T TE x t dt e dt P ∞-∞∞→∞-====⎰⎰(b) dt t x TP T TT ⎰-∞→∞=2)(21lim121lim ==⎰-∞→dt T TTT∞===⎰⎰∞∞--∞→∞dt t x dt t x E TTT 22)()(lim(c).222lim()cos (),111cos(2)1lim()lim2222TT TTTT T TTE x t dt t dt t P x t dt dt TT∞∞→∞--∞∞→∞→∞--===∞+===⎰⎰⎰⎰(d) 034121lim )21(121lim ][121lim 022=⋅+=+=+=∞→=∞→-=∞→∞∑∑N N n x N P N Nn n N N N n N 34)21()(lim202===∑∑-∞=∞→∞nNNn N n x E (e). 2()1,x n E ∞==∞211lim []lim 112121N NN N n N n NP x n N N ∞→∞→∞=-=-===++∑∑ (f) ∑-=∞→∞=+=NNn N n x N P 21)(121lim 2∑-=∞→∞∞===NNn N n x E 2)(lim1.9. a). 00210,105T ππω===; b) 非周期的; c) 00007,,22mN N ωωππ=== d). 010;N = e). 非周期的; 1.12 解:∑∞=--3)1(k k n δ对于4n ≥时,为1即4≥n 时,x(n)为0,其余n 值时,x(n)为1易有:)3()(+-=n u n x , 01,3;M n =-=- 1.15 解:(a)]3[21]2[][][222-+-==n x n x n y n y , 又2111()()2()4(1)x n y n x n x n ==+-, 1111()2[2]4[3][3]2[4]y n x n x n x n x n ∴=-+-+-+-,1()()x n x n = ()2[2]5[3]2[4]y n x n x n x n =-+-+- 其中][n x 为系统输入。
奥本海姆《信号与系统(第二版)》习题参考答案.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Z变换
1. 双边Z变换及其收敛域ROC。
本章主要内容
1. 双边Z变换及其收敛域ROC。
2. ROC的特征,各类信号的ROC,零极点图。
3. Z反变换,利用部分分式展开进行反变换。
4. 由零极点图分析系统的特性。
5. 常用信号的Z变换,Z变换的性质。
6. 用Z变换表征LTI系统,系统函数,LTI系统 的Z变换分析法,系统的级联与并联型结构。
7. 单边Z变换,增量线性系统的分析。
引言
Z 变换与拉氏变换相对应,是离散时间傅里叶变换的推广。
Z 变换的基本思想、许多性质及其分析方法都与拉氏变换有相似之处。
当然,Z 变换与拉氏变换也存在着一些重要的差异。
当 时, 即为离散时间傅里叶变换。
这表明:DTFT 就是在单位圆上进行的Z 变换。
1r j z e
()()[()]
j n j n
n
n X re x n r
e
x n r
F ()()n
n X z x n z
j z re
其中 是一个复数。
一.双边Z变换的定义:
可见:对
做 Z 变换就等于对 做DTFT 。
因此,Z 变换是对DTFT 的推广。
()x n ()n
x n r 有缘学习更多+谓ygd3076考证资料或关注桃报:奉献教育(店铺)
例1.()()n
x n a u n 11()1n n
n X z a
z
az
时收敛
z a 当 时, ROC包括了单位圆。
1a 1()1j j X e ae
此时, 的DTFT存在。
()x n ()|()
j
j z e X z X e 显然有
例2.()()
x n u n 10
1()1n
n X z z
z
此时,ROC不包括单位圆,所以不能简单地从
通过将 得到 。
()X z z j e
()j X e
1
()(2)1j j k X e k e
1
z ROC:
例3.()(1)
n
x n a u n 1
1
()n n
n n
n n X z a z a z
1
11
111a z a z az
z a
ROC:
例4.1()()()2(1)
2
n n
x n u n u n 1
0111()()
21111212
n n n n X z z z z
1
ROC :2
2
z 双边信号的ROC如果存在,是 Z 平面上一个以原点为中心的圆环。
有缘学习更多+谓ygd3076考证资料或关注桃报:奉献教育(店铺)
结 论:
1)Z变换存在着收敛问题,不是任何信号都存 在Z
变换,也不是任何复数Z都能使 收敛。
()X z ()X z ()X z ()x n 2)仅仅由 的表达式不能唯一地确定一个信号,只有 连同相应的ROC一道,才能与信号
建立一一对应的关系。
3)Z变换的ROC,一般是Z平面上以原点为中心的环形区域。
4)如果 ,则其ROC是各个 的ROC
的公共部分。
若没有公共区域则表明 的Z 变换不
存在。
()()i i
x n x n
()i x n ()x n ()X z ()X z 5)当 是有理函数时,其ROC的边界总是由
的极点所在的圆周界定的。
6)若 的ROC包括单位圆,则有
()X z ()()|j j z e X e X z。
