数学分析简明教程答案(尹小玲邓东皋)第四章
数学分析简明教程答案(尹小玲 邓东皋)第一二章

5.在半径为r得瑟球内嵌入一内接圆柱,试将圆柱的体积表示为其高的函数,并求此函数 的定义域。
h2 解:设其高为h, 那么圆柱的底面半径为R r ; 于是圆柱体积 4 2 V R h
2
hr 2
4
h3
由于圆柱为球的内接圆柱,故有h (0, 2r ).
-2-
6.某公交车路线全长为20 Km, 票价规定如下:乘坐5 Km以下(包含5 Km)者收费1元;超过 5 Km但在15 Km以下(包含15Km)者收费2元;其余收费2元5角。试将票价表示成路线的 函数,并作出函数的图像。 解:设y为票价,x为路程,则有 1 y ( x) 2 2.5 它的函数图像如下: x (0,5] x (5,15] . x (15, 20]
画图板作图
7.一脉冲发生器产生一个三角波,若记它随时间t的变化规律为f (t ), 且三个角分别对应关 系f (0) 0, f (10) 20, f (20) 0, 求f (t )(0 t 20), 并作出函数的图形。 解:由题意可知所求函数为: 2t f (t ) 40 2t 其函数图像为:
2 2 2 2
(2). x1 x2 xn x1 x2 xn ; 证明:使用数学归纳法; i.对于x, y , 总有 x y xy, 于是有 x 2 x y y x 2 2 xy y 2 ; 整理后可得 x y x y ,即当n 2时所证成立。 ii.假设当n k时所证不等式也成立,即 x1 x2 xk x1 x2 xk . iii.当n k 1时,取y x1 x2 xk , 于是有: x1 x2 xk xk 1 y xk 1 y xk 1 x1 x2 xk xk 1 x1 x2 xk xk 1 即当n k 1时所证不等式也成立。 那么由数学归纳法可知题证成立。
数学分析简明教程答案

第二十一章曲线积分与曲面积分§1 第一型曲线积分与曲面积分1.对照定积分的基本性质写出第一型曲线积分和第一型曲面积分的类似性质。
解:第一型曲线积分的性质:1(线性性)设⎰L ds z y x f ),,(,⎰L ds z y x g ),,(存在,21,k k 是实常数,则[]ds z y x g k z y x f kL ⎰+),,(),,(21存在,且[]ds z y x g k z y x f k L⎰+),,(),,(21⎰⎰+=LLds z y x g kds z y x f k ),,(),,(21;2l ds L=⎰1,其中l 为曲线L 的长度;3(可加性)设L 由1L 与2L 衔接而成,且1L 与2L 只有一个公共点,则⎰Lds z y x f ),,(存在⇔⎰1),,(Lds z y x f 与⎰2),,(L ds z y x f 均存在,且=⎰Lds z y x f ),,(⎰1),,(L ds z y x f +⎰2),,(L ds z y x f ;4(单调性)若⎰L ds z y x f ),,(与⎰L ds z y x g ),,(均存在,且在L 上的每一点p 都有),()(p g p f ≤则⎰⎰≤L L ds p g ds p f )()(;5若⎰L ds p f )(存在,则⎰L ds p f )(亦存在,且≤⎰ds p f L)(⎰Ldsp f )(6(中值定理)设L 是光滑曲线,)(p f 在L 上连续,则存在L p ∈0,使得l p f ds p f L)()(0=⎰,l 是L 的长度;第一型曲面积分的性质: 设S 是光滑曲面,⎰⎰S ds p f )(,⎰⎰S ds p g )(均存在,则有1(线性性)设21,k k 是实常数,则[]⎰⎰+Sds p g k p f k)()(21存在, 且[]⎰⎰+Sds p g k p f k )()(21⎰⎰⎰⎰+=SSds p g k ds p f k )()(21;2s ds S=⎰1, 其中s 为S 的面积;3(可加性)若S 由1S ,2S 组成21S S S =,且1S ,2S 除边界外不相交,则⎰⎰Sds p f )(存在⇔⎰⎰1)(S ds p f 与⎰⎰2)(S ds p f 均存在,且⎰⎰Sds p f )(=⎰⎰1)(S ds p f +⎰⎰2)(S ds p f4 (单调性)若在S 上的的每一点p 均有),()(p g p f ≤则⎰⎰⎰⎰≤SSds p g ds p f )()(;5⎰⎰S ds p f )(也存在,且≤⎰⎰Sdsp f )(⎰⎰Sds p f )(;6 (中值定理)若)(p f 在S 上连续,则存在S p ∈0,使得使得s p f ds p f S⎰⎰=)()(0,其中s 为S 的面积。
数学分析简明教程答案(尹小玲 邓东皋)

第九章 再论实数系§1 实数连续性的等价描述2211.{}({},{})1(1).1; sup 1,inf 0;(2)[2(2)]; sup ,inf ;1(3),1,(1,2,); sup ,inf 2;1(4)[1(1)]; n n n n n n n n n n k k n n n n x x x x x x nx n x x x k x k x x k n x n ++∞-∞=-===+-=+∞=-∞==+==+∞=+=+- 求数列的上下确界若无上下确界则称,是的上下确界: sup 3,inf 0;(5) sup 2,inf 1;12(6)cos ; sup 1,inf .132n n n n n n n n x x x x x n n x x x n π=====-===-+2.(),(1)sup{()}inf (); (2)inf{()}sup ().(1)sup{()},.,();.0,()..,();.x Dx Dx Dx Dx Df x D f x f x f x f x A f x i x D f x A ii x D f x A i x D f x A ii εεε∈∈∈∈∈-=--=-=-∀∈-≤∀>∃∈->-∀∈≥-∀>设在上定义求证:证明:设即有对有 对使得 于是有对有 对0,().inf (),inf (),sup{()}inf ()x Dx Dx Dx Dx D f x A A f x A f x f x f x ε∈∈∈∈∃∈<-+-==--=-使得 那么即因此有成立。
(2)inf{()},.,();.0,()..,();.0,().sup (),sup (),x Dx Dx DB f x i x D f x B ii x D f x B i x D f x B ii x D f x B B f x A f x εεεε∈∈∈=-∀∈-≥∀>∃∈-<+∀∈≤-∀>∃∈>---==-设即有对有 对使得 于是有对有 对使得 那么即因此有inf{()}sup ()x Dx Df x f x ∈∈-=- 成立。
数学分析简明教程答案(尹小玲 邓东皋)第11章

x x x 2 0 , 而 lim x 1 , 无 穷 积 分 2 x 1 x 2 1 x sin x x 1 x x 发散,由比较判别法知 dx 0 x 2 1 0 1 x 2 sin 2 x dx 发散.
( 5 ) x 0 , 有
2
xn (6)因为 lim 1 ,所以, x 1 x n
第十一章 广义积分
§11.1 1. 求下列无穷积分的值: (1) 无穷限广义积分
2
1 dx ; x 1
2
(2)
2
1 dx ; x(1 x 2 )
xe ax dx (a 0) ; e
ax
2
(3) (4) . (5)
0
0
sin bxdx (a 0) ;
(2) lim x
2
(4) x 0 ,有
1 1 0 ,且 1 x sin x x 1
A dx dx lim lim ln(1 A) , 1 x A 0 1 x A
即
0
0
dx dx 发散,由比较判别法知 发散. 0 1 x 1 x sin x
y x
所以,
2 2 (1 2 x x) 2 ln [arctan( 2 x 1) arctan( 2 x 1)] C , 2 4 1 x 2
A
0
2 (1 2 A A) 2 x ln [arctan( 2 A 1) arctan( 2 A 1)] dx 2 2 4 2 1 x 1 A 2 2 ( ) 2 2 2 2 ( A ) ,
数值分析简明教程第二版课后习题答案(供参考)
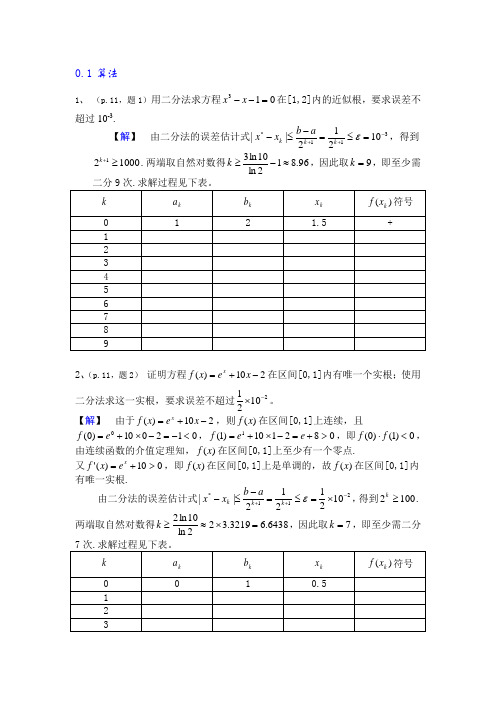
0.1算法1、 (p.11,题1)用二分法求方程013=--x x 在[1,2]内的近似根,要求误差不超过10-3.【解】 由二分法的误差估计式311*10212||-++=≤=-≤-εk k k a b x x ,得到100021≥+k .两端取自然对数得96.812ln 10ln 3≈-≥k ,因此取9=k ,即至少需2、(p.11,题2) 证明方程210)(-+=x e x f x在区间[0,1]内有唯一个实根;使用二分法求这一实根,要求误差不超过21021-⨯。
【解】 由于210)(-+=x e x f x ,则)(x f 在区间[0,1]上连续,且012010)0(0<-=-⨯+=e f ,082110)1(1>+=-⨯+=e e f ,即0)1()0(<⋅f f ,由连续函数的介值定理知,)(x f 在区间[0,1]上至少有一个零点.又010)('>+=x e x f ,即)(x f 在区间[0,1]上是单调的,故)(x f 在区间[0,1]内有唯一实根.由二分法的误差估计式211*1021212||-++⨯=≤=-≤-εk k k a b x x ,得到1002≥k .两端取自然对数得6438.63219.322ln 10ln 2=⨯≈≥k ,因此取7=k ,即至少需二分0.2误差1.(p.12,题8)已知e=2.71828…,试问其近似值7.21=x ,71.22=x ,x 2=2.71,718.23=x 各有几位有效数字?并给出它们的相对误差限。
【解】有效数字:因为11102105.001828.0||-⨯=<=-K x e ,所以7.21=x 有两位有效数字; 因为12102105.000828.0||-⨯=<=-K x e ,所以71.22=x 亦有两位有效数字;因为3310210005.000028.0||-⨯=<=-K x e ,所以718.23=x 有四位有效数字;%85.17.205.0||111=<-=x x e r ε; %85.171.205.0||222=<-=x x e r ε; %0184.0718.20005.0||333=<-=x x e r ε。
数学分析简明教程答案(尹小玲 邓东皋)

即
un vn un vn .
n 1 n 1 n 1
D
4.设级数 un 各项是正的, 把级数的项经过组合而得到的新级数 U n ,即
n 1 n 1
U n 1 ukn 1 ukn 2 ukn1 , n 0,1, 2, , 其中k0 0, k0 k1 k2 kn kn 1 . 若级数 U n收敛,证明原来的级数也收敛。
(2)
n 1
1 4n 2 1
1 1 1 2 n 1 2n 1 2n 1
1 1 1 1 1 1 1 1 lim 1 2 n 3 3 5 5 7 2n 1 2n 1 1 1 1 lim 1 . 2 n 2n 1 2
n
于是可得 Sn 由于 r 1,因此有
r
n 1
n
r cos x r 2 . 1 r 2 2r cos x
2.讨论下列级数的敛散性: (1) n ; n 1 2n 1
lim
n 1 0, 故原级数发散。 n 2n 1 2 由于级数 lim cos
第十章 数项级数
§1 级数问题的提出
1.证明:若微分方程xy '' y ' xy 0有多项式解 y a0 a1 x a2 x 2 an x n ; 则必有ai 0, i 1, 2, , n. 证明:若y a0 a1 x a2 x 2 an x n 微分方程的一个解, 那么 y ' a1 2a2 x 3a3 x 2 nan x n 1 y '' 2a2 6a3 x n(n 1)an x n 2 ; 于是可得 xy '' 2a2 x 6a3 x 2 n(n 1)an x n 1 xy a0 x a1 x 2 a2 x 3 an x n 1. 因此可知 xy '' y ' xy a1 (4a2 a0 ) x (9a3 a1 ) x 2 (n 2 an an 2 ) x n 1 an x n 0 那么由多项式相等可知有 a1 0 2 n an an 2 0 a 0 n 递推可知有ai 0, i 1, 2, , n成立。 n 2.
2020北大数院金融硕士考研难度深度分析
2020北大数院金融硕士考研难度深度分析本文重点讲解北大数院金融专硕介绍、北大数院金融专硕课程设置、北大数院金融专硕初试考试科目、北大数院金融专硕参考书、北大数院金融专硕复习规划、北大数院金融专硕复试情况及北大数院金融专硕的奖助学金等信息,下面凯程老师就详细的给大家介绍一下。
一、院校介绍北大数学学院暨北京国际数学研究中心拥有一支实力雄厚的师资队伍,现有教师119人,其中中科院院士7人,长江特聘教授11人,国家杰出青年基金获得者24人,他们不仅在数学研究的前沿领域上取得了杰出的成就,还长期坚持在教学岗位上,为国家培养了一批又一批高素质、高水平的创新型人才。
1952年以来,数学科学学院先后为国家培养了一万多名毕业生,他们奋斗在国家建设的各条战线上,其中包括30余名两院院士。
获得国家最高科技奖的吴文俊院士和王选院士是数学科学学院校友中的杰出代表。
数学科学学院在2001年获得国家优秀教学成果特等奖;在教育部学科评估中,2002年、2007年、2012年北大数学均名列全国首位;2017年北大数学和统计学均获评A+并入选国家“一流学科”建设名单。
二、数院金融硕士介绍金融数学是近年来蓬勃发展的新学科,在国际金融界和应用数学界受到高度重视。
北大数学科学院金融数学系除培养金融数学本科生外,还通过金融数学与精算学应用硕士项目培养面向金融业的高级人才。
金融数学系将培养学生不仅具有扎实的现代数学基础,熟练使用计算机的技能,而且具有深厚的金融专业知识,文理并茂,全面发展。
分系后除继续开设概率统计、随机分析、微分方程等数学基础课外,还将开设利息、证券、汇率、保险精算等金融数学的专业课程,一些经济与金融的基础课由经济学院及光华管理学院开设。
金融数学系本科毕业生将能熟练运用数学知识和数据分析方法,从事某些金融保险实际工作,并可继续深造,到高等学校和科研机构应用数学、经济和金融管理等专业攻读硕士或博士学位。
三、课程设置本项目的学习期间为两年(4个学期),前三个学期以课堂学习为主,课程包括必修课(30学分)和专业选修课(10学分)两类。
数值分析简明教程课后习题答案
比较详细的数值分析课后习题答案0.1算法1、 (p.11,题1)用二分法求方程013=--x x 在[1,2]内的近似根,要求误差不超过10-3.【解】 由二分法的误差估计式311*10212||-++=≤=-≤-εk k k a b x x ,得到100021≥+k .两端取自然对数得96.812ln 10ln 3≈-≥k ,因此取9=k ,即至少需2、(p.11,题2) 证明方程210)(-+=x e x f x在区间[0,1]内有唯一个实根;使用二分法求这一实根,要求误差不超过21021-⨯。
【解】 由于210)(-+=x e x f x ,则)(x f 在区间[0,1]上连续,且012010)0(0<-=-⨯+=e f ,082110)1(1>+=-⨯+=e e f ,即0)1()0(<⋅f f ,由连续函数的介值定理知,)(x f 在区间[0,1]上至少有一个零点.又010)('>+=x e x f ,即)(x f 在区间[0,1]上是单调的,故)(x f 在区间[0,1]内有唯一实根.由二分法的误差估计式211*1021212||-++⨯=≤=-≤-εk k k a b x x ,得到1002≥k .两端取自然对数得6438.63219.322ln 10ln 2=⨯≈≥k ,因此取7=k ,即至少需二分0.2误差1.(p.12,题8)已知e=2.71828…,试问其近似值7.21=x ,71.22=x ,x 2=2.71,718.23=x 各有几位有效数字?并给出它们的相对误差限。
【解】有效数字:因为11102105.001828.0||-⨯=<=- x e ,所以7.21=x 有两位有效数字; 因为12102105.000828.0||-⨯=<=- x e ,所以71.22=x 亦有两位有效数字;因为3310210005.000028.0||-⨯=<=- x e ,所以718.23=x 有四位有效数字;%85.17.205.0||111=<-=x x e r ε; %85.171.205.0||222=<-=x x e r ε; %0184.0718.20005.0||333=<-=x x e r ε。
实变函数简明教程(邓东皋)新版答案
E(f
≥
c)
表示
{x
∈
E|f
>
c}
和
{x
∈
E|f
≥
c},
并令
En,k
=
E(fn
>
c
−
1 k
),
试证
∩∞
∩∞
∩∞
limn→∞En,k = limn→∞En,k, E(f ≥ c) = limn→∞En,k.
k=1
k=1
k=1
证明: 由 limn→∞En,k ⊆ limn→∞En,k, 知
∩∞
∩∞
limn→∞En,k ⊇ limn→∞En,k;
且为偶
数时,有
0
>
1 n2
−
2x0
(−1)n
1 n
>
δ
>
−ε;
4
√
x0 < 0 时,令 n 取奇数,则 y = −x0 ±
x20 + δ,
则当
n>
√1
−x0− x20+δ
且
为奇数时,有
0
>
1 n2
−
2x0
(−1)n
1 n
>
δ
>
−ε
从而
limn→∞An ⊆ E2.
再证
limn→∞An ⊇ E2.
∀Q ∈ (x0, y0) ∈ E2, 即 x20 + y02 ≤ 1, 且 (x0, y0) ̸= (0, ±1), 若 x0 = 0, y02 < 1, 故
n
n
n=1
n=1
.
证明: 对任意正整数
数值分析简明教程---课后答案
0.1算法1、 (p.11,题1)用二分法求方程013=--x x 在[1,2]内的近似根,要求误差不超过10-3.【解】 由二分法的误差估计式311*10212||-++=≤=-≤-εk k k a b x x ,得到100021≥+k .两端取自然对数得96.8110ln 3≈-≥k ,因此取9=k ,即至少需二分9次.求解过程见下表。
2、(p.11,题2) 证明方程210)(-+=x e x f x在区间[0,1]内有唯一个实根;使用二分法求这一实根,要求误差不超过21021-⨯。
【解】 由于210)(-+=x e x f x ,则)(x f 在区间[0,1]上连续,且012010)0(0<-=-⨯+=e f ,082110)1(1>+=-⨯+=e e f ,即0)1()0(<⋅f f ,由连续函数的介值定理知,)(x f 在区间[0,1]上至少有一个零点.又010)('>+=x e x f ,即)(x f 在区间[0,1]上是单调的,故)(x f 在区间[0,1]内有唯一实根.由二分法的误差估计式211*1021212||-++⨯=≤=-≤-εk k k a b x x ,得到1002≥k .两端取自然对数得6438.63219.3210ln 2=⨯≈≥k ,因此取7=k ,即至少需二分7次.求解过程见下表。
0.2误差1.(p.12,题8)已知e=2.71828…,试问其近似值7.21=x ,71.22=x ,x 2=2.71,718.23=x 各有几位有效数字?并给出它们的相对误差限。
【解】有效数字:因为11102105.001828.0||-⨯=<=- x e ,所以7.21=x 有两位有效数字; 因为12102105.000828.0||-⨯=<=- x e ,所以71.22=x 亦有两位有效数字;因为3310210005.000028.0||-⨯=<=- x e ,所以718.23=x 有四位有效数字;%85.17.205.0||111=<-=x x e r ε; %85.171.205.0||222=<-=x x e r ε; %0184.0718.20005.0||333=<-=x x e r ε。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x0
x
lim
x0
3x02x 3x2 x0 x
x3
3x02 ;
f '(0 0) lim f (0 x) f (x) lim x3 0 0,
x0
x
x0 x
f '(0 0) lim f (0 x) f (x) lim x3 0 0,
第四章 微商与微分
第一节 微商的概念及其计算
1.求抛物线y x2在A(1,1)点和B(2, 4)点的切线方程和法线方程。
解:函数y x2的导函数为y ' 2x,则它在A(1,1), B(2, 4)的切线斜率分别为
y '(1) 2, y '(2) 4;
于是由点斜式可以求得在这两点的切线方程分别为y 2x 1, y 4x 4.
由于法线斜率与切线斜率的乘积为 1, 故可以求得在这两点的法线斜率分别为
k1
1 2
,
k2
1; 4
那么由点斜式可以求得在这两点的法线方程分别为y 1 x 3 , y 1 x 9 . 22 42
2.若S vt 1 gt2,求 2
(1)在t 1,t 1 t之间的平均速度(设t 1, 0.1, 0.01); (2)在t 1的瞬时速度。 解:(1)可以求得
x
令
lim f (3 x) f (3) lim a(3 x) b 32 lim 3a a x b 9 6,
x0
x
x0
x
x0
x
那么必有
解得:a 6,b 9.
3a b 9 0 a 6
5.求下列曲线在指定点P的切线方程和法线方程。
为y x 1, y x 3.
(2)函数y cos x的导函数为y ' sin x,则在P点的切线斜率为k y '(0) 0;因此由点斜式
可以求得在P点的切线为y 1.
由于在同一点的法线与切线相垂直,于是在此点的法线为x 0.
2
6.求下列函数的导函数: (1) f (x) x 3
x0
x
x0 x
f '(0 0) lim f (0 x) f (x) lim 11 0,
x0
x
x0 x
综上可得
f
'( x)
1 0
x0 .
x0
4
7.设函数f
(
x)
xm
sin
1 x
x
0 ,
(m为正整数).
(1) y x2 , 4
P(2,1);
(2) y cos x, P(0,1).
解:(1)函数y x2 的导函数为y ' x ,则在P点的切线斜率为k y '(2) 1;由于同一点的切线与
4
2
法线相垂直,于是法线斜率为k1
1 k
1.因此由点斜式可以求得在P点的切线与法线分别
x
2
2
1
4.设f
(
x)
x2 ax
b
x 3 ,试确定a,b的值,使f (x)在x 3处可导。 x3
解:可以求得 lim f (3 x) f (3) lim (3 x)2 32 lim 6x x2 6;
x0
x
x0
x
x0
x0
x
x0 x
f
'( x)
3x2 3x2
x0 .
x0
3
(2)
f
(
x)
x 1
1
x0 x0
解:对于x0 R有 对于x0 R有 当x 0时有
f
'(x0 )
lim
x0
f
( x0
x) x
f
(x0 )
lim (x0 x) 1 (x0 1)
S (1)
v
1.05g
;
v3
S (1
0.01) 0.01
S (1)
v
1.005g
(2)由于S ' dS y gt,于是S '(1) v g,在t 1的瞬时速度为v g. dt
3.试确定曲线y ln x在哪些点的切线平行于下列直线:(1) y x 1, (2) y 2x 3
解:函数y ln x的导函数为y ' 1 ; x
(1)令y ' 1 1,可得x 1; y(1) ln1 0,故曲线在点(1,0)的切线平行于直线y x 1; x
(1)令y ' 1 2,可得x 1 ; y(1) ln 1 ln 2,故曲线在点(2, ln 2)的切线平行于y 2x 3.
x0
x
lim x 1; x0 x
f
'(x0 )
lim
x0
f
( x0
x) x
f
(x0 )
lim 11 lim 0 0; x0 x x0 x
因此f '(0)不存在.
f '(0 0) lim f (0 x) f (x) lim x 11 1,
于是有
S S
(1) v 1 g 2
(11) 2v
2g
S
(1
0.1)
1.1v
1.21 2
g
;
S
(1
0.01)
1.01v
1.0201 2
g
v1
S(11) 1
S (1)
v
1.5g
v2
S (1
0.1) 0.1
解:f (x)
x3
x3
x3
对于x0 R有
当x 0时有
因此f '(0) 0. 综上可得
x x
0 0
,
那么对于x0
R
有
f
'(x0 )
lim
x0
f
( x0
x) x
f
(x0 )
lim (x0 x)3 x03
x0
x
lim x03 3x02x 3x2 x0 x3 x03
x0
x
lim 3x02x 3x2 x0
x0
x
x3
3x02;
f
'(x0 )
lim
x0
f
( x0
x) x
f
(x0 )
lim (x0 x)3 (x03 )
x0
x
lim x03 3x02x 3x2 x0 x3 x03
