12.2 第1课时 “边边边”精选练习1
12.2 边边边 第1课时同步练习(含答案)

12.2 第1课时 边边边(SSS )一、选择题1.如图,ABC △中,AB AC =,EB EC =,则由“SSS ”可以判定( ) A .ABD ACD △≌△ B .ABE ACE △≌△ C .BDE CDE △≌△D .以上答案都不对2.如图,在ABC △和DCB △中,AB DC =,AC 与BD 相交于点E ,若不再添加任何字母与辅助线,要使ABC DCB △≌△,则还需增加的一个条件是( ) A .AC =BD B .AC =BC C .BE =CE D .AE =DE3.如图,已知AB =AC ,BD =DC ,那么下列结论中不正确的是( ) A .△ABD ≌△ACD B .∠ADB =90° C .∠BAD 是∠B 的一半D .AD 平分∠BAC4. 如图,AB =AD ,CB =CD ,∠B =30°,∠BAD =46°,则∠ACD 的度数是( )A .120°B .125°C .127°D .104°5. 如图,线段AD 与BC 交于点O ,且AC =BD ,AD =BC , 则下面的结论中不正确的是( ) A .△ABC ≌△BAD B .∠CAB =∠DBA C .OB =OC D .∠C =∠D6. 如图,AB =CD ,BC =DA ,E 、F 是AC 上的两点,且AE =CF ,DE =BF ,,那么图中全等三角形共有( )对A .4对B .3对C .2对D .1对A EC第1题图第2题图 第3题图第4题图第5题图7. 如图 ,AB =CD ,BC =AD ,则下列结论不一定正确的是( ). A .AB ∥DC B . ∠B =∠D C . ∠A =∠C D . AB =BC8. 如果△ABC 的三边长分别为3,5,7,△DEF 的三边长分别为3,3x -2,2x -1,若这两个三角形全等,则x 等于( ) A .73B .3C .4D .5 二、填空题9.工人师傅常用角尺平分一个任意角。
人教版八年级上数学12.2 第1课时 “边边边”2
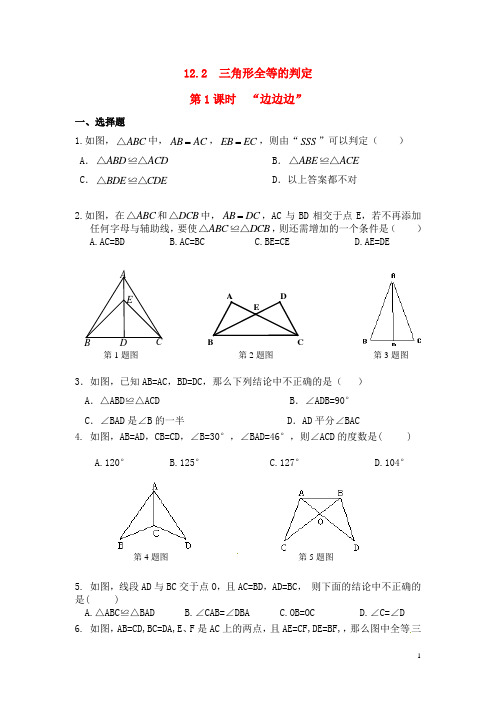
12.2 三角形全等的判定 第1课时 “边边边”一、选择题1.如图,ABC △中,AB AC =,EB EC =,则由“SSS ”可以判定( ) A .ABD ACD △≌△ B .ABE ACE △≌△ C .BDE CDE △≌△ D .以上答案都不对2.如图,在ABC △和DCB △中,AB DC =,AC 与BD 相交于点E ,若不再添加任何字母与辅助线,要使ABC DCB △≌△,则还需增加的一个条件是( ) A.AC=BD B.AC=BC C.BE=CE D.AE=DE3.如图,已知AB=AC ,BD=DC ,那么下列结论中不正确的是( ) A .△ABD ≌△ACD B .∠ADB=90° C .∠BAD 是∠B 的一半D .AD 平分∠BAC4. 如图,AB=AD ,CB=CD ,∠B=30°,∠BAD=46°,则∠ACD 的度数是( )A.120°B.125°C.127°D.104°5. 如图,线段AD 与BC 交于点O ,且AC=BD ,AD=BC , 则下面的结论中不正确的是( )A.△ABC ≌△BADB.∠CAB=∠DBAC.OB=OCD.∠C=∠D6. 如图,AB=CD,BC=DA,E 、F 是AC 上的两点,且AE=CF,DE=BF,,那么图中全等三EDCB AAEB DC第1题图第2题图 第3题图第4题图第5题图角形共有( )对A .4对B .3对C .2对D .1对7. 如图 ,AB=CD ,BC=AD ,则下列结论不一定正确的是( ).A.AB ∥DCB. ∠B =∠DC. ∠A =∠CD. AB=BC8. 如果△ABC 的三边长分别为3,5,7,△DEF 的三边长分别为3,3x -2,2x -1,若这两个三角形全等,则x 等于( ) A .73B . 3C .4D .5二、填空题9.(2011湖北十堰)工人师傅常用角尺平分一个任意角。
人教版八年级上数学12.2 第1课时 “边边边”2

12.2 三角形全等的判定 第1课时 “边边边”一、选择题1.如图,ABC △中,AB AC =,EB EC =,则由“SSS ”可以判定( ) A .ABD ACD △≌△ B .ABE ACE △≌△ C .BDE CDE △≌△ D .以上答案都不对2.如图,在ABC △和DCB △中,AB DC =,AC 与BD 相交于点E ,若不再添加任何字母与辅助线,要使ABC DCB △≌△,则还需增加的一个条件是( ) A.AC=BD B.AC=BC C.BE=CE D.AE=DE3.如图,已知AB=AC ,BD=DC ,那么下列结论中不正确的是( ) A .△ABD ≌△ACD B .∠ADB=90° C .∠BAD 是∠B 的一半D .AD 平分∠BAC4. 如图,AB=AD ,CB=CD ,∠B=30°,∠BAD=46°,则∠ACD 的度数是( )A.120°B.125°C.127°D.104°5. 如图,线段AD 与BC 交于点O ,且AC=BD ,AD=BC , 则下面的结论中不正确的是( )A.△ABC ≌△BADB.∠CAB=∠DBAC.OB=OCD.∠C=∠D6. 如图,AB=CD,BC=DA,E 、F 是AC 上的两点,且AE=CF,DE=BF,,那么图中全等三EDCB AAEB DC第1题图第2题图 第3题图第4题图第5题图角形共有( )对A .4对B .3对C .2对D .1对7. 如图 ,AB=CD ,BC=AD ,则下列结论不一定正确的是( ).A.AB ∥DCB. ∠B =∠DC. ∠A =∠CD. AB=BC8. 如果△ABC 的三边长分别为3,5,7,△DEF 的三边长分别为3,3x -2,2x -1,若这两个三角形全等,则x 等于( ) A .73B . 3C .4D .5二、填空题9.(2011湖北十堰)工人师傅常用角尺平分一个任意角。
2019秋人教版八年级数学上册作业课件:12.2 第1课时 “边边边”

15.如图,AD=CB,E,F是AC上的两动点,且有DE=BF. (1)若E,F运动至如图①所示的位置,有AF=CE, 求证:△ADE≌△CBF; (2)若E,F运动至如图②所示的位置,仍有AF=CE, 那么△ADE≌△CBF还成立吗?为什么? (3)若E,F不重合,且AF=CE,那么AD和CB平行吗?请说明理由.
AB=DE
5.(教材P45习题13变式)如图,AB=AC,DB=DC,EB=EC. (1)图中有几对全等三角形?请一一写出来; (2)选择(1)中的一对全等三角形加以证明.
解:(1)3 对,△ABD≌△ACD,△ABE≌△ACE,△DBE≌△DCE (2)以△ABD≌△ACD 为例,
AB=AC, 证明:在△ABD 与△ACD 中,DB=DC,∴△ABD≌△ACD(SSS)
AD=AD,
6.如图是用直尺和圆规作一个角等于已知角的示意图, 要证明∠A′O′B′=∠AOB,就要先证明△C′O′D′≌△COD, 那么判定△C′O′D′≌△COD的依据是_______S_S_S.
7.已知∠AOB,点C是OB边上的一点. 用尺规作图画出经过点C与OA平行的直线.
解: ①以点O为圆心,任意长为半径,弧交OA于点E,交OB于点D; ②以点C为圆心,OD的长为半径画弧交OB于点G; ③以点G为圆心,DE的长为半径,交前弧于点H,连接CH,则CH∥OA.
则△_____≌△_____,∠2=___°.
ABD ACE
20
10.如图,在△ABC中,AB=AC,AD是BC边上的中线, 求证:△ABD≌△ACD.
解:∵AD 是 BC 边上的中线,∴BD=CD.
AB=AC, 在△ABD 和△ACD 中,AD=AD,∴△ABD≌△ACD(SSS)
(精)初中数学同步训练人教8年级上册: 12.2.1三角形全等的判定——边边边
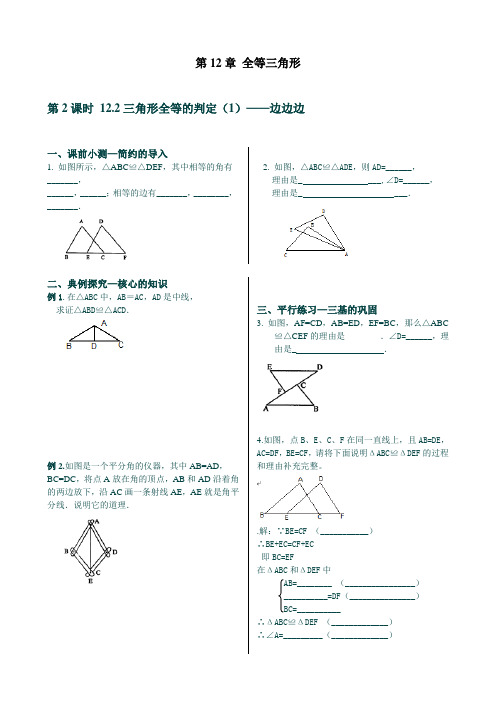
第12章全等三角形第2课时12.2三角形全等的判定(1)——边边边一、课前小测—简约的导入1. 如图所示,△ABC≌△DEF,其中相等的角有_______,______,______;相等的边有_______,________,_______.2.如图,△ABC≌△ADE,则AD=______,理由是_ ___,∠D=______,理由是_ ___.二、典例探究—核心的知识例1.在△ABC中,AB=AC,AD是中线,求证△ABD≌△ACD.例2.如图是一个平分角的仪器,其中AB=AD,BC=DC,将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是角平分线.说明它的道理.三、平行练习—三基的巩固3. 如图,AF=CD,AB=ED,EF=BC,那么△ABC≌△CEF的理由是________.∠D=______,理由是_ .4.如图,点B、E、C、F在同一直线上,且AB=DE,AC=DF,BE=CF,请将下面说明ΔABC≌ΔDEF的过程和理由补充完整。
.解:∵BE=CF (___________)∴BE+EC=CF+EC即BC=EF在ΔABC和ΔDEF中AB=________ (________________)__________=DF(_______________)BC=__________∴ΔABC≌ΔDEF (_____________)∴∠A=_________(_____________)5.如图,AB=CD,AC=DB,∠1与∠2相等吗?为什么?四、变式练习—拓展的思维例3如图四边形ABCD中,AB=CD,AD=BC,你能把四边形ABCD分成两个相互全等的三角形吗?你有几种方法?变式1.如图四边形ABCD中,AB=CD,AD=BC,则∠D=∠B,试说明理由.变式2.如图,已知在四边形ABCD中,AD=AB,CD=CB,则∠D=∠B,试说明理由.变式3.如图,已知CA=CB,AD=BD,M,N分别为CB,CA的中点.试问DN与DM•的大小关系如何?请说明道理.五、课时作业—必要的再现6. 如图,AB=AD,CB=CD,∠B=30°,∠BAD=46°,则∠ACD的度数是()A.120°B.125°C.127°D.104°7.如图,AB=DE,AC=DF,BF=CE.(1)若BC=18cm,则FE=______;(2)若∠B=50°,∠D=70°,则∠DFE=_______.8.如图,已知AB=CD,AE=CF,DE=BF.请证明:AB∥CD.。
“边边边” 精品导学案及练习

第十二章 全等三角形•归纳获得. ) ) . : .(画完归纳总结:只有一条边或一个角对应相等的两个三角形不一定全等2:给出两个条件画三角形做一做:符号表示:如图,如果DEFABC∆∆⇒⎪⎭⎪⎬⎫===________________________________________例1:如图, C是BF的中点,AB =DC,AC=DF.求证:△ABC≌△DCF.F【变式题】已知: 如图,点B、E、C、F在同一直线上 , AB = DE , AC = DF ,BE = CF . 求证: (1)△ABC ≌ △DEF;(2)∠A=∠D.AC=FE探究点2:尺规作图作一个角等于已知角画一画:已知:∠BAC.求作:∠B'A'C',使∠B'A'C'=∠BAC.作一个角等于已知角的依据是___________.. 第1题图 第2题图,AD =BC , 则下列结论:①△ABC ≌△CDB ;②△C=AD FDE; :如图 第3课时 “角边角”和“角角边”学习目标:1.了解1.探索三角形全等的“角边角”和“角角边”的条件温馨提示:配套课件及全册导学案WORD 版见光盘或网站下载:(无须登录,直接下载)DC O2.应用“角边角”和“角角边”证明两个三角形全等,进而证线段或角相等.重点:已知两角一边的三角形全等探究.难点:理解,掌握三角形全等的条件:“ASA”“AAS”.一、知识链接1.能够的两个三角形叫做全等三角形.2.判定两个三角形全等方法有哪些?边边边:对应相等的两个三角形全等.边角边:和它们的对应相等的两个三角形全等.二、新知预习1.在三角形中,已知三个元素的四种情况中,我们研究了三种,今天我们接着探究已知两角一边是否可以判断两三角形全等呢?三角形中已知两角一边又分成哪两种呢?2.现实情境一张教学用的三角板硬纸不小心被撕坏了,如图:你能制作一张与原来同样大小的新道具吗?能恢复原来三角形的原貌吗?(2)以②为模板,画一画,能还原吗?(3)以③为模板,画一画,能还原吗?(4)第③块中,三角形的边角六个元素中,固定不变的元素是_____________.猜想:两角及夹边对应相等的两个三角形_______.三、我的疑惑______________________________________________________________________________________________________________________________________________________B=∠C,求证:AD=AE.证明线段或角度相等,可先证两个三角形全等,利用对应边或对应角相等来CBE.探究点2:三角形全等的判定定理3的推论--“角角边”做一做:已知一个三角形的两个内角分别是60°和45°,且45°所对的边的边长为3cm,你能画出这个三角形吗?追问:这里的条件与“角边角”中的条件有什么相同点与不同点?你能将它转化为“角边角”中的条件吗?要点归纳:相等的两个三角形全等(简称“角角边”或“AAS”).几何语言:如图,在△ABC和△DEF中,ABC≌△DEF.例3:在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF.求证:△ABC≌△DEF.例4:如图,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.求证:(1)△BDA≌△AEC;(2)DE=BD+CE.如图,已知△ABC的六个元素,则下面甲、乙、丙三个三角形中,和△ABC全等的图形是()二、课堂小结“角角边”是利用三角形内角和定理转化成“角边角”来证明两个三角形全等1.△ABC 和△DEF 中,AB =DE ,∠B =∠E ,要使△ABC≌△DEF ,则下列补充的条件中错误的是( )A .AC =DFB .BC =EF C .∠A=∠D D .∠C =∠F2. 在△ABC 与△A′B′C′中,已知∠A=44°,∠B=67°,∠C′=69° ,∠A′=44°, 且AC =A′C′,那么这两个三角形( )A .一定不全等B .一定全等C .不一定全等D .以上都不对 3.如图,已知∠ACB=∠DBC,∠ABC=∠CDB,判别下面的 两个三角形是否全等,并说明理由.4.如图∠ACB=∠DFE ,BC=EF ,那么应补充一个条件 , 才能使△ABC ≌△DEF (写出一个即可),并说明理由.5.已知:如图, AB ⊥BC ,AD ⊥DC ,∠1=∠2, 求证:AB=AD. 拓展提升6.已知:如图,△ABC ≌△A′B′C′ ,AD 、A′ D′ 分别是△ABC 和△A′B′C′的高.试说明AD = A′D′ ,并用一句话说出你的发现.当堂检测 温馨提示:配套课件及全册导学案WORD 版见光盘或网站下载:(无须登录,直接下载)。
人教版八年级上数学12.2 第1课时 “边边边”2

12.2 三角形全等的判定 第1课时 “边边边”一、选择题1.如图,ABC △中,AB AC =,EB EC =,则由“SSS ”可以判定( ) A .ABD ACD △≌△ B .ABE ACE △≌△ C .BDE CDE △≌△ D .以上答案都不对2.如图,在ABC △和DCB △中,AB DC =,AC 与BD 相交于点E ,若不再添加任何字母与辅助线,要使ABC DCB △≌△,则还需增加的一个条件是( ) A.AC=BD B.AC=BC C.BE=CE D.AE=DE3.如图,已知AB=AC ,BD=DC ,那么下列结论中不正确的是( ) A .△ABD ≌△ACD B .∠ADB=90° C .∠BAD 是∠B 的一半D .AD 平分∠BAC4. 如图,AB=AD ,CB=CD ,∠B=30°,∠BAD=46°,则∠ACD 的度数是( )A.120°B.125°C.127°D.104°5. 如图,线段AD 与BC 交于点O ,且AC=BD ,AD=BC , 则下面的结论中不正确的是( )A.△ABC ≌△BADB.∠CAB=∠DBAC.OB=OCD.∠C=∠D6. 如图,AB=CD,BC=DA,E 、F 是AC 上的两点,且AE=CF,DE=BF,,那么图中全等三CB AEB DC第1题图第2题图 第3题图第4题图第5题图角形共有( )对A .4对B .3对C .2对D .1对7. 如图 ,AB=CD ,BC=AD ,则下列结论不一定正确的是( ).A.AB ∥DCB. ∠B =∠DC. ∠A =∠CD. AB=BC8. 如果△ABC 的三边长分别为3,5,7,△DEF 的三边长分别为3,3x -2,2x -1,若这两个三角形全等,则x 等于( ) A .73B .3C .4D .5二、填空题9.(2011湖北十堰)工人师傅常用角尺平分一个任意角。
人教版八年级上册数学人教版八年级上册数学 12.2 第1课时 “边边边”精选练习1

12.2 三角形全等的判定 第1课时 “边边边”一、选择题1.如图1,AB=AD ,CB=CD ,∠B=30°,∠BAD=46°,则∠ACD 的度数是( )A .120°B .125°C .127°D .104°DCBAODCBAFEDC BA(1) (2) (3)2.如图2,线段AD 与BC 交于点O ,且AC=BD ,AD=BC ,•则下面的结论中不正确的是( ) A .△ABC ≌△BAD B .∠CAB=∠DBA C .OB=OC D .∠C=∠D 二、填空题 3.在△ABC 和△A 1B 1C 1中,已知AB=A 1B 1,BC=B 1C 1,则补充条件____________,可得到△ABC ≌△A 1B 1C 1. 4.如图3,AB=CD ,BF=DE ,E 、F 是AC 上两点,且AE=CF .欲证∠B=∠D ,可先运用等式的性质证明AF=________,再用“SSS ”证明________≌_________•得到结论. 三、解题题5.如图,在四边形ABCD 中AB=CD ,AD=BC ,求证:①AB ∥CD ;②AD ∥BC .DCBA6.如图,已知AB=CD ,AC=BD ,求证:∠A=∠D .E DBA7.如图,AC 与BD 交于点O ,AD=CB ,E 、F 是BD 上两点,且AE=CF ,DE=BF .•请推导下列结论:(1)∠D=∠B ;(2)AE ∥CF .O F ED CBA答案:1.C 2.C 3.AC=AC 4.CE;△ABF≌△CDE5.连接AC(或BD) 6.连接BC后证明△ABC≌△DCB7.①证明△ADE≌△CBF;②证明∠AEF=∠CFE。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
12.2 三角形全等的判定 第1课时 “边边边”
一、选择题
1.如图1,AB =AD ,CB =CD ,∠B =30°,∠BAD =46°,则∠ACD 的度数是( )
A .120°
B .125°
C .127°
D .104°
D
C
B
A
O
D
C
B
A
F
E
D
C B
A
(1) (2) (3)
2.如图2,线段AD 与BC 交于点O ,且AC =BD ,AD =BC ,•则下面的结论中不正确的是( ) A .△ABC ≌△BAD ;B .∠CAB =∠DBA C .OB =OC D .∠C =∠D 二、填空题
3.在△ABC 和△A 1B 1C 1中,已知AB =A 1B 1,BC =B 1C 1,则补充条件____________,可得到△ABC ≌△A 1B 1C 1.
4.如图3,AB =CD ,BF =DE ,E 、F 是AC 上两点,且AE =CF .欲证∠B =∠D ,可先运用等式的性质证明AF =________,再用“SSS ”证明________≌_________•得到结论.
三、解题题
5.如图,在四边形ABCD 中AB =CD ,AD =BC ,求证:①AB ∥CD ;②AD ∥B C .
D
C
B A
6.如图,已知AB=CD,AC=BD,求证:∠A=∠D.
E
D
B
A
7.如图,AC与BD交于点O,AD=CB,E、F是BD上两点,且AE=CF,DE=BF.•请推导下列结论:
(1)∠D=∠B;(2)AE∥CF.
O F E
D C
B A
参考答案
1.C2.C3.AC=AC4.CE;△ABF≌△CDE
5.连接AC(或BD)6.连接BC后证明△ABC≌△DCB 7.①证明△ADE≌△CBF;②证明∠AEF=∠CFE。
