利用一次函数图象解决实际问题专项训练(含答案)
4.5 第1课时 利用一次函数解决实际问题 湘教版数学八年级下册课时习题(含答案)
4.5 一次函数的应用第1课时利用一次比例函数解决实际问题要点感知1函数图象由两个一次函数拼接在一起，我们要按照图象实行分段处理，每段看它适合哪种函数模型.预习练习1-1如图所示中的折线ABC为甲地向乙地打长途电话需付的电话费y(元)与通话时间t(分钟)之间的函数关系，则通话8分钟应付电话费__________元.要点感知2 同一坐标系中若有多条直线，我们要对每条直线进行处理，重在找出这些函数的交点坐标和每个图形的起始坐标(交点的求法一般将两个函数的表达式联立在一起，组成方程组，方程组的解便是交点坐标).预习练习2-1在同一平面直角坐标系中，若一次函数y=-x+3与y=3x-5的图象交于点M，则点M的坐标为( )A.(-1，4)B.(-1，2)C.(2，-1)D.(2，1)2-2 如图，l1反映了某公司的销售收入与销量的关系，l2反映了该公司产品的销售成本与销量的关系，当该公司赢利(收入＞成本)时，销售量必须__________.知识点1 利用一次函数解决分段计费问题1.如图是某复印店复印收费y(元)与复印面数(8开纸)x(面)的函数图象，那么从图象中可看出，复印超过100面的部分，每面收费( )A.0.4元B.0.45元C.约0.47元D.0.5元2.某城市按以下规定收取每月煤气费，用煤气不超过60立方米，按每立方米0.8元收费；如果超过60立方米，超过部分按每立方米1.2元收费.已知甲用户某月份用煤气80立方米，那么这个月甲用户应交煤气费__________元.3.为了鼓励居民节约用水，某市采用“阶梯水价”的方法按月计算每户家庭的水费：每月用水量不超过20吨时，按每吨2元计费；每月用水量超过20吨时，其中的20吨仍按每吨2元计费，超过部分按每吨2.8元计费.设每户家庭月用水量为x吨时，应交水费y元.(1)分别求出0≤x≤20和x＞20时，y与x之间的函数表达式；(2)小颖家四月份、五月份分别交水费45.6元、38元，问小颖家五月份比四月份节约用水多少吨？知识点2 利用一次函数解决相交直线问题4. “五一节”期间，王老师一家自驾游去了离家170千米的某地，下面是他们离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象.当他们离目的地还有20千米时，汽车一共行驶的时间是( )A.2小时B.2.2小时C.2.25小时D.2.4小时第4题图第5题图5.某市政府决定实施供暖改造工程，现甲、乙两工程队分别同时开挖两条600米长的管道，所挖管道长度y(米)与挖掘时间x(天)之间的关系如图，则下列说法中错误的是( )A.甲队每天挖100米B.乙队开挖两天后，每天挖50米C.甲队比乙队提前2天完成任务D.当x=3时，甲、乙两队所挖管道长度相同6.某市出租车起步价是5元(3公里及3公里以内为起步价)，以后每公里收费1.6元，不足1公里按1公里收费，小明乘出租车到达目的地时计价器显示为11.4元，则此出租车行驶的路程可能为( )A.5.5公里B.6.9公里C.7.5公里D.8.1公里7.甲乙两地相距50千米.星期天上午8：00小聪同学在父亲陪同下骑山地车从甲地前往乙地.2小时后，小明的父亲骑摩托车沿同一路线也从甲地前往乙地，他们行驶的路程y(千米)与小聪行驶的时间x(小时)之间的函数关系如图所示，小明父亲出发________小时时，行进中的两车相距8千米.8.小李和小陆沿同一条路行驶到B地，他们离出发地的距离s和行驶时间t之间的函数关系的图象如图.已知小李离出发地的距离s和行驶时间t之间的函数关系为s=2t+10.则：(1)小陆离出发地的距离s和行驶时间t之间的函数关系为：_________________；(2)他们相遇的时间t=__________.9.学生甲、乙两人跑步的路程s与所用时间t的函数关系图象表示如图(甲为实线，乙为虚线).根据图象判断：如果两人进行一百米赛跑，当甲跑到终点时，乙落后甲多少米？10.电信公司推出两种手机收费方式：A种方式是月租20元，B种方式是月租0元.一个月的本地网内打出电话时间t(分钟)与打出电话费s(元)的函数关系如图，当打出电话150分钟时，这两种方式电话费相差__________元.11.为了促进节能减排，倡导节约用电，某市将实行居民生活用电阶梯电价方案，图中折线反映了每户每月用电电费y(元)与用电量x(度)间的函数关系式.(1)根据图象，阶梯电价方案分为三个档次，填写下表：档次第一档第二档第三档每月用电量x(度)0＜x≤140(2)小明家某月用电120度，需交电费__________元；(3)求第二档每月电费y(元)与用电量x(度)之间的函数关系式；(4)在每月用电量超过230度时，每多用1度电要比第二档多付电费M元，小刚家某月用电290度，交电费153元，求M的值.参考答案预习练习1-17.4预习练习2-1 D2-2大于41.A2.723.(1)当0≤x≤20时，y与x之间的函数表达式为：y=2x(0≤x≤20)；当x＞20时，y与x之间的函数表达式为：y=2.8(x-20)＋40=2.8x-16(x＞20)；(2)∵小颖家四月份、五月份分别交水费45.6元、38元，∴小颖家四月份用水超过20吨，五月份用水没有超过20吨.∴45.6=2.8(x1-20)＋40，38=2x2.∴x1=22,x2=19.∵22-19=3，∴小颖家五月份比四月份节约用水3吨.4.C5.D6.B7.或8.（1）s=10t（2）9.根据图形可得：甲的速度是=8(米/秒)，乙的速度是：=7(米/秒)，∴根据题意得：100-×7=12.5(米).当甲跑到终点时，乙落后甲12.5米.答：当甲跑到终点时，乙落后甲12.5米.10.1011.（1）140＜x≤230x＞230（2）54(3)设第二档每月电费y(元)与用电量x(度)之间的函数关系式为：y=ax+c，将(140，63)，(230，108)代入，得解得则第二档每月电费y(元)与用电量x(度)之间的函数关系式为：y=x-7(140＜x≤230).(4)根据图象可得出：用电230度，需要付费108元，用电140度，需要付费63元，故108-63=45(元)，230-140=90(度)，45÷90=0.5(元)，则第二档电费为0.5元/度；∵小刚家某月用电290度，交电费153元，290-230=60(度)，153-108=45(元)，45÷60=0.75(元)，M=0.75-0.5=0.25.答：M的值为0.25.。
一次函数的图象专题练习题(最新版) 含答案
一次函数的图象专题练习题1．画函数图象的方法．可以概括为_______，__ __，__ __三步，通常称为__ __．2．如果点M 在函数y ＝x －1的图象上，则M 点的坐标可以是( )A ．(－1，0)B ．(0，1)C ．(1，0)D ．(1，－1)3．(1)若点A(a ，－3)在函数y ＝－3x的图象上，则a ＝____； (2)下列各点M (1，2)，N (3，32)，P (1，－1)，Q (－2，－4)中，在函数y ＝2x x ＋1的图象上的点是__________. 4. 小明骑自行车上学，开始以正常速度匀速行驶，但行至中途自行车出了故障，只好停下来修车，车修好后，因怕耽误上课，加快了骑车速度，下面是小明离家后他到学校剩下的路程s 关于时间t 的函数图象，那么符合小明行驶情况的图象大致是( )5. 小明的父亲从家走了20分钟到一个离家900米的书店，在书店看了10分钟书后，用15分钟返回家，下列图中表示小明的父亲离家的距离与时间的函数图象是( )6. 某星期六上午，小明从家出发跑步去公园，在公园停留了一会儿打车回家．图中折线表示小明离开家的路程y(米)和所用时间x(分)之间的函数关系，则下列说法中错误的是()A．小明在公园休息了5分钟B．小明乘出租车用了17分C．小明跑步的速度为180米/分D．出租车的平均速度是900米/分7. 一段笔直的公路AC长20千米，途中有一处休息点B，AB长15千米，甲、乙两名长跑爱好者同时从点A出发，甲以15千米/时的速度匀速跑至点B，原地休息半小时后，再以10千米/时的速度匀速跑至终点C；乙以12千米/时的速度匀速跑至终点C，下列选项中，能正确反映甲、乙两人出发后2小时内运动路程y(千米)与时间x(小时)函数关系的图象是()8. 李老师为锻炼身体一直坚持步行上下班．已知学校到李老师家总路程为2000米．一天，李老师下班后，以45米/分的速度从学校往家走，走到离学校900米时，正好遇到一个朋友，停下又聊了半小时，之后以110米/分的速度走回了家．李老师回家过程中，离家的路程s(米)与所用时间t(分)之间的关系如图所示．(1)求a，b，c的值；(2)求李老师从学校到家的总时间．9. 如果两个变量x，y之间的函数关系如图，则函数值y的取值范围是() A．－3≤y≤3 B．0≤y≤2C．1≤y≤3 D．0≤y≤310. 如图是甲、乙两车在某时段速度随时间变化的图象，下列结论错误的是()A．乙前4秒行驶的路程为48米B．在0到8秒内甲的速度每秒增加4米/秒C．两车到第3秒时行驶的路程相等D．在4至8秒内甲的速度都大于乙的速度11. 甲骑摩托车从A地去B地，乙开汽车从B地去A地，同时出发，匀速行驶，各自到达终点后停止，设甲、乙两人间距离为s(单位：千米)，甲行驶的时间为t(单位：小时)，s与t之间的函数关系如图所示，有下列结论：①出发1小时时，甲、乙在途中相遇；②出发1.5小时时，乙比甲多行驶了60千米；③出发3小时时，甲、乙同时到达终点；④甲的速度是乙速度的一半．其中，正确结论的个数是()A．4B．3C．2D．112. 有一个水箱，它的容积是500升，水箱内原有水200升，现需将水箱注满，已知每分钟注入水10升．(1)写出水箱内水量Q(升)与时间t(分)的函数关系式；(2)求自变量t的取值范围；(3)画出函数的图象．13.如图，在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG，动点P从点A出发，沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止(不含点A和点B)，则△ABP的面积S随着时间t变化的函数图象大致是()14. 如图①，底面积为30 cm2的空圆柱形容器内水平放置着由两个实心圆柱组成的“几何体”，现向容器内匀速注水，注满为止，在注水过程中，水面高度h(cm)与注水时间t(s)之间的关系如图②所示．请根据图中提供的信息，解答下列问题：(1)圆柱形容器的高为____cm，匀速注水的水流速度为____cm3/s；(2)若“几何体”的下方圆柱的底面积为15 cm2，求“几何体”上方圆柱的高和底面积．答案：1. 描点 连线 描点法2. C3. (1) 1 (2) 点N4. D5. B6. B7. A8. (1)李老师停留地点离他家路程为：2000－900＝1100(米)，900÷45＝20(分)．a ＝20，b ＝1100，c ＝20＋30＝50 (2)20＋30＋1100110＝60(分)．答：李老师从学校到家共用60分钟 9. D10. C11. B 点拨：①②④正确12. (1)Q ＝200＋10t (2)令200≤Q≤500，则0≤t≤30 (3)图略13. B14. (1) 14 5(2) “几何体”下方圆柱的高为a ，则a·(30－15)＝18×5，解得a ＝6，所以“几何体”上方圆柱的高为11 cm－6 cm ＝5 cm ，设“几何体”上方圆柱的底面积为S cm 2，根据题意得5(30－S )＝5×(24－18)，解得S ＝24，即“几何体”上方圆柱的底面积为24 cm 2。
2024学年九年级中考数学专题复习：行程问题(一次函数的综合实际应用)(提升篇)(含答案)
2024学年九年级中考数学专题复习：行程问题（一次函数的综合实际应用）姓名：___________班级：___________考号：___________1．一列快车从甲地驶往乙地，一列慢车从乙地驶往甲地，两车同时出发，图中的折线表示两车之间距离()kmy与慢车行驶时间()h x之间的函数关系图象，请根据图象提供的信息回答：（1）快车的速度是______km/h．（2）求线段BC所表示的函数关系式．（3）若在第一列快车与慢车相遇时，第二列快车从乙地出发驶往甲地，速度与第一列快车相同，直接写出第二列快车出发多长时间与慢车相距200km．2．A、B两地相距60km，甲从A地去B地，乙从B地去A地，图中12，分别表示甲、乙l l两人离B地的距离y（km）与甲出发时间x（h）的函数关系图象．（1）求点A的坐标，并说明其实际意义；（2）甲出发多少时间，两人之间的距离恰好相距5km；（3）若用y3（km）表示甲、乙两人之间的距离，请在坐标系（图3）中画出y3（km）关于时间x（h）的函数关系图象，注明关键点的数据．3．快车甲和慢车乙分别从A、B两站同时出发，相向而行．快车到达B站后，停留1小时，然后原路原速返回A站，慢车到达A站即停运休息．下图表示的是两车之间的距离y（千米）与行驶时间x（小时）的函数图象．请结合图象信息．解答下列问题：（1）直接写出快、慢两车的速度及A、B两站间的距离；（2）求快车从B返回A站时，y与x之间的函数关系式；（3）出发几小时，两车相距200千米？请直接写出答案．4．甲、乙两人从相距4千米的两地同时、同向出发，乙每小时走4千米，小狗随甲一起同向出发，小狗追上乙的时候它就往甲这边跑，遇到甲时又往乙这边跑，遇到乙的时候再往甲这边跑…就这样一直匀速跑下去．如图，折线A B C--，A D E--分别表示甲、小狗在行进过程中，y与甲行进时间x(h)之间的部分函数图象．离乙的路程()km(1)求AB所在直线的函数解析式；(2)小狗的速度为______km/h；求点E的坐标；(3) 小狗从出发到它折返后第一次与甲相遇的过程中，求x为何值时，它离乙的路程与离甲的路程相等？5．甲、乙两地高速铁路建设成功，一列动车从甲地开往乙地，一列普通列车从乙地开往甲地，两车均匀速行驶并同时出发．设普通列车行驶的时间为x（小时），两车之间的距离为y（千米）．图中的折线表示y与x之间的函数关系图像．求：(1)甲、乙两地相距______千米；(2)求动车和普通列车的速度；(3)求C点坐标和直线CD解析式；(4)求普通列车行驶多少小时后，两车相距1000千米．6．甲、乙两车分别从A，B两地同时出发，匀速行驶，先相向而行．途中乙车因故停留1小时，然后以原速继续向A地行驶，甲车到达B地后，立即按原路原速返回A地（甲车掉头的时间忽略不计），到达A地后停止行驶，原地休息；甲、乙两车距B地的路程y（千米）与所用时间x （时）之间的函数图象如图，请结合图象信息解答下列问题：(1)乙车的速度为千米/时，在图中的（）内应填上的数是．(2)求甲车从B地返回A地的过程中，y与x的函数关系式．(3)两车出发后几小时相距120千米，请直接写出答案：时．7．甲、乙两人从A地前往B地，先到终点的人在原地休息．已知甲先出发30s后，乙才出发．在运动过程中，甲、乙两人离A地的距离分别为1y（单位：m）、2y（单位：m），都是甲出发时间x（单位：s）的函数，它们的图象如图①．设甲的速度为1v m/s，乙的速度为2v m/s．(1)12:v v=______，=a______；(2)求2y与x之间的函数表达式；(3)在图②中画出甲、乙两人之间的距离s（单位：m）与甲出发时间x（单位：s）之间的函数图象．8．小明从学校出发，匀速骑行前往距离学校2400米的图书馆，小明出发的同时，同学小阳以每分钟80米的速度从图书馆沿同一条道路步行回学校，两人距离学校的路程y（单位：米）与小明从学校出发的时间x（单位：分钟）的函数图象如图所示．(1)点C的坐标为_________；(2)求直线BC的表达式；(3)若小明在图书馆停留7分钟后沿原路按原速返回，请补全小明距离学校的路程y与x的函数图象；(4)在（3）的基础上，小明能否在返校途中追上小阳？若能，请计算此时两人与学校之间的距离；若不能，请说明理由．9．如图，已知：平面直角坐标系中，正比例函数y＝kx（k≠0）的图象经过点A（﹣2，﹣2），点B是第二象限内一点，且点B的横、纵坐标分别是一元二次方程x2﹣36＝0的两个根．过点B作BC⊥x轴于点C．（1）直接写出k的值和点B的坐标：k＝；B（，）；（2）点P从点C出发，以每秒1个单位长度的速度沿x轴向右运动，设运动时间为t，若△BPO 的面积是S，试求出S关于t的函数解析式（直接写出t的取值范围）（3）在（2）的条件下，当S＝6时，以PQ为一边向直线PQ下方作正方形PQRS，求点R 的坐标．10．甲、乙两车从A地出发，匀速驶向B地．甲车以80km/h的速度行驶1h后，乙车才沿相同路线行驶，乙车先到达B地并停留1h后，再以原速按原路返回，直至与甲车相遇．在此过程中，两车之间的距离y（km）与乙车行驶时间x（h）之间的函数关系如图所示．根据图像回答下列问题：（1）乙车行驶小时追上了甲车．（2）乙车的速度是；（3）m=；（4）点H的坐标是；（5）n=．11．已知矩形ABCD中，AB＝4米，BC＝6米，E为BC中点，动点P以2米/秒的速度从A 出发，沿着△AED的边，按照A→E→D→A顺序环行一周，设P从A出发经过x秒后，△ABP 的面积为y（平方米），求y与x间的函数关系式．12．某兴趣小组利用计算机进行电子虫运动实验．如图1，在相距100个单位长度的线段AB 上，电子虫甲从端点A出发，匀速往返于端点A、B之间，电子虫乙同时从端点B出发，设定不低于甲的速度匀速往返于端点B、A之间．他们到达端点后立即转身折返，用时忽略不计．兴趣小组成员重点探究了甲、乙迎面相遇的情况，这里的“迎面相遇”包括面对面相遇、在端点处相遇这两种．设甲、乙第一次迎面相遇时，相遇地点与点A之间的距离为x个单位长度，他们第二次迎面相遇时，相遇地点与点A之间的距离为y个单位长度．(1)请直接写出：当x＝20时，y的值为_________；当x＝40时，y的值为________；(2)兴趣小组成员发现了y与x的函数关系，并画出了部分函数图像（如图2中的线段OM，但不包括点O，因此点O用空心画出）①请直接写出：a＝_______；②分别求出各部分图像对应的函数解析式，并在图2中补全函数图像，标出关键点的坐标；(2)小黄在距离学校多少米处遭遇堵车？从小黄遇到堵车到小吴追上小黄用了多少时间？(3)小吴和小黄何时相距520m？15．甲、乙两人计划8：00一起从学校出发，乘坐班车去博物馆参观，乙乘坐班车准时出发，但甲临时有事没赶上班车，8：45甲沿相同的路线自行驾车前往，结果比乙早1小时到达．甲、乙两人离学校的距离y（千米）与甲出发时间x（小时）的函数关系如图所示．（1）点A的实际意义是什么？（2）求甲、乙两人的速度；（3）求OC和BD的函数关系式；（4）求学校和博物馆之间的距离．16．甲乙两人沿相同的路线同时登山甲、乙两人距地面的高度y（米）与登山时间x（分钟）之间的函数图象如图所示，根据图象所提供的信息解答下列问题：（1）甲距地面的高度y（米）与登山时间x（分）之间的函数关系式为：y 甲．（2）若乙提速后，乙的速度是甲登山速度的3倍，登山多长时间时，乙追上了甲?此时乙距A 地的高度为多少米？答案：21200 430v=15 6v∴=⨯30 a∴=⨯。
一次函数实际应用(带解析)
一次函数实际应用（解析版）1．已知A、B两地之间有一条长270千米的公路．甲、乙两车同时出发，甲车以60千米/时的速度沿此公路从A 地匀速开往B地，乙车从B地沿此公路匀速开往A地，两车分别到达目的地后停止．甲、乙两车相距的路程y（千米）与甲车的行驶时间x（时）之间的函数关系如图所示．（1）乙车的速度为千米/时，a=，b=（2）求甲、乙两车相遇后y与x之间的函数关系式．（3）当甲车到达距B地70千米处时，求甲、乙两车之间的路程．2．（8.00分）某种水泥储存罐的容量为25立方米，它有一个输入口和一个输出口．从某时刻开始，只打开输入口，匀速向储存罐内注入水泥，3分钟后，再打开输出口，匀速向运输车输出水泥，又经过2.5分钟储存罐注满，关闭输入口，保持原来的输出速度继续向运输车输出水泥，当输出的水泥总量达到8立方米时，关闭输出口．储存罐内的水泥量y（立方米）与时间x（分）之间的部分函数图象如图所示．（1）求每分钟向储存罐内注入的水泥量．（2）当3≤x≤5.5时，求y与x之间的函数关系式．（3）储存罐每分钟向运输车输出的水泥量是立方米，从打开输入口到关闭输出口共用的时间为分钟．3．（8分）甲、乙两车间同时开始加工一批服装．从开始加工到加工完这批服装甲车间工作了9小时，乙车间在中途停工一段时间维修设备，然后按停工前的工作效率继续加工，直到与甲车间同时完成这批服装的加工任务为止．设甲、乙两车间各自加工服装的数量为y （件），甲车间加工的时间为x (时），y 与x 之间的函数图象如图所示．（1）甲车间每小时加工服装的件数为 件；这批服装的总件数为 件． （2）求乙车间维修设备后，乙车间加工服装的数量y 与x 之间的函数关系式． （3）求甲、乙两车间共同加工完1 000件服装时甲车间所用的时间．4.实验室里，水平桌面上有甲、乙、丙三个高都是10cm 的圆柱形容器（甲、丙的底面积相同），用两个相同的管子在容器的6cm 高度处连通（即管子底离容器底6cm ，管子的体积忽略不计），、现在三个容器中，只有甲中有水，水位高2cm ，如图①所示，若每分钟同时向乙、丙中注入相同量的水，到三个容器都注满水停止，乙、丙容器中的水位h （cm ）与注水时间t （min ）的图象如图②所示．（1）乙、丙两个容器的底面积之比为 ． （2）图②中a 的值为 ，b 的值为 ． （3）注水多少分钟后，乙与甲的水位相差2cm ？y (件)5.小明在练习操控航拍无人机，该型号无人机在上升和下落时的速度相同，设无人机的飞行高度为y （米），小明操控无人飞机的时间为x（分），y与x之间的函数图象如图所示．（1）无人机上升的速度为米/分，无人机在40米的高度上飞行了分．（2）求无人机下落过程中，y与x之间的函数关系式．（3）求无人机距地面的高度为50米时x的值．6.某加工厂为赶制一批零件，通过提高加工费标准的方式调动工人的积性．工人每天加工零件获得的加工费y（元）与加工个数x（个）之间的函数图像为折线OA-AB-BC，如图所示．（1）求工人一天加工费不超过20个时零件的加工费．（2）求40≤x≤60时y与x的函数关系式．（3）小王两天一共加工了60个零件，共得到加工费220元，在这两天中，小王一天加工的零件不足20个，求小王第一天加工零件的个数。
一次函数图像应用题(带解析版答案)
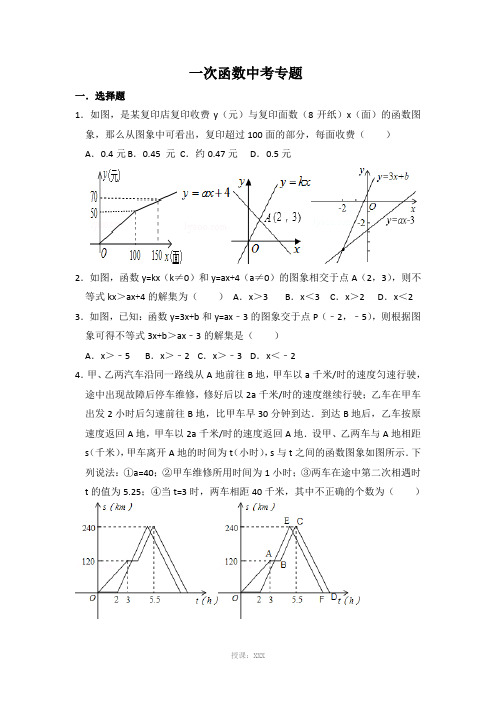
一次函数中考专题一．选择题1．如图，是某复印店复印收费y（元）与复印面数（8开纸）x（面）的函数图象，那么从图象中可看出，复印超过100面的部分，每面收费（）A．0.4元 B．0.45 元C．约0.47元D．0.5元2．如图，函数y=kx（k≠0）和y=ax+4（a≠0）的图象相交于点A（2，3），则不等式kx＞ax+4的解集为（）A．x＞3 B．x＜3 C．x＞2 D．x＜2 3．如图，已知：函数y=3x+b和y=ax﹣3的图象交于点P（﹣2，﹣5），则根据图象可得不等式3x+b＞ax﹣3的解集是（）A．x＞﹣5 B．x＞﹣2 C．x＞﹣3 D．x＜﹣24．甲、乙两汽车沿同一路线从A地前往B地，甲车以a千米/时的速度匀速行驶，途中出现故障后停车维修，修好后以2a千米/时的速度继续行驶；乙车在甲车出发2小时后匀速前往B地，比甲车早30分钟到达．到达B地后，乙车按原速度返回A地，甲车以2a千米/时的速度返回A地．设甲、乙两车与A地相距s（千米），甲车离开A地的时间为t（小时），s与t之间的函数图象如图所示．下列说法：①a=40；②甲车维修所用时间为1小时；③两车在途中第二次相遇时t的值为5.25；④当t=3时，两车相距40千米，其中不正确的个数为（）A．0个B．1个 C．2个 D．3个【解答】①由函数图象，得a=120÷3=40故①正确，②由题意，得5.5﹣3﹣120÷（40×2），=2.5﹣1.5，=1．∴甲车维修的时间为1小时；故②正确，③如图：∵甲车维修的时间是1小时，∴B（4，120）．∵乙在甲出发2小时后匀速前往B地，比甲早30分钟到达．∴E（5，240）．∴乙行驶的速度为：240÷3=80，∴乙返回的时间为：240÷80=3，∴F（8，0）．设BC的解析式为y1=k1t+b1，EF的解析式为y2=k2t+b2，由图象，得，解得，，∴y1=80t﹣200，y2=﹣80t+640，当y1=y2时，80t﹣200=﹣80t+640，t=5.25．∴两车在途中第二次相遇时t的值为5.25小时，故弄③正确，④当t=3时，甲车行的路程为120km，乙车行的路程为80×（3﹣2）=80km，∴两车相距的路程为：120﹣80=40千米，故④正确，故选：A．5．甲、乙两车从A地驶向B地，并以各自的速度匀速行驶，甲车比乙车早行驶2h，并且甲车途中休息了0.5h，如图是甲乙两车行驶的距离y（km）与时间x（h）的函数图象．则下列结论：（1）a=40，m=1；（2）乙的速度是80km/h；（3）甲比乙迟h到达B地；（4）乙车行驶小时或小时，两车恰好相距50km．正确的个数是（）A．1 B．2 C．3 D．4【解答】（1）由题意，得m=1.5﹣0.5=1．120÷（3.5﹣0.5）=40（km/h），则a=40，故（1）正确；（2）120÷（3.5﹣2）=80km/h（千米/小时），故（2）正确；（3）设甲车休息之后行驶路程y（km）与时间x（h）的函数关系式为y=kx+b，由题意，得解得：∴y=40x﹣20，根据图形得知：甲、乙两车中先到达B地的是乙车，把y=260代入y=40x﹣20得，x=7，∵乙车的行驶速度80km/h，∴乙车行驶260km需要260÷80=3.25h，∴7﹣（2+3.25）=h，∴甲比乙迟h到达B地，故（3）正确；（4）当1.5＜x≤7时，y=40x﹣20．设乙车行驶的路程y与时间x之间的解析式为y=k'x+b'，由题意得解得：∴y=80x﹣160．当40x﹣20﹣50=80x﹣160时，解得：x=．当40x﹣20+50=80x﹣160时，解得：x=．∴﹣2=，﹣2=．所以乙车行驶或小时，两车恰好相距50km，故（4）错误．故选（C）二．填空题（共3小题）6．如图，已知A1，A2，A3，…，A n是x轴上的点，且OA1=A1A2=A2A3=…=A n A n+1=1，分别过点A1，A2，A3，…，A n+1作x 轴的垂线交一次函数的图象于点B1，B2，B3，…，B n+1，连接A1B2，B1A2，A2B3，B2A3，…，A n B n+1，B n A n+1依次产生交点P1，P2，P3，…，P n，则P n 的坐标是（n+，）．【解答】由已知得A1，A2，A3，…的坐标为：（1，0），（2，0），（3，0），…，又得作x轴的垂线交一次函数y=x的图象于点B1，B2，B3，…的坐标分别为（1，），（2，1），（3，），…．由此可推出A n，B n，A n+1，B n+1四点的坐标为（n，0），（n ，），（n+1，0），（n+1，）．所以得直线A n B n+1和A n+1B n的直线方程分别为解得故答案为：（n+，）．7. 下图是护士统计一病人的体温变化图，这位病人中午12时的体温约为℃．8．某高速铁路即将在2019年底通车，通车后，重庆到贵阳、广州等地的时间将大大缩短．5月初，铁路局组织甲、乙两种列车在该铁路上进行试验运行，现两种列车同时从重庆出发，以各自速度匀速向A地行驶，乙列车到达A地后停止，甲列车到达A地停留20分钟后，再按原路以另一速度匀速返回重庆，已知两种列车分别距A地的路程y（km）与时间x（h）之间的函数图象如图所示．当乙列车到达A地时，则甲列车距离重庆km．【解答】设乙列车的速度为xkm/h，甲列车以ykm/h的速度向A地行驶，到达A 地停留20分钟后，以zkm/h的速度返回重庆，则根据3小时后，乙列车距离A地的路程为240，而甲列车到达A地，可得3x+240=3y，①根据甲列车到达A地停留20分钟后，再返回重庆并与乙列车相遇的时刻为4小时，可得x+（1﹣）z=240，②根据甲列车往返两地的路程相等，可得（﹣3﹣）z=3y，③由①②③，可得x=120，y=200，z=180，∴重庆到A地的路程为3×200=600（km），∴乙列车到达A地的时间为600÷120=5（h），∴当乙列车到达A地时，甲列车距离重庆的路程为600﹣（5﹣3﹣）×180=300（km），故答案为：300．三．解答题（共10小题）9．为倡导绿色出行，某共享单车近期登陆徐州，根据连续骑行时长分段计费：骑行时长在2h以内（含2h）的部分，每0.5h计费1元（不足0.5h按0.5h计算）；骑行时长超出2h的部分，每小时计费4元（不足1h按1h计算）．根据此收费标准，解决下列问题：（1）连续骑行5h，应付费多少元？（2）若连续骑行xh（x＞2且x为整数）需付费y元，则y与x的函数表达式为；（3）若某人连续骑行后付费24元，求其连续骑行时长的范围．【解答】（1）当x=5时，y=2×2+4×（5﹣2）=16，∴应付16元；（2）y=4（x﹣2）+2×2=4x﹣4；故答案为：y=4x﹣4；（3）当y=24，24=4x﹣4，x=7，∴连续骑行时长的范围是：6＜x≤7．10．如图，“十一”期间，小明一家乘坐高铁前往某市旅游，计划第二天租用新能源汽车自驾出游．根据以上信息，解答下列问题：（1）设租车时间为x小时，租用甲公司的车所需费用为y1元，租用乙公司的车所需费用为y2元，分别求出y1，y2关于x的函数表达式；（2）当租车时间为多少小时时，两种方案所需费用相同；（3）根据（2）的计算结果，结合图象，请你帮助小明选择怎样的出游方案更合算．【解答】（1）设y1=k1x+80，把点（1，95）代入，可得：95=k1+80，解得k1=15，∴y1=15x+80（x≥0）；设y2=k2x，把（1，30）代入，可得30=k2，即k2=30，∴y2=30x（x≥0）；（2）当y1=y2时，15x+80=30x，解得x=；答：当租车时间为小时时，两种方案所需费用相同；（3）由（2）知：当y1=y2时，x=；当y1＞y2时，15x+80＞30x，解得x＜；当y1＜y2时，15x+80＜30x，解得x＞；∴当租车时间为小时，任意选择其中的一个方案；当租车时间小于小时，选择方案二合算；当租车时间大于小时，选择方案一合算．11．如表给出A、B、C三种上网的收费方式：收费方式月使用费/元包时上网时间/小时超时费/（元/分钟）A30250.05B50500.05C120不限时（1）假设月上网时间为x小时，分别直接写出方式A、B、C三种上网方式的收费金额分别为y1、y2、y3与x的函数关系式，并写出自变量的范围（注意结果要化简）；（2）给出的坐标系中画出这三个函数的图象简图；（3）结合函数图象，直接写出选择哪种上网方式更合算．【分析】从题意可知，本题中的一次函数又是分段函数，关键是理清楚自变量的取值范围，由取值来确定函数值，从而作出函数图象．【解答】（1）收费方式A：y=30 （0≤x≤25），y=30+3x （x＞25）；收费方式B：y=50 （0≤x≤50），y=50+3x （x＞50）；收费方式C：y=120 （0≤x）；（2）函数图象如图：（3）由图象可知，上网方式C更合算。
初三数学中考复习《一次函数的应用》专项训练（含答案）
初三数学中考复习 一次函数的应用 专项训练1. 大剧院举行专场音乐会，成人票每张20元，学生票每张5元，暑假期间，为了丰富广生的业余文化生活，大剧院制定了两种优惠方案，方案①：购买一张成人票赠送一张学生票；方案②：按总价的90%付款，某校有4名老师与若干名(不少于4人)学生听音乐会．(1)设学生人数为x(人)，付款总金额为y(元)，分别求出两种优惠方案中y 与x 的函数关系式；(2)请计算并确定出最节省费用的购票方案．2. 小李是某服装厂的一名工人，负责加工A ，B 两种型号服装，他每月的工作时间为22天，月收入由底薪和计件工资两部分组成，其中底薪900元，加工A 型服装1件可得20元，加工B 型服装1件可得12元．已知小李每天可加工A 型服装4件或B 型服装8件，设他每月加工A 型服装的时间为x 天，月收入为y 元． (1)求y 与x 的函数关系式；(2)根据服装厂要求，小李每月加工A 型服装数量应不少于B 型服装数量的35，那么他的月收入最高能达到多少元？3. 某汽车运输公司根据实际需要计划购买大、中型两种客车共20辆，已知大型客车每辆62万元，中型客车每辆40万元，设购买大型客车x(辆)，购车总费用为y(万元)．(1)求y与x的函数关系式；(不要求写出自变量x的取值范围)(2)若购买中型客车的数量少于大型客车的数量，请你给出一种费用最省的方案，并求出该方案所需费用．4. 昨天早晨7点，小明乘车从家出发，去西安参加中学生科技创新大赛，赛后，他当天按原路返回，如图，是小明昨天出行的过程中，他距西安的距离y(千米)与他离家的时间x(时)之间的函数图象．根据下面图象，回答下列问题：(1)求线段AB所表示的函数关系式；(2)已知昨天下午3点时，小明距西安112千米，求他何时到家？5. 胡老师计划组织朋友暑假去革命圣地两日游，经了解，现有甲、乙两家旅行社比较合适，报价均为每人640元，且提供的服务完全相同，针对组团两日游的游客，甲旅行社表示，每人都按八五折收费；乙旅行社表示，若人数不超过20人，每人都按九折收费，超过20人，则超出部分每人按七五折收费，假设组团参加甲、乙两家旅行社两日游的人数均为x人．(1)请分别写出甲、乙两家旅行社收取组团两日游的总费用y(元)与x(人)之间的函数关系式；(2)若胡老师组团参加两日游的人数共有32人，请你计算，在甲、乙两家旅行社中，帮助胡老师选择收取总费用较少的一家．6. 科学研究发现，空气含氧量y(克/立方米)与海拔高度x(米)之间近似地满足一次函数关系．经测量，在海拔高度为0米的地方，空气含氧量约为299克/立方米；在海拔高度为2000米的地方，空气含氧量约为235克/立方米．(1)求出y与x的函数关系式；(2)已知某山的海拔高度为1200米，请你求出该山山顶处的空气含氧量约为多少？7. 小李从西安通过某快递公司给在南昌的外婆寄一盒樱桃，快递时，他了解到这个公司除收取每次6元的包装费外，樱桃不超过1 kg收费22元，超过1 kg，则超出部分按每千克10元加收费用．设该公司从西安到南昌快递樱桃的费用为y(元)，所寄樱桃为x(kg)．(1)求y与x之间的函数关系式；(2)已知小李给外婆快寄了2.5 kg樱桃，请你求出这次快寄的费用是多少元？8. “十一节”期间，申老师一家自驾游去了离家170千米的某地，下面是他们离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象．(1)求他们出发半小时时，离家多少千米？(2)求出AB段图象的函数表达式；(3)他们出发2小时时，离目的地还有多少千米？9. 由于持续高温和连日无雨，某水库的蓄水量随时间的增加而减少，已知原有蓄水量y1(万m3)与干旱持续时间x(天)的关系如图中线段l1所示，针对这种干旱情况，从第20天开始向水库注水，注水量y2(万m3)与时间x(天)的关系如图中线段l2所示(不考虑其他因素)．(1)求原有蓄水量y1(万m3)与时间x(天)的函数关系式，并求当x＝20时的水库总蓄水量；(2)求当0≤x≤60时，水库的总蓄水量y(万m3)与时间x(天)的函数关系式(注明x的范围)，若总蓄水量不多于900万m3为严重干旱，直接写出发生严重干旱时x 的范围．10. 周末，小芳骑自行车从家出发到野外郊游，从家出发0.5小时到达甲地，游玩一段时间后按原速前往乙地，小芳离家1小时20分钟后，妈妈驾车沿相同路线前往乙地，行驶10分钟时，恰好经过甲地，如图是她们距乙地的路程y(km)与小芳离家时间x(h)的函数图象．(1)小芳骑车的速度为____km/h，H点坐标为__________________；(2)小芳从家出发多少小时后被妈妈追上？此时距家的路程多远？(3)相遇后，妈妈载上小芳和自行车同时到达乙地(彼此交流时间忽略不计)，求小芳比预计时间早几分钟到达乙地？11. 根据卫生防疫部门要求，游泳池必须定期换水、清洗．某游泳池周五早上8：00打开排水孔开始排水，排水孔的排水速度保持不变，期间因清洗游泳池需要暂停排水，游泳池的水在11：30全部排完．游泳池内的水量Q(m3)和开始排水后的时间t(h)之间的函数图象如图所示，根据图象解答下列问题：(1)暂停排水需要多少时间？排水孔排水速度是多少？(2)当2≤t≤3.5时，求Q关于t的函数表达式．12. 小明和爸爸从家步行去公园，爸爸先出发一直匀速前行，小明后出发．家到公园的距离为2500 m，如图是小明和爸爸所走的路程s(m)与小明的步行时间t(min)的函数图象．(1)直接写出小明所走路程s与时间t的函数关系式；(2)小明出发多少时间与爸爸第三次相遇？(3)在速度都不变的情况下，小明希望比爸爸早20 min到达公园，则小明在步行过程中停留的时间需作怎样的调整？13. 某物流公司引进A，B两种机器人用来搬运某种货物，这两种机器人充满电后可以连续搬运5小时，A种机器人于某日0时开始搬运，过了1小时，B种机器人也开始搬运，如图，线段OG表示A种机器人的搬运量y A(千克)与时间x(时)的函数图象，根据图象提供的信息，解答下列问题：(1)求y B关于x的函数解析式；(2)如果A，B两种机器人连续搬运5个小时，那么B种机器人比A种机器人多搬运了多少千克？14. 某学校计划组织500人参加社会实践活动，与某公交公司接洽后，得知该公司有A，B型两种客车，它们的载客量和租金如表所示：A型客车B型客车载客量(人/辆) 45 28租金(元/辆) 400 250经测算，租用A，B型客车共13辆较为合理，设租用A型客车x辆，根据要求回答下列问题：(1)用含x的代数式填写下表：车辆数(辆) 载客量(人) 租金(元)A型客车x 45x 400xB型客车13－x ____________ ______________ (2)采用怎样的租车方案可以使总的租车费用最低，最低为多少？15. 为了节约资源，科学指导居民改善居住条件，小强向房管部门提出了一个购买商品房的政策性方案：人均住房面积(平方米) 单价(万元/平方米)不超过30(平方米)部分0.4超过30平方米部分0.9设一个3口之家购买商品房的人均面积为x平方米，缴纳房款y万元．(1)请求出y关于x的函数关系式；(2)若某3口之家欲购买120平方米的商品房，求其应缴纳的房款．16. 保障我国海外维和官兵的生活，现需通过A港口、B港口分别运送100吨和50吨生活物资．已知该物资在甲仓库存有80吨，乙仓库存有70吨，若从甲、乙两仓库运送物资到港口的费用(元/吨)如表所示：运费(元/吨)港口甲库乙库A港14 20B港10 8(1)设从甲仓库运送到A港口的物资为x吨，求总运费y(元)与x(吨)之间的函数关系式，并写出x 的取值范围；(2)求出最低费用，并说明费用最低时的调配方案． 参考答案：1. 解：(1)按优惠方案①可得y 1＝20×4＋(x －4)×5＝5x ＋60(x≥4)，按优惠方案②可得y 2＝(5x ＋20×4)×90%＝4.5x ＋72(x≥4) (2)因为y 1－y 2＝0.5x －12(x≥4)，①当y 1－y 2＝0时，得0.5x －12＝0，解得x ＝24，∴当x ＝24时，两种优惠方案付款一样多．②当y 1－y 2＜0时，得0.5x －12＜0，解得x ＜24，∴4≤x ＜24时，y 1＜y 2，优惠方案①付款较少．③当y 1－y 2＞0时，得0.5x －12＞0，解得x ＞24，当x ＞24时，y 1＞y 2，优惠方案②付款较少2. 解：(1)由题意得y ＝20×4x＋12×8×(22－x)＋900，即y ＝－16x ＋3012 (2)依题意得4x≥35×8×(22－x)，∴x≥12.在y ＝－16x ＋3012中，∵－16＜0，∴y 随x 的增大而减小．∴当x ＝12时，y 取最大值，此时y ＝－16×12＋3012＝2820.答：当小李每月加工A 型服装12天时，月收入最高，可达2820元 3. 解：(1)因为购买大型客车x 辆，所以购买中型客车(20－x)辆．y ＝62x ＋40(20－x)＝22x ＋800(2)依题意得20－x ＜x.解得x ＞10，∵y ＝22x ＋800，y 随着x 的增大而增大，x 为整数，∴当x ＝11时，购车费用最省，为22×11＋800＝1042(万元)，此时需购买大型客车11辆，中型客车9辆，答：购买大型客车11辆，中型客车9辆时，购车费用最省为1042万元4. 解：(1)设线段AB 所表示的函数关系式为y ＝kx ＋b ，依题意有⎩⎪⎨⎪⎧b ＝192，2k ＋b ＝0，解得⎩⎪⎨⎪⎧k ＝－96，b ＝192.故线段AB 所表示的函数关系式为：y ＝－96x ＋192(0≤x≤2)(2)12＋3－(7＋6.6)＝1.4(小时)，112÷1.4＝80(千米/时)，(192－112)÷80＝1(小时)，3＋1＝4(时)．答：他下午4时到家 5. 解：(1)甲旅行社的总费用：y 甲＝640×0.85x＝544x ；乙旅行社的总费用：当0≤x≤20时，y乙＝640×0.9x＝576x ；当x ＞20时，y 乙＝640×0.9×20＋640×0.75(x－20)＝480x ＋1920(2)当x ＝32时，y 甲＝544×32＝17408(元)，y 乙＝480×32＋1920＝17280，因为y 甲＞y 乙，所以胡老师选择乙旅行社6. 解：(1)设y ＝kx ＋b(k≠0)，则⎩⎪⎨⎪⎧b ＝299，2000k ＋b ＝235，解得⎩⎪⎨⎪⎧k ＝－4125，b ＝299，∴y＝－4125x ＋299(2)当x ＝1200时，y ＝－4125×1200＋299＝260.6(克/立方米)，答：该山山顶处的空气含氧量约为260.6克/立方米7. 解：(1)由题意得，当0＜x≤1时，y ＝22＋6＝28；当x ＞1时，y ＝28＋10(x－1)＝10x ＋18.∴y＝⎩⎪⎨⎪⎧28（0＜x≤1）10x ＋18（x ＞1）(2)当x ＝2.5时，y ＝10×2.5＋18＝43，∴这次快寄的费用是43元8. 解：(1)设OA 段图象的函数表达式为y ＝kx ，∵当x ＝1.5时，y ＝90，∴1.5k ＝90，∴k＝60，∴y＝60x(0≤x≤1.5)，∴当x ＝0.5时，y ＝60×0.5＝30，故他们出发半小时时，离家30千米(2)设AB 段图象的函数表达式为y ＝k′x＋b ，∵A(1.5，90)，B(2.5，170)在AB上，∴⎩⎪⎨⎪⎧1.5k′＋b ＝90，2.5k′＋b ＝170，解得⎩⎪⎨⎪⎧k′＝80，b ＝－30，∴y＝80x －30(1.5≤x≤2.5) (3)∵当x ＝2时，y ＝80×2－30＝130，∴170－130＝40，故他们出发2小时时，离目的地还有40千米9. 解：(1)设y 1＝k 1x ＋b 1，把(0，1200)和(60，0)代入到y 1＝k 1x ＋b 1，得⎩⎪⎨⎪⎧b 1＝1200，60k 1＋b 1＝0，解得⎩⎪⎨⎪⎧k 1＝－20，b 1＝1200.∴y 1＝－20x ＋1200，当x ＝20时，y 1＝－20×20＋1200＝800(2)设y 2＝k 2x ＋b 2，把(20，0)和(60，1000)代入到y 2＝k 2x ＋b 2中，得⎩⎪⎨⎪⎧20k 2＋b 2＝0，60k 2＋b 2＝1000， 解得⎩⎪⎨⎪⎧k 2＝25，b 2＝－500，∴y 2＝25x －500，当0≤x≤20时，y ＝－20x ＋1200，当20＜x≤60时，y ＝y 1＋y 2＝－20x ＋1200＋25x －500＝5x ＋700，y≤900，则5x ＋700≤900，x≤40，当y 1＝900时，900＝－20x ＋1200，x ＝15，∴发生严重干旱时x 的范围为15≤x≤4010. 解：(1)由函数图象可以得出，小芳家距离甲地的路程为10 km ，花费时间为0.5 h ，故小芳骑车的速度为：10÷0.5＝20(km/h)，由题意可得出，点H 的纵坐标为20，横坐标为：43＋16＝32，故点H 的坐标为(32，20)(2)设直线AB 的解析式为：y 1＝k 1x ＋b 1，将点A(0，30)，B(0.5，20)代入得：y 1＝－20x ＋30，∵AB∥CD，∴设直线CD 的解析式为：y 2＝－20x ＋b 2，将点C(1，20)代入得：b 2＝40，故y 2＝－20x ＋40，设直线EF 的解析式为：y 3＝k 3x ＋b 3，将点E(43，30)，H(32，20)代入得：k 3＝－60，b 3＝110，∴y 3＝－60x ＋110，解方程组⎩⎪⎨⎪⎧y ＝－60x ＋110，y ＝－20x ＋40，得⎩⎪⎨⎪⎧x ＝1.75，y ＝5，∴点D 坐标为(1.75，5)，30－5＝25(km )，所以小芳出发1.75小时候被妈妈追上，此时距家25 km (3)将y ＝0代入直线CD 的解析式有：－20x ＋40＝0，解得x ＝2，将y ＝0代入直线EF 的解析式有：－60x ＋110＝0，解得x ＝116，2－116＝16(h )＝10(分钟)，故小芳比预计时间早10分钟到达乙地11. 解：(1)暂停排水需要的时间为：2－1.5＝0.5(小时)．∵排水时间为：3.5－0.5＝3(小时)，一共排水900 m 3，∴排水孔排水速度是：900÷3＝300(m 3/h ) (2)当2≤t≤3.5时，设Q 关于t 的函数表达式为Q ＝kt ＋b ，易知图象过点(3.5，0)．∵t ＝1.5时，排水300×1.5＝450，此时Q ＝900－450＝450(m 3)，∴(2，450)在直线Q ＝kt ＋b 上．把(2，450)，(3.5，0)代入Q ＝kt ＋b ，得⎩⎪⎨⎪⎧2k ＋b ＝450，3.5k ＋b ＝0，解得⎩⎪⎨⎪⎧k ＝－300，b ＝1050，∴Q 关于t 的函数表达式为Q ＝－300t ＋105012. 解：(1)s ＝⎩⎪⎨⎪⎧ 50t （0≤t≤20），1000（20＜t≤30），50t －500（30＜t≤60）(2)设小明的爸爸所走的路程s 与小明的步行时间t 的函数关系式为：s ＝kt ＋b ，则⎩⎪⎨⎪⎧25k ＋b ＝1000，b ＝250，解得，⎩⎪⎨⎪⎧k ＝30，b ＝250，则小明的爸爸所走的路程与小明的步行时间的关系式为：s ＝30t ＋250，当50t －500＝30t ＋250，即t ＝37.5 min 时，小明与爸爸第三次相遇(3)30t ＋250＝2500，解得t ＝75，则小明的爸爸到达公园需要75 min ，∵小明到达公园需要的时间是60 min ，∴小明希望比爸爸早20 min 到达公园，则小明在步行过程中停留的时间需减少5 min13. 解：(1)设y B 关于x 的函数解析式为y B ＝kx ＋b(k≠0)．将点(1，0)，(3，180)代入得⎩⎪⎨⎪⎧k ＋b ＝0，3k ＋b ＝180.解得k ＝90，b ＝－90.所以y B 关于x 的函数解析式为y B ＝90x－90(1≤x≤6)(2)设y A 关于x 的解析式为y A ＝k 1x.根据题意得3k 1＝180.解得k 1＝60.所以y A ＝60x.当x ＝5时，y A ＝60×5＝300(千克)；x ＝6时，y B ＝90×6－90＝450(千克).450－300＝150(千克)．答：如果A ，B 两种机器人各连续搬运5小时，B 种机器人比A 种机器人多搬运了150千克14. (1) 28(13－x) 250(13－x)(2) 解：设租车的总费用为W 元，则有：W ＝400x ＋250(13－x)＝150x ＋3250.由已知得：45x＋28(13－x)≥500，解得：x≥8.∵在W＝150x＋3250中150＞0，∴当x＝8时，W取最小值，最小值为4450元．故租A型车8辆，B型车5辆时，总的租车费用最低，最低为4450元15. 解：(1)当0≤x≤30时，y＝3×0.4x＝1.2x；当x＞30时，y＝3×0.9×(x －30)＋3×0.4×30＝2.7x－45(2)由题意知：该3口之家人均住房面积为：120÷3＝40＞30，在y＝2.7x－45中，令x＝40，则y＝2.7×40－45＝63.∴应缴纳的房款为63万元16. 解：(1)设从甲仓库运x吨往A港口，则从甲仓库运往B港口的有(80－x)吨，从乙仓库运往A港口的有(100－x)吨，运往B港口的有50－(80－x)＝(x－30)吨，所以y＝14x＋20(100－x)＋10(80－x)＋8(x－30)＝－8x＋2560，x的取值范围是30≤x≤80(2)由(1)得y＝－8x＋2560，y随x的增大而减少，所以当x＝80时总运费最小，当x＝80时，y＝－8×80＋2560＝1920，此时方案为：把甲仓库的物资全部运往A港口，再从乙仓库运20吨往A港口，乙仓库余下的物资全部运往B港口。
2022-2023学年苏科版八年级数学上册《6-4用一次函数解决问题》解答题专题提升训练(附答案)
2022-2023学年苏科版八年级数学上册《6.4用一次函数解决问题》解答题专题提升训练（附答案）1．小明和爸爸进行登山锻炼，两人同时从山脚下出发，沿相同路线匀速上山，小明用8分钟登上山顶，此时爸爸距出发地280米，小明登上山顶立即按原路匀速下山，与爸爸相遇后，和爸爸一起以原下山速度返回出发地．小明、爸爸在锻炼过程中离出发地的路程y1（米），y2（米）与小明出发的时间x（分）的函数关系如图所示．（1）图中a＝，b＝；（2）小明上山的速度米/分；小明下山的速度米/分；爸爸上山的速度米/分．（3）小明的爸爸下山所用的时间．2．小李、小王两人从学校出发去图书馆，小李步行一段时间后，小王骑电动车沿相同路线行进，两人均匀速前行，他们的路程差s（米）与小李出发时间t（分）之间的函数关系如图所示．（1）请直接写出小李、小王两人的前行速度；（2）请直接写出小李、小王两人前行的路程y1（米），y2（米）与小李出发时间t（分）之间的函数关系式；（3）求小王出发多长时间，两人的路程差为240米．3．小刚家、学校、图书馆依次在一条直线上，小刚骑自行车匀速从学校到图书馆，到达图书馆还完书后，再以相同的速度原路返回家中，小刚离家的距离y（m）与他所用的时间x（min）的函数关系如图所示．（1）求小刚从图书馆返回家的过程中，y与x之间的关系式；（2）小刚出发35分钟时，他离家有多远？4．如图，甲、乙两人分别从同一公路上的A、B两地同时出发骑车前往c地，两人行驶的路程y（km）与甲行驶的时间x（h）之间的关系如图所示，请根据图象所提供的信息解答下列问题：（1）A、B两地相距km，乙骑车的速度是km/h；（2）求甲在0≤x≤6的时间段内的函数关系式；（3）在0≤x≤6的时间段内，当x（h）为何值时甲、乙两人相距5千米．5．甲、乙两地相距300千米，一辆货车和一辆轿车先后从甲地出发向乙地．如图，线段OA 表示货车离甲地距离y（千米）与时间x（小时）之间的函数关系；折线BCD表示轿车离甲地距离y（千米）与x（小时）之间的函数关系．请根据图象解答下列问题：（1）货车的速度是km/h；轿车提速后的速度是km/h；（2）轿车到达乙地后，货车距乙地千米；（3）线段CD对应的函数解析式为；（4）货车从甲地出发后小时与轿车相遇．6．某移动通讯公司开设了两类通讯业务，A类收费标准为不管通话时间多长，使用者都应缴50元月租费，然后每通话1分钟，付0.4元；B类收费标准为用户不缴月租费，每通话1分钟，付话费0.6元，若一个月通讯x分钟，两种方式的费用分别为y A和y B元．（1）分别写出y A，y B与x之间的函数关系式；（2）某人估计一个月内通话时间为300分钟，应选哪种移动通讯方式合算些？请书写计算过程；（3）李师傅用的是A卡，他计算了一下，若是用B卡，他本月的话费将会比现在多100元，请算一下本月李师傅实际的话费是多少元？7．已知A、B两地相距120km，甲、乙两人沿同一条道路从A地到B地．l1、l2分别表示甲、乙两人离开A地的距离S（km）与时间t（h）之间的关系．请根据图象填空：（1）大约在甲出发h后，两人相遇，这时他们离B地km；（2）甲的速度是km/h；乙的速度是km/h；（3）l1对应的表达式为：，l2对应的表达式为：．8．甲、乙两车从A城出发匀速行驶至B城．在整个行驶过程中，甲、乙两车离开A城的距离y（千米）与甲车行驶的时间t（小时）之间的函数关系如图所示．（1）甲车出发小时后，乙车才出发；（2）甲车的速度为km/h，乙车的速度为km/h；（3）甲、乙两车经过小时后第一次相遇；（4）当t为何值时，甲、乙两车相距20千米．（直接写出t的值）9．随着春节临近，某儿童游乐场推出了甲、乙两种消费卡，其中，甲为按照次数收费，乙为收取办卡费用以后每次打折收费．设消费次数为x时，所需费用为y元，且y与x的函数关系如图所示．根据图中信息，解答下列问题．（1）分别求出选择这两种卡消费时，y关于x的函数表达式；（2）求出入园多少次时，两者花费一样？费用是多少？（3）洋洋爸准备了240元，请问选择哪种划算？10．甲、乙两车从A地出发，沿同一路线驶向B地．甲车先出发匀速驶向B地，40min后乙出发，匀速行驶一段时间后，在途中的货站装货耗时半小时．由于满载货物，为了行驶安全，速度减少了50km/h，结果与甲车同时到达B地，甲乙两车距A地的路程y（km）与乙车行驶时间x（h）之间的函数图象如图所示．（1）a的值是，甲的速度是km/h．（2）求线段EF所表示的y与x的函数关系式；（3）若甲乙两车距离不超过10km时，车载通话机可以进行通话，则两车在行驶过程中可以通话的总时长为多少小时？11．某商品共200吨，经市场调查，可采用批发、零售、冷库储藏后销售三种方式，并且按这三种方式销售，计划每吨的平均售价及成本如下表：销售方式批发零售储藏后销售售价/（元/吨）300045005500成本/（元/吨）200030003500若经过一段时间，商品按计划全部售出获得的总利润为y（元），其中零售x（吨），且零售量是批发量的一半．（1）求y与x之间的函数关系式；（2）由于受条件限制，经冷库储藏售出的商品数量最多为80吨，求该生产基地按计划全部售完商品获得的最大利润．12．为了传承中华优秀传统文化，增强文化自信，某中学举办了以“争做时代先锋少年”为主题的演讲比赛，并为获奖的同学颁发奖品．张老师去商店购买甲、乙两种笔记本作为奖品，已知该商店甲种笔记本的单价为5元/个，乙种笔记本的单价为3元/个，张老师准备购买甲、乙两种笔记本共100个．因张老师购买的数量多，实际付款时按原价的九折付款．设张老师购买x个甲种笔记本，购买这两种笔记本所需费用为y元．（1）求y与x之间的关系式；（2）若本次购买甲种笔记本的数量不少于乙种笔记本数量的3倍，为了使所花费用最低，应如何购买？最低费用是多少元？13．“中国海带之乡”霞浦县今年又迎来一个丰收年．某海带养殖专业村为保障养殖户收益，联系了村海带加工厂，收购养殖户每天收割的鲜海带．该加工厂主要以加工干海带和盐渍海带两种方式处理每天收购的30吨鲜海带，工厂现有12名工人，每位工人在同一天中只能选择一种加工方式．若生产干海带，每人每天可加工2吨鲜海带，每吨可获利250元；若加工盐渍海带，每人每天可加工0.6吨鲜海带，每吨可获利600元；每天加工不完的鲜海带直接续给鲍鱼养殖场作饲料．若安排所有的工人都加工干海带，则加工厂当天可获利6300元．（1）求加工不完的鲜海带直接卖给鲍鱼养殖场作饲料，每吨可获利多少元；（2）根据市场销售情况，该加工厂决定生产干海带的人数不超过盐渍海带人数的2倍．问加工厂如何安排工人，可使每天生产的利润最大？最大利润是多少元？14．学校计划组织七年级学生到“万州三峡移民纪念馆”参加“追寻先辈足迹，传承三峡精神”的活动．在此活动中，若每位老师带队14名学生，则还有10名学生没有老师带队；若每位老师带队15名学生，就有一位老师少带6名学生．（1）参加此次活动的老师和学生各多少名？（2）现计划租用两种客车共8辆，一辆甲型客车可以载35人，租金400元，一辆乙型客车可以载30人，租金320元．计划此次活动的租金总费用不超过3000元，学校共有哪几种租车方案？最少租车费用是多少？15．一条笔直的公路上依次有A、B、C三地，甲车从A地驶往C地，乙车从A地驶往B地，两车同时出发并以各自的速度匀速行驶．乙车中途因汽车故障停下来修理，修好后立即以原速的两倍继续前进到达B地；如图是甲、乙两车与A地的距离y（千米）与出发时间x（小时）之间的大致图象．（1）求B、C两地之间的距离；（2）什么时候乙追上甲；（3）当两车相距40千米时，甲车行驶了多长时间．16．复课第一天，马小虎同学从家出发，骑车匀速前往学校上学，出发几分钟后，爸爸发现马小虎的健康卡落在家里，于是骑车沿相同的路线匀速去追马小虎．爸爸刚出发2分钟，马小虎也发现自己健康卡落在家里，立刻原路原速骑车返回，2分钟后马小虎遇到爸爸，爸爸把健康表给马小虎后立即原路原速返家中，马小虎继续原路原速赶往学校．马小虎与爸爸相距的路程y（米）与马小虎出发的时间x（分）之间的关系如图所示（爸爸给马小虎健康卡的时间忽略不计）．（1）马小虎出发分钟后，爸爸追上他．（2）求马小虎骑车的速度．（3）若爸爸到家4分钟后，马小虎才到学校，求马小虎家到学校的路程．17．如图，直线与x轴、y轴分别交于A、B两点，OM⊥AB于点M，点P 为直线l上不与点A、B重合的一个动点．（1）求线段OM的长；（2）当△BOP的面积是3时，求点P的坐标；（3）当点P在线段AB上且△BOP的面积为3时，在x轴上是否存在点Q，使得△OPQ 是以OP为腰的等腰三角形，若存在，请直接写出Q点的坐标，若不存在，请说明理由．18．如图1，在平面直角坐标系中，一次函数y＝3x+6分别与x轴和y轴交于点C和点B，已知A（6，0），（1）写出点B，点C的坐标和△ABC的面积；（2）直线l经过A、B两点，求直线AB的解析式；（3）点D是在直线AB上的动点，是否存在动点D，使得？若存在，求出点D的坐标；若不存在，请说明理由；（4）如图2，P为A点右侧x轴上的一动点，以P为直角顶点、BP为腰在第一象限内作等腰直角三角形△BPQ，连接QA并延长交y轴于点K．当P点运动时，K点的位置是否发生变化？如果不变，请求出它的坐标；如果变化，请说明理由．19．如图所示，在平面直角坐标系中，直线y＝x+1与y＝﹣x+3分别交x轴于点B和点C，点D是直线y＝﹣x+3与y轴的交点．（1）求点B、C、D的坐标；（2）设M（x，y）是直线y＝x+1上一点，当△BCM的面积为10时，求点M的坐标；（3）线段CD上是否存在点P，使△CBP为等腰三角形，如果存在，直接写出P点的坐标；如果不存在，请说明理由．20．问题提出：如图1，等腰Rt△ABC中，∠ACB＝90°，CB＝CA，直线ED经过点C，过点A作AD ⊥ED于点D，过点B作BE⊥ED于点E，求证：△BEC≌△CDA；问题探究：如图2，在平面直角坐标系中，一次函数y＝x+1与x轴交于点A，与y轴交于点B，以AB为腰在第二象限作等腰直角△ABC，∠BAC＝90°，求点C的坐标；问题解决：古城西安已经全面迎来地铁时代！继西安地铁2号线于2011年9月16日通车试运行以来，共有八条线路开通运营，极大促进了西安市的交通运输，目前还有多条线路正在修建中．如图3，地铁某线路原计划按OA﹣AB的方向施工，由于在AB方向发现一处地下古建筑，地铁修建须绕开此区域．经实地勘测，若将AB段绕点A顺时针或逆时针方向旋转45°至AC或AD方向，则可以绕开此区域．已知OA长为1千米，以点O为原点，OA所在直线为x轴，1千米为单位长度，建立平面直角坐标系，且射线AB与直线y＝﹣2x平行，请帮助施工队计算出AC和AD所在直线的解析式．参考答案1．解：（1）由图象可以得到，a＝8，b＝280，故答案为：8，280；（2）由图象可以得出爸爸上山的速度是：280÷8＝35（米/分），小明上山的速度为：400÷8＝50（米/分），小明下山的速度是：400÷（24﹣8）＝25（米/分），故答案为：50，25，35；（3）∵小明从下山到与爸爸相遇用的时间是：（400﹣280）÷（35+25）＝2分，∵小明与爸爸相遇后，和爸爸一起以原下山速度返回出发地，∴小明的爸爸下山所用的时间：24﹣8﹣2＝14（分）．故答案为：14．2．解：（1）由图象得出小李步行720米，需要9分钟，所以小李的运动速度为：720÷9＝80（米/分），当第15分钟时，小王运动15﹣9＝6（分钟），运动距离为：15×80＝1200（m），∴小王的运动速度为：1200÷6＝200（米/分）；（2）根据题意得y1＝80t，y2＝200（t﹣9）＝200t﹣1800；（3）当相遇前两人的路程差为240米时，得y1﹣y2＝240，即80t﹣（200t﹣1800）＝240，解得t＝13，当相遇前两人的路程差为240米时，得y2﹣y1＝240，即（200t﹣1800）﹣80t＝240，解得t＝17，∴小王出发13分钟或17分钟时，两人的路程差为240米．3．解：（1）由题意得，小刚家与学校的距离为3000m，小刚骑自行车的速度为：（5000﹣3000）÷10＝200（m/min），小刚从图书馆返回家的时间：5000÷200＝25（min），总时间：25+20＝45（min），设小刚从图书馆返回家的过程中，y与x的函数表达式为y＝kx+b，把（20，5000），（45，0）代入得：，解得，∴y＝﹣200x+9000（20≤x≤45）；（2）小刚出发35分钟时，即当x＝35时，y＝﹣200×35+9000＝2000．答：他离家2000m．4．解：（1）由图象可得，A、B两地相距20km，乙骑车的速度是（30﹣20）÷2＝10÷2＝5（km/h），故答案为：20，5；（2）设甲在0≤x≤6时，y与x之间的函数关系式是y＝kx，∵点（6，60）在该函数图象上，∴6k＝60，解得k＝10，即甲在0≤x≤6时，y与x之间的函数关系式是y＝10x；（3）设乙在0≤x≤6时，y与x之间的函数关系式是y＝ax+b，∵点（2，30），（6，50）在函数图象上，∴，解得，即乙在0≤x≤6时，y与x之间的函数关系式是y＝5x+20；相遇之前两人相距5km，则（5x+20）﹣10x＝5，解得x＝3；相遇之后且甲到达C地之前相距5km，则10x﹣（5x+20）＝5，解得x＝5；答：当乙行驶3小时或5小时时甲、乙两人相距5千米．5．解：（1）货车的速度为300÷5＝60（km/h）；轿车提速后的速度为＝110（km/h）．故答案为：60，110；（2）从图象上看轿车比货车早0.5h到达乙地，∴轿车到达乙地后，货车距乙地有0.5×60＝30（千米），故答案为：30；（3）设CD段函数解析式为y＝kx+b（k≠0）（2.5≤x≤4.5）．∵C（2.5，80），D（4.5，300）在其图象上，∴，解得，∴CD段函数解析式：y＝110x﹣195（2.5≤x≤4.5），故答案为：y＝110x﹣195；（4）设OA段函数解析式为y＝mx，代入A（50，300），得5m＝300，解得m＝60，∴OA段函数解析式为y＝60x；联立方程组，得，解得，故货车从甲地出发后3.9小时与轿车相遇．故答案为：3.9．6．解：（1）由题意可得，y A＝0.4x+50，y B＝0.6x；（2）当x＝300时，y A＝0.4×300+50＝170，y B＝0.6×300＝180，∵170＜180，∴某人估计一个月内通话时间为300分钟，应选A种移动通讯方式合算些；（3）设本月李师傅实际的话费是a元，，解得a＝350，答：本月李师傅实际的话费是350元．7．解：（1）由图象可知，大约在甲出发3﹣2＝1（h）后，两人相遇，这时他们离B地120﹣30＝90（km）；故答案为：1，90；（2）甲的速度是30÷（3﹣2）＝30（km/h），乙的速度是30÷3＝10（km/h），故答案为：30，10；（3）设l1对应的表达式为s＝kt+b，将（3，30），（6，120）代入得：，解得，∴l1对应的表达式为：s＝30t﹣60，设l2对应的表达式为s＝k't，将（3，30）代入得：30＝3k'，解得k'＝10，∴l2对应的表达式为s＝10t，故答案为：s＝30t﹣60，s＝10t．8．解：（1）由图象可直接得出：甲车出发1小时后，乙车才出发；故答案为：1；（2）由图象可知，甲车的速度为240÷5＝48（km/h），乙车的速度为240÷（4﹣1）＝80（km/h）；故答案为：48；80；（3）甲所在的直线为y＝48x，乙所在的直线为：y＝80x﹣80，令48x＝80x﹣80，解得x＝2.5，故答案为：2.5；（4）当乙车开始行驶前，令48x＝20，解得x＝，符合题意，当甲、乙两车相遇前，48x﹣（80x﹣80）＝20，解得x＝，符合题意，当甲、乙两车相遇后，80x﹣80﹣48x＝20，解得x＝，符合题意，当乙到达目的地后，48x+20＝240，解得x＝，符合题意．∴当t的值为或或或，甲、乙两车相距20千米．9．解：（1）设y甲＝k1x，根据题意得4k1＝80，解得k1＝20，∴y甲＝20x；设y乙＝k2x+80，根据题意得：12k2+80＝200，解得k2＝10，∴y乙＝10x+80；（2）解方程组解得：，∴出入园8次时，两者花费一样，费用是160元；（3）当y＝240时，y甲＝20x＝240，∴x＝12；当y＝240时，y乙＝10x+80＝240，解得x＝16；∵12＜16，∴选择乙种更合算．10．解：（1）∵线段DE代表乙车在途中的货站装货耗时半小时，∴a＝4+0.5＝4.5（小时），∴甲车的速度＝＝60（千米/小时）；故答案为：4.5；60；（2）设乙开始的速度为v千米/小时，则4v+（7﹣4.5）（v﹣50）＝460，解得v＝90（千米/小时），∴4v＝360，∴D（4，360），E（4.5，360），设直线EF的解析式为y＝kx+b，把E（4.5，360），F（7，460）代入得：，解得，∴线段EF所表示的y与x的函数关系式为y＝40x+180（4.5≤x≤7）；（3）∵60×＝40，∴C（0，40），设线段CF的解析式为y＝kx+40，根据题意得：7k+40＝460，解得k＝60，∴线段CF的解析式为y＝60x+40，∵甲乙两车距离不超过10km时，车载通话机可以进行通话，由，解得1≤x≤，由，解得≤x≤7，∴两车在行驶过程中可以通话的总时长为：（﹣1）+（7﹣）＝（小时）．11．解：（1）设零售x吨，则批发2x吨，储藏后销售（200﹣x﹣2x）吨，根据题意得：y＝2x（3000﹣2000）+x（4500﹣3000）+（200﹣3x）（5500﹣3500）＝﹣2500x+400000；即y＝﹣2500x+400000；（2）∵冷库储藏售出的商品数量最多为80吨，∴200﹣3x≤80，∴x≥40，，∵y＝﹣2500x+400000中，﹣2500＜0，∴y的值随x的值增大而减小，∴当x＝40时，y最大值＝﹣2500×40+400000＝300000（元）；答：该生产基地按计划全部售完商品获得的最大利润为300000元．12．解：（1）设张老师购买x个甲种笔记本，则购买（100﹣x）个乙种笔记本，由题意可得：y＝5×0.9x+3×0.9（100﹣x）＝1.8x+270．即y与x之间的关系式为y＝1.8x+270；（2）由（1）知：y＝1.8x+270，∴y随x的增大而增大，∵甲种笔记本的数量不少于乙种笔记本数量的3倍，∴x≥3（100﹣x），解得x≥75．∴当x＝75时，y取得最小值，此时y＝405，100﹣x＝25，答：购买75个甲种笔记本、25个乙种笔记本，所花费用最低，最低费用是405元．13．解：（1）设加工不完的鲜海带直接卖给鲍鱼养殖场作饲料，每吨可获利x元，根据题意得：12×2×250+（30﹣12×2）x＝6300，解得x＝50，答：加工不完的鲜海带直接卖给鲍鱼养殖场作饲料，每吨可获利50元；（2）设生产盐渍海带的m人，每天生产的利润是w元，则生产干海带的（12﹣m）人，∵生产干海带的人数不超过盐渍海带人数的2倍，∴12﹣m≤2m，解得m≥4，根据题意得：w＝0.6m×600+2（12﹣m）×250+50[30﹣0.6m﹣2（12﹣m）]＝﹣70m+6300，∵﹣70＜0，∴当m＝4时，w取最大值，最大值为﹣70×4+6300＝6020（元），此时12﹣m＝8，答：生产盐渍海带的4人，生产干海带的8人，可使每天生产的利润最大，最大利润是6020元．14．解：（1）设参加此次研学活动的老师有x人，学生有y人，依题意，得：，解得．答：参加活动的老师有16人，学生有234人；（2）设租甲种车型n辆，依题意得，解这个不等式组得：2≤n≤5.5，∵n为正整数，∴n＝2，3，4，5，即学校共有一下四种租车方案：方案①：2辆甲车，6辆乙车；方案②：3辆甲车，5辆乙车；方案③：4辆甲车，5辆乙车；方案④：5辆甲车，3辆乙车；设租车费用为W元，则W＝400n+320（8﹣n）＝80n+2560，∵80＞0，∴W随n的增大而增大，∴当n＝2时费用最低，最少费用为W＝160+2560＝2720（元）．答：学校共有四种租车方案，最少费用为2720元．15．解：（1）乙前面的速度为：100÷2＝50（千米/小时），乙后来的速度为：50×2＝100（千米/小时），BC＝360﹣100﹣100×（4.8﹣2.8）＝60（千米），答：B、C两地之间的距离为60千米；（2）甲的速度为：360÷6＝60（千米/小时），设乙t小时追上甲，根据题意得60t＝100+100（t﹣2.8），解得t＝4.5，答：出发后4.5小时乙追上甲；（3）当0＜x≤2时，两车距离小于40，①当2＜x≤2.8时，设甲距离A地的距离y（千米）与出发时间x（小时）之间的关系式为y＝k1x，代入（6，360）可得k1＝60，∴y＝60x，60x﹣100＝40，解得x＝；②当2.8＜x≤4.8时，由（1）可得，A、B两地之间的距离为：360﹣60＝300（km），设乙与A地距离与出发时间x之间的函数关系式为y＝k2x+b，代入（2.8，100）和（4.8，300），得，解得，∴y＝100x﹣180，解方程100x﹣180﹣60x＝40得x＝5.2（不合题意，舍去），解方程60x﹣（100x﹣180）＝40得x＝3.5；③当x＞4.8时，解方程60x＝360﹣20得x＝．答：当两车相距40千米时，甲车行驶了小时或3.5小时或小时．16．解：（1）由题意可知，当y＝0时，x＝10，所以马小虎出发10分钟后，爸爸追上他．故答案为：10；（2）由题意得，2400÷6＝400（米/分钟），即马小虎骑车的速度为400米/分钟；（3）∵由题意可知，相遇4分钟后，爸爸到家，∴相遇后马小虎又骑行了8分钟才到学校，2400+2×400﹣2×400+8×400＝5600（米），答：马小虎家到学校的路程为5600米．17．解：（1）对于直线y＝﹣x+3，令x＝0，则y＝3，令y＝0，则﹣x+3＝0，解得：x＝4，∴点A、B的坐标分别是（4，0），（0，3），∴OA＝4，OB＝3，∴AB＝＝＝5，∵S△OAB＝AB•OM，∴OM＝；（2）过P作PC⊥y轴于C，如图1，∴S△BOP＝OB•PC＝3，∴PC＝2，∴点P的横坐标为2或﹣2，∴P（2，）或（﹣2，）；（3）存在，理由如下：∵P点在线段AB上，∴P（2，），设Q（x，0），∴OP＝，OQ＝|x|，PQ＝，当OP＝OQ时，|x|＝，解得x＝或x＝﹣，∴Q（，0）或（﹣，0）；当OP＝PQ时，＝，解得x＝0（舍）或x＝4，∴Q（4，0）；综上所述：Q点坐标为（，0）或（﹣，0）或（4，0）．18．解：（1）对于y＝3x+6，令x＝0，则y＝6，故点B（0，6），令y＝3x+6＝0，解得：x＝﹣2，故点C（﹣2，0）；则△ABC的面积＝×AC×OB＝×（6+2）×6＝24；（2）设直线AB的表达式为y＝kx+b（k≠0），则，解得：，故直线AB的表达式为y＝x+6；（3）存在，理由：∵，∴|y D|＝|y B|＝3，即|x+6|＝3，解得：x＝3或9，故点D的坐标为（3，3）或（9，﹣3）；（4）K点的位置不发生变化，理由：设点P的坐标为（t，0），过点Q作QH⊥x轴于点H，∵∠BPO+∠QPH＝90°，∠PBO+∠BPO＝90°，∴∠QPH＝∠PBO，在Rt△BOP和Rt△PHQ中，，∴△BOP≌△PHQ（AAS），∴PH＝BO＝6，QH＝OP＝t，则点Q的坐标为（t+6，t），设直线AQ的表达式为y＝mx+n，则，解得，故点K的坐标为（0，﹣6）．19．解：（1）y＝x+1中当y＝0时，x＝﹣1，∴B（﹣1，0），y＝﹣x+3中y＝0时，则x＝4，x＝0时，则y＝3，∴C（4，0），D（0，3）；（2）∵B（﹣1，0），C（4，0），∴BC＝5，∵M（x，y），∴S△BCM＝×5×|x+1|，∵△BCM的面积为10，∴×5×|x+1|＝10，解得x＝3或x＝﹣5，∴M（3，4）或（﹣5，﹣4）；（3）线段CD上存在点P，使△CBP为等腰三角形，理由如下：设P（t，﹣t+3）（0≤t≤4），∴BP＝，CP＝，当BC＝BP时，＝5，解得t＝4（舍）或t＝﹣（舍），∴此时不存在P点满足题意；当BC＝CP时，＝5，解得t＝0或t＝8（舍），∴P（0，3）；当BP＝CP时，＝，解得t＝，∴P（，）；综上所述：P点坐标为（0，3）或（，）．20．问题提出：证明：∵∠ACB＝90°，∴∠ACD+∠BCE＝90°，∵AD⊥ED，BE⊥ED，∴∠BEC＝∠ADC＝90°，∴∠BCE+∠CBE＝90°，∴∠ACD＝∠CBE，∵AC＝BC，∴△BEC≌CDA（SAS）；问题探究：解：过C点作CD⊥x轴交于点D，∵∠BAC＝90°，CD⊥x轴，BO⊥x轴，AC＝AB，由问题提出可得△CAD≌△ABO（SAS），∴CD＝OA，AD＝BO，∵y＝x+1与x轴交于点A（﹣4，0），与y轴交于点B（0，1），∴AO＝4，OB＝1，∴C（﹣5，4）；问题解决：解：设线段AB绕点A顺时针旋转后的线段为AC，绕A点逆时针旋转后的线段为AD，过点C作CN⊥x轴交于点N，过D点作DM⊥x轴交于点M，∵∠CAB＝∠DAB＝45°，∴∠CAD＝90°，由问题提出可得△ACN≌△DAM（SAS），设C点坐标为（m，n），∴DM＝AN，CN＝AM，∵OA＝1，∴A（﹣1，0），∴D（﹣n﹣1，m+1），∵射线AB与直线y＝﹣2x平行，∴直线AB的解析式为y＝﹣2x﹣2，连接CD交AB于点E，∵△ACD是等腰直角三角形，∴∠ADC＝45°，∵∠BAD＝45°，∴∠AED＝90°，∴E是CD的中点，∴E（，），∴E点在直线AB上，∴＝﹣2•﹣2，整理得n＝3m+3，∴直线AC的解析式为y＝3x+3，设y＝m+1，x＝﹣n﹣1，∴﹣x﹣1＝3（y﹣1）+3，整理得y＝﹣x﹣，∴直线AD的解析式为y＝﹣x﹣．。
中考数学总复习《行程问题(一次函数实际综合应用)》专项提升训练(带答案)
中考数学总复习《行程问题（一次函数实际综合应用）》专项提升训练（带答案)学校:___________班级：___________姓名：___________考号：___________1．李师傅将容量为60升的货车油箱加满后，从工厂出发运送一批物资到某地．行驶过程中，货车离目的地的路程s（千米）与行驶时间t（小时）的关系如图所示（中途休息、加油的时间不计）．当油箱中剩余油量为10升时，货车会自动显示加油提醒．设货车平均耗油量为0.1升/千米，请根据图象解答下列问题：(1)直接写出工厂离目的地的路程；(2)求s关于t的函数表达式；(3)当货车显示加油提醒后，问行驶时间t在怎样的范围内货车应进站加油？2．一辆快车从甲地出发驶向乙地，在到达乙地后，立即按原路原速返回到甲地，快车出发一段时间后一辆慢车从甲地驶向乙地，中途因故停车1h后，继续按原速驶向乙地，两车距甲地4的路程kmy与慢车行驶时间()h x之间的函数图象如图所示，请结合图象解答下列问题：(1)甲乙两地相距______km，快车行驶的速度是______ km/h，图中括号内的数值是______ ；(2)求快车从乙地返回甲地的过程中，y与x的函数解析式；(3)慢车出发多长时间，两车相距120km3．甲、乙两地之间是一条直路，王明跑步从甲地往乙地，陈星骑自行车从乙地往甲地，两人同时出发，陈星先到达目的地，设两人的在行进过程中保持匀速，两人之间的距离()km y 与运动时间()h x 的函数关系大致如图所示，请你根据图形进行探究：(1)王明和陈星的速度分别是多少？(2)请写出线段BC 所表示的y 与x 之间的函数关系式，并写出自变量x 的取值范围． 4．某次无人机展演活动中，Ⅰ号无人机从海拔10m 处出发，以12m/min 的速度匀速上升，Ⅱ号无人机从海拔30m 处同时出发，以()m/min a 的速度匀速上升，经过5min 两架无人机位于同一海拔高度()m b ．无人机海拔高度()m y 与时间()min x 的关系如图．两架无人机都上升了15min ．(1)求b 的值及Ⅱ号无人机海拔高度()m y 与时间()min x 的关系式； (2)问无人机上升了多少时间，两无人机高度相差32m ．5．现有A 、B 两种品牌的共享电动车，收费y (元)与骑行时间(min)x 之间的函数关系如图所示，其中A 品牌收费方式对应1y ，B 品牌的收费方式对应2y ．(1)直接写出A 品牌收费方式对应的函数关系式为 ．(2)如果小致每天早上需要骑共享电动车去上班，已知两种品牌共享电动车的平均行驶速度均为30km /h ，小致家到学校的距离为6km ，那么小致选择 (填“A 品牌”或“B 品牌”)的共享电动车更省钱．(3)求出两种收费相差0.5元时x 的值．6．如图，小李和小赵相约去农庄游玩．小李从甲小区骑电动车出发，同时小赵从乙小区开车出发，途中去超市购物，购物后仍按原速继续驶向农庄，甲乙小区、超市和农庄之间的路程如图①所示，图②中线段OD 、BC 分别表示小李、小赵行驶中离甲小区的路程()km s 与出发时间t （分）之间的函数图象（或部分图象）．根据图象回答问题：(1)分别求出线段OD 、BC 的函数表达式；(2)请补全小赵离甲小区的路程为()km s 与出发时间t （分）的函数图象，并写出小赵在超市购物，用时______分钟．7．甲、乙两人同时开车从A 地出发，沿同一条道路去B 地，途中都以两种不同的速度1V 与212()V V V >行驶．甲前一半路程以速度1V 匀速行驶，后一半路程以速度2V 匀速行驶；乙前一半时间以速度匀速2V 行驶，后一半时间用以速度1V 匀速行驶．(1)设甲乙两人从A 地到B 地的平均速度分别为V 甲和V 乙，则V =甲___________；___________(V =乙用含1V 、2V 的式子表示)．2(1)当04t<≤时，求2v关于t的函数关系式；(2)求图中a的值；(3)小明每次踢球都能使球的速度瞬间增加6m/s，球运动方向不变，当小明带球跑完200m，写出小明踢球次数共有____次，并简要说明理由．10．已知甲、乙、丙三地依次在同一直线上，乙地离甲地260km，丙地离乙地160km．一艘游轮从甲地出发，途经乙地前往丙地．当游轮到达乙地时，一艘货轮沿着同样的线路从甲地出发前往丙地．已知游轮的速度为20km/h，离开甲地的时间记为t（单位：h），两艘轮船离甲地的距离y（单位：km）关于t的图象如图所示（游轮在停靠前后的行驶速度不变）．货轮比游轮早2.6h到达丙地．根据相关信息，解答下列问题：(1)填表：游轮离开甲地的时间/h 6 13 16 22 24游轮离甲地的距离/km120 260(2)填空：①游轮在乙地停靠的时长为_______h；②货轮从甲地到丙地所用的时长为_______h，行驶的速度为_______km/h；③游轮从乙地出发时，两艘轮船的距离为_______km．13．我国已取得脱贫攻坚的全面胜利，国家已进入乡村振兴实施阶段，现代物流的高速发展，为乡村振兴的实施提供了良好条件．某物流公司的汽车在市区行驶20km后进入高速路，在高速路上匀速行驶一段时间后，再在乡村道路上行驶1h到达目的地，汽车行驶的时间x（单位：h）与行驶的路程y（单位：km）之间的关系如图所示．请结合图象，回答下列问题：(1)汽车在乡村道路上行驶的平均速度是______ km/h；(2)求汽车在高速路上行驶的路程y与行驶的时间x之间的函数关系式，并写出自变量x的取值范围；(3)当该物流车行驶到距离出发地120km时，请问该车再过1.5小时能不动达目的地，如果能，写出计算过程；如果不能，直接写出1.5小时后该车离目的地还有多远？14．甲、乙两车分别从相距15km的大连北站和大连广播电视中心同时匀速相向而行．甲车出发10min后，由于交通管制，停止了2min，再出发时速度比原来减少15km/h，并安全到达终点．甲、乙两车距大连北站的路程y（单位：km）与两车行驶时间x（单位：h）的图象如图所示．(1)填空： a______；(2)求乙车距大连北站的路程y与两车行驶时间x的函数解析式，并直接写出自变量x的取值范围；(3)求甲、乙两车相遇时，乙车距大连北站的路程．15．随着疫情的消失，三年的管控使人们的消费和旅游在2023年的“五一”假期得以全面释放．小明和小军分别骑车和驾车从本村出发，沿同一条公路去东门外生态公园游玩．小明骑一段时间后，小军驾车出发，结果半路遭遇堵车，当小明迫上小军后，小军坐小明的自行车一起去生态公园(小军泊车时间忽略不计)，如图是小明、小军两人在去生态公园过程中经过的路程()my与小明出发时间()s x之间的函数图像．请结合图像回答：(1)村与公园的距离为______ ，小明骑车速度是______ m/s．(2)小军在离开村多少公里处遭遇堵车？从小军遇到堵车到追上小明用了多长时间？(3)直接写出两人何时相距520m？16．甲、乙两地相距320km，A，B两辆货车同时分别从甲、乙两地相向而行，货车A先出发，一个小时后，货车B也出发，若它们都保持匀速行驶，货车A、货车B距乙地的距离()y km与时x h之间的关系如图所示．间()(1)求货车B距乙地的距离y与时间x的关系式；(2)求货车B到甲地后，货车A还需多长时间到达乙地．参考答案：1．(1)工厂离目的地的路程为880千米 (2)s 关于t 的函数表达式：()80880011s t t =-+≤≤ (3)t 的取值范围是254t ≤≤1522．(1)400，100，7(2)快车从乙地返回甲地的过程中，y 与x 的函数解析式为100400y x =-+ (3)慢车出发1小时或103小时或143小时，两车相距120km3．(1)王明跑步的速度为8km/h ，陈星的速度为16km/h ． (2)()24241 1.5y x x =-≤≤ 4．(1)70 830y x =+(2)无人机上升了13min ，两无人机高度相差32m ． 5．(1)10.2y x =(2)小明选择A 品牌的共享电动车更省钱 (3)两种收费相差0.5元时，x 的值为15或25；6．(1)线段OD 的函数表达式为()0.5020y x x =≤≤；线段BC 函数表达式为()81218y x x =-≤≤； (2)小赵在超市购物，用时10min ． 7．(1)12121222VV V V V V ++，(2)乙(3)①1210050300V V S ===，，，②3.5小时 8．(1)20a = 140b =； (2)2020y x =+甲1550y x =+乙；(3)飞行1分钟或者11分钟时，两架航模飞行高度相差25米。
中考数学总复习训练 一次函数的实际应用含解析
一次函数的实际应用一、利用函数的解析式解决问题1．某市种植某种绿色蔬菜，全部用来出口．为了扩大出口规模，该市决定对这种蔬菜的种植实行政府补贴，规定每种植﹣亩这种蔬菜一次性补贴菜农若干元．经调查，种植亩数y（亩）与补贴数额x（元）之间大致满足如图1所示的一次函数关系．随着补贴数额x的不断增大，出口量也不断增加，但每亩蔬菜的收益z（元）会相应降低，且z与x之间也大致满足如图2所示的一次函数关系．（1）在政府未出台补贴措施前，该市种植这种蔬菜的总收益额为多少？（2）分别求出政府补贴政策实施后，种植亩数y和每亩蔬菜的收益z与政府补贴数额x之间的函数关系式；（3）要使全市这种蔬菜的总收益w（元）最大，政府应将每亩补贴数额x定为多少？并求出总收益w的最大值．2．某产品每件成本10元，试销阶段每件产品的销售价x（元）与产品的日销售量y（件）之间的关系如下表：x （元）15 20 25 …y （件）25 20 15 …若日销售量y是销售价x的一次函数．（1）求出日销售量y（件）与销售价x（元）的函数关系式；（2）求销售价定为30元时，每日的销售利润．3．如图，两摞相同规格的饭碗整齐地叠放在桌面上，请根据图中给的数据信息，解答下列问题：（1）求整齐摆放在桌面上饭碗的高度y（cm）与饭碗数x（个）之间的一次函数解析式；（2）把这两摞饭碗整齐地摆成一摞时，这摞饭碗的高度是多少？4．鞋子的“鞋码”和鞋长（cm）存在一种换算关系，下表是几组“鞋码”与鞋长换算的对应数值：（注：“鞋码”是表示鞋子大小的一种号码）鞋长（cm） 16 19 21 24鞋码（号） 22 28 32 38（1）设鞋长为x，“鞋码”为y，试判断点（x，y）在你学过的哪种函数的图象上；（2）求x、y之间的函数关系式；（3）如果某人穿44号“鞋码”的鞋，那么他的鞋长是多少？5．某市为了鼓励居民节约用水，采用分段计费的方法按月计算每户家庭的水费，月用水量不超过20m3时，按2元/m3计费；月用水量超过20m3时，其中的20m3仍按2元/m3收费，超过部分按2.6元/m3计费．设每户家庭用水量为xm3时，应交水费y元．（1）分别求出0≤x≤20和x＞20时y与x的函数表达式；（2）小明家第二季度交纳水费的情况如下：月份四月份五月份六月份交费金额30元34元42.6元小明家这个季度共用水多少立方米？6．一辆客车从甲地开往乙地，一辆出租车从乙地开往甲地，两车同时出发，设客车离甲地的距离为y1（km），出租车离甲地的距离为y2（km），客车行驶时间为x（h），y1，y2与x 的函数关系图象如图所示：（1）根据图象，直接写出y1，y2关于x的函数关系式．（2）分别求出当x=3，x=5，x=8时，两车之间的距离．（3）若设两车间的距离为S（km），请写出S关于x的函数关系式．（4）甲、乙两地间有A、B两个加油站，相距200km，若客车进入A站加油时，出租车恰好进入B站加油．求A加油站到甲地的距离．7．我国是世界上严重缺水的国家之一．为了增强居民节水意识，某市自来水公司对居民用水采用以户为单位分段计费办法收费．即一月用水10吨以内（包括10吨）的用户，每吨收水费a元；一月用水超过10吨的用户，10吨水仍按每吨a元收费，超过10吨的部分，按每吨b元（b＞a）收费．设一户居民月用水x吨，应收水费y元，y与x之间的函数关系如图所示．（1）求a的值；某户居民上月用水8吨，应收水费多少元；（2）求b的值，并写出当x＞10时，y与x之间的函数关系式；（3）已知居民甲上月比居民乙多用水4吨，两家共收水费46元，求他们上月分别用水多少吨？二、利用函数的增减性解决问题8．某饮料厂为了开发新产品，用A种果汁原料和B种果汁原料试制新型甲、乙两种饮料共50千克，设甲种饮料需配制x千克，两种饮料的成本总额为y元．（1）已知甲种饮料成本每千克4元，乙种饮料成本每千克3元，请你写出y与x之间的函数关系式．（2）若用19千克A种果汁原料和17.2千克B种果汁原料试制甲、乙两种新型饮料，下表是试验的相关数据；请你列出关于x且满足题意的不等式组，求出它的解集，并由此分析如何配制这两种饮料，可使y值最小，最小值是多少？甲乙每千克饮料果汁含量果汁A 0.5千克0.2千克B 0.3千克0.4千克9．某厂工人小王某月工作的部分信息如下：信息一：工作时间：每天上午8：00～12：00，下午14：00～18：00，每月25天；信息二：生产甲、乙两种产品，并且按规定每月生产甲产品的件数不少于60件．生产产品件数与所用时间之间的关系见下表：生产甲产品数（件）生产乙产品数（件）所用时间（分）10 10 35030 20 850信息三：按件计酬，每生产一件甲产品可得1.50元，每生产一件乙产品可得2.80元．根据以上信息，回答下列问题：（1）小王每生产一件甲种产品，每生产一件乙种产品分别需要多少分；（2）小王该月最多能得多少元此时生产甲、乙两种产品分别多少件．10．“5.12”汶川特大地震灾害发生后，社会各界积极为灾区捐款捐物，某经销商在当月销售的甲种啤酒尚有2万元货款未收到的情况下，先将销售甲种啤酒全部应收货款的70%捐给了灾区，后又将该月销售乙种啤酒所得的全部货款的80%捐给了灾区．已知该月销售甲、乙两种啤酒共5000件，甲种啤酒每件售价为50元，乙种啤酒每件售价为35元，设该月销售甲种啤酒x件，共捐助救灾款y元．（1）该经销商先捐款元，后捐款元；（用含x的式子表示）（2）写出y与x的函数关系式，并求出自变量x的取值范围；（3）该经销商两次至少共捐助多少元？11．为支持四川抗震救灾，重庆市A、B、C三地现在分别有赈灾物资100吨、100吨、80吨，需要全部运往四川重灾地区的D、E两县．根据灾区的情况，这批赈灾物资运往D县的数量比运往E县的数量的2倍少20吨．（1）求这批赈灾物资运往D、E两县的数量各是多少？（2）若要求C地运往D县的赈灾物资为60吨，A地运往D的赈灾物资为x吨（x为整数），B地运往D县的赈灾物资数量小于A地运往D县的赈灾物资数量的2倍．其余的赈灾物资全部运往E县，且B地运往E县的赈灾物资数量不超过25吨．则A、B两地的赈灾物资运往D、E两县的方案有几种？请你写出具体的运送方案；（3）已知A、B、C三地的赈灾物资运往D、E两县的费用如下表：A地B地C地运往D县的费用（元/吨）220 200 200运往E县的费用（元/吨）250 220 210为及时将这批赈灾物资运往D、E两县，某公司主动承担运送这批赈灾物资的总费用，在（2）问的要求下，该公司承担运送这批赈灾物资的总费用最多是多少？12．某电脑公司经销甲种型号电脑，受经济危机影响，电脑价格不断下降．今年三月份的电脑售价比去年同期每台降价1000元，如果卖出相同数量的电脑，去年销售额为10万元，今年销售额只有8万元．（1）今年三月份甲种电脑每台售价多少元？（2）为了增加收入，电脑公司决定再经销乙种型号电脑，已知甲种电脑每台进价为3500元，乙种电脑每台进价为3000元，公司预计用不多于5万元且不少于4.8万元的资金购进这两种电脑共15台，有几种进货方案？（3）如果乙种电脑每台售价为3800元，为打开乙种电脑的销路，公司决定每售出一台乙种电脑，返还顾客现金a元，要使（2）中所有方案获利相同，a值应是多少此时，哪种方案对公司更有利？13．“5•12”四川汶川大地震的灾情牵动全国人民的心，某市A、B两个蔬菜基地得知四川C、D两个灾民安置点分别急需蔬菜240吨和260吨的消息后，决定调运蔬菜支援灾区．已知A蔬菜基地有蔬菜200吨，B蔬菜基地有蔬菜300吨，现将这些蔬菜全部调往C、D两个灾民安置点．从A地运往C、D两处的费用分别为每吨20元和25元，从B地运往C、D两处的费用分别为每吨15元和18元．设从B地运往C处的蔬菜为x吨．（1）请填写下表，并求两个蔬菜基地调运蔬菜的运费相等时x的值；C D 总计A 200吨B x吨300吨总计240吨260吨500吨（2）设A、B两个蔬菜基地的总运费为w元，写出w与x之间的函数关系式，并求总运费最小的调运方案；（3）经过抢修，从B地到C处的路况得到进一步改善，缩短了运输时间，运费每吨减少m 元（m＞0），其余线路的运费不变，试讨论总运费最小的调运方案．14．某公司有A型产品40件，B型产品60件，分配给下属甲、乙两个商店销售，其中70件给甲店，30件给乙店，且都能卖完．两商店销售这两种产品每件的利润（元）如下表：A型利润B型利润甲店200 170乙店160 150（1）设分配给甲店A型产品x件，这家公司卖出这100件产品的总利润为W（元），求W 关于x的函数关系式，并求出x的取值范围；（2）若公司要求总利润不低于17560元，说明有多少种不同分配方案，并将各种方案设计出来；（3）为了促销，公司决定仅对甲店A型产品让利销售，每件让利a元，但让利后A型产品的每件利润仍高于甲店B型产品的每件利润．甲店的B型产品以及乙店的A，B型产品的每件利润不变，问该公司又如何设计分配方案，使总利润达到最大？一次函数的实际应用参考答案与试题解析一、利用函数的解析式解决问题1．某市种植某种绿色蔬菜，全部用来出口．为了扩大出口规模，该市决定对这种蔬菜的种植实行政府补贴，规定每种植﹣亩这种蔬菜一次性补贴菜农若干元．经调查，种植亩数y（亩）与补贴数额x（元）之间大致满足如图1所示的一次函数关系．随着补贴数额x的不断增大，出口量也不断增加，但每亩蔬菜的收益z（元）会相应降低，且z与x之间也大致满足如图2所示的一次函数关系．（1）在政府未出台补贴措施前，该市种植这种蔬菜的总收益额为多少？（2）分别求出政府补贴政策实施后，种植亩数y和每亩蔬菜的收益z与政府补贴数额x之间的函数关系式；（3）要使全市这种蔬菜的总收益w（元）最大，政府应将每亩补贴数额x定为多少？并求出总收益w的最大值．【考点】二次函数的应用；一次函数的应用．【专题】压轴题．【分析】（1）根据题意可知直接计算这种蔬菜的收益额为3000×800=2400000（元）；（2）设种植亩数y和每亩蔬菜的收益z与政府补贴数额x之间的函数关系式分别为：y=kx+800，z=k1x+3000，并根据图象上点的坐标利用待定系数法求函数的解析式即可；（3）表示出蔬菜的总收益w（元）与x之间的关系式，w=﹣24x2+21600x+2400000，利用二次函数最值问题求最大值．【解答】解：（1）政府没出台补贴政策前，这种蔬菜的收益额为3000×800=2400000（元）（2）设种植亩数y和每亩蔬菜的收益z与政府补贴数额x之间的函数关系式分别为：y=kx+800，z=k1x+3000，分别把点（50，1200），（100，2700）代入得，50k+800=1200，100k1+3000=2700，解得：k=8，k1=﹣3，种植亩数与政府补贴的函数关系为：y=8x+800每亩蔬菜的收益与政府补贴的函数关系为z=﹣3x+3000（x＞0）（3）由题意：w=yz=（8x+800）（﹣3x+3000）=﹣24x2+21600x+2400000=﹣24（x﹣450）2+7260000，∴当x=450，即政府每亩补贴450元时，总收益额最大，为7260000元．【点评】主要考查利用一次函数和二次函数的模型解决实际问题的能力．要先根据题意列出函数关系式，再代数求值．解题的关键是要分析题意根据实际意义准确的列出解析式，再把对应值代入求解．利用二次函数的顶点坐标求最值是常用的方法之一．2．某产品每件成本10元，试销阶段每件产品的销售价x（元）与产品的日销售量y（件）之间的关系如下表：x （元）15 20 25 …y （件）25 20 15 …若日销售量y是销售价x的一次函数．（1）求出日销售量y（件）与销售价x（元）的函数关系式；（2）求销售价定为30元时，每日的销售利润．【考点】一次函数的应用．【专题】压轴题；图表型．【分析】（1）已知日销售量y是销售价x的一次函数，可设函数关系式为y=kx+b（k，b 为常数，且k≠0），代入两组对应值求k、b，确定函数关系式．（2）把x=30代入函数式求y，根据：（售价﹣进价）×销售量=利润，求解．【解答】解：（1）设此一次函数解析式为y=kx+b（k，b为常数，且k≠0）．（1分）则．（2分）解得k=﹣1，b=40（4分）即一次函数解析式为y=﹣x+40（5分）（2）当x=30时，每日的销售量为y=﹣30+40=10（件）（6分）每日所获销售利润为（30﹣10）×10=200（元）（8分）【点评】本题主要考查用待定系数法求一次函数关系式，并会用一次函数研究实际问题．3．如图，两摞相同规格的饭碗整齐地叠放在桌面上，请根据图中给的数据信息，解答下列问题：（1）求整齐摆放在桌面上饭碗的高度y（cm）与饭碗数x（个）之间的一次函数解析式；（2）把这两摞饭碗整齐地摆成一摞时，这摞饭碗的高度是多少？【考点】一次函数的应用．【专题】应用题；压轴题．【分析】（1）可设y=kx+b，因为由图示可知，x=4时y=10.5；x=7时，y=15，由此可列方程组，进而求解；（2）令x=4+7，求出相应的y值即可．【解答】解：（1）设y=kx+b（k≠0）．（2分）由图可知：当x=4时，y=10.5；当x=7时，y=15．（4分）把它们分别代入上式，得（6分）解得k=1.5，b=4.5．∴一次函数的解析式是y=1.5x+4.5（x是正整数）．（8分）（2）当x=4+7=11时，y=1.5×11+4.5=21（cm）．即把这两摞饭碗整齐地摆成一摞时，这摞饭碗的高度是21cm．（10分）【点评】本题意在考查学生利用待定系数法求解一次函数关系式，并利用关系式求值的运算技能和从情景中提取信息、解释信息、解决问题的能力．而它通过所有学生都熟悉的摞碗现象构造问题，将有关数据以直观的形象呈现给学生，让人耳目一新．从以上例子我们看到，数学就在我们身边，只要我们去观察、发现，便能找到它的踪影；数学是有用的，它可以解决实际生活、生产中的不少问题．4．鞋子的“鞋码”和鞋长（cm）存在一种换算关系，下表是几组“鞋码”与鞋长换算的对应数值：（注：“鞋码”是表示鞋子大小的一种号码）鞋长（cm） 16 19 21 24鞋码（号） 22 28 32 38（1）设鞋长为x，“鞋码”为y，试判断点（x，y）在你学过的哪种函数的图象上；（2）求x、y之间的函数关系式；（3）如果某人穿44号“鞋码”的鞋，那么他的鞋长是多少？【考点】一次函数的应用．【专题】压轴题；图表型．【分析】（1）可利用函数图象判断这些点在一条直线上，即在一次函数的图象上；（2）可设y=kx+b，把两个点的坐标代入，利用方程组即可求解；（3）令（2）中求出的解析式中的y等于44，求出x即可．【解答】解：（1）如图，这些点在一次函数的图象上；（2）设y=kx+b，由题意得，解得，∴y=2x﹣10．（x是一些不连续的值．一般情况下，x取16、16.5、17、17.5、26、26.5、27等）；（3）y=44时，x=27．答：此人的鞋长为27cm．【点评】本题首先利用待定系数法确定一次函数的解析式，然后利用函数实际解决问题．5．某市为了鼓励居民节约用水，采用分段计费的方法按月计算每户家庭的水费，月用水量不超过20m3时，按2元/m3计费；月用水量超过20m3时，其中的20m3仍按2元/m3收费，超过部分按2.6元/m3计费．设每户家庭用水量为xm3时，应交水费y元．（1）分别求出0≤x≤20和x＞20时y与x的函数表达式；（2）小明家第二季度交纳水费的情况如下：月份四月份五月份六月份交费金额30元34元42.6元小明家这个季度共用水多少立方米？【考点】一次函数的应用．【专题】应用题．【分析】（1）因为月用水量不超过20m3时，按2元/m3计费，所以当0≤x≤20时，y与x 的函数表达式是y=2x；因为月用水量超过20m3时，其中的20m3仍按2元/m3收费，超过部分按2.6元/m3计费，所以当x＞20时，y与x的函数表达式是y=2×20+2.6（x﹣20），即y=2.6x ﹣12；（2）由题意可得：因为四月份、五月份缴费金额不超过40元，所以用y=2x计算用水量；六月份缴费金额超过40元，所以用y=2.6x﹣12计算用水量．【解答】解：（1）当0≤x≤20时，y与x的函数表达式是：y=2x；当x＞20时，y与x的函数表达式是：y=2×20+2.6（x﹣20）=2.6x﹣12；（2）因为小明家四、五月份的水费都不超过40元，故0≤x≤20，此时y=2x，六月份的水费超过40元，x＞20，此时y=2.6x﹣12，所以把y=30代入y=2x中得，2x=30，x=15；把y=34代入y=2x中得，2x=34，x=17；把y=42.6代入y=2.6x﹣12中得，2.6x﹣12=42.6，x=21．所以，15+17+21=53．答：小明家这个季度共用水53m3．【点评】本题是贴近社会生活的应用题，赋予了生活气息，使学生真切地感受到“数学来源于生活”，体验到数学的“有用性”．这样设计体现了《新课程标准》的“问题情景﹣建立模型﹣解释、应用和拓展”的数学学习模式．6．一辆客车从甲地开往乙地，一辆出租车从乙地开往甲地，两车同时出发，设客车离甲地的距离为y1（km），出租车离甲地的距离为y2（km），客车行驶时间为x（h），y1，y2与x 的函数关系图象如图所示：（1）根据图象，直接写出y1，y2关于x的函数关系式．（2）分别求出当x=3，x=5，x=8时，两车之间的距离．（3）若设两车间的距离为S（km），请写出S关于x的函数关系式．（4）甲、乙两地间有A、B两个加油站，相距200km，若客车进入A站加油时，出租车恰好进入B站加油．求A加油站到甲地的距离．【考点】一次函数的应用．【分析】（1）可根据待定系数法来确定函数关系式；（2）可依照（1）得出的关系式，得出结果；（3）要根据图象中自变量的3种不同的取值范围，分类讨论；（4）根据（3）中得出的函数关系式，根据自变量的取值范围分别计算出A加油站到甲地的距离．【解答】解：（1）y1=60x（0≤x≤10），y2=﹣100x+600（0≤x≤6）（2）当x=3时，y1=180，y2=300，∴y2﹣y1=120，当x=5时y1=300，y2=100，∴y1﹣y2=200，当x=8时y1=480，y2=0，∴y1﹣y2=480．（3）当两车相遇时耗时为x，y1=y2，解得x=，S=y2﹣y1=﹣160x+600（0≤x≤）S=y1﹣y2=160x﹣600（＜x≤6）S=60x（6＜x≤10）；（4）由题意得：S=200，①当0≤x≤时，﹣160x+600=200，∴x=，∴y1=60x=150．②当＜x≤6时160x﹣600=200，∴x=5，∴y1=300，③当6＜x≤10时，60x≥360不合题意．即：A加油站到甲地距离为150km或300km．【点评】本题通过考查一次函数的应用来考查从图象上获取信息的能力．借助函数图象表达题目中的信息，读懂图象是关键．注意自变量的取值范围不能遗漏．7．我国是世界上严重缺水的国家之一．为了增强居民节水意识，某市自来水公司对居民用水采用以户为单位分段计费办法收费．即一月用水10吨以内（包括10吨）的用户，每吨收水费a元；一月用水超过10吨的用户，10吨水仍按每吨a元收费，超过10吨的部分，按每吨b元（b＞a）收费．设一户居民月用水x吨，应收水费y元，y与x之间的函数关系如图所示．（1）求a的值；某户居民上月用水8吨，应收水费多少元；（2）求b的值，并写出当x＞10时，y与x之间的函数关系式；（3）已知居民甲上月比居民乙多用水4吨，两家共收水费46元，求他们上月分别用水多少吨？【考点】一次函数的应用；二元一次方程组的应用；分段函数．【分析】（1）由图中可知，10吨水出了15元，那么a=15÷10=1.5元，用水8吨，应收水费1.5×8元；（2）由图中可知当x＞10时，有y=b（x﹣10）+15．把（20，35）代入一次函数解析式即可．（3）应先判断出两家水费量的范围．【解答】解：（1）a=15÷10=1.5．（1分）用8吨水应收水费8×1.5=12（元）．（2分）（2）当x＞10时，有y=b（x﹣10）+15．（3分）将x=20，y=35代入，得35=10b+15．b=2．（4分）故当x＞10时，y=2x﹣5．（5分）（3）∵假设甲乙用水量均不超过10吨，水费不超过46元，不符合题意；假设乙用水10吨，则甲用水14吨，∴水费是：1.5×10+1.5×10+2×4＜46，不符合题意；∴甲、乙两家上月用水均超过10吨．（6分）设甲、乙两家上月用水分别为x吨，y吨，则甲用水的水费是（2x﹣5）元，乙用水的水费是（2y﹣5）元，则（8分）解得：（9分）故居民甲上月用水16吨，居民乙上月用水12吨．（10分）【点评】本题主要考查了一次函数与图形的结合，应注意分段函数的计算方法．二、利用函数的增减性解决问题8．某饮料厂为了开发新产品，用A种果汁原料和B种果汁原料试制新型甲、乙两种饮料共50千克，设甲种饮料需配制x千克，两种饮料的成本总额为y元．（1）已知甲种饮料成本每千克4元，乙种饮料成本每千克3元，请你写出y与x之间的函数关系式．（2）若用19千克A种果汁原料和17.2千克B种果汁原料试制甲、乙两种新型饮料，下表是试验的相关数据；请你列出关于x且满足题意的不等式组，求出它的解集，并由此分析如何配制这两种饮料，可使y值最小，最小值是多少？甲乙每千克饮料果汁含量果汁A 0.5千克0.2千克B 0.3千克0.4千克【考点】一元一次不等式组的应用．【专题】应用题；压轴题．【分析】（1）由题意可知y与x的等式关系：y=4x+3（50﹣x）化简即可；（2）根据题目条件可列出不等式方程组，推出y随x的增大而增大，根据实际求解．【解答】解：（1）依题意得y=4x+3（50﹣x）=x+150；（2）依题意得解不等式（1）得x≤30解不等式（2）得x≥28∴不等式组的解集为28≤x≤30∵y=x+150，y是随x的增大而增大，且28≤x≤30∴当甲种饮料取28千克，乙种饮料取22千克时，成本总额y最小，即y最小=28+150=178元．【点评】解决问题的关键是读懂题意，找到关键描述语，进而找到所求的量的等量关系．注意本题的不等关系为：甲种果汁不超过19，乙种果汁不超过17.2．9．某厂工人小王某月工作的部分信息如下：信息一：工作时间：每天上午8：00～12：00，下午14：00～18：00，每月25天；信息二：生产甲、乙两种产品，并且按规定每月生产甲产品的件数不少于60件．生产产品件数与所用时间之间的关系见下表：生产甲产品数（件）生产乙产品数（件）所用时间（分）10 10 35030 20 850信息三：按件计酬，每生产一件甲产品可得1.50元，每生产一件乙产品可得2.80元．根据以上信息，回答下列问题：（1）小王每生产一件甲种产品，每生产一件乙种产品分别需要多少分；（2）小王该月最多能得多少元此时生产甲、乙两种产品分别多少件．【考点】二元一次方程组的应用；一次函数的应用．【专题】压轴题；阅读型；图表型．【分析】（1）设生产一件甲种产品需x分，生产一件乙种产品需y分，利用待定系数法求出x，y的值．（2）设生产甲种产品用x分，则生产乙种产品用（25×8×60﹣x）分，分别求出甲乙两种生产多少件产品．【解答】解：（1）设生产一件甲种产品需x分，生产一件乙种产品需y分．由题意得：（2分）即：解这个方程组得：答：生产一件甲产品需要15分，生产一件乙产品需要20分．（4分）（2）设生产甲种产品共用x分，则生产乙种产品用（25×8×60﹣x）分．则生产甲种产品件，生产乙种产品件．（5分）∴w总额===0.1x+1680﹣0.14x=﹣0.04x+1680（7分）又，得x≥900，由一次函数的增减性，当x=900时w取得最大值，此时w=0.04×900+1680=1644（元）此时甲有（件），乙有：（件）（9分）答：小王该月最多能得1644元，此时生产甲、乙两种产品分别60，555件．【点评】通过表格当中的信息，我们可以利用列方程组来求出生产甲、乙两种产品的时间，然后利用列函数关系式表示出小王得到的总钱数，然后利用一次函数的增减性求出钱数的最大值．10．“5.12”汶川特大地震灾害发生后，社会各界积极为灾区捐款捐物，某经销商在当月销售的甲种啤酒尚有2万元货款未收到的情况下，先将销售甲种啤酒全部应收货款的70%捐给了灾区，后又将该月销售乙种啤酒所得的全部货款的80%捐给了灾区．已知该月销售甲、乙两种啤酒共5000件，甲种啤酒每件售价为50元，乙种啤酒每件售价为35元，设该月销售甲种啤酒x件，共捐助救灾款y元．（1）该经销商先捐款元，后捐款元；（用含x的式子表示）（2）写出y与x的函数关系式，并求出自变量x的取值范围；（3）该经销商两次至少共捐助多少元？【考点】一次函数的应用．【专题】压轴题．【分析】（1）根据题意可直接得出经销商先捐款50x•70%=35x元，后捐款35（5000﹣x）•80%或（140000﹣28x）元；（2）根据题意可列出式子为y=7x+140000，根据“50x﹣20000≥0”，“5000﹣x＞0”求出自变量取值范围为400≤x＜5000；（3）当x=400时，y最小值=142800．【解答】解：（1）50x•70%或35x，35（5000﹣x）•80%或（140000﹣28x）；（2）y与x的函数关系式为：y=7x+140000，由题意得解得400≤x＜5000，∴自变量x的取值范围是400≤x＜5000；（3）∵y=7x+140000是一个一次函数，且7＞0，400≤x＜5000，∴当x=400时，y最小值=142800．答：该经销商两次至少共捐款142800元．【点评】主要考查利用一次函数的模型解决实际问题的能力．要先根据题意列出函数关系式，再代数求值．解题的关键是要分析题意根据实际意义求解．注意要根据自变量的实际范围确定函数的最值．11．为支持四川抗震救灾，重庆市A、B、C三地现在分别有赈灾物资100吨、100吨、80吨，需要全部运往四川重灾地区的D、E两县．根据灾区的情况，这批赈灾物资运往D县的数量比运往E县的数量的2倍少20吨．（1）求这批赈灾物资运往D、E两县的数量各是多少？（2）若要求C地运往D县的赈灾物资为60吨，A地运往D的赈灾物资为x吨（x为整数），B地运往D县的赈灾物资数量小于A地运往D县的赈灾物资数量的2倍．其余的赈灾物资全部运往E县，且B地运往E县的赈灾物资数量不超过25吨．则A、B两地的赈灾物资运往D、E两县的方案有几种？请你写出具体的运送方案；（3）已知A、B、C三地的赈灾物资运往D、E两县的费用如下表：A地B地C地运往D县的费用（元/吨）220 200 200运往E县的费用（元/吨）250 220 210为及时将这批赈灾物资运往D、E两县，某公司主动承担运送这批赈灾物资的总费用，在（2）问的要求下，该公司承担运送这批赈灾物资的总费用最多是多少？【考点】一元一次不等式组的应用；一次函数的应用．【专题】压轴题；方案型．【分析】（1）设这批赈灾物资运往D县的数量为a吨，运往E县的数量为b吨，得到一个二元一次方程组，求解即可．（2）根据题意得到一元二次不等式，再找符合条件的整数值即可．（3）求出总费用的函数表达式，利用函数性质可求出最多的总费用．【解答】解：（1）设这批赈灾物资运往D县的数量为a吨，运往E县的数量为b吨．（1分）由题意，得（2分）解得（3分）答：这批赈灾物资运往D县的数量为180吨，运往E县的数量为100吨．（4分）（2）由题意，得（5分）解得即40＜x≤45．∵x为整数，∴x的取值为41，42，43，44，45．（6分）则这批赈灾物资的运送方案有五种．具体的运送方案是：方案一：A地的赈灾物资运往D县41吨，运往E县59吨；B地的赈灾物资运往D县79吨，运往E县21吨．。
一次函数综合题(解析版)--2024年中考数学压轴题专项训练
一次函数综合题通用的解题思路：(1)一次函数与几何图形的面积问题首先要根据题意画出草图，结合图形分析其中的几何图形，再求出面积．(2)一次函数的优化问题通常一次函数的最值问题首先由不等式找到x 的取值范围，进而利用一次函数的增减性在前面范围内的前提下求出最值．(3)用函数图象解决实际问题从已知函数图象中获取信息，求出函数值、函数表达式，并解答相应的问题．1(2024•鼓楼区一模)如图，直线y =-3x +6与⊙O 相切，切点为P ，与x 轴y 轴分别交于A 、B 两点．⊙O 与x 轴负半轴交于点C ．(1)求⊙O 的半径；(2)求图中阴影部分的面积．【分析】(1)由OP =OA ⋅sin60°，即可求解；(2)由图中阴影部分的面积=S 扇形COP -S ΔPOC ，即可求解．【解答】解：(1)对于直线y =-3x +6，令y =-3x +6=0，则x =23，即OA =23，由一次函数的表达式知，OB =6，则tan ∠BAC =OB AO =623=3，则∠BAC =60°连接OP ，则OP ⊥AB ，则OP =OA ⋅sin60°=23×32=3；(2)过点P 作PH ⊥AC 于点H ，∵∠POH =30°，则∠POC =150°，PH =12OP =32，则图中阴影部分的面积=S 扇形COP -S ΔPOC =150°360°×π×32-12×3×32=15π-94．【点评】本题考查了一次函数和圆的综合运用，涉及到圆切线的和一次函数的性质，解直角三角形，面积的计算等，综合性强，难度适中．2(2023•宿豫区三模)如图①，在平面直角坐标系中，直线l 1:y =x +1与直线l 2:x =-2相交于点D ，点A 是直线l 2上的动点，过点A 作AB ⊥l 1于点B ，点C 的坐标为(0,3)，连接AC ，BC ．设点A 的纵坐标为t ，ΔABC 的面积为s ．(1)当t =2时，求点B 的坐标；(2)s 关于t 的函数解析式为s =14t 2+bt -54t -1或t 5 a t +1 t -5 (-1<t <5)，其图象如图②所示，结合图①、②的信息，求出a 与b 的值；(3)在直线l 2上是否存在点A ，使得∠ACB =90°，若存在，请求出此时点A 的坐标；若不存在，请说明理由．【分析】(1)解法一：先根据t =2可得点A (-2,2)，因为B 在直线l 1上，所以设B (x ,x +1)，利用y =0代入y =x +1可得G 点的坐标，在Rt ΔABG 中，利用勾股定理列方程可得点B 的坐标；解法二：根据可以使用y =x +1与x 轴正半轴夹角为45度来解答；(2)先把(7,4)代入s =14t 2+bt -54中计算得b 的值，计算在-1<t <5范围内图象上一个点的坐标值：当t =2时，根据(1)中的数据可计算此时s =94，可得坐标2,94，代入s =a (t +1)(t -5)中可得a 的值；(3)存在，设B (x ,x +1)，如图5和图6，分别根据两点的距离公式和勾股定理列方程可解答．【解答】解：(1)解法一：如图1，连接AG ，当t =2时，A (-2,2)，设B (x ,x +1)，在y =x +1中，当x =0时，y =1，∴G (0,1)，∵AB ⊥l 1，∴∠ABG =90°，∴AB 2+BG 2=AG 2，即(x +2)2+(x +1-2)2+x 2+(x +1-1)2=(-2)2+(2-1)2，解得：x 1=0(舍)，x 2=-12，∴B -12，12；解法二：如图1-1，过点B 作BE ⊥x 轴于E ，过点A 作AH ⊥BE 于H ，当x =0时，y =1，当y =0时，x +1=0，则x =-1，∴OF =OG =1，∵∠GOF =90°，∴∠OGF =∠OFG =45°，∴BE =EF ，∵∠ABD =90°，∴∠ABH =∠BAH =45°，∴ΔABH 是等腰直角三角形，∴AH =BH ，当t =2时，A (-2,2)，设B (x ,x +1)，∴x +2=2-(x +1)，∴x =-12，∴B -12，12 ；(2)如图2可知：当t =7时，s =4，把(7,4)代入s =14t 2+bt -54中得：494+7b -54=4，解得：b =-1，如图3，过B 作BH ⎳y 轴，交AC 于H ，由(1)知：当t =2时，A (-2,2)，B -12，12 ，∵C (0,3)，设AC 的解析式为：y =kx +n ，则-2k +n =2n =3 ，解得k =12n =3 ，∴AC 的解析式为：y =12x +3，∴H -12，114，∴BH =114-12=94，∴s=12BH⋅|x C-x A|=12×94×2=94，把2,9 4代入s=a(t+1)(t-5)得：a(2+1)(2-5)=94，解得：a=-1 4；(3)存在，设B(x,x+1)，当∠ACB=90°时，如图5，∵∠ABD=90°，∠ADB=45°，∴ΔABD是等腰直角三角形，∴AB=BD，∵A(-2,t)，D(-2,-1)，∴(x+2)2+(x+1-t)2=(x+2)2+(x+1+1)2，(x+1-t)2=(x+2)2，x+1-t=x+2或x+1-t=-x-2，解得：t=-1(舍)或t=2x+3，RtΔACB中，AC2+BC2=AB2，即(-2)2+(t-3)2+x2+(x+1-3)2=(x+2)2+(x+1-t)2，把t=2x+3代入得：x2-3x=0，解得：x=0或3，当x=3时，如图5，则t=2×3+3=9，∴A(-2,9)；当x=0时，如图6，此时，A(-2,3)，综上，点A的坐标为：(-2,9)或(-2,3)．【点评】本题考查二次函数综合题、一次函数的性质、等腰直角三角形的判定和性质、三角形的面积、两点间距离公式等知识，解题的关键是灵活运用所学知识解决问题．3(2023•溧阳市一模)如图1，将矩形AOBC放在平面直角坐标系中，点O是原点，点A坐标为(0,4)，点B坐标为(5,0)，点P是x轴正半轴上的动点，连接AP，ΔAQP是由ΔAOP沿AP翻折所得到的图形．(1)当点Q落在对角线OC上时，OP= 165 ；(2)当直线PQ经过点C时，求PQ所在的直线函数表达式；(3)如图2，点M是BC的中点，连接MP、MQ．①MQ的最小值为；②当ΔPMQ是以PM为腰的等腰三角形时，请直接写出点P的坐标．【分析】(1)通过Q 点在OC 上，可以通过∠BOC 的三角函数和∠OAP 的三角函数来导出对应的边的关系，求得结果；(2)通过直角ΔAQC 中，得到QC 的长度，然后通过OP =PQ =x ，可以在Rt ΔBCP 中，得到对应的x 值然后求出结果；(3)通过QA =OA =4，可得出Q 点的运动轨迹，是以A 点为圆心，4为半径长度的圆弧，从而可知，MA 的连线上的Q 点为最短的MQ 长度，通过分类讨论，PM =PQ ，PM =QM ，PQ =QM 来求得对应的P 的坐标．【解答】解：(1)如图1，∵∠OAP +∠AOE =90°，∠BOC +∠AOE =90°，∴∠OAP =∠BOC ，又∵∠AOP =∠OBC =90°，∴ΔOAP ∽ΔBOC ，∴OP BC =OA OB ，即OP 4=45，∴OP =165，故答案为：165；(2)如图，∵AQ ⊥PQ ，∴∠AQC =90°，∴QC =AC 2-AQ 2=52-42=3，∵AQ =AO =4，设OP =PQ =x ，则CP =3+x ，PB =5-x ，∴CP 2=BP 2+BC 2，(3+x )2=(5-x )2+42，x =2，∴P 点的坐标为(2,0)，将P (2,0)和C (5,4)代入y =kx +b 中，0=2k +b 4=5k +b ，解得：k =43b =-83，∴PQ 所在直线的表达式为：y =43x -83；(3)如图，①∵AQ =AO =4，∴Q 点的运动轨迹，是以A 为圆心，4为半径的圆弧，∴MQ 的最小值在AM 的连线上，如图，MQ ′即为所求，∵M 是BC 中点，CM =12BC =2，∴AM =52+22=29，MQ ′=MA -AQ ′=29-4，故答案为：29-4；②如图，设OP =PQ =x ，BP =5-x ，∴PM 2=(5-x )2+22=x 2-10x +29，当PM =PQ 时，PM 2=PQ 2，∴x 2-10x +29=x 2，x =2910，∴P 2910，0，当MP =MQ 时，如图，若点Q 在AC 上，则AQ =OA =4，∵MP =MQ ，MB =MC ，∠PBM =∠QCM ，∴ΔPMB ≅ΔQMC (HL )，∴PB =QC ，QC =AC -AQ =5-4=1，∴PB =1，∴OP =BO -PB =5-1=4，∴P (4,0)；若点Q 在AC 上方时，由对称性可知OM =MQ ，∵MQ =MQ ，∴MO =MP ，∴P (10,0)；当MQ =PQ 时，不符合题意，不成立，故P 点坐标为P 2910，0或P (4,0)或(10,0)．【点评】本题考查一次函数的图象及应用，通过一次函数坐标图象的性质，三角函数的性质，全等三角形的性质和勾股定理，来求得对应的解．4(2022•启东市模拟)我们知道一次函数y =mx +n 与y =-mx +n (m ≠0)的图象关于y 轴对称，所以我们定义：函数y =mx +n 与y =-mx +n (m ≠0)互为“M ”函数．(1)请直接写出函数y =2x +5的“M ”函数；(2)如果一对“M ”函数y =mx +n 与y =-mx +n (m ≠0)的图象交于点A ，且与x 轴交于B ，C 两点，如图所示，若∠BAC =90°，且ΔABC 的面积是8，求这对“M ”函数的解析式；(3)在(2)的条件下，若点D 是y 轴上的一个动点，当ΔABD 为等腰三角形时，请求出点D 的坐标．【分析】(1)根据互为“M ”函数的定义，直接写出函数y =2x +5的“M ”函数；(2)现根据已知条件判断ΔABC 为等腰直角三角形，再根据互为“M ”函数的图象关于y 轴对称，得出OA =OB =OC ，再根据函数解析式求出点A 、B 、C 的坐标，再根据ΔABC 的面积是8求出m 、n 的值，从而求出函数解析式；(3)ΔABD 为等腰三角形，分以A 为顶点，以B 为顶点，以D 为顶点三种情况讨论即可．【解答】(1)解：根据互为“M ”函数的定义，∴函数y =2x +5的“M ”函数为y =-2x +5；(2)解：根据题意，y =mx +n 和y =-mx +n 为一对“M 函数”．∴AB =AC ，又∵∠BAC =90°，∴ΔABC 为等腰直角三角形，∴∠ABC =∠ACB =45°，∵OB =OC ，∴∠BAO =∠CAO =45°，∴OA =OB =OC ，又∵S ΔABC =12×BC ×AO =8且BC =2AO ，∴AO =22，∵A 、B 、C 是一次函数y =mx +n 与y =-mx +n (m ≠0)的图象于坐标轴的交点，∴A (0,n )，B -n m ，0 ，C n m ，0，∵OA =OB =n ，∴n m=22，∴m =1，∴y =x +22和y =-x +22；(3)解：根据等腰三角形的性质，分情况，∵AO =BO =22，∴AB =4，由(2)知，A (0，22)，B (-22，0)，C (22，0)，∴①以A 为顶点，则AB =AD ，当点D 在点A 上方时，AD =22+4，当点D 在点A 下方时，AD =22-4，∴D 1(0，22+4)，D 2(0，22-4)，②以B 为顶点，则BA =BD ，此时点D 在y 轴负半轴，∴D 3(0,-22)，③以D 为顶点，则DA =DB ，此时D 为坐标原点，∴D 4(0,0)．∴D 点坐标为D 1(0，22+4)，D 2(0，22-4)，D 3(0,-22)，∴D 4(0,0)．【点评】本题考查一次函数的综合应用，以及新定义、等腰三角形的性质等知识，关键是理解新定义，用新定义解题．5(2024•新北区校级模拟)如图①，动点P 从矩形ABCD 的顶点A 出发，以v 1的速度沿折线A -B -C 向终点C 运动；同时，一动点Q 从点D 出发，以v 2的速度沿DC 向终点C 运动，当一个点到达终点时，另一个点也停止运动．点E 为CD 的中点，连接PE ，PQ ，记ΔEPQ 的面积为S ，点P 运动的时间为t ，其函数图象为折线MN -NF 和曲线FG (图②)，已知，ON =4，NH =1，点G 的坐标为(8,0)．(1)点P 与点Q 的速度之比v 1v 2的值为 85 ；AB AD的值为；(2)如果OM =15．①求线段NF 所在直线的函数表达式；②求FG 所在曲线的函数表达式；③是否存在某个时刻t ，使得S ≥154？若存在，求出t 的取值范围：若不存在，请说明理由．【分析】(1)由函数图象可知t =3时，Q 与E 重合，t =4时，P 与B 重合，t =6时，P 与C 重合，则Q 的速度v 2=DE 4，P 的速度v 1=AB 4，从而得出答案；(2)①当t =0时，P 与A 重合，Q 与D 重合，此时S ΔADE =2，可得AD =BC =DE =15，AB =CD =53AD =10，从而得出点P 与Q 的速度，即可得出点F 的坐标，利用待定系数法可得答案；②设FG 所在的曲线的数解析式为S =a (t -6)2+k (a ≠0)，把F 5,154，G (8,0)代入解析式求得a ，k 值即可求解答；③利用待定系数法求出直线MN 的函数解析式，当S =154时，可得t 的值，根据图象可得答案．【解答】解：(1)∵ON =4，NH =1，G (8,0)，∴N (4,0)，H (5,0)，由图象可知：t =4时，Q 与E 重合，t =5时，P 与B 重合，t =8时，P 与C 重合，∴Q 的速度v 2=DE 4，P 的速度v 1=AB 5，∵四边形ABCD 是矩形，∴AB =CD ，AD =BC ，∵E 为CD 的中点，∴DE =12CD =12AB ，∴v 1v 2=AB5DE 4=AB 5⋅4DE =85，∵P 从A 到B 用了5秒，从B 到C 用了3秒，∴AB =5v 1，BC =3v 1，∴AB =53BC ，∴AB :AD 的值为53，故答案为：85，53；(2)①∵OM =15，∴M (0,15)，由题知，t =0时，P 与A 重合，Q 与D 重合，∴S ΔEPQ =12AD ⋅DE =15，∵AB :AD =53，DE =12AB ，∴DE =56AD ，∴12AD ⋅56AD =15，∴AD =BC =6(舍去负值)，∴AB =CD =53AD =10，∴v 2=DE 4=54，当t =5时，DQ =v 2t =54×5=254，∴QE =DQ -DE =254-5=54，此时P 与B重合，∴S ΔEPQ =12EQ ⋅BC =12×54×6=154，∴F 5,154 ，设直线NF 的解析式为S =kt +b (k ≠0)，将N (4,0)与F 5,154 代入得：4k +b =05k +b =154，∴k =154b =-15 ，∴线段NF 所在直线的函数表达式为S =154t -15(4<t ≤5)；②设FG所在的曲线的数解析式为S=1254t-5(16-2t)=-54t2+15t-40，∴FG所在的曲线的函数解析式为S=-54t2+15t-40(5≤t≤8)；③存在，分情况讨论如下：当Q在DE上，P在AB上时，∵直线MN经过点M(0,15)，N(4,0)，可求得直线MN的解析式为S=-54t+15(0≤t≤4)，当s=154时，-154t+15=154，∴x=3，∵s随x的增大而减小，∴当0≤x≤3时，S≥154，当Q在CE上，P在BC上时，直线NF的解析式为S=154t-15(4<t≤5)；由F5,15 4知：当t=5时，S=154，当S=154时，-54t2+15t-40=154，∴t=7或5，由图象知：当5≤x≤7，x的取值范围为0≤t≤3或5≤t≤7．【点评】本题是一次函数综合题，主要考查了待定系数法求函数解析式，三角形的面积，矩形的性质等知识，理解函数图象中每一个拐点的意义是解题的关键．6(2024•梁溪区校级模拟)在平面直角坐标系xOy 中，二次函数y =-ax 2+3ax +4a 的图象与x 轴交于A 、B 两点(点A 在点B 的左侧)，与y 轴正半轴交于点C ，直线y =12x 交于第一象限内的D 点，且ΔABC 的面积为10．(1)求二次函数的表达式；(2)点E 为x 轴上一点，过点E 作y 轴的平行线交线段OD 于点F ，交抛物线于点G ，当GF =5OF 时，求点G 的坐标；(3)已知点P (n ,0)是x 轴上的点，若点P 关于直线OD 的对称点Q 恰好落在二次函数的图象上，求n 的值．【分析】(1)在y =-ax 2+3ax +4a 中，令y =0得A (-1,0)，B (4,0)，根据ΔABC 的面积为10，即得OC =4，C (0,4)，用待定系数法即得二次函数的表达式为y =-x 2+3x +4；(2)设E (m ,0)，则F m ,12m ，G (m ,-m 2+3m +4)，由GF =5OF ，可得-m 2+52m +4=5×52m ，即可解得G (2,6)；(3)连接PQ 交直线OD 于K ，过Q 作QT ⊥x 轴于T ，设Q (r ,s )，可得K n +r 2，s 2 ，即得s 2=12×n +r 2，n +r =2s ①，又r 2+s 2=n 2，(n +r )(n -r )=s 2②，可解得r =35n ，s =45n ，故Q 35n ，45n ，代入y =-x 2+3x +4得45n =-35n 2+3×35n +4，解得n =5或n =-209．【解答】解：(1)如图：在y =-ax 2+3ax +4a 中，令y =0得-ax 2+3ax +4a =0，解得x =4或x =-1，∴A (-1,0)，B (4,0)，∴AB =5，∵ΔABC 的面积为10，∴12AB ⋅OC =10，即12×5⋅OC =10，∴OC =4，∴C (0,4)，把C (0,4)代入y =-ax 2+3ax +4a 得：4a =4，∴a =1，∴二次函数的表达式为y =-x 2+3x +4；(2)如图：设E (m ,0)，则F m ,12m ，G (m ,-m 2+3m +4)，∴OF =m 2+12m 2=52m ，GF =-m 2+3m +4-12m =-m 2+52m +4，∵GF =5OF ，∴-m 2+52m +4=5×52m ，解得m =2或m =-2(舍去)，∴G (2,6)；(3)连接PQ 交直线OD 于K ，过Q 作QT ⊥x 轴于T ，如图：∵P (n ,0)关于直线对称点为Q ，∴OQ =OP =|n |，K 是PQ 中点，设Q (r ,s )，∴K n +r 2，s 2，∵K 在直线y =12x 上，∴s 2=12×n +r 2，整理得：n +r =2s ①，∵OT 2+QT 2=OQ 2，∴r 2+s 2=n 2，变形得：(n +r )(n -r )=s 2②，把①代入②得：2s (n -r )=s 2，∵s ≠0，∴n -r =s2③，由①③可得r =35n ，s =45n ，∴Q 35n ，45n ，∵Q 在抛物线y =-x 2+3x +4上，∴45n =-35n 2+3×35n +4，解得n =5或n =-209，答：n 的值为5或-209．【点评】本题考查一次函数、二次函数综合应用，涉及待定系数法，三角形面积，对称变换等知识，解题的关键是用含n 的代数式表示Q 的坐标．7(2023•邗江区校级一模)如图1，在平面直角坐标系中，直线l :y =-33x +43分别与x 轴、y 轴交于点A 点和B 点，过O 点作OD ⊥AB 于D 点，以OD 为边构造等边ΔEDF (F 点在x 轴的正半轴上)．(1)求A 、B 点的坐标，以及OD 的长；(2)将等边ΔEDF ，从图1的位置沿x 轴的正方向以每秒1个单位的长度平移，移动的时间为t (s )，同时点P 从E 出发，以每秒2个单位的速度沿着折线ED -DF 运动(如图2所示)，当P 点到F 点停止，ΔDEF 也随之停止．①t =3或6(s )时，直线l 恰好经过等边ΔEDF 其中一条边的中点；②当点P 在线段DE 上运动，若DM =2PM ，求t 的值；③当点P 在线段DF 上运动时，若ΔPMN 的面积为3，求出t 的值．【分析】(1)把x =0，y =0分别代入y =-33x +43，即可求出点A 、B 的坐标，求出∠BAO =30°，根据直角三角形的性质，即可得出OD =12OA =6；(2)①当直线l 分别过DE 、DF 、EF 的中点，分三种情况进行讨论，得出t 的值，并注意点P 运动的最长时间；②分点P 在直线l 的下方和直线l 上方两种情况进行讨论，求出t 的值即可；③分点P 在DN 之间和点P 在NF 之间两种情况进行讨论，求出t 的值即可．【解答】解：(1)令x =0，则y =43，∴点B 的坐标为(0,43)，令y =0，则-33x +43=0，解得x =12，∴点A 的坐标为(12,0)，∵tan ∠BAO =OB OA=4312=33，∴∠BAO =30°，∵OD ⊥AB ，∴∠ODA =90°，∴ΔODA 为直角三角形，∴OD =12OA =6；(2)①当直线l 过DF 的中点G 时，∵ΔDEF 为等边三角形，∴∠DFE =60°，∵∠BAO =30°，∴∠FGA =60°-30°=30°，∴∠FGA =∠BAO ，∴FA =FG =12DF =3，∴OF =OA -FA =9，∴OE =OF -EF =9-6=3，∴t =3；当l 过DE 的中点时，∵DE ⊥l ，DG =EG ，∴直线l 为DE 的垂直平分线，∵ΔDEF 为等边三角形，∴此时点F 与点A 重合，∴t =12-61=6；当直线l 过EF 的中点时，运动时间为t =12-31=9；∵点P 从运动到停止用的时间为：6+62=6，∴此时不符合题意；综上所述，当t =3s 或6s 时，直线l 恰好经过等边ΔEDF 其中一条边的中点，故答案为：3或6；②∵OE =t ，AE =12-t ，∠BAO =30°，∴ME =6-t2，∴DM =DE -EM =t2，∵EP =2t ，∴PD =6-2t ，当P 在直线l 的下方时，∵DM =23DP ，∴t 2=23(6-2t )，解得：t =2411；当P 在直线l 的上方时，∵DM =2DP ，∴t2=2(6-2t )，解得t =83；综上所述：t 的值为2411或83；③当3<t ≤6时，∵∠D =60°，∠DMN =90°，DM =t2，∴∠DNM =90°-60°=30°，∴MN =DM ×tan60°=32t ，DN =2DM =2×t2=t ，∵DP =2t -6，∴PN =DN -DP =t -(2t -6)=6-t ，∵∠DNM =30°，∴边MN 的高h =12PN =3-12t ，∵ΔPMN 的面积为3，∴12×32t 3-12t =3，整理得：t 2-6t +8=0，解得t =2(舍)或t =4当点P 在NF 之间时，∵∠D =60°，∠DMN =90°，DM =t2，∴∠DNM =90°-60°=30°，∴MN =DM ×tan60°=32t ，DN =2DM =2×t2=t ，∵DP =2t -6，∴PN =DP -DN =2t -6-t =t -6，∵∠DNM =30°，∴∠FNA =∠DNM =30°，∴边MN 的高h =12PN =12t -3，∵ΔPMN 的面积为3，∴12×32t 12t -3 =3，解得t =3+17(舍)或t =3-17(舍)，综上所述，t 的值为4s ．【点评】本题主要考查了一次函数的性质、等边三角形的性质、直角三角形的性质、利用三角函数解直角三角形，熟练掌握含30°的直角三角形的性质并注意进行分类讨论是解题的关键．8(2023•武进区校级模拟)在平面直角坐标系xOy 中，对于任意两点P 1(x 1，y 1)与P 2(x 2，y 2)的“非常距离”，给出如下定义：若|x 1-x 2|≥|y 1-y 2|，则点P 1与点P 2的“非常距离”为|x 1-x 2|；若|x 1-x 2|<|y 1-y 2|，则点P 1与点P 2的“非常距离”为|y 1-y 2|．例如：点P 1(1,2)，点P 2(3,5)，因为|1-3|<|2-5|，所以点P 1与点P 2的“非常距离”为|2-5|=3，也就是图1中线段P 1Q 与线段P 2Q 长度的较大值(点Q 为垂直于y 轴的直线P 1Q 与垂直于x 轴的直线P 2Q 交点)．(1)已知点A -12，0，B 为y 轴上的一个动点，①若点A 与点B 的“非常距离”为2，写出一个满足条件的点B 的坐标；②直接写出点A 与点B 的“非常距离”的最小值；(2)已知C 是直线y =34x +3上的一个动点，①如图2，点D 的坐标是(0,1)，求点C 与点D 的“非常距离”的最小值及相应的点C 的坐标；②如图3，E 是以原点O 为圆心，1为半径的圆上的一个动点，求点C 与点E 的“非常距离”的最小值及相应的点E 与点C 的坐标．【分析】(1)①根据点B 位于y 轴上，可以设点B 的坐标为(0,y )．由“非常距离”的定义可以确定|0-y |=2，据此可以求得y 的值；②设点B 的坐标为(0,y )．因为-12-0 ≥|0-y |，所以点A 与点B 的“非常距离”最小值为-12-0 =12；(2)①设点C 的坐标为x 0，34x 0+3 ．根据材料“若|x 1-x 2|≥|y 1-y 2|，则点P 1与点P 2的“非常距离”为|x 1-x 2|”知，C 、D 两点的“非常距离”的最小值为-x 0=34x 0+2，据此可以求得点C 的坐标；②根据“非常距离”的定义，点E 在过原点且与直线y =34x +3垂直的直线上，且C 与E 的横纵坐标差相等时，点C 与点E 的“非常距离”取最小值，据此求出C 与E 的坐标及“非常距离”的最小值．【解答】解：(1)①∵B 为y 轴上的一个动点，∴设点B 的坐标为(0,y )．∵-12-0 =12≠2，∴|0-y |=2，解得，y =2或y =-2；∴点B 的坐标是(0,2)或(0,-2)；②点A 与点B 的“非常距离”的最小值为12．(2)①如图2，当点C 与点D 的“非常距离”取最小值时，需要根据运算定义“若|x 1-x 2|≥|y 1-y 2|，则点P 1与点P 2的“非常距离”为|x 1-x 2|”解答，此时|x 1-x 2|=|y 1-y 2|．即AC =AD ，∵C 是直线y =34x +3上的一个动点，点D 的坐标是(0,1)，∴设点C 的坐标为x 0，34x 0+3 ，∴-x 0=34x 0+2，此时，x 0=-87，∴点C 与点D 的“非常距离”的最小值为：|x 0|=87，此时C -87，157；②如图3，当点E 在过原点且与直线y =34x +3垂直的直线上，且CF =EF 时，点C 与点E 的“非常距离”最小，设E (x ,y )(点E 位于第二象限)．则y x=-43x 2+y 2=1 ，解得x =-35y =45，故E -35，45．设点C 的坐标为x 0，34x 0+3 ，-35-x 0=34x 0+3-45，解得x0=-8 5，则点C的坐标为-8 5，95，点C与点E的“非常距离”的最小值为1．【点评】本题考查了一次函数综合题．对于信息给予题，一定要弄清楚题干中的已知条件．本题中的“非常距离”的定义是正确解题的关键．9(2023•海安市一模)对于平面直角坐标系xOy中的图形W和点P，给出如下定义：F为图形W上任意一点，将P，F两点间距离的最小值记为m，最大值记为M，称M与m的差为点P到图形W的“差距离”，记作d(P,W)，即d(P,W)=M-m，已知点A(2,1)，B(-2,1)(1)求d(O,AB)；(2)点C为直线y=-1上的一个动点，当d(C,AB)=1时，点C的横坐标是 (2-5)或(5-2，) ；(3)点D为函数y=x+b(-2≤x≤2)图象上的任意一点，当d(D,AB)≤2时，直接写出b的取值范围．【分析】(1)画出图形，根据点P到图形W的“差距离”的定义即可解决问题．(2)如图2中，设C(m,-1)．由此构建方程即可解决问题．(3)如图3中，取特殊位置当b=6时，当b=-4时，分别求解即可解决问题．【解答】解：(1)如图1中，∵A(2,1)，B(-2,1)，∴AB⎳x轴，∴点O到线段AB的最小距离为1，最大距离为5，∴d(O,AB)=5-1．(2)如图2中，设C(m,-1)．当点C在y轴的左侧时，由题意AC-2=1，∴AC=3，∴(2-m)2+22=9，∴m=2-5或2+5(舍弃)，∴C(2-5，-1)，当点C在y轴的右侧时，同法可得C(5-2，-1)，综上所述，满足条件的点C的坐标为(2-5，-1)或(5-2，-1)．故答案为：(2-5，-1)或(5-2，-1)．(3)如图3中，当b=6时，线段EF:y=x+6(-2≤x≤2)上任意一点D，满足d(D,AB)≤2，当b=-4时，线段E′F′:y=x-4(-2≤x≤2)上任意一点D′，满足d(D′,AB)≤2，观察图象可知：当b≥6或b≤-4时，函数y=x+b(-2≤x≤2)图象上的任意一点，满足d(D,AB)≤2．【点评】本题属于一次函数综合题，考查了一次函数的性质，点P到图形W的“差距离”的定义等知识，解题的关键是理解题意，学会利用参数解决问题，学会寻找特殊位置解决问题，属于中考创新题型．10(2022•姑苏区校级模拟)平面直角坐标系xOy中，对于任意的三个点A、B、C，给出如下定义：若矩形的任何一条边均与某条坐标轴平行，且A，B，C三点都在矩形的内部或边界上，则称该矩形为点A，B，C的“三点矩形”．在点A，B，C的所有“三点矩形”中，若存在面积最小的矩形，则称该矩形为点A，B，C的“最佳三点矩形”．如图1，矩形DEFG，矩形IJCH都是点A，B，C的“三点矩形”，矩形IJCH是点A，B，C的“最佳三点矩形”．如图2，已知M(4,1)，N(-2,3)，点P(m,n)．(1)①若m=2，n=4，则点M，N，P的“最佳三点矩形”的周长为18，面积为；②若m=2，点M，N，P的“最佳三点矩形”的面积为24，求n的值；(2)若点P在直线y=-2x+5上．①求点M，N，P的“最佳三点矩形”面积的最小值及此时m的取值范围；②当点M，N，P的“最佳三点矩形”为正方形时，求点P的坐标；(3)若点P(m,n)在抛物线y=ax2+bx+c上，当且仅当点M，N，P的“最佳三点矩形”面积为12时，-2≤m≤-1或1≤m≤3，直接写出抛物线的解析式．【分析】(1)①利用“最佳三点矩形”的定义求解即可，②利用“最佳三点矩形”的定义求解即可；(2)①利用“最佳三点矩形”的定义求得面积的最小值为12，②由“最佳三点矩形”的定义求得正方形的边长为6，分别将y=7，y=-3代入y=-2x+5，可得x分别为-1，5，点P的坐标为(-1,7)或(4,-3)；(3)利用“最佳三点矩形”的定义画出图形，可分别求得解析式．【解答】解：(1)①如图，画出点M，N，P的“最佳三点矩形”，可知矩形的周长为6+6+3+3=18，面积为3×6=18；故答案为：18，18．②∵M(4,1)，N(-2,3)，∴|x M-x N|=6，|y M-y N|=2．又∵m=2，点M，N，P的“最佳三点矩形”的面积为24．∴此矩形的邻边长分别为6，4．∴n=-1或5．(2)如图，①由图象可得，点M，N，P的“最佳三点矩形”面积的最小值为12；分别将y=3，y=1代入y=-2x+5，可得x分别为1，2；结合图象可知：1≤m≤2；②当点M，N，P的“最佳三点矩形”为正方形时，边长为6，分别将y=7，y=-3代入y=-2x+5，可得x分别为-1，4；∴点P的坐标为(-1,7)或(4,-3)；(3)设抛物线的解析式为y=ax2+bx+c，经过点(-1,1)，(1,1)，(3,3)，∴a -b +c =1a +b +c =19a +3b +c =3，a =14b =0c =34，∴y =14x 2+34，同理抛物线经过点(-1,3)，(1,3)，(3,1)，可求得抛物线的解析式为y =-14x 2+134，∴抛物线的解析式y =14x 2+34或y =-14x 2+134．【点评】本题主要考查了一次函数的综合题，涉及点的坐标，正方形及矩形的面积及待定系数法求函数解析式等知识，解题的关键是理解运用好“最佳三点矩形”的定义．11(2022•太仓市模拟)如图①，动点P 从矩形ABCD 的顶点A 出发，以v 1的速度沿折线A -B -C 向终点C 运动；同时，一动点Q 从点D 出发，以v 2的速度沿DC 向终点C 运动，当一个点到达终点时，另一个点也停止运动．点E 为CD 的中点，连接PE ，PQ ，记ΔEPQ 的面积为S ，点P 运动的时间为t ，其函数图象为折线MN -NF 和曲线FG (图②)，已知，ON =3，NH =1，点G 的坐标为(6,0)．(1)点P 与点Q 的速度之比v 1v 2的值为 32 ；AB :AD 的值为；(2)如果OM =2．①求线段NF 所在直线的函数表达式；②是否存在某个时刻t ，使得S ≥23？若存在，求出t 的取值范围；若不存在，请说明理由．【分析】(1)由函数图象可知t =3时，Q 与E 重合，t =4时，P 与B 重合，t =6时，P 与C 重合，则Q 的速度v 2=DE 3，P 的速度v 1=AB4，从而得出答案；(2)①当t =0时，P 与A 重合，Q 与D 重合，此时S ΔADE =2，可得AD =BC =DE =2，AB =CD =2AD =4，从而得出点P 与Q 的速度，即可得出点F 的坐标，利用待定系数法可得答案；②利用待定系数法求出直线MN 的函数解析式，当S =23时，可得t 的值，根据图象可得答案．【解答】解：(1)∵ON =3，NH =1，G (6,0)，∴N (3,0)，H (4,0)，由图象可知：t =3时，Q 与E 重合，t =4时，P 与B 重合，t =6时，P 与C 重合，∴Q 的速度v 2=DE 3，P 的速度v 1=AB4，∵四边形ABCD 是矩形，∴AB =CD ，AD =BC ，∵E 为CD 的中点，∴DE =12CD =12AB ，∴v 1v 2=AB4DE 3=AB 4⋅3DE =AB 4⋅312AB =32，∵P 从A 到B 用了4秒，从B 到C 用了2秒，∴AB =4v 1，BC =2v 1，∴AB =2BC ，∴AB :AD 的值为2，故答案为：32,2；(2)①∵OM =2，∴M (0,2)，由题知，t =0时，P 与A 重合，Q 与D 重合，∴S ΔEPQ =12AD ⋅DE =2，∵AB :AD =2，∴AD =DE =12AB ，∴12AD 2=2，∴AD =BC =DE =2，AB =CD =2AD =4，∴v 2=DE 3=23，当t =4时，DQ =v 2t =23×4=83，∴QE =DQ -DE =83-2=23，此时P 与B 重合，∴S ΔEPQ =12EQ ⋅BC =12×23×2=33，∴F 4,23，设直线NF 的解析式为S =kx +b (k ≠0)，将N (3,0)与F 4,23 代入得：3k +b =04k +b =23 ，∴k =23b =-2，∴线段NF 所在直线的函数表达式为S =23x -2(3<x ≤4)；②存在，分情况讨论如下：当Q 在DE 上，P 在AB 上时，∵直线MN 经过点M (0,2)，N (3,0)，同理求得直线MN 的解析式为S =-23x +2(0≤x ≤3)，当s =23时，-23x +2=2，∴x =2，∵s随x的增大而减小，∴当0≤x≤2时，S≥23，当Q在CE上，P在AB上时，直线NF的解析式为S=23x-2(3<x≤4)，由F4,2 3知：当x=4时，S=23，当Q在CE上，P在BC上时，SΔEPQ=12EQ⋅CP，∵DQ=v2t=23t，∴EQ=DQ-DE=23t-2，∵v1=AB4=44=1，∴AB+BP=v1t=t，∵AB+BC=4+2=6，∴CP=6-t，∴S=1223t-2(6-t)=-13t2+3t-6(4<x≤6)，当S=23时，-13t2+3t-6=23，∴t=4或5，由图象知：当4<x≤5时，S≥2 3，综上，S≥23时，x的取值范围为0≤x≤2或4≤x≤5．【点评】本题是一次函数综合题，主要考查了待定系数法求函数解析式，三角形的面积，矩形的性质等知识，理解函数图象中每一个拐点的意义是解题的关键．12(2022•邗江区校级一模)在平面直角坐标系xOy中，对于点P和线段ST，我们定义点P关于线段ST的线段比k=PSST(PS<PT)PTST(PS≥PT) ．(1)已知点A(0,1)，B(1,0)．①点Q(2,0)关于线段AB的线段比k= 22 ；②点C(0,c)关于线段AB的线段比k=2，求c的值．(2)已知点M(m,0)，点N(m+2,0)，直线y=x+2与坐标轴分别交于E，F两点，若线段EF上存在点使得这一点关于线段MN的线段比k≤14，直接写出m的取值范围．【分析】(1)①求出QA、QB、AB，根据线段比定义即可得到答案；②方法同①，分c>0和c≤0讨论；(2)分两种情况，画出图象，根据线段比定义，分别在M(N)为“临界点”时列出不等式，即可得到答案．【解答】解：(1)①∵A(0,1)，B(1,0)，Q(2,0)，∴AB=2，QA=5，QB=1，根据线段比定义点Q(2,0)关于线段AB的线段比k=QBAB=22；故答案为：22；②∵A (0,1)，B (1,0)，C (0,c )，∴AB =2，AC =|1-c |，BC =1+c 2，AC 2=1+c 2-2c ，BC 2=1+c 2，当c >0时，AC 2<BC 2，即AC <BC ，由C (0,c )关于线段AB 的线段比k =2可得：|1-c |2=2，解得c =3或c =-1(舍去)，∴c =3，当c ≤0时，AC 2≥BC 2，即AC ≥BC ，由C (0,c )关于线段AB 的线段比k =2可得：1+c 22=2，解得c =3(舍去)或c =-3，∴c =-3，综上所述，点C (0,c )关于线段AB 的线段比k =2，c =3或c =-3；(2)∵直线y =x +2与坐标轴分别交于E ，F 两点，∴E (-2,0)，F (0,2)，∵点M (m ,0)，点N (m +2,0)，∴MN =2，N 在M 右边2个单位，当线段EF 上的点到N 距离较小时，分两种情况：①当M 、N 在点E 左侧时，如图：线段EF 上存在点使得这一点关于线段MN 的线段比k ≤14，∴NE MN≤14，即-2-(m +2)2≤14，解得：m ≥-92，②当N 在E 右侧，M 在E 左侧时，过M 作MG ⊥EF 于G ，如图：线段EF 上存在点使得这一点关于线段MN 的线段比k ≤14，∴GM MN ≤14，即GM 2≤14，∴GM ≤12，而E (-2,0)，F (0,2)，∴∠FEO =45°，∴ΔHEM 时等腰直角三角形，∴GM =22EM ，∴22EM ≤12，即22[(m +2)-(-2)]≤12，解得m ≤-4+22，∴线段EF 上存在点使得这一点关于线段MN 的线段比k ≤14，线段EF 上的点到N 距离较小时，-92≤m ≤-4+22，当线段EF 上的点到M 距离较小时，也分两种情况：①当N 在E 右侧，M 在E 左侧时，如图：线段EF 上存在点使得这一点关于线段MN 的线段比k ≤14，∴ME MN≤14，即-2-m 2≤14，解得m ≥-52，②当M 、N 在点E 右侧时，过M 作MH ⊥EF 于H ，如图：线段EF 上存在点使得这一点关于线段MN 的线段比k ≤14，∴HM MN ≤14，即HM 2≤14，∴HM ≤12，而E (-2,0)，F (0,2)，∴∠FEO =45°，∴ΔHEM 时等腰直角三角形，∴HM =22EM ，∴22EM ≤12，即22[m -(-2)]≤12，解得：m ≤-2+22，∴线段EF 上存在点使得这一点关于线段MN 的线段比k ≤14，线段EF 上的点到M 距离较小时，-52≤m ≤-2+22，综上所述，线段EF 上存在点使得这一点关于线段MN 的线段比k ≤14，则-92≤m ≤-4+22或-52≤m ≤-2+22．【点评】本题考查一次函数应用，解题的关键是读懂线段比的定义，找出“临界点”列不等式．13(2022•泰州)定义：对于一次函数y 1=ax +b 、y 2=cx +d ，我们称函数y =m (ax +b )+n (cx +d )(ma +nc ≠0)为函数y 1、y 2的“组合函数”．(1)若m =3，n =1，试判断函数y =5x +2是否为函数y 1=x +1、y 2=2x -1的“组合函数”，并说明理由；(2)设函数y 1=x -p -2与y 2=-x +3p 的图像相交于点P ．①若m +n >1，点P 在函数y 1、y 2的“组合函数”图像的上方，求p 的取值范围；②若p ≠1，函数y 1、y 2的“组合函数”图像经过点P ．是否存在大小确定的m 值，对于不等于1的任意实数p ，都有“组合函数”图像与x 轴交点Q 的位置不变？若存在，请求出m 的值及此时点Q 的坐标；若不存在，请说明理由．【分析】(1)由y =5x +2=3(x +1)+(2x -1)，可知函数y =5x +2是函数y 1=x +1、y 2=2x -1的“组合函数”；(2)①由y =x -p -2y =-x +3p得P (2p +1,p -1)，当x =2p +1时，y =m (2p +1-p -2)+n (-2p -1+3p )=(p-1)(m +n )，根据点P 在函数y 1、y 2的“组合函数”图象的上方，有p -1>(p -1)(m +n )，而m +n >1，可得p <1；②由函数y 1、y 2的“组合函数” y =m (x -p -2)+n (-x +3p )图象经过点P ，知p -1=m (2p +1-p -2)+n (-2p -1+3p )，即(p -1)(1-m -n )=0，而p ≠1，即得n =1-m ，可得y =(2m -1)x +3p -(4p +2)m ，令y =0得(2m -1)x +3p -(4p +2)m =0，即(3-4m )p +(2m -1)x -2m =0，即可得m =34时，“组合函数”图象与x 轴交点Q 的位置不变，Q (3,0)．【解答】解：(1)函数y =5x +2是函数y 1=x +1、y 2=2x -1的“组合函数”，理由如下：∵3(x +1)+(2x -1)=3x +3+2x -1=5x +2，∴y =5x +2=3(x +1)+(2x -1)，∴函数y =5x +2是函数y 1=x +1、y 2=2x -1的“组合函数”；(2)①由y =x -p -2y =-x +3p得x =2p +1y =p -1 ，∴P (2p +1,p -1)，∵y 1、y 2的“组合函数”为y =m (x -p -2)+n (-x +3p )，∴x =2p +1时，y =m (2p +1-p -2)+n (-2p -1+3p )=(p -1)(m +n )，∵点P 在函数y 1、y 2的“组合函数”图象的上方，∴p -1>(p -1)(m +n )，∴(p -1)(1-m -n )>0，∵m +n >1，∴1-m -n <0，∴p -1<0，∴p <1；②存在m =34时，对于不等于1的任意实数p ，都有“组合函数”图象与x 轴交点Q 的位置不变，Q (3,0)，理由如下：由①知，P (2p +1,p -1)，∵函数y 1、y 2的“组合函数”y =m (x -p -2)+n (-x +3p )图象经过点P ，∴p -1=m (2p +1-p -2)+n (-2p -1+3p )，∴(p -1)(1-m -n )=0，∵p ≠1，∴1-m -n =0，有n =1-m ，∴y =m (x -p -2)+n (-x +3p )=m (x -p -2)+(1-m )(-x +3p )=(2m -1)x +3p -(4p +2)m ，令y =0得(2m -1)x +3p -(4p +2)m =0，变形整理得：(3-4m )p +(2m -1)x -2m =0，∴当3-4m =0，即m =34时，12x -32=0，∴x =3，∴m =34时，“组合函数”图象与x 轴交点Q 的位置不变，Q (3,0)．【点评】本题考查一次函数综合应用，涉及新定义，函数图象上点坐标的特征，一次函数与一次方程的关系等，解题的关键是读懂“组合函数“的定义．14(2024•钟楼区校级模拟)在同一平面内，具有一条公共边且不完全重合的两个全等三角形，我们称这两个三角形叫做“共边全等”．(1)下列图形中两个三角形不是“共边全等”是③；AB，点E、F分别在AC、BC边(2)如图1，在边长为6的等边三角形ABC中，点D在AB边上，且AD=13上，满足ΔBDF和ΔEDF为“共边全等”，求CF的长；(3)如图2，在平面直角坐标系中，直线y=-3x+12分别与直线y=x、x轴相交于A、B两点，点C是OB 的中点，P、Q在ΔAOB的边上，当以P、B、Q为顶点的三角形与ΔPCB“共边全等”时，请直接写出点Q 的坐标．【分析】(1)由于第③个图不符合共边要求，所以图③即为答案；(2)DF为两个全等三角形的公共边，由于F点在BC边上，E在AC边上，两个三角形的位置可以如图②，在公共边异侧，构成一个轴对称图形，也可以构成一个平行四边形(将图③的两条最长边重合形成)，分两类讨论，画出图形，按照图②构图，会得到一个一线三等角模型，利用相似，列出方程来解决，按照平行四边形构图，直接得到ΔADE为等边三角形，计算边长即可求得；(3)由题目要求，可以知道两个全等三角形的公共边为PB边，由于要构成ΔPCB，所以P点只能在OA和OB边上，当P在OA边上，两个三角形可以在PB同侧，也可以在PB异侧，当在PB异侧构图时，可以得到图3和图4，在图3中，当在PB同侧构图时，可以得到图6，当P在OB边上时，Q只能落在OA上，得到图7，利用已知条件，解三角形，即可求出Q点坐标．【解答】解：(1)①②均符合共边全等的特点，只有③，没有公共边，所以③不符合条件，∴答案是③；(2)①如图1，当ΔBDF≅ΔEFD，且是共边全等时，∠BFD=∠EDF，∴DE⎳BC，∵ΔABC是等边三角形，∴ΔADE是等边三角形，AB=2，∵AD=13∴DE=AE=BF=2，∴CF=BC-BF=4，②如图2，当ΔBDF≅ΔEDF，且是共边全等时，BD=DE=6-AD=4，∠DEF=∠B=60°，EF=BF，∴∠AED+∠FEC=120°，又∠AED+∠EDA=120°，。
人教版初二下《第19章一次函数》专项训练含答案
人教版初二下《第19章一次函数》专项训练含答案专训1.用一次函数巧解实际中方案设计的应用名师点金：做一件情况，有时有不同的方案，比较这些方案，从中选择最佳方案作为行动打算，是专门必要的．解决这些问题时，先要弄清题意，依照题意构建恰当的函数模型，求出自变量的取值范畴，然后再结合实际问题确定最佳方案．合理决策问题1．某商场打算投入一笔资金采购一批紧俏商品，经市场调研发觉，假如本月初出售，可获利10%，然后将本利再投资其他商品，到下月初又可获利10%；假如下月初出售可获利25%，但要支付仓储费8 000元．设商场投入资金x元，请你依照商场的资金情形，向商场提出合理化建议，说明何时出售获利较多．选择方案问题2．某教育行政部门打算今年暑假组织部分教师到外地进行学习，预订宾馆住宿时，有住宿条件一样的甲、乙两家宾馆供选择，其收费标准均为每人每天120元，同时各自推出不同的优待方案．甲家是35人(含35人)以内的按标准收费，超过35人的，超出部分按九折收费；乙家是45人(含45人)以内的按标准收费，超过45人的，超出部分按八折收费．假如你是那个部门的负责人，你应选择哪家宾馆更实惠些？最佳效益问题3．甲、乙两个商场出售相同的某种商品，每件售价均为3 000元，同时多买都有一定的优待．甲商场的优待条件是：第一件按原售价收费，其余每件优待30%；乙商场的优待条件是：每件优待25%.设所买商品为x件时，甲商场收费为y元，乙商场收费为y2元．1(1)分别求出y1，y2与x之间的关系式．(2)当甲、乙两个商场的收费相同时，所买商品为多少件？(3)当所买商品为5件时，应选择哪个商场更优待？请说明理由．专训2.全章热门考点整合应用名师点金：本章内容是中考的必考内容，要紧考查一次函数的图象与性质，求函数解析式及建立一次函数模型解决利润大小、方案选择等实际问题，题型涉及选择题、填空题与解答题．其热门考点可概括为：三个概念，两个图象，一个性质，四个关系，一个方法，两个应用．三个概念概念1变量与常量1．(1)设圆柱的底面半径R不变，圆柱的体积V与圆柱的高h的关系式是V ＝πR2h，在那个变化过程中常量和变量分别是什么？(2)设圆柱的高h不变，在圆柱的体积V与圆柱的底面半径R的关系式V＝πR2h中，常量和变量分别又是什么？概念2函数2．两个变量之间存在的关系式是y2＝x＋1(其中x是非负整数)，y是不是x 的函数？假如变为用含y的代数式表示x的形式，x是不是y的函数？请说明缘故．3．求下列函数中自变量的取值范畴：(1)y＝－12x2－x＋6；(2)y＝－112x－3；(3)y＝16x－9 3x－2.概念3一次函数4．当m，n为何值时，y＝(5m－3)x2－n＋(m＋n)是关于x的一次函数？当m，n为何值时，y是关于x的正比例函数？两个图象图象1函数的图象5．小张的爷爷每天坚持体育锤炼，星期天爷爷从家里跑步到公园，打了一会儿太极拳，然后沿原路慢步走到家，下面能反映当天爷爷离家的距离y(米)与时刻x(分钟)之间关系的大致图象是( )图象2一次函数的图象6．(中考·阜新)关于一次函数y＝kx＋k－1(k≠0)，下列叙述正确的是( )A．当0<k<1时，函数图象通过第一、二、三象限B．当k>0时，y随x的增大而减小C．当k<1时，函数图象一定交于y轴的负半轴D．函数图象一定通过点(－1，－2)7．若有理数a，b，c满足a＋b＋c＝0，且a＜b＜c，则函数y＝ax＋c的图象可能是( )一个性质8．已知点M(1，a)和点N(2，b)是一次函数y＝－2x＋1的图象上的两点，则a与b的大小关系是( )A．a＞b B．a＝bC．a＜b D．以上都不对9．已知一次函数的解析式是y＝(k－2)x＋12－3k.(1)当图象与y轴的交点位于原点下方时，判定函数值随着自变量的增大而变化的趋势；(2)假如函数值随着自变量的增大而增大，且函数图象与y轴的交点位于原点上方，确定满足条件的正整数k的值．四个关系关系1一次函数与正比例函数的关系10．下列函数中，哪些是一次函数？哪些是正比例函数？①y＝－2x－1；②y＝12x；③y＝2x；④y＝－x2－1；⑤2x－y＝0；⑥y＝－2(x－1)．11．如图，过A点的一次函数的图象与正比例函数y＝2x的图象相交于点B.(1)求一次函数的解析式；(2)判定点C(4，－2)是否在该一次函数的图象上，说明理由；(3)若该一次函数的图象与x轴交于D点，求△BOD的面积．(第11题)关系2 一次函数与一元一次方程的关系12．如图，在平面直角坐标系xOy 中，直线y ＝x ＋1与y ＝－34x ＋3交于点A ⎝ ⎛⎭⎪⎫87，157，两直线分别交x 轴于点B 和点C. (1)求点B ，C 的坐标； (2)求△ABC 的面积．(第12题)关系3 一次函数与二元一次方程(组)的关系13．下列各个选项中的网格差不多上边长为1的小正方形，利用函数的图象解方程5x －1＝2x ＋5，其中正确的是( )关系4 一次函数与不等式(组)的关系14．已知一次函数y ＝kx ＋3的图象通过点(1，4)．(1)求那个一次函数的解析式；(2)求关于x 的不等式kx ＋3≤6的解集．15．在同一平面直角坐标系中，画出一次函数y 1＝2x －4，y 2＝x ＋1的图象，依照图象求解下列问题：(1)二元一次方程组⎩⎨⎧y ＝2x －4，y ＝x ＋1的解；(2)一元一次不等式组⎩⎨⎧2x －4＞0，x ＋1＞0的解集．一个方法——待定系数法16．如图，一个正比例函数图象与一个一次函数图象交于点A(3，4)，且一次函数的图象与y 轴相交于点B(0，－5)．(1)求这两个函数的解析式； (2)求三角形AOB 的面积．(第17题)两个应用应用1给出解析式(或图象)解实际问题17．某游泳馆一般票价20元/张，暑期为了促销，新推出两种优待卡：①金卡售价600元/张，每次凭卡不再收费；②银卡售价150元/张，每次凭卡另收10元．暑期一般票正常出售，两种优待卡仅限暑期使用，不限次数．设游泳x次时，所需总费用为y元．(1)分别写出选择银卡、一般票消费时，y与x之间的函数关系式；(2)在同一个坐标系中，若三种消费方式对应的函数图象如图所示，要求出点A，B，C的坐标；(3)请依照函数图象，直截了当写出选择哪种消费方式更合算．(第18题)应用2只给语言叙述或图表情境解实际问题18．为改善生态环境，防止水土流失，某村打算在河堤坡面种植白杨树，现有甲、乙两家林场可提供相同质量的白杨树苗，其具体销售方案如下：(1)该村需要购买1 500棵白杨树苗，若都在甲林场购买所需费用为________元，若都在乙林场购买所需费用为________元；(2)分别求出y甲、y乙与x之间的函数关系式；(3)假如你是该村的负责人，应该选择到哪家林场购买树苗合算，什么缘故？答案专训11．解：设假如商场本月初出售，下月初可获利y1元，则y1＝10%x＋(1＋10%)x·10%＝0.1x＋0.11x＝0.21x，设假如商场下月初出售，可获利y2元，则y2＝25%x－8 000＝0.25x－8 000.当y1＝y2时，0.21x＝0.25x－8 000，解得x＝200 000；当y1>y2时，0.21x>0.25x－8 000，解得x<200 000；当y1<y2时，0.21x<0.25x－8 000，解得x>200 000.因此若商场投入资金为20万元，两种出售方式获利相同；若商场投入资金少于20万元，本月初出售获利较多；若投入资金多于20万元，下月初出售获利较多．2．分析：设总人数是x人，当x≤35时，选择两家宾馆是一样的；当35＜x≤45时，选择甲宾馆比较实惠；当x>45时，两家宾馆的收费能够表示成人数x 的函数，比较两个函数值的大小即可．解：设总人数是x人，甲宾馆的收费为y甲元，乙宾馆的收费为y乙元，当x≤35时，两家宾馆的费用是一样的；当35<x ≤45时，选择甲宾馆比较实惠；当x>45时，甲宾馆的收费y 甲＝35×120＋0.9×120×(x －35)，即y 甲＝108x ＋420，乙宾馆的收费y 乙＝45×120＋0.8×120(x －45)＝96x ＋1 080. 当y 甲＝y 乙时，108x ＋420＝96x ＋1 080，解得x ＝55； 当y 甲>y 乙时，108x ＋420>96x ＋1 080，解得x>55； 当y 甲<y 乙时，108x ＋420<96x ＋1 080，解得x<55.综上可得，当x ≤35或x ＝55时，两家宾馆的费用是一样的； 当35<x<55时，选择甲宾馆比较实惠； 当x>55时，选择乙宾馆比较实惠．3．解：(1)当x ＝1时，y 1＝3 000；当x ＞1时，y 1＝3 000＋3 000(x －1)×(1－30%)＝2 100x ＋900.因此y 1＝⎩⎨⎧3 000（x ＝1），2 100x ＋900（x ＞1，x 为整数）.y 2＝3 000x (1－25%)＝2 250x (x 为正整数)．(2)当甲、乙两个商场的收费相同时，2 100x ＋900＝2 250x ，解得x ＝6.故甲、乙两个商场的收费相同时，所买商品为6件．(3)应选择乙商场更优待，理由如下：当x ＝5时，y 1＝2 100x ＋900＝2 100×5＋900＝11 400，y 2＝2 250x ＝2 250×5＝11 250，因为11 400＞11 250，因此当所买商品为5件时，应选择乙商场更优待．专训21．解：(1)常量是π和R ，变量是V 和h. (2)常量是π和h ，变量是V 和R.2．解：在y 2＝x ＋1中，当x 的值是0时，y 的值为±1，现在y 的值有两个，并不是唯独确定的，因此y 不是x 的函数．y 2＝x ＋1变形为x ＝y 2－1后，关于y 的每一个值，另一个变量x 都有唯独确定的值与其对应，因此x 是y 的函数．5．B 6.C 7.A8．A 点拨：∵点M(1，a)和点N(2，b)在一次函数y ＝－2x ＋1的图象上，由一次函数图象性质可知一次函数y ＝－2x ＋1中函数值y 随x 的增大而减小，∴a>b.9．解：(1)因为图象与y 轴的交点位于原点下方，即点(0，12－3k)位于原点下方，因此12－3k<0，解得k>4.因此k －2>4－2>0，因此函数值随着自变量的增大而增大．(2)因为函数值随着自变量的增大而增大，因此k －2>0，解得k>2. 因为函数图象与y 轴的交点位于原点上方，因此12－3k>0，解得k<4. 因此k 的取值范畴为2<k<4. 因此满足条件的正整数k 的值为3. 10．解：一次函数：①②⑤⑥ 正比例函数：②⑤11．解：(1)在y ＝2x 中，令x ＝1，得y ＝2，则点B 的坐标是(1，2)， 设一次函数的解析式是y ＝kx ＋b(k ≠0)， 则⎩⎨⎧b ＝3，k ＋b ＝2，解得⎩⎨⎧b ＝3，k ＝－1. 故一次函数的解析式是y ＝－x ＋3.(2)点C(4，－2)不在该一次函数的图象上．理由：关于y ＝－x ＋3，当x ＝4时，y ＝－1≠－2，因此点C(4，－2)不在该函数的图象上．(3)在y ＝－x ＋3中，令y ＝0，得x ＝3，则点D 的坐标是(3，0)，的交点的横坐标，因此画出y＝5x－1与y＝2x＋5的图象即可．14．解：(1)把点(1，4)的坐标代入y＝kx＋3中，得4＝k＋3.∴k＝1.∴一次函数的解析式为y＝x＋3.(2)由(1)知k＝1，∴原不等式为x＋3≤6.∴x≤3.点拨：(1)把点(1，4)的坐标代入y＝kx＋3中，用待定系数法求出k的值．(2)把求出的k值代入不等式kx＋3≤6中，求出不等式的解集．15．解：图象略．(2)因为A点横坐标为3，因此A点到OB的距离为3.又因为B点纵坐标为－5，因此OB＝5.一般票：y ＝20x.(2)把x ＝0代入y ＝10x ＋150，得y ＝150， ∴A(0，150)． ∵⎩⎨⎧y ＝20x ，y ＝10x ＋150，∴⎩⎨⎧x ＝15，y ＝300.∴B(15，300)．把y ＝600代入y ＝10x ＋150，得x ＝45.∴C(45，600)．(3)当0<x<15时，选择购买一般票更合算；(注：若写成0≤x ＜15，也正确) 当x ＝15时，选择购买银卡、一般票的总费用相同，均比金卡合算； 当15<x<45时，选择购买银卡更合算；当x ＝45时，选择购买金卡、银卡的总费用相同，均比一般票合算； 当x>45时，选择购买金卡更合算．18．解：(1)5 900；6 000(2)当0≤x ≤1 000时，y 甲＝4x ，当x>1 000时，y 甲＝4 000＋3.8(x －1 000)＝3.8x ＋200，∴y 甲＝ ⎩⎨⎧4x （0≤x ≤1 000且x 为整数），3.8x ＋200（x>1 000且x 为整数）.当0≤x ≤2 000时，y 乙＝4x ，当x>2 000时，y 乙＝8 000＋3.6(x －2 000)＝3.6x ＋800，∴y 乙＝⎩⎨⎧4x （0≤x ≤2 000且x 为整数），3.6x ＋800（x>2 000且x 为整数）.(3)由题意，得当0≤x ≤1 000时，两家林场白杨树苗单价一样，∴到两家林场购买所需费用一样．当1 000<x≤2 000时，甲林场有优待而乙林场无优待，∴当1 000<x≤2 000时，到甲林场购买合算；当x>2 000时，y甲＝3.8x＋200，y乙＝3.6x＋800，当y甲＝y乙时3．8x＋200＝3.6x＋800，解得x＝3 000，∴当x＝3 000时，到两家林场购买所需费用一样；当y甲<y乙时，3．8x＋200＜3.6x＋800，解得x<3 000.∴当2 000<x<3 000时，到甲林场购买合算；当y甲>y乙时，3．8x＋200>3.6x＋800，解得x>3 000.∴当x>3 000时，到乙林场购买合算．综上所述，当0≤x≤1 000或x＝3 000时，到两家林场购买所需费用一样，当1 000<x<3 000时，到甲林场购买合算；当x>3 000时，到乙林场购买合算．。
初中数学一次函数的图像专项练习30题(有答案)
初中数学一次函数的图像专项练习30题(有答案)1.本题为选择题，无需改写。
2.在图中，当x＞2时，y2＞y1，因此结论③正确。
由于y1=kx+b与y2=x+a的图象相交于第三象限，因此a＜0，结论②也正确。
而k＜0，因此结论①错误。
因此选项C正确。
3.根据题目中的条件，k＜0，b＞0，因此函数的图象是下降的直线，截距为正数，应该是选项A。
4.本题为选择题，无需改写。
5.根据题目中的条件，k＜0，b＞0，因此函数的图象是下降的直线，截距为正数，斜率的绝对值小于1，应该是选项B。
6.将直线l1和直线l2的方程化简可得y=2x+1和y=-x-1，因此直线l1的斜率为2，直线l2的斜率为-1.由于x+y=0，因此该点在第三部分。
因此选项C正确。
7.根据两个函数的表达式可知它们的图象分别是斜率为负数的直线和斜率为正数的直线，应该是选项B。
8.函数y=2x+3的斜率为2，截距为3，应该是选项A。
9.根据图象可知，选项C表示的是y=-x-1的图象，因此选项C正确。
10.将函数kx-y=2化简可得y=kx-2，因此函数的图象是斜率为正数的直线，截距为-2，应该是选项C。
11.由于b1＜b2，因此直线y1在直线y2的下方。
由于k1k2＜0，因此直线y1和直线y2的斜率异号，相交于第二象限。
因此选项B正确。
12.根据图象可知，选项D表示的是y=abx的图象，因此选项D正确。
13.根据图象可知，降雨后，蓄水量每天增加5万立方米，因此选项B正确。
14.本题为选择题，无需改写。
15.将y=kx代入y=kx-k可得y=k(x-1)，因此函数的图象是斜率为正数的直线，截距为-k，应该是选项C。
16.当x增加时，y的值也会增加，且当x大于某个值时，y会大于2.17.当x增加时，y的值也会增加，但当x大于某个值时，y会小于某个值。
18.当x增加时，y的值也会增加，且当x大于某个值时，y会大于某个值。
19.正确的判断是：①k0；③当x=3时，y1=y2；④当03时，y1>y2.20.当x增加时，y1的值也会增加，且当x大于某个值时，y1会大于y2.21.当y小于某个值时，x的取值范围是一定的，具体取值范围需要根据具体函数图象来确定。
第19章 一次函数 解题技巧专题：利用一次函数解决实际问题(含答案)
解题技巧专题：利用一次函数解决实际问题——明确不同类型的图象的端点、折点、交点等的意义 ◆类型一 费用类问题一、建立一次函数模型解决问题1．某市为了鼓励居民节约用水，决定实行两级收费制度．若每月用水量不超过14吨(含14吨)，则每吨按政府补贴优惠价m元收费；若每月用水量超过14吨，则超过部分每吨按市场价n元收费．小明家3月份用水20吨，交水费49元；4月份用水18吨，交水费42元．(1)求每吨水的政府补贴优惠价和市场价；(2)设每月用水量为x吨，应交水费为y元，请写出y与x之间的函数解析式；(3)小明家5月份用水26吨，则他家应交水费多少元？二、分段函数问题2．为更新果树品种，某果园计划新购进A，B两个品种的果树苗栽植培育，若计划购进这两种果树苗共45棵，其中A种树苗的单价为7元/棵，购买B种树苗所需费用y(元)与购买数量x(棵)之间存在如图所示的函数关系．(1)求y与x的函数解析式；(2)若在购买计划中，B种树苗的数量不超过35棵，但不少于A种树苗的数量，请设计购买方案，使总费用最低，并求出最低费用．三、两个一次函数图象结合的问题3．随着互联网的发展，互联网消费逐渐深入人们生活，如图是“滴滴顺风车”与“滴滴快车”的行驶里程x(公里)与计费y(元)之间的函数关系图象，下列说法：①“快车”行驶里程不超过5公里计费8元；②“顺风车”行驶里程超过2公里的部分，每公里计费1.2元；③A点的坐标为(6.5，10.4)；④从哈尔滨西站到会展中心的里程是15公里，则“顺风车”要比“快车”少用3.4元．其中正确的个数有( )A．1个B．2个C．3个D．4个四、分类讨论思想4．江汉平原享有“中国小龙虾之乡”的美称，甲、乙两家农贸商店，平时以同样的价格出售品质相同的小龙虾，“龙虾节”期间，甲、乙两家商店都让利酬宾，付款金额y甲，y乙(单位：元)与原价x(单位：元)之间的函数关系如图所示：(1)直接写出y甲，y乙关于x的函数关系式；(2)“龙虾节”期间，如何选择甲、乙两家商店购买小龙虾更省钱？一、两个一次函数图象结合的问题5．A，B两地相距60 km，甲、乙两人从两地出发相向而行，甲先出发，图中l1，l2表示两人离A地的距离s(km)与时间t(h)的关系，请结合图象解答下列问题：(1)表示乙离A地的距离与时间关系的图象是________(填l1或l2)；甲的速度是________km/h，乙的速度是________km/h；(2)甲出发多长时间两人恰好相距5 km?二、分段函数问题6．暑假期间，小刚一家乘车去离家380 km的某景区旅游，他们离家的距离y(km)与汽车行驶的时间x(h)之间的函数图象如图所示．(1)从小刚家到该景区乘车一共用了多少时间？(2)求线段AB对应的函数解析式；(3)小刚一家出发2.5 h后离目的地有多远？一、两个一次函数图象结合的问题7．甲、乙两工程队分别同时开挖两条600米长的管道，所挖管道长度y(米)与挖掘时间x(天)之间的关系如图所示，则下列说法中：①甲队每天挖100米；②乙队开挖2天后，每天挖50米；③甲队比乙队提前3天完成任务；④当x＝2或6时，甲、乙两队所挖管道长度都相差100米．正确的有________(填序号)．二、分段函数问题8．根据卫生防疫部门的要求，游泳池必须定期换水、清洗．某游泳池周五早上8：00打开排水孔开始排水，排水孔的排水速度保持不变，期间因清洗游泳池需要暂停排水，游泳池的水在11：30全部排完．游泳池内的水量Q(m3)和开始排水后的时间t(h)之间的函数图象如图所示，根据图象解答下列问题：(1)暂停排水需要多少时间？排水孔的排水速度是多少？(2)当2≤t≤3.5时，求Q关于t的函数解析式．参考答案与解析1．解：(1)设每吨水的政府补贴优惠价为m 元，市场价为n 元．由题意得{14m ＋（20－14）n ＝49，14m ＋（18－14）n ＝42，解得{m ＝2，n ＝3.5.答：每吨水的政府补贴优惠价为2元，市场价为3.5元．(2)当0≤x ≤14时，y ＝2x ；当x ＞14时，y ＝14×2＋(x －14)×3.5＝3.5x －21.综上所述，y ＝{2x （0≤x ≤14），3.5x －21（x >14）.(3)∵26＞14，∴小明家5月份水费为3.5×26－21＝70(元)．答：小明家5月份应交水费70元．2．解：(1)当0≤x ≤20时，设y 与x 的函数解析式为y ＝ax ，把(20，160)代入y ＝ax 中，得a ＝8.即y 与x 的函数解析式为y ＝8x ；当x >20时，设y 与x 的函数解析式为y ＝kx ＋b ，把(20，160)，(40，288)代入y ＝kx ＋b 中，得{20k ＋b ＝160，40k ＋b ＝288，解得{k ＝6.4，b ＝32，即y 与x 的函数解析式为y ＝6.4x ＋32.综上所述，y 与x 的函数解析式为y ＝{8x （0≤x ≤20），6.4x ＋32（x >20）.(2)∵B 种树苗的数量不超过35棵，但不少于A 种树苗的数量，∴{x ≤35，x ≥45－x ，∴22.5≤x ≤35.设总费用为W 元，则W ＝6.4x ＋32＋7(45－x )＝－0.6x ＋347.∵k ＝－0.6<0，∴y 随x 的增大而减小，∴当x ＝35，45－x ＝10时，总费用最低，即购买B 种树苗35棵，A 种树苗10棵时，总费用最低，W 最低＝－0.6×35＋347＝326(元)．3．D4．解：(1)设y 甲＝kx ，把(2000，1600)代入，得2000k ＝1600，解得k ＝0.8，所以y 甲＝0.8x .当0＜x ＜2000时，设y 乙＝ax ，把(2000，2000)代入，得2000k ＝2000，解得k ＝1，所以y 乙＝x .当x ≥2000时，设y 乙＝mx ＋n ，把(2000，2000)，(4000，3400)代入，得{2000m ＋n ＝2000，4000m ＋n ＝3400，解得{m ＝0.7，n ＝600，所以y 乙＝{x （0<x <2000），0.7x ＋600（x ≥2000）.(2)当0＜x ＜2000时，0.8x ＜x ，到甲商店购买更省钱；当x ≥2000时，若到甲商店购买更省钱，则0.8x ＜0.7x ＋600，解得x ＜6000；若到乙商店购买更省钱，则0.8x ＞0.7x ＋600，解得x ＞6000；若到甲、乙两商店购买一样省钱，则0.8x ＝0.7x ＋600，解得x ＝6000；故当购买金额按原价小于6000元时，到甲商店购买更省钱；当购买金额按原价大于6000元时，到乙商店购买更省钱；当购买金额按原价等于6000元时，到甲、乙两商店购买花钱一样．5．解：(1)l 2 30 20 解析：由题意可知，乙的函数图象是l 2，甲的速度是602＝30(km/h)，乙的速度是603＝20(km/h)．故答案为l 2，30，20.(2)设甲出发x h 两人恰好相距5 km.由题意30x ＋20(x －0.5)＋5＝60或30x ＋20(x －0.5)－5＝60，解得x ＝1.3或1.5.答：甲出发1.3 h 或1.5 h 两人恰好相距5 km.6．解：(1)从小刚家到该景区乘车一共用了4 h.(2)设线段AB 对应的函数解析式为y ＝kx ＋b .把点A (1，80)，B (3，320)代入得{k ＋b ＝80，3k ＋b ＝320，解得{k ＝120，b ＝－40.∴y ＝120x －40(1≤x ≤3)．(3)当x ＝2.5时，y ＝120×2.5－40＝260，380－260＝120(km)．故小刚一家出发2.5h 后离目的地120km.7．①②④8．解：(1)暂停排水需要的时间为2－1.5＝0.5(h)．∵排水时间为3.5－0.5＝3(h)，一共排水900m 3，∴排水孔的排水速度是900÷3＝300(m 3/h)．(2)当2≤t ≤3.5时，设Q 关于t 的函数解析式为Q ＝kt ＋b ，易知图象过点(3.5，0)．∵当t ＝1.5时，排水300×1.5＝450(m 3)，此时Q ＝900－450＝450，∴点(2，450)在直线Q ＝kt ＋b 上．把(2，450)，(3.5，0)代入Q ＝kt ＋b ，得{2k ＋b ＝450，3.5k ＋b ＝0，解得{k ＝－300，b ＝1050，∴Q 关于t 的函数解析式为Q ＝－300t ＋1050.。
2024学年九年级中考数学专题复习：分配方案问题(一次函数实际综合应用)(含答案)
2024 学年九年级中考数学专题复习:分配方案问题（一次函数实际综合应用）1．春天来了，学校计划用两种花卉对校园进行美化．已知用600元购买A 种花卉与用900元购买B 种花卉的数量相等，且B 种花卉每盆的价格比A 种花卉每盆的价格多0.5元．(1)求A ，B 两种花卉每盆的价格各是多少元；(2)学校计划购买A ，B 两种花卉共6000盆，其中A 种花卉的数量不超过B 种花卉数量的13，请你给出购买这批花卉费用最低的方案，并求出最低费用． 2．某市的A 县和B 县春季育苗，急需化肥分别为90t 和60t ，该市的C 县和D 县分别储存化肥100t 和50t ，全部调配给A 县和B 县．已知从C 县运化肥到A 县的运费为35元/t ，从C 县运化肥到B 县的运费为30元/t ，从D 县运化肥到A 县的运费为40元/t ，从D 县运化肥到B 县的运费为45元/t ．(1)设C 县运到A 县的化肥为x t ，求总运费W （单位：元）关于x （单位：t ）的函数解析式，并写出自变量x 的取值范围；(2)求最低总运费，并说明总运费最低时的运送方案．3．为加强学生的劳动教育，某校准备开展以“种下希望，共建美好家园”为主题的义务植树活动． 经了解，购买2棵枣树和3棵石榴树共需44元；购买5棵枣树和6棵石榴树共需98元，该校决定购买(0)m m 棵枣树和50棵石榴树．(1)求枣树和石榴树的单价；(2)实际购买时，商家给出了如下优惠方案：方案一：均按原价的九折销售；方案二：如果购买的枣树不超过50棵，按原价销售． 如果购买的枣树超过50棵，则超出的部分按原价的八折销售，石榴树始终按原价销售．分别求出两种方案的费用1W ，2W 关于m 的函数解析式．4．“一骑红尘妃子笑，无人知是荔枝来”，夏季是盛产荔枝的季节，某县城为尽快打开市场，对本地的荔枝品种妃子笑进行线上和线下销售相结合的模式，具体费用标准如下：线上销售模式：不超过6千克时，按原价出售，超过6千克时，超出部分每千克再让利3.5元；线下销售模式：一律九折出售．购买妃子笑x 千克，所需费用为y 元，y 与x 之间的函数关系如图所示．根据以上信息回答下列问题：(1)请问妃子笑的标价为多少？(2)请求出线上销售模式所需费用y关于x的函数解析式；(3)若想购买妃子笑40千克，请问选择哪种模式购买最省钱？5．某公司为改善办公条件，计划采购一批A，B两种型号的电脑，已知1台A型电脑比1台B型电脑的便宜1200元；采购4台A型电脑与采购3台B型电脑的费用一样多．(1)求A型电脑和B型电脑每台各需多少元；(2)若公司计划采购A、B两种型号电脑共50台，且A型电脑的台数不超过B型电脑的4倍，两种型号电脑的采购总费用不超过200000元，该公司共有几种采购方案？哪种采购方案可使总费用最低，最低费用是多少元？6．希望艺术团准备采购甲，乙两种道具，某经销商知道了活动的方案后，主动联系希望艺术团，对甲种道具的出售价格根据购买量给予优惠，对乙种道具按25元/件的价格出售．设希望艺术团购买甲种道具x件，付款y元，y与x之间的函数关系如图所示．(1)直接写出当0≤x≤50和x>50时，y与x之间的函数关系式；(2)若希望艺术团计划一次性购买甲，乙两种道具共100件，且甲种道具不少于40件，但又不超过60件．如何分配甲，乙两种道具的购买量，才能使希望艺术团付款总金额w（元）最少？(3)若甲、乙两种道具的进货价格分别为22元/件和18元/件．经销商按（2）中甲，乙两种道具购买量的分配比例卖出两种道具共a件，且销售完a件道具获得的利润不少于1050元，求a的最小值．7．我市某中学计划举行以“奋斗百年路，启航新征程”为主题的知识竞赛，并对获奖的同学给予奖励．现要购买A，B两种奖品．已知2件A种奖品和3件B种奖品共需41元，5件A种奖品和2件B种奖品共需53元．(1)这两种奖品的单价各是多少元？(2)学校准备购进这两种奖品共90件，且B种奖品的数量不少于A种奖品数量的13，请设计出最省钱的购买方案，并求出最少费用．8．我市是福建省茶叶的主要产区，清明过后就是春茶的采摘季节．已知熟练采茶工人每天采茶的数量是新手采茶工人的3倍，每个熟练采茶工人采摘600斤鲜叶比新手采茶工人采摘450斤鲜叶少用25天．(1)求熟练采茶工人和新手采茶工人一天分别能采摘鲜叶的斤数；(2)某茶厂计划一天采摘鲜叶600斤，该茶厂有20名熟练采茶工人和15名新手采茶工人，按点工制度付给熟练采茶工人每人每天的工资为300元，付给新手采茶工人每人每天的工资为80元，应如何安排熟练采茶工人和新手采茶工人能使费用最少？9．为了方便老师工作，某中学决定购进一批教学用具，在购买教学用具时，该校从甲、乙、丙三家商场了解到同一种型号教学用具的优惠条件如下：甲：定价为90元，超过5个，超过的部分每个优惠20%；乙：定价为90元，每个优惠10% ；丙：购会员卡100元，每个教学用具70元．(1)设该校购买x个教学用具，选择甲商场时，所需费用为y1元；选择乙商场时，所需费用为y2元；选择丙商场时，所需费用为y3元；请分别求出y1，y2，y3与x之间的函数关系式；(2)当购买教学用具数量大于多少件时，y2＞y3？10．某年级430名师生秋游，计划租用8辆客车，现有甲、乙两种型号客车，它们的载客量和租金如下表：(1)设租用甲种客车x辆，租车总费用为y元．求出y（元）与x（辆）之间的函数表达式；(2)当甲种客车有多少辆时，能保障所有的师生能参加秋游且租车费用最少，最少费用是多少元？11．目前，全国各地都在积极开展新冠肺炎疫苗接种工作，某生物公司接到批量生产疫苗任务，要求5天内加工完成22万支疫苗，该公司安排甲，乙两车间共同完成加工任务，乙车间加工过程中停工一段时间维修设备，然后提高效率继续加工，直到与甲车间同时完成加工任务为止，设甲，乙两车间各自生产疫苗y （万支）与甲车间加工时间x （天）之间的关系如图1所示；两车间未生产疫苗w （万支）与甲车间加工时间x （天）之间的关系如图2所示，请结合图象回答下列问题：(1)甲车间每天生产疫苗 万支，第一天甲、乙两车间共生产疫苗 万支，=a ；(2)当3x =时，求甲、乙车间生产的疫苗数（万支）之差12y y -；(3)若5.5万支疫苗恰好装满一辆货车，那么加工多长时间装满第一辆货车？再加工多长时间恰好装满第三辆货车？12．某校准备在健康大药房购买口罩和水银体温计发放给每个学生．已知每盒口罩有100只，每盒水银体温计有10支，每盒口罩价格比每盒水银体温计价格多150元．用1200元购买口罩盒数与用300元购买水银体温计所得盒数相同．(1)求每盒口罩和每盒水银体温计的价格各是多少元？(2)如果给每位学生发放2只口罩和1支水银体温计，且口罩和水银体温计均整盒购买．设购买口罩m 盒（m 为正整数），则购买水银体温计多少盒能和口罩刚好配套？请用含m 的代数式表示．(3)在健康大药房累计购医用品超过1800元后，超出1800元的部分可享受8折优惠．该校按（2）中的配套方案购买，共支付w 元，求w 关于m 的函数关系式．若该校九年级有1000名学生，需要购买口罩和水银体温计各多少盒？所需总费用为多少元？ 13．某商场销售一种夹克和衬衣，夹克每件定价100元，衬衣每件定价50元，商场在开展促销活动期间，向顾客提供两种优惠方案．方案一：买一件夹克送一件衬衣方案二：夹克和衬衣均按定价的80%付款现有顾客要到该商场购买夹克30件，衬衣x件（x>30）（1）用含x的代数式表示方案一购买共需付款y1元和方案二购买共需付款y2元；（2）通过计算说明，购买衬衣多少件时，两种方案付款一样多？（3）当x=40时，哪种方案更省钱？请说明理由．14．灵宝寺河山被誉为“亚洲第一高山果园”，海拔800﹣1200米，土质肥沃，雨量充沛，日照充足，昼夜温差大，气候条件得天独厚，是苹果的最佳适生地．寺河山苹果，是三门峡市灵宝苹果的龙头品牌，素有“天下苹果属灵宝，灵宝苹果属寺河”之说．在苹果收获季节，为了保证苹果的新鲜度，需要将苹果运送至冷库进行保存，现有A，B两个果园，若A果园有苹果120吨，B果园有苹果60吨．现将A，B两个果园的苹果全部运往C，D两个冷库进行冷藏保存，已知C仓库可储存100吨，D仓库可储存80吨，A，B 两个果园到C，D两个冷藏仓库的运费如下表：设从A果园运往C仓库的苹果重量为x吨．（1）用含x（吨）的代数式表示总运费W（元），并写出自变量x的取值范围；（2）如何进行运送才能使总运费最少？求出最低总运费．15．学习贯彻习近平总书记关于生态文明建设系列重要讲话精神，牢固树立“绿水青山就是金山银山”理念，把生态文明建设融入经济建设、政治建设、文化建设、社会建设各个方面和全过程．在建设美丽中国的活动中，某学校计划组织全校1450名师生到相关部门规划的林区植树，经过研究，决定在当地租车公司租用62辆A、B两种型号的客车作为交通工具．下表是租车公司提供给学校有关A、B两种型号客车的载客量和租金信息：注：载客量指的是每辆客车最多可载该校师生的人数；（1）设租用A型号客车x辆，租车总费用为y元，求y与x之间的函数表达式，并通过计算求出x的取值范围；（2）若要使租车总费用不超过13460元，则共有几种租车方案？哪种租车方案最省钱？参考答案：1．(1)A 种花卉每盆1元，B 种花卉每盆1.5元(2)当购买A 种花卉1500盆，B 种花卉4500盆时购买这批花卉总费用最低，最低费用为8250元．2．(1)W ＝10x +4800（40≤x ≤90）(2)最低总运费为5200元，此时的运送方案是：C 县的100t 化肥40t 运往A 县，60t 运往B 县，D 县的50t 化肥全部运往A 县3．(1)枣树的单价为10元，石榴树的单价为8元(2)19360W m =+，210400(050),8500(50).m m W m m +<≤⎧=⎨+>⎩4．(1)25元/千克(2)()()250621.5216x x y x x ⎧≤<⎪=⎨+>⎪⎩(3)线上购买5．(1)购买1台A 型电脑需要3600元，购买1台B 型电脑需要4800元．(2)该公司共有7种采购方案. 购买A 型电脑40台，B 型电脑10台方案可使总费用最低，最低费用是192000元6．(1)30(050)24300(50)x x y x x ≤≤⎧=⎨+>⎩ (2)购进甲道具40件，乙道具60件时，才能使希望艺术团付款总金额w （元）最少；(3)a 的最小值为2107．(1)A ：7元，B ：9元(2)购进A 种奖品67件，购进B 种奖品23件；676元8．(1)每名熟练的采茶工人一天能采摘鲜叶30斤，每名新手采茶工人一天能采摘鲜叶10斤(2)茶厂应安排15名熟练的采茶工人采摘鲜叶，15名新手采茶工人采摘鲜叶能使得费用最少9．(1)190(05)7290(5)x x y x x <≤⎧=⎨+>⎩；290(110%)81y x x =⨯-=；370100y x =+ (2)1010．(1)y ＝100x +3600(2)当甲种客车有5辆时，能保障所有的师生能参加秋游且租车费用最少，最少费用是4100元11．(1)2，3.5，1.5(2)1(3)2天，2天12．(1)每盒口罩和每盒水银体温计的价格各是200元，50元(2)5m(3)当m ≤4时，则w=450m ；当m ＞4时，w =360m +360，需要购买口罩20盒，水银体温计100盒，所需总费用为7560元13．（1）12501500402400y x y x =+⎧⎨=+⎩；（2）当90x =时12y y =；（3）当x =40时，方案一更省钱． 14．（1）43400W x =+，40100x ≤≤；（2）运送方案为A 果园将40吨苹果运往C 仓库，80吨运往D 仓库，B 果园的60吨苹果全部运往C 仓库，此时总运费最低，最低是3560元 15．（1）y ＝100x ＋11160（21≤x ≤62且x 为整数）；（2）3种，租用A 型号客车21辆。
初中数学一次函数的图像专项练习30题(有答案)ok
一次函数的图像专项练习30题（有答案）1．函数y=ax+b与y=bx+a的图象在同一坐标系内的大致位置正确的是（）A．B．C．D．2．一次函数y1=kx+b与y2=x+a的图象如图，则下列结论：①k＜0；②a＞0；③当x＞2时，y2＞y 1，其中正确的个数是（）A．0B．1C．2D．33．一次函数y=kx+b，y随x的增大而减小，且kb＞0，则在直角坐标系内它的大致图象是（）A．B．C．D．4．下列函数图象不可能是一次函数y=ax﹣（a﹣2）图象的是（）A．B．C．D．5．如图所示，如果k•b＜0，且k＜0，那么函数y=kx+b的图象大致是（）A．B．C．D．6．如图，直线l1：y=x+1与直线l2：y=﹣x﹣把平面直角坐标系分成四个部分，则点（，）在（）A ． 第一部分B ． 第二部分C ． 第三部分D ． 第四部分7．已知正比例函数y=﹣kx 和一次函数y=kx ﹣2（x 为自变量），它们在同一坐标系内的图象大致是（ ） A ． B ． C ． D ．8．函数y=2x+3的图象是（ ） A ．过点（0，3），（0，﹣）的直线 B ．过点（1，5），（0，﹣）的直线C ．过点（﹣1，﹣1），（﹣，0）的直线D ． 过点（0，3），（﹣，0）的直线9．下列图象中，与关系式y=﹣x ﹣1表示的是同一个一次函数的图象是（ ） A ． B ． C ． D ．10．函数kx ﹣y=2中，y 随x 的增大而减小，则它的图象是下图中的（ ） A ．B ．C ．D ．11．已知直线y 1=k 1x+b 1，y 2=k 2x+b 2，满足b 1＜b 2，且k 1k 2＜0，两直线的图象是（ ） A ．B ．C ．D ．A．B．C．D．13．连降6天大雨，某水库的蓄水量随时间的增加而直线上升．若该水库的蓄水量V（万米3）与降雨的时间t（天）的关系如图所示，则下列说法正确的是（）A．降雨后，蓄水量每天减少5万米3B．降雨后，蓄水量每天增加5万米3C．降雨开始时，蓄水量为20万米3D．降雨第6天，蓄水量增加40万米314．拖拉机开始行驶时，油箱中有油4升，如果每小时耗油0.5升，那么油箱中余油y（升）与它工作的时间t（时）之间的函数关系的图象是（）A．B．C．D．15．已知正比例函数y=kx的图象经过第一、三象限，则y=kx﹣k的大致图象可能是下图的（）A．B ．C．D．16．一次函数y=kx+b的图象如图所示，当x_________时，y＞2．17．一次函数的图象如图所示，根据图象可知，当x_________时，有y＜0．18．如图，直线l是一次函数y=kx+b的图象，当x_________时，y＞0．19．一次函数y1=kx+b与y2=x+a的图象如图所示，则下列结论：①k＜0；②a＞0；③当x=3时，y1=y2；④当x＞3时，y1＜y2中，正确的判断是_________．20．如图，已知函数y1=ax+b和y2=kx的图象交于点P，则根据图象可得，当x_________时，y1＞y2．21．已知一次函数y=kx+b的图象如图所示，当y＜0时，x的取值范围是_________．22．在平面直角坐标系中画出函数的图象．（1）在图象上标出横坐标为﹣4的点A，并写出它的坐标；（2）在图象上标出和y轴的距离是2个单位长度的点，并写出它的坐标．23．作函数y=2x﹣4的图象，并根据图象回答下列问题．（1）当﹣2≤x≤4，求函数y的取值范围．（2）当x取何值时，y＜0？y=0？y＞0？24．如图是一次函数y=﹣x+5图象的一部分，利用图象回答下列问题：（1）求自变量的取值范围．（2）在（1）在条件下，y是否有最小值？如果有就求出最小值；如果没有，请说明理由．25．已知函数y1=﹣x+和y2=2x﹣1．（1）在同一个平面直角坐标系中画出这两个函数的图象；（2）根据图象，写出它们的交点坐标；（3）根据图象，试说明当x取什么值时，y1＞y2？26．作出函数y=3﹣3x的图象，并根据图象回答下列问题：（1）y的值随x的增大而_________；（2）图象与x轴的交点坐标是_________；与y轴的交点坐标是_________；（3）当x_________时，y≥0；（4）函数y=3﹣3x的图象与坐标轴所围成的三角形的面积是多少？27．已知函数y=2x﹣1．（1）在直角坐标系中画出这函数的图象；（2）判断点A（﹣2.5，﹣4），B（2.5，4）是否在函数y=2x﹣1的图象上；（3）当x取什么值时，y≤0．28．已知函数y=﹣2x﹣6．（1）求当x=﹣4时，y的值，当y=﹣2时，x的值．（2）画出函数图象．（3）如果y的取值范围﹣4≤y≤2，求x的取值范围．29．已知一次函数的图象经过点A（﹣3，0），B（﹣1，1）两点．（1）画出图象；（2）x为何值时，y＞0，y=0，y＜0？30．已知一次函数y=﹣2x+2，（1）在所给的平面直角坐标系中画出它的图象；（2）根据图象回答问题：①图象与x轴的交点坐标是_________，与y轴的交点坐标是_________；②当x_________时，y＞0．参考答案：1．分四种情况：①当a＞0，b＞0时，y=ax+b的图象经过第一、二、三象限，y=bx+a的图象经过第一、二、三象限，无选项符合；②当a＞0，b＜0时，y=ax+b的图象经过第一、三、四象限；y=bx+a的图象经过第一、二、四象限，C选项符合；③当a＜0，b＞0时，y=ax+b的图象经过第一、二、四象限；y=bx+a的图象经过第一、三、四象限，无选项符合；④当a＜0，b＜0时，y=ax+b的图象经过第二、三、四象限；y=bx+a的图象经过第二、三、四象限，无选项符合．故选C2．由一次函数y1=kx+b与y2=x+a的图象可知k＜0，a＜0，当x＞2时，y2＞y1，①③正确．故选C3．∵一次函数y=kx+b，y随x的增大而减小，∴k＜0，又∵kb＞0，∴b＜0，∴函数的图象经过第二、三、四象限．故选C4．根据图象知：A、a＞0，﹣（a﹣2）＞0．解得0＜a＜2，所以有可能；B、a＜0，﹣（a﹣2）＜0．解得两不等式没有公共部分，所以不可能；C、a＜0，﹣（a﹣2）＞0．解得a＜0，所以有可能；D、a＞0，﹣（a﹣2）＜0．解得a＞2，所以有可能．故选B5．∵k•b＜0，且k＜0，∴b＞0，k＜0，∴函数y=kx+b的图象经过第一、二、四象限，故选D6．由题意可得，解得，故点（，）应在交点的上方，即第二部分．故选B．7．分两种情况：（1）当k＞0时，正比例函数y=﹣kx的图象过原点、第一、三象限，一次函数y=kx﹣2的图象经过第一、三、四象限，选项A符合；（2）当k＜0时，正比例函数y=﹣kx的图象过原点、第二、四象限，一次函数y=kx﹣2的图象经过第二、三、四象限，无选项符合．故选A．8．A、把x=0代入函数关系式得2×0+3=3，故函数图象过点（0，3），不过（0，﹣），故错误；B、由A知函数图象不过点（0，﹣），故错误；C、把x=﹣1代入函数关系式得，2×（﹣1）+3=1，故（﹣1，﹣1）不在函数图象上，故错误；D、分别令x=0，y=0，此函数成立，故正确．故选D9．函数y=﹣x﹣1是一次函数，其图象是一条直线．当x=0时，y=﹣1，所以直线与y轴的交点坐标是（0，﹣1）；当y=0时，x=﹣1，所以直线与x轴的交点坐标是（﹣1，0）．由两点确定一条直线，连接这两点就可得到y=﹣x﹣1的图象．故选D10．整理为y=kx﹣2∵y随x的增大而减小∴k＜0又因为图象过2，4，3象限故选D．11．k1k2＜0，则k1与k2异号，因而两个函数一个y随x的增大而增大，另一个y随x的增大而减小，因而A是错误的；b1＜b2，则y1与y轴的交点在y2与y轴的交点的下边，因而B、C都是错误的．12．①当ab＞0，正比例函数y=abx过第一、三象限；a与b同号，同正时y=ax+b过第一、二、三象限，故D错误；同负时过第二、三、四象限，故B错误；②当ab＜0时，正比例函数y=abx过第二、四象限；a与b异号，a＞0，b＜0时y=ax+b过第一、三、四象限，故C错误；a＜0，b＞0时过第一、二、四象限．故选A13．A、根据图象知，水库的蓄水量因该随着降雨的时间的增加而增多；故本选项错误；B、本图象的直线，所以每天的降雨量是相等的，所以，蓄水库每天的增加的水的量是（40﹣10）÷6=5；故本选项正确；C、根据图示知，降雨开始时，蓄水量为10万米3，故本选项错误；D、根据图示知，降雨第6天，蓄水量增加了40万米3﹣30万米3=10万米3，故本选项错误；故选B14．根据题意列出关系式为：y=40﹣5t，考虑实际情况：拖拉机开始工作时，油箱中有油4升，即开始时，函数图象与y轴交于点（0，40），如果每小时耗油0.5升，且8小时，耗完油，故函数图象为一条线段．故选D15．∵正比例函数y=kx的图象经过第一、三象限，∴k＞0，∴﹣k＜0，∴y=kx﹣k的大致图象经过一、三、四象限，故选：B．16．由图形可知，该函数过点（0，2），（3，0），故斜率k==，所以解析式为y=，令y＞2，即＞2，解之得：x＜017．根据题意，要求y＜0时，x的范围，即：x+3＜0，解可得：x＜﹣2，故答案为x＜﹣218．根据题意，观察图象，可得直线l过点（2，0），且y随x的增大而增大，分析可得，当x＞2时，有y＞0 19．根据图示及数据可知：①一次函数y1=kx+b的图象经过第二、四象限，则k＜0正确；②y2=x+a的图象经与y轴交与负半轴，则a＞0错误；③一次函数y1=kx+b与y2=x+a的图象交点的横坐标是3，所以当x=3时，y1=y2正确；④当x＞3时，y1＜y2正确；故正确的判断是①，③，④20．根据图示可知点P的坐标是（﹣4，2），所以y1＞y2即直线1在直线2的上方，则x＜﹣4．21．根据图象和数据可知，当y＜0即图象在x轴下侧，x＜1．故答案为x＜122．函数与坐标轴的交点的坐标为（0，3），（6，0）．（1）点A的坐标（﹣4，5）；（2）和y轴的距离是2个单位长度的点的坐标M（2，2），N（﹣2，4）23．当x=0时，y=﹣4；当y=0时，2x﹣4=0，解得x=2，∴函数图象与两坐标轴的交点为（0，﹣4）（2，0）．图象如下：（1）x=﹣2时，y=2×（﹣2）﹣4=﹣8，x=4时，y=2×4﹣4=4，∵k=2＞0，∴y随x的增大而增大，∴﹣8≤y≤4；24．（1）由图象可看出当y=2.5时，x=5，因此x的取值范围应该是0＜x≤5（y轴上的点是空心圆，因此x≠0）；（2）由图象可看出，当x=5时，函数的值最小，是y=2.525．（1）如图所示：（2）由（1）中两函数图象可知，其交点坐标为（1，1）；（3）由（1）中两函数图象可知，当x＞1时，y1＞y2．26．如图．（1）因为一次项系数是﹣3＜0，所以y的值随x的增大而减小；（2）当y=0时，x=1，所以图象与x轴的交点坐标是（1，0）；当x=0时，y=3，所以图象与y轴的交点坐标是（0，3）；（3）由图象知，在A点左边，图象在x轴上方，函数值大于0．所以x≤1时，y≥0．（4）∵OA=1，OB=3，∴函数y=3﹣3x的图象与坐标轴所围成的三角形的面积是S△AOB=×1×3=．27．（1）函数y=2x﹣1与坐标轴的坐标为（0，﹣1）（，0），描点即可，如图所示；（2）将A、B的坐标代入函数式中，可得出A点不在直线y=2x﹣1的图象上，B点在直线y=2x﹣1的图象上，A代入函数后发现﹣2.5×2﹣1=﹣6≠﹣4，因此A点不在函数y=2x﹣1的图象上，然后用同样的方法判定B是否在函数的图象上；（3）当y≤0时，2x﹣1≤0，因此x≤．28．（1）当x=﹣4时，y=2；当y=﹣2时，x=﹣2；（2）由（1）可知函数图象过（﹣4，2）、（﹣2，﹣2），由此可画出函数的图象，如下图所示：（3）∵y=﹣2x﹣6，﹣4≤y≤2∴﹣4≤﹣2x﹣6≤22≤﹣2x≤8﹣4≤x≤﹣129．（1）图象如图：（2）观察图象可得，当x＞﹣3时，y＞0；当x=﹣3时，y=0；当x＜﹣3时，y＜0．30．（1）列表：x 0 1y 2 0描点，连线（如图）…（也可以写成过点（0，2）和（1，0）画直线）（2）①（1，0）；（0，2）②＜1。
苏科版数学八年级上册6.4《用一次函数解决问题》解答题专项练习
《用一次函数解决问题》解答题专题练习1．星期天，李玉刚同学随爸爸妈妈回老家探望爷爷奶奶，爸爸8：30骑自行车先走，平均每小时骑行20km ；李玉刚同学和妈妈9：30乘公交车后行，公交车平均速度是40km/h ．爸爸的骑行路线与李玉刚同学和妈妈的乘车路线相同，路程均为40km ．设爸爸骑行时间为x （h ）．（1）请分别写出爸爸的骑行路程y 1（km ）、李玉刚同学和妈妈的乘车路程y 2（km ）与x （h ）之间的函数解析式，并注明自变量的取值范围；（2）请在同一个平面直角坐标系中画出（1）中两个函数的图象；（3）请回答谁先到达老家．2．有一科技小组进行了机器人行走性能试验，在试验场地有A 、B 、C 三点顺次在同一笔直的赛道上，甲、乙两机器人分别从A 、B 两点同时同向出发，历时7分钟同时到达C 点，乙机器人始终以60米/分的速度行走，如图是甲、乙两机器人之间的距离y （米）与他们的行走时间x （分钟）之间的函数图象，请结合图象，回答下列问题：（1）A 、B 两点之间的距离是 米，甲机器人前2分钟的速度为 米/分；（2）若前3分钟甲机器人的速度不变，求线段EF 所在直线的函数解析式；（3）若线段FG ∥x 轴，则此段时间，甲机器人的速度为 米/分；（4）求A 、C 两点之间的距离；（5）直接写出两机器人出发多长时间相距28米．3．甲、乙两人利用不同的交通工具，沿同一路线从A 地出发前往B 地，甲出发1h 后，y 甲、y 乙与x 之间的函数图象如图所示．（1）甲的速度是 km/h ；（2）当1≤x≤5时，求y关于x的函数解析式；乙（3）当乙与A地相距240km时，甲与A地相距km．4．环保局对某企业排污情况进行检测，结果显示：所排污水中硫化物的浓度超标，即硫化物的浓度超过最高允许的1.0mg/L．环保局要求该企业立即整改，在15天以内（含15天）排污达标．整改过程中，所排污水中硫化物的浓度y（mg/L）与时间x（天）的变化规律如图所示，其中线段AB表示前3天的变化规律，从第3天起，所排污水中硫化物的浓度y与时间x成反比例关系．（1）求整改过程中硫化物的浓度y与时间x的函数表达式；（2）该企业所排污水中硫化物的浓度，能否在15天以内不超过最高允许的1.0mg/L？为什么？5．某家具商场计划购进某种餐桌、餐椅进行销售，有关信息如表：已知用600元购进的餐桌数量与用160元购进的餐椅数量相同．（1）求表中a的值；（2）若该商场购进餐椅的数量是餐桌数量的5倍还多20张，且餐桌和餐椅的总数量不超过200张．该商场计划将一半的餐桌成套（一张餐桌和四张餐椅配成一套）销售，其余餐桌、餐椅以零售方式销售．请问怎样进货，才能获得最大利润？最大利润是多少？（3）由于原材料价格上涨，每张餐桌和餐椅的进价都上涨了10元，按照（2）中获得最大利润的方案购进餐桌和餐椅，在调整成套销售量而不改变销售价格的情况下，实际全部售出后，所得利润比（2）中的最大利润少了2250元．请问本次成套的销售量为多少？6．根据卫生防疫部门要求，游泳池必须定期换水，清洗．某游泳池周五早上8：00打开排水孔开始排水，排水孔的排水速度保持不变，期间因清洗游泳池需要暂停排水，游泳池的水在11：30全部排完．游泳池内的水量Q（m3）和开始排水后的时间t（h）之间的函数图象如图所示，根据图象解答下列问题：（1）暂停排水需要多少时间？排水孔排水速度是多少？（2）当2≤t≤3.5时，求Q关于t的函数表达式．7．公司有330台机器需要一次性运送到某地，计划租用甲、乙两种货车共8辆，已知每辆甲种货车一次最多运送机器45台、租车费用为400元，每辆乙种货车一次最多运送机器30台、租车费用为280元（Ⅰ）设租用甲种货车x辆（x为非负整数），试填写表格．表一：表二：（Ⅱ）给出能完成此项运送任务的最节省费用的租车方案，并说明理由．8．暑假期间，小刚一家乘车去离家380公里的某景区旅游，他们离家的距离y （km）与汽车行驶时间x（h）之间的函数图象如图所示．（1）从小刚家到该景区乘车一共用了多少时间？（2）求线段AB对应的函数解析式；（3）小刚一家出发2.5小时时离目的地多远？9．小李是某服装厂的一名工人，负责加工A，B两种型号服装，他每月的工作时间为22天，月收入由底薪和计件工资两部分组成，其中底薪900元，加工A型服装1件可得20元，加工B型服装1件可得12元．已知小李每天可加工A型服装4件或B型服装8件，设他每月加工A型服装的时间为x天，月收入为y元．（1）求y与x的函数关系式；（2）根据服装厂要求，小李每月加工A型服装数量应不少于B型服装数量的，那么他的月收入最高能达到多少元？10．都匀某校准备组织学生及家长代表到桂林进行社会实践活动，为便于管理，所有人员必须乘坐同一列高铁，高铁单程票价格如表所示，二等座学生票可打7.5折，已知所有人员都买一等座单程火车票需6175元，都买二等座单程火车票需3150元；如果家长代表与教师的人数之比为2：1．（1）参加社会实践活动的老师、家长代表与学生各有多少人？（2）由于各种原因，二等座单程火车票只能买x张（x＜参加社会实践的总人数），其余的须买一等座单程火车票，在保证所有人员都有座位的前提下，请你设计最经济的购票方案，并写出购买单程火车票的总费用y与x之间的函数关系式．（3）在（2）的方案下，请求出当x=30时，购买单程火车票的总费用．11．我省某苹果基地销售优质苹果，该基地对需要送货且购买量在2000kg﹣5000kg（含2000kg和5000kg）的客户有两种销售方案（客户只能选择其中一种方案）：方案A：每千克5.8元，由基地免费送货．方案B：每千克5元，客户需支付运费2000元．（1）请分别写出按方案A，方案B购买这种苹果的应付款y（元）与购买量x（kg）之间的函数表达式；（2）求购买量x在什么范围时，选用方案A比方案B付款少；（3）某水果批发商计划用20000元，选用这两种方案中的一种，购买尽可能多的这种苹果，请直接写出他应选择哪种方案．12．某市为了鼓励居民节约用水，决定实行两级收费制度．若每月用水量不超过14吨（含14吨），则每吨按政府补贴优惠价m元收费；若每月用水量超过14吨，则超过部分每吨按市场价n元收费．小明家3月份用水20吨，交水费49元；4月份用水18吨，交水费42元．（1）求每吨水的政府补贴优惠价和市场价分别是多少？（2）设每月用水量为x吨，应交水费为y元，请写出y与x之间的函数关系式；（3）小明家5月份用水26吨，则他家应交水费多少元？13．某学校计划组织500人参加社会实践活动，与某公交公司接洽后，得知该公司有A，B型两种客车，它们的载客量和租金如表所示：经测算，租用A，B型客车共13辆较为合理，设租用A型客车x辆，根据要求回答下列问题：（1）用含x的代数式填写下表：（2）采用怎样的租车方案可以使总的租车费用最低，最低为多少？14．我州某养殖场计划购买甲、乙两种鱼苗600条，甲种鱼苗每条16元，乙种鱼苗每条20元，相关资料表明：甲、乙两种鱼苗的成活率为80%，90%（1）若购买这两种鱼苗共用去11000元，则甲、乙两种鱼苗各购买多少条？（2）若要使这批鱼苗的总成活率不低于85%，则乙种鱼苗至少购买多少条？（3）在（2）的条件下，应如何选购鱼苗，使购买鱼苗的总费用最低？最低费用是多少？15．周末，小芳骑自行车从家出发到野外郊游，从家出发0.5小时到达甲地，游玩一段时间后按原速前往乙地，小芳离家1小时20分钟后，妈妈驾车沿相同路线前往乙地，行驶10分钟时，恰好经过甲地，如图是她们距乙地的路程y（km）与小芳离家时间x（h）的函数图象．（1）小芳骑车的速度为km/h，H点坐标．（2）小芳从家出发多少小时后被妈妈追上？此时距家的路程多远？（3）相遇后，妈妈载上小芳和自行车同时到达乙地（彼此交流时间忽略不计），求小芳比预计时间早几分钟到达乙地？16．某校准备组织师生共60人，从南靖乘动车前往厦门参加夏令营活动，动车票价格如表所示：（教师按成人票价购买，学生按学生票价购买）．若师生均购买二等座票，则共需1020元．（1）参加活动的教师有人，学生有人；（2）由于部分教师需提早前往做准备工作，这部分教师均购买一等座票，而后续前往的教师和学生均购买二等座票．设提早前往的教师有x人，购买一、二等座票全部费用为y元．①求y关于x的函数关系式；②若购买一、二等座票全部费用不多于1032元，则提早前往的教师最多只能多少人？17．为保障我国海外维和部队官兵的生活，现需通过A港口、B港口分别运送100吨和50吨生活物资．已知该物资在甲仓库存有80吨，乙仓库存有70吨，若从甲、乙两仓库运送物资到港口的费用（元/吨）如表所示：（1）设从甲仓库运送到A港口的物资为x吨，求总运费y（元）与x（吨）之间的函数关系式，并写出x的取值范围；（2）求出最低费用，并说明费用最低时的调配方案．18．某公司今年如果用原线下销售方式销售一产品，每月的销售额可达100万元．由于该产品供不应求，公司计划于3月份开始全部改为线上销售，这样，预计今年每月的销售额y（万元）与月份x（月）之间的函数关系的图象如图1中的点状图所示（5月及以后每月的销售额都相同），而经销成本p（万元）与销售额y（万元）之间函数关系的图象图2中线段AB所示．（1）求经销成本p（万元）与销售额y（万元）之间的函数关系式；（2）分别求该公司3月，4月的利润；（3）问：把3月作为第一个月开始往后算，最早到第几个月止，该公司改用线上销售后所获得利润总额比同期用线下方式销售所能获得的利润总额至少多出200万元？（利润=销售额﹣经销成本）19．荔枝是深圳的特色水果，小明的妈妈先购买了2千克桂味和3千克糯米糍，共花费90元；后又购买了1千克桂味和2千克糯米糍，共花费55元．（每次两种荔枝的售价都不变）（1）求桂味和糯米糍的售价分别是每千克多少元；（2）如果还需购买两种荔枝共12千克，要求糯米糍的数量不少于桂味数量的2倍，请设计一种购买方案，使所需总费用最低．20．甲、乙两车分别从A、B两地同时出发，甲车匀速前往B地，到达B地立即以另一速度按原路匀速返回到A地；乙车匀速前往A地，设甲、乙两车距A地的路程为y（千米），甲车行驶的时间为x（时），y与x之间的函数图象如图所示（1）求甲车从A地到达B地的行驶时间；（2）求甲车返回时y与x之间的函数关系式，并写出自变量x的取值范围；（3）求乙车到达A地时甲车距A地的路程．21．（列方程（组）及不等式解应用题）春节期间，某商场计划购进甲、乙两种商品，已知购进甲商品2件和乙商品3件共需270元；购进甲商品3件和乙商品2件共需230元．（1）求甲、乙两种商品每件的进价分别是多少元？（2）商场决定甲商品以每件40元出售，乙商品以每件90元出售，为满足市场需求，需购进甲、乙两种商品共100件，且甲种商品的数量不少于乙种商品数量的4倍，请你求出获利最大的进货方案，并确定最大利润．22．一茶叶专卖店经销某种品牌的茶叶，该茶叶的成本价是80元/kg，销售单价不低于120元/kg．且不高于180元/kg，经销一段时间后得到如下数据：设y与x的关系是我们所学过的某一种函数关系．（1）直接写出y与x的函数关系式，并指出自变量x的取值范围；（2）当销售单价为多少时，销售利润最大？最大利润是多少？23．某花店准备购进甲、乙两种花卉，若购进甲种花卉20盆，乙种花卉50盆，需要720元；若购进甲种花卉40盆，乙种花卉30盆，需要880元．（1）求购进甲、乙两种花卉，每盆各需多少元？（2）该花店销售甲种花卉每盆可获利6元，销售乙种花卉每盆可获利1元，现该花店准备拿出800元全部用来购进这两种花卉，设购进甲种花卉x盆，全部销售后获得的利润为W元，求W与x之间的函数关系式；（3）在（2）的条件下，考虑到顾客需求，要求购进乙种花卉的数量不少于甲种花卉数量的6倍，且不超过甲种花卉数量的8倍，那么该花店共有几种购进方案？在所有的购进方案中，哪种方案获利最大？最大利润是多少元？24．A城有某种农机30台，B城有该农机40台，现要将这些农机全部运往C，D 两乡，调运任务承包给某运输公司．已知C乡需要农机34台，D乡需要农机36台，从A城往C，D两乡运送农机的费用分别为250元/台和200元/台，从B城往C，D两乡运送农机的费用分别为150元/台和240元/台．（1）设A城运往C乡该农机x台，运送全部农机的总费用为W元，求W关于x 的函数关系式，并写出自变量x的取值范围；（2）现该运输公司要求运送全部农机的总费用不低于16460元，则有多少种不同的调运方案？将这些方案设计出来；（3）现该运输公司决定对A城运往C乡的农机，从运输费中每台减免a元（a ≤200）作为优惠，其它费用不变，如何调运，使总费用最少？25．甲、乙两车从A城出发前往B城，在整个行程中，两车离开A城的距离y与t的对应关系如图所示：（1）A、B两城之间距离是多少千米？（2）求乙车出发多长时间追上甲车？（3）直接写出甲车出发多长时间，两车相距20千米．26．下表是世界人口增长趋势数据表：（1）请你认真研究上面数据表，求出从1960年到2010年世界人口平均每年增长多少亿人；（2）利用你在（1）中所得到的结论，以1960年30亿人口为基础，设计一个最能反映人口数量y关于年份x的函数关系式，并求出这个函数的解析式；（3）利用你在（2）中所得的函数解析式，预测2020年世界人口将达到多少亿人．27．某公司有A型产品40件，B型产品60件，分配给甲、乙两个商店销售，其中70件给甲店，30件给乙店，且全部售出，两种产品的利润如表所示：（1）设分配给甲店A型产品x件，这家公司卖出这100件产品的总利润为W（元），求W关于x的函数关系式，并求x的取值范围．（2）为了促销，公司决定仅对甲店A型产品让利销售，每件让利a元，但让利后A型产品每件的利润仍高于甲店B型产品每件的利润，其它利润不变，问该公司如何设计分配方案，可使得总利润最大？28．某农机租赁公司共有50台收割机，其中甲型20台、乙型30台，现将这50台联合收割机派往A、B两地区收割水稻，其中30台派往A地区，20台派往B 地区，两地区与该农机公司商定的每天租赁价格如下表：（1）设派往A地区x台乙型联合收割机，租赁公司这50台联合收割机一天获得的租金为y元，求y关于x的函数关系式；（2）若使农机租赁公司这50台收割机一天所获租金不低于79600元，试写出满足条件的所有分派方案；（3）农机租赁公司拟出一个分派方案，使该公司50台收割机每天获得租金最高，并说明理由．29．甲、乙两组同学玩“两人背夹球”比赛，即：每组两名同学用背部夹着球跑完规定的路程，若途中球掉下时须捡起并回到掉球处继续赛跑，用时少者胜．结果：甲组两位同学掉了球；乙组两位同学则顺利跑完．设比赛距出发点用y表示，单位是米；比赛时间用x表示，单位是秒．两组同学比赛过程用图象表示如下．（1）这是一次米的背夹球比赛，获胜的是组同学；（2）请直接写出线段AB的实际意义；（3）求出C点坐标并说明点C的实际意义．30．某商店销售10台A型和20台B型电脑的利润为4000元，销售20台A型和10台B型电脑的利润为3500元．（1）求每台A型电脑和B型电脑的销售利润；（2）该商店计划一次购进两种型号的电脑共100台，其中B型电脑的进货量不超过A型电脑的2倍，设购进A型电脑x台，这100台电脑的销售总利润为y 元．①求y关于x的函数关系式；②该商店购进A型、B型电脑各多少台，才能使销售总利润最大？参考答案与解析1．（2016•滨州）星期天，李玉刚同学随爸爸妈妈回老家探望爷爷奶奶，爸爸8：30骑自行车先走，平均每小时骑行20km ；李玉刚同学和妈妈9：30乘公交车后行，公交车平均速度是40km/h ．爸爸的骑行路线与李玉刚同学和妈妈的乘车路线相同，路程均为40km ．设爸爸骑行时间为x （h ）．（1）请分别写出爸爸的骑行路程y 1（km ）、李玉刚同学和妈妈的乘车路程y 2（km ）与x （h ）之间的函数解析式，并注明自变量的取值范围；（2）请在同一个平面直角坐标系中画出（1）中两个函数的图象；（3）请回答谁先到达老家．【分析】（1）根据速度乘以时间等于路程，可得函数关系式，（2）根据描点法，可得函数图象；（3）根据图象，可得答案．【解答】解；（1）由题意，得y 1=20x （0≤x ≤2）y 2=40（x ﹣1）（1≤x ≤2）；（2）由题意得；（3）由图象可得李玉刚和妈妈乘车和爸爸骑行同时到达老家．【点评】本题考查了一次函数图象，利用描点法是画函数图象的关键．2．（2016•齐齐哈尔）有一科技小组进行了机器人行走性能试验，在试验场地有A 、B 、C 三点顺次在同一笔直的赛道上，甲、乙两机器人分别从A 、B 两点同时同向出发，历时7分钟同时到达C 点，乙机器人始终以60米/分的速度行走，如图是甲、乙两机器人之间的距离y（米）与他们的行走时间x（分钟）之间的函数图象，请结合图象，回答下列问题：（1）A、B两点之间的距离是70 米，甲机器人前2分钟的速度为95 米/分；（2）若前3分钟甲机器人的速度不变，求线段EF所在直线的函数解析式；（3）若线段FG∥x轴，则此段时间，甲机器人的速度为60 米/分；（4）求A、C两点之间的距离；（5）直接写出两机器人出发多长时间相距28米．【分析】（1）结合图象得到A、B两点之间的距离，甲机器人前2分钟的速度；（2）根据题意求出点F的坐标，利用待定系数法求出EF所在直线的函数解析式；（3）根据一次函数的图象和性质解答；（4）根据速度和时间的关系计算即可；（5）分前2分钟、2分钟﹣3分钟、4分钟﹣7分钟三个时间段解答．【解答】解：（1）由图象可知，A、B两点之间的距离是70米，甲机器人前2分钟的速度为：（70+60×2）÷2=95米/分；（2）设线段EF所在直线的函数解析式为：y=kx+b，∵1×（95﹣60）=35，∴点F的坐标为（3，35），则，解得，，∴线段EF所在直线的函数解析式为y=35x﹣70；（3）∵线段FG∥x轴，∴甲、乙两机器人的速度都是60米/分；（4）A、C两点之间的距离为70+60×7=490米；（5）设前2分钟，两机器人出发x分钟相距28米，由题意得，60x+70﹣95x=28，解得，x=1.2，前2分钟﹣3分钟，两机器人相距28米时，35x﹣70=28，解得，x=2.8．4分钟﹣7分钟，直线GH经过点（4，35）和点（7，0），则直线GH的方程为y=﹣x+，当y=28时，解得x=4.6，答：两机器人出发1.2分或2.8分或4.6分相距28米．【点评】本题考查的是一次函数的综合运用，掌握待定系数法求一次函数解析式、正确列出一元一次方程、灵活运用数形结合思想是解题的关键．3．（2016•吉林）甲、乙两人利用不同的交通工具，沿同一路线从A地出发前往B地，甲出发1h后，y甲、y乙与x之间的函数图象如图所示．（1）甲的速度是60 km/h；（2）当1≤x≤5时，求y乙关于x的函数解析式；（3）当乙与A地相距240km时，甲与A地相距220 km．【分析】（1）根据图象确定出甲的路程与时间，即可求出速度；关于x的函数解析式即可；（2）利用待定系数法确定出y乙（3）求出乙距A地240km时的时间，加上1，再乘以甲的速度即可得到结果．【解答】解：（1）根据图象得：360÷6=60km/h；（2）当1≤x≤5时，设y=kx+b，乙把（1，0）与（5，360）代入得：，解得：k=90，b=﹣90，=90x﹣90；则y乙（3）∵乙与A地相距240km，且乙的速度为360÷（5﹣1）=90km/h，∴乙用的时间是240÷90=h，则甲与A地相距60×（+1）=220km，故答案为：（1）60；（3）220【点评】此题考查了一次函数的应用，弄清图象中的数据是解本题的关键．4．（2016•连云港）环保局对某企业排污情况进行检测，结果显示：所排污水中硫化物的浓度超标，即硫化物的浓度超过最高允许的1.0mg/L．环保局要求该企业立即整改，在15天以内（含15天）排污达标．整改过程中，所排污水中硫化物的浓度y（mg/L）与时间x（天）的变化规律如图所示，其中线段AB表示前3天的变化规律，从第3天起，所排污水中硫化物的浓度y与时间x成反比例关系．（1）求整改过程中硫化物的浓度y与时间x的函数表达式；（2）该企业所排污水中硫化物的浓度，能否在15天以内不超过最高允许的1.0mg/L？为什么？【分析】（1）分情况讨论：①当0≤x≤3时，设线段AB对应的函数表达式为y=kx+b；把A（0，10），B（3，4）代入得出方程组，解方程组即可；②当x＞3时，设y=，把（3，4）代入求出m的值即可；（2）令y==1，得出x=12＜15，即可得出结论．【解答】解：（1）分情况讨论：①当0≤x≤3时，设线段AB对应的函数表达式为y=kx+b；把A（0，10），B（3，4）代入得，解得：，∴y=﹣2x+10；②当x＞3时，设y=，把（3，4）代入得：m=3×4=12，∴y=；综上所述：当0≤x≤3时，y=﹣2x+10；当x＞3时，y=；（2）能；理由如下：令y==1，则x=12＜15，故能在15天以内不超过最高允许的1.0mg/L．【点评】本题考查了扬州市的应用、反比例函数的应用；根据题意得出函数关系式是解决问题的关键．5．（2016•达州）某家具商场计划购进某种餐桌、餐椅进行销售，有关信息如表：已知用600元购进的餐桌数量与用160元购进的餐椅数量相同．（1）求表中a的值；（2）若该商场购进餐椅的数量是餐桌数量的5倍还多20张，且餐桌和餐椅的总数量不超过200张．该商场计划将一半的餐桌成套（一张餐桌和四张餐椅配成一套）销售，其余餐桌、餐椅以零售方式销售．请问怎样进货，才能获得最大利润？最大利润是多少？（3）由于原材料价格上涨，每张餐桌和餐椅的进价都上涨了10元，按照（2）中获得最大利润的方案购进餐桌和餐椅，在调整成套销售量而不改变销售价格的情况下，实际全部售出后，所得利润比（2）中的最大利润少了2250元．请问本次成套的销售量为多少？【分析】（1）根据餐桌和餐椅数量相等列出方程求解即可；（2）设购进餐桌x张，餐椅（5x+20）张，销售利润为W元．根据购进总数量不超过200张，得出关于x的一元一次不等式，解不等式即可得出x的取值范围，再根据“总利润=成套销售的利润+零售餐桌的利润+零售餐椅的利润”即可得出W关于x的一次函数，根据一次函数的性质即可解决最值问题；（3）设本次成套销售量为m套，先算出涨价后每张餐桌及餐椅的进价，再根据利润间的关系找出关于m的一元一次方程，解方程即可得出结论．【解答】解：（1）由题意得=，解得a=150，经检验，a=150是原分式方程的解；（2）设购进餐桌x张，则购进餐椅（5x+20）张，销售利润为W元．由题意得：x+5x+20≤200，解得：x≤30．∵a=150，∴餐桌的进价为150元/张，餐椅的进价为40元/张．依题意可知：W=x•（500﹣150﹣4×40）+x•（270﹣150）+（5x+20﹣x•4）•（70﹣40）=245x+600，∵k=245＞0，∴W 关于x 的函数单调递增，∴当x=30时，W 取最大值，最大值为7950．故购进餐桌30张、餐椅170张时，才能获得最大利润，最大利润是7950元．（3）涨价后每张餐桌的进价为160元，每张餐椅的进价为50元，设本次成套销售量为m 套．依题意得：（500﹣160﹣4×50）m+（30﹣m ）×（270﹣160）+（170﹣4m ）×（70﹣50）=7950﹣2250，即6700﹣50m=5700，解得：m=20．答：本次成套的销售量为20套．【点评】本题考查了一次函数的应用、解一元一次不等式、一次函数的性质及解一元一次方程，解题的关键是：（1）由数量相等得出关于a 的分式方程；（2）根据数量关系找出W 关于x 的函数解析式；（3）根据数量关系找出关于m 的一元一次方程．本题属于中档题，难度不大，但较繁琐，解决该题型题目时，根据数量关系找出函数关系式（方程或方程组）是关键．6．（2016•绍兴）根据卫生防疫部门要求，游泳池必须定期换水，清洗．某游泳池周五早上8：00打开排水孔开始排水，排水孔的排水速度保持不变，期间因清洗游泳池需要暂停排水，游泳池的水在11：30全部排完．游泳池内的水量Q （m 3）和开始排水后的时间t （h ）之间的函数图象如图所示，根据图象解答下列问题：（1）暂停排水需要多少时间？排水孔排水速度是多少？（2）当2≤t ≤3.5时，求Q 关于t 的函数表达式．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
一次函数专项训练专训1.一次函数的两种常见应用名师点金：一次函数的两种常见应用主要体现在解决实际问题和几何问题．能够从函数图象中得到需要的信息，并求出函数解析式从而解决实际问题和几何问题，是一次函数应用价值的体现，这种题型常与一些热点问题结合，考查学生综合分析问题、解决问题的能力．利用函数图象解决实际问题题型1行程问题(第1题)1．甲、乙两车从A城出发匀速行驶至B城，在整个行驶过程中，甲、乙两车离开A城的距离y(km)与甲车行驶的时间t(h)之间的函数关系如图所示，则下列结论①A，B两城相距300 km；②乙车比甲车晚出发1 h，却早到1 h；③乙车出发后2.5 h追上甲车；④当甲、乙两车相距50 km时，t＝54或154.其中正确的结论有( )A．1个B．2个C．3个D．4个2．甲、乙两地相距300 km，一辆货车和一辆轿车先后从甲地出发驶向乙地．如图，线段OA表示货车离甲地的距离y(km)与时间x(h)之间的函数关系，折线BCDE表示轿车离甲地的距离y(km)与时间x(h)之间的函数关系，根据图象，解答下列问题：(1)线段CD表示轿车在途中停留了________h；(2)求线段DE对应的函数解析式；(3)求轿车从甲地出发后经过多长时间追上货车．(第2题)题型2工程问题3．甲、乙两组工人同时加工某种零件，乙组在工作中有一段时间停产更换设备，更换设备后，乙组的工作效率是原来的2倍．两组各自加工零件的数量y(件)与时间x(h)之间的函数图象如图所示．(1)求甲组加工零件的数量y与时间x之间的函数解析式．(2)求乙组加工零件总量a的值．(3)甲、乙两组加工出的零件合在一起装箱，每够300件装一箱，零件装箱的时间忽略不计，经过多长时间恰好装满第1箱？再经过多长时间恰好装满第2箱？(第3题)题型3实际问题中的分段函数4．某种铂金饰品在甲、乙两个商店销售．甲店标价为477元/g，按标价出售，不优惠；乙店标价为530元/g，但若买的铂金饰品质量超过3 g，则超出部分可打八折．(1)分别写出到甲、乙两个商店购买该种铂金饰品所需费用y(元)和质量x(g)之间的函数解析式；(2)李阿姨要买一条质量不少于4 g且不超过10 g的此种铂金饰品，到哪个商店购买合算？5．我国是世界上严重缺水的国家之一．为了增强居民的节水意识，某市自来水公司对居民用水采用以户为单位分段计费办法收费．即一个月用水10 t以内(包括10 t)的用户，每吨收水费a元；一个月用水超过10 t的用户，10 t水仍按每吨a元收费，超过10 t的部分，按每吨b(b＞a)元收费．设一户居民月用水x t，应交水费y元，y与x之间的函数关系如图所示．(1)求a的值；某户居民上月用水8 t，应交水费多少元？(2)求b的值，并写出当x＞10时，y与x之间的函数解析式．(第5题)利用一次函数解几何问题题型4利用图象解几何问题6．如图①所示，正方形ABCD的边长为6 cm，动点P从点A出发，在正方形的边上沿A→B→C→D运动，设运动的时间为t(s)，三角形APD的面积为S(cm2)，S与t的函数图象如图②所示，请回答下列问题：(1)点P在AB上运动的时间为________s，在CD上运动的速度为________cm/s，三角形APD的面积S的最大值为________cm2；(2)求出点P在CD上运动时S与t之间的函数解析式；(3)当t为何值时，三角形APD的面积为10 cm2?(第6题)题型5利用分段函数解几何问题(分类讨论思想、数形结合思想)7．在长方形ABCD中，AB＝3，BC＝4，动点P从点A开始按A→B→C→D的方向运动到点D.如图，设动点P所经过的路程为x，△APD 的面积为y.(当点P与点A或D重合时，y＝0)(1)写出y与x之间的函数解析式；(2)画出此函数的图象．(第7题)专训2.二元一次方程(组)与一次函数的四种常见应用名师点金：二元一次方程(组)与一次函数的关系很好地体现了“数”与“形”的结合，其常见应用有：利用两条直线的交点坐标确定方程组的解；利用方程(组)的解求两直线的交点坐标；方程组的解与两个一次函数图象位置的关系；利用二元一次方程组求一次函数的解析式．利用两直线的交点坐标确定方程组的解1．已知直线y ＝－x ＋4与y ＝x ＋2如图所示，则方程组⎩⎪⎨⎪⎧y ＝－x ＋4，y ＝x ＋2 的解为( )(第1题)A .⎩⎪⎨⎪⎧x ＝3y ＝1 B .⎩⎪⎨⎪⎧x ＝1y ＝3 C .⎩⎪⎨⎪⎧x ＝0y ＝4 D .⎩⎪⎨⎪⎧x ＝4y ＝0 2．已知直线y ＝2x 与y ＝－x ＋b 的交点坐标为(1，a)，试确定方程组⎩⎪⎨⎪⎧2x －y ＝0，x ＋y －b ＝0的解和a ，b 的值．3．在平面直角坐标系中，一次函数y ＝－x ＋4的图象如图所示．(1)在同一坐标系中，作出一次函数y ＝2x －5的图象；(2)用作图象的方法解方程组⎩⎪⎨⎪⎧x ＋y ＝4，2x －y ＝5； (3)求一次函数y ＝－x ＋4与y ＝2x －5的图象与x 轴所围成的三角形的面积．(第3题)利用方程(组)的解求两直线的交点坐标4．已知方程组⎩⎪⎨⎪⎧－mx ＋y ＝n ，ex ＋y ＝f 的解为⎩⎪⎨⎪⎧x ＝4，y ＝6，则直线y ＝mx ＋n 与y ＝－ex ＋f 的交点坐标为( )A ．(4，6)B ．(－4，6)C ．(4，－6)D ．(－4，－6)5．已知⎩⎪⎨⎪⎧x ＝3，y ＝－2和⎩⎪⎨⎪⎧x ＝2，y ＝1是二元一次方程ax ＋by ＝－3的两个解，则一次函数y ＝ax ＋b 的图象与y 轴的交点坐标是( )A ．(0，－7)B ．(0，4)C .⎝ ⎛⎭⎪⎫0，－37D .⎝ ⎛⎭⎪⎫－37，0 方程组的解与两个一次函数图象位置的关系6．若方程组⎩⎪⎨⎪⎧x ＋y ＝2，2x ＋2y ＝3没有解，则一次函数y ＝2－x 与y ＝32－x 的图象必定( )A ．重合B ．平行C ．相交D ．无法确定7．直线y ＝－a 1x ＋b 1与直线y ＝a 2x ＋b 2有唯一交点，则二元一次方程组⎩⎪⎨⎪⎧a 1x ＋y ＝b 1，a 2x －y ＝－b 2的解的情况是( ) A ．无解 B ．有唯一解C ．有两个解D ．有无数解利用二元一次方程组求一次函数的解析式8．已知一次函数y ＝kx ＋b 的图象经过点A(1，－1)和B(－1，3)，求这个一次函数的解析式．9．已知一次函数y ＝kx ＋b 的图象经过点A(3，－3)，且与直线y ＝4x －3的交点B 在x 轴上．(1)求直线AB 对应的函数解析式；(2)求直线AB 与坐标轴所围成的三角形BOC(O 为坐标原点，C 为直线AB 与y 轴的交点)的面积．答案专训11．B2．解：(1)0.5(2)设线段DE对应的函数解析式为y＝kx＋b(2.5≤x≤4.5)．将D(2.5，80)，E(4.5，300)的坐标分别代入y＝kx＋b可得，80＝2.5k ＋b，300＝4.5k＋b.解得k＝110，b＝－195.所以y＝110x－195(2.5≤x≤4.5)．(3)设线段OA对应的函数解析式为y＝k1x(0≤x≤5)．将A(5，300)的坐标代入y＝k1x可得，300＝5k1，解得k1＝60.所以y＝60x(0≤x≤5)．令60x＝110x－195，解得x＝3.9.故轿车从甲地出发后经过3.9－1＝2.9(h)追上货车．3．解：(1)设甲组加工零件的数量y与时间x之间的函数解析式为y＝kx，因为当x＝6时，y＝360，所以k＝60.即甲组加工零件的数量y与时间x之间的函数解析式为y＝60x(0≤x≤6)．(2)a＝100＋100÷2×2×(4.8－2.8)＝300.(3)当工作2.8 h时共加工零件100＋60×2.8＝268(件)，所以装满第1箱的时刻在2.8 h 后．设经过x 1 h 装满第1箱．则60x 1＋100÷2×2(x 1－2.8)＋100＝300，解得x 1＝3.从x ＝3到x ＝4.8这一时间段内，甲、乙两组共加工零件(4.8－3)×(100＋60)＝288(件)，所以x>4.8时，才能装满第2箱，此时只有甲组继续加工． 设装满第1箱后再经过x 2 h 装满第2箱．则60x 2＋(4.8－3)×100＝300，解得x 2＝2.故经过3 h 恰好装满第1箱，再经过2 h 恰好装满第2箱．4．解：(1)y 甲＝477x ，y 乙＝⎩⎪⎨⎪⎧530x （0≤x ≤3），424x ＋318（x ＞3）. (2)当477x ＝424x ＋318时，解得x ＝6.即当x ＝6时，到甲、乙两个商店购买所需费用相同； 当477x<424x ＋318时，解得x<6，又x ≥4，于是，当4≤x ＜6时，到甲商店购买合算； 当477x>424x ＋318时，解得x>6，又x ≤10，于是，当6＜x ≤10时，到乙商店购买合算．5．解：(1)当x ≤10时，由题意知y ＝ax.将x ＝10，y ＝15代入，得15＝10a ，所以a ＝1.5.故当x ≤10时，y ＝1.5x.当x ＝8时，y ＝1.5×8＝12. 故应交水费12元．(2)当x ＞10时，由题意知y ＝b(x －10)＋15.将x ＝20，y ＝35代入，得35＝10b ＋15，所以b ＝2.故当x ＞10时，y 与x 之间的函数解析式为y ＝2x －5.点拨：本题解题的关键是从图象中找出有用的信息，用待定系数法求出解析式，再解决问题．6．解：(1)6；2；18(2)PD ＝6－2(t －12)＝30－2t ，S ＝12AD·PD＝12×6×(30－2t)＝90－6t ，即点P 在CD 上运动时S 与t 之间的函数解析式为S ＝90－6t(12≤t ≤15)．(3)当0≤t ≤6时易求得S ＝3t ，将S ＝10代入，得3t ＝10，解得t ＝103；当12≤t ≤15时，S ＝90－6t ，将S ＝10代入，得90－6t ＝10，解得t ＝403.所以当t 为103或403时，三角形APD 的面积为10 cm 2. 7．解：(1)点P 在边AB ，BC ，CD 上运动时所对应的y 与x 之间的函数解析式不相同，故应分段求出相应的函数解析式．①当点P 在边AB 上运动，即0≤x ＜3时，y ＝12×4x ＝2x ； ②当点P 在边BC 上运动，即3≤x ＜7时，y ＝12×4×3＝6； ③当点P 在边CD 上运动，即7≤x ≤10时，y ＝12×4(10－x)＝－2x ＋20. 所以y 与x 之间的函数解析式为y ＝⎩⎪⎨⎪⎧2x （0≤x ＜3），6 （3≤x ＜7），－2x ＋20 （7≤x ≤10）.(2)函数图象如图所示．(第7题)点拨：本题考查了分段函数在动态几何中的运用，体现了数学中的分类讨论思想和数形结合思想．根据点P 在边AB ，BC ，CD 上运动时所对应的y 与x 之间的函数解析式不相同，分段求出相应的函数解析式，再画出相应的函数图象．专训21．B2．解：将(1，a)代入y ＝2x ，得a ＝2.所以直线y ＝2x 与y ＝－x ＋b 的交点坐标为(1，2)，所以方程组⎩⎪⎨⎪⎧2x －y ＝0，x ＋y －b ＝0的解是⎩⎪⎨⎪⎧x ＝1，y ＝2. 将(1，2)代入y ＝－x ＋b ，得2＝－1＋b ，解得b ＝3.3．解：(1)画函数y ＝2x －5的图象如图所示．(2)由图象看出两直线的交点坐标为(3，1)，所以方程组的解为⎩⎪⎨⎪⎧x ＝3，y ＝1.(第3题)(3)直线y ＝－x ＋4与x 轴的交点坐标为(4，0)，直线y ＝2x －5与x 轴的交点坐标为⎝ ⎛⎭⎪⎫52，0，又由(2)知，两直线的交点坐标为(3，1)，所以三角形的面积为12×⎪⎪⎪⎪⎪⎪4－52×1＝34. 4．A 5.C 6.B 7.B8．解：依题意将A(1，－1)与B(－1，3)的坐标代入y ＝kx ＋b 中，得⎩⎪⎨⎪⎧k ＋b ＝－1，－k ＋b ＝3，解得k ＝－2，b ＝1， 所以这个一次函数的解析式为y ＝－2x ＋1.9．解：(1)因为一次函数y ＝kx ＋b 的图象与直线y ＝4x －3的交点B 在x 轴上，所以将y ＝0代入y ＝4x －3中，得x ＝34，所以B ⎝ ⎛⎭⎪⎫34，0，把A(3，－3)，B ⎝ ⎛⎭⎪⎫34，0的坐标分别代入y ＝kx ＋b 中，得⎩⎪⎨⎪⎧3k ＋b ＝－3，34k ＋b ＝0，解得⎩⎪⎨⎪⎧k ＝－43，b ＝1.则直线AB 对应的函数解析式为y ＝－43x ＋1.(2)由(1)知直线AB 对应的函数解析式为y ＝－43x ＋1，所以直线AB 与y 轴的交点C 的坐标为(0，1)，所以OC ＝1，又B ⎝ ⎛⎭⎪⎫34，0，所以OB ＝34.所以S 三角形BOC ＝12OB·OC＝12×34×1＝38.即直线AB 与坐标轴所围成的三角形BOC 的面积为38.。