凸轮机构例题
凸轮例题
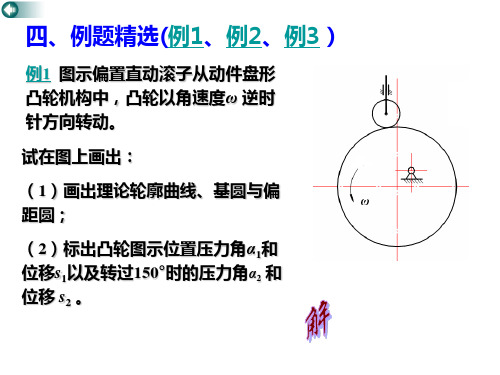
例1 图示偏置直动滚子从动件盘形 凸轮机构中，凸轮以角速度ω 逆时 针方向转动。 试在图上画出：
（1）画出理论轮廓曲线、基圆与偏 距圆；
（2）标出凸轮图示位置压力角α1和 位移s1以及转过150°时的压力角α2 和位移 s2 。
本题目主要考察对凸轮廓线、基圆、偏距 圆、压力角及位移等基本概念的理解和对反转 法原理的灵活运用。 解
解
本题目主要考察对摆动从动件凸轮机构的 基圆、行程运动角、压力角及角位移等基本概 念的理解。
O
（1）图示位置的r0 、s 和α如图。 （2）r0 、s 与α之间的关系式为：
v tan lOP e r0 e s
2 2
1
பைடு நூலகம்
e
s r02 e 2
例3 图示为摆动滚子从动件盘形凸轮机构，凸轮为偏心圆盘， 且以角速度ω逆时针方向回转。
试在图上标出：
1. 凸轮基圆； 2. 升程运动角和回程运动角； 3. 图示位置时从动件的初始位置 角0和角位移 ； 4. 图示位置从动件的压力角α； 5. 从动件的最大角位移max 。
例2 已知图示凸轮机构标出基圆半径r0，图示位置从动件位移s 和机构的压力角，并求出它们之间的关系式。。 试求： 1.标出基圆半径r0？ 2.标出图示位置从动件位移s 和机构 的压力角α ？
3.求出r0 、s 和α之间的关系式？
本题目主要考察对基圆、压力角及位移等 基本概念的理解和压力角的计算方法。 解
凸轮机构作业!
凸轮作业2：
图示凸轮机构中，试求： (1)凸轮的基圆； (2)凸轮从图示位置转过60 度时，机构的压力角α； (3)滚子从图示位置翻转到B 处时，对应的凸轮转角δ
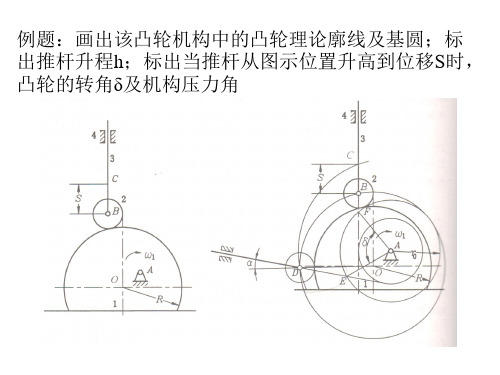
例题：画出该凸轮机构中的凸轮理论廓线及基圆；标 出推杆升程h；标出当推杆从图示位置升高到位移S时， 凸轮的转角δ及机构压力角
凸轮章节作业！
凸轮作业1：
图示凸轮机构中，比例尺为1mm/mm， ω=1rad/s。试求： (1)凸轮的理论廓线和基圆； (2)图示位置时机构压力角α； (3)凸轮从图示位置转过90度时的位移s； (4)其他条件不变：①若改变滚子半径， 从动件运动规律是否改变？②若改变凸 轮转向，从动件运动规律是否改变？ ③ 若改变凸轮偏心距，从动件运动规律是 否改变？
机械原理典型例题凸轮
hk
αk
α max k
90°
θ
V
(P)
h
F αF=0
(1)凸轮偏心距。利用速度瞬心 ，几何 中心O即为速度瞬心p，可得ν=eω，求 得e=25mm。
（2）凸轮转过90°时，从动件在K点 接触，其压力角为αk。
e/sinαk =R/sinθ；
当θ=90°时，αk达到最大值。
αk=arcsin(e/R)=30°
接触时的压力角αC；比较αB，αC大小，说明题意中的偏置是否合理。 （3）如果偏距e=-5mm，此时的偏置是否合理
αB αC
αD
B
C
D
hB
e
R
r0 O
A
解：
αC> αB。该偏置有利 减小压力角，改善受力，
故偏置合理。
α D> α C> αB，故偏置 不合理。
例4 凸轮为偏心轮如图，已知参数R=30mm，loA=10mm，e=15mm，rT=5mm， E，F为凸轮与滚子的两个接触点。求 （1）画出凸轮轮廓线（理论轮廓线），求基园r0；（2）E点接触时从动件的压力角 αE； (3) 从E到F接触凸轮所转过的角度φ； （4）由E点接触到F点接触从动件的位 移S；(5）找出最大αmax的位置。
αE
hE E
e
ω
Oθ
F
φ
r0
A
αmax
S=hF-hE Sin α =(e-loAcos θ)/(R+rT)
θ =180时,α为 αmax
R
hF
例5 ：图示为一直动推杆盘形凸轮机构。若一直凸轮基
推程
圆半径r0，推杆的运动规律s=S(δ)，为使设计出的凸轮
机构受力状态良好，试结合凸轮机构压力角的计算公式
机械原理凸轮机构习题与答案（五篇材料）
机械原理凸轮机构习题与答案（五篇材料）第一篇：机械原理凸轮机构习题与答案解：曲柄的存在的必要条件是1）最短杆与追长杆的杆长之和应小于或等于其余两杆的长度之和；2)连架杆与机架必有最短杆1）.杆件1为曲柄2）.在各杆长度不变的情况下，选取c杆做为机架就可以实现双摇杆机构试以作图法设计一偏置尖底推杆盘形凸轮的轮廓曲线。
已知凸轮以等角速度顺时针回转，正偏距e=10,基园半径r0=30mm.推杆运动规律为：凸轮转角δ=0~150时，推杆00.凸轮转角δ=180~300时推杆等速上升16mm;.凸轮转角δ=150~180时推杆远休；等加速回程16mm;.凸轮转角δ=300~360时推杆近休。
解：解题步骤1）首先绘制位移S与转角δ的关系曲线S-δ曲线。
2）根据S-δ曲线、凸轮基园半径和正偏距，绘制凸轮的轮廓曲线。
000000凸轮仅用了0度，90度，150度，180度，300度几个点绘制轮廓曲线，同学们绘制时英多用些点（一般取12个点，再勾画轮廓曲线）第二篇：机械原理_凸轮机构设计机械原理课程设计——凸轮机构设计（一）目录 (1)＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿（一）、题目及原始数据 (2)（二）、推杆运动规律及凸轮廓线方程 (3)（三）、（四）、（五）、（六）、（七）、（八）、计算程序方框图..........................5 计算源程序..............................6 程序计算结果及分析......................10 凸轮机构图..............................15 心得体会................................16 参考书. (16)（一）、题目及原始数据试用计算机辅助设计完成偏置直动滚子推杆盘形凸轮机构的设计，凸轮以1rad/s的角速度沿逆时针方向转动。
要求：（1）、推程运动规律为等加速等减速运动，回程运动规律为五次多项式运动规律；（2）、打印出原始数据；（3）、打印出理论轮廓和实际轮廓的坐标值；（4）、打印出推程和回程的最大压力角，以及出现最大压力角时凸轮的相应转角；（5）、打印出凸轮实际轮廓曲线的最小曲率半径，以及相应的凸轮转角；（6）、打印出凸轮运动的位移；（7）、打印最后所确定的凸轮的基圆半径。
凸轮机构例题
凸轮机构例题1、已知题4图所示的直动平底推杆盘形凸轮机构，凸轮为R= 30mm的偏心圆盘,20mm，试求：（1）基圆半径和升程；（2）推程运动角、回程运动角、远休止角和近休止角；（3）凸轮机构的最大压力角和最小压力角；（4）推杆的位移s、速度v和加速度a方程；（5）若凸轮以W = IOrad/s回转，当AO成水平位置时推杆的速度。
7匕题」图题4图解1、解:⑴ x0 = 10 = 2AO= 40mnit⑺ 推程J药角心=lS（r ,回程运动角<5；=180° 1近休止角九=0° ,远休止角玄a才-⑶由于平底垂盲于导路的平底推杆凸轮机构的圧力甫恒等于零，所以弧二％0U）如團所示，取旦唯钱与水平线的夹角肯凸轮的转角G M：推杆的位務右程再5 = x3+x3sh^-20（145b^推杆的速度方程対V =20&JCOS^推杆的加速度肓程为口一2%%航<5）当也=1[|曲创池碇于水平位貫时，5M}°或顷° ,所以推杆的速度为v= (20X LOcasS) mm.?«±20Uiiitn/82、10图所示对心直动尖顶推杆盘形凸轮机构中，凸轮为一偏心圆，O为凸轮的几何中心，O i为凸轮的回转中心。
直线AC与BD垂直，且Q试计算：=30tnnb（1）该凸轮机构中B、D两点的压力角;（2）该凸轮机构推杆的行程h。
⑴由區可加.氷口两掠的巫和闻次）母沖== arct吕［OQ# OB =arctgO. 5 = 25.565°(2) IT S h = = (2 > 30)mir = GG ITJTI3.如题13图所示的凸轮机构，设凸轮逆时针转动。
要求:画出凸轮的基圆半径，在图示位置时推杆的位移推杆开始上升时总=0°,以及传动角y题H團解s,凸轮转角厲（设。
机械原理-凸轮机构例题
第三章凸轮机构典型例题例 1 在图示的对心移动滚子从动件盘形凸轮机构中，凸轮的实际廓线为一圆，其圆心在A点，半径R=40mm，凸轮转动方向如图所示，l OA=25mm，滚子半径r t=10mm，试问：（1）凸轮的理论廓线为何种曲线？（2）凸轮的基圆半径r b=?（3）从动件的升距h=?解：选取适当的比例尺作机构图如图（b）所示（1）理论廓线η为半径为R+r t =40+10=50mm的圆。
（2）凸轮的基圆半径r b凸轮理论廓线的最小向径称为凸轮的基圆半径，如图所示线段OC即为理论廓线η的最小向径，也就是凸轮的基圆半径r b。
由图（b）可知r b=l AC－l AO =（R+r t）－l AO=（40+10）－25=25mm（3）从动件的升距h从动件上升的最大距离h称为从动件的升距，它等于理论廓线η的最大与最小向径之差。
因此，h=（l AO+R+r t）－r b=25+40+10－25=50mm例 2 如图（a）所示为凸轮机构推杆的速度曲线，它由四段直线组成。
要求：画出推杆的位移线图和加速度线图；判断那几个位置有冲击存在，是刚性冲击还是柔性冲击；在图示的F位置。
凸轮与推杆之间有无惯性力作用，有无冲击存在。
解：由图（a）所示推杆的速度线图可知在OA段内，因推杆的速度v=0，故此段为推杆的近休止，推杆的位移及加速度均为零，即s=0，a=0，如图（b）（c）所示。
在AD段内，因v>0，故为推杆的推程段。
且在AB段内，因速度线图为上升的斜直线，故推杆先等加速上升，位移线图为抛物线运动曲线，而加速度线图为正的水平直线段；在BC线段内，速度线图为水平直线段，故推杆继续等速上升，位移线图为上升的斜直线，而加速度线图为与δ轴重合的线段；在CD 段内，因速度线图为下降的斜直线，故推杆继续等减速上升，位移线图为抛物线运动曲线，而加速度线图为负的水平直线段。
做出推杆的推程段的位移及加速度线图，如图（b）（c）所示。
凸轮机构习题解
在图示旳凸轮机构中，圆弧底摆动推杆与凸轮在B点接触。当 凸轮从图示位置逆时针转过900时，试用图解法标出：1）推杆 在凸轮上旳接触点；2）摆杆位移角旳大小；3）凸轮机构旳压 力角。
解：1）接触点：
2）摆杆位移角:
y
3）压力角:
r
v
B
o’
B’
a
o
例已知图示偏心圆盘凸轮机构旳各部分尺寸，试在图上用 作图法求： （1）凸轮机构在图示位置时旳压力角 ； （2）凸轮旳基圆；
解：
例 在图示凸轮机构中，画出凸轮从图示位置转 过90°时凸轮机构旳压力角。
解：
例 图示偏置直动滚子从动件盘形凸轮机构中，凸轮以角速度 逆时针方向转动。试在图上：
（1）画出理论轮廓曲线、基圆与偏距圆； （2）标出凸轮从图示位置转过90°时旳压力角 和位移 s。
解：
例 偏心圆盘凸轮机构，凸轮旳回转方向如图所示。 要求（1）阐明该机构旳详细名称；
凸轮机构
例 用作图法求出图 示两凸轮机构从图 示位置转过45°时旳 压力角。
解：
例 画出图示凸轮机构旳基圆半径r0及示凸轮机构中标出凸轮转过90°时凸轮 机构旳压力角
解：
例 在图示旳凸轮机构中，画出凸轮从图示位 置转过60°时从动件旳位置及从动件旳 位移s。
（3）从动件从最下位置摆到图示位置时所摆过旳角度y；
（4）凸轮相应转过旳角度。
解：
试以作图法设计一偏置直动滚子推杆盘形凸轮机构凸轮旳轮廓曲线。 已知凸轮以等角速度顺时针回转，正偏距e=10mm，基圆半径ro=30mm，滚 子半径rr=10mm：推杆运动规律为：凸轮转角d=00～1500时，推杆等速上升 16mm；d=1500一1800时推杆远休；d=1800～3000时推杆等加速等减速回程 16mm；d=3000～3600时推杆近休。
第五章凸轮机械原理典型例题
推程
r0
O
ω
S,V, a 是确定的
B
B
S
B
α
S0 δ
S δ
S
S0
α1
O’ e O ω
O
α2
δ ω e O’
S0
O
ω
P
tan OP / OB (ds / d ) / (r0 s)
P
P
tan (OP e) / O ' B ((ds / d ) e) / ( r02 e 2 s)
A'
φ Cr B -ω O' A B' V
C' O
α
滚子中心C，半径r 理论轮廓，R=LO'C 基园R0， 推杆中心位置园， R=LOA 凸轮逆时90，推杆 中心A'，推杆位置 接触点B' 摆动角φ 压力角α
2 2 tan 假设凸轮轮廓已经做出，要求在凸轮转过δ角时， (OP e) / O ' B ((ds / d ) e) / ( r0 e s) 位移为S，速度为V， V=ω×Lop ，压力角为α。 适当偏距e（左移），使凸轮转过δ角，此时应有 可知：采用适当的偏距且使推杆偏向凸轮轴心 的左侧，可使推程压力角减小，从而改善凸轮 相同位移S，相同速度V。此时压力角为α1； 的受力情况，但使回程的压力角增大，由于回 P为瞬心位置，相同的速度即瞬心P位置是固定的。程的许用压力角很大，故对机构的受力情况影 响不大。 右移，使凸轮转过δ角，此时压力角为α2；
基本概念题
1.选择题
（1）对于远、近休止角均不为零的凸轮机构，当从动件推程按简谐运动 C 规律运动时，在推程开始和结束位置______。 A.不存在冲击 B.存在刚性冲击 C.存在柔性冲击 （2）已知一滚子接触摆动从动件盘形凸轮机构，因滚子损坏，更换了一 个外径与原滚子不同的新滚子，则更换滚子后________。 D A. 从动件运动规律发生变化，而从动件最大摆角不变 B. 从动件最大摆角发生变化，而从动件运动规律不变 C. 从动件最大摆角和从动件运动规律均不变 D. 从动件最大摆角和从动件运动规律均发生变化 (3)已知一滚子接触偏置直动从动件盘形凸轮机构，若将凸轮转向由顺 时针改为逆时针，则_________。 D A. 从动件运动规律发生变化，而从动件最大行程不变 B. 从动件最大行程发生变化，而从动件运动规律不变 C. 从动件最大行程和从动件运动规律均不变 D. 从动件最大行程和从动件运动规律均发生变化
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第三章凸轮机构典型例题
例 1 在图示的对心移动滚子从动件盘形凸轮机构中，凸轮的实际廓线为一圆，其圆心在A点，半径R=40mm，凸轮转动方向如图所示，l OA=25mm，滚子半径r t=10mm，试问：
（1）凸轮的理论廓线为何种曲线？
（2）凸轮的基圆半径r b=?
（3）从动件的升距h=?
解：选取适当的比例尺作机构图如图（b）所示
（1）理论廓线η为半径为R+r t =40+10=50mm的圆。
（2）凸轮的基圆半径r b
凸轮理论廓线的最小向径称为凸轮的基圆半径，如图所示线段OC即为理论廓线η的最小向径，也就是凸轮的基圆半径r b。
由图（b）可知
r b=l AC－l AO =（R+r t）－l AO=（40+10）－25=25mm
（3）从动件的升距h
从动件上升的最大距离h称为从动件的升距，它等于理论廓线η的最大与最小向径之差。
因此，
h=（l AO+R+r t）－r b=25+40+10－25=50mm
例 2 如图（a）所示为凸轮机构推杆的速度曲线，它由四段直线组成。
要求：画出推杆的位移线图和加速度线图；判断那几个位置有冲击存在，是刚性冲击还是柔性冲击；在图示的F位置。
凸轮与推杆之间有无惯性力作用，有无冲击存在。
解：由图（a）所示推杆的速度线图可知
在OA段内，因推杆的速度v=0，故此段为推杆的近休止，推杆的位移及加速度均为零，即s=0，a=0，如图（b）（c）所示。
解：
在AD段内，因v>0，故为推杆的推程段。
且在AB段内，因速度线图为上升的斜直线，故推杆先等加速上升，位移线图为抛物线运动曲线，而加速度线图为正的水平直线段；在BC线段内，速度线图为水平直线段，故推杆继续等速上升，位移线图为上升的斜直线，而加速度线图为与δ轴重合的线段；在CD 段内，因速度线图为下降的斜直线，故推杆继续等减速上升，位移线图为抛物线运动曲线，而加速度线图为负的水平直线段。
做出推杆的推程段的位移及加速度线图，如图（b）（c）所示。
在DE段内，因v<0，故为推杆的回程段，且速度线图为水平线段，推杆作等速下降运动。
位移线图为下降的斜直线，而加速度线图为与δ轴重合的线段，且在D和E处其加速度分别为负无穷大和正无穷大，如图（b）（c）所示。
由推杆速度线图（a）和加速度线图（c）可知，在D及E处，有速度突变，且在加速度线图上分别为负无穷大和正无穷大。
故在在D及E处有刚性冲击。
在加速度线图上A"，B"，C"，处有加速度值的有限值突变，故在这几处凸轮机构有柔性冲击。
在F处有正的加速度值，故有惯性力，但既无速度突变，也无加速度突变，因此，F处无冲击存在。
例3 图示为一移动滚子从动件盘形凸轮机构，滚子中心位于B0点时为该机构的起始位置。
试求：
（1）滚子与凸轮廓线在B1' 点接触时，所对应的凸轮转角φ1。
（2）当滚子中心位于B2点时，凸轮机构的压力角α2。
解（1）这是灵活运用反转法的一种情况，即已知凸轮廓线，求当从动件与凸轮廓线上从一点到另一点接触时，凸轮转过的角度。
求解步骤如下：
1）正确作出偏距圆，如图（b）所示
2）用反向包络法求处在B1'点附近的部分理论廓线η。
3）找出滚子与凸轮在B1'点接触时滚子中心的位置B1。
4）过B1点作偏心圆的切线，该切线即为滚子与凸轮在B1' 点接触时从动件的位置。
该位置与从动件起始位置线间的夹角，即为所求得凸轮转角φ1。
如图所示，φ1也可在偏心圆上度量。
（2）这是灵活运用反转法的另一种情况，即已知凸轮廓线，求当凸轮从图示位置转过某一角度到达另一位置时，凸轮机构的压力角。
求解步骤如下：1）过B2点作偏心圆的切线，该切线即为滚子中心位于B2点时从动件的位置。
2）过B2点作出凸轮廓线的法线nn，该法线必通过滚子中心B2，同时通过滚子与凸轮廓线的切点，它代表从动件的受力方向。
3）该法线与从动件位置线间所夹的锐角即为机构在该点处的压力角α2，如图（b）所示。
例4在图（a）示的凸轮机构中，从动件的起始上升点为C点。
（1）试在图上标出从C点接触到D点接触时，凸轮转过的转角φ，及从动
件走过的位移；
（2）标出在D点接触时凸轮机构的压力角α。
解：具体解法如图（b）所示。
摆线运动规律位移线图作图方法： 以
2h 为半径画圆并将其6等分。