山东省济南市山东建筑大学电气工程及其自动化07-08代数B+答案
山东建筑大学电气工程及其自动化专业2020-2021第二学期自动控制原理

山东建筑大学电气工程及其自动化专业2020-2021第二学期自动控制原理一、单选题1.下面哪种控制属于自动控制() [单选题]A.自行车速度控制B.收音机音量控制C.汽车驾驶控制D.空调器的温度控制(正确答案)2.下列不是对自动控制系统性能的基本要求的是() [单选题]A.稳定性B.复现性(正确答案)C.快速性D.准确性3.下列常用来描述静态特性的数学模型是() [单选题]A.微分方程B.代数方程(正确答案)C.差分方程D.传递函数4.指数函数.其拉氏变换为() [单选题]A. 1B.(正确答案)C.D5.典型的二阶振荡环节的传递函数为()。
[单选题]A.(正确答案)B.C.D.6.下列不属于动态性能指标的是() [单选题]A稳态误差(正确答案)B上升时间C峰值时间D最大超调量7.不属于控制系统设计过程步骤的是() [单选题]A根据需要制定技术指标B根据技术指标设计若干解决方案C根据理论分析选择解决方案(正确答案)D对所选择方案做细节设计8.系统的闭环传递函数为,则系统的极点为()。
[单选题]A.B.(正确答案)C.D.9.根轨迹的分支与()数目相等。
[单选题]A开环极点(正确答案)B闭环极点C开环零点D闭环零点10.某环节传递函数,则其频率特征的奈奎斯特图终点坐标为()。
[单选题] A.B.C.D.(正确答案)11.下面哪种控制属于人工控制() [单选题]A导弹飞行控制B 汽轮机的转速控制C 人造卫星控制D汽车驾驶控制(正确答案)12.自动控制系统不稳定的过渡过程是()。
[单选题]A.发散振荡过程(正确答案)B.衰减振荡过程C.单调过程D.以上都不是13.下列不是用来描述动态方程的数学模型是() [单选题]A差分方程B传递函数(正确答案)C状态方程D代数方程14.最大超调量的大小直接描述了系统的() [单选题]A快速性B准确性C相对稳定性(正确答案)D鲁棒性15.一阶系统的放大系数K越大,则其()。
山东省济南市山东建筑大学电气工程及其自动化概率论08-09-1 试卷B
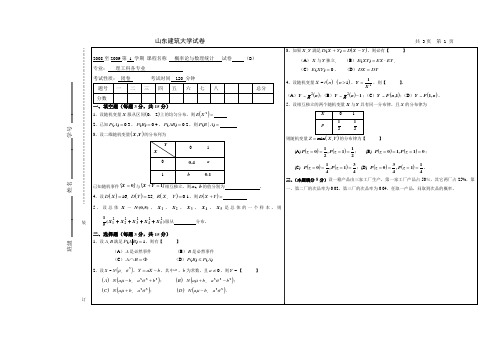
···········································································································装订山东建筑大学试卷 共 3页 第 1 页2008至2009第 1 学期 课程名称 概率论与数理统计 试卷 (B ) 专业: 理工科各专业 考试性质: 闭卷 考试时间 120 分钟 题号 一 二 三 四 五 六 七 八 总分 分数一、填空题(每题3分,共15分)1、设随机变量X 服从区间()20,上的均匀分布,则()=2XE .2、已知()0.3P A =,()0.4P B =,()0.2P AB =,则(|)P B A =3、设二维随机变量()Y X ,的分布列为YX0 10 4.0 a1b 1.0已知随机事件{}0=X 与{}1=+Y X 相互独立,则b a 、的值分别为 。
山东建筑大学电力电子试题06级B卷

4..维持晶闸管导通的条件是什么?怎样使晶闸管由导通变为关断?
5.三相桥式全控整流电路,若其中一只晶闸管短路时,电路会发生什么情况?
6.交流调压和交流调功电路有何异同?
8.什么叫同步调制?
得分
阅卷人
三.计算题(共34分)
1.(10分)有一三相半波可控整流电路,带大电感负载不接续流二极管, ,变压器二次侧相电压有效值 ,电路工作在 ,求电路的负载电流值 ,并选择合适的晶闸管元件。
···········································································································装订线··································································································
得分
阅卷人
四.分析说明题(共16分)
1.(6分)说明图示电路的名称,简述其工作原理。
2..(10分)三相半波可控整流电路中,整流变压器TR的接法为D,y5,触发电路采用NPN管锯齿波同步移相触发电路,考虑锯齿波起始段的非线性,预留60°角的裕量,且同步电压又经过阻容移相滞后了30°。求:
(1)同步电压与对应主电压的相位关系;(2)用矢量图确定同步变压器Ts的接法与钟点数;(3)完成系统连线图。
二、
10.电压型逆变电路交流侧输出电压波形为。
A.矩形波B.因负载阻抗情况的不同而不同C.锯齿波D.正弦波
得分
阅卷人
二.简答题(每题5分,共40分)
1.如图单相桥式半控整流电路,电路在带电感性负载时会出现什么问题?说明如何解决?并在图中标明。
山东建筑大学模拟电子技术期末考试试题B卷及答案
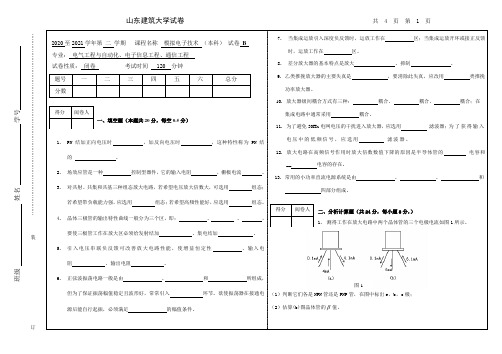
···········································································································装订线山东建筑大学试卷 共 4 页 第 1 页2020至2021学年第 二 学期 课程名称 模拟电子技术 (本科) 试卷 B 专业: 电气工程与自动化、电子信息工程、通信工程 试卷性质: 闭卷 考试时间 120 分钟 题号 一 二 三 四 五 六 总分 分数得分 阅卷人一、填空题(本题共20分,每空0.5分)1. PN 结加正向电压时 ,加反向电压时 ,这种特性称为PN 结的 。
电气工程及其自动化基础知识单选题100道及答案解析

电气工程及其自动化基础知识单选题100道及答案解析1. 以下哪个不是电路的基本组成部分?()A. 电源B. 负载C. 导线D. 电阻器答案:D解析:电路的基本组成部分包括电源、负载和导线,电阻器是负载的一种。
2. 正弦交流电的三要素是()A. 最大值、频率、初相位B. 有效值、周期、相位C. 平均值、角频率、相位差D. 瞬时值、周期、初相位答案:A解析:正弦交流电的三要素是最大值、频率和初相位。
3. 纯电感电路中,电流与电压的相位关系是()A. 电流超前电压90°B. 电流滞后电压90°C. 电流与电压同相D. 电流与电压反相答案:B解析:在纯电感电路中,电流滞后电压90°。
4. 三相交流电源的星形连接中,线电压与相电压的关系是()A. 线电压等于相电压B. 线电压是相电压的根号3 倍,且超前30°C. 线电压是相电压的根号3 倍,且滞后30°D. 线电压是相电压的3 倍答案:B解析:三相交流电源星形连接时,线电压是相电压的根号3 倍,且线电压超前相电压30°。
5. 变压器的基本作用是()A. 变电压B. 变电流C. 变阻抗D. 以上都是答案:D解析:变压器可以实现变电压、变电流和变阻抗的作用。
6. 异步电动机的转差率S 的范围是()A. 0 < S < 1B. -1 < S < 1C. 0 <= S <= 1D. -∞< S < +∞答案:A解析:异步电动机正常运行时,转差率0 < S < 1。
7. 直流电机的换向器的作用是()A. 改变电流方向B. 改变磁场方向C. 改变电枢绕组中的电动势方向D. 以上都是答案:C解析:直流电机的换向器主要是改变电枢绕组中的电动势方向。
8. 电力系统中,无功功率的主要作用是()A. 提高功率因数B. 提高设备利用率C. 维持电压水平D. 减少线路损耗答案:C解析:无功功率主要用于维持电力系统的电压水平。
山东省济南市山东建筑大学电气工程及其自动化2010~2011-2-线代A卷+答案

1 2 1 r 1 2 1 r 0 1 1 r 0 1 1
1 1 2
2 1 1
0 0 0
0 0 0
1 得基础解系: 3 1 ; 1
分)
单位化得
1
3
p3
1
3 1
3
;
………………(10
1
2
得到正交矩阵
P
1 2
0
1 6
1
6 2
6
1
3
1
3 1
3
量的个数为
。
5.已知二次型 f (x1, x2 , x3 ) (k 1)x12 (k 1)x22 (k 3)x32 正定,则数 k 的
取值范围为________。 三、综合题(60 分)
1 234 2341 1.(10 分)计算行列式: D 3412 4123
姓名 装订线
班级
考场 装订线
4. 设 =2 是可逆矩阵 A 的一个特征值,则矩阵 A2 1 必有一个特征值等于
(
)
装订线
山东建筑大学试卷
3.(10 分)设向量组
共 4 页第 2 页
1 2,3,1,2T ,2 1,1,4,0T ,3 3,3,12,0T ,4 5,10,1,6T ;
求该向量组的秩 R1 , 2 , 3 , 4 ,并求出该向量组的一个最大无关组.
学号
1 0 1
2.(10 分)设 A 和 B 都是 3 阶方阵 AB E A2 B ,若 A 0 2 0 ,
4.解
A,
b
1
1
1
3 r 1
1
1
3
1 1 1
1 1
1 0
1 1
山东建筑大学复变函数与积分变换A(07-08-01)答案

一、选择题(4分×6=24分)CDACCB二、填空题(4分×4=16分)1.2. 03.__1_ 42π三、计算题(6分×8=48分)1. 计算解: =----------------------------------------------------------------------------------2分22ii keπππ⎛⎫⎛⎫+⎪⎪⎝⎭⎭⎝⎭==-----------------------------------------------------4分cos sin22iππππ⎛⎛⎫=+++⎪⎪ ⎪⎝⎭⎝⎭---------------------------6分2. 利用高阶导数公式计算积分()341zzdzz=-⎰ ,积分曲线取正向.解:()()()213222!1zzz iI dz zzπ====-⎰ --------------------------------------------4分=---------------------------------------------------------------------------------6分3. 利用柯西积分公式计算32sin241zze zdzz z=⎛⎫+⎪++⎝⎭⎰ ,积分曲线取正向.解: 两个奇点-1,-4 其中-4在曲线外边,所以---------------------------------------------2分3322sin22411zz ze zdz dzz z z==⎛⎫⎛⎫+=⎪ ⎪+++⎝⎭⎝⎭⎰⎰-----------------------------------------4分4iπ=----------------------------------------------------------6分4. 已知调和函数22u x xy=-,求()f z u iv=+解: 222u vf i y i xx x∂∂'=+=-+∂∂-------------------------------------------------------2分()2222i x iy iz=++=+---------------------------------------------------------4分所以2222iz dz iz z C+=++⎰,则()22f z iz z C=++-----------------------------6分5. 将函数()()112z z--在环域2z<<+∞内展开为洛朗级数解: 在2z<<+∞环域上, ()()()1111212f zz z z z==---------------------------2分21111111111z z z z z z ⎛⎫=-=-+++ ⎪-⎝⎭- 221111221221z z z z z z ⎛⎫=-=-+++ ⎪-⎝⎭- ----------------------------------------------4分 所以()234137f z z z z=+++ -----------------------------------------------------------6分 6. 留用留数定理计算()220sin 0x x dx a x a +∞>+⎰解: 函数()22z f z z a =+在上半平面有一级极点ai ,故 ()222R e ,ix iz x e dx i s R z e ai x a π+∞-∞⎡⎤=⎣⎦+⎰22aae i i e ππ--==----------------------------------------------------------2分 ()22sin x xf x x a =+为偶函数,所以22220sin 1R e 2ix x x x dx e dx x a x a +∞+∞-∞⎡⎤=⎢⎥++⎣⎦⎰⎰----------4分 而原积分12a I e π-==---------------------------------------------------------------------------6分 7.()() 0 0,0, 0t t f t et ββ-<⎧=>⎨≥⎩求傅氏变换 解:()F ω()j t f t edt ω+∞--∞=⎰ ---------------------------------------------------------------------2分0t j t e e dt βω+∞--=⎰()0j t e dt ωβ+∞-+=⎰()()0j t e j ωβωβ+∞-+⎡⎤=⎢⎥-+⎣⎦--------------------------4分 ()01j ωβ-=-+22j βωβω-=+----------------------------------------------------------6分8.()()sin f t kt k =求正弦函数的拉氏变换为实数解:[sin ]L kt 0sin st kte dt +∞-=⎰------------------------------------------------------------------2分()220sin cos st e s kt k kt s k +∞-=-⋅-⋅+------------------------------------------4分 22ks k =+(Re()0)s >----------------------------------------------------------6分四、证明题(6分×2=12分)1证明拉普拉斯变换得微分性质.()()()0L f t sF s f '=-⎡⎤⎣⎦证明:()()0st L f t f t e dt +∞-''=⎡⎤⎣⎦⎰---------------------------------------------------------------------2分()()00st st f t e s f t e dt +∞+∞--=+⎰-------------------------------------------------------------------------4分()()0(Re())sL f t f s c =->⎡⎤⎣⎦()()0sF s f =-------------------------------------------------6分2、若在1z <内,()f z 解析,并且1()1f z z ≤-, 则()(0)(1)!n f e n <+证: 因 ()1||1!()(0)d 2πi n n n z n n f z f z z +=+=⎰-----------------------------------------------------------------2分故11||1||1!|(0)||d |2π||z (n)n n z n n f z z -+=+≤⎰11111!n 2π2π()n+1n n n nn n +-++≤------------------------------------------------------------------4分1(1)!1e(1)!n n n n ⎛⎫=++<+ ⎪⎝⎭ ----------------6分。
山东建筑大学《建筑电气安装技术》课后题答案

作业19.解冷加工设备属长期负荷,Pe=(10×3)+(4×8)+(1.5×10)+(2.8×11)=107.8KW查表2-2,大批量生产冷加工设备Kx=0.18,cosφ=0.5,tgφ=1.73,Pc=Kx×Pe=19.4KW,Qc=Pc×tgφ=33.61KVar,Sc=(Pc2+Qc2)1/2=38.81KVAIc=Sc/(1.73×0.38)=58.96A10.解1)冷加工机床属长期负荷,Pe1=(7.5×4)+(4×6)=54.0KW查表2-2,大批量生产冷加工设备Kx1=0.18,cosφ1=0.5,tgφ1=1.73,Pc1=Kx1×Pe1=9.72KW,Qc1=Pc1×tgφ1=16.84KVar,Sc1=(Pc12+Qc12)1/2=19.44KVAIc1=Sc1/(1.73×0.38)=29.54A2)生产用通风机属长期负荷,Pe2=(4.5×3)=13.5KW查表2-2,生产用通风机Kx2=0.8,cosφ2=0.8,tgφ2=0.75,Pc2=Kx2×Pe2=10.8KW,Qc2=Pc2×tgφ2=8.1KVar,Sc2=(Pc22+Qc22)1/2=13.5KVAIc2=Sc2/(1.73×0.38)=20.54A3)生产用水泵属长期负荷,Pe3=(2.8×2)=5.6KW查表2-2,生产用水泵Kx3=0.8,cosφ3=0.8,tgφ3=0.75,Pc3=Kx3×Pe3=4.48KW,Qc3=Pc3×tgφ3=3.36KVar,Sc3=(Pc32+Qc32)1/2=5.6KVAIc3=Sc3/(1.73×0.38)=8.52A4)同期系数KΣp=0.9,KΣq=0.95,Pc=KΣp(Pc1+Pc2+Pc3)=0.9×25=22.5KWQc=KΣq(Qc1+Qc2+Qc3)=0.95×25=28.3KvarSc=(Pc2+Qc2)1/2=36.15KVAIc=Sc/(1.73×0.38)=55.0A120户平均分配在3相供电线路,每相供电线路为40户;每户4KW,A相供电线路Pe A=40×4=160KW查表2-6,Kx=0.45,cosφ=0.9,tgφ=0.48,每相供电线路Pc A=Pe A×Kx=72KWQc A=Pc A×tgφ=34.56KvarSc A=(Pc A2+Qc A2)1/2=79.86KVAIc A=Sc A/(0.22)=363.02A三相供电线路总计算负荷Pc=Pc A×3=216KWQc=Qc A×3=103.68KvarSc=(Pc2+Qc2)1/2=239.59KVAIc=Sc/(1.732×0.38)=363.02A15.解第1单元Pe A1=3×2×6=36KWPe B1=2×2×6=24KWPe C1=2×2×6=24KW第2单元Pe A2=2×2×6=24KWPe B2=3×2×6=36KWPe C2=2×2×6=24KW住宅各相总负荷Pe A=Pe A1+Pe A2=36+24=60KWPe B=Pe B1+Pe B2=24+36=60KWPe C=Pe C1+Pe C2=24+24=48KW最大相与最小相之差ΔP=60-48=12KW住宅三相总负荷Pe=Pe A+Pe B+Pe C=60+60+48=168KWΔP/Pe=12/168=7.14%<10%按三相对称负荷计算,三相总负荷为168KW。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2007-2008学年第二学期线性代数试题(B 卷)
一、单项选择题(每小题4分,本大题共20分)
1. 行列式0
010213
21=A 的值为( )
(A) 1 ; (B) 2 ; (C) 0 ; (D) -6.
2. 设A ,B 为n 阶方阵,则下列式子成立的是( ) (A )||||||B A B A +=+; (B )111)(---+=+B A B A ; (C )||||||B A AB ⋅=; (D )BA AB =.
3.当=λ( )时,方程组⎪⎩
⎪
⎨⎧-=---=+=-+4
)3)(2)(1(2212332321λλλλx x x x x x 有唯一解. (A) 1; (B) 2; (C) 3; (D) 4.
4.设1ξ,2ξ是矩阵A 的属于特征值λ的特征向量,则以下结论正确的是( ) (A)12ξξ+是λ对应的特征向量; (B) 22ξ是λ对应的特征向量; (C) 1ξ,2ξ一定线性相关; (D) 1ξ,2ξ一定线性无关. 5. 设A 是正交矩阵,则下列结论错误的是( )
(A) 2||A 必为1;
(B) |A|必为1;
(C) 1A -=T A ; (D) A 的行(列)向量组是正交单位向量组.
二、填空题(每小题4分,本大题共20分)
1. 设矩阵200020002A ⎛⎫ ⎪
= ⎪ ⎪⎝⎭
,则行列式12A -= .
2.矩阵⎪⎪⎭
⎫
⎝⎛-θθθθcos sin sin cos 的逆矩阵为 .
3、若n 元齐次线性方程组的系数矩阵A 的秩为r ,且n r <,则方程组的基础解
系中有 个解. 4.设3阶矩阵A 的特征值为1,3,5,则A 的行列式|A |等于 .
5.当t 满足 时,二次型 22
1212
12(,)2f x x x x tx x =++是正定的.
三、(本题10分)计算4阶行列式11
223344
00000000a b a b D b a b a =
.
四、(本题10分)解矩阵方程 B X AX +=2,其中⎪⎪⎪⎭⎫ ⎝⎛-=410110004A ,
⎪⎪⎪
⎭
⎫
⎝⎛-=321163B .
五、(本题12分) 求线性方程组⎪⎩
⎪
⎨⎧=--+=+-+=+-+1
222241
2432143214321x x x x x x x x x x x x 的通解.
六、(本题12分).
求三阶方阵⎪⎪⎪
⎭
⎫ ⎝⎛----=163053064
A 的特征值与特征向量,并判断A 是否与对角形矩阵相似?
七、(本题8分)
求向量组 )1,3,1,1(1=α,)3,1,1,1(2--=α,)9,8,2,5(3--=α,
)7,1,3,1(4-=α的一个极大线性无关组,并将其余向量用该极大线性无关组线性表示. 八、(本题8分) 证明:向量组121,,,(0)s αααα≠线性相关的充分必要条件是至少有一个
(1)i i s α<≤可由向量组121,,,i ααα-线性表示.
2007-2008学年第二学期线性代数试卷B 参考答案和评分标准
一、单项选择题(每小题4分,本大题共20分) 1. D. 2. C. 3.D. 4.B. 5. B 二、填空题(每小题4分,本大题共20分)
1. 1. 2.⎪⎪⎭
⎫
⎝⎛-θθ
θθ
cos sin sin cos . 3、r n -. 4.15. 5.11t -<<. 三、(本题10分)计算4阶行列式11223344
00000000a b a b D b a b a =
解:0
000
00
0033221
44
33221a b b a b b a a b b a a D -= ………………………………(3分)
142323142323()()a a a a b b b b a a b b =---………………………………….…(6分) ))((32324141b b a a b b a a --=……………………………………………..(10分)
四、(本题10分)解矩阵方程B X AX +=2,其中⎪⎪⎪⎭⎫ ⎝⎛-=410110004A ,⎪⎪⎪
⎭⎫
⎝⎛-=321163B .
解. 因为2002011012A E ⎛⎫
⎪
-=-- ⎪ ⎪⎝⎭
……………………………………….…..(3分)
求得其逆矩阵为()1
1
0220
21011A E -⎛⎫ ⎪ ⎪
-=-- ⎪ ⎪
⎪⎝⎭…………………………….…(7分) 于是所求的矩阵()B I A X 1
2--= =⎪⎪⎪⎪⎪⎭⎫
⎝⎛--2314323……………………………(10分)
五、(本题12分) 求线性方程组⎪⎩
⎪
⎨⎧=--+=+-+=+-+1
2222412432143214321x x x x x x x x x x x x 的通解.
解
(1) B =⎪⎪⎭⎫ ⎝⎛----111122122411112~⎪⎪⎭
⎫
⎝⎛-00000010002/102/12/11 …………………
(2分) 所以原方程组等价于 1
2322334111222
x x x x x x x x ⎧
=-++⎪⎪⎪
=⎨⎪=⎪=⎪⎩………………………………(5分)
取231,0x x ==得141
,02x x =-=;………………………………………….…(7分)
取230,1x x ==得141
,02x x ==.………………………………………………(9分)
因此通解为121234111222100010000x x k k x x ⎛⎫⎛⎫⎛⎫-⎛⎫ ⎪ ⎪ ⎪
⎪ ⎪ ⎪ ⎪ ⎪=++ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭
⎝⎭⎝⎭⎝⎭
(k 1, k 2为任意常数)。
……..(12分) 六、(本题12分).
求三阶方阵⎪⎪⎪
⎭
⎫ ⎝⎛----=163053064A 的特征值与特征向量,并判断A 是否与对角形矩阵相似?
解.A 的特征方程为1
6
3
05
30
64
||-+--=
-λλλλA E =0)1)(2(2=-+λλ,…..(2分)
故A 的特征值为21-=λ,132==λλ. ……………………………………….(5分) (1) 对于特征值21-=λ,
属于特征值2-的全部特征向量为,111⎪⎪⎪
⎭
⎫
⎝⎛-k (0≠k ).…………….…………..(7分)
(2) 对于特征值132==λλ,
属于特征值1的全部特征向量为,10001221⎪⎪⎪
⎭
⎫ ⎝⎛+⎪⎪⎪⎭⎫ ⎝⎛-k k (21,k k 不全为零).……….(9分)
因此A 与对角形矩阵相似. .…………….……………………………….(12分) 七、(本题8分)
求向量组 )1,3,1,1(1=α,)3,1,1,1(2--=α,)9,8,2,5(3--=α,
)7,1,3,1(4-=α的一个极大线性无关组,并将其余向量用该极大线性无关组线性表示.
解. 把向量4321,,,αααα按列排,进行初等行变换,化简为
()⎪⎪⎪⎪
⎪⎭
⎫
⎝⎛-----=79311
813321115114321αααα ⎪⎪⎪⎪⎪
⎪⎭
⎫ ⎝⎛
-→00
00002271012301……….………(2分) 因此21,αα为一个极大线性无关组 …………………………………….…(4分)
且 2132
7
23ααα-= ……………………………….……..…....(6分)
2142ααα+= ……………………………………………….(8分)
八、(本题8分) 证明:向量组121,,
,(0)s αααα≠线性相关的充分必要条件是至少有一个
(1)i i s α<≤可由向量组121,,
,i ααα-线性表示.
证明:“必要性”: 向量组121,,
,(0)s αααα≠线性相关,即存在不全为零的常数12,,
,,s k k k 使11220,s s k k k ααα++
=……….…………….…..…(2分)
则有0i k ≠,而0(),j k j i =>(1)i s <≤, 从而
1
12121i i i i i
i
k k k
k k k αααα--=-
---
……….………………………....…(4分) “充分性” : 设i α可由向量组121,,,i ααα-线性表示,
则向量组121,,,,i i αααα-线性相关,……….…………………………….…(6分) 从而向量组12,,,s ααα线性相关. ……………………..………………..(8分)。
