阵列信号处理-1
相关的重要学术会议
• IEEE Sensor Array and Multichannel Signal Processing Workshop –SAM • IEEE Workshop On Statistical Signal Processing –SSP (Formerly IEEE Workshop On Statistical Signal And Array Processing –SSAP) • IEEE International Conference on Acoustics, Speech, and Signal Processing –ICASSP • Workshop on Adaptive Sensor Array Processing –ASAP (Lincoln Laboratory –MIT) • MTS/IEEE Oceans Conference
M −1 m =0
∑n
m
(t )
1.2 阵列处理提取信号特征 1）信号的传播方向 2）速度 3）距离 4）频谱
小结： 1 阵列信号处理的发展； 2 两个几个基本概念； 3 简单介绍了阵列信号处理的研究内容和应 用领域；
第二章 信号的空间和时间特性 1）波动方程 2）波的色散与衰减 3）信号的时、空付氏变换 第三章 阵列 1）有限连续孔径阵列 2）空间采样 3）离散阵列
多普勒对传播特性的影响 当感应器沿电波传播的方向运动，其频率变 为：
vs ω ' = ω (1 − ) c
当感应器的运动方向与电波传播的方向相反 时，其频率变为
ω' =
ω
1 − vs / c
通过波动方程，得到如下结论： 传播信号是时间和空间的函数； 传播速度是传播媒质的函数； 利用波动方程可得到传播函数、速度。 应用波动方程的注意事项: 介质是无耗的 介质是单色的，即传播速度是定值 结论： 利用空时采样可得到信号的特性；
其中：
n = −∞
∑A
∞
n
exp[ jnω 0 (t − α ⋅ x )]
（2.15） 由以上分析可以得到如下结论：传播的电 磁波 ，无论其信号是何种形式，均满足波 动方程。且任意方向传播的电磁波可同时 存在。
1 T An = ∫ s(u) exp(− jnω0u)du T 0
球面波波动方程： 球面波波动方程：
阵列信号处理的应用领域 雷达；目标参数、抗干扰。 通讯；抗干扰、定向通讯等 导航；目标方位等 侦查；干扰、雷达、通讯等设备方位 医疗诊断；提高分辨率、增加信噪比等 声纳；目标定位等 射电天文学；提高分辨率、抗干扰等 地震：震源方位、增加信噪比等
基本概念： • 感应器（Sensor） 转换通常为线性： • 阵列 （Array）
s ( t ) = Kf ( t )
1.1 阵列处理提高信噪比 由感应器感应的外部有用信号，往往伴随 着干扰和噪声，对于一个由M个感应器组成 的阵列，每个单元的输出可以表示为。
ym (t) = s(t) + nm (t)
将各感应器所感应的信号简单叠加，得 到：
1 z (t ) = M
M −1
1 ∑ ym (t ) = s(t ) + M m=0
第一章
绪论
信号处理研究的内容
信号处理主要 研究方向
从复杂环境中 提取有用信号
由检测到的信号中 提取信息
信号处理的发展
起源于17世纪 50年代前期 分离元件 速度低 体积大 可靠性差
速度高 体积小 可靠性高
60年代后期 集成电路
信号处理的发展
信号处理前期
信号处理后期
时域信号处理 （一维）
图像处理
2.3波的色散和衰减 波的色散是指电磁波在传播过程其传播特 性随频率变化； 衰减是指电磁波在传播过程中随着传播距 离的增加，能量不断的减小。 其特点如信号在RCL电路中传播。 2．3．1 电磁波的色散 电磁波的色散是由于不同频率的电磁波， 在介质中的传播速度不同产生的。
通过波动方程：
∂H ∇ × E = −µ ∂t
∆ x ∆ t = c
（2.12）
这里的c即为电磁波的传播速度。
电磁波的波长： 波长定义为一个周期T=1/f=2π/ω内(f为频率) 电磁波传播的距离。假设电磁波的传播速度 为c，则在一个周期内，电磁波的传播距离为：
λ = T ⋅ c = 2π / k = c / f
（2.13）
波数（Wavenumber）（空间频率）： 空间频率为在空间电磁波的相位分布特性。
s ( x , y , z , t ) = f ( x ) g ( y )h ( z ) p (t )
(k + k + k )s( x, y, z, t ) =
2 x 2 y 2 z
ω
c
=
2
2
s( x, y, z, t ) 2.7
ω
z
由该式可以看出，只要 k x ，k y ，k 满足下式
k
2 x
+ k
2 2
应用球面波方程一般都是球对称的，简化为：
1 ∂ 1 ∂ s 2 ∂s (r )= 2 2 2 ∂r r ∂r c ∂t
2
经过变化，可得：
∂ rs 1 ∂ rs = 2 2 ∂r c ∂t 2 该方程的一个解为：
2 2
A s = exp[ j (ωt − kr ) r
同样有如下关系：
k =ω/c
第二章
信号的空间和时间特性
由辐射源辐射的电磁波沿一定的方向传播， 这些波均带有一定的信息，它们是位置和 时间的函数。 2.1 坐标系 1）直角坐标系 2）球坐标系
z θ r y φ x
2．2 波传播方程 电磁波特性满足Maxwell 方程，其微分形式表示 为：
∂H ∇ × E = −µ ∂t
∂E ∇× H = ε +J ∂t
2 2 2 c 2
为其解，可以得到的k 与ω的关系为：
ω = c
2
k
+
ω
c
2 c 2
相速
对色散媒质常用相速描述：即等位面或平面波的传 播速度。
ω (t 0 + ∆ t ) − k ⋅ ( x + ∆ x ) = C
得到：
vp =
ω
k
2
v
p
=
2 c
ω k
k
2
k
2
1 = (ω 2 c
v
p
− ω
)
c 2ω k = ω 2 − ω
参考资料
L. C. Godara, Smart Attennas, CRC Press, 2004 P. S. Naidu, Sensor Array Signal Processing, CRC Press, 2001 张贤达,保铮. 通信信号处理, 国防工业出版 社,2000 王永良,陈辉,彭应宁,万群. 空间谱估计理论 与算法, 清华大学出版社, 2004
相关的重要学术刊物
• IEEE Transactions on Signal Processing • IEEE Transactions on Antennas and Propagation (AP) • IEEE Transactions on Aerospace and Electronic Systems (AES) • 电子学报 • 声学学报
(2.14） 波动方程是线形方程，即如果两个方程的解 分别为： S1 ( x , t ) 和 S 2 ( x , t ) ，则其线性 组合：
aS1 ( x , t ) + bS 2 ( x , t )
仍然是该方程的解。
由付氏变换理论可知，任意的周期函数均可 以用一组正弦函数的组合来表示：
s( x , t ) =
（2.1）
（2.2）
这里，J为电流密度： 2.3 进一步可推导出电磁波的波动方程表示式：
J = σE
∂ ∂ ∂ 1 ∂ E ( 2 + 2 + 2 )E = 2 2 ∂x ∂y ∂z c ∂t
2 2 2 2
2.4
假设波动方程的解为： 2.5 为计算方便，对这种形式的方程解作进一步的假 设，将解用指数形式表示：即 s ( x , y , z , t ) = A exp[ j (ω t − k x x − k y y − k z z )Байду номын сангаас 2.6 将其带入波动方程 (2.4)中，可以得到：
特点： 与时间频率相对应，反映相位在空间的变化； 其值为：
k = 2π / λ
是矢量函数，与方向有关； 与波长成反比； 是传播媒质的函数； 也称为相位常数；
慢矢量： 慢矢量： 定义 α = k / ω 示为：
，则波动方程的解可以表
s( x, t ) = A exp[ jω(t − α ⋅ x )]
2 c
• 假设信号为：
s( x, t ) = exp[ j(ω1t − ϕ0 − k ⋅ x)] + exp[ jω2t − k ⋅ x]
当该信号在无色散媒质中传播时，两个信号 的传播速度相同，电磁波经过∆t时间，两个 信号传播的距离相同，均为x0，这时信号可 以表示为;
s( x0 , t ) = exp[ jω1 (t − ∆t ) − ϕ0 − jk ⋅ x0 ] + exp[ jω2 (t − ∆t ) − jk ⋅ x0 ] = s( x0 , t − ∆t )
阵列信号处理
哈工大（威海）
2010年3月
教 材
• 主要教材 H.L. Van Trees, Optimum Array Processing, John Wiley & Sons, 2002 D.H. Johnson and D.E. Dudgeon, Array Signal Processing: Concepts and Techniques, Prentice-Hall, 1993
阵列信号处理
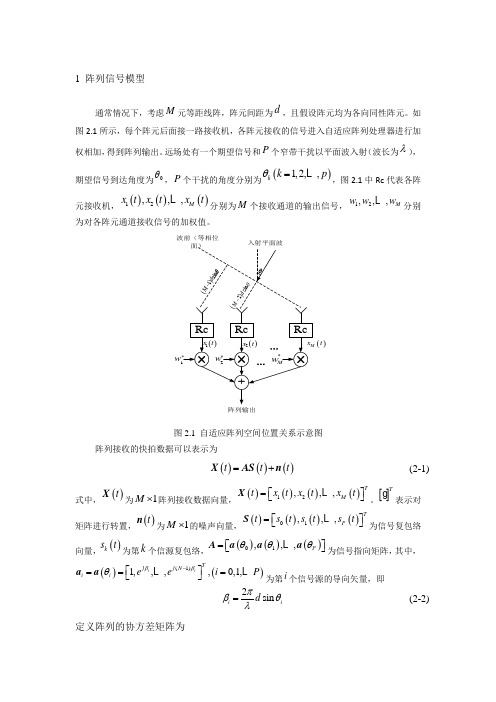
1 阵列信号模型通常情况下，考虑M 元等距线阵，阵元间距为d ，且假设阵元均为各向同性阵元。
如图2.1所示，每个阵元后面接一路接收机，各阵元接收的信号进入自适应阵列处理器进行加权相加，得到阵列输出。
远场处有一个期望信号和P 个窄带干扰以平面波入射（波长为λ），期望信号到达角度为0θ，P 个干扰的角度分别为()1,2,,k k p θ= ，图2.1中Rc 代表各阵元接收机，()()()12,,,M x t x t x t 分别为M 个接收通道的输出信号，12,,,M w w w 分别为对各阵元通道接收信号的加权值。
()t w 阵列输出波前（等相位图2.1 自适应阵列空间位置关系示意图阵列接收的快拍数据可以表示为()()()t t t =+X AS n(2-1)式中，()t X 为1M ⨯阵列接收数据向量，()()()()12,,,TM t x t x t x t =⎡⎤⎣⎦X 。
[]T表示对矩阵进行转置，()t n 为1M ⨯的噪声向量，()()()()01,,,TP t s t s t s t =⎡⎤⎣⎦S 为信号复包络向量，()k s t 为第k 个信源复包络，()()()01,,,P θθθ=⎡⎤⎣⎦A a a a 为信号指向矩阵，其中，()()(1)1,,,,0,1,i iTj j N i i e e i P ββθ-⎡⎤===⎣⎦a a 为第i 个信号源的导向矢量，即2sin i i d πβθλ=(2-2)定义阵列的协方差矩阵为()()2H H x s n E t t σ⎡⎤==+⎣⎦R X X AR A I (2-3)式中，()()H s E t t ⎡⎤=⎣⎦R S S 为信号的协方差矩阵，I 为M 维单位矩阵，2n σ为阵元的噪声功率，本文中约定，[]T表示转置，[]*表示共轭，[]H表示共轭转置。
式(2-3)常由接收数据采样协方差矩阵ˆx R 代替，即()()11ˆNH xiii t t N==∑R x x(2-4)如图2.1所示的自适应阵列模型，阵列的M 个通道接收信号经加权处理后，最后的输出信号为()()()1MH i i i y t w x t t *===∑w x(2-5)阵列的方向图()p θ定义为()()H p θθ=w a(2-6)调整自适应阵列的权矢量w ，可以改变阵列的方向图，即改变各个方向上入射信号增益。
阵列信号处理
B
B
1 有 zB t 2
B
2
z e jt d z B t
因此
s r , t z B t e j0t e j0 s 0, t e j0
2
小结： 信号带宽足够小使得波到达 r 处时的复包络基本 不变。 T r 表示了波传播的空间信息（方向、位置）， 它仅含于载波项中，而与信号复包络无关。
s exp[ j t r ]d
T
这里函数 s 是任意的，只要其Fourier变换存在即 可。该式表达了沿同一方向 传播的任意波形（信 号），其频率分量任意。
B. 波动方程球坐标系中的解
球坐标系 r , , ，但是，当波动方程的解具有球形 对称时,函数s r , , , t 并不依赖于 和 ，使解简化， 这时波动方程可简化为：
T
波动方程的任意解可以分解为无穷多个“单频” 解的迭加（传播方向和频率分量均任意）。
波动方程的单频解可以写成单变量的函数：
s r , t A exp[ j (t k r ) A exp[ j t r ]
T T
k ，其大小等于传播速度的倒数，其方向与 式中
时间频率 空间频率
b) 任意解：由四维Fourier变换表示： j t k r 1 s r, t s u , e d kd 4 2 j t k r s k , s t , r e d rdt 其中
T
a t 带宽越宽，信号起伏越快。窄带条件即要求a t cos 变化比 0t t 变化慢。
阵列信号处理 psf 点扩散函数 反卷积
阵列信号处理（Array Signal Processing）1. 简介阵列信号处理是一种利用多个传感器或微phones接收到的信号进行处理的技术。
这些传感器通常以阵列的形式排列在一起，可以在空间上对信号进行采样。
阵列信号处理技术可以用于各种应用，包括无线通信、雷达、声音定位和语音增强等领域。
在阵列信号处理中，经常会使用到点扩散函数（Point Spread Function，PSF）和反卷积（Deconvolution）等概念。
本文将详细介绍这些特定函数的定义、用途和工作方式。
2. 点扩散函数（Point Spread Function，PSF）2.1 定义点扩散函数（PSF）是指在观察到一个点源时，系统输出的响应。
点源可以是一个理想的点光源、点声源或点热源等。
PSF描述了系统对于一个点源的感知能力，可以用于评估系统的分辨率和信号传输特性。
2.2 用途PSF在阵列信号处理中具有广泛的应用，主要用于以下几个方面：2.2.1 分辨率评估PSF可以用于评估系统的分辨率，即系统能够分辨并显示的最小特征尺寸。
通过分析PSF的形状和尺寸，可以确定系统的分辨率限制，进而优化系统设计和参数设置。
2.2.2 反卷积PSF还可以用于图像或信号的反卷积处理。
在实际应用中，由于传感器和系统的限制，观测到的信号往往受到模糊和失真的影响。
通过将观测到的信号与PSF进行卷积运算的逆过程，可以恢复出原始信号的更清晰的图像或声音。
2.2.3 信号重构PSF在阵列信号处理中也可以用于信号重构。
通过对多个传感器接收到的信号进行处理和分析，可以利用PSF将信号的不同成分分离出来，从而实现信号的重构和定位。
2.3 工作方式PSF的工作方式可以通过以下几个步骤来理解：2.3.1 系统建模首先，需要对阵列系统进行建模。
这包括确定阵列的几何结构、传感器的位置和响应特性等。
通过建模，可以得到系统的传递函数，即系统对于输入信号的响应。
2.3.2 点源输入接下来，将一个点源输入到系统中，观察系统的输出。
基于MATLAB阵列信号处理研究1
基于MATLAB阵列信号处理研究1基于MATLAB阵列信号处理研究1MATLAB是一种广泛应用于科学和工程领域的编程语言和开发环境。
它在信号处理领域有着广泛的应用，可以用于信号的生成、滤波、变换、分析和可视化等方面。
本文将基于MATLAB介绍阵列信号处理的研究内容，包括阵列信号模型、阵列信号参数估计、波束形成和空间谱估计等。
首先，阵列信号模型是研究阵列信号处理的基础。
阵列信号模型描述了信号在阵列中的传播和接收过程。
常见的阵列信号模型有基于阵列几何结构的波达模型和基于信号方向的自相关函数模型。
波达模型假设信号到达阵列的时间差和入射角与信号源之间的关系，自相关函数模型则描述了信号在阵列中的空间相关性。
其次，阵列信号参数估计是研究阵列信号处理的关键环节。
信号参数估计是指在阵列接收到信号之后，通过分析接收到的信号来估计信号的到达角度、入射波的相位和幅度等参数。
常用的信号参数估计方法有基于阵列输出的MUSIC算法、基于最小二乘法的MVDR算法和基于梯度的阵列信号处理算法等。
这些方法可以有效地提取出信号的参数信息并进行分析。
波束形成是阵列信号处理的一个重要任务。
波束形成是指通过对阵列接收到的信号进行加权和相干性处理，实现对特定方向信号的增强，从而抑制其他方向的干扰信号。
常用的波束形成方法有波束形成权向量设计、线性约束波束形成和非线性约束波束形成等。
这些方法可以实现对特定方向的信号进行增强，并提高抗干扰能力和信噪比。
最后，空间谱估计是一种用于估计信号频谱特性的方法。
空间谱估计可以通过阵列接收到的信号的二阶统计特性来计算信号的功率谱密度。
常用的空间谱估计方法有基于传统阵列信号处理方法的峰值检测算法、基于最大似然法的多传感器信号处理算法和基于SVD分解的阵列信号处理算法等。
这些方法可以提供信号的频谱信息，为信号处理和分析提供重要的依据。
总之，基于MATLAB的阵列信号处理研究涉及到阵列信号模型、信号参数估计、波束形成和空间谱估计等多个方面。
阵列信号处理(知识点)
信号子空间：设N 元阵接收p 个信源，则其信号模型为：()()()()1piiii x t s t a N t θ==+∑在无噪声条件下，()()()()()12,,,P x t span a a a θθθ∈称()()()()12,,,P span a a a θθθ为信号子空间，是N 维线性空间中的P 维子空间，记为P N S 。
P N S 的正交补空间称为噪声子空间，记为N P N N -。
正交投影设子空间m S R ∈，如果线性变换P 满足，()1),,,2),,,0m mx R Px S x S Px x x R y S x Px y ∀∈∈∀∈=∀∈∀∈-=且则称线性变换P 为正交投影。
导向矢量、阵列流形设N 元阵接收p 个信源，则其信号模型为：()()()()1piiii x t s t a N t θ==+∑，其中矢量()i ia θ称为导向矢量，当改变空间角θ，使其在空间扫描，所形成的矩阵称为阵列流形，用符号A 表示，即(){|(0,2)}a A θθπ=∈波束形成波束形成（空域滤波）技术与时间滤波相类似，是对采样数据作加权求和,以增强特定方向信号的功率，即()()()()HHy t W X t s t W a θ==，通过加权系数W 实现对θ的选择。
最大似然已知一组服从某概率模型()f X θ的样本集12,,,N X X X ，其中θ为参数集合，使条件概率()12,,,N f X X X θ最大的参数θ估计称为最大似然估计。
不同几何形态的阵列的阵列流形矢量计算问题假设有P 个信源，N 元阵列，则先建立阵列的几何模型求第i 个信源的导向矢量()i i a θ 选择阵元中的一个作为第一阵元，其导向矢量()1[1]i a θ=然后根据阵列的几何模型求得其他各阵元与第一阵元之间的波程差n ∆，则确定其导向矢量()2jn i a eπλθ∆=最后形成N 元阵的阵列流形矢量()11221N j j N Pe A e πλπλθ-∆∆⨯⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦ 例如各向同性的NxM 元矩形阵，阵元间隔为半个波长，当信源与阵列共面时：首先建立阵列几何模型：对于第m 行、第n 列的阵元，其与第1行、第1列阵元之间的波程差为(1)sin()(1)cos()mn i i n d m d θθ∆=---故：()1122(sin()cos())22((1)sin()(1)cos())11N j j d j j d N M NM P NM Pe e A e e ππθθλλππθθλλθ-∆-∆---⨯⨯⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦而当信源与阵列不共面时： 首先将信源投影到阵列平面然后建立阵列模型对于第m 行、第n 列的阵元，其与第1行、第1列阵元之间的波程差为[(1)sin()(1)cos()]sin()mn i i i n d m d θθϕ∆=-+-故：()1122(sin()cos())cos()22((1)sin()(1)cos())cos()11N j j d j j d N M NM P NM Pe e A e e ππθθϕλλππθθϕλλθ-∆-∆---⨯⨯⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦线性约束最小方差准则（LCMV ）的自适应波束形成算法： 对于信号模型：()()()0X t s t a J N θ=++， 波束形成输出：()()()()0()H H H yt W X t s t W a W J N θ==++LCMV 准则实际上是使()0HW a θ为一个固定值的条件下，求取使得()HWJ N +方差最小的W 作为最有权值，即：()0min .H X W HW R Ws t W a Fθ⎧⎪⎨⎪=⎩，其中F 为常数利用拉格朗日乘子法可解得：()10X opt W R a μθ-=当取1F =时，则()()11H X a R a μθθ-=，μ的取值不影响SNR 和方向图。
阵列信号处理 ARRAYppt课件
其中： SNRomni——接收机入口处的信噪比
CBlo(g 1SNR ) C——信道容量：bps B——接收机2 带宽：Hz
Omni
;.
25
波束成形天线示意图 天线阵的各个单元间距小于/2
发送波束成形
接收波束成形
;.
26
多天线系统的信道容量（2）
波束成形天线系统：将发射功率相等的分配到M个全向发射天线上，M个 全向收、发天线采用相位波束成形技术，则信道容量为：
;.
为什么要进行阵列信号处场的有用特征，获取信号源的属性等信息。 改善蜂窝和个人通信服务系统质量、覆盖范围和容量的强有力的工具。
研究兴趣：将接收天线阵列用于反向连接（客户到基站）
;.
;.
来看两个阵列在天线方面的应用
智能天线阵 分布多天线阵
智能天线阵 ;.
;.
29
多天线系统的信道容量比较
;.
30
传输环境对天线系统的影响
MIMO与波束成形天线的频谱效率 （[4,6]，SNR=10dB,中断率 10% ）
15
d
频谱效率 b/s/Hz
CBe a m sBlo2g(1M2SNORm)n i SN足 R 够B大 {2lo2g(M.SNORm}ni
;.
27
MIMO天线系统示意图
独立信道
天线阵
天线阵2
;.
28
多天线系统的信道容量（3）
如果发射功率分散到M个独立的信道中，并且各个信道具有相同的路径 损耗，则信道容量为：
CMIMOMlBo2g(1SNORm)ni S N足 R 够M 大{Blo2(gSNORm}n i
;.
平面波与阵列 天线应具有方向性——定向发射和接收 采用阵列天线——易于控制波束 阵列处理的对象——空间信号
现代数字信号处理课件：阵列信号处理
阵列信号处理
2. 阵列信号协方差矩阵分解 阵列信号协方差矩阵R=E[XXH]可以写作
R
E[ x1 x1 ] E[x2 x1]
E[ x1 x2 ] E[x2 x2]
E[ x1 xM E[x2 xM
] ]
E[
xM
x1
]
E[xM x2]
E[
xM
xM
]
(7.1.11)
这是一个Hermitian方阵，则其特征分解为
di l c
1 c
( xi
sin
cosj
yi
cos
cosj
zi
sinj )
(7.1.4)
通常情况下，考虑空间有N个独立远场窄带信号入射到
M个阵元的阵列上，且有零均值高斯白噪声n(t)，可以得到
阵列的输出为
x1(t) exp( j2πf011)
x2 (t
)
exp(
j2πf0
21 )
UHRU=Σ
(7.1.13)
将R=ARSAH+σ2I代入上式，可得
UH(ARSAH+σ2I)U=Σ 而酉矩阵U满足UHU=I，因此
(7.1.14)
UHARSAHU=Σ－σ2I
(7.1.15)
由上面的分析可知，Σ可分为两部分: 一是与信号对应
的大特征值，由ARSAH和RN提供；二是与噪声对应的小特征 值σ2，由RN提供。即
则各阵元第k次快拍的采样值的矩阵形式为
X(k)=AS(k)+N(k)
(7.1.7)
由于S(k)随k变化，且其初相通常为均匀分布，一阶统
计量(均值)为零，所以不能直接采用一阶统计量来提取方向
信息。而二阶统计量可以消除信号S(k)的随机初相，可以用
第四章 阵列信号处理
通常信号的频带B比载波 ω 小很多，即s(t)变化 相对 ω 缓慢，则延时
1 c
r α <<
T
1 B
则可以认为 s (t − r α ) ≈ s (t ) 即信号包络 在各阵元上差异可忽略——窄带信号。
4.2 等距线阵与均匀圆阵
一、等距线阵 M个阵元等距排成一直线，阵元间距为d，到达波 的方向角定义为与阵列法线的夹角 θ ，称为波 达方向（DOA）。 在三维空间中还可以 θ θ 确定信源方位角 ψ
d
5
4
y
ψ
2
1
x
等距线阵（ULA）的方向向量
aULA (θ ) = [1, e = [1, e
−j 2π − j k d sin θ −j
,L, e
2π
− j k ( M −1) d sin θ T
]
λ
d sin θ
,L, e
λ
( M −1) d sin θ
]T
若有多个信源(p个),波达方向分别为 θ i (i − 1, L, p) 方向矩阵为
A = [a(θ1 ), a(θ 2 ),L, a(θ p )] = 1 ⎡ ⎢ e − j 2λπ d sin θ1 =⎢ ⎢ L ⎢ − j 2λπ ( M −1) d sin θ1 ⎣e ⎤ π − j 2λ d sin θ p ⎥ L e ⎥ ⎥ L L π − j 2λ ( M −1) d sin θ p ⎥ L e ⎦ L 1
θ
d sin θ
Vandermonde矩阵
阵列结构不允许其方向向量和空间角之间模糊， 等距线阵阵元间距不能大于 λ ，则可以保证 2 方向矩阵中各个列向量线性独立。 二、等距线阵的阵列响应与方向图 在单个信源情况下，阵列输出为各阵元信号的加 权和（不考虑噪声），
阵列接收信号处理流程
阵列接收信号处理流程一、信号接收阵列接收信号处理的第一步是信号接收。
在阵列中，有多个接收器同时接收信号。
这些接收器可以是天线、传感器或其他接收设备。
每个接收器都可以独立地接收到信号，并将信号传输到后续的信号处理单元。
二、信号预处理接收到的信号可能会受到噪声、干扰或其他不完美因素的影响，因此需要进行信号预处理。
信号预处理的目的是提高信号的质量和准确性。
常见的信号预处理方法包括滤波、增益控制、噪声消除和时序校正等。
滤波是信号预处理的一种常用方法。
通过滤波可以去除信号中的噪声和干扰，提高信号的清晰度和可辨识度。
常见的滤波方法有低通滤波、高通滤波和带通滤波等。
增益控制是调整信号强度的方法。
通过增益控制可以使信号的强度达到最佳状态，避免信号过强或过弱的问题。
噪声消除是去除信号中噪声成分的方法。
噪声是信号中的不完美因素，可能会干扰信号的质量和准确性。
通过噪声消除可以提高信号的清晰度和准确性。
时序校正是调整信号的时序关系的方法。
在多个接收器同时接收信号时，由于信号传输路径的不同，信号到达各个接收器的时间可能存在微小的差异。
通过时序校正可以使信号的时序关系达到一致，提高信号的同步性和准确性。
三、信号合并经过信号预处理后，接收到的信号可以进行合并。
信号合并是将多个接收器接收到的信号进行综合和整合的过程。
通过信号合并可以提高信号的强度和准确性，增加信号的可靠性和鲁棒性。
常见的信号合并方法有加权平均法、最大比例合并法和最大比例合并法等。
加权平均法是将每个接收器接收到的信号按照一定的权重进行加权平均，得到综合的信号。
最大比例合并法是选择接收到信号强度最大的接收器的信号作为综合的信号。
最大比例合并法是根据接收到信号的强度比例进行综合，提高信号的强度和准确性。
四、信号解调和解码信号合并后，接下来需要进行信号的解调和解码。
信号解调是将调制信号转化为原始信号的过程。
常见的调制方式有频率调制、相位调制和振幅调制等。
通过信号解调可以恢复出原始信号的特征和信息。
阵列信号处理
阵列信号处理是信号处理的一个年青的分支，属于现代信号处理的重要研究内容之一，其应用范围很广，可用于雷达、声呐、通信、地震勘察、射电天文和医用成像等众多领域。
阵列信号处理是将一组传感器在空间的不同位置按一定规则布置形成的传感器阵列（尽管采用的传感器的类型可以不同，如天线、水听器、听地器、超声探头、X射线检测器，但是传感器的功能是相同的，它是连接信号处理器和感兴趣的空间纽带），用传感器阵列发射能量和（或）接收空间信号，获得信号源的观测数据并加以处理。
阵列信号处理的目的是从这些观测数据中提取信号的有用特征，获取信号源的属性等信息。
目前，阵列信号处理在雷达及移动通信等领域有着广泛而重要的应用。
在相控阵雷达体制中，自适应波束形成技术在抑制杂波干扰方面起着关键的作用。
在移动通信中，基于阵列信号处理的波达方向估计技术，使移动通信进入一个崭新的阶段。
本论文首先介绍阵列信号处理的基础知识。
在此基础上，着重讨论阵列波束形成技术，非理想线性阵列的雷达信号波达方向和多普勒频率估计，均匀圆形阵列的信号波达方向估计和复杂信号的波达方向及参数估计等四方面内容。
这些内容都是阵列信号处理领域的研究热点。
它们无论对阵列信号处理的理论发展还是实际应用，都有重要的意义。
目前，人们普遍关注在阵列响应矢量未知情况下，自适应波束形成问题，即盲自适应波束形成技术。
本文第一方面介绍了最基本的阵列波束形成方法，即最小均方误差波束形成器，线性约束最小方差波束形成器和基于特征空间的波束形成器（ESB）。
在此基础上，提出一个基于特征空间的盲自适应波束形成算法。
此算法首先根据高分辨波达方向估计方法，估计信号源的波达方向，然后以此方向形成约束导向矢量，进而计算出ESB波束形成算法的最优权矢量，最后，对期望目标形成笔状波束。
此算法能够有效地抑制信号的对消现象，并且能够应用于在波束中有多个期望信号的场合。
当阵列存在各种误差时，一般高分辨波达方向估计方法（如MUSIC）的估计性能严重下降。