混凝土应力应变弯矩
钢筋混凝土梁正截面抗弯实验

钢筋混凝土梁正截面抗弯实验一、引言钢筋混凝土梁是建筑结构中常见的承重构件,其正截面的抗弯强度是评价梁的性能指标之一。
为了确定梁的正截面抗弯性能,需要进行相应的实验研究。
本文将详细介绍钢筋混凝土梁正截面抗弯实验,包括实验目的、实验步骤、实验装置及方法、实验数据处理等内容。
二、实验目的通过本次实验,旨在研究钢筋混凝土梁正截面的抗弯性能,并得出相应的结论。
具体目的包括: 1. 掌握梁正截面抗弯实验的基本原理和方法; 2. 测定梁在不同加载荷载下的挠度和应变; 3. 绘制梁在不同荷载下的弯曲应力-应变曲线; 4. 对比分析不同梁的抗弯性能。
三、实验步骤1. 实验准备1.根据设计要求制作梁模具;2.准备好所需的混凝土和钢筋材料;3.检查实验装置和测量仪器的工作状态。
2. 梁制作1.在模具内放置钢筋,按照设计要求确定钢筋的布置方式和数量;2.注入混凝土,在振捣混凝土的同时,注意排除气泡;3.需要制作多个相同规格的梁,以保证实验结果的可靠性。
3. 实验装置与测试途径1.将制作好的梁放置在抗弯实验机的两个支座上,并调整支座的间距;2.通过加载装置施加荷载于梁上,使其弯曲;3.使用传感器测量梁的挠度和应变。
4. 实验进行1.自由挠度测量:在没有加载荷载作用时,测量梁的自由挠度;2.逐级加荷:依次增加加载荷载,记录每一级荷载下梁的挠度和应变;3.荷载卸载:依次减小荷载直至荷载卸载。
5. 实验数据处理1.计算梁的弯矩、弯曲应力和应变等参数;2.绘制荷载-挠度曲线和应力-应变曲线;3.分析比较不同梁之间的抗弯性能。
四、实验装置与方法1. 实验装置•抗弯实验机:用于施加加载荷载于梁上,实现梁的弯曲。
•挠度传感器:用于测量梁的挠度变化,通常采用电阻应变片传感器。
•应变传感器:用于测量梁中钢筋和混凝土的应变变化,通常采用电阻应变片传感器。
2. 实验方法•自由挠度测量方法:在没有加载荷载时,测量梁的自由挠度。
•加载荷载方法:逐级增加加载荷载,记录每一级荷载下梁的挠度和应变。
第三章 钢筋混凝土受弯构件正截面承载力计算

第三章钢筋混凝土受弯构件正截面承载力计算受弯构件(bendingmember)是指截面上通常有弯矩和剪力共同作用而轴力可以忽视不计的构件。
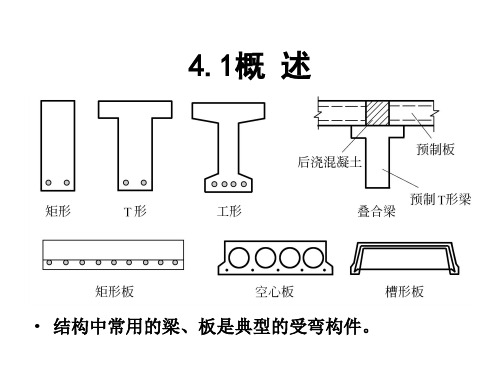
钢筋混凝土受弯构件的主要形式是板(Slab)和梁(beam),它们是组成工程结构的基本构件,在桥梁工程中应用很广。
在荷载作用下,受弯构件的截面将承受弯矩M和V的作用。
因此设计受弯构件时,一般应满意下列两方面的要求:(1)由于弯矩M的作用,构件可能沿弯矩最大的截面发生破坏,当受弯构件沿弯矩最大的截面发生破坏时,破坏截面与构件轴线垂直,称为正截面破坏。
故需进行正截面承载力计算。
(2)由于弯矩M和剪力V的共同作用,构件可能沿剪力最大或弯矩和努力都较大的截面破坏,破坏截面与构件的轴线斜交,称为沿斜截面破坏,故需进行斜截面承载力计算。
为了保证梁正截面具有足够的承载力,在设计时除了适当的选用材料和截面尺寸外,必需在梁的受拉区配置足够数量的纵向钢筋,以承受因弯矩作用而产生的拉力;为了防止梁的斜截面破坏,必需在梁中设置肯定数量的箍筋和弯起钢筋,以承受由于剪力作用而产生的拉力。
第一节受弯构件的截面形式与构造一、钢筋混凝土板的构造板是在两个方向上(长、宽)尺度很大,而在另一方向上(厚度)尺寸相对较小的构件。
钢筋混凝土板可分为整体现浇板和预制板。
在施工场地现场搭支架、立模板、配置钢筋,然后就地浇筑混凝土的板称为整体现浇板。
通常这种板的截面宽度较大,在计算中常取单位宽度的矩形截面进行计算。
预制板是在预制厂和施工场地现场预先制好的板,板宽度一般掌握在Inl左右,由于施工条件好,预制板不仅能采纳矩形实心板,还能采纳矩形空心板,以减轻板的自重。
板的厚度h由截面上的最大弯矩和板的刚度要求打算,但是为了保证施工质量及耐久性的要求,《大路桥规》规定了各种板的最小厚度;行车道板厚度不小于IOOmm人行道板厚度,就地浇注的混凝土板不宜小于80mm,预制不宜小于60mm。
空心板桥的顶板和底板厚度,均不宜小于80mm。
钢筋混凝土梁正截面抗弯实验

钢筋混凝土梁正截面抗弯实验一、实验目的本实验旨在通过对钢筋混凝土梁正截面抗弯实验的进行,掌握梁的正截面抗弯性能及其影响因素。
二、实验原理1.受力分析当梁受到外力作用时,梁内部会产生内力,其中最重要的是弯矩。
在梁的中性轴处,弯矩为0,在上部纤维和下部纤维处则呈现相反的符号。
因此,在不同位置上的混凝土和钢筋所承受的应力也不同。
2.截面抗弯性能分析在梁受到外力作用时,由于混凝土与钢筋之间具有良好的黏结性能,因此混凝土与钢筋共同工作以形成一个整体。
当外力超过一定值时,由于混凝土本身脆性较大,容易产生裂缝,进而导致整个梁失效。
3.影响因素分析(1)截面形状:不同形状的截面对于抵抗外力有着不同的效果。
(2)材料特性:混凝土和钢筋材料特性的不同,会影响其受力性能。
(3)受力状态:梁在不同受力状态下的抗弯性能也不同。
(4)配筋率:钢筋的数量和分布方式对于梁的抗弯性能有着重要的影响。
三、实验步骤1.制作试件根据实验要求,制作出符合要求的试件。
一般而言,试件应该采用正方形或矩形截面,并且在试件中应该按照一定比例配筋。
2.实验测量将试件放置在测试机上,并加载到规定荷载值。
通过测试机上的传感器和测量仪器,可以得到试件在不同荷载下的变形情况和荷载值。
同时,还需要记录下试件断裂时所承受的最大荷载值。
3.数据处理根据测试结果,可以计算出试件在不同荷载下的应变、应力和变形等数据。
通过这些数据可以得到试件在正截面抗弯方面的性能表现。
四、实验注意事项1.制作试件时需要严格按照要求进行操作,以保证测试结果具有可靠性和可重复性。
2.在进行实验前需要对测试设备进行校准,以确保测量结果的准确性。
3.在进行实验时需要严格控制荷载值的大小和速率,以避免试件过早失效。
4.在记录测试数据时需要注意精度和准确性,以保证数据处理的准确性。
五、实验结果分析通过对正截面抗弯实验的进行,可以得到试件在不同荷载下的应变、应力和变形等数据。
通过这些数据可以计算出试件在不同荷载下的截面抗弯性能表现。
混凝土受弯构件正截面承载力计算
r As f y As a1 fcbx x a1 fc
bh0 bh0 f y bh0 f y h0 f y
令
x
h0
则
r
a1 fc
fy
令b为 = r max时的相对受压区高度,即
rmax
b
a1
f
fc
y
= r max时的破坏形态为受压区边缘混凝土达到极限压
c fc e0 e ecu
n
2
1 60
(
fcu,k
50)
2.0
各系数查表4-3
e0 0.002 0.5( fcu,k 50)105 0.002
ecu 0.0033 0.5( fcu,k 50)105 0.0033
4.钢筋应力—应变关系的假定(本构关系)
Ese e e y fy e ey
4.3钢筋混凝土受弯构件正截面试验研究
一、受弯构件正截面破坏过程
受弯构件正截面破坏分为三个阶段 • 第一阶段:裂缝开裂前 • 第二阶段:从开裂到钢筋屈服 • 第三阶段:从钢筋屈服到梁破坏
(1)第I阶段
当荷载比较小时,混凝土基本处 于弹性阶段,截面上应力分布为三 角形,荷载-挠度曲线或弯矩-曲率 曲线基本接近直线。截面抗弯刚度 较大,挠度和截面曲率很小,钢筋 的应力也很小,且都于弯矩近似成 正比。
My
Mu
Failure”,破坏前
可吸收较大的应变
能。
0
f
2.超筋梁(Over reinforced)破坏
钢筋配置过多,将发生这种破坏。 破坏特征:破坏时钢筋没有达到屈服强度,破坏是由 于压区混凝土被压碎引起,没有明显预兆,为脆性破 坏。
混凝土结构设计原理

混凝土结构设计原理
9.变形和裂缝宽度的计算
4、保证使用者的感觉在可接受的程度之内。过大振动、变形 会引起使用者的不适或不安全感。
《规范》3.3.2 受弯构件的挠度限值
构 件 类 型 挠度限值(以计算跨度 l0 计算) l0/500 吊车梁:手动吊车 l0/600 电动吊车 屋盖、楼盖及楼梯构件: l0/200( l0/250) 当 l0≤7m 时 l0/250( l0/300) 当 7m≤l0≤9m 时 l0/300( l0/400) 当 l0 > 9m 时 注:1、表中括号内数值适用于使用上对挠度有较高要求的构件; 2、悬臂构件的挠度限值按表中相应数值乘以系数 2.0 取用。
以简支梁 为例:
f
M 2 f S l Sf l 2 EI
M M EI M EI f f f EI
截面抗弯刚度EI 体现了截面抵抗弯曲变形的能力,同时也反映了 截面弯矩与曲率之间的物理关系。 ⑴对于弹性均质材料截面,EI为常数,M-f 关系为直线。
混凝土结构设计原理
9.变形和裂缝宽度的计算
⑵钢筋混凝土构件曲率与弯矩关系的推导 ①几何关系: f e sm e cm 符合平截面假定 h0
②物理关系: 请看动画
εcm
φ h0
es
s
Es
,
c ec Ec
h0
c c
εsm
③平衡关系:根据裂缝截面的应力分布
C
M k T hh0 s As hh0
Mk c hbh02
混凝土结构设计原理
9.变形和裂缝宽度的计算
9.2 受弯构件的变形验算
9.2.1变形限值
f ≤ f lim
(S C )
混凝土构件的变形

混凝土构件的变形、裂缝宽度验算和耐久性概念设计1.混凝土构件裂缝形成的原因?答:目前,混凝土是抗压性能大大优于抗拉性能的材料。
由于其极限拉伸变形很小,当混凝土构件受到弯矩、剪力、拉力和扭矩等荷载效应作用,或由于地基不均匀沉降、混凝土收缩和温度变化而产生的外加变形受到钢筋或其它构件约束,以及钢筋锈蚀体积膨胀时,混凝土中便产生拉应力,该拉应力超过其极限抗拉强度时就会开裂。
同时,混凝土材料来源广泛,成分多样,施工工序繁多,养护硬化需要较长时间,受环境影响较大,混凝土自身构成机理,以及冻融和化学作用等也往往是混凝土开裂的原因。
所以,钢筋混凝土构件截面在施工中和正常使用阶段难免出现荷载和非荷载因素导致的裂缝。
2.为什么要对混凝土构件进行裂缝宽度控制?答:对裂缝宽度进行控制的原因:(1)使用功能的要求有些使用上要求不出现渗漏的贮液(气)容器或输送管道,裂缝的存在会直接影响其使用功能,因此,要对其控制裂缝的出现。
(2)建筑外观要求外观是评价混凝土质量的重要因素之一,裂缝过宽会影响建筑的外观,引起人们的不安全感。
满足外观要求的裂缝宽度限值选取,取决于多种原因。
调查表明,控制裂缝宽度在0.3mm以内,对外观没有显著影响,一般不会引起人们的特别注意。
(3)耐久性要求这是控制裂缝最主要的原因。
化学介质、气体和水分侵入裂缝,破坏了钢筋的钝化膜,会在钢筋表面发生电化学反应,引起钢筋锈蚀,使构件发生破坏,影响结构的使用寿命。
3.混凝土构件裂缝控制的标准如何?答:混凝土构件的裂缝控制统一划分成三级,分别用应力及裂缝宽度进行控制。
一级:严格要求不出现裂缝的构件,按荷载效应标准组合进行计算时,构件受拉边缘混凝土不应产生拉应力;二级:一般要求不出现裂缝的构件,按荷载效应标准组合进行计算时,构件受拉边缘混凝土的拉应力不应超过混凝土的抗拉强度标准值f tk,按荷载效应准永久组合下进行计算时,构件受拉边缘混凝土不应产生拉应力;三级:允许出现裂缝的构件,最大裂缝宽度按荷载效应标准组合并考虑长期作用组合影响计算,并符合下列规定w max w lim式中w max—在荷载效应的标准组合并考虑长期作用影响计算得到的最大裂缝宽度;w l im—最大裂缝宽度限值,设计时应根据结构构件的具体情况按教材附表17选用。
第八章 钢筋混凝土受弯构件变形与裂缝宽度计算汇总

y —裂缝间纵向受拉钢筋应变不均匀系数
f tk y 1.1 0.65 sq te
当y <0.2时,取y =0.2; 当y >1.0时,取y =1.0; 对直接承受重复荷载作
用的构件,取y =1.0。
sq ——按荷载准永久组合计算的钢筋混凝土
构件纵向受拉普通钢筋应力。 对于受弯构件
sq
M M EI M EI EI
截面弯曲刚度EI 就是使截面产生单位曲率所施 加的弯矩值体现了截面抵抗弯曲变形的能力,同时 也反映了截面弯矩与曲率之间的物理关系。 对于弹性均质材料截面,EI为常数,M- 关系 为直线。如下图中的黑线所示。
②钢筋混凝土构件
由于混凝土开裂、弹塑性应力-应变关系和钢筋 屈服等影响,钢筋混凝土适筋梁的M-f 关系不再是直 线,而是随弯矩增大,截面曲率呈曲线变化。如下图 红线所示。
★如果两条裂缝的间距小于2 l,则由于粘结应力传递 长度不够,混凝土拉应力不可能达到ft,因此将不会出 现新的裂缝,裂缝的间距最终将稳定在(l ~ 2 l)之间, 平均间距可取1.5 l。 ★粘接应力传递长度l越短,裂缝分布越密。粘接强度 越高, l越短;钢筋面积相同时小直径钢筋表面积大些, l就短些;低配筋率钢筋, l长些。
8.3.3平均裂缝宽度Wm
c wm s lm clm s (1 )lm s
c (1 ) 0.85 s
s y s y
sk
Es
◆平均裂缝宽度
wm 0.85 y
sk
Es
lm
8.3.4最大裂缝宽度及其验算 实测表明,裂缝宽度具有很大的离散性。取实测 裂缝宽度wt与上述计算的平均裂缝宽度wm的比值 为 s l 。
容许应力计算法

混凝土结构设计原理(容许应力计算法)混凝土结构设计原理(容许应力计算法)混凝土结构设计原理(容许应力计算法)混凝土轴心抗压极限强度比较38.535.532.429.626.823.420.116.713.410GB 50010-200250454036322824201612CEB -FIP 1990403733.5302723.5201713.510.1TB 10002.3-2005C60C55C50C45C40C35C30C25C20C15混凝土强度等级轴心抗压极限强度f c (MPa)序号应力种类中心受压弯曲受压及偏心受压有箍筋及斜筋时的主拉应力无箍筋及斜筋时的主拉应力梁部分长度中全由混凝土承受的主拉应力纯剪应力][c σ][b σ][1-tp σ][2-tp σ][3-tp σ][c τ123456C15C20C25C30C35C40C45C50C55混凝土强度等级符号混凝土的容许应力4.6 6.17.69.010.311.613.214.617.46.17.89.511.213.014.716.518.220.01.3 1.55 1.78 1.992.21 2.42 2.59 2.77 2.950.470.570.660.730.820.890.96 1.03 1.090.240.290.330.370.410.450.480.520.550.710.860.991.10 1.22 1.34 1.441.54 1.64混凝土结构设计原理(容许应力计算法)钢筋的容许应力Ⅰ级钢筋Ⅱ级钢筋主力作用下主力加附加作用下130180 160230][sσ桥梁承受的荷载大致可分为主要荷载(主力)、附加荷载(附加力)和特殊荷载三种。
混凝土结构设计原理(容许应力计算法)主要荷载包括恒载和活载。
恒载包括桥梁自重、土压力、静水压力和浮力。
预应力混凝土结构的桥梁还包括预应力、混凝土收缩力和徐变的影响所产生的力等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0.6 0.4 0.2
h0
Mcr/Mu
9
8
7
6
5
4 3 2 e / ×10-3
1
0
1
2
3
0
0.1 0.2 0.3 0.4 0.5 0.6 0.7
j =xc/h0
纵向应变
1.0 0.8
中和轴位置
Mu/Mu My/Mu
1.0 0.8 钢筋屈服
Mu/Mu My/Mu
b
As bh0
4.1试验测试及结果
n 三种破坏形态 p 素混凝土梁 p 少筋梁 p 适筋梁 p 超筋梁 n 适筋梁的配筋率范围 p 最大配筋率rmax p 最小配筋率rmin p 适筋梁的配筋率
p
rmax ≤ r ≤rmin
M
超筋梁 适筋梁 适筋梁
n 三种破坏形态的比较
少筋梁
f
4.1试验测试及结果
My
Mcu
f yAs
f y As
4. 2 适筋梁正截面工作的三个阶段
适筋梁的破坏特征、破坏性质
受拉区纵筋应力首先达到屈服强度,然后受压区 混凝土被压坏。 塑性破坏:梁破坏前有明显的塑性变形和裂缝预 兆。 材料利用情况:两种材料都得到了充分利用
4. 3 超筋梁和少筋梁的破坏特征
超筋梁的受弯性能
破坏过程:从加载到第Ⅱ阶段,应力、应变的变化与适筋梁相 同。继续加载,由于受拉钢筋量过多,钢筋应力达不到屈服, 裂缝开展与向上延伸不明显,而受压区混凝土应力继续增大, 最后梁因受压区混凝土被压坏而破坏(受拉钢筋仍未屈服)。 破坏特征 受压区混凝土被压坏,受拉钢筋应力达不到屈服强度 破坏性质 脆性破坏,无明显预兆 材料利用情况 钢筋强度未充分利用
As / bh0
4. 3 超筋梁和少筋梁的破坏特征
少筋梁的受弯性能
破坏过程:从加载到Ⅰa阶段,应力、应变的变化与适筋梁相 同。当荷载稍微增加一点,由于受拉钢筋量过少,钢筋应力 很快达到屈服强度,甚至达到强化阶段,梁由于过度变形而 达到承载力极限状态。 破坏特征:瞬拉破坏(混凝土拉裂,钢筋拉断) 破坏性质:脆性破坏(一裂即坏) 材料利用情况:混凝土强度未充分利用,钢筋作用不大
<ey
ey
> ey
> ey
M1
Mcr s sA s
M2
My
My
Mcu
s sA s
s sAs
f yAs
f yAs
f yAs
I
Ia
I I
IIa
III
IIIa
4. 4 试验测试及结果
n 试验曲线
M / Mu
0.11 0.22 0.54 0.95 1.0
Mu/Mu
My/Mu
xc 1.00
0.8
M / Mu
钢筋混凝土结构的一个重要特点
受力性能与两种材料的强度和数量配比有关。
As / bh0
设计时,通过控制配筋率来控制构件的受力性能。
4. 3 超筋梁和少筋梁的破坏特征 梁的破坏形态
适筋梁:配筋率适当,受拉区裂缝发展充分。 ● 超筋梁:配筋率过大,受拉区裂缝发展不充分。 ● 少筋梁:配筋率过小,裂缝贯通,断裂破坏。
中和轴位置
Mu/Mu
My/Mu
1.0 0.8
Mu/Mu
钢筋屈服
My/Mu
M / Mu
0.6 0.4 0.2 0 100 200 300 400 500
M / Mu
Mcr/Mu
0.6 0.4 0.2 0 混凝土开裂 10 20 30 40 50 60 70
Mcr/Mu
ss / N/mm2
f /mm
纵筋应力
第 4章
p
梁受弯性能的试验研究
适筋梁正截面工作的三个阶段
p
p p
适筋梁的截面应力分布
正截面受弯的破坏形态 适筋梁的配筋率范围
内容提要
试验目的:建立正截面承载力计算公式 试验方法及测试内容 试验结果分析
●
截面应力变化过程:钢筋应力、应变;混凝土应力、应变;
弯矩-挠度曲线 梁三个受力阶段的受力性能
● ●
M1
Mcr
s sA s
s sA s
et
4. 2 适筋梁正截面工作的三个阶段
■第Ⅱ阶段—裂缝出现→受拉钢筋屈服
受压区混凝土出现塑性,应力为曲线分布; 受拉区混凝土退出工作(中和轴附近还有一小部分混凝土 承受拉力),拉力由钢筋承受; 第Ⅱ阶段末称为梁的屈服状态,以Ⅱa表示,特点是受拉钢 筋应力达到屈服强度; 工程意义:变形和裂缝宽度验算的依据
●
M
超筋梁 适筋梁 适筋梁
少筋梁
f
4. 4 适筋梁的截面应力分布
n 混凝土与钢筋的应力-应变曲线
sc
c max
fy
ss
cu
e0 2
4ecu
ec
ey 2
es
4
混凝土的应力-应变曲线
钢筋的理想应力-应变曲线
4. 4 适筋梁的截面应力分布
n 梁各阶段的截面应变及对应的应力分布
ecu
h0
h
b
et
跨中挠度
4.1 试验测试及结果
三阶段截面应力及应变分布
h0 ecu
et
<ey
ey
> ey
> ey
M1
Mcr s sA s
M2
My
My
Mcu
s sA s
s sAsபைடு நூலகம்
f yAs
f yAs
f yAs
I
Ia
I I
IIa
III
IIIa
4. 2 适筋梁正截面工作的三个阶段
第Ⅰ阶段—开始加载→受拉边缘混凝土达到极限拉应变 受压区混凝土处于弹性工作阶段,应力为三角形分布; 第Ⅰ阶段末称为梁的开裂极限状态,以Ⅰa表示,特点是混 凝土应变达到极限拉应变,受拉区混凝土应力为曲线分布 (塑性状态)。 钢筋处于弹性状态。 工程意义:抗裂验算的依据
4.1试验测试及结果
n 试验方案
百分表
P
应变测点
P
百分表
h0
位移计
b l /3 l /3
l /3
弯矩图
纯弯段
剪力图
•钢筋、混凝土 应变 •跨中挠度 •梁端转角
h
4.1试验测试及结果
n 试件的主要变化参数:配筋率的定义 配筋率:受拉钢筋面积 与截面有效面积之比。
截面有效面积: bh0
h0 h
截面有效高度 h0 :受 拉钢筋合力点距截面受 压边缘的距离。
n 试验曲线
M / Mu
0.11 0.22 0.54 0.95 1.0
Mu/Mu My/Mu
xc 1.00
0.8
M / Mu
0.6 0.4
0.2
h0
Mcr/Mu
9
8
7
6
5
4 3 2 e / ×10-3
1
0
1
2
3
0
0.1 0.2 0.3 0.4 0.5 0.6 0.7
j =xc/h0
纵向应变
1.0 0.8
M2
My
s sA s
f yAs
4. 2 适筋梁正截面工作的三个阶段
第Ⅲ阶段—受拉钢筋屈服→受压边缘混凝土达极限压应变
受压区混凝土应力图形为较丰满的曲线;前期应力峰值在 边缘,后期应力峰值内移; 第Ⅲ阶段末称为梁的承载能力极限状态,以Ⅲa表示,特点 是受压区边缘混凝土达到其极限压应变。 工程意义:承载能力极限状态计算的依据
