欧拉_拉格朗日方程的推广_张露萍
欧拉-拉格朗日方法and欧拉-欧拉方法

欧拉-拉格朗⽇⽅法and欧拉-欧拉⽅法
欧拉-拉格朗⽇⽅法
在Fluent中的拉格朗⽇离散相模型遵循欧拉-拉格朗⽇⽅法。
流体相被处理为连续相,直接求解时均纳维-斯托克斯⽅程,⽽离散相是通过计算流场中⼤量的粒⼦,⽓泡或是液滴的运动得到的。
离散相和流体相之间可以有动量、质量和能量的交换。
该模型的⼀个基本假设是,作为离散的第⼆相的体积⽐率应很低,即便如此,较⼤的质量加载率仍能满⾜。
粒⼦或液滴运⾏轨迹的计算是独⽴的,它们被安排在流相计算的指定的间隙完成。
这样的处理能较好的符合喷雾⼲燥,煤和液体燃料燃烧,和⼀些粒⼦负载流动,但是不适⽤于流-流混合物,流化床和其他第⼆相体积率不容忽略的情形。
欧拉-欧拉⽅法
在欧拉-欧拉⽅法中,不同的相被处理成互相贯穿的连续介质。
由于⼀种相所占的体积⽆法再被其他相占有,故此引⼊相体积率(phasic volume fraction)的概念。
体积率是时间和空间的连续函数,各相的体积率之和等于1。
从各相的守恒⽅程可以推导出⼀组⽅程,这些⽅程对于所有的相都具有类似的形式。
从实验得到的数据可以建⽴⼀些特定的关系,从⽽能使上述⽅程封闭,另外,对于⼩颗粒流(granular flows),则可以通过应⽤分⼦运动论的理论使⽅程封闭。
在FLUENT中, 共有三种欧拉-欧拉多相流模型,分别为:流体体积模型(VOF),混合物模型,以及欧拉模型。
欧拉-拉格朗日方程在一维波动方程中的应用

欧拉-拉格朗日方程在一维波动方程中的应用王颖;史旭光【摘要】In this paper,the one-dimensional wave function is studied in frame of the kinetic energy and potential energy.In general,one-dimensional wave equation is obtained through the force analysis of an arbitrary string element and Newton's second law.In this paper,we introduce the Lagrangian of a particle,which moves in the potential V.Then Euler-Lagrange equation,Which is also the motion equation of particle,is given based on the principle of the least action.In the frame of this theory,we give the kinetic energy and potential energy of the string element.Then the Lagrange density function of the 1-dimension string element is de-fined.The Euler-Lagrange equation to describe a system with infinite degrees of freedom is obtained.Based on these,the one-dimensional wave equation is revealed.At last,we give the relations between Lagrange density function in one-dimensional wave and Lagrange density function in Polyakov interaction in string theory.%本文以一维弦上微元的动能和势能为基础,推导出了一维波动方程.文章首先介绍了通过力学分析得到一维波动方程的方法.然后分析了一维自由运动粒子的动能和势能,引入系统的哈密顿量和拉格朗日函数,由最小作用原理得到了欧拉-拉格朗日方程,也就是粒子的运动方程.将这一方法用于分析一维弦上波动,给出微元的拉格朗日密度函数,得到可以描写无穷多自由度系统的欧拉-拉格朗日方程,从而导出了一维波动方程.最后分析了一维弦上波动的拉格朗日密度与弦理论中Polyakov作用量中的拉格朗日密度的关系.【期刊名称】《物理与工程》【年(卷),期】2017(027)006【总页数】4页(P41-44)【关键词】波动方程;拉格朗日函数;最小作用量原理;欧拉-拉格朗日方程【作者】王颖;史旭光【作者单位】北京林业大学理学院,北京 100083;北京林业大学理学院,北京100083【正文语种】中文波动是物理学中的重要概念。
拉格朗日方程推导

拉格朗日方程推导一、引言拉格朗日方程是数学物理中最重要的方程之一,它以数学形式描述了物理系统的运动规律。
拉格朗日方程的应用范围广泛,从经典力学到量子力学,从电磁场到弹性力学,都有着重要的应用。
本文将对拉格朗日方程进行推导,并介绍其应用。
二、拉格朗日方程的定义与意义拉格朗日方程是由法国数学家拉格朗日于1797年提出,它是一种描述物理系统运动规律的方程。
拉格朗日方程的意义在于,它提供了一种通过最小化泛函来求解物理系统运动状态的方法。
三、拉格朗日方程的推导过程1.泛函与变分首先,我们需要引入泛函的概念。
泛函是一个关于函数的函数,它表示了一个物理系统的能量。
我们可以通过求泛函的极小值来找到系统的运动状态。
然后,我们引入变分原理,它是这样一种原理:如果一个物理系统的运动方程可以表示为某个泛函的极小值问题,那么这个物理系统在任意运动状态下的变分满足拉格朗日方程。
2.欧拉方程欧拉方程是拉格朗日方程的一个特殊情况,它描述了流体力学中流体的运动。
欧拉方程可以通过求解泛函的极小值来得到。
3.拉格朗日方程的得出通过对泛函求导,并令导数为零,我们可以得到拉格朗日方程。
这个方程描述了物理系统在任意状态下的运动规律。
四、拉格朗日方程的应用1.力学系统拉格朗日方程在力学系统中有着广泛的应用,它可以描述质点、刚体、弹性体等的运动。
2.电磁场方程拉格朗日方程也可以应用于电磁场,通过最小化泛函,我们可以得到电磁场的运动状态。
3.量子力学在量子力学中,拉格朗日方程可以用于描述粒子的运动,并通过求解拉格朗日方程,我们可以得到量子力学方程。
五、结论与展望拉格朗日方程是一种重要的物理方程,它通过数学形式描述了物理系统的运动规律。
其在各个领域的应用表明,拉格朗日方程是一种具有广泛实用性的方程。
欧拉 拉格朗日方程

欧拉拉格朗日方程一、欧拉拉格朗日方程的定义欧拉拉格朗日方程是经典力学中的一个重要概念,由两位著名的数学家和物理学家欧拉和拉格朗日分别独立提出。
它是描述系统运动的一个重要原理,可以从系统的动能和势能出发,推导出系统的运动方程。
欧拉拉格朗日方程的形式简洁,适用于各种复杂的物理系统,对于解决实际问题具有广泛的应用价值。
二、欧拉拉格朗日方程的推导1. 动能和势能的定义首先,我们需要定义系统的动能和势能。
动能是描述物体运动状态的量,通常用T 表示,它的定义为:T=12mv2其中,m是物体的质量,v是物体的速度。
势能是描述物体位置的量,通常用V表示,它的定义为:V=V(x,y,z)其中,V是关于物体位置(x,y,z)的函数。
2. 拉格朗日函数的定义为了方便推导,我们引入拉格朗日函数L的概念,它定义为系统的动能T减去势能V,即:L=T−V3. 欧拉拉格朗日方程的表达式根据最小作用量原理,系统的运动路径使得作用量S取得极值。
作用量S定义为:S=∫Lt2t1dt其中,t1和t2是选取的两个时刻。
根据变分法,我们可以得到欧拉拉格朗日方程的表达式:∂L ∂q −ddt(∂L∂q̇)=0其中,q是描述系统的广义坐标,q̇是q对时间t的导数。
三、欧拉拉格朗日方程的应用欧拉拉格朗日方程的应用非常广泛,以下是一些例子:1. 单摆的运动考虑一个质点在一根轻绳上进行简谐摆动的情况。
我们可以选择以初始位置为参考点,将质点位置与竖直线之间的夹角作为广义坐标q,则拉格朗日函数为:L=T−V=12ml2q̇2−mgl(1−cosq)根据欧拉拉格朗日方程,我们可以推导出质点的角加速度与夹角q的关系,从而描述单摆的运动。
2. 刚体的运动刚体是一个具有固定形状的物体,它的运动涉及到旋转和平动。
欧拉拉格朗日方程可以用来描述刚体的运动,有助于求解刚体的角速度和平动速度。
3. 量子力学中的波函数在量子力学中,波函数描述了微观粒子的运动状态。
欧拉拉格朗日方程可以应用于波函数的变分原理,从而得到薛定谔方程,进而推导出量子力学的基本原理。
欧拉–拉格朗日方程
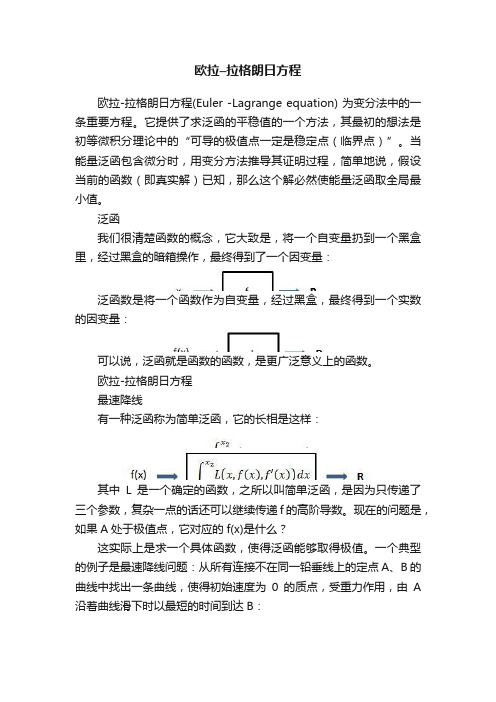
欧拉–拉格朗日方程欧拉-拉格朗日方程(Euler -Lagrange equation) 为变分法中的一条重要方程。
它提供了求泛函的平稳值的一个方法,其最初的想法是初等微积分理论中的“可导的极值点一定是稳定点(临界点)”。
当能量泛函包含微分时,用变分方法推导其证明过程,简单地说,假设当前的函数(即真实解)已知,那么这个解必然使能量泛函取全局最小值。
泛函我们很清楚函数的概念,它大致是,将一个自变量扔到一个黑盒里,经过黑盒的暗箱操作,最终得到了一个因变量:泛函数是将一个函数作为自变量,经过黑盒,最终得到一个实数的因变量:可以说,泛函就是函数的函数,是更广泛意义上的函数。
欧拉-拉格朗日方程最速降线有一种泛函称为简单泛函,它的长相是这样:其中L是一个确定的函数,之所以叫简单泛函,是因为只传递了三个参数,复杂一点的话还可以继续传递f的高阶导数。
现在的问题是,如果A处于极值点,它对应的f(x)是什么?这实际上是求一个具体函数,使得泛函能够取得极值。
一个典型的例子是最速降线问题:从所有连接不在同一铅垂线上的定点A、B的曲线中找出一条曲线,使得初始速度为0的质点,受重力作用,由A 沿着曲线滑下时以最短的时间到达B:这里我们将曲线看作路径f关于时间t的函数:ΔSi是在极短时间Δti内沿着曲线移动的微小弧长,此时的瞬时速度是ΔVi,距离=速度×时间:重力加速的推论,在t时间处的速度v2 = 2gh:质点从A点到B点的总时间:根据弧长公式,可以将dS化简,进一步写成把结论和简单泛函做个对比,可以看到二者形式相吻合:最右侧的式子并没有严格映射到L(x,f(x),f’(x)),因为在函数中并没有直接使用到参数t,这无所谓了,可以理解成虽然传递了参数t,但实际上t并没有起任何作用,就像y (x) = 1一样,无论传递任何x,最终结果都是1,但它仍然是一个y关于x的函数。
现在回到最初的问题,AB间有无数条曲线,每条曲线都可以求得时间T[f],在众多的曲线中,有一条唯一的曲线能够使得T[f]取得最小值,这个f(x)应该长成什么样?EL方程的推导这里暂且耍一下流氓,抛开具体的速降问题,只看A[f],并且假设f0(x)就是符合条件的最优函数。
欧拉拉格朗日方程小时百科

欧拉-拉格朗日方程什么是欧拉-拉格朗日方程欧拉-拉格朗日方程(Euler-Lagrange equation)是经典力学中的一个重要定律,用于描述质点或系统在势能场中的运动。
它由瑞士数学家欧拉和法国数学家拉格朗日在18世纪中叶独立提出,并成为经典力学的基础之一。
欧拉-拉格朗日方程可以从变分原理(principle of least action)推导而来,该原理认为自然界中的运动路径是使作用量(action)取极小值的路径。
作用量定义为质点或系统在一段时间内所受到的所有力所做的功之和。
欧拉-拉格朗日方程的表达式对于一个质点或系统,在广义坐标q i和广义速度q̇i下,其动能T和势能V可以表示为:T=T(q1,q2,…,q n,q̇1,q̇2,…,q̇n)V=V(q1,q2,…,q n)其中n表示系统自由度的数量。
根据变分原理,作用量可以表示为:S=∫Lt2t1(q1,q2,…,q n,q̇1,q̇2,…,q̇n)dt其中L=T−V称为拉格朗日函数(Lagrangian),它是动能和势能的差。
欧拉-拉格朗日方程可以通过对作用量进行变分,使其取极值,得到:∂L ∂q i −ddt(∂L∂q̇i)=0对于每一个广义坐标q i,都有一个对应的欧拉-拉格朗日方程。
这些方程描述了系统在广义坐标和时间上的运动规律。
欧拉-拉格朗日方程的意义与应用欧拉-拉格朗日方程是经典力学的重要工具,它具有以下几个重要意义和应用:1. 简化运动方程相比于牛顿力学中的运动方程,欧拉-拉格朗日方程更加简洁、优雅,并且适用于复杂系统。
通过引入广义坐标和广义速度,可以将系统的自由度从直角坐标系中解放出来,从而简化了运动方程的表达。
2. 描述约束系统在经典力学中,约束系统是指由于各种限制条件而使得系统自由度减少的情况。
欧拉-拉格朗日方程可以很好地描述约束系统的运动,通过引入拉格朗日乘子(Lagrange multiplier)来处理约束条件。
关于拉格朗日法与欧拉法相互变换的研究
关于拉格朗日法与欧拉法相互变换的研究
樊斌
【期刊名称】《纺织高校基础科学学报》
【年(卷),期】1996(009)001
【摘要】描述流体运动状态有两种方法:拉格朗日法与欧拉法。
它们分别将物理量表示为拉格朗日变数的函数和欧拉变数的函数。
本文研究流体中传播的平面简谐声波,求出描述这种运动的拉格朗日法与欧拉法相互变换的方法,其结果可推广到有限振幅声波的传播中。
【总页数】3页(P93-94,98)
【作者】樊斌
【作者单位】无
【正文语种】中文
【中图分类】O35
【相关文献】
1.一种"准拉格朗日法"和"欧拉法"统一算法时间积分方案 [J], 辜旭赞
2.欧拉法融合拉格朗日法高效模拟灌溉二维地表水运动规律 [J], 史源;章少辉;白美健;李益农
3.虚轴上具有重极点的拉普拉斯变换与傅里叶变换相互计算的方法 [J], 陈绍荣; 何健; 朱行涛; 刘郁林
4.声传播研究中拉格朗日法与欧拉法的区别 [J], 樊斌
5.采用拉格朗日法与欧拉法模拟旋风筒内气固两相流的对比研究 [J], 毛娅;陈家乐;陈作炳;刘宁;吕银雷
因版权原因,仅展示原文概要,查看原文内容请购买。
欧拉拉格朗日方程推导
欧拉拉格朗日方程推导欧拉-拉格朗日方程(Euler-Lagrange equation)是用于描述物理系统的经典力学问题的定律,它的推导基于变分原理和拉格朗日函数。
在物理学中,我们经常需要找到一个系统的最优路径,即该路径下其中一物理量的变分问题。
为此,拉格朗日引入了一个新的函数,即拉格朗日函数(Lagrange function),它是系统的广义坐标(generalized coordinates)和广义速度(generalized velocities)的函数,记作L(q, q ̇)。
广义坐标是指描述系统的自由度的坐标,坐标的个数与系统自由度的数量相等。
广义速度是广义坐标对时间的导数。
这个拉格朗日函数可以看作系统的动能(kinetic energy)和势能(potential energy)的代数和。
我们希望通过求解拉格朗日函数的变分问题,来得到系统的最优路径。
变分问题的解就是能够使拉格朗日函数满足对应的极值条件的路径。
这个变分问题可以用欧拉方程来描述。
首先,我们需要定义一个定义域中的路径,路径上的点可以由广义坐标 q 的函数表示,即 q(t)。
接下来,引入一个新的函数,广义速度v(t),它表示路径上其中一点的广义坐标 q 对时间的导数,即 v(t) =dq(t)/dt。
这个函数可以用来表示路径上其中一点的切矢量。
在此基础上,我们可以定义一个新的函数,即作用量(action),记作S。
作用量是广义坐标 q 和广义速度 v 的函数,定义为路径上各个点的拉格朗日函数在时间间隔 t1 到 t2 上的积分:S[q(t)] = ∫L(q, v) dt, t1到t2上式描述了广义坐标和广义速度在整个路径上的变化,我们希望找到一个路径使得作用量最小化。
为了求解这个变分问题,我们需要引入变分运算符(variational operator),记作δ。
变分运算符作用在函数上得到函数的变分值(函数的微小变化)。
对于一些函数 f(x),它的变分值可以表示为:δf(x)=f(x+δx)-f(x)其中,δx是函数x的变分值。
欧拉方法和拉格朗日方法
欧拉方法和拉格朗日方法欧拉方法是一种简单的近似方法,用于求解常微分方程的初值问题。
它基于一个重要的数值近似原理,即在一个小区间上,如果函数的导数变化不太大,那么可以将函数的变化等同于导数的变化。
具体来说,欧拉方法将原始的微分方程转化为离散的差分方程,并根据初始条件逐步逼近问题的解。
对于一个一阶常微分方程dy/dx = f(x, y),欧拉方法将自变量x和因变量y分成若干个小区间,每个小区间的长度为h。
利用微分方程的性质,我们可以将函数在每个小区间上进行线性近似。
具体来说,我们从初始点(x0, y0)出发,根据微分方程的定义,计算出斜率k1=f(x0, y0),然后根据该斜率近似得到在下个小区间上的函数值y1=y0 + k1 * h。
以此类推,我们可以得到在每个小区间上的近似函数值。
欧拉方法的一个明显局限是误差较大,特别是在相对大的步长h下。
这是因为欧拉方法只考虑了导数在小区间上的线性变化,忽略了更高阶的项,导致近似解与真实解的误差随着步长的增加而累积。
拉格朗日方法是一种改进的近似方法,用于求解微分方程的数值解。
它基于拉格朗日插值多项式的思想,通过将微分方程中的函数y(x)近似为一个多项式函数来逼近实际解。
具体而言,拉格朗日方法通过利用初始点(x0,y0)的函数值和导数值,在每个小区间上构造一个插值多项式L(x),该多项式是一个关于x的n次多项式,其中n是方程的阶数。
在拉格朗日方法中,我们首先确定每个小区间的节点,例如选取三个节点x0,x1,x2,并计算出这些节点上的函数值y0,y1,y2、然后我们利用这些节点构造一个三次拉格朗日插值多项式L(x),具体形式为:L(x)=L0(x)*y0+L1(x)*y1+L2(x)*y2,其中L0(x),L1(x),L2(x)是三个插值基函数。
通过这个多项式L(x),我们可以逐步计算出每个小区间上的函数值,并不断迭代得到近似解。
与欧拉方法相比,拉格朗日方法考虑了更高阶的项,在相对大的步长下,其近似解与真实解的误差更小。
欧拉 拉格朗日方程
欧拉拉格朗日方程欧拉拉格朗日方程欧拉方程和拉格朗日方程是经典力学中的两个重要方程,它们被广泛应用于物理学、工程学、数学等领域。
欧拉方程描述了质点在空间中的运动,而拉格朗日方程则描述了质点在势能场中的运动。
一、欧拉方程1.1 定义欧拉方程是经典力学中描述质点在空间中运动的基本方程。
它由牛顿第二定律和牛顿第三定律推导得出,表达式为:F = ma其中,F表示作用于质点上的合力,m表示质点的质量,a表示质点的加速度。
这个公式可以解释为:物体所受合外力等于物体的惯性乘以加速度。
1.2 推导过程欧拉方程可以从牛顿第二定律和牛顿第三定律推导得出。
首先,根据牛顿第二定律:F = ma其中F表示作用于物体上的合力,m表示物体的质量,a表示物体的加速度。
然后根据牛顿第三定律:F12 = - F21其中F12和F21分别表示物体1对物体2的作用力和物体2对物体1的作用力。
将这两个公式代入欧拉方程中,可以得到:m1a1 = F12m2a2 = F21这就是欧拉方程的推导过程。
二、拉格朗日方程2.1 定义拉格朗日方程是经典力学中描述质点在势能场中运动的基本方程。
它由哈密顿原理推导得出,表达式为:d/dt(∂L/∂q') - ∂L/∂q = 0其中,L表示系统的拉格朗日函数,q表示广义坐标,q'表示广义速度。
这个公式可以解释为:系统在满足最小作用量原理下,其运动轨迹应该满足使作用量取极值的条件。
2.2 推导过程拉格朗日方程可以从哈密顿原理推导得出。
哈密顿原理是指,在所有可能的路径中,粒子实际上只会沿着使作用量取极值的路径运动。
因此,如果我们假设系统在某一瞬间处于广义坐标q和广义速度q'处,并且在接下来的一段时间内沿着某条路径运动,则该路径所对应的作用量为:S = ∫L(q,q',t)dt其中,L(q,q',t)表示系统的拉格朗日函数。
根据哈密顿原理,该路径所对应的作用量应该取极值,即:δS = 0将S展开,并对广义坐标和广义速度求偏导数,可以得到:δS = ∫[∂L/∂q δq + ∂L/∂q' δq']dt其中δq和δq'分别表示广义坐标和广义速度的微小变化量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
i,j=1 Ω
-
n
-
-
-
∑ … ,uxkxl(x),… ))φ(x))dx= 蘩(鄣xjxjfuxixj(x,u(x),ux1(x),… ,uxn
i,j=1 Ω
-
-
(x),… ,uxkxl(x),… ))φ(x))dx从 而 在 u(x)=u(x)
n
n
∑ ∑ L′(0)=Ⅰ+Ⅱ+Ⅲ=蘩Ω(fu-
i=1
i,j=1
蘩
Ω
(
鄣
xi
f
uxixj
(x,
u
(x),
u
x1
(x),
…
,
u
xn
(x),
…
,
u xkxl
(x),
n
-
-
-
-
∑ … ))φxj(x)dx=- 蘩 鄣xj(鄣xjfuxixj(x,u(x),ux1(x),… ,uxn(x),… ,u
i,j=1 Ω
n
-
-
-
∑ xkxl (x), … )φ (x))dx+ 蘩 (鄣 f xjxj uxixj (x,u (x),ux1 (x), … ,uxn (x),
n
-
-
-
-
-
-
∑鄣xixjfuxiuxj (x, u (x), ux1 (x), … , uxn (x), u x1x1 (x), u x2x2 (x), u xnxn
i,j=1
(x))=0定 理 2:设 f是 关 于 自 变 量 的 2k次 连 续 可 微 函 数 ,若
S=L(u
)=蘩f(x,u
Ω
新高中数学课程标准在“基本理念”中强调数学的人文价 值 ,并 提 出 “数 学 是 全 人 类 的 共 同 财 富 ,也 是21世 纪 公 民 必 备 的科学、文化素养。 应当通过介绍数学发展的历史……包括了 解数学在推动当代社会发展中的社会价值。 在整个数学教学 中,都要注意体现数学的社会需要,数学科学的重大作用、美 学 价 值 、正 确 数 学 观 ,并 使 之 成 为 正 确 世 界 观 的 一 部 分 ”[4]。
i,j=1
+Ⅱ+Ⅲ=0
由定理1
∑n
-
-
-
-
Ⅱ=- 蘩(鄣xifuxi(x,u(x),ux1(x),… ,uxn(x),… ,uxkxl(x))φ
i=1 Ω
(x)dx
同 理 对 Ⅲ式 运 用 Gauss公 式 及 φ∈C0(Ω), 得
n
-
-
-
-Байду номын сангаас
∑ Ⅲ=蘩 Ω
i,j=1
fuxixj(x
,u
(x
),ux1(x)
-
-
-
L (a) =L ( u +aφ) = 蘩 f (x, u (x) +aφ (x),
鄣[u(x)+aφ(x)]
,…,
Ω
鄣x1
-
鄣[u(x)+aφ(x)]
,…
2-
鄣 [u(x)+aφ(x)]
-
… )dx 即 L (u+aφ) 为 a 的
鄣xn
鄣xi鄣xj
函 数 ,且 当 a=0时 函 数 L(a)取 极 值 .故 有
其中L为拉格朗日量,T为动能,V为势能. 拉格朗日量是动能T 与 势 能 V的 差 值 L=T-V[2].
一个物理系统的拉格朗日函数所构成的泛函的变分问
题 :在 时 间 段 [t1,t2]内 的 一 切 容 许 运 动 中 ,真 实 的 运 动 必 使 L 取 极值对应于寻求泛函的临界点, 在寻找函数的极大、 极小值 时,一个解附近的微小变 化 的 分 析 给 出 一 阶 的 一 个 近 似 [3],借
面拒人千里之外,使人望而生畏,另一方面美丽动人,让人流 连忘返。 数学极其重要的价值正是体现在数学为社会发展和 人类文明进步提供动力,以及许多基础学科、工程技术和整个 社会日益增长的数学文化需求上的。 在这一过程中,数学文化 体现了以下重要特征,可以概括为:数学文化具有相对的稳定 性和连续性,其基本观点、思想方法交叉组合而成的具有丰富 内容和强烈应用价值的技术系统。
关键词: 数学文化 数学教学 渗透策略
数学作为一种文化研究最早出现在西方哲学研究中。 美 国数学家怀尔德受到科学哲学研究发展的启示, 出版了他的 代表作《作为一种文 化 体 系 的 数 学 》[1]。 斯 默 瑞 恩 斯 基 对 其 给 予高度评价, 认为是二十世纪三十年代以来第一个成熟的数 学哲学观[2]。 中国的数学文化作为一种学术研究的内容、作为 一种教学形式, 在二三十年的时间里迅速发展成大学乃至中 学教学中受重视的教学内容, 成为数学教育领域发展比较迅 速的数学分支。 在新课程改革中,数学文化研究的范畴如何界 定? 在新课标下的数学教学中如何渗透数学文化? 本文将从以 下几个方面做探讨。
○ 数学教学与研究 2013年第35期
周刊
欧 拉—拉 格 朗 日 方 程 的 推 广
张露萍
(江西科技学院 公共教学部,江西 南昌 330098)
摘 要: 变分法是处理泛函极值的一种数学方法,欧拉— 拉格朗日方程是基于变分法得到的, 该方程在除数学外的很 多其他领域有着广泛的运用. 如果能将欧拉—拉格朗日方程 的应用范围进一步扩大,即条件减弱或者放松限制条件,就可 以使已有的结论更完善.本文运用变分法,得到更普遍适用的 欧拉—拉格朗日方程.
,…
uxi
,…
,uxjxl,
u … , xmlxm2…xmk
…
)dx
-
-
在 u(x)=u(x)取 极 值 ,则 在 u(x)
n
n
n
∑ ∑ ∑ 2
k
fu- 鄣xifuxi+ 鄣xixjfuxiuxj+(-1)
k
鄣xm1…xmkfuxm1…umk=0.
i=1
i,j=1
m1,…mk=1
参考文献: [1]Fomin,S.V.and Gelfand,I.M.:Calculus of Variations,
i,j=1
-
-
-
-
-
-
鄣xixjfuxiuxj(x,u(x),ux1(x),… ,uxn(x),ux1x1(x),ux1x2(x),uxnxn(x))=0
68
-
证明:设在u=(x)=u(x)时L(u)取 极 值 ,取φ∈C0(Ω),取 绝
-
对 值 分 小 的 a,使 得 u+aφ属 于 容 许 函 数 类 ,则
鄣xifuxi+ 鄣xixjfuxiuxj)φdx=0 i,j=1
由引理,在Ω上恒有
-
-
-
-
-
-
fu (x,u (x),ux1 (x), … ,uxn (x),ux1x1 (x),ux2x2 (x),uxnxn (x))-
∑n
-
-
-
-
-
-
鄣xjfuxi(x,u(x),ux1(x),… ,uxn(x),ux1x1(x),ux2x2(x),uxnxn(x))+
i=1
周刊 2013年第35期 ○ 数学教学与研究
新课标下的高中数学文化渗透
任淑萍 李全林
(甘肃省庆阳第一中学,甘肃 庆阳 745000)
摘 要: 数学文化可以张扬数学思考的魅力,拓展思考 视角,增强思考动力,提升思考品位。 本文对数学文化做了定 位,分析了数学文化的特点,提出了在高中数学教学中渗透数 学文化的策略,对当前的数学教学改革具有现实指导意义。
(x)dx=0,
其
中
f∈C
(Ω),
则 在 Ω上 f≡0[5].
2.主 要 结 论
上述得到的欧拉—拉格朗日方程涉及的是变量的一阶偏
导, 如果L涉及变量的高阶偏导那么上述方程就不适用了.为
了使其运用范围进一步扩大,本文通过运用变分法,得到更普
遍适用的欧拉—拉格朗日方程.
定理1:设f是关于自变量的四次连续可微函数,若
i=1
这里我们采用下述记号,设f为在Ω上定义的连续函数,记
—— —— —— ———— —— —— —
k
f的支集suppf为suppf={x;f(x)≠0}, 记C 为Ω上 定 义 的 直 到k阶
k
k
导数都连续的函数的集合,记C0(Ω)为C (Ω)中其函数的支集
为 包 含 在 Ω内 的 紧 集 的 函 数 的 集 合 [4].fu为 函 数 f 对 变 量 u 的 一 阶
,
…
,uxn
(x),…
,uxkxl
(x)
,
…
)φxixj
∑n
-
-
-
-
(x)dx= 鄣(xifuxixj(x,u(x),ux1(x),… ,uxn(x),… ,uxkxl(x),… )φxj
i,j=1
∑n
-
-
-
-
(x)dx- (鄣xifuxixj(x,u(x),ux1(x),…,uxn(x),…,uxkxl(x),…))φxj
1.数 学 文 化 的 界 定 和 特 点 1.1数 学 文 化 的 界 定 数学科学是以人们的社会生活需要及客观现象为研究对 象。 它作为人类文明的一个组成部分,与一定的社会历史发展 水平相适应;它作为一种文化现象,又受到整个文化结构的影 响。 数学文化是数学史、数学教育、数学哲学和文化学的交叉 领域,它把数学史、数学教育、数学哲学作为一种文化现象进 行分析研究。 与一般文化物相比较,数学对象并非世界中的真 实存在,而是抽象思维的产物。 张楚廷先生的《数学文化》一 书,强调在数学是一种文化的理解下,数学不只是数的世界, 形的世界,或更广阔世界的科学,还是一门充满了人文精神的 科学[3]。 我国著名 数 学 哲 学 教 授 郑 毓 信 对 数 学 文 化 观 念 做 了 描述,数学应主要看成人类的一种活动,一种以数学共同体为 主体,并在一定的文化环境中所从事的创造性活动。 高中数学新课程标准中特别增加了“数学建模”、“探究性 课 题 ”、“数 学 文 化 ”三 个 模 块 ,为 学 生 提 供 了 更 广 阔 的 发 展 空 间,也为改变学生的学习方式提供了素材[4]。 美国数学史学家 莫里斯·克莱因(M·Kline)出版了专著《古今数学思想》、《西 方 文化中的数学》,还有我国的数学哲学家郑毓信先生出版的专 著《数学文化学》,从不同侧面力图增添数学文化的人文色彩, 充分揭示数学的文化内涵,肯定数学作为文化存在的价值,为 数学文化的发展奠定了基础。 1.2数 学 文 化 的 特 点 数学文化具有明显的特点,直接支配着人们的行动。 一方
