用几何画板七步快速绘出太极图
几何画板快速教程概要

几何画板快速教程第八课 变换菜单的使用方法几何画板中画图可以用画图工具,也可以用构造菜单中的作图功能。
另一种作图的方法是运用“变换”工具或“变换”菜单。
在几何画板中变换有“平移”、“旋转”、“缩放”、与“对称”等,在特定的条件下,还可以进行“自定义变换”。
下面分别作一介绍。
1.用变换工具进行作图:用鼠标左键选中选择键,不要松开,这时将出现三个供选择的工具,它们分别是“平移选择”、“旋转选择”、“ 缩放选择”。
图3-1正确使用后两个工具,就可以完成图形的旋转和放缩。
无论是旋转或是放缩,都需要设定旋转中心或缩放中心。
设定中心的方法是在画面内选中一个点,用变换菜单中的“标记中心”功能定义这个点。
然后将选择键的箭头显示转换成“旋转选择”或“缩放选择”,用鼠标选中需要变换的图形,拖动到相应的位置就完成了旋转或放缩。
如图所示,是把三角形进行了旋转。
图3-2 图3-32.用变换菜单进行变换:用鼠标选中变换菜单,下拉可以看到如下的下拉菜单: T 变换 功能标记中心——标记已选择的点为中心标记镜面——标记已选择的线为对称轴标记角度——标记角度已选择的角度标记线段——比标记已选择的两条线段的比值标记向量——标记已选择的线段为向量标记距离——标记已选择的线段的长度平移——将选定的图形按规定方向平移旋转——将选定的图形按标记中心旋转规定的角度缩放——将选定的图形按标记中心缩放规定的比例反射——将选定的图形按标记镜面作轴对称图形迭代——先后作了两个以上的变换后连接几个变换(1)平移:所有的几何对象都可以平移,但轨迹、文字、表格、操作类按钮不能平移。
在这里特别要注意的是轨迹不能平移,若强行平移,会出现不可逆转的错误。
若画图中确实想看到轨迹平移后的效果,可以把生成轨迹的点平移,用平移后的点与原轨迹的路径上的点对应,得到一个新的轨迹,这个轨迹就是原来轨迹平移后的图形。
中心点 中心点当选定了要平移的图形后,用鼠标选中变换菜单中的“平移”工具,得到如下的对话框,里面有三种平移的方式,即按直角坐标向量平移、按极坐标向量平移、按标记的向量平移(只有在事先标记了向量之后,按标记的向量平移才有效)。
(完整版)几何画板教程

几何画板教程第一章用工具作图第一节几何画板的启动和绘图工具的介绍1、启动几何画板:单击桌面左下角的【开始】按钮,选择【所有程序】|【GSP4.05】应用程序后,启动几何画板。
如图1所示,是打开一个几何画板文件的截图。
菜单栏工具框工作区状态栏图1几何画板的窗口是不是和其他Windows应用程序窗口十分类似?有控制菜单、最大/最小化以及标题栏,画板窗口的左侧是画板工具栏,画板的右边和下边可以有滚动条可以使小画板处理更大的图形。
画板的左侧是画板工具箱,把光标移动到工具的上面,一会儿就会显示工具的名称,看看它们分别是什么?它们分别是【选择箭头工具】、【点工具】、【圆规工具】、【直尺工具】、【文本工具】、【自定义画图工具】。
和一般的绘图软件相比,你会不会感觉它的工具是不是少了点?几何画板的主要用途之一是用来绘制几何图形。
而几何图形的绘制,我们通常是用直尺和圆规,它们的配合几乎可以画出所有的欧氏几何图形。
因为任何欧氏几何图形最后都可归结为“点”、“线”、“圆”。
这种公里化作图思想因为“三大作图难题”曾经吸引无数数学爱好者的极大兴趣从而在数学历史上影响重大,源远流长。
从某种意义上讲几何画板绘图是欧氏几何“尺规作图”的一种现代延伸。
因为这种把所有绘图建立在基本元素上的做法和数学作图思维中公里化思想是一脉相承的。
按住工具框的边缘,可随意拖动到画板窗口的任何位置,不同位置形状不同。
试一试,能否拖到某一个地方,工具框变成图2所示的形状?图2顾名思义,猜测一下它们都有何功能?:选择对象这是它的主要功能,当然还有其他:画点可以在画板绘图区任何空白的地方或“线”上画点。
“线”可以是线段、射线、圆、轨迹、函数图像:画圆只能画正圆不能画椭圆,是不是有点遗憾?(几何画板也能画椭圆,请看第二章):画线直尺工具当然用于画线段,还不仅仅如此!:加标注(即说明性的文字)或给对象标标签:自定义工具如果你觉得上述工具不够(如:不能直接画正方形),你可以定义新的工具选择某项绘图工具时,用鼠标单击一下该工具即可。
《几何画板教程》课件

《几何画板教程》课件目录1. 几何画板简介 (2)1.1 什么是几何画板 (3)1.2 几何画板的界面介绍 (4)2. 基本绘图工具 (5)2.1 点、线、圆、弧等基本图形绘制 (7)2.2 图形的编辑与操作 (8)3. 基本变换 (9)3.1 平移、旋转、缩放等基本变换操作 (10)3.2 利用坐标系统进行变换 (11)4. 图形的度量与计算 (12)4.1 测量长度、面积、体积等 (13)4.2 图形的代数运算 (14)5. 几何图形的动画与动态效果 (16)5.1 动画制作基础 (17)5.2 制作动态几何模型 (18)6. 交互式教学功能 (20)6.1 创建交互式课件 (21)6.2 利用教学模板进行教学设计 (22)7. 几何图形的性质与证明 (24)7.1 探究图形的性质 (25)7.2 使用几何画板进行数学证明 (27)8. 几何画板在教学中的应用 (28)8.1 制作几何教学课件 (29)8.2 利用几何画板提高教学效果 (31)9. 几何画板教案设计 (33)9.1 如何设计几何画板教案 (33)9.2 教案示例分析 (35)10. 课程设计与资源整合 (37)10.1 如何整合教学资源 (38)10.2 设计综合性几何画板课程 (39)11. 几何画板常见导致问题及解决方法 (40)11.1 常见导致问题 (40)11.2 解决方法 (41)12. 如何提高学习效率与兴趣 (42)12.1 提高学习效率的技巧 (43)12.2 激发学习兴趣的方法 (44)1. 几何画板简介几何画板是一款强大的数学教学软件,它以直观、生动的方式呈现几何图形,帮助学生更好地理解几何概念。
通过几何画板,用户可以创建、编辑和分析各种几何图形,如点、线、圆、多边形等。
几何画板还支持丰富的几何变换和计算功能,为教师和学生提供了一个便捷的数学工具。
直观易用:几何画板采用图形化界面设计,用户无需编程知识即可轻松上手。
几何画板使用指南

几何画板使用指南
《几何画板使用指南》
嘿呀,今天来给大家讲讲这个几何画板咋用哈!
先来说说我第一次接触几何画板的时候吧,那可真是有点懵圈呀。
我就像个小迷糊似的,看着那些个图标和工具,完全不知道从哪儿下手。
记得有一次,我想要画个三角形,哎呀,我就在那捣鼓半天,不是这里点错了,就是那里拉歪了。
我那个着急呀,心想这玩意儿咋这么难搞呢!但咱可不能轻易放弃呀,我就慢慢摸索,一点点试。
然后我发现呀,要先找到那个画线段的工具,嘿,就那个小图标,点一下,然后在画板上轻轻一拖,一条线段就出来啦。
接着再用同样的方法画另外两条线段,把它们连起来,嘿,一个三角形就有啦!当时我那个高兴呀,就像发现了新大陆似的。
之后呢,我又学会了用几何画板来测量角度呀、长度呀啥的。
每次测量出一个准确的数值,我都觉得特别有成就感。
而且哦,还能在上面进行各种变换,把图形转来转去的,可有意思啦。
总之呀,几何画板就是个很有趣的工具,只要你有耐心,慢慢去琢磨,就能发现它的好多好玩的地方。
大家也赶紧去试试吧,说不定你也会像我一样爱上它呢!哈哈!
哎呀,说了这么多,希望对你们有用呀,拜拜啦!。
几何画板绘制几何图形教程
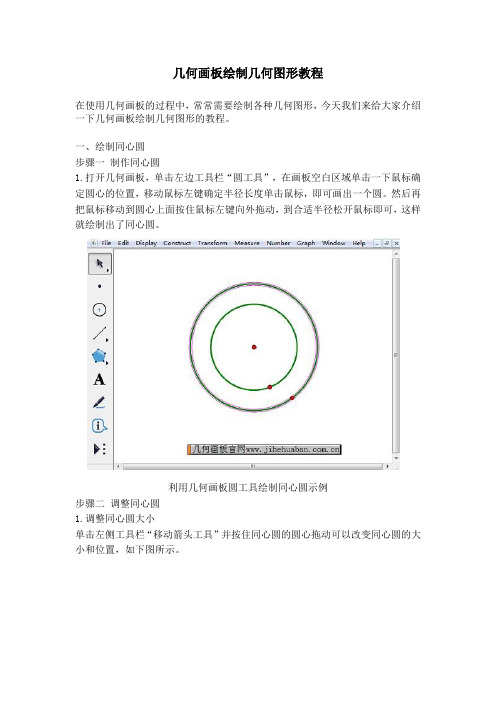
几何画板绘制几何图形教程在使用几何画板的过程中,常常需要绘制各种几何图形,今天我们来给大家介绍一下几何画板绘制几何图形的教程。
一、绘制同心圆步骤一制作同心圆1.打开几何画板,单击左边工具栏“圆工具”,在画板空白区域单击一下鼠标确定圆心的位置,移动鼠标左键确定半径长度单击鼠标,即可画出一个圆。
然后再把鼠标移动到圆心上面按住鼠标左键向外拖动,到合适半径松开鼠标即可,这样就绘制出了同心圆。
利用几何画板圆工具绘制同心圆示例步骤二调整同心圆1.调整同心圆大小单击左侧工具栏“移动箭头工具”并按住同心圆的圆心拖动可以改变同心圆的大小和位置,如下图所示。
在几何画板中调整同心圆示例2.调整大圆大小单击左侧工具栏“移动箭头工具”并按住同心圆大圆边上的红点拖动可以改变大圆的大小和位置,如下图所示。
在几何画板中调整同心圆大圆大小示例3.调整小圆大小单击左侧工具栏“移动箭头工具”并按住同心圆小圆边上的红点拖动可以改变小圆的大小,如下图所示。
在几何画板中调整同心圆小圆大小示例二、绘制三角形比如已知三角形三边长度为3、4、5,具体的绘制步骤如下:1.打开几何画板软件,执行“数据”——“新建参数”,新建参数a=3;b=4;c=5,单位选择“距离”;选中参数a,执行“变换”——“标记距离”。
新建参数a、b、c表示三边距离示例2.使用“点工具”画一个点并选中,然后执行“变换”——“平移”,角度为0,得到另一个点。
以参数a的标记距离平移点示例3.选中上面两点执行“构造”——“线段”命令构造线段,得到定长为3的线段。
构造线段长度为3的线段示例4.选中长度为3的线段一端点和参数b,执行“构造”——“以圆心和半径绘圆”画圆,接着选中线段的另一端点和参数c,执行“构造”——“以圆心和半径绘圆”画圆,两圆交点就是三角形的第三个顶点。
以参数b、c为半径构造两圆得到交点示例5.使用“线段工具”连接线段端点和交点,得到三边长为3,4,5的三角形。
最后隐藏不必要对象即可。
运用几何画板绘制圆锥曲线的十种方法

运用几何画板绘制圆锥曲线的十种方法几何画板可以利用来绘制几何图形,其中最经典的图形就是圆锥曲线。
它是一种圆形曲线,它的特殊性在于它的曲线上可以保持一致的宽度和长度,因此它的外形很漂亮,而且易于控制。
下面就介绍一下,如何运用几何画板绘制圆锥曲线,有十种不同的方法。
1. 使用圆角形状:首先,在几何画板上选择椭圆形状,然后调整圆角形状范围,以达到需要的圆锥曲线。
2. 使用椭圆形状:打开几何画板,选择椭圆形状,将其大小拖拽调整,就可以得到合适的圆锥曲线。
3. 使用多段线:先选择多段线工具,然后在几何画板上通过拖拽,将多段线的每一段拖拽成圆弧的形状,就可以达到圆锥曲线的效果。
4. 使用Bézier曲线:先选择几何画板中的Bézier曲线,然后调整Bézier曲线的控制点,就可以获得想要的圆锥曲线图形。
5. 使用圆弧:将几何画板中的圆弧形状移动到要制作的位置,然后调整圆弧的半径,以绘制任何形状的圆锥曲线。
6. 使用抛物线:选择几何画板中的抛物线工具,然后将抛物线的焦点移动到圆锥曲线所需的位置,就可以绘制出圆锥曲线的形状。
7. 使用圆点:选择几何画板中的圆点工具,然后通过拖拽调整圆点的大小和位置,就可以制作出任何形状的圆锥曲线。
8. 使用多边形:在几何画板中选择多边形工具,然后调整点的位置,拖动顶点,以获得想要的圆锥曲线。
9. 使用齿轮:选择一个合适的大小的齿轮模型,然后在几何画板上调整模型的尺寸,移动齿轮的中心点,就可以得到想要的圆锥曲线。
10. 使用螺旋线:可以先选择几何画板中的螺旋线工具,然后调整螺旋线的曲线度,调整起始点的位置,它就可以变成圆锥曲线了。
上述十种方法,分别介绍了如何运用几何画板绘制圆锥曲线,不管是初学者还是专业设计师,都可以适当选择其中任一种方法快速简便地制作出圆锥曲线。
圆锥曲线多用于图形设计、广告牌设计、影视特效、AI领域等,它给制作各种类型场景增添了许多美感,是受到广泛欢迎的一种设计手法。
几何画板基本操作

几何画板基本操作
1.创建几何图形:首先,在几何画板中选择一个几何图形的绘制工具,比如点、线、圆、多边形等。
然后,在绘图区域点击并拖动鼠标,确定几
何图形的位置和尺寸。
最后,松开鼠标按钮,完成几何图形的创建。
3.添加文本:几何画板还支持在绘图区域添加文本。
你可以选择一个
文本工具,在绘图区域点击并拖动鼠标,确定文本的位置和大小。
然后,
输入想要添加的文本内容,并根据需要调整文本的字体、颜色和样式。
4.绘制图表:几何画板通常还提供了一些绘制常见图表的工具,如条
形图、折线图、饼图等。
你可以选择一个适合的图表工具,在绘图区域点
击并拖动鼠标,确定图表的位置和尺寸。
然后,根据数据输入图表的具体
数值,并选择图表的样式和颜色。
最后,完成绘制并呈现出一个漂亮的图表。
6.图层管理:几何画板通常支持图层的创建和管理,用于对绘制的几
何图形进行分组和层次化管理。
你可以创建多个图层,并为每个图层添加
不同的几何图形。
这样可以方便地控制图形的显示和隐藏,或者修改各个
图层中的几何图形而不影响其他图层的内容。
10.自定义设置:几何画板通常提供一些自定义选项,允许用户根据
自己的需求进行个性化设置。
例如,你可以调整绘图区域的背景颜色、网
格线的间距和颜色,或者设置默认文本字体和大小等。
如何利用《几何画板》作图

如何利用《几何画板》作图在中学数学教学工作中,我们经常会遇到需要画图的情况.笔者以自己在工作中所遇到的实际问题为例,说明如何应用几何画板画出符合要求的图形,并简要说明这些画图方法正确及可行的理论依据. 一 画简单的几何图形 1.按已知条件画几何图形例1.已知:梯形ABCD 中.AD ∥BC .AB=AD+BC .E 是CD 的中点.求证:AE 、BE 分别平分∠BAD 、∠ABC .如图1,我们可以从已知条件出发,按照以下操作步骤,画出符合例1的题意的图形.(1)画出腰AB 和两底所在的射线;(2)在线段AB 上任取一点F ,分别以点A 、B 为圆心,以AF 、BF 长为半径作圆,与两底所在的射线交于点D 、C .显然,AD+BC=AB .(3)取线段CD 的中点E ,连结AE 、BE ;(4)将作图过程中的辅助图形隐藏,即可得到符合题目要求的图形(如图2).FED CBA E D CBAG E D CB AEDCB A图(1) 图(2) 图(3) 图(4)2.从结论出发画几何图形若要证明的命题的逆命题也成立,则可以从结论出发画出几何图形. 仍以例1为例.例1的逆命题是:在梯形ABCD 中,AD ∥BC ,∠DAB 和∠CBA 的平分线交于点E ,点E 恰好在腰CD 上.则:AB=AD+BC ,E 是CD 的中点.显然,∠AEB=90°.如图3,设线段AB 的中点是点G ,连结EG ,则AG=EG ,即:∠AEG=∠EAG=∠EAD .所以AD ∥EG ,因此,CE=DE ,AD+BC=2EG=AB .由于例1的逆命题是真命题,所以我们可以从例1的结论出发画出符合题意的几何图形.画图步骤如下:(1)如图4,画出腰AB 和两底所在的射线; (2)作∠A 和∠B 的角平分线,交于点E ;(3)在一底所在的射线上任取一点C ,作射线CE ,交另一底所在的射线于ED CB A点D ;(4)连结相关线段,并将作图过程中的辅助图形隐藏,即可得到符合题意的图形.从以上例题可以看出,平面几何作图问题通常可以化归为确定某些点的位置的问题.而一个点的位置往往是由两个条件决定的.如果放弃了条件2,让这个点按照条件1而运动起来,即可以生成轨迹1;同样的,如果放弃了条件1,让这个点按照条件2而运动起来,即可以生成轨迹2.轨迹1和轨迹2的交点即为符合题意的点.通常情况下,这个点往往是两条直线的交点,或一条直线与一个圆的交点,或两个圆的交点.这种作图方法叫做轨迹交截法,简称交轨法. 作为练习,读者可以试一试画出符合下题题意的图形.如图5,梯形ABCD 中,∠ADC =90°,∠AEC=3∠BAE ,AB ∥CD ,E 是BC 的中点.求证:CD=CE . 图(5) 二 检验几何命题的正确性有时我们费尽心机地试图证明一个几何命题,结果却发现这是个假命题.我们能否尽力避免这一情况的发生呢?几何画板可以准确快速地画出动态图形,并且在图形的运动变化中保持给定的几何性质不变.因此,我们可以利用几何画板来检验几何命题是否正确.例2.以任意三角形的三条中线为边,可以构成新的三角形.以任意三角形的三条角平分线(或高)为边,能否构成新的三角形呢?用几何画板画图进行验证.如图6,AD 、BE 、CF 分别是△ABC 三个内角的角平分线.以点B 为圆心,以CF 长为半径画圆;以点E 为圆心,AD 长为半径画圆.拖动点A ,改变△ABC 的形状,发现两圆不一定有交点.这说明:以任意三角形的三条角平分线为边,不一定能构成三角形.用类似方法可以验证以任意三角形的三条高为边,不一定能构成三角形(如图7).A BCD EF FEDC BA图(6) 图(7)三 画函数图象1.画定义域为R 的函数的图象例3.画函数y =x 2+3x -2的图象.在几何画板中选择“图表”菜单中的“绘制新函数”命令,然后在弹出的对话框(如图8)中直接输入函数解析式“x^2+3x-2”,再按“确定”按钮,即可以画出函数图象(如图9).图(8)图(9)2.画定义域为限定区间的函数的图象例4.画函数y=x2+3x-2(-4≤x≤1.5)的图象.将鼠标指针移动到上面画出的函数图象上,然后按鼠标右键,选择“属性”命令,在弹出的对话框(如图10)中指定自变量x的取值范围.将x的取值范围改成-4≤x≤1.5后,相应的图象变为如图11所示的一段曲线.图(10)图(11)如果只需要粗略地指定限定区间,可以用鼠标选择函数图象上的箭头,然后按住鼠标左键拖动即可.四画复杂的几何图形1.用自定义工具画图“几何画板”允许用户创建自定义的工具,这使简单图形(如图12)的绘制可以非常快捷,也使绘制由一系列重复的简单图形构成的复杂图形(如图13)成为可能.用户还可以用复杂图形(如图14)创建新的“自定义工具”,从而大大降低绘图工作的劳动强度,节约大量的时间.创建用户自定义工具的方法如下(以创建画正方体的工具为例):(1)在几何画板中画一个正方体(如图12);(2)选择这个正方体的所有顶点和棱;(3)点击几何画板窗体左侧的“自定义工具”按钮,选择“创建新工具”命令;(4)在弹出的对话框(如图15)中将工具名称改为正方体.然后按“确定”按钮.(5)点击几何画板窗体左侧的“自定义工具”按钮,就可以看到新建立的“正方体”画图工具.这样建立的自定义工具存储在当前几何画板文件中,所以只有在当前几何画板文件打开时才能使用.如果要求能在几何画板文件不打开时也能使用存储在其中的自定义工具,必须将这个文件保存在几何画板可执行文件(.exe文件)所在目录的“Tool Folder”子目录中.图(12)图(13)图(14)图(15)2.用“迭代”的方法画图例5.如图16,OA=OB,将线段OA和OB分成n等分,按照图中的方法连结.包络围成的图形是什么?n-2 = 3t1+1()n= 0.2t1+1 = 1t1 = 0n = 5O'BAO图(16)这是一个典型的“参数迭代”构造.操作过程如下:(1)选择“图表”菜单中的“新建参数”命令,新参两个参数n和t1.其初始值分别为5和0.参数t1将作为迭代的初始值;(2)选择“度量”菜单中的“计算”命令,分别计算t1+1、nt11+,n-2.其中t1+1指定迭代的步长为1,nt11+指定缩放比例,n-2指定迭代次数为3.(3)画线段OA 、OB ;(4)双击点O 或选择点O 后再选择“变换”菜单中的“标记中心”命令,将点O 设定为缩放的中心.选择nt 11+,然后选择“变换”菜单中的“标记比值”命令,将nt 11+的值设为缩放参数.图(17) 图(18)(5)选择点A ,然后选择“变换”菜单中的“缩放”命令(如图17),将点A 以点O 为中心,以nt 11+为缩放参数进行缩放,得到点A ’; (6)用同样的方法将点O 以点B 为中心,以nt 11+为缩放参数进行缩放,得到点O ’;(7)连结A ’O ’;(8)依次选择t 1和n -2,然后按住<Shift>键,并选择“变换”菜单中的“带参数的迭代”命令.弹出对话框后,用鼠标选择t 1+1,将它指定为迭代的初象(如图18).(9)按“迭代”按钮退出,即可得到如图16所示的图形.(10)选择n ,然后按“+”或“-”键,可以增大或减小n 的值.图19是当n =20时的图象.O'BAO图(19)五 经典尺规作图题尺规作图问题以其工具的简单、规则的简洁和问题本身的高度挑战性而吸引了无数数学爱好者去研究.三大尺规作图不能问题更成为经典中的经典,时至今日仍不时有人宣称解决了三等分角问题.下面我们也来研究一个经典的尺规作图问题:求作线段AB 的n1(n 是正整数).据报道:1995年夏季学期,美国格林法姆学校的两名相当于中国初中二年级的学生David Goldenheim 和Dan Litchfiled 在完成老师布置的“把一条给定的线段分成任意等份”的几何任务时,发现了“任意等分线段”的新方法,在这以前人们通常采用欧几里德在2500年前所用的方法,他们的构造(已经被命名为GlaD 构造)是“自古以来第二种构造等分的方法”.不仅如此,他们还发现了构造Fibonacci 序列的独创方法.为此,还和他们的辅导老师Dietrich 应邀参加NCTM 的74、75次年会,并应邀在“技术与数学”第12次年会上发言,这也是该会议中的一次邀请学生进行演讲.而这一切并没有使用传统工具直尺和圆规,完全是在GSP 的帮助下完成的.“50%的数学知识是1940年以后出现的,而在这其中99.9%是由博士级的人物发现的.Dan 和David 的发现是非常值得注意的,因为这些发现可以运用中学数学知识通过第三种方法证明:代数、几何、推理.”[1]GlaD 构造的简化画法如下(如图20):F 5F 4F 3F 2B图(20)(1)以线段AB 为一边构造一个矩形ABCD ;(2)连结AC 、BD ,相交于点E 2;(3)过点E 2作E 2F 2⊥AB ,点F 2为垂足,则AF 2=21AB ; (4)连结DF 2,交AC 于点E 3;(5)过点E 3作E 3F 3⊥AB ,点F 3为垂足,则AF 3=31AB ;……依次类推,可以作出线段AB 的4等分点、5等分点……n 等分点. Glad 构造确实简洁精妙,然而将之称为“自古以来的第二种构造等分的方法”未免言过其实.事实上,早在18世纪,数学家白朗松便提出了如下更简洁、漂亮的解法(如图21)[2]:F 5F 4F 32AB图(21)(1)在直线AB 之外任取一点P ,连结AP 、BP ;(2)在线段AP 上任取一点D ,作DC ∥AB ,交BP 于点C ; (3)连结AC 、BD ,相交于点E 2,作射线PE 2交线段AB 于点F 2,则AF 2=21AB ; (4)连结DF 2,交线段AC 于点E 3,作射线PE 3交线段AB 于点F 3,则AF 3=31AB ;……显然,如果点P 位于无限远处,白朗松构造变成了Glad 构造.即Glad 构造是白朗松构造的特例.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
用几何画板七步快速绘出太极图
——找对方法就是快哟
一、打开几何画板程序,菜单栏“绘图”——点“显示网格”和“自动吸附网格”。
工具栏选“点工具”,在网格上任取一点,选“圆工具”以这一点为中心四个单元格为半径,拖动作圆。
二、在工具栏的“自定义工具”中选“圆工具——弓形”,在圆内的两个半径上绘出弓形。
选取两个半径的中点A、B做两个I小圆。
在工具栏的“自定义工具”中选“圆工具——弓形”,以O点为中心大○半径为半径绘出上半部分弓形。
选取全部图形点“显示——线型——中等、实线”。
选中不必要的线段和点按“Ctrl——H”隐藏。
三、选择大弓形,点“构造——弧内部——弓形内部”,填充颜色,右键单击大弓形内,菜单选“颜色——黑色、属性——不透明度——不透明”;选择左边的小弓形,点“构造——弧内部——弓形内部”,填充颜色,右键单击小弓形内,菜单选“颜色——黑色、属性——不透明度——不透明”。
四、点选左边的小圆,点“构造——圆内部”,填充颜色,右键单击小圆内,菜单选“颜色——其它——红色、绿色、蓝色的值全改为255(白色值);属性——不透明度——不透明”
五、选择右边的小弓形,点“构造——弧内部——弓形内部”,填充颜色,右键单击小弓形内,菜单选“颜色——其它——红色、绿色、蓝色的值全改为255(白色值);属性——不透明度——不透明”。
六、点选右边的小圆,点“构造——圆内部”,填充颜色,右键单击小圆内,菜单选“颜色——黑色、属性——不透明度——不透明”。
怎么样图形基本完成了。
七、点“绘图——隐藏网格”,点选轮廓线并选“显示——颜色——黑色“。
大功告成!。
