高考数学柱坐标系和球坐标系
高中数学新人教A版选修4-4 柱坐标系与球坐标系简介

四柱坐标系与球坐标系简介1.柱坐标系(1)定义:建立空间直角坐标系Oxyz .设P 是空间任意一点,它在Oxy 平面上的射影为Q ,用(ρ,θ)(ρ≥0,0≤θ<2π)表示点Q 在平面Oxy 上的极坐标,这时点P 的位置可用有序数组(ρ,θ,z )(z ∈R)表示,这样,我们建立了空间的点与有序数组(ρ,θ,z )之间的一种对应关系,把建立上述对应关系的坐标系叫做柱坐标系,有序数组(ρ,θ,z )叫做点P 的柱坐标,记作P (ρ,θ,z ),其中ρ≥0,0≤θ<2π,z ∈R.(2)空间任意一点P 的直角坐标(x ,y ,z )与柱坐标(ρ,θ,z )之间的变换公式为⎩⎪⎨⎪⎧x =ρcos θ,y =ρsin θ,z =z.2.球坐标系(1)定义:建立空间直角坐标系Oxyz .设P 是空间任意一点,连接OP ,记|OP |=r ,OP 与Oz 轴正向所夹的角为φ,设P 在Oxy 平面上的射影为Q ,Ox 轴按逆时针方向旋转到OQ 时所转过的最小正角为θ.这样点P 的位置就可以用有序数组(r ,φ,θ)表示.这样,空间的点与有序数组(r ,φ,θ)之间建立了一种对应关系,把建立上述对应关系的坐标系叫做球坐标系(或空间极坐标系),有序数组(r ,φ,θ)叫做点P 的球坐标,记作P (r ,φ,θ),其中r ≥0,0≤φ≤π,0≤θ<2π.(2)空间点P 的直角坐标(x ,y ,z )与球坐标(r ,φ,θ)之间的变换关系为⎩⎪⎨⎪⎧x =r sin φcos θ,y =r sin φsin θ,z =r cos φ.[例1] (1)设点A 的直角坐标为(1,3,5),求它的柱坐标. (2)已知点P 的柱坐标为⎝⎛⎭⎫4,π3,8,求它的直角坐标. [思路点拨] 直接利用变换公式求解.[解] (1)由变换公式⎩⎪⎨⎪⎧x =ρcos θ,y =ρsin θ,得ρ2=x 2+y 2,z =z ,即ρ2=12+(3)2=4,∴ρ=2. tan θ=yx =3,又x >0,y >0.∴θ=π3,∴点A 的柱坐标为⎝⎛⎭⎫2,π3,5. (2)由变换公式⎩⎪⎨⎪⎧x =ρcos θ,y =ρsin θ,z =z得x =4cos π3=2,y =4sin π3=23,z =8.∴点P 的直角坐标为(2,23,8).由直角坐标系中的直角坐标求柱坐标,可设点的柱坐标为(ρ,θ,z ),代入变换公式⎩⎪⎨⎪⎧x =ρcos θ,y =ρsin θ,z =z求ρ,也可利用ρ2=x 2+y 2,求ρ.利用tan θ=yx 求θ,在求θ的时候特别注意角θ所在的象限,从而确定θ的值;同理,可由柱坐标转化为直角坐标.1.已知点M 的直角坐标为(0,1,2),求它的柱坐标. 解:ρ=x 2+y 2=02+12=1.∵x =0,y >0,∴θ=π2,∴点M 的柱坐标为⎝⎛⎭⎫1,π2,2. 2.将下列各点的柱坐标分别化为直角坐标. (1)⎝⎛⎭⎫2,π6,1;(2)⎝⎛⎭⎫6,5π3,-2;(3)()1,π,0. 解:设点的直角坐标为(x ,y ,z ). (1)∵(ρ,θ,z )=⎝⎛⎭⎫2,π6,1,∴⎩⎪⎨⎪⎧x =ρcos θ=2cos π6=3,y =ρsin θ=2sin π6=1,z =1,∴(3,1,1)为所求.(2)∵(ρ,θ,z )=⎝⎛⎭⎫6,5π3,-2, ∴⎩⎪⎨⎪⎧x =ρcos θ=6cos 5π3=3,y =ρsin θ=6sin 5π3=-33,z =-2,∴(3,-33,-2)为所求.(3)∵(ρ,θ,z )=(1,π,0),∴⎩⎪⎨⎪⎧x =ρcos θ=cos π=-1,y =ρsin θ=sin π=0,z =0,∴(-1,0,0)为所求.[例2] (1)已知点P 的球坐标为⎝⎛⎭⎫4,3π4, π4,求它的直角坐标; (2)已知点M 的直角坐标为(-2,-2,-22),求它的球坐标. [思路点拨] 直接套用坐标变换公式求解. [解] (1)由坐标变换公式得, x =r sin φcos θ=4sin3π4cos π4=2, y =r sin φsin θ=4sin 3π4sin π4=2,z =r cos φ=4cos 3π4=-22,故其直角坐标为(2,2,-22). (2)由坐标变换公式得,r =x 2+y 2+z 2=(-2)2+(-2)2+(-22)2=4. 由r cos φ=z =-22,得cos φ=-22r =-22,φ=3π4. 又tan θ=y x =1,则θ=5π4(M 在第三象限),从而知M 点的球坐标为⎝⎛⎭⎫4,3π4,5π4.由直角坐标化为球坐标时,可设点的球坐标为(r ,φ,θ),利用变换公式⎩⎪⎨⎪⎧x =r sin φcos θ,y =r sin φsin θ,z =r cos φ求出r ,φ,θ即可;也可以利用r 2=x 2+y 2+z 2,tan θ=y x ,cos φ=zr来求.要特别注意由直角坐标求球坐标时,要先弄清楚φ和θ所在的位置.3.将下列各点的球坐标分别化为直角坐标. (1)⎝⎛⎭⎫2,π6,π3;(2)⎝⎛⎭⎫6,π3,2π3. 解:设点的直角坐标为(x ,y ,z ). (1)∵(r ,φ,θ)=⎝⎛⎭⎫2,π6,π3, ∴⎩⎪⎨⎪⎧x =r sin φcos θ=2sin π6cos π3=12,y =r sin φsin θ=2sin π6sin π3=32,z =r cos φ=2cos π6=3,∴⎝⎛⎭⎫12,32,3为所求.(2)∵(r ,φ,θ)=⎝⎛⎭⎫6,π3,2π3, ∴⎩⎪⎨⎪⎧x =r sin φcos θ=6sin π3cos 2π3=-332,y =r sin φsin θ=6sin π3sin 2π3=92,z =r cos φ=6cos π3=3,∴⎝⎛⎭⎫-332,92,3为所求.4.求下列各点的球坐标.(1)M (1,3,2);(2)N (-1,1,-2). 解:(1)由变换公式得,r =x 2+y 2+z 2=12+(3)2+22=2 2. 由z =r cos φ,得cos φ=z r =222=22,∴φ=π4,又tan θ=y x =31=3,x >0,y >0,∴θ=π3,∴它的球坐标为⎝⎛⎭⎫22,π4,π3. (2)由变换公式得,r =x 2+y 2+z 2=(-1)2+12+(-2)2=2. 由z =r cos φ,得cos φ=z r =-22,∴φ=3π4.又tan θ=y x =1-1=-1,x <0,y >0,∴θ=3π4,∴它的球坐标为⎝⎛⎭⎫2,3π4,3π4.一、选择题1.在球坐标系中,方程r =2表示空间的( ) A .球 B .球面 C .圆D .直线解析:选B r =2,表示空间的点到原点的距离为2,即表示球心在原点,半径为2的球面.2.设点M 的直角坐标为(-1,-3,3),则它的柱坐标是( ) A.⎝⎛⎭⎫2,π3,3 B.⎝⎛⎭⎫2,2π3,3 C.⎝⎛⎭⎫2,4π3,3 D.⎝⎛⎭⎫2,5π3,3 解析:选C ρ=(-1)2+(-3)2=2,∵tan θ=y x =3,x <0,y <0,∴θ=4π3,又z=3,∴点M 的柱坐标为⎝⎛⎭⎫2,4π3,3. 3.若点M 的球坐标为⎝⎛⎭⎫8,π3,5π6,则它的直角坐标为( ) A .(-6,23,4) B .(6,23,4) C .(-6,-23,4)D .(-6,23,-4)解析:选A 由x =8sin π3cos 5π6=-6,y =8sin π3sin 5π6=23,z =8cos π3=4,得点M 的直角坐标为(-6,23,4).4.若点M 的直角坐标为(3,1,-2),则它的球坐标为( ) A.⎝⎛⎭⎫22,3π4,π6 B.⎝⎛⎭⎫22,π4,π6C.⎝⎛⎭⎫22,π4,π3D.⎝⎛⎭⎫22,3π4,π3 解析:选A 设M 的球坐标为(r ,φ,θ),r ≥0,0≤φ≤π,0≤θ<2π,则r =(3)2+12+(-2)2=22, 由22cos φ=-2得φ=3π4, 又tan θ=13=33,x >0,y >0,得θ=π6,∴点M 的球坐标为⎝⎛⎭⎫22,3π4,π6.故选A. 二、填空题5.点P 的柱坐标为⎝⎛⎭⎫4,π6,3,则点P 到原点的距离为________. 解析:x =ρcos θ=4cos π6=23,y =ρsin θ=4sin π6=2.即点P 的直角坐标为(23,2,3),其到原点的距离为(23-0)2+(2-0)2+(3-0)2=25=5.答案:56.点M (-3,-3,3)的柱坐标为________. 解析:ρ=x 2+y 2=(-3)2+(-3)2=32,∵tan θ=-3-3=1,x <0,y <0,∴θ=5π4,∴点M 的柱坐标为⎝⎛⎭⎫32,5π4,3. 答案:⎝⎛⎭⎫32,5π4,3 7.已知点M 的直角坐标为(1,2,3),球坐标为(r ,φ,θ),则tan φ=________,tan θ=________.解析:如图所示,tan φ=x 2+y 2z =53,tan θ=y x =2.答案:532 三、解答题8.设点M 的直角坐标为(1,1,2),求点M 的柱坐标与球坐标. 解:由坐标变换公式,可得ρ=x 2+y 2=2, ∵tan θ=y x =1,x >0,y >0,∴θ=π4.r =x 2+y 2+z 2=12+12+(2)2=2. 由r cos φ=z =2(0≤φ≤π),得cos φ=2r =22,φ=π4. 所以点M 的柱坐标为⎝⎛⎭⎫2,π4,2,球坐标为⎝⎛⎭⎫2,π4,π4. 9.已知点M 的柱坐标为⎝⎛⎭⎫2,π4,3,点N 的球坐标为⎝⎛⎭⎫2,π4,π2,求线段MN 的长度. 解:设点M 的直角坐标为(x ,y ,z ),由变换公式得,x =ρcos θ=2cos π4=1,y =ρsin θ=2sin π4=1,z =3,∴点M 的直角坐标为(1,1,3),设点N 的直角坐标为(a ,b ,c ), 则a =ρsin φ·cos θ=2×22×0=0,b =ρsin φ·sin θ=2×22×1=2,c =ρcos φ=2×22=2,∴点N 的直角坐标为(0,2,2).∴|MN |=12+(1-2)2+(3-2)2=15-8 2.10.已知正方体ABCD -A 1B 1C 1D 1的棱长为1,如图所示建立空间直角坐标系A -xyz ,以Ax 为极轴.求点C 1的直角坐标,柱坐标以及球坐标.解:点C 1的直角坐标为(1,1,1),设点C 1的柱坐标为(ρ,θ,z ),球坐标为(r ,φ,θ),其中ρ≥0,r ≥0,0≤φ≤π,0≤θ<2π,由坐标变换公式⎩⎪⎨⎪⎧x =ρcos θ,y =ρsin θ,z =z ,且⎩⎪⎨⎪⎧x =r sin φcos θ,y =r sin φsin θ,z =r cos φ,得⎩⎪⎨⎪⎧ ρ=x 2+y 2,tan θ=y x (x ≠0),且⎩⎪⎨⎪⎧r =x 2+y 2+z 2,cos φ=z r ,得⎩⎨⎧ρ=2,tan θ=1,且⎩⎪⎨⎪⎧r =3,cos φ=33.结合图形,得θ=π4,由cos φ=33得tan φ= 2.所以点C 1的直角坐标为(1,1,1),柱坐标为⎝⎛⎭⎫2,π4,1,球坐标为⎝⎛⎭⎫3,φ,π4,其中tan φ=2,0≤φ≤π.。
高中数学人教新课标A版选修4-4第一章坐标系1.1.6柱坐标系与球坐标系课件2

3.坐标系是联系数与形的桥梁,利用坐标系可以实现几何
问题与代数问题的相互转化.但不同的坐标系有不同的特点,
在实际应用时,要根据问题的特点选择适当的坐标系,使
研究过程方便、简捷.
提高训练
设地球的半径为R,在球坐标系中,点A的坐标为(R,45°,
70°),点B的坐标为(R,45°,160°),求A,B两点间的球
故点 M 的柱坐标为
π
1, ,5
2
2
.
[A
基础达标]
5π
4, ,3
1.点 P 的柱坐标是
4
,则其直角坐标为(
)
A . 2 2,2 2,3
B . -2 2,2 2,3
C . -2 2,-2 2,3
D . 2 2,-2 2,3
5π
5π
解析:选 C.x=ρcos θ=4cos
=-2 2,y=ρsin θ=4sin
π
6
.故点 M 的球坐标为 2 2, ,
6
7π
4
.
B基础训练达标
4.已知点
则|P1P2|=(
π 5π
π
P1 的球坐标为4, 2, 3 ,P2 的柱坐标为2, 6,1,
)
A. 21
B. 29
C. 30
D.4 2
解析:选 A.设点 P1 的直角坐标为(x1,y1,z1),
数学选修4-4:坐标系与参数方程
第一章 坐标系
1.1.6 柱坐标系与球坐标系
学习目标
思维脉络
1.了解在柱坐标系、
球坐标系中刻画空间 柱坐标系与球坐标系
柱坐标系和球坐标系

上一页
返回首页
下一页
图 1-5-2
如图 1-5-2 所示,设 z 轴的正向与向量O→M的夹角为 φ,x 轴的正向与O→M0的 夹角为 θ,M 点到原点 O 的距离为 r,则由三个数 r,θ,φ 构成的有序数组 (r,θ,φ)称为空间中点 M 的球坐标.若设投影点 M0 在 xOy 平面上的极坐标为(ρ, θ),则极坐标 θ 就是上述的第二个球坐标 θ.在球坐标中限定 r≥0,0≤θ<2π, 0≤φ≤π.
则有11= =ρρcsions
θ, θ,
z=1,
解之得,ρ= 2,θ=π4.
因此,点 M 的柱坐标为( 2,π4,1).
上一页
返回首页
下一页
由直角坐标系中的直角坐标求柱坐标,可以先设出点 M 的柱坐标为ρ,θ,
z代入变换公式xy= =ρρcsions
θ, θ,
z=z.
求 ρ;也可以利用 ρ2=x2+y2,求 ρ.利用 tan θ=yx,
∵(r,θ,φ)=(3,53π,56π),
x=rsin φcos θ=3sin56πcos53π=34,
y=rsin φsin θ=3sin56πsin53π=-343,
z=rcos
φ=3cos56π=-3
2
3 .
∴点
M
的直角坐标为(34,-3
4
3,-3
2
3 ).
上一页
返回首页
下一页
类型三 空间点的直角坐标化为球坐标 已知长方体 ABCD-A1B1C1D1 中,底面正方形 ABCD 的边长为 1,
下一页
[质疑·手记] 预习完成后,请将你的疑问记录,并与“小伙伴们”探讨交流: 疑问 1: _____________________________________________________ 解惑: _______________________________________________________ 疑问 2: _____________________________________________________ 解惑: _______________________________________________________ 疑问 3: ______________________________________________________ 解惑: _______________________________________________________
圆柱,圆球坐标系
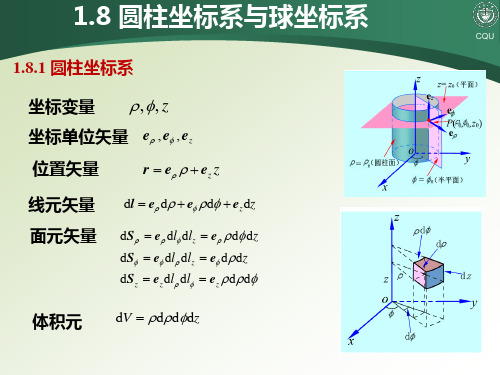
1 ∂ 1 ∂Fφ ∂Fz ∇ ⋅ F (ρ ,φ ,z) = (ρ Fρ ) + + ρ ∂ρ ρ ∂φ ∂z
1
ρ
eρ
eφ ∂ ∂φ ρ Fφ
1
ρ
ez
∇ × F (ρ ,φ ,z )
=
∂ ∂ρ Fρ
∂ ∂z Fz
1.8 圆柱坐标系与球坐标系
CQU
1.8.2 球面坐标系 坐标变量
r ,θ , φ
坐标单位矢量 er , eθ , eφ 位置矢量 线元矢量 面元矢量
= 0, ∂ρ ∂e z = 0, ∂ρ
= −eρ , ∂φ ∂e z = 0, ∂φ
1.8 圆柱坐标系与球坐标系
CQU
圆柱坐标系中的三度表达式
∇ = eρ
∇f =
∂ 1 ∂ ∂ + eφ + ez ∂ρ ρ ∂φ ∂z
∂f 1 ∂f ∂f eρ + eφ + ez ∂ρ ρ ∂φ ∂z
(ρ ≠ 0)
e ρ = cos φ e x + sin φ e y eφ = −sin φ e x + cosφ e y
∂e ρ ∂ρ ∂eφ = 0, ∂e ρ ∂φ ∂eϕ = eφ , =0 ∂z ∂eφ = 0 ∂z ∂e z =0 ∂z ∂e ρ
eρ、eφ、ez对坐标ρ、φ、z求偏导 求偏导
1.8 圆柱坐标系与球坐标系
1.8.1 圆柱坐标系 坐标变量
1
CQU
ρ ,φ , z
r = eρ ρ + ez z
dl = eρ dρ + eφ ρ dφ + e z dz
坐标单位矢量 eρ , eφ , e z 位置矢量 线元矢量 面元矢量
柱坐标系和球坐标系

§3柱坐标系和球坐标系1.柱坐标系如图1-3-1,建立空间直角坐标系O -xyz .设M (x ,y ,z )为空间一点,并设点M 在xOy 平面上的投影点P 的极坐标为(r ,θ),则这样的三个数r ,θ,z 构成的有序数组(r ,θ,z )就叫作点M 的柱坐标,这里规定r ,θ,z 的变化范围为0≤r <+∞,0≤θ<2π,-∞<z <+∞.图1-3-1特别地,r =常数,表示的是以z 轴为轴的圆柱面;θ=常数,表示的是过z 轴的半平面; z =常数,表示的是与xOy 平面平行的平面. 2.球坐标系设M (x ,y ,z )为空间一点,点M 可用这样三个有次序的数r ,φ,θ来确定,其中r 为原点O 到点M 间的距离,φ为有向线段OM →与z 轴正方向所夹的角,θ为从z 轴正半轴看,x 轴正半轴按逆时针方向旋转到有向线段O P →的角,这里P 为点M 在xOy 平面上的投影(如图1-3-2).这样的三个数r ,φ,θ构成的有序数组(r ,φ,θ)叫作点M 的球坐标,这里r ,φ,θ的变化范围为0≤r <+∞,0≤φ≤π,0≤θ<2π.图1-3-2特别地,r =常数,表示的是以原点为球心的球面;φ=常数,表示的是以原点为顶点,z 轴为轴的圆锥面; θ=常数,表示的是过z 轴的半平面. 3.空间中点的坐标之间的变换公式设空间一点M 的直角坐标为(x ,y ,z ),柱坐标为(r ,θ,z ),球坐标为(r ,φ,θ),则1.空间中点的三种坐标各有何特点?【提示】 设空间中点M 的直角坐标为(x ,y,z ),柱坐标为(r ,θ,z ),球坐标为(r ,φ,θ),它们都是有序数组,但意义不同.直角坐标为三个实数;柱坐标分别表示距离、角、实数;球坐标分别表示距离、角、角.2.在空间的柱坐标系中,方程r =r 0(r 0为不等于0的常数),θ=θ0,z =z 0分别表示什么图形?【提示】 在空间的柱坐标系中,方程r =r 0表示中心轴为z 轴,底半径为r 0的圆柱面,它是上述圆周沿z 轴方向平行移动而成的.方程θ=θ0表示与zOx 坐标面成θ0角的半平面.方程z =z 0表示平行于xOy 坐标面的平面,如图所示.常把上述的圆柱面、半平面和平面称为柱坐标系的三族坐标面. 3.在空间的球坐标系中,方程r =r 0(r 0为正常数),θ=θ0(0≤θ0<2π),φ=φ0(0≤φ0<π),各表示什么图形?【提示】 在空间的球坐标系中,方程r =r 0(r 0为正常数),表示球心在原点,半径为r 0的球面;方程θ=θ0(0≤θ0<2π),表示过z 轴的半平面,它与zOx 坐标面的夹角为θ0;方程φ=φ0(0≤φ0≤π),表示顶点在原点,半顶角为φ0的圆锥面,它的中心轴是z 轴,φ0<π2时它在上半空间,φ0>π2时它在下半空间,φ0=π2时它是xOy 平面(如图所示).根据下列点的柱坐标,分别求直角坐标:(1)(2,5π6,3);(2)(2,π4,5). 【思路探究】柱坐标――→x =r cos θy =r sin θz =z直角坐标 【自主解答】 设点的直角坐标为(x ,y ,z ). (1)∵(r ,θ,z )=(2,5π6,3),∴⎩⎪⎨⎪⎧x =r cos θ=2cos 5π6=-3,y =r sin θ=2sin 5π6=1,z =3,∴(-3,1,3)为所求.(2)∵(r ,θ,z )=(2,π4,5),∴⎩⎪⎨⎪⎧x =r cos θ=2cos π4=1,y =r sin θ=2sin π4=1,z =5,∴(1,1,5)为所求.点(r ,θ,z )是三维空间坐标系中的点的坐标,在平面xOy 内实际为极坐标系,且r ≥0,0≤θ<2π,在竖直方向上,z 为任意实数.化点的柱坐标(r ,θ,z )为直角坐标(x ,y ,z ),需要运用公式⎩⎪⎨⎪⎧x =r cos θy =r sin θz =z 转化为三角函数的求值与运算即得.将下列各点的柱坐标分别化为直角坐标: (1)(2,π6,1);(2)(1,π,0).【解】 设点的直角坐标为(x ,y ,z ), (1)∵(r ,θ,z )=(2,π6,1),∴⎩⎪⎨⎪⎧x =r cos θ=2cos π6=3,y =r sin θ=2sin π6=1,z =1,∴(3,1,1)为所求.(2)∵(r ,θ,z )=(1,π,0), ∴⎩⎪⎨⎪⎧x =r cos θ=cos π=-1,y =r sin θ=sin π=0,z =0,∴(-1,0,0)为所求.把下列各点的球坐标化为直角坐标.(1)(2,34π,54π);(2)(6,π3,π6). 【思路探究】球坐标――→x =r sin φcos θy =r sin φsin θz =r cos φ直角坐标【自主解答】 设点的直角坐标为(x ,y ,z ), (1)∵(r ,φ,θ)=(2,3π4,5π4),∴⎩⎪⎨⎪⎧x =r sin φcos θ=2sin 3π4cos 5π4=-1,y =r sin φsin θ=2sin 3π4sin 5π4=-1,z =r cos φ=2cos 3π4=-2,∴(-1,-1,-2)为所求. (2)∵(r ,φ,θ)=(6,π3,π6),∴⎩⎪⎨⎪⎧x =r sin φcos θ=6sin π3cos π6=364,y =r sin φsin θ=6sin π3sin π6=324,z =r cos φ=6cos π3=62,∴(364,324,62)为所求.首先要明确点的球坐标(r ,φ,θ)中角φ,θ的边与数轴Oz ,Ox 的关系,注意各自的限定范围,即0≤φ≤π,0≤θ<2π.化点的球坐标(r ,φ,θ)为直角坐标(x ,y ,z ),需要运用公式⎩⎪⎨⎪⎧x =r sin φcos θ,y =r sin φsin θ,z=r cos φ转化为三角函数的求值与运算.将下列各点的球坐标分别化为直角坐标: (1)(6,π3,23π);(2)(3,π,π). 【解】 设点的直角坐标为(x ,y ,z ) (1)∵(r ,φ,θ)=(6,π3,2π3),∴⎩⎪⎨⎪⎧x =r sin φcos θ=6sin π3cos 2π3=-332,y =r sin φsin θ=6sin π3sin 2π3=92,z =r cos φ=6cos π3=3,∴(-332,92,3)为所求. (2)∵(r ,φ,θ)=(3,π,π),∴⎩⎪⎨⎪⎧x =r sin φcos θ=3sin πcos π=0,y =r sin φsin θ=3sin πsin π=0,z =r cos φ=3cos π=-3,∴(0,0,-3)为所求.坐标图1-3-3已知正方体ABCD -A 1B 1C 1D 1的棱长为1,如图1-3-3,建立空间直角坐标系A -xyz ,以Ax 为极轴,求点C 1的直角坐标、柱坐标以及球坐标.【思路探究】 先求C 1的直角坐标,再根据柱坐标、球坐标与直角坐标的关系,求得其柱坐标、球坐标.【自主解答】 点C 1的直角坐标为(1,1,1).设点C 1的柱坐标为(r ,θ,z ),球坐标为(r ,φ,θ),其中r ≥0,r ≥0,0≤φ≤π,0≤θ<2π.由公式⎩⎪⎨⎪⎧x =r cos θ,y =r sin θ,z =z及⎩⎪⎨⎪⎧x =r sin φcos θ,y =r sin φsin θ,z =r cos φ,得⎩⎨⎧r =x 2+y 2,tan θ=yx (x ≠0),及⎩⎨⎧r =x 2+y 2+z 2,cos φ=z r ,得⎩⎪⎨⎪⎧r =2,tan θ=1,及⎩⎨⎧r =3,cos φ=33,结合图形,得θ=π4, 由cos φ=33得tan φ= 2.所以点C 1的直角坐标为(1,1,1),柱坐标为(2,π4,1),球坐标为(3,φ,π4),其中tan φ=2,0≤φ≤π.化点M 的直角坐标(x ,y ,z )为柱坐标(r ,θ,z )或球坐标(r ,φ,θ),需要对公式⎩⎪⎨⎪⎧x =r cos θy =r sin θz =z以及⎩⎪⎨⎪⎧x =r sin φcos θy =r sin φsin θz =r cos φ进行逆向变换,得到⎩⎪⎨⎪⎧r =x 2+y 2tan θ=yx(x ≠0)z =z以及⎩⎨⎧r =x 2+y 2+z 2,cos φ=zr .提醒在由三角函数值求角时,要结合图形确定角的范围再求值.若本例中条件不变,求点C 、D 的柱坐标与球坐标.【解】 结合图形知点C 的直角坐标为(1,1,0),柱坐标为(2,π4,0),球坐标为(2,π2,π4),同样点D的直角坐标为(0,1,0),柱坐标为(1,π2,0),球坐标为(1,π2,π2).(教材第22页练习第1题)如图1-3-4,把边长为1个单位长度的正方体分别放到空间直角坐标系中的不同位置,试说出正方体各个顶点的柱坐标和球坐标.图1-3-4(2013·镇江模拟)结晶体的基本单位称为晶胞,如图1-3-5是食盐晶胞的示意图(可看成是八个棱长为12的小正方体堆积成的正方体).图形中的点代表钠原子,如图1-3-6,建立空间直角坐标系O —xyz 后,试写出下层钠原子所在位置的球坐标、柱坐标.图1-3-5图1-3-6【命题意图】 本题以食盐晶胞为载体,主要考查柱坐标系及球坐标系在确定空间点的位置中的应用.【解】 下层的原子全部在xOy 平面上,它们所在位置的竖坐标全是0,所以这五个钠原子所在位置的球坐标分别为(0,0,0),(1,π2,0),(2,π2,π4),(1,π2,π2),(22,π2,π4);它们的柱坐标分别为(0,0,0),(1,0,0),(2,π4,0),(1,π2,0),(22,π4,0).1.要刻画绕地球运转的某气象卫星的位置,应适合运用( ) A .极坐标系 B .空间直角坐标系 C .柱坐标系D .球坐标系【解析】 由题意知D 正确. 【答案】 D2.已知点A 的柱坐标为(1,0,1),则点A 的直角坐标为( )A .(1,1,0)B .(1,0,1)C .(0,1,1)D .(1,1,1)【解析】 由点A 的柱坐标为(1,0,1)知,r =1,θ=0,z =1, 故x =r cos θ=1,y =r sin θ=0,z =1,所以直角坐标为(1,0,1). 【答案】 B3.已知点A 的球坐标为(3,π2,π2),则点A 的直角坐标为( ) A .(3,0,0) B .(0,3,0) C .(0,0,3)D .(3,3,0)【解析】 ∵x =3×sin π2×cos π2=0,y =3×sin π2×sin π2=3,z =2×cos π2=0,∴直角坐标为(0,3,0).故选B. 【答案】 B4.设点M 的直角坐标为(1,1,2),则点M 的柱坐标为________,球坐标为________.【解析】 由坐标变换公式,可得ρ=x 2+y 2=2,tan θ=y x =1,θ=π4(点(1,1)在平面xOy 的第一象限),r =x 2+y 2+z 2=12+12+(2)2=2. 由r cos φ=z =2, 得cos φ=2r =22,φ=π4.∴点M 的柱坐标为(2,π4,2),球坐标为(2,π4,π4). 【答案】 (2,π4,2) (2,π4,π4)一、选择题1.在空间球坐标系中,方程r =2(0≤φ≤π2,0≤θ<2π)表示( ) A .圆 B .半圆 C .球面 D .半球面【解析】 由球坐标系的定义知,r =2(0≤φ≤π2,0≤θ<2π)表示半球面,故选D.【答案】 D2.设点M 的直角坐标为(-1,-3,3),则它的柱坐标是( ) A .(2,π3,3) B .(2,2π3,3)C .(2,4π3,3)D .(2,5π3,3)【解析】 ∵r =(-1)2+(-3)2=2,θ=4π3,z =3,∴M 的柱坐标为(2,4π3,3),故选C. 【答案】 C3.设点M 的直角坐标为(-1,-1,2),则它的球坐标为( ) A .(2,π4,π4) B .(2,π4,5π4) C .(2,5π4,π4) D .(2,3π4,π4)【解析】 由坐标变换公式,得r =x 2+y 2+z 2=2,cos φ=zr =22,∴φ=π4.∵tan θ=y x =-1-1=1,∴θ=54π,∴M 的球坐标为(2,π4,54π),故选B. 【答案】 B4.已知点M 的球坐标为(4,π4,3π4),则点M 到Oz 轴的距离为( ) A .2 2 B. 2 C .2 D .4【解析】 设点M 的直角坐标为(x ,y ,z ), ∵(r ,φ,θ)=(4,π4,3π4),∴⎩⎪⎨⎪⎧x =r sin φcos θ=4sin π4cos 3π4=-2,y =r sin φsin θ=4sin π4sin 3π4=2,z =r cos φ=4cos π4=22,∴M (-2,2,22),到Oz 轴的距离为(-2)2+22=2 2.故选A. 【答案】 A 二、填空题5.若点M 的球坐标为(3,5π6,5π3),则点M 的直角坐标为________. 【解析】 设M 的直角坐标为(x ,y ,z )则⎩⎪⎨⎪⎧x =r sin φcos θ=3sin 5π6cos 5π3=34,y =r sin φsin θ=3sin 5π6sin 5π3=-334,z =r cos φ=3cos 5π6=-332.∴点M 的直角坐标为(34,-334,-332). 【答案】 (34,-334,-332)6.(2013·长春检测)在柱坐标系中,点M 的柱坐标为(2,23π,5),则|OM |=________.【解析】 设点M 的直角坐标为(x ,y ,z ). 由(r ,θ,z )=(2,23π,5)知x =r cos θ=2cos 23π=-1, y =2sin 23π= 3. 因此|OM |=x 2+y 2+z 2 =(-1)2+(3)2+(5)2=3. 【答案】 3 三、解答题7.已知点P 的柱坐标为(2,π4,5),点B 的球坐标为(6,π3,π6),求这两个点的直角坐标.【解】 设点P 的直角坐标为(x ,y ,z ), 则x =2cos π4=2×22=1, y =2sin π4=1,z =5.设点B 的直角坐标为(x ,y ,z ),则x =6sin π3cos π6=6×32×32=364, y =6sin π3sin π6=6×32×12=324, z =6cos π3=6×12=62.所以点P 的直角坐标为(1,1,5),点B 的直角坐标为(364,324,62). 8.经过若干个固定和流动的地面遥感观测站监测,并通过数据汇总,计算出一个航天器在某一时刻的位置,离地面2 384千米,地球半径为6 371千米,此时经度为80°,纬度为75°.试建立适当的坐标系,确定出此时航天器点P 的坐标.【解】 在赤道平面上,选取地球球心为极点,以O 为原点且与零子午线相交的射线Ox 为极轴,建立球坐标系.由已知航天器位于经度为80°,可知θ=80°=49π.由航天器位于纬度75°,可知,φ=90°-75°=15°=π12,由航天器离地面2 384千米,地球半径为6 371千米,可知r =2 384+6 371=8 755千米.所以点P 的球坐标为(8 755,π12,4π9).9.在柱坐标系中,求满足⎩⎪⎨⎪⎧r =1,0≤θ<2π0≤z ≤2,的动点M (r ,θ,z )围成的几何体的体积.【解】 根据柱坐标系与点的柱坐标的意义可知,满足r =1,0≤θ<2π,0≤z ≤2的动点M (r ,θ,z )的轨迹如图所示,是以直线Oz 为轴,轴截面为正方形的圆柱.圆柱的底面半径r =1,h =2. 所以V =Sh =πr 2h =2π.教师备选10.已知在球坐标系Oxyz 中,M (6,π3,π3),N (6,2π3,π3),求|MN |. 【解】 法一 由题意知,|OM |=|ON |=6,∠MON =π3, ∴△MON 为等边三角形,∴|MN |=6. 法二 设M 点的直角坐标为(x ,y ,z ),则⎩⎪⎨⎪⎧x =6sin π3cos π3=332,y =6sin π3sin π3=92,z =6cos π3=3.故点M 的直角坐标为(332,92,3), 同理得点N 的直角坐标为(332,92,-3), ∴|MN |=(323-323)2+(92-92)2+(3+3)2=0+0+62=6.。
人教版高中数学选修4-4《1.4柱坐标系与球坐标系简介》

φ r o θ
P(r,φ,θ) y Q
x OP与Oz轴正向所夹的角为φ
转过的最小正角为θ
Ox轴按逆时针方向旋转到OQ时所
点P的位置可以用有序数组(r,φ,θ)表示 我们把建立上述对应关系的坐标系叫 球坐标系(或空间极坐标系) 有序数组(r,φ,θ)叫做点P的球坐标
其中 r 0, 0 , 0 2
5 5 3 点M的直角坐标为(- , ) 2 2
如图,建立空间直角坐标系Oxyz, z 设P是空间任意一点, P(ρ,θ,Z) p在平面Oxy的射影为Q o θ Q x 用(ρ,θ)(ρ≥0,0≤θ<2π)表示点Q 在平面Oxy上的极坐标,
y
点P的位置可用有序数组(ρ,θ,Z)表示
把建立上述对应关系的坐标系叫做 柱坐标系.
空间点P的直角坐标(x, y, z)与球坐标
(r,φ,θ)之间的变换关系为
x r sin cos y r sin sin z r cos
3、已知点 N的球坐标是(2, , ), 3 4 求它的直角坐标。
3
1、通过这节课的学习, 我们知道, 为了表示空间中所有的 点,我们可 以建立 _______________________ 、 ______________ 和 ______________ 来表示这些点。
2、这节课我们需要了解 的内容有:
谢谢
有序数组(ρ,θ,Z)叫点P的柱坐标.
其中ρ≥0, 0≤θ<2π, -∞<Z<+∞
注:柱坐标系又称半极坐标系,它是由 平面极坐标系及空间直角坐标系中的 一部分建立z)与柱坐标
(ρ,θ,Z)之间的变换关系为
x cos y sin zz
高中数学第一章坐标系1.3柱坐标系和球坐标系课件北师大选修4_4 (1)

������ = ������sin������, ������ = ������.
在柱坐标(ρ,θ,z)中,ρ=|OA|= |������������|2 + |������������|2 = ������2 + ������2, ������ =∠
POA,其中 x,y,z 的值与直角坐标中的相同.在球坐标(r,φ,θ) 中,r=|OM|= |������������|2 + |������������|2 = ������2 + ������2 + ������2, ������ =∠ROM,θ=∠ POA,其中 θ 与柱坐标中的 θ 相同,x,y,z 的值与直角坐标中的相同.
-1 = ������cos������,
������ = ������
【例1】 将点M的直角坐标化为柱坐标,将点P的柱坐标化为直
角坐标.
(1)M(-1, 3, 2); (2)������ 2,π4 ,1 .
分析:利用相关公式代入进行转化求值.
������ = ������cos������, 解:(1)设点 M 的柱坐标为(r,θ,z),则有 ������ = ������sin������,
特别地,r=常数,表示的是以原点为球心的球面; φ=常数,表示的是以原点为顶点,z轴为轴的圆锥面; θ=常数,表示的是过z轴的半平面. 点M的直角坐标与球坐标的关系为
������ = |������������|cos������ = ������sin������cos������,
圆柱坐标系和球坐标系

圆柱坐标系和球坐标系球坐标系的定义:球坐标是三维坐标系的一种,用以确定三维空间中点、线、面以及体的位置,它以坐标原点为参考点,由方位角、仰角和距离构成。
假设P(x,y,z)为空间内一点,则点P也可用这样三个有次序的数r,θ,φ来确定,其中r为原点O与点P间的距离,r∈[0,+∞)θ为有向线段OP与z轴正向的夹角,θ∈[0,π]φ为从正z轴来看自x轴按逆时针方向转到OM所转过的角,φ∈[0,2π]这里M为点P在xOy面上的投影。
这样的三个数r,φ,θ叫做点P的球面坐标。
当r,θ或φ分别为常数时,可以表示如下特殊曲面:r = 常数,即以原点为心的球面;θ= 常数,即以原点为顶点、z轴为轴的圆锥面;φ= 常数,即过z轴的半平面。
球坐标系与直角坐标系间的转换1).球坐标系(r,θ,φ)与直角坐标系(x,y,z)的转换关系:x= r sinθ cosφy= r sinθsinφz = r cosθ球坐标系下的微分关系在球坐标系中,沿基矢方向的三个线段元为:dl(r)=dr,dl(θ)=rdθ,dl(φ)=rsinθdφ球坐标的面元面积是:dS=dl(θ)* dl(φ)=r^2*sinθdθdφ体积元的体积为:dV=dl(r)*dl(θ)*dl(φ)=r^2*sinθdrdθdφ圆柱坐标系的定义:它是二维极坐标系往z-轴的延伸。
添加的第三个坐标专门用来表示P点离xy-平面的高低。
按照国际标准化组织建立的约定(ISO 31-11) ,径向距离、方位角、高度,分别标记为。
如图右,P 点的圆柱坐标是。
是P 点与z-轴的垂直距离。
是线OP 在xy-面的投影线与正x-轴之间的夹角。
与直角坐标的等值。
圆柱坐标系与直角坐标系间的转换1).圆柱坐标系(r,φ,z)与直角坐标系(x,y,z)的转换关系:x=r co sφy=r sinφz=z圆柱坐标系下的微分关系在球坐标系中,沿基矢方向的三个线段元为:dl(r)=dr,dl(φ)=rdφ,dl(z)= dz球坐标的面元面积是:dS=dl(θ)* dl(z)=r dφ dz体积元的体积为:dV=dl(r)*dl(φ)*dl(z)=r dr dφ dz。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
自主预习
讲练互动
课堂达标
教材链接
1.将下列各点的柱坐标化为直角坐标.
π 2 P2,6,1,Q4,3π,-3
解
x=ρcos θ 直接代入互化公式y=ρsin θ , z=z
可得 P 的直角坐标为( 3,1,1),Q 点的直角 坐标为(-2,2 3,-3).
§3 柱坐标系和球坐标系
自主预习
讲练互动
课堂达标
教材链接
1.柱坐标系
(1)定义:在平面极坐标系的基础上,通过极点O,再增加 一条与极坐标系所在平面垂直的z轴,这样就建立了柱坐 标系.设M(x,y,z)为空间一点,并设点M在xOy平面上的 投影点P的极坐标为(r,θ),则这样的三个数r,θ,z构成 (r,θ,z)就叫作点M的柱坐标 的有序数组________ ______,这里规定r,θ, 0≤r<+∞,________ 0≤θ<2π, -∞<z<+∞ . z的变化范围为__________ 特别地,r=常数,表示的是以z轴为轴的圆柱面;θ=常 数,表示的是 过z轴的半平面 xOy平面平行的平面 .
;
φ=常数,表示的是以原点为顶点,z轴为轴的圆锥面;
(2)空间点P的直角坐标(x,y,z)与球坐标(r,φ,θ)之间 的变换关系为
sin φ· cos θ, x=r· sin φ· sin θ, y=r· z=rcos φ.
自主预习
讲练互动
课堂达标
教材链接
【思维导图】
自主预习
讲练互动
自主预习
讲练互动
课堂达标
教材链接
【反思感悟】 写空间任一点的球半径,就是 求该点到点O的距离和方位角、高低角.两个角 可以和地球的经纬度相结合,要搞清它们的联
系和区别.
自主预习
讲练互动
课堂达标
教材链接
2.在赤道平面上,我们选取地球球心 O 为极点,以 O 为端点且与零子午线相交的射线 Ox 为极轴,建 立坐标系.有 A, B 两个城市, 它们的球坐标分别为
纬度为75°.试建立适当的坐标系,确定出此时航天器点P 的坐标.
自主预习
讲练互动
课堂达标
教材链接
解
在赤道平面上, 我们选取地球球心为极点, 以O
为端点且与零子午线相交的射线 Ox 为极轴, 建立平 面极坐标系,在此基础上,取以 O 为端点且经过北 极的射线 Oz(垂直于赤道平面)为另一条极轴,如图 所示建立一个球坐标系 . 由已知航天器位于经度为 80° ,可知 θ=80° ,由航天器位于纬度 75° ,可知,φ =90° -75° =15° ,由航天器离地面 2 384 千米,地 球半径为 6 371 千米,可知 r=2 384+6 371=8 755 千米.所以点 P 的球坐标为(8 755,15° ,80° ).
题型三
空间点的坐标
1.空间直角坐标系中点的坐标是由横坐标、 纵坐标和竖坐标三 度来确定的,即(x,y,z). 2.空间点的柱坐标是由平面极坐标系及空间直角坐标系中的 竖坐标组成的,即(ρ,θ,z). 3.(1)空间点的球坐标是点和原点的连线与 x 轴正方向所成的 角 θ,与 z 轴的正方向所成的角 φ,以及点到原点的距离 r 组成的,即(r,φ,θ). (2)注意球坐标的顺序为:①到原点的距离 r;②与 z 轴正方 向所成的角 φ;③与 x 轴正方向所成的角 θ.
自主预习
;z=常数,表示的是与
讲练互动
课堂达标
教材链接
(2)空间点 M 的直角坐标(x,z)与柱坐标(ρ,
x=ρcos θ, y=ρsin θ, z=z. θ,z)之间的变换公式为_____________.
自主预习
讲练互动
课堂达标
教材链接
2.球坐标系
(1)定义:设 M(x,y,z)为空间一点,点 M 可用这样三个有 次序的数 r,φ,θ 来确定,其中 r 为原点 O 到点 M 间的距 → 离,φ 为有向线段OM与 z 轴正方向所夹的角,θ 为从 z 轴正 → 半轴看,x 轴正半轴按逆时针方向旋转到有向线段OP的角, 这里 P 为点 M 在 xOy 平面上的投影.这样的三个数 r,φ,θ
π π π 2π AR,4,6,BR,4, 3 ,飞机应该走怎样的航
线最快,所走的路程有多远?
自主预习
讲练互动
课堂达标
教材链接
解 由题意可知面 AOO1,面 BOO1 都垂直于两圆平面, ∴∠AO1B 是两平面 AOO1 和 BOO1 的夹角,
π π π 2π 又∵AR,4,6,BR,4, 3 ,
自主预习
讲练互动
课堂达标
教材链接
【例1】 柱坐标满足方程ρ=2的点所构成的图形是什么?
解 在平面极坐标系中,ρ=2表示以极点为圆心,2为半径
的圆.因此,在柱坐标系中,设Oz轴所在的直线为l,则方程 ρ=2表示以l为轴,且垂直于轴的截面是半径为2的圆柱面. 【反思感悟】 柱坐标满足ρ=2的点可以和平面直角坐标系 中满足x=1的点构成一条直线,空间直角坐标系中满足y=2 的点构成的图形是一个平面结合考虑.
2π π π π ∴∠AO1B= 3 -6=2,∠AOO1=∠BOO1=4, 2 ∠AO1O=∠BO1O,∴小圆 O1 的半径 r= 2 R,∴AB=R, π π ∴∠AOB= ,则经过 A、B 两地的球面距离为 R. 3 3 π 故飞机经过 A、B 两地的大圆,航线最短,其路程为 R. 3
自主预习 讲练互动 课堂达标 教材链接
自主预习
讲练互动
课堂达标
教材链接
题型二
球坐标系
球坐标系又称空间极坐标系,用空间任意一点P到O的距离r以 及两个角θ,φ来刻画点P的位置. 【例2】 经过若干个固定和流动的地面遥感观测站监测, 并通过数据汇总,计算出一个航天器在某一时刻离地面2
384千米的位置,地球半径为6 371千米,此时经度为80°,
r,φ,θ 叫作点 M 的_________ 球坐标 , 构成的有序数组(_______) 这里 r, φ, 0≤r<+∞ , 0≤φ≤π , 0 ≤θ<2π 特别地, θ 的变化范围为__________ _________ ________.
自主预习
讲练互动
课堂达标
教材链接
r=常数,表示的是 以原点为球心的球面 θ=常数,表示的是过z轴的半平面 .
课堂达标
教材链接
【知能要点】
1.柱坐标系. 2.球坐标系.
3.空间点的坐标的确定.
自主预习
讲练互动
课堂达标
教材链接
题型一
柱坐标系
柱坐标系又称半极坐标系,它是由平面极坐标系
及空间直角坐标系中的一部分建立起来的. 空间任一点P的位置可以用有序数组(ρ,θ,z)表 示,(ρ,θ)是点P在Oxy平面上的射影Q的极坐标, z是P在空间直角坐标系中的竖坐标.
