最优化计算方法课后习题答案----高等教育出版社。施光燕
最优化方法及其应用课后答案
1 2( ( ⎨最优化方法部分课后习题解答1.一直优化问题的数学模型为：习题一min f (x ) = (x − 3)2 + (x − 4)2⎧g (x ) = x − x − 5 ≥ 0 ⎪ 11 2 2 ⎪试用图解法求出：s .t . ⎨g 2 (x ) = −x 1 − x 2 + 5 ≥ 0 ⎪g (x ) = x ≥ 0 ⎪ 3 1 ⎪⎩g 4 (x ) = x 2 ≥ 0（1） 无约束最优点，并求出最优值。
（2） 约束最优点，并求出其最优值。
（3） 如果加一个等式约束 h (x ) = x 1 −x 2 = 0 ，其约束最优解是什么？ *解 ：（1）在无约束条件下， f (x ) 的可行域在整个 x 1 0x 2 平面上，不难看出，当 x =（3，4） 时， f (x ) 取最小值，即，最优点为 x * =（3，4）：且最优值为： f (x * ) =0（2）在约束条件下， f (x ) 的可行域为图中阴影部分所示，此时，求该问题的最优点就是在约束集合即可行域中找一点 (x 1 ,x 2 ) ，使其落在半径最小的同心圆上，显然，从图示中可以看出，当 x *=15 , 5 ) 时， f (x ) 所在的圆的半径最小。
4 4⎧g (x ) = x −x − 5 = 0⎧ 15 ⎪x 1 = 其中：点为 g 1 (x) 和 g 2 (x ) 的交点，令 ⎪ 1 1 2 ⎨2 求解得到： ⎨ 45即最优点为 x *= ⎪⎩g 2 (x ) = −x 1 −x 2 + 5 = 015 , 5 ) ：最优值为： f(x * ) = 65 ⎪x =⎪⎩ 2 44 48（3）.若增加一个等式约束，则由图可知，可行域为空集，即此时最优解不存在。
2.一个矩形无盖油箱的外部总面积限定为 S ，怎样设计可使油箱的容量最大？试列出这个优化问题的数学模型，并回答这属于几维的优化问题. 解：列出这个优化问题的数学模型为：max f (x ) = x 1x 2 x 3⎧x 1x 2 + 2x 2 x 3 + 2x 1x 3 ≤ S ⎪ s .t . ⎪x 1 > 0⎪x 2 > 0 ⎪⎩x 3 > 0该优化问题属于三维的优化问题。
数学建模B题：人员安排问题
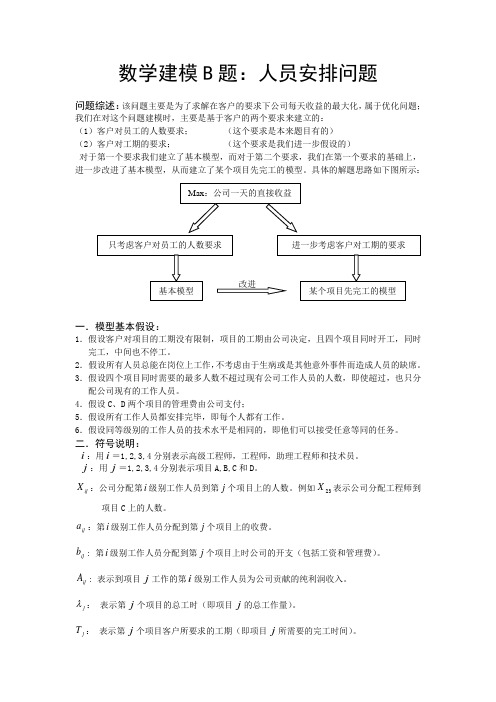
数学建模B 题：人员安排问题问题综述：该问题主要是为了求解在客户的要求下公司每天收益的最大化，属于优化问题；我们在对这个问题建模时，主要是基于客户的两个要求来建立的： （1）客户对员工的人数要求； （这个要求是本来题目有的） （2）客户对工期的要求； （这个要求是我们进一步假设的）对于第一个要求我们建立了基本模型，而对于第二个要求，我们在第一个要求的基础上，进一步改进了基本模型，从而建立了某个项目先完工的模型。
具体的解题思路如下图所示：一．模型基本假设：1．假设客户对项目的工期没有限制，项目的工期由公司决定，且四个项目同时开工，同时完工，中间也不停工。
2． 假设所有人员总能在岗位上工作，不考虑由于生病或是其他意外事件而造成人员的缺席。
3．假设四个项目同时需要的最多人数不超过现有公司工作人员的人数，即使超过，也只分配公司现有的工作人员。
4．假设C 、D 两个项目的管理费由公司支付；5．假设所有工作人员都安排完毕，即每个人都有工作。
6．假设同等级别的工作人员的技术水平是相同的，即他们可以接受任意等同的任务。
二．符号说明：i ：用i ＝1,2,3,4分别表示高级工程师，工程师，助理工程师和技术员。
j ：用j ＝1,2,3,4分别表示项目A,B,C 和D 。
ij X ：公司分配第i 级别工作人员到第j 个项目上的人数。
例如23X 表示公司分配工程师到项目C 上的人数。
ij a ：第i 级别工作人员分配到第j 个项目上的收费。
ij b : 第i 级别工作人员分配到第j 个项目上时公司的开支（包括工资和管理费）。
ij A : 表示到项目j 工作的第i 级别工作人员为公司贡献的纯利润收入。
j ： 表示第j 个项目的总工时（即项目j 的总工作量）。
j T ： 表示第j 个项目客户所要求的工期（即项目j 所需要的完工时间）。
j M ： 表示客户要求第j 个项目一天所必须完成的工作量。
j m ： 表示公司分配给第j 个项目的所有工作人员一天能够完成的工作量。
数学建模B题：人员安排问题
数学建模B 题：人员安排问题问题综述：该问题主要是为了求解在客户的要求下公司每天收益的最大化，属于优化问题；我们在对这个问题建模时，主要是基于客户的两个要求来建立的： （1）客户对员工的人数要求； （这个要求是本来题目有的） （2）客户对工期的要求； （这个要求是我们进一步假设的）对于第一个要求我们建立了基本模型，而对于第二个要求，我们在第一个要求的基础上，进一步改进了基本模型，从而建立了某个项目先完工的模型。
具体的解题思路如下图所示：一．模型基本假设：1．假设客户对项目的工期没有限制，项目的工期由公司决定，且四个项目同时开工，同时完工，中间也不停工。
2． 假设所有人员总能在岗位上工作，不考虑由于生病或是其他意外事件而造成人员的缺席。
3．假设四个项目同时需要的最多人数不超过现有公司工作人员的人数，即使超过，也只分配公司现有的工作人员。
4．假设C 、D 两个项目的管理费由公司支付；5．假设所有工作人员都安排完毕，即每个人都有工作。
6．假设同等级别的工作人员的技术水平是相同的，即他们可以接受任意等同的任务。
二．符号说明：i ：用i ＝1,2,3,4分别表示高级工程师，工程师，助理工程师和技术员。
j ：用j ＝1,2,3,4分别表示项目A,B,C 和D 。
ij X ：公司分配第i 级别工作人员到第j 个项目上的人数。
例如23X 表示公司分配工程师到项目C 上的人数。
ij a ：第i 级别工作人员分配到第j 个项目上的收费。
ij b : 第i 级别工作人员分配到第j 个项目上时公司的开支（包括工资和管理费）。
ij A : 表示到项目j 工作的第i 级别工作人员为公司贡献的纯利润收入。
j ： 表示第j 个项目的总工时（即项目j 的总工作量）。
j T ： 表示第j 个项目客户所要求的工期（即项目j 所需要的完工时间）。
Max ：公司一天的直接收益 只考虑客户对员工的人数要求 基本模型 进一步考虑客户对工期的要求 某个项目先完工的模型改进j M ： 表示客户要求第j 个项目一天所必须完成的工作量。
最优化方法练习题答案
练习题一1建立优化模型应考虑哪些要素？ 答：决策变量、目标函数和约束条件。
2、讨论优化模型最优解的存在性、迭代算法的收敛性及停止准则。
min f(x)答：针对一般优化模型s.t g i (x )臭0,i =1,2,…m ，讨论解的可行域D ，若存在一点h j x =0, j =1;, pX D ，对于-X • D 均有f (X ) < f (X)则称X 为优化模型最优解，最优解存在；迭 代算法的收敛性是指迭代所得到的序列X ⑴,X ⑵，…，X (K)…，满足f (X (K °)乞f (X (K))，|x (5 _x (k)||则迭代法收敛；收敛的停止准则有X(k)||c s —— < sx ()练习题二1某公司看中了例2.1中厂家所拥有的3种资源R i 、R 2、和R 3,欲出价收购(可 能用于生产附加值更高的产品)。
如果你是该公司的决策者，对这 3种资源的收购报价 是多少？(该问题称为例2.1的对偶问题)。
对3种资源报价y ,, y 2, y 3作为本问题的决策变量。
问题的目标很清楚一一“收购价最小”。
资源的报价至少应该高于原生产产品的利润，这样原厂家才可能因此有如下线性规划问题： min w = 170比• 100y 2 • 150y 35y , 2y 2 y 3 -10 s.t <2y 1 +3y 2 +5y 3 =1871, 丫2,丫3 -0*2、研究线性规划的对偶理论和方法(包括对偶规划模型形式、对偶理论和对偶单 纯形法)。
答：略。
f x (k 1)x (k)f x (k 1)-f x (k)f x (k)\ f x (k)：：：；等等解：确定决策变量 确定目标函数 确定约束条件3、用单纯形法求解下列线性规划问题:min z = X [ - x 2 x 3 +x 2 _2x 3 兰2/ 八 2x ^ +x 2 +x 3 兰3(1)s.t. 12 3 .； -x 1 + x 3 兰 4X i , X 2,X 3 — 0解：(1)引入松弛变量X 4, X 5, X 6 min z =捲-x 2 x 3 0* x 4 0* x 5 0* x 6乂 +x 2 -2x 3 +x 4=22捲 +x 2 +x 3+x5 =3st <123—x1 +x3+x6=4x1,x2, x3,x4,x5,x6 30(2) min z = 4 - X 2X 3% - 2X 2 + X 3=2x 2 — 2x 3 + x 4=2s.t.234x2 X3X 5 = 5X i -0 (i =1,2/ ,5)因检验数q>o,表明已求得最优解：X、(0,8/3,1/3,0,0,11/3)，去除添加的松弛变量，原问题的最优解为：X* =(0,8/3,1/3)。
最优化计算方法课后习题答案----高等教育出社。施光燕
习题二包括题目： P36页 5（1）（4）5（4）习题三包括题目：P61页 1(1)(2); 3; 5; 6; 14；15(1) 1(1)(2)的解如下3题的解如下5,6题14题解如下14. 设22121212()(6)(233)f x x x x x x x =+++---, 求点在(4,6)T-处的牛顿方向。
解：已知 (1)(4,6)T x=-，由题意得121212212121212(6)2(233)(3)()2(6)2(233)(3)x x x x x x x f x x x x x x x x +++-----⎛⎫∇= ⎪+++-----⎝⎭∴ (1)1344()56g f x -⎛⎫=∇=⎪⎝⎭21212122211212122(3)22(3)(3)2(233)()22(3)(3)2(233)22(3)x x x x x x x f x x x x x x x x +--+--------⎛⎫∇= ⎪+--------+--⎝⎭∴ (1)2(1)1656()()564G x f x --⎛⎫=∇=⎪-⎝⎭(1)11/8007/400()7/4001/200G x --⎛⎫= ⎪--⎝⎭∴ (1)(1)11141/100()574/100d G x g -⎛⎫=-=⎪-⎝⎭15（1）解如下15. 用DFP 方法求下列问题的极小点（1）22121212min 353x x x x x x ++++解：取 (0)(1,1)T x=，0H I =时，DFP 法的第一步与最速下降法相同2112352()156x x f x x x ++⎛⎫∇= ⎪++⎝⎭， (0)(1,1)T x =，(0)10()12f x ⎛⎫∇= ⎪⎝⎭(1)0.07800.2936x -⎛⎫= ⎪-⎝⎭， (1)1.3760() 1.1516f x ⎛⎫∇= ⎪-⎝⎭以下作第二次迭代(1)(0)1 1.07801.2936x x δ-⎛⎫=-= ⎪-⎝⎭， (1)(0)18.6240()()13.1516f x f x γ-⎛⎫=∇-∇= ⎪-⎝⎭0110111011101T T T TH H H H H γγδδδγγγ=+- 其中，111011126.3096,247.3380T T TH δγγγγγ===111.1621 1.39451.3945 1.6734Tδδ⎛⎫= ⎪⎝⎭ ， 01101174.3734113.4194113.4194172.9646T TH H γγγγ⎛⎫== ⎪⎝⎭所以10.74350.40560.40560.3643H -⎛⎫= ⎪-⎝⎭(1)(1)1 1.4901()0.9776dH f x -⎛⎫=-∇= ⎪⎝⎭令 (2)(1)(1)1xx d α=+ ， 利用 (1)(1)()0df x d d αα+=，求得 10.5727α=-所以 (2)(1)(1)0.77540.57270.8535xx d⎛⎫=-= ⎪-⎝⎭ ， (2)0.2833()0.244f x ⎛⎫∇= ⎪-⎝⎭以下作第三次迭代(2)(1)20.85340.5599x x δ⎛⎫=-= ⎪-⎝⎭ ， (2)(1)2 1.0927()()0.9076f x f x γ-⎛⎫=∇-∇= ⎪⎝⎭22 1.4407T δγ=- ， 212 1.9922T H γγ=220.72830.47780.47780.3135T δδ-⎛⎫=⎪-⎝⎭1221 1.39360.91350.91350.5988T H H γγ-⎛⎫= ⎪-⎝⎭所以22122121222120.46150.38460.38460.1539T T T TH H H H H δδγγδγγγ-⎛⎫=+-= ⎪-⎝⎭(2)(2)20.2246()0.1465d H f x ⎛⎫=-∇= ⎪-⎝⎭令 (3)(2)(2)2xxdα=+ ， 利用(2)(2)()0df x d d αα+=，求得 21α=所以 (3)(2)(2)11x x d ⎛⎫=+=⎪-⎝⎭， 因为 (3)()0f x ∇=，于是停止 (3)(1,1)T x =-即为最优解。
最优化习题答案及复习资料
6
,12
T
)
17 17
g
=(
6
,12
T
)
2 17 17
β g d = −
(d ) d 1
T
A
2
(1) T
(1)
A
(1)
=
1 298
− 90
d g β d (2) = −
+
2
1
(1)
=
−
289 210 289
α 线性搜索得步长：
= 1.7
2
x x α d (3) = (2) +
2 (2) = 11
x(1) = (1,1,1)T
.验证
d x x d (1) =(1,0,-1)是 f(x)在点 (1) 处的一个下降方向,并计算 min f( (1) +t (1) )
t>0
证明:
∇f (x) =
(2
x1,3x
2 2
+
2
x3−1,4
x
3+
2
x
2−1)T
∇f (x1) = (2,4,5)T
2
d
∇f
(
x
=
x2
−
(x2 − x1) f ′(x2) −
f f
′( x2) ′( x1)
或者
x
=
x1
−
(x2 − x1) f ′(x2) −
f f
′( x1) ′( x1)
证明：1）设ϕ(x) = a x2 + bx + c （ a ≠ 0 ）
则 ϕ ′(x) = 2ax + b
ϕ ′(x1) = 2a x1 + b = f ′(x1)
最优化计算方法
ymax=subs(y,x,xmax)
Newton 法
求方程F(x)=0的根.
牛顿法： x(n)=x(n-1)-F(x(n-1))/F’(x(n-1))
F = dydx; F1 = diff(F,x); format long N = 10; % number of iterations x0 = 19 % initial guess fprintf(' iteration xvalue\n\n'); for i=1:N x1=x0-subs(F,x,x0)/subs(F1,x,x0); fprintf('%5.0f %1.16f\n', i, x1); x0 = x1; end display('Hence, the critical point (solution of F=0) is (approx)'), x1
xmax figure, ezcontourf(z,[0.1 10 0.1 10]) hold on plot3(xmax(1),xmax(2),zmax, 'mo', 'LineWidth',2,... 'MarkerEdgeColor','k', 'MarkerFaceColor',[.49 1 .63],... 'MarkerSize',12); title('Countour plot and optimal value');
a=0; b=6; c=0; d=6; N=1000; x0 = a+(b-a)*rand(1); y0 = c+(d-c)*rand(1); zmin = subs(z,[x,y],[x0,y0]); fprintf(' Iteration xmin ymin zmin value\n\n'); for n=1:N xnew=a+(b-a)*rand(1); ynew=c+(d-c)*rand(1); znew=subs(z,[x,y],[xnew,ynew]); if znew<zmin xmin=xnew; ymin=ynew; zmin=znew; fprintf('%4.0f %1.6f %1.6f %1.6f\n', n, xmin, ymin, zmin); end end
最优化计算方法
grid on
A
3
ezplot(y,[0,20])
(130-2 x) exp(1/40 x)-9/20 x 140 139 138 137 136 135 134 133 132 131 130
0
2
4
6
ห้องสมุดไป่ตู้
8
10 12 14 16 18 20
x
A
4
ezplot(y,[0,40])
18 18.5 19 19.5 20 20.5 21 21.5 22 x
A
6
ezplot(y,[19,20]); grid on
(130-2 x) exp(1/40 x)-9/20 x
139.395 139.394 139.393 139.392 139.391 139.39 139.389 139.388 139.387 139.386 139.385
A
8
Newton 法
?求方程F(x)=0的根. ?牛顿法： x(n)=x(n-1)-F(x(n-1))/F'(x(n-1))
A
9
F = dydx;
F1 = diff(F,x);
format long
N = 10; % number of iterations
x0 = 19 % initial guess
xvalues = [xvalues; xmaxc];
end xvalues = xvalues(2:end);
A
12
(130-2 x) exp(1/40 x)-9/20 x 140
135
130
125
120
0
5
最优化计算方法(工程优化) 第4章
f ( x)T p f ( x) p cos(f ( x), p)
f ( x) f ( x) ，此时由f ( x) p f ( x) 可得 p f ( x)
T
当 cos(f ( x), p) 1 时，f ( x)T p 最小，最小值为
最速下降法
最速下降法是求多元函数极值的最古老的数值算 法，早在1847年法国数学家Cauchy提出该算法，后来 Curry作了进一步的研究。 该方法直观，简单，计算方便，而且后来的一些新的 有效的方法大多数是对它的改进，或受它的启发而得到 的。
2 2
2 0 f x1 , 0 2
0 , 2 0 . 2
1 1 1 1 x1 , x2 , x3 , x4 . 0 2 0 2
无约束优化的最优性条件
2 0 2 2 0 f x1 , f x4 的行列式小于0； 0 2 0 2
无约束优化的最优性条件----一阶必要条件
定理(一阶必要条件) 设 f : R n R ，若 x 为 f ( x) 的局部极小点，且在 N ( x*)
内连续可微，则
f ( x* ) 0.
无约束优化的最优性条件----二阶必要条件
定理（二阶必要条件） 若 x * 为 f x 的局部极小点，且在 N x* 内 f x 二次连续 可微，则 f ( x* ) 0, 2 f ( x* ) 半正定。
4 d = f x , 2
1 1
=40 2 20 3 令 0= ' ( ) 80 20, 得 1 =1/4,
第2次迭代：
2 x1 2 x2 4 f ( x) , 2 x1 +4x2 1 1 4 2 2 x 2 =x1 +1d 1 = +1/4 = ， f x 2 , 1 2 1/2
最优化方法习题答案
习题一1.1利用图解法求下列线性规划问题： （1）21x x z max +=⎪⎪⎩⎪⎪⎨⎧≥≤+≥+0x ,x 5x 2x 2x x 3.t .s 212121 解：根据条件，可行域为下面图形中的阴影部分，，有图形可知，原问题在A 点取得最优值，最优值z=5（2）21x 6x z min -=⎪⎪⎩⎪⎪⎨⎧≥≤+-≤+0x ,x 7x x 1x x 2.t .s 212121 解：图中阴影部分表示可行域，由图可知原问题在点A 处取得最优值，最优值z=-6.（3）21x 2x 3z max +=⎪⎪⎩⎪⎪⎨⎧≥-≥-≤+-0x ,x 4x 2x 1x x .t .s 212121 解：如图所示，可行域为图中阴影部分，易得原线性规划问题为无界解。
（4）21x 5x 2z min -=⎪⎪⎩⎪⎪⎨⎧≥≤+≥+0x ,x 2x x 6x 2x .t .s 212121 解：由图可知该线性规划可行域为空，则原问题无可行解。
1.2 对下列线性规划问题，找出所有的基解，基可行解，并求出最优解和最优值。
（1）4321x 6x 3x 2x 5z min -+-=⎪⎪⎩⎪⎪⎨⎧≥=+++=+++0x ,x ,x ,x 3x 2x x x 27x 4x 3x 2x .t .s 432143214321 解：易知1x 的系数列向量⎪⎪⎭⎫ ⎝⎛=21p 1，2x 的系数列向量⎪⎪⎭⎫ ⎝⎛=12p 2，3x 的系数列向量⎪⎪⎭⎫⎝⎛=13p 3，4x 的系数列向量⎪⎪⎭⎫⎝⎛=24p 4。
①因为21p ,p 线性无关，故有⎪⎩⎪⎨⎧--=+--=+43214321x 2x 3x x 2x 4x 37x 2x ，令非基变量为0x x 43==，得⎪⎪⎩⎪⎪⎨⎧=-=311x 31x 21，所以得到一个基解)0,0,311,31(x )1(-=是非基可行解； ②因为31p ,p 线性无关，可得基解)0,511,0,52(x)2(=，543z 2=；③因为41p ,p 线性无关，可得基解611,0,0,31(x )3(-=，是非基可行解；④因为32p ,p 线性无关，可得基解)0,1,2,0(x )4(=，1z 4-=；⑤因为42p ,p 线性相关，42x ,x 不能构成基变量； ⑥因为43p ,p 线性无关，可得基解)1,1,0,0(x )6(=，3z 6-=；所以)6()4()2(x ,x ,x是原问题的基可行解，)6(x 是最优解，最优值是3z -=。
最优化计算方法课后习题答案----高等教育出版社。施光燕
习题二包括题目: P36页5(1）（4）5（4)习题三包括题目：P61页1（1）（2)；3；5; 6；14；15(1) 1（1)（2)的解如下3题的解如下5,6题14题解如下14。
设22121212()(6)(233)f x x x x x x x =+++---， 求点在(4,6)T -处的牛顿方向。
解：已知 (1)(4,6)T x =-，由题意得121212212121212(6)2(233)(3)()2(6)2(233)(3)x x x x x x x f x x x x x x x x +++-----⎛⎫∇= ⎪+++-----⎝⎭∴ (1)1344()56g f x -⎛⎫=∇=⎪⎝⎭21212122211212122(3)22(3)(3)2(233)()22(3)(3)2(233)22(3)x x x x x x x f x x x x x x x x +--+--------⎛⎫∇= ⎪+--------+--⎝⎭∴ (1)2(1)1656()()564G x f x --⎛⎫=∇=⎪-⎝⎭(1)11/8007/400()7/4001/200G x --⎛⎫= ⎪--⎝⎭∴ (1)(1)11141/100()574/100d G x g -⎛⎫=-=⎪-⎝⎭15（1）解如下15. 用DFP 方法求下列问题的极小点（1）22121212min353x x x x x x ++++ 解:取 (0)(1,1)T x=，0H I =时，DFP 法的第一步与最速下降法相同2112352()156x x f x x x ++⎛⎫∇= ⎪++⎝⎭， (0)(1,1)T x =，(0)10()12f x ⎛⎫∇= ⎪⎝⎭(1)0.07800.2936x -⎛⎫= ⎪-⎝⎭， (1)1.3760() 1.1516f x ⎛⎫∇= ⎪-⎝⎭以下作第二次迭代(1)(0)1 1.07801.2936x xδ-⎛⎫=-= ⎪-⎝⎭, (1)(0)18.6240()()13.1516f x f x γ-⎛⎫=∇-∇= ⎪-⎝⎭0110111011101T T T TH H H H H γγδδδγγγ=+-其中，111011126.3096,247.3380T T T H δγγγγγ===11 1.1621 1.39451.3945 1.6734T δδ⎛⎫= ⎪⎝⎭ ， 01101174.3734113.4194113.4194172.9646T TH H γγγγ⎛⎫== ⎪⎝⎭所以10.74350.40560.40560.3643H -⎛⎫= ⎪-⎝⎭(1)(1)1 1.4901()0.9776d H f x -⎛⎫=-∇= ⎪⎝⎭令 (2)(1)(1)1xx d α=+ , 利用(1)(1)()0df x d d αα+=，求得 10.5727α=- 所以 (2)(1)(1)0.77540.57270.8535x x d ⎛⎫=-= ⎪-⎝⎭ ， (2)0.2833()0.244f x ⎛⎫∇= ⎪-⎝⎭以下作第三次迭代(2)(1)20.85340.5599xx δ⎛⎫=-= ⎪-⎝⎭ ， (2)(1)2 1.0927()()0.9076f x f x γ-⎛⎫=∇-∇= ⎪⎝⎭22 1.4407T δγ=- ， 212 1.9922T H γγ= 220.72830.47780.47780.3135T δδ-⎛⎫=⎪-⎝⎭1221 1.39360.91350.91350.5988T H H γγ-⎛⎫= ⎪-⎝⎭所以22122121222120.46150.38460.38460.1539T T T T H H H H H δδγγδγγγ-⎛⎫=+-= ⎪-⎝⎭(2)(2)20.2246()0.1465d H f x ⎛⎫=-∇= ⎪-⎝⎭令 (3)(2)(2)2xxdα=+ ， 利用(2)(2)()0df x d d αα+=，求得 21α= 所以 (3)(2)(2)11xx d ⎛⎫=+= ⎪-⎝⎭, 因为 (3)()0f x ∇=，于是停止(3)(1,1)T x =-即为最优解.习题四包括题目: P95页 3;4；8；9(1);12选做；13选做 3题解如下3.考虑问题21),(2)(min 21x x x f sx x -=∈，其中{}{}.10,1),(1),(2121222121≤≤≤≤+=x x x x x x x x S T T（1）画出此问题的可行域和等值线的图形；（2）利用几何图形求出此问题的最优解及最优值;(3）分别对点,)1,0(,)0,0(,)1,1(,)0,1(4321T T T T x x x x -==-==指出哪些约束是紧约束和松约束。
最优化方法习题答案
x3
-M
0
0
0
5
-1
1
2
x4
x5
1+ 2 M
0
3
ห้องสมุดไป่ตู้
x2
1 3
1
x5
2 3
0
以 x1 为换入基， x5 作为换出基有
-1- M 3
1 3 1
3
-M
0
0
0
5
3
-1
1
1
3
x1
x2
x3
x4
x5
0
x2
0
x1
1
0
1
2
1
1
2
0
1
2
3
3 M
-5.5
2
2
1
1
1.5
2
2
3 3
0.5
22
以 x 4 换入， x 2 换出有
⑤因为 p2 , p4 线性相关， x 2 , x 4 不能构成基变量；
⑥因为 p3, p4 线性无关，可得基解 x(6) (0,0,1,1) ， z6 3 ；
所以 x(2) , x(4) , x(6) 是原问题的基可行解， x(6) 是最优解，最优值是 z 3 。
（2） max z x1 x2 2x3 x4 x5
x1 2x2 3x3 4x4 7 s.t.2x1 x2 x3 2x4 3
x1, x2 , x3, x4 0
解：易知
x1 的系数列向量
p1
1
2
，x 2
的系数列向量
p2
2
1
最优化方法练习题答案
练习题一1、建立优化模型应考虑哪些要素“答：决策变量、目标函数和约束条件。
2、讨论优化模型最优解的存在性、迭代算法的收敛性及停顿准则。
答：针对一般优化模型，讨论解的可行域，假设存在一()()min ()..0,1,2, 0,1,,i j f x s t g x i m h x j p≥===L L D 点，对于均有则称为优化模型最优解，最优解存在；*X D ∈X D ∀∈*()()f X f X ≤*X 迭代算法的收敛性是指迭代所得到的序列，满足，(1)(2)(),,,K X X X L L (1)()()()K K f X f X +≤则迭代法收敛；收敛的停顿准则有，，(1)()k k x x ε+-<(1)()()k k k x x xε+-<，，等等。
()()(1)()k k f x f x ε+-<()()()(1)()()k k k f x f x f x ε+-<()()k f x ε∇<练习题二1、*公司看中了例2.1中厂家所拥有的3种资源R 1、R2、和R 3，欲出价收购〔可能用于生产附加值更高的产品〕。
如果你是该公司的决策者，对这3种资源的收购报价是多少？〔该问题称为例2.1的对偶问题〕。
解：确定决策变量对3种资源报价作为本问题的决策变量。
123,,y y y 确定目标函数问题的目标很清楚——“收购价最小〞。
确定约束条件资源的报价至少应该高于原生产产品的利润，这样原厂家才可能卖。
因此有如下线性规划问题：123min 170100150w y y y =++*2、研究线性规划的对偶理论和方法〔包括对偶规划模型形式、对偶理论和对偶单纯形法〕。
答：略。
3、用单纯形法求解以下线性规划问题：〔1〕⎪⎪⎩⎪⎪⎨⎧≥≤+-≤++≤-++-=0,,43222..min32131321321321x x x x x x x x x x x t s x x x z ；〔2〕⎪⎪⎩⎪⎪⎨⎧=≥=++=+-=+-+-=)5,,2,1(052222..4min 53243232132 i x x x x x x x x x x t s x x z i 解：〔1〕引入松弛变量*4，*5，*6c j →1-11C B基b*1*2*3*4*5*60*421[1]-21000*532110100*64-101001c j -z j1-11因检验数σ2<0，故确定*2为换入非基变量，以*2的系数列的正分量对应去除常数列，最小比值所在行对应的基变量*4作为换出的基变量。
最优化计算方法课后习题集答案解析
解：取 ， 时，DFP法的第一步与最速下降法相同
， ，
，
以下作第二次迭代
，
其中，
，
所以
令 ， 利用 ，求得
所以 ，
以下作第三次迭代
，
，
所以
令 ， 利用 ，求得
所以 ， 因为 ，于是停止
即为最优解。
习题四
包括题目： P95页 3；4；8；9(1)；12选做；13选做
3题解如下
3.考虑问题 ，其中
X1,x2,x3≥0 （3）
求出点（1,1,0）处的一个下降可行方向.
解：首先检查在点（1,1,0）处哪些约束为有效约束。检查易知（1），X3≥0为有效约束。设所求可行方向d=(d1,d2,d3)T。根据可行方向d的定义，应存在a>0，使对∀t∈（0，a）能有
X+td=(1+td1,1+td2,0+td3)T
（1）
s.t.
（2）
s.t.
（1）解：非线性规划的K-T条件如下：
（1）
（2）
（3）
再加上约束条件 （4）
为求出满足（1）~（4）式的解，分情况考虑：
①若（4）式等号不成立，即 ，那么由（2）式得 ，将 代入（1）式解得 ， ，所得值不满足 的条件，故舍去。
②若（4）式等号成立，由（1）式可以解得 ， ，代入（4）式有：
JBi
1
2
3
4
5
6
7
8
9
di0
1
1
0
-5/6
-1/6
1
10/6
4
0
0
38/6
2
0
1
-9/6
最优化方法练习题答案
最优化⽅法练习题答案精⼼整理练习题⼀1、建⽴优化模型应考虑哪些要素? 答：决策变量、⽬标函数和约束条件。
2、讨论优化模型最优解的存在性、迭代算法的收敛性及停⽌准则。
min ()f x D ∈，对于则有(f ?1例2.1解：*2、研究线性规划的对偶理论和⽅法（包括对偶规划模型形式、对偶理论和对偶单纯形法）。
答：略。
3、⽤单纯形法求解下列线性规划问题：（1）≥≤+-≤++≤-++-=0,,43222..min32131321321321x x x x x x x x x x x t s x x x z ；（2）=≥=++=+-=+-+-=)5,,2,1(052222..4min 53243232132Λi x x x x x x x x x x t s x x z i解：（1）引⼊松弛变量x 4，x 5，x 6因检验数σj >0，表明已求得最优解：*(0,8/3,1/3,0,0,11/3)X =，去除添加的松弛变量，原问题的最优解为：*(0,8/3,1/3)X =。
（2）根据题意选取x 1，x 4，x 5，为基变量：因检验数σ2<0最⼩，故确定x 2为换⼊⾮基变量，以x 2的系数列的正分量对应去除常数列，最⼩⽐值所在⾏对应的基变量x 4作为换出的基变量。
4根据题意约束条件1和2可以合并为1，引⼊松弛变量x 3，x 4，构造新问题。
因检验数σj>0，表明已求得最优解：*(3/5,6/5)X 。
Matlab调⽤代码：Matlab调⽤代码：f=[-10;-15;-12];A=[5,3,1;-5,6,15;-2,-1,-1];b=[9;15;-5];lb=[0;0;0];x=linprog(f,A,b,[],[],lb)输出结果：原题⽆可⾏解。
5、⽤内点法和Matlab软件求解下列线性规划问题：解：⽤内点法的过程⾃⼰书写，参考答案：最优解[4/3 7/3 0] X=；最优值5 Matlab调⽤代码：f=[2;1;1];Aeq=[1,2,2;2,1,0];beq=[6;5]; Array 6解：（x=33y=-39最优解[33]；最优值39（2）调⽤matlab编译程序bbmethodf=[-7;-9];G=[-13;71];h=[6;35][x,y]=bbmethod(f,G,h,[],[],[0;0],[],[1;0],1)x=50y=-35最优解[50]；最优值357、⽤隐枚举法和Matlab软件求解下列问题：0）（1，2.1，1，输出结果x=1fval=2（2）调⽤代码：f=[-3;-2;5;2;3]; %价值向量fA=[1,1,1,2,1;7,0,3,-4,3;-11,6,0,-3,3]; %不等式约束系数矩阵A，[]中的分号“；”%为⾏分隔符b=[4;8;-1]; %不等式约束右端常数向量b[x,fval]=bintprog(f,A,b,[],[]); %调⽤函数bintprog。
机械优化设计习题参考答案 第五版
结构优化设计structural optimal design (optimum structural design)参考书：1. 孙靖民：机械优化设计，机械工业出版社，20032. 孙德敏：工程最优化方法和应用，中国科大出版社，19973. 施光燕：最优化方法，高教出版社，1999绪论1. 内容基本概念：结构(structure) 广义—系统组成；窄义—承受载荷、维持系统几何形状不变的部分，如梁杆板壳及其组合。
结构是用来支承有效载荷的。
设计(design) 完成一项新产品、新工程前的方案构思（如大小、尺寸、形状、材料、工艺过程等）。
数据—数字化--CAE优化(optimization) 从几种方案中选出最好的—优选；从设计空间中的无数种方案中用计算机选出最好的—优化。
2. 工程中的优化问题1） 桥梁2） 等强度梁，铁塔 3） 飞机、航天器4） 其他领域（控制、化工）3. 发展史: 牛顿，计算机， 钱令希；MATLAB —优化工具箱；遗传算法MATLAB —面向工程的高级语言 Optimization Toolbox 主要功能：1） 线性规划 x c TbAx ⋅≤min —— ()b Ac lp x ,,*=2） 二次规划 ⎪⎭⎫⎝⎛+≤x c x H x T T b Ax 21min —— ),,,(*b A c H qp x =一、概述（入门实例）一、 举例 1. 人字架优化已知：2B=152cm, T=0.25cm, E=2.1×105Mpa, ρ=7.8×103kg/m 3, σ=420Mpa, 2F=3×105N求：min [m(D,h)] 满足强度和稳定要求 解：变量 D,h载荷 ()hh BFF F 21221cos /+==θ--单杆内力应力 ()hTDh B F A F πσ21221+==临界应力 )(8)(22222h B D T E A F e e ++==πσ 强度条件 y σσ≤()hTDhB F π2122+y σ≤稳定条件 e σσ≤()hTDhB F π2122+)(8)(22222h B D T E ++≤π目标函数：2122)(22),(min h B TD AL h D m +==πρρ● 解析法：2122)(22),(min h B TD AL h D m +==πρρ不考虑稳定条件，由强度条件建立D,h 关系极限情况 y h D σσ=),(Thh B F D y πσ2/122)(+=→→hh B F h B TD AL h m y 2221222)(22)(+⋅=+==σρπρρ 012)(22=⎪⎪⎭⎫ ⎝⎛-=h B F dh h dm y σρcm B h 76*==→→ cm D 43.6*=校核稳定条件 ),(),(****h D h D e σσ≤，没问题。
最优化方法部分课后习题解答(1-7)
最优化方法部分课后习题解答习题一1.一直优化问题的数学模型为：22121122123142min ()(3)(4)5()02()50..()0()0f x x xg x x x g x x x s t g x x g x x =−+−⎧=−−≥⎪⎪⎪=−−+≥⎨⎪=≥⎪=≥⎪⎩试用图解法求出：（1）无约束最优点，并求出最优值。
（2）约束最优点，并求出其最优值。
（3）如果加一个等式约束，其约束最优解是什么？12()0h x x x =−=解：（1）在无约束条件下，的可行域在整个平面上，不难看出，当=（3，4）()f x 120x x *x 时，取最小值，即，最优点为=（3，4）：且最优值为：=0()f x *x *()f x （2）在约束条件下，的可行域为图中阴影部分所示，此时，求该问题的最优点就是()f x 在约束集合即可行域中找一点，使其落在半径最小的同心圆上，显然，从图示中可12(,)x x 以看出，当时，所在的圆的半径最小。
*155(,)44x =()f x 其中：点为和的交点，令求解得到：1()g x 2()g x 1122125()02()50g x x x g x x x ⎧=−−=⎪⎨⎪=−−+=⎩1215454x x ⎧=⎪⎪⎨⎪=⎪⎩即最优点为：最优值为：=*155(,)44x =*()f x 658（3）.若增加一个等式约束，则由图可知，可行域为空集，即此时最优解不存在。
2.一个矩形无盖油箱的外部总面积限定为S，怎样设计可使油箱的容量最大？试列出这个优化问题的数学模型，并回答这属于几维的优化问题.解：列出这个优化问题的数学模型为：该优化问题属于三维的优化问题。
123122313123max ()220..00f x x x x x x x x x x S x s t x x =++≤⎧⎪>⎪⎨>⎪⎪>⎩32123sx y z v⎛⎞=====⎜⎟⎝⎠习题二3.计算一般二次函数的梯度。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
习题二包括题目： P36页 5（1）（4）5（4）习题三包括题目：P61页 1(1)(2); 3; 5; 6; 14；15(1) 1(1)(2)的解如下3题的解如下5,6题14题解如下14. 设22121212()(6)(233)f x x x x x x x =+++---, 求点在(4,6)T-处的牛顿方向。
解：已知 (1)(4,6)T x=-，由题意得121212212121212(6)2(233)(3)()2(6)2(233)(3)x x x x x x x f x x x x x x x x +++-----⎛⎫∇= ⎪+++-----⎝⎭∴ (1)1344()56g f x -⎛⎫=∇=⎪⎝⎭21212122211212122(3)22(3)(3)2(233)()22(3)(3)2(233)22(3)x x x x x x x f x x x x x x x x +--+--------⎛⎫∇= ⎪+--------+--⎝⎭∴ (1)2(1)1656()()564G x f x --⎛⎫=∇=⎪-⎝⎭(1)11/8007/400()7/4001/200G x --⎛⎫= ⎪--⎝⎭∴ (1)(1)11141/100()574/100d G x g -⎛⎫=-=⎪-⎝⎭15（1）解如下15. 用DFP 方法求下列问题的极小点（1）22121212min 353x x x x x x ++++解：取 (0)(1,1)T x=，0H I =时，DFP 法的第一步与最速下降法相同2112352()156x x f x x x ++⎛⎫∇= ⎪++⎝⎭， (0)(1,1)T x =，(0)10()12f x ⎛⎫∇= ⎪⎝⎭(1)0.07800.2936x -⎛⎫= ⎪-⎝⎭， (1)1.3760() 1.1516f x ⎛⎫∇= ⎪-⎝⎭以下作第二次迭代(1)(0)1 1.07801.2936x x δ-⎛⎫=-= ⎪-⎝⎭， (1)(0)18.6240()()13.1516f x f x γ-⎛⎫=∇-∇= ⎪-⎝⎭0110111011101T T T TH H H H H γγδδδγγγ=+- 其中，111011126.3096,247.3380T T TH δγγγγγ===111.1621 1.39451.3945 1.6734Tδδ⎛⎫= ⎪⎝⎭ ， 01101174.3734113.4194113.4194172.9646T TH H γγγγ⎛⎫== ⎪⎝⎭所以10.74350.40560.40560.3643H -⎛⎫= ⎪-⎝⎭(1)(1)1 1.4901()0.9776dH f x -⎛⎫=-∇= ⎪⎝⎭令 (2)(1)(1)1xx d α=+ ， 利用 (1)(1)()0df x d d αα+=，求得 10.5727α=-所以 (2)(1)(1)0.77540.57270.8535xx d⎛⎫=-= ⎪-⎝⎭ ， (2)0.2833()0.244f x ⎛⎫∇= ⎪-⎝⎭以下作第三次迭代(2)(1)20.85340.5599x x δ⎛⎫=-= ⎪-⎝⎭ ， (2)(1)2 1.0927()()0.9076f x f x γ-⎛⎫=∇-∇= ⎪⎝⎭22 1.4407T δγ=- ， 212 1.9922T H γγ=220.72830.47780.47780.3135T δδ-⎛⎫=⎪-⎝⎭1221 1.39360.91350.91350.5988T H H γγ-⎛⎫= ⎪-⎝⎭所以22122121222120.46150.38460.38460.1539T T T TH H H H H δδγγδγγγ-⎛⎫=+-= ⎪-⎝⎭(2)(2)20.2246()0.1465d H f x ⎛⎫=-∇= ⎪-⎝⎭令 (3)(2)(2)2xxdα=+ ， 利用(2)(2)()0df x d d αα+=，求得 21α=所以 (3)(2)(2)11x x d ⎛⎫=+=⎪-⎝⎭， 因为 (3)()0f x ∇=，于是停止 (3)(1,1)T x =-即为最优解。
习题四包括题目： P95页 3；4；8；9(1)；12选做；13选做 3题解如下3.考虑问题21),(2)(min 21x x x f sx x -=∈，其中{}{}.10,1),(1),(2121222121≤≤≤≤+=x x x x x x x x S T T I（1）画出此问题的可行域和等值线的图形；（2）利用几何图形求出此问题的最优解及最优值；（3）分别对点,)1,0(,)0,0(,)1,1(,)0,1(4321TTTTx x x x -==-==指出哪些约束是紧约束和松约束。
解：（1）如图所示，此问题的可行域是以O 点为圆心，1为半径的圆的上半部分；等值线是平行于直线x 2=2x 1的一系列平行线，范围在如图所示的两条虚线内。
（2）要求f 的最小值，即求出这一系列平行线中与x 2轴相交，所得截点纵坐标的最大值。
显然当直线在虚线1的位置，能取得极值。
如图求出切点⎪⎭⎫ ⎝⎛-51,52P ，此点即为最优解Tx )51,52(-=*，解得最优值5-=*f（3）对于区间集S 可以简化为g 1:012221≥--x xg 2:02≥-x对于点Tx )0,1(1=，g 1和g 2均为该点处的紧约束； 对于点Tx )1,1(2-=，g 1和g 2均为该点处的松约束；对于点Tx )0,0(3=，g 1为该点的松约束，g 2为该点的紧约束； 对于点Tx )1,0(4-=，g 1为该点的紧约束，g 2为该点的松约束。
4题解如下4.试写出下列问题的K-T 条件，并利用所得到的表达式求出它们的最优解： （1）()();12min 2221-+-x x. 012221≥--x x （2）()();12min 2221-+-x x. 092221≥--x x（1）解：非线性规划的K-T 条件如下：022********=⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛--x x x x λ （1）0)1(2221=--x x λ （2）0≥λ （3）再加上约束条件 012221≥--x x （4） 为求出满足（1）~（4）式的解，分情况考虑：①若（4）式等号不成立，即012221>--x x ，那么由（2）式得0=λ，将0=λ代入（1）式解得21=x ，12=x ，所得值不满足012221>--x x 的条件，故舍去。
②若（4）式等号成立，由（1）式可以解得121+=λx ，112+=λx ，代入（4）式有： 1111222=⎪⎭⎫⎝⎛++⎪⎭⎫ ⎝⎛+λλ 解得5151--+-=或λ 因为0≥λ，所以51+-=λ，那么521=x ，512=x ，满足以上所有条件。
综上所述，所求非线性规划有唯一的K-T 点为：Tx )51,52(=*(2)解：非线性规划的K-T 条件如下：022********=⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛--x x x x λ （1）0)9(2221=--x x λ （2）0≥λ （3）再加上约束条件092221≥--x x （4） 为求出满足（1）~（4）式的解，分情况考虑：①若（4）式等号不成立，即092221>--x x ，那么由（2）式得0=λ，将0=λ代入（1）式解得21=x ，12=x ，所得值满足以上所有约束。
②若（4）式等号成立，由（1）式可以解得121+=λx ，112+=λx ，代入（4）式有： 9111222=⎪⎭⎫⎝⎛++⎪⎭⎫ ⎝⎛+λλ 解得351±-=λ 因为0≥λ，所以所得λ值均舍去，该情况不成立。
综上所述，所求非线性规划有唯一的K-T 点为：T x )1,2(=*8题解如下 8 考虑问题Min x12+x1x2+2x22-6x1-2x2-12x3 . X1+x2+x3=2 （1） -x1+2x2≤3 （2） X1,x2,x3≥0 （3）求出点（1,1,0）处的一个下降可行方向.解：首先检查在点（1,1,0）处哪些约束为有效约束。
检查易知（1），X3≥0为有效约束。
设所求可行方向d=(d1,d2,d3)T 。
根据可行方向d 的定义，应存在a>0，使对?t ∈（0，a ）能有X+td=(1+td1,1+td2,0+td3)T 也能满足所有有效约束：(1+td1)+(1+td2)+(0+td3)=2 td3≥0 经整理即为d1+d2+d3=0 d3≥0满足上述不等式组的d=(d1,d2,d3)T 均为可行方向。
现只求一个可行方向，所以任取d3=1，求解d1+d2=-d3得d1+d2=-1，可任取d1=1，d2=-2得一可行方向d=（1，-2，1）T考虑下降性由题可知：将目标函数化为f(x)=1/2XTQX+bTX+C从而▽f=QX+b即▽f（1,1,0）=（-3,3，-12）因为▽f（1,1,0）Td=-21<0表明d=（1,-2，1）T为原问题在x=（1,1,0）T处的一个下降可行方向9题解如下9 用lemke算法解下列问题：（1）min 2x12+2x22-2x1x2-4x1-6x2. X1+x2≤2X1+5x2≤5X1,x2≥0解：，，，于是，，，与本题相应的线性互补问题为：W-MZ=qW≥0,Z≥0WTZ=0写成表格为由上表可看出仅w4，z4这一对变量全部不是基变量，因此从它们之中选一个进基，由于第一次碰到这一对变量，故选z4进基.在所选列中，有 Min {8/5,11/9,2/6,6/4}=2/6故选相应的第3行第8列元素作主元，再进行旋转，得由于W0仍在基变量中，故继续运算.由于这时仅有W3，Z3这一对变量全不在基中，故仍在它们之中选一变量进基，由于是第一次从这一对变量选取，故也选Z3进基，再由Min {38/6/4,8/8，28/6/2}=8/8再继续，得优解：y1=-208/93，x1=35/31，x2=24/31，u2=32/31，y2=v2=v2=u1=0,即x*=（35/31,24/31）T12题解如下12.(1）外点法min =)(f x 2221x x + . 11≥x解： 定义惩罚函数 F( )(){}[]2122211,0max ,--++=x x x x σσ=2221x x + 当 11≥x()2122211-++x x x σ 当11<x用解析法求解 min F(σ,x ),有=∂∂1x F12x 当11≥x()11221x x σ+- 当11<x222x x F=∂∂ 令01=∂∂x F ，02=∂∂x F得到 =*σx ()21,x x T⎪⎭⎫ ⎝⎛+=0,1σσT 易见，当+∞→σ时，()0,1=→**x x σT*x 恰为所求费线性规划的最优解。