第一章误差-精选
计算方法第一章误差

例:重力加速度常数g。g 9.80米 秒2 , g 980厘米 秒2
两者均有三位有效数字
g 9.80 0.5 102 米 秒2
g 980 0.5厘米 秒2
后者的绝对误差大,而相对误差分别为
0.5 102 0.5 和 9.80 980
两者相等,与量纲的选取无关
有效数字
取 r 5% 。
定理 2 若近似数 x 0.x1 x2
xn 10m ,的相对误差限
r
则它至少具有 n 位有效数字。 证 x 0.x1 x2 则 xx
1 10 ( n 1) 2( x1 1)
xn 10m 有 x ( x1 1) 10m 1
1. 2.
3.
4.
数值分析需要考虑哪些问题
1. 计算速度 例如:求解一个20阶线性方程组,20个未知量, 用加减消原法需3000次乘法运算,用行列式求 解需进行9.7*1020次运算,如果用每秒1亿次乘 法运算的计算机要30万年。 说明了算法方法的重要性 2. 存储量。大型问题有必要考虑 例如算法所需要保留的中间结果比较少,则可 以省下为保留中间结果所需要的额外的存储空 间。
0.3529 10 , 0.352900 10
2
2
当 x 0.a1a2
al
an 10m , ai为数字01 , , 2, , 9,a1 0.
其中,有效数字的个数是l,即 a1, , al是有效的。
则 e x x * 0.510
ml
有效数字:由绝对误差决定
此定理说明,相对误差限是由有效数字决定。
例:用 3.14 作为 的近似值,求其相 对误差。 解:四舍五入的近似值各位都是有效 数字,即 n=3,由定理 1 (31) r 10 0.17% 23 x 有两位有效数字,求其相对误差限。 解
第1章 误差分析

第1章误差分析利用计算机进行数值计算几乎全都是近似计算:计算机所能表示的数的个数是有限的,我们需要用到的数的个数是无限的,所以在绝大多数情况下,计算机不可能进行绝对精确的计算。
定义:设x *为某个量的真值,x为x *的近似值,称x *- x为近似值x的误差,通常记为e(x),以表明它是与x有关的量。
与误差作斗争是时计算方法研究的永恒的主体,由于时间和经验的关系,我们仅对这方面的只是做一个最基本的介绍。
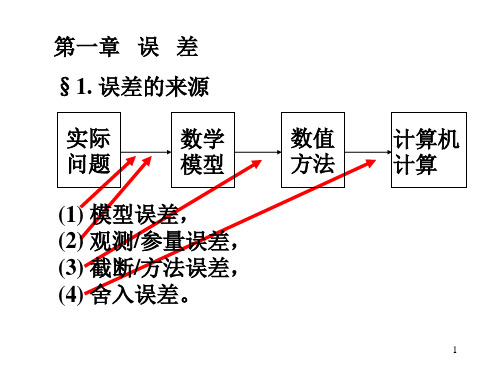
1.1 误差的来源误差的来源是多方面的,但主要来源为:描述误差,观测误差,截断误差和舍入误差。
1描述误差为了便于数学分析和数值计算,人们对实际问题的数学描述通常只反映出主要因素之间的数量关系,而忽略次要因素的作用,由此产生的误差称为描述误差。
对实际问题进行数学描述通常称为是建立数学模型,所以描述误差也称为是模型误差。
2观测误差描述实际问题或实际系统的数学模型中的某些参数往往是通过实验观测得到的。
由试验得到的数据与实际数据之间的误差称为观测误差。
比如我们用仪表测量电压、电流、压力、温度时,指针通常会落在两个刻度之间,读数的最后一位只能是估计值,从而也产生了观测误差。
3.舍入误差几乎所有的计算工具,当然也包括电子计算机,都只能用一定数位的小数来近似地表示数位较多或无限的小数,由此产生的误差称为舍入误差。
4.截断误差假如真值x*为近似值系列{x n}的极限,由于计算机只能执行有限步的计算过程,所以我们只能选取某个x N作为x*的近似值,由此产生的误差称为截断误差。
我们可以通过函数的泰勒展式来理解截断误差:设f(x)可以在x=x0处展开为泰勒级数,记f N(x)为前N+1项的和,R N(x)为余项,如果用f N(x)近似表示f(x),则R N(x)就是截断误差。
提示:在我们的课程中,重点是考虑尽可能减小截断误差,尽可能消除舍入误差的副作用。
1.2 误差基本概念1.绝对误差与相对误差定义:设x*为某个量的真值,x为x*的近似值,我们称|x*- x|为近似值x的绝对误差;称|x *- x|/|x*|为近似值x的相对误差。
第一章误差分析的基本概念

计算方法-1 -第一章 误差分析的基本概念§ 1误差的来源1. 误差概念:精确值与近似值之差称为误差,也叫绝对误差。
2. 产生误差的主要原因① 模型误差:在解决实际问题时,在一定条件下抓住主要因素将现实系统理想化的数学描述称为实 际问题的数学模型,这种数学描述常常是近似的,数学模型与实际系统之间存在误差,这种误差称为模 型误差。
② 观测误差:数学模型中往往含有一些由观测得到的物理量(如温度、电阻、长度)或由物理量估 算出的模型参数,这些观测物理量或模型参数常常与实际数据存在误差。
这种由观察产生的误差称为观 测误差。
③ 截断误差:数值计算中用有限运算近似代替无穷过程产生的误差。
例如计算一个无穷次可微函数 的函数值时,理论上只要能算出这个函数的泰勒级数值即可,但是实际工程上仅用泰勒级数中前面有限 项来近似计算函数值,而舍去高阶无穷小量。
这个被舍的高阶无穷小量正是截断误差。
④ 舍入误差:计算中按四舍五入进行舍入而引起的误差或因计算机字长有限,数据在内存中存放时 进行了舍入而引起的误差。
3. 举例说明例1设一根铝棒在温度t 时的实际长度为L t ,在t=0 C 时的实际长度为 L o ,用i t 来表示铝棒在温度为t 时的长度计算值,并建立一个数学模型: I tL °(1「.t ),其中a 是由实验观察得到的常数:-二(0.0000238 ± 0.0000001 ) 1/ C,称L t —I t 为模型误差,0.0000001/ C 是a 的观测误差。
这个问题中模型 误差产生的原因是:实际上 L t 与t 2有微弱关系,也就是说模型未能完全反映物理过程。
为了计算近似值,可取前面有限项计算•如取前面五项计算,计算过程中与计算结果都取五位小数得e ~1+1 + 1/2+1/6+1/24疋2.7083, e 取五位小数时的准确值为~ =2.71828,于是截断误差为:□0' —:2.71828 -2.7083 = 0.00995 n总n !这表明:只要在计算中采用了有限步运算近似代替无限步运算的方法,截断误差就一定存在。
计算方法-误差
举例4:计算 tg(1.57079),tg(1.57078)
x 1.57079 , x* 1.57078
(x*) | x x* | 0.00001
r (x*) | (x x*) / x* | 6.410-6
| f ' (x*) | 1 3.8 109
c os2 ( x*)
15
( y*) | f ' (x*) | (x*) 3.8 104
| x * f ' (x*) / f (x*) |
1
9.6 104
s in( x*) c os (x*)
r ( y*) 0.6
y = tan(x) 1.580579134162482e+ 005
y* = tan(x*) 6.124900853150305e+ 004
( y*) =| y-y* | 9.680890488474515e+ 004
1 22
x2 2!
1 x2 3 x3 35 x4
22 2! 23 3! 24
4!
6.172839438271605e-16
3 23
x3 3!
35 24
x4 4!
6.1728394382716030948026634659e-16 3
• 举例3-1:计算机的精度限制(舍入误差)
-- 在matlab中运行计算:
f ( x1, x2 ) f ( x1*, x2 ) f ( x1*, x2 ) f ( x1*, x2*)
f
(1, x2 )
x1
( x1
x1*)
f
( x1*,2 )
x2
( x2
x2*)
f
( x1*, x2*) x1
第一章误差x的相对误差为求xln...

第一章 误差1、设0>x ,x 的相对误差为δ,求x ln 的误差 [解]设0*>x为x 的近似值,则有相对误差为δε=)(*x r ,绝对误差为**)(x x δε=,从而x ln 的误差为δδεε=='=*****1)()(ln )(ln x xx x x ,相对误差为****ln ln )(ln )(ln xxx x r δεε==。
2、设x 的相对误差为2%,求nx 的相对误差。
[解]设*x 为x 的近似值,则有相对误差为%2)(*=x r ε,绝对误差为**%2)(x x =ε,从而nx 的误差为nn x x nxn xx n x x x **1***%2%2)()()()(ln *⋅=='=-=εε,相对误差为%2)()(ln )(ln ***n x x x nr ==εε。
3、计算球体积要使相对误差限为1%,问度量半径R 允许的相对误差是多少?[解]由3*3**3**)(34))(34())(34(%1R R R r ππεπε==可知,)()(4)()(34)(34%1))(34(**2***3*3*3**R R R R R R επεπππε⨯='⎥⎦⎤⎢⎣⎡=⨯=, 从而***31%1)(R R ⨯=ε,故300131%1)()(*****=⨯==RR R r εε。
4、设280=Y ,按递推公式),2,1(78310011 =-=-n Y Y n n 计算到100Y ,若取982.27783≈(五位有效数字,)试问计算100Y 将有多大误差?[解]令n Y 表示n Y 的近似值,n n n Y Y Y e -=)(*,则0)(0*=Y e ,并且由 982.2710011⨯-=-n n Y Y ,78310011⨯-=-n n Y Y 可知,)783982.27(100111-⨯--=---n n n n Y Y Y Y ,即=-⨯-=-⨯-=--)783982.27(1002)()783982.27(1001)()(2*1**n n n Y e Y e Y e ,从而982.27783)783982.27()()(0*100*-=--=Y e Y e ,而31021982.27783-⨯≤-,所以3100*1021)(-⨯=Y ε。
误差理论与数据处理-第一章误差的基本概念ppt课件.ppt

病原体侵 入机体 ,消弱 机体防 御机能 ,破坏 机体内 环境的 相对稳 定性, 且在一 定部位 生长繁 殖,引 起不同 程度的 病理生 理过程
第二节 测量误差的定义及基本概念
一、测量误差
定义
δ=x-a
测量误差
被测量 的真值
测量结果
病原体侵 入机体 ,消弱 机体防 御机能 ,破坏 机体内 环境的 相对稳 定性, 且在一 定部位 生长繁 殖,引 起不同 程度的 病理生 理过程
根据测量条件是否发生变化分类
等权测量
指在测量过程中,测量仪器、测量方法、测量条 件和操作人员都保持不变。因此,对同一被测量进 行的多次测量结果可认为具有相同的信赖程度,应 按同等原则对待。
不等权测量
指测量过程中测量仪器、测量方法、测量条件或 操作人员某一因素或某几因素发生变化,使得测量结 果的信赖程度不同。对不等权测量的数据应按不等权 原则进行处理。
δ≤2.5%×[0.1-(-0.1)]=0.005(MPa) 引用误差专用于仪器仪表误差的描述。
病原体侵 入机体 ,消弱 机体防 御机能 ,破坏 机体内 环境的 相对稳 定性, 且在一 定部位 生长繁 殖,引 起不同 程度的 病理生 理过程
第三节 测量误差的来源
为了减小测量误差,提高测量准确度,就必须了解误差 来源。而误差来源是多方面的,在测量过程中,几乎所有 因素都将引入测量误差。
测量方法误差
病原体侵 入机体 ,消弱 机体防 御机能 ,破坏 机体内 环境的 相对稳 定性, 且在一 定部位 生长繁 殖,引 起不同 程度的 病理生 理过程
按测量结果的获取方式分类
直接测量
指被测量与该标准量直接进行比较的 测量,指该被测量的测量结果可以直接 由测量仪器输出得到,而不再需要经过
第一章 误差分析与数据分析

(a)
(b )
23.5m的近似值,其绝对误差限等于该近似 值末位的半个单位。
截断误差求解数学模型所用的数值计算方法如果是近似的方法那么只能得到数学模型的近似解由此产生的误差称为截断误差或方法误差
第一章
误差分析与数据分析
第一节 误差分析 1.1 误差的来源和分析 1 模型误差
反映实际问题有关量之间的计算公式,即 数学模型,通常只是近似的。由此产生的 数学模型的解与实际问题的解之间的误差, 称为模型误差。
a
称为近似值 a 的相对误差限和相对误差界,有er r 。
例 1 用最小刻度为毫米的卡尺测量直杆甲和直杆乙,分别读出长度 r ( a) 、 r (b) 各是多少?两杆的实 a=312mm 和 b=24mm,问 (a) 、 (b) 、 际长度 x 和 y 的范围?
解: (a) = (b) =0.5mm
5 尽量减少运算次数
定义 设 a 是数 x 的近似值,如果 a 的绝对误差限是它的某一位的半个 单位,并且从该位到它的第一位非零数字共有 n 位,则称用 a 近似 x 时具有 n 位有效数字。
数 a 可以写成如下形式: 0.a1a2…ak × a= 10m a 其中 m 是整数,ai 是 0 到 9 中的一个数字, 1 0。 如果 a 作为 x 的近似值,且
如,由Taylor(泰勒)公式,函数f(x)可表示为,
为简化计算,当误差不大时,去掉上式 右端的最后一项,得近似公式:
此近似公式的误差就是截断误差。
4 舍入误差 由于计算机的字长有限,参加运算的数据 以及运算结果在计算机上存放会产生误差, 这种误差称为舍入误差或计算误差。 如 1/3=0.333333333 (1.000002)2-1.000004=0 在数值分析中,主要研究截断误差和舍入误 差对计算结果的影响,而一般不考虑模型误 差和观测误差。
第一章 误差

出,但往往可以估计出������∗(������)的上界:
即存在正数 ������∗,使得
|������∗(������)| = |������ − ������∗| ≤ ℰ∗
(1.3)
称������∗为近似值������∗的绝对误差限,简称误差限或精度。
4
������∗越小,表示近似值������∗的精度越高。 在 工 程 技 术 中 , 常 将 ������∗ − ������∗ ≤ ������ ≤ ������∗ + ������∗ , 表 示 为 ������ = ������∗ ������∗ 表示近似值������∗的精度或精确值 x 的所在范围,绝对误 差是有量纲的。 例如,������ = (100 ± 2)������ 表示 ������∗ = 100������是电压������的一个近 似值,2������是近似值 ������∗ 的一个绝对误差限,即:|������ − ������∗| ≤ 2������; 又如,用毫米刻度的直尺去测量一个长度为 x 的物体,测得其近 似值为������∗ = 84������������,由于直尺以毫米为刻度,所以其误差不超过 0.5mm,即 x 84 0.5(mm) 。这样,虽然不能得出准确值 x 的长 度是多少,但可以知道 x 范围是 83.5mm x 84.5mm ,即 x 必 在[83.5mm,84.5mm]内。 例 求 ������∗ = 3.14 与 的绝对误差。 解 由于 3.1415 3.1416 ,得
|���������∗��� (������)|
=
������ |
− ������∗ ������∗ |
≤
1 2
× 10������−������+1 ������1 × 10������
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 nx2n
cosx1 L 2 4! 6!
2n!
L
当 x 很小时,可以用 1 x 2 作为 coxs 近似值。
2
由交错级数判断的莱布尼兹(Leibniz)准则, 它的截断误差的绝对值不超过 x 4
24
6
误差的来源
4.舍入误差 在计算过程中往往要对数字进行舍入。 如受机器
字长的限制,无穷小数和位数很多的数必须舍入成 一定的位数。 这样产生的误差称为“舍入误差”。
x * 的第一位非零数字共有q位,则称近似值 x * 有q
位有效数字。
16
绝对误差、相对误差和有效数字
例如, 2 的近似值1.414准确到小数点后第3位, 它具有4位有效数字。
1.4142136作为 2 的近似值精确到小 数点后第7位,有8位有效数字。
准确值之比为近似值 x * 的相对误差,记为 er ( x* )
即
erx*exx*xxx*
(1-3)
relative error
11
绝对误差、相对误差和有效数字
由于在计算过程中准确值x总是未知的,
故一般取相对误差为
er x*
ex* x*
xx* x*
可以证明当 er
x*
e x*
1.模型误差 实际问题的解与数学模型的解之差称为
“模型误差”。 2.观测误差
数学问题中总包含一些参量,它们的值往 往是由观测得到的, 而观测不可能绝对准确, 由此产生的误差称为“观测误差”。
4
误差的来源
3.截断误差
由于实际问题建立起来的数学模型,在很多情况 下得到准确解是困难的,通常要用数值方法求它的 近似解.
数值计算方法是应用数学研究的一个重要分 支(又称数值分析或计算方法), 是研究科学与 工程技术中数学问题的数值解及其理论的,
或者说是“研究用于求得数学问题近似解的 方法和过程”。
用数学方法解决实际问题,常按以下过程 进行:
实际问题 抽象、简化 数学模型 数值计算 问题近似解
3
误差的来源
因此,在计算过程中,误差是不可避免的。 在此过程中,引起误差的因素很多,主要有以 下几种:
很小时, x
e x* x*
是 er
x*
的高阶无穷小,可以忽略不计。
所以,取绝对误差与近似值之比为相对误 差是合理的。
12
绝对误差、相对误差和有效数字
同样,相对误差也只能估计其上限。 如果存在正
数 r , 使得
erx*
ex*
x*
r
(1-4)
则称 r为 x *的相对误差限。
显然,误差限与近似值绝对值之比 x * 为 x *的 一
15
绝对误差、相对误差和有效数字
前面已经提到,通过四舍五入得到的数,其绝对
误差均不超过末位数字的半个单位,
21.4141103 2
3.14161104
2
如果近似值 x *
的误差限是
1 2
1
0
n
,
则称
x*
准
确到小数点后第n位,并从第一个非零数字到这
一位的所有数字均称为有效数字。
定义: 若x的某一近似值 x * 的绝对误差限是某一位 的半个单位, 则称其“准确”到这一位,且从该位直到
例如,常用有限过程逼近无限过程,
用能计算的问题代替不能计算的问题. 这种数学模型的精确解与由数值方法求出的
近似解之间的误差称为截断误差。
由于截断误差是数值方法固有的, 故又称方法误差.
如求一个收敛的无穷级数之和, 总是用它
的部分和作为近似值,也就是截去该级数后面
的无穷多项。
5
误差的来源
例如
x2 x4 x6
数值分析 (54学时)
主 讲: 董 亚 丽
理学院 数学系
教材:《数值计算方法》, 第2版, 丁丽娟 程杞元 编著 北京理工大学 出版社
参考书目: 1、《数值分析原理》,封建湖等 科学出版社
2、《数值计算方法》,吕同富等,清华大学出版社
3、《数值计算方法》,合肥工业大学出版社
误差的来源
第一章误差
§1.1 误差的来源
本课程只讨论截断误差与舍入误差对计算结 果的影响。
§1.2 绝对误差、相对误差和有效数字
7
绝对误差、相对误差和有效数字
1.2.1 绝对误差与相对误差
定义1 设 x * 为准确值 x 的一个近似值,称
e(x*)xx*
(1-1)
为近似值 x * 的绝对误差,简称误差。
当 e(x*) 0 时 ,称 x * 为弱近似值或亏近似值.
个相对误差限。
例 取3.14作为 的四舍五入的近似值,试求其
相对误差限.
13
绝对误差、相对误差和有效数字
解:
3.14 0.00 116 1 02
相对误差限
x*
1102 2
3.14
2 0.159%
又如
由实验测得光速近似值为 c*2.99792 15 05公里/秒, 其误差限为0.1公里/秒, 于是
当 e(x*) 0时 ,称 x * 为强近似值或盈近似值. 一般情况下 准确值 x难以求出,从而也不
能算出绝对误差 e ( x * ) 的准确值,但可以根据测量 工具或计算的情况估计出它的取值范围,
8
绝对误差、相对误差和有效数字
即估计出误差绝对值的一个上界
e(x*)xx*
(1-2)
通常称为近似值 x * 的绝对误差限,简称误差限。
3.140.0016 1 1 0 2
2
若取 3.142, 则
3.142 0.000 1411 0 3
2
10
绝对误差、相对误差和有效数字
误差限的大小不能完全反映近似值的精确程度。 要刻画近似值的精确程度,不仅要看绝对误差的
大小,还必须考虑所测量本身的大小, 由此引出 了相对误差的概念。
定义2 设 x *为准确值 x 的近似值,称绝对误差与
显然误差限不是唯一的。
有了误差限及近似值,就可以得到准确值
的范围
x * x x *
即准确值 x 必定在区间 x*,x*内,
也常ቤተ መጻሕፍቲ ባይዱ作:
xx*
9
绝对误差、相对误差和有效数字
容易看出,经过四舍五入得到的数,其误差必定 不超过被保留的最后数位上的半个单位, 即 最后数位上的半个单位为其误差限。 例如若取 的近似值为3.14,则
0.1 41 07
c* 2.997 912505
所以,4107是 c * 的一个相对误差限。
14
绝对误差、相对误差和有效数字
1.2.2 有效数字 有效数字是近似值的一种表示法。它既能表
示近似值的大小,又能表示其精度程度。 在计算过程中,常常按四舍五入的原则取数
x的前几位数 x *为其近似值。
例如,x 21.414213562L ,取前四位数得 x* 1.414. 取前八位数得近似值 x* 1.4142136
