2019年《南方新课堂·高考总复习》数学(理科)作业及测试:课时作业 第六章不等式
2019年《南方新课堂·高考总复习》数学(理科)作业及测试:课时作业 专题六立体几何 Word版含解析
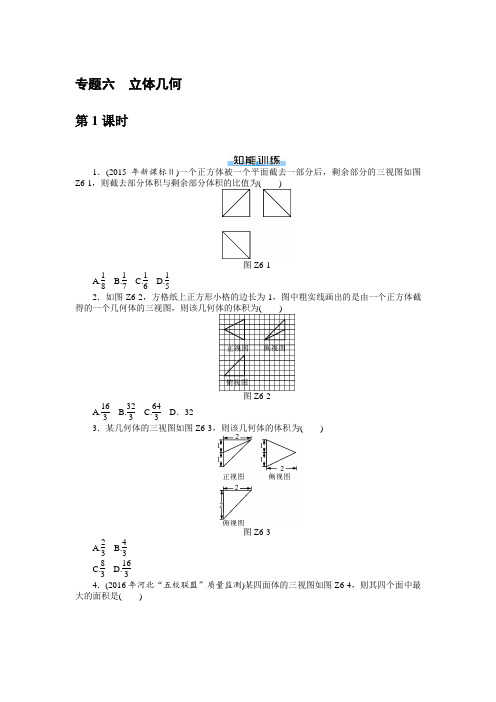
专题六 立体几何第1课时1.(2015年新课标Ⅱ)一个正方体被一个平面截去一部分后,剩余部分的三视图如图Z6-1,则截去部分体积与剩余部分体积的比值为( )图Z6-1 A.18 B.17 C.16 D.152.如图Z6-2,方格纸上正方形小格的边长为1,图中粗实线画出的是由一个正方体截得的一个几何体的三视图,则该几何体的体积为( )图Z6-2 A.163 B.323 C.643D .32 3.某几何体的三视图如图Z6-3,则该几何体的体积为( )图Z6-3 A.23 B.43C.83D.1634.(2016年河北“五校联盟”质量监测)某四面体的三视图如图Z6-4,则其四个面中最大的面积是( )图Z6-4 A .2 B .2 2 C. 3 D .2 35.已知一个几何体的三视图如图Z6-5,则该几何体的体积为( )图Z6-5 A .8 B.223 C.233D .7 6.点A ,B ,C ,D 均在同一球面上,且AB ,AC ,AD 两两垂直,且AB =1,AC =2,AD =3,则该球的表面积为( )A .7πB .14π C.72π D.714π3 7.(2013年新课标Ⅰ)如图Z6-6,有一个水平放置的透明无盖的正方体容器,容器高8 cm ,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6 cm ,如果不计容器厚度,则球的体积为( )图Z6-6 A.500π3 cm 3 B.866π3cm 3 C.1372π3 cm 3 D.2048π3cm 3 8.(2016年北京)某四棱柱的三视图如图Z6-7,则该四棱柱的体积为________.图Z6-79.球O 半径为R =13,球面上有三点A ,B ,C ,AB =12 3,AC =BC =12,则四面体OABC 的体积是( )A .60 3B .50 3C .60 6D .50 610.如图Z6-8,已知正三角形ABC 三个顶点都在半径为2的球面上,球心O 到平面ABC 的距离为1,点E 是线段AB 的中点,过点E 作球O 的截面,则截面面积的最小值是( )图Z6-8 A.7π4 B .2π C.9π4D .3π 11.(2017年广东茂名一模)过球O 表面上一点A 引三条长度相等的弦AB ,AC ,AD ,且两两夹角都为60°,若球半径为R ,则△BCD 的面积为____________.12.已知三棱柱ABC -A 1B 1C 1的侧棱垂直于底面,各顶点都在同一球面上,若该棱柱的体积为3,AB =2,AC =1,∠BAC =60°,则此球的表面积等于________.第2课时1.在直三棱柱ABC -A 1B 1C 1中,若∠BAC =90°,AB =AC =AA 1,则异面直线BA 1与AC 1所成的角等于( )A .30°B .45°C .60°D .90°2.(2016年天津模拟)如图Z6-9,以等腰直角三角形ABC 的斜边BC 上的高AD 为折痕,把△ABD 和△ACD 折成互相垂直的两个平面后,某学生得出下列四个结论:图Z6-9 ①BD ⊥AC ;②△BAC 是等边三角形;③三棱锥D -ABC 是正三棱锥;④平面ADC ⊥平面ABC .其中正确的是( )A .①②④B .①②③C .②③④D .①③④3.三棱锥的三组相对的棱(相对的棱是指三棱锥中成异面直线的一组棱)分别相等,且长各为2,m ,n ,其中m 2+n 2=6,则三棱锥体积的最大值为( )A.33B.12C.8 327D.234.(2016年辽宁葫芦岛统测)已知四棱锥P -ABCD 的五个顶点都在球O 的球面上,底面ABCD 是矩形,平面P AD 垂直于平面ABCD ,在△P AD 中,P A =PD =2,∠APD =120°,AB =2,则球O 的外接球的表面积等于( )A .16πB .20πC .24πD .36π5.在矩形ABCD 中,AD =2,AB =4,E ,F 分别为边AB ,AD 的中点,将△ADE 沿DE 折起,点A ,F 折起后分别为点A ′,F ′,得到四棱锥A ′-BCDE .给出下列几个结论:①A ′,B ,C ,F ′四点共面;②EF ′∥平面A ′BC ;③若平面A ′DE ⊥平面BCDE ,则CE ⊥A ′D ;④四棱锥A ′-BCDE 体积的最大值为2,其中正确的是________(填上所有正确的序号).6.(2017年广东梅州一模)如图Z6-10所示的多面体是由一个直平行六面体被平面AEFG所截后得到的,其中∠BAE =∠GAD =45°,AB =2AD =2,∠BAD =60°.(1)求证:BD ⊥平面ADG ;(2)求平面AEFG 与平面ABCD 所成锐二面角的余弦值.图Z6-107.(2017年广东广州二模)如图Z6-11,ABCD是边长为a的菱形,∠BAD=60°,EB⊥平面ABCD,FD⊥平面ABCD,EB=2FD=3a.(1)求证:EF⊥AC;(2)求直线CE与平面ABF所成角的正弦值.图Z6-118.(2017年广东揭阳一模)如图Z6-12,在直三棱柱ABC-A1B1C1中,AB=BC=BB1,AB1∩A1B=E,D为AC上的点,B1C∥平面A1BD;(1)求证:BD⊥平面A1ACC1;(2)若AB=1,且AC·AD=1,求二面角B-A1D-B1的余弦值.图Z6-12专题六 立体几何第1课时1.D 解析:由三视图,得在正方体ABCD -A 1B 1C 1D 1中,截去四面体A -A 1B 1D 1,如图D164,图D164设正方体棱长为a ,则111-A A B D V =13×12a 3=16a 3. 则剩余几何体体积为a 3-16a 3=56a 3.所以截去部分体积与剩余部分体积的比值为15.故选D.2.B 解析:几何体为如图D165所示的正方体中的三棱锥E -BB 1C (E 为AA 1的中点),它的体积为13×12×4×4×4=323.故选B.图D165 图D1663.B 解析:由三视图知对应的几何体为如图D166所示的正方体中的三棱锥P -ABC ,其中PC ⊥平面P AB ,P A =AB ,PC =PB =2,A 到PB 的距离为2,故该几何体的体积为13×12×2×2×2=43.故选B. 4.D 解析:如图D167,在正方体ABCD -A 1B 1C 1D 1中还原出三视图的直观图,其是一个三个顶点在正方体的右侧面、一个顶点在左侧面的三棱锥,即D 1-BCB 1,其四个面的面积分别为2,2 2,2 2,2 3.故选D.图D1675.D 解析:由三视图可知该几何体是一个由棱长为2的正方体截去两个三棱锥A -A 1PQ 和D -PC 1D 1后剩余的部分,如图D168,其中Q 是棱A 1B 1的中点,P 是A 1D 1的中点,所以该几何体的体积为V =8-13×12×1×1×2-13×12×1×2×2=7.故选D.图D1686.B 解析:三棱锥A -BCD 的三条侧棱两两互相垂直,所以把它扩展为长方体,它也外接于球,长方体的对角线长为其外接球的直径,所以长方体的对角线长是12+22+32=14,它的外接球半径是142,外接球的表面积是4π×⎝⎛⎭⎫1422=14π.故选B. 7.A 解析:如图D169,作出球的一个截面,则MC =8-6=2(cm),BM =12AB =12×8=4(cm).设球的半径为R cm ,则R 2=OM 2+MB 2=(R -2)2+42,∴R =5.∴V 球=43π×53=500π3(cm 3).图D169 8.32解析:由已知的三视图,得该几何体上部是一个以俯视图为底面的四棱柱,其高为1,故该四棱柱的体积V =Sh =12×(1+2)×1×1=32. 9.A 解析:设△ABC 外接圆半径为r ,由AB =12 3,AB =BC =12,得A =B =30°,C =120°.所以2r =12 3sin 120°=24.解得r =12.则O 到平面ABC 的距离d =R 2-r 2=132-122=5.又S △ABC =12×12×12×sin 120°=36 3,所以V O -ABC =13×36 3×5=60 3.故选A. 10.C 解析:根据球的截面圆性质、正三角形的性质与勾股定理,知经过点E 的球O 的截面与OE 垂直时截面圆的半径最小,相应的截面圆的面积有最小值,由此算出截面圆半径的最小值,从而可得截面面积的最小值.设正三角形ABC 的中心为O 1,连接O 1A ,连接O 1O ,O 1C ,OC ,∵O 1是正三角形ABC 的中心,A ,B ,C 三点都在球面上,∴O 1O ⊥平面ABC .结合O 1C ⊂平面ABC ,可得O 1O ⊥O 1C .∵球的半径R =2,球心O 到平面ABC 的距离为1,∴O 1O =1.∴Rt △O 1OC 中,O 1C =R 2-O 1O 2= 3.又∵E 为AB 的中点,△ABC 是等边三角形.∴O 1E =AO 1sin 30°=32.∴OE =OO 21+O 1E 2=72.过E 作球O 的截面,当截面与OE 垂直时,截面圆的半径最小,此时截面圆的半径r =R 2-OE 2=32.可得截面面积为S =πr 2=94π.故选C. 11.2 33R 2 解析:方法一,由条件知A -BCD 是正四面体,△BCD 是正三角形,A ,B ,C ,D 为球上四点,将正三棱锥A -BCD 补充成一个正方体AGBH -FDEC ,如图D170.则正三棱锥A -BCD 和正方体AGBH -FDEC 有共同的外接球,△BCD 的边长就是正方体面的对角线,设正方体AGBH -FDEC 的棱长为a ,则正方体外接球半径R 满足:a 2+a 2+a 2=(2R )2,解得a 2=43R 2.所以BC 2=a 2+a 2=83R 2.所以△BCD 的面积S =12BC ×BD sin 60°=12×83R 2×32=2 33R 2.图D170 图D171方法二,由条件A -BCD 是正四面体,△BCD 是正三角形,A ,B ,C ,D 为球上四点,球心O 在正四面体中心,如图D171.设BC =a ,CD 的中点为E ,O 1为过点B ,C ,D 截面圆的圆心,则截面圆半径r =O 1B =23BE =23×32a =33a . 正四面体A -BCD 的高AO 1=a 2-⎝⎛⎭⎫33a 2=63a . ∴截面BCD 与球心的距离d =OO 1=63a -R . 在Rt △BOO 1中,⎝⎛⎭⎫33a 2=R 2-⎝⎛⎭⎫63a -R 2,解得a =2 63R . ∴△BCD 的面积为S =12BC ×BC sin 60°=12×⎝⎛⎭⎫2 63R 2×32=2 33R 2. 12.8π 解析:∵三棱柱ABC -A 1B 1C 1的侧棱垂直于底面,棱柱的体积为3,AC =1,AB =2,∠BAC =60°,∴12×1×2×sin 60°×AA 1= 3.∴AA 1=2.∵BC 2=AB 2+AC 2-2AB ·AC cos 60°=4+1-2=3,∴BC = 3.设△ABC 外接圆的半径为R ,则BC sin 60°=2R .∴R =1.故外接球的半径为12+12=2,外接球的表面积等于4π×(2)2=8π.第2课时1.C 解析:延长CA 到D ,使得AD =AC ,则ADA 1C 1为平行四边形,∠DA 1B 就是异面直线BA 1与AC 1所成的角.又△A 1DB 为等边三角形.∴∠DA 1B =60°.2.B 解析:由题意知,BD ⊥平面ADC ,故BD ⊥AC ,①正确;AD 为等腰直角三角形斜边BC 上的高,平面ABD ⊥平面ACD ,所以AB =AC =BC ,△BAC 是等边三角形,②正确;易知DA =DB =DC ,又由②知③正确;由①知④错.3.D 解析:直接求三棱锥的体积很困难,因为不知三棱锥的形状,也没有数据,将该三棱锥放进长方体模型,如图D172,三棱锥A -CB 1D 1符合题意,设AA 1=x ,A 1D 1=y ,A 1B 1=z ,有⎩⎪⎨⎪⎧ x 2+y 2=2,x 2+z 2=m 2,y 2+z 2=n 2,x 2+y 2+2z 2=m 2+n 2=6,2z 2=4,z =2,x 2+y 2=2≥2xy ,∴xy ≤1.三棱锥体积V =13V 长方体=13xyz =23xy ≤23.所以三棱锥体积的最大值为23.故选D.图D1724.B 解析:取AD 的中点为E ,连接PE ,则由平面P AD 垂直于平面ABCD 可得,PE⊥平面ABCD ,于是以点E 为原点,以ED ,EP 分别为x ,z 轴建立空间直角坐标系,其中AC 与BD 相交于F 点.于是可得E (0,0,0),D (3,0,0),A (-3,0,0),P (0,0,1),C (3,2,0),B (-3,2,0),F (0,1,0),设球O 的球心的坐标为O (0,1,z 0),则OP →=(0,-1,1-z 0),OB →=(-3,1,-z 0),由|OP →|=|OB →|,得(-1)2+(1-z 0)2=3+1+z 20.解之,得z 0=-1.所以球心O (0,1,-1).于是其半径为|OP →|=5,由球的表面积公式知,S =4πr 2=4π×(5)2=20π.故选B.5.②③6.(1)证明:在△BAD 中,∵AB =2AD =2,∠BAD =60°,∴由余弦定理,可得BD = 3.∵AB 2=AD 2+BD 2,∴AD ⊥BD .又在直平行六面体中,GD ⊥平面ABCD ,BD ⊂平面ABCD ,∴GD ⊥BD .又AD ∩GD =D ,∴BD ⊥平面ADG .(2)解:以D 为坐标原点,建立如图D173所示的空间直角坐标系D -xyz .图D173∵∠BAE =∠GAD =45°,AB =2AD =2,∴A (1,0,0),B (0,3,0),G (0,0,1),E (0,3,2),C (-1,3,0).∴AE →=(-1,3,2),AG →=(-1,0,1).设平面AEFG 的法向量为n =(x ,y ,z ),故有⎩⎪⎨⎪⎧n ·AE →=-x +3y +2z =0,n ·AG →=-x +z =0. 令x =1,得y =-33,z =1.n =(1,-33,1). 而平面ABCD 的一个法向量为DG →=(0,0,1),∴cos 〈DG →,n 〉=DG →·n |DG →|·|n |=217. 故平面AEFG 与平面ABCD 所成锐二面角的余弦值为217. 7.解:(1)证明:连接BD ,如图D174.因为ABCD 是菱形,所以AC ⊥BD .因为FD ⊥平面ABCD ,AC ⊂平面ABCD ,所以AC ⊥FD .因为BD ∩FD =D ,所以AC ⊥平面BDF .因为EB ⊥平面ABCD ,FD ⊥平面ABCD ,所以EB ∥FD .所以B ,D ,F ,E 四点共面.因为EF ⊂平面BDFE ,所以EF ⊥AC .图D174 图D175(2)如图D175,以D 为坐标原点,分别以DC →,DF →的方向为y 轴,z 轴的正方向,建立空间直角坐标系D -xyz .可以求得A ⎝⎛⎭⎫32a ,-12a ,0,B ⎝⎛⎭⎫32a ,12a ,0,F ⎝⎛⎭⎫0,0,32a ,C (0,a,0),E ⎝⎛⎭⎫32a ,12a ,3a .所以AB →=(0,a,0),AF →=⎝⎛⎭⎫-32a ,12a ,32a .设平面ABF 的法向量为n =(x ,y ,z ),则⎩⎪⎨⎪⎧n ·AB →=0,n ·AF →=0,即⎩⎪⎨⎪⎧ay =0,-32ax +12ay +32az =0.取x =1,则平面ABF 的一个法向量为n =(1,0,1).因为CE →=⎝⎛⎭⎫32a ,-12a ,3a ,所以||cos 〈n ,CE →〉=||n ·CE →||n ||CE →=3 68.所以直线CE 与平面ABF 所成角的正弦值为3 68.8.(1)证明:如图D176,连接ED ,∵平面AB 1C ∩平面A 1BD =ED ,B 1C ∥平面A 1BD ,∴B 1C ∥ED .∵E 为AB 1的中点,∴D 为AC 的中点.∵AB =BC ,∴BD ⊥AC .①方法一,由A 1A ⊥平面ABC ,BD ⊂平面ABC ,得A 1A ⊥BD ,②由①②及A 1A ,AC 是平面A 1ACC 1内的两条相交直线,∴BD ⊥平面A 1ACC 1.方法二,∵A 1A ⊥平面ABC ,A 1A ⊂平面A 1ACC 1,∴平面A 1ACC 1⊥平面ABC .又平面A 1ACC 1∩平面ABC =AC , ∴BD ⊥平面A 1ACC 1.图D176 图D177 (2)由AB =1,得BC =BB 1=1.由(1)知DA =12AC ,由AC ·DA =1,得AC 2=2. ∵AC 2=2=AB 2+BC 2,∴AB ⊥BC .以B 为原点,建立空间直角坐标系B -xyz 如图D177,则A 1(1,0,1),B 1(0,0,1),D ⎝⎛⎭⎫12,12,0.所以B 1A 1→=(1,0,0),B 1D →=⎝⎛⎭⎫12,12,-1. 设m =(x ,y ,z )是平面A 1B 1D 的一个法向量,则⎩⎪⎨⎪⎧ m ⊥B 1A 1→,m ⊥B 1D →,得⎩⎪⎨⎪⎧m ·B 1A 1→=x =0,m ·B 1D →=12x +12y -z =0. 令z =1,得m =(0,2,1).设n =(a ,b ,c )为平面A 1BD 的一个法向量,则⎩⎪⎨⎪⎧ n ⊥BD →,n ⊥BA 1→,得⎩⎪⎨⎪⎧n ·BD →=a 2+b 2=0,n ·BA 1→=a +c =0.令c =1,得n =(-1,1,1).依题意知二面角B -A 1D -B 1为锐二面角,设其大小为θ,则cos θ=|cos 〈n ,m 〉|=|n ·m ||n |·|m |=35×3=155. 即二面角B -A 1D -B 1的余弦值为155.。
2019年《南方新课堂·高考总复习》数学(理科)作业及测试课时作业 专题三数列与不等式 Word版含解析

专题三数列与不等式
.已知等差数列{},{}的前项和分别为,,且=,则使得
为整数的正整数的个数是( )
....
.已知等差数列{}的公差≠,且,,成等比数列,若=,为数列{}的前项和,则
的最小值为( )
...-
.(年新课标Ⅱ)设是数列{}的前项和,且=-,+=+,则=.
.设数列{}的前项和为,且满足+=,则的取值范围是( )
.() .(,+∞)
.(年广东调研)设是等比数列{}的前项的积,若(+)=,=,则当取最小值时,=..(年新课标
Ⅰ)几名大学生响应国家的创业号召,开发了一款应用软件.为激发大家学习数学的兴趣,他们推出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案:已知数列,…,其中第一项是,接下来的两项是,再接下来的三项是,依此类推.求满足如下条件的最小整数:>且该数列的前项和为的整数幂.那么该款软件的激活码是(
)
....
.(年新课标Ⅲ)已知各项都为正数的数列{}满足=,-(+-)-+=.
()求,;
()求{}的通项公式.
.(年广东揭阳一模)设等差数列{}的前项和为,且=,=+-.
()求数列{}的通项公式;
()设数列{}满足++…+=-,求{}的前项和.
.(年广东汕头一模)已知数列{}的前项和为,=,+=+.
()求数列{}的通项公式;
()已知=,求数列的前项和.
.(年天津)已知{}为等差数列,前项和为(∈
*),{}是首项为的等比数列,且公比大于,+=,=-,=.
()求{}和{}的通项公式;
()求数列{-}的前项和(∈*).。
2019年《南方新课堂·高考总复习》数学(理科)作业及测试:课时作业 专题五圆锥曲线的综合及应用问题含解析

专题五 圆锥曲线的综合及应用问题第1课时1.已知点F 1,F 2分别为双曲线x 2-y 23=1的左、右焦点,点P 为双曲线右支上的任意一点,则|PF 1|2|PF 2|的最小值为( )A .8B .5C .4D .92.已知点F 1,F 2是x 24+y 2=1的左、右焦点,点P 在椭圆上运动,则PF 1→·PF 2→的最大值是( )A .4B .5C .2D .13.(2017年广东揭阳一模)已知双曲线x 24-y 22=1右焦点为F ,P 为双曲线左支上一点,点A (0,2),则△APF 周长的最小值为( )A .4(1+2)B .4+ 2C .2(2+6) D.6+3 2 4.(2016年四川)设O 为坐标原点,P 是以F 为焦点的抛物线y 2=2px (p >0) 上任意一点,M 是线段PF 上的点,且|PM |=2|MF |,则直线OM 的斜率的最大值为( )A.33B.23C.22 D .1 5.设F 1,F 2分别是椭圆x 225+y 216=1的左、右焦点,P 为椭圆上任一点,点M 的坐标为(6,4),则|PM |+|PF 1|的最大值为________.6.已知F 是双曲线x 24-y 212=1的左焦点,A (1,4),P 是双曲线右支上的动点,则|PF |+|PA |的最小值为________.7.(2014年新课标Ⅰ)已知点A (0,-2),椭圆E :x 2a 2+y 2b 2=1(a >b >0)的离心率为32,F 是椭圆的焦点,直线AF 的斜率为2 33,O 为坐标原点. (1)求E 的方程;(2)设过点A 的直线l 与E 相交于P ,Q 两点,当△OPQ 的面积最大时,求l 的方程.8.(2017年广东广州二模)已知双曲线x 25-y 2=1的焦点是椭圆C :x 2a 2+y 2b2=1(a >b >0)的顶点,且椭圆与双曲线的离心率互为倒数.(1)求椭圆C 的方程;(2)设动点M ,N 在椭圆C 上,且|MN |=4 33,记直线MN 在y 轴上的截距为m ,求m的最大值.第2课时1.(2017年广东调研)已知椭圆C :x 2a 2+y 2b2=1(a >b >0)的右焦点到直线x -y +3 2=0的距离为5,且椭圆C 的一个长轴端点与一个短轴端点间的距离为10.(1)求椭圆C 的标准方程;(2)给出定点Q ⎝⎛⎭⎪⎫6 55,0,对于椭圆C 的任意一条过Q 的弦AB ,1|QA |2+1|QB |2是否为定值?若是,求出该定值,若不是,请说明理由.2.已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)的离心率为22,且过点P (2,1).(1)求椭圆C 的方程;(2)若A 1,A 2分别是椭圆C 的左、右顶点,动点M 满足MA 2⊥A 1A 2,且MA 1交椭圆C 于不同于A 1的点R ,求证:OR →·OM →为定值.3.(2017年广东广州一模)过点P (a ,-2)作抛物线C :x 2=4y 的两条切线,切点分别为A (x 1,y 1), B (x 2,y 2).(1)证明:x 1x 2+y 1y 2为定值;(2)记△PAB 的外接圆的圆心为点M ,点F 是抛物线C 的焦点, 对任意实数a ,试判断以PM 为直径的圆是否恒过点F? 并说明理由.4.(2017年广东广州华附执信深外联考)已知椭圆x 2a 2+y 2b 2=1,离心率为63,点A ,B分别是椭圆与x 轴,y 轴的交点,且原点O 到AB 的距离为62. (1)求椭圆方程;(2)如图Z51若F 是椭圆的右焦点,过F 的直线l 交椭圆于M ,N 两点,当直线l 绕着点F 转动过程中,试问在直线x =3上是否存在点P ,使得△PMN 是以P 为顶点的等腰直角三角形,若存在,求出直线l 的方程;若不存在,请说明理由。
2019年《南方新课堂·高考总复习》数学(理科)作业及测试:课时作业 专题三数列与不等式含解析

专题三 数列与不等式1.已知等差数列{a n },{b n }的前n 项和分别为S n ,T n ,且S n T n =7n +45n -3,则使得a nb n为整数的正整数n 的个数是( )A .3B .4C .5D .62.已知等差数列{a n }的公差d ≠0,且a 1,a 3,a 13成等比数列,若a 1=1,S n 为数列{a n }的前n 项和,则2S n +16a n +3的最小值为( )A .4B .3C .2 3-2 D.923.(2015年新课标Ⅱ)设S n 是数列{a n }的前n 项和,且a 1=-1,a n +1=S n S n +1,则S n=________.4.设数列{a n }的前n 项和为S n ,且满足a n +S n =1,则S n 的取值范围是( ) A .(0,1) B .(0,+∞) C.⎣⎢⎡⎭⎪⎫12,1 D.⎣⎢⎡⎭⎪⎫12,+∞ 5.(2017年广东调研)设R n 是等比数列{a n }的前n 项的积,若25(a 1+a 3)=1,a 5=27a 2,则当R n 取最小值时,n =______.6.(2017年新课标Ⅰ)几名大学生响应国家的创业号召,开发了一款应用软件.为激发大家学习数学的兴趣,他们推出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案:已知数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,…,其中第一项是20,接下来的两项是20,21,再接下来的三项是20,21,22,依此类推.求满足如下条件的最小整数N :N >100且该数列的前N 项和为2的整数幂.那么该款软件的激活码是( )A .440B .330C .220D .1107.(2016年新课标Ⅲ)已知各项都为正数的数列{a n }满足a 1=1,a 2n -(2a n +1-1)a n -2a n +1=0.(1)求a 2,a 3;(2)求{a n }的通项公式.8.(2017年广东揭阳一模)设等差数列{a n }的前n 项和为S n ,且S 4=4S 2,a 2n =2a n +1-3.(1)求数列{a n }的通项公式;(2)设数列{b n }满足a 1b 1+a 2b 2+…+a n b n =3-2n +32n ,求{b n }的前n 项和T n .9.(2017年广东汕头一模)已知数列{a n }的前n 项和为S n ,a 1=2,a n +1=S n +2. (1)求数列{a n }的通项公式;(2)已知b n =log 2a n ,求数列⎩⎨⎧⎭⎬⎫1b n b n +1的前n 项和T n .10.(2017年天津)已知{a n }为等差数列,前n 项和为S n (n ∈N *),{b n }是首项为2的等比数列,且公比大于0,b 2+b 3=12,b 3=a 4-2a 1,S 11=11b 4.(1)求{a n }和{b n }的通项公式;(2)求数列{a 2n b 2n -1}的前n 项和(n ∈N *).专题三 数列与不等式1.B 解析:a n b n =2a n 2b n =a 1+a 2n -1b 1+b 2n -1=S 2n -1T 2n -1=14n +382n -4=7n +19n -2=7+33n -2,∴n -2=-1或1或3或11或33,∴n =1或3或5或13或35.当n =3时,S n T n =T n +45n -3中分母为零,所以舍去.2.A 解析:由a 1,a 3,a 13成等比数列,得a 23=a 1a 13⇒(a 1+2d )2=a 1(a 1+12d )⇒4d2=8a 1d .因为d ≠0,因此d =2a 1=2,S n =n 2,a n =2n -1,从而2S n +16a n +3=n 2+8n +1=(n +1)+9n +1-2≥2n +9n +1-2=4,当且仅当n =2时取等号.故选A. 3.-1n解析:由已知,得a n +1=S n +1-S n =S n +1·S n ,两边同时除以-S n +1·S n ,得1S n +1-1S n=-1,故数列⎩⎨⎧⎭⎬⎫1S n 是以-1为首项,-1为公差的等差数列.则1S n=-1-(n -1)=-n .所以S n =-1n.4.C 解析:当n =1时,a 1=12.当n ≥2时,a n -1+S n -1=1,得a n -a n -1+a n =0,即2a n =a n -1.∴数列{}a n 是首项为12,公比为12的等比数列.∴S n =12×⎣⎢⎡⎦⎥⎤1-⎝ ⎛⎭⎪⎫12n 1-12=1-⎝ ⎛⎭⎪⎫12n.∴S n ∈⎣⎢⎡⎭⎪⎫12,1. 5.6 解析:设公比为q ,则q 3=a 5a 2=27.所以q =3.由25(a 1+a 3)=1,得25(a 1+a 1·32)=1,解得a 1=1250.则a n =3n -1250.则要使R n 取得最小值,必有⎩⎪⎨⎪⎧a n ≤1,a n +1>1,即⎩⎪⎨⎪⎧3n -1250≤1,3n250>1,所以250<3n≤750,解得n =6.6.A 解析:由题意,得数列如下: 1, 1,2, 1,2,4, …则该数列的前1+2+…+k =k k +2项和为S ⎝ ⎛⎭⎪⎫k k +2=1+(1+2)+…+(1+2+…+2k )=2k +1-k -2. 要使k k +2>100,有k ≥14,此时k +2<2k +1.所以k +2是之后的等比数列1,2,…,2k +1的部分和,即k +2=1+2+…+2t -1=2t-1.所以k =2t -3≥14,则t ≥5,此时k =25-3=29.对应满足的最小条件为N =29×302+5=440.故选A.7.解:(1)由题意,得a 2=12,a 3=14.(2)由a 2n -(2a n +1-1)a n -2a n +1=0,得 2a n +1(a n +1)=a n (a n +1).因为{a n }的各项都为正数,所以a n +1a n =12.故{a n }是首项为1,公比为12的等比数列.因此a n =12n -1.8.解:(1)设{a n }的公差为d ,则有 ⎩⎪⎨⎪⎧4a 1+6d =a 1+d ,a 1+n -d =a 1+nd -3, 解得⎩⎪⎨⎪⎧a 1=1,d =2.故a n =a 1+(n -1)d =2n -1.(2)a 1b 1+a 2b 2+…+a n b n =3-2n +32n , ①当n =1时,a 1b 1=12,所以b 1=12.当n ≥2时,a 1b 1+a 2b 2+…+a n -1b n -1=3-2n +12n -1. ②①式减去②式,得a n b n =2n -12n .求得b n =12n ,易知当n =1时也成立,所以数列{b n }为等比数列.其前n 项和T n =b 1+b 2+…+b n =12⎣⎢⎡⎦⎥⎤1-⎝ ⎛⎭⎪⎫12n 1-12=1-⎝ ⎛⎭⎪⎫12n.9.解:(1)∵a n +1=S n +2,∴a n =S n -1+2(n ≥2). 两式作差,得a n +1-a n =S n -S n -1=a n .∴a n +1=2a n ,即a n +1a n=2(n ≥2). 又当n =1时,a 2=S 1+2=4,∴a 2a 1=2成立.∴数列{a n }是公比为2,首项为2的等比数列.∴a n =a 1q n -1=2n (n ∈N *).(2)由(1),可得b n =log 2a n =n .∴1b n b n +1=1n n +=1n -1n +1.∴T n =⎝ ⎛⎭⎪⎫11-12+⎝ ⎛⎭⎪⎫12-13+…+⎝ ⎛⎭⎪⎫1n -1n +1=1-1n +1=n n +1. 10.解:(1)设等差数列{a n }的公差为d ,等比数列{b n }的公比为q .由已知b 2+b 3=12,得b 1(q +q 2)=12.因为b 1=2,所以q 2+q -6=0.又因为q >0,解得q =2.所以b n =2n. 由b 3=a 4-2a 1,可得3d -a 1=8.① 由S 11=11b 4,可得a 1+5d =16.②联立①②,解得a 1=1,d =3.由此可得a n =3n -2.所以数列{a n }的通项公式为a n =3n -2,数列{b n }的通项公式为b n =2n. (2)设数列{a 2n b 2n -1}的前n 项和为T n ,因为a 2n =6n -2,b 2n -1=2×4n -1,所以a 2n b 2n -1=(3n -1)×4n.故T n =2×4+5×42+8×43+…+(3n -1)×4n,4T n =2×42+5×43+8×44+…+(3n -4)×4n +(3n -1)×4n +1,上述两式相减,得-3T n =2×4+3×42+3×43+…+3×4n -(3n -1)×4n +1=-4n 1-4-4-(3n -1)×4n +1=-(3n -2)×4n +1-8.得T n =3n -23×4n +1+83.所以数列{a 2n b 2n -1}的前n 项和为3n -23×4n +1+83.。
2019年《南方新课堂·高考总复习》数学(理科)课件:第六章 第4讲 简单的线性规划

图 6-4-2 其中点 A(1,1),B(-1,-1),C-1,151.z=x-y 2表示△ABC 区 域 内 ( 含 边 界 ) 的 点 与 点 M(2,0) 的 连 线 的 斜 率 , 显 然 kMA≤z≤kMB,即1-1 2≤z≤--1-1 2.化简,得-1≤z≤13.
答案:-1,13
答案:3
图 6-4-1
(2)(2017 年湖北七市联考)若变量 x,y 满足约束条件
xy≥ ≥- x,1, 3x+5y≤8,
则 z=x-y 2的取值范围是__________.
解 析 : 作 出 不 等 式 组 xy≥ ≥- x,1, 3x+5y≤8
所表示的区域,如图
6-4-2 中△ABC 所表示的区域(含边界).
1.不等式组xx- -3y+y+26≥<00, 表示的平面区域是( C )
A
B
C
D
解析:x-3y+6<0 表示直线 x-3y+6=0 左上方的平面区
域,x-y+2≥0 表示直线 x-y+2=0 及其右下方的平面区域.
故选 C.
2.(2016 年辽宁沈阳四校联考)下列各点中,与点(1,2)位于直
能用平面区域表示 2015年新课标Ⅰ第15题考查简单线 二元一次不等式组. 性规划求截距的最大值; 3.会从实际情境中 2016年新课标Ⅱ第14题考查简单线 抽象出一些简单的 性规划求最值,山东、江苏考查非
二元线性规划问题,线性规划的最值(距离);
并能加以解决
2017年新课标Ⅰ第14题考查简单线
性规划求截距的最小值
(2)因为对直线 Ax+By+C=0 同一侧的所有点(x,y),把它 的坐标(x,y)代入 Ax+By+C 所得到实数的符号都相同,所以 只需在此直线的某一侧取一个特殊点(x0,y0),由Ax0+By0+C 的符号即可判断不等式表示的平面区域.
2019年《南方新课堂·高考总复习》数学(理科)作业及测试:课时作业 第三章 三角函数与解三角形含解析

第三章 三角函数与解三角形第1讲 弧度制与任意角的三角函数1.设集合M =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x =k2·180°+45°,k ∈Z,N =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x =k4·180°+45°,k ∈Z,则( ) A .M =N B .M ⊆NC .N ⊆MD .M ∩N =∅2.(2017年青海西宁复习检测)若cos θ>0,且sin 2θ<0,则角θ的终边所在象限为( )A .第一象限B .第二象限C .第三象限D .第四象限 3.若角α是第一象限角,则α2是( )A .第一象限角B .第二象限角C .第一或第三象限角D .第二或第四象限角4.(2016年四川成都模拟)若α是第三象限角,则下列各式中不成立的是( ) A .sin α+cos α<0 B .tan α-sin α<0 C .cos α-tan α<0 D .tan αsin α<05.若角α的终边经过点P (1,m ),且tan α=-2,则sin α=( )A.55 B .-55 C.2 55 D .-2 556.(2014年新课标Ⅰ)若tan α>0,则( ) A .sin α>0 B .cos α>0 C .sin 2α>0 D .cos 2α>07.设α是第二象限角,点P (x,4)为其终边上的一点,且cos α=15x ,则tan α=( )A.43B.34 C .-34 D .-438.(2016年河北衡水二中模拟)已知角φ的终边经过点P (-4,3),函数f (x )=sin(ωx +φ)(ω>0)图象的相邻两条对称轴之间的距离等于π2,则f ⎝ ⎛⎭⎪⎫π4的值为( ) A.35 B.45 C .-35 D .-459.(2017年广东深圳二模)以角θ的顶点为坐标原点,始边为x 轴的非负半轴,建立平面直角坐标系,角θ的终边过点P (1,2),则tan ⎝ ⎛⎭⎪⎫θ+π4=________.10.在如图X311的算法中,令a =tan θ,b =sin θ,c =cos θ,若在集合⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫θ⎪⎪⎪0<θ<3π2中任取θ的一个值,输出的结果是sin θ的概率是( )图X311A.13B.12C.23D.3411.判断下列各式的符号:(1)tan 125°·sin 278°; (2)cos 7π12tan23π12sin11π12.12.(1)已知扇形的周长为10,面积为4,求扇形圆心角的弧度数;(2)已知扇形的周长为40,当它的半径和圆心角取何值时,才能使扇形的面积最大?最大面积是多少?第2讲 同角三角函数的基本关系式与诱导公式1.sin 2013°的值属于区间( )A.⎝ ⎛⎭⎪⎫-12,0B.⎝⎛⎭⎪⎫-1,-12 C.⎝ ⎛⎭⎪⎫12,1 D.⎝ ⎛⎭⎪⎫0,12 2.下列关系式中,正确的是( ) A .sin 11°<cos 10°<sin 168° B .sin 168°<sin 11°<cos 10° C .sin 11°<sin 168°<cos 10° D .sin 168°<cos 10°<sin 11°3.已知sin α-cos α=2,α∈(0,π),则tan α=( )A .-1B .-22 C.22D .14.(2014年大纲)设a =sin 33°,b =cos 55°,c =tan 35°,则( ) A .a >b >c B .b >c >a C .c >b >a D .c >a >b5.(2011年新课标)已知角θ的顶点与原点重合,始边与x 轴的正半轴重合,终边在直线y =2x 上,则cos 2θ=( )A .-45B .-35 C.35 D.456.下列不等式成立的是( )A .tan ⎝ ⎛⎭⎪⎫9π8>tan ⎝ ⎛⎭⎪⎫π6B .sin ⎝ ⎛⎭⎪⎫-3π10>sin ⎝ ⎛⎭⎪⎫-π5C .sin π18>sin π10D .cos ⎝ ⎛⎭⎪⎫-7π4>cos ⎝ ⎛⎭⎪⎫-23π5 7.(2012年大纲)已知α为第二象限角,sin α+cos α=33,则cos 2α=( ) A .-53 B .-59 C.59 D.538.(2017年浙江绍兴二模)已知sin α+cos α=15,α∈(0,π),则tan α=( )A .-43B .-34 C.43 D.349.(2013年新课标Ⅱ)设θ为第二象限角,若tan ⎝⎛⎭⎪⎫θ+π4=12,则sin θ+cos θ=________.10.(2016年广东惠州三调)已知sin θ+cos θ=43(0<θ<π4),则sin θ-cos θ的值为( )A.23 B .-23 C.13 D .-1311.已知函数f (x )=1-2sin ⎝ ⎛⎭⎪⎫2x -π4cos x.(1)求函数f (x )的定义域;(2)设α是第四象限角,且tan α=-43,求f (α)的值.12.已知tan α=2.(1)求tan ⎝⎛⎭⎪⎫α+π4的值; (2)求sin 2αsin α+sin αcos α-cos 2α-1的值.第3讲 三角函数的图象与性质1.下列四个函数中,最小正周期为π,且图象关于直线x =π12对称的是( )A .y =sin ⎝ ⎛⎭⎪⎫x 2+π3B .y =sin ⎝ ⎛⎭⎪⎫x 2-π3 C .y =sin ⎝ ⎛⎭⎪⎫2x +π3 D .y =sin ⎝⎛⎭⎪⎫2x -π3 2.(2017年重庆适应性测试)若函数f (x )=sin ⎝⎛⎭⎪⎫ωx +π6-cos ωx (ω>0)的图象相邻两个对称中心之间的距离为π2,则f (x )的一个单调递增区间为( )A.⎝ ⎛⎭⎪⎫-π6,π3B.⎝ ⎛⎭⎪⎫-π3,π6C.⎝ ⎛⎭⎪⎫π6,2π3D.⎝ ⎛⎭⎪⎫π3,5π63.(2016年新课标Ⅱ)函数y =A sin(ωx +φ)的部分图象如图X331,则( )图X331A .y =2sin ⎝ ⎛⎭⎪⎫2x -π6B .y =2sin ⎝ ⎛⎭⎪⎫2x -π3C .y =2sin ⎝ ⎛⎭⎪⎫2x +π6D .y =2sin ⎝⎛⎭⎪⎫2x +π3 4.(2017年广东茂名一模)已知函数f (x )=3cos ⎝⎛⎭⎪⎫ωx +π3(ω>0)和g (x )=2sin(2x+φ)+1的图象的对称轴完全相同,若x ∈⎣⎢⎡⎦⎥⎤0,π3,则f (x )的取值范围是( )A .[-3,3] B.⎣⎢⎡⎦⎥⎤-32,3 C.⎣⎢⎡⎦⎥⎤-3,3 32 D.⎣⎢⎡⎦⎥⎤-3,32 5.(2013年大纲)若函数y =sin(ωx +φ)(ω>0)的部分图象如图X332,则ω=( )图X332A .5B .4C .3D .26.函数y =|tan x |cos x ⎝⎛⎭⎪⎫0≤x <3π2,且x ≠π2的图象是( )A BC D7.(2017年新课标Ⅲ)设函数f (x )=cos ⎝⎛⎭⎪⎫x +π3,则下列结论错误的是( )A .f (x )的一个周期为-2πB .y =f (x )的图象关于直线x =8π3对称C .f (x +π)的一个零点为x =π6D .f (x )在⎝ ⎛⎭⎪⎫π2,π上单调递减 8.(2016年江苏)定义在区间[0,3π]上的函数y =sin 2x 的图象与函数y =cos x 的图象的交点个数是______.9.(2017年浙江温州中学统测)已知函数f (x )=sin ωx -3cos ωx (ω>0)的图象与x轴的两个相邻交点的距离等于π2,若将函数y =f (x )的图象向左平移π6个单位长度得到函数y =g (x )的图象,则y =g (x )是减函数的区间为( )A.⎝ ⎛⎭⎪⎫π4,π3B.⎝ ⎛⎭⎪⎫-π4,π4C.⎝ ⎛⎭⎪⎫0,π3D.⎝ ⎛⎭⎪⎫-π3,010.(2012年新课标)已知ω>0,函数f (x )=sin ⎝ ⎛⎭⎪⎫ωx +π4在⎝ ⎛⎭⎪⎫π2,π上单调递减,则ω的取值范围是( )A.⎣⎢⎡⎦⎥⎤12,54B.⎣⎢⎡⎦⎥⎤12,34C.⎝ ⎛⎭⎪⎫0,12 D .(0,2] 11.已知函数f (x )=(sin x +cos x )2+cos 2x . (1)求f (x )的最小正周期;(2)求f (x )在区间⎣⎢⎡⎦⎥⎤0,π2上的最大值和最小值.12.是否存在实数a,使得函数y=sin2x+a cos x+58a-32在闭区间⎣⎢⎡⎦⎥⎤0,π2上的最大值是1?若存在,求出对应的a值;若不存在,请说明理由.第4讲 函数y =A sin(ωx +φ)的图象1.函数y =sin(ωx +φ)(x ∈R ,ω>0,0≤φ<2π)的部分图象如图X341,则( )图X341A .ω=π2,φ=π4B .ω=π3,φ=π6C .ω=π4,φ=π4D .ω=π4,φ=5π42.为了得到函数y =sin 3x +cos 3x 的图象,可以将函数y =2cos 3x 的图象( )A .向右平移π12个单位长度B .向右平移π4个单位长度C .向左平移π12个单位长度D .向左平移π4个单位长度3.(2017年四川眉山中学统测)将函数f (x )=3sin ⎝⎛⎭⎪⎫2x +π3 的图象向右平移π2个单位长度,所得图象对应的函数( )A .其一条对称轴方程为x =-π6B .在区间⎣⎢⎡⎦⎥⎤π12,7π12上单调递增C .当x =π12+k π(k ∈Z )时取得最大值D .在区间⎣⎢⎡⎦⎥⎤-π6,π3上单调递增 4.(2015年湖南)将函数f (x )=sin 2x 的图象向右平移φ⎝⎛⎭⎪⎫0<φ<π2个单位长度后得到函数g (x )的图象,若对满足|f (x 1)-g (x 2)|=2的x 1,x 2,有|x 1-x 2|min =π3,则φ=( )A.5π12B.π3C.π4D.π65.(2017年湖北咸宁模拟)已知函数f (x )=sin(ωx +φ)⎝⎛⎭⎪⎫ω>0,-π2<φ<π2的最小正周期为π,将该函数的图象向左平移π6个单位长度后,得到的图象对应的函数为奇函数,则f (x )的图象( )A .关于点⎝ ⎛⎭⎪⎫π12,0对称 B .关于直线x =5π12对称 C .关于点⎝ ⎛⎭⎪⎫5π12,0对称 D .关于直线x =π12对称6.设f (x )=3sin 3x +cos 3x ,若对任意实数x 都有|f (x )|≤a ,则实数a 的取值范围是________.7.已知函数f (x )=sin ⎝ ⎛⎭⎪⎫2x +π6,其中x ∈⎣⎢⎡⎦⎥⎤-π6,a .当a =π3时,f (x )的值域是__________;若f (x )的值域是⎣⎢⎡⎦⎥⎤-12,1,则a 的取值范围是__________. 8.(2015年湖南)已知ω>0,在函数y =2sin ωx 与y =2cos ωx 的图象的交点中,距离最短的两个交点的距离为2 3,则ω=________.9.(2015年天津)已知函数f (x )=sin ωx +cos ωx (ω>0),x ∈R ,若函数f (x )在区间(-ω,ω)内单调递增,且函数f (x )的图象关于直线x =ω对称,则ω的值为____________.10.(2014年北京)函数f (x )=3sin ⎝⎛⎭⎪⎫2x +π6的部分图象如图X342. (1)写出f (x )的最小正周期及图中x 0,y 0的值;(2)求f (x )在区间⎣⎢⎡⎦⎥⎤-π2,-π12上的最大值和最小值.图X34211.(2017年山东)设函数f (x )=sin ⎝ ⎛⎭⎪⎫ωx -π6+sin ⎝⎛⎭⎪⎫ωx -π2,其中0<ω<3,已知f ⎝ ⎛⎭⎪⎫π6=0.(1)求ω;(2)将函数y =f (x )的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),再将得到的图象向左平移π4个单位,得到函数y =g (x )的图象,求g (x )在⎣⎢⎡⎦⎥⎤-π4,3π4上的最小值.第5讲 两角和与差及二倍角的三角函数公式1.(2016年新课标Ⅱ)若cos ⎝ ⎛⎭⎪⎫π4-α=35,则sin 2α=( )A.725B.15 C .-15 D .-7252.4cos 50°-tan 40°=( )A. 2B.2+32C. 3 D .2 2-13.(2017年上海师大附中统测)函数y =2cos 2⎝⎛⎭⎪⎫x -π4-1是( ) A .最小正周期为π的奇函数 B .最小正周期为π的偶函数C .最小正周期为π2的奇函数D .最小正周期为π2的偶函数4.(2015年上海)已知点A 的坐标为(4 3,1),将OA 绕坐标原点O 逆时针旋转π3至OB ,则点B 的纵坐标为( )A.3 32B.5 32C.112D.1325.(2017年江苏)若tan ⎝⎛⎭⎪⎫α-π4=16, 则tan α=________. 6.(2017年北京)在平面直角坐标系xOy 中,角α与角β均以Ox 为始边,它们的终边关于y 轴对称.若sin α=13,cos(α-β)=________.7.(2016年新课标Ⅲ)函数y =sin x -3cos x 的图象可由函数y =2sin x 的图象至少向右平移______个单位长度得到.8.(2016年上海)若函数f (x )=4sin x +a cos x 的最大值为5,则常数a =________. 9.(2016年上海)方程3sin x =1+cos 2x 在区间[0,2π]上的解为__________.10.(2015年浙江)函数f (x )=sin 2x +sin x cos x +1的最小正周期是________,最小值是________,单调递减区间是____________________.11.(2014年江苏)已知α∈⎝⎛⎭⎪⎫π2,π,sin α=55.(1)求sin ⎝ ⎛⎭⎪⎫π4+α的值;(2)求cos ⎝ ⎛⎭⎪⎫5π6-2α的值.12.(2017年北京)已知函数f (x )=3cos ⎝⎛⎭⎪⎫2x -π3-2sin x cos x . (1)求f (x )的最小正周期;(2)求证:当x ∈⎣⎢⎡⎦⎥⎤-π4,π4时,f (x )≥-12.第6讲 简单的三角恒等变换1.若sin α2=33,则cos α=( )A .-23B .-13 C.13 D.232.(2016年山东)函数f (x )=(3sin x +cos x )(3cos x -sin x )的最小正周期是( )A.π2 B .π C.3π2D .2π 3.(2017年广东广州一模)已知函数f (x )=sin(ωx +φ)+cos(ωx +φ)(ω>0,0<φ<π)是奇函数,直线y =2与函数f (x )的图象的两个相邻交点的横坐标之差的绝对值为π2,则( )A .f (x )在⎝⎛⎭⎪⎫0,π4上单调递减B .f (x )在⎝ ⎛⎭⎪⎫π8,3π8上单调递减C .f (x )在⎝⎛⎭⎪⎫0,π4上单调递增D .f (x )在⎝ ⎛⎭⎪⎫π8,3π8上单调递增4.(2017年河北石家庄一模)函数f (x )=A sin(ωx +φ)(A >0,ω>0)的部分图象如图X361,则f ⎝ ⎛⎭⎪⎫11π24的值为( )图X361A .-62 B .-32 C .-22D .-1 5.若将函数y =tan ⎝⎛⎭⎪⎫ωx +π4(ω>0)的图象向右平移π6个单位长度后,与函数y =tan ⎝ ⎛⎭⎪⎫ωx +π6的图象重合,则ω的最小值为( ) A.16 B.14 C.13 D.126.(2016年山西四校联考)已知函数f (x )=cos ⎝⎛⎭⎪⎫ωx +φ-π2⎝ ⎛⎭⎪⎫ω>0,|φ|<π2的部分图象如图X362,则y =f ⎝⎛⎭⎪⎫x +π6取得最小值时x 的取值集合为( )图X362A.⎩⎨⎧⎭⎬⎫x |x =k π-π6,k ∈ZB.⎩⎨⎧⎭⎬⎫x |x =k π-π3,k ∈ZC.⎩⎨⎧⎭⎬⎫x |x =2k π-π6,k ∈Z D.⎩⎨⎧⎭⎬⎫x |x =2k π-π3,k ∈Z7.已知α∈R ,sin α+2cos α=102,则tan 2α=( ) A.43 B.34 C .-34 D .-438.(2012年大纲)当函数y =sin x -3cos x (0≤x <2π)取最大值时,x =________.9.(2016年江西九江模拟)化简sin 235°-12cos10°cos80°=________.10.若函数y =cos 2x +3sin 2x +a 在⎣⎢⎡⎦⎥⎤0,π2上有两个不同的零点,则实数a 的取值范围为____________.11.(2014年四川)已知函数f (x )=sin ⎝⎛⎭⎪⎫3x +π4. (1)求f (x )的单调递增区间;(2)若α是第二象限角,f ⎝ ⎛⎭⎪⎫α3=45cos ⎝⎛⎭⎪⎫α+π4cos 2α,求cos α-sin α的值.12.(2017年浙江)已知函数f (x )=sin 2x -cos 2x -2 3 sin x cos x (x ∈R ).(1)求f ⎝ ⎛⎭⎪⎫2π3的值; (2)求f (x )的最小正周期及单调递增区间.第7讲 正弦定理和余弦定理1.设△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,若2sin A cos B =sin C ,则△ABC 一定是( )A .直角三角形B .等腰三角形C .等腰直角三角形D .等边三角形2.(2017年山东)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c .若△ABC 为锐角三角形,且满足sin B (1+2cos C )=2sin A cos C +cos A sin C ,则下列等式成立的是( )A .a =2bB .b =2aC .A =2BD .B =2A3.(2016年新课标Ⅲ)在△ABC 中,B =π4,BC 边上的高等于13BC ,则sin A =( )A.310B.1010C.55 D.310104.(2017年河南郑州模拟)已知a ,b ,c 分别为△ABC 三个内角A ,B ,C 的对边,且 (b -c )(sin B +sin C )=(a -3c )sin A ,则角B 的大小为( )A .30° B.45° C.60° D.120° 5.(2013年新课标Ⅰ)已知锐角三角形ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,23cos 2A +cos 2A =0,a =7,c =6,则b =( )A .10B .9C .8D .56.(2016年山东德州模拟)在△ABC 中,AB =3,AC =1,B =π6,则△ABC 的面积是( )A.32B.34C.32或34D.32或 3 7.(2017年湖北孝感一模)在锐角三角形ABC 中,已知AB =2 3,BC =3,其面积S△ABC =3 2,则AC =________.8.(2015年重庆)在△ABC 中,B =120°,AB =2,角A 的平分线AD =3,则AC =________.9.(2017年北京)在△ABC 中,∠A =60°,c =37a .(1)求sin C 的值;(2)若a =7,求△ABC 的面积.10.(2017年新课标Ⅱ)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知sin(A +C )=8sin 2B2.(1)求cos B ;(2)若a +c =6,△ABC 的面积为2,求b .第8讲 解三角形应用举例1.某人向正东方向走x km 后,顺时针转150°,然后朝新方向走3 km ,结果他离出发点恰好 3 km ,则x =( )A. 3 B .2 3 C .2 3或 3 D .32.两座灯塔A 和B 与海洋观察站C 的距离都等于a km ,灯塔A 在观察站C 的北偏东20°的方向,灯塔B 在观察站C 的南偏东40°的方向,则灯塔A 与灯塔B 的距离为( )A .a km B.2a km C .2a km D.3a km3.如图X381,一艘海轮从A 处出发,以40海里/时的速度沿南偏东40°方向直线航行,30分钟后到达B 处.在C 处有一座灯塔,海轮在A 处观察灯塔,其方向是南偏东70°,在B 处观察灯塔,其方向是北偏东65°,那么B ,C 两点间的距离是( )图X381A .10 2海里B .10 3海里C .20 2海里D .20 3海里4.(2014年四川)如图X382,从气球A 上测得正前方的河流的两岸B ,C 的俯角分别为67°,30°,此时气球的高是46 m ,则河流的宽度BC 约等于________m .(用四舍五入法将结果精确到个位.参考数据:sin 67°≈0.92,cos 67°≈0.39,sin 37°≈0.60,cos 37°≈0.80,3≈1.73)图X3825.(2016年河南信阳模拟)某舰艇在A 处测得遇险渔船在北偏东45°距离为10海里的C 处,该渔船沿北偏东105°方向,以每小时9海里的速度向一小岛靠近,舰艇时速21海里,则舰艇到达渔船的最短时间是________分钟.6.(2017年浙江)已知△ABC ,AB =AC =4,BC =2.点D 为AB 延长线上一点,BD =2,连接CD ,则△BDC 的面积是________,cos ∠BDC =________.7.(2016年上海)已知△ABC 的三边长分别为3,5,7,则该三角形的外接圆半径等于________.8.(2017年广东揭阳一模)如图X383,在△ABC 中,∠B =π6,AC =1,点D 在边AB上,且DA =DC ,BD =1,则∠DCA =________.图X3839.(2017年新课标Ⅲ)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .已知sin A +3cos A =0,a =2 7,b =2.(1)求c ;(2)设D 为BC 边上一点,且AD ⊥AC ,求△ABD 的面积.10.(2017年广东广州一模)如图X384,在△ABC 中, 点P 在BC 边上, ∠PAC =60°,PC =2,AP +AC =4.(1)求∠ACP ;(2)若△APB 的面积是3 32, 求sin ∠BAP .图X384第三章 三角函数与解三角形 第1讲 弧度制与任意角的三角函数1.B 解析:方法一,由于M =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x =k2·180°+45°,k ∈Z ={…,-45°,45°,135°,225°,…},N =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x =k4·180°+45°,k ∈Z ={…,-45°,0°,45°,90°,135°,180°,225°,…},显然有M ⊆N .故选B.方法二,在M 中,x =k2·180°+45°=k ·90°+45°=(2k +1)·45°,2k +1是奇数;在N 中,x =k4·180°+45°=k ·45°+45°=(k +1)·45°,k +1是整数,因此必有M ⊆N .故选B.2.D 解析:由cos θ>0,sin 2θ=2sin θcos θ<0,得sin θ<0,则角θ的终边在第四象限.故选D.3.C 解析:∵α是第一象限角,∴2k π<α<π2+2k π,k ∈Z ,∴k π<α2<π4+k π,k ∈Z .当k 为偶数时,α2是第一象限角;当k 为奇数时,α2是第三象限角.4.B 解析:在第三象限,sin α<0,cos α<0,tan α>0,则tan α-sin α>0,故B 错误.故选B.5.D 解析:由三角函数的定义,得tan α=m =-2.∴r =5,sin α=-25=-2 55.故选D.6.C 解析:tan α=sin αcos α>0,而sin 2α=2sin αcos α>0.故选C.7.D 解析:∵α是第二象限角,∴cos α=15x <0,即x <0.又cos α=15x =xx 2+16,解得x =-3.∴tan α=4x =-43.8.D 解析:由于角φ的终边经过点P (-4,3),所以cos φ=-45.再根据函数f (x )=sin(ωx +φ)(ω>0)图象的相邻两条对称轴之间的距离等于π2,可得2πω=2×π2,所以ω=2.所以f (x )=sin(2x +φ).所以f ⎝ ⎛⎭⎪⎫π4=sin ⎝ ⎛⎭⎪⎫π2+φ=cos φ=-45.故选D. 9.-3 解析:由题意知tan θ=21=2,所以tan ⎝⎛⎭⎪⎫θ+π4=tan θ+tanπ41-tan θtanπ4=2+11-2×1=-3.10.A 解析:该程序框图的功能是比较a ,b ,c 的大小并输出最大值,因此要使输出的结果是sin θ,需sin θ>tan θ,且sin θ>cos θ.∵当θ∈⎝⎛⎭⎪⎫0,π2时,总有tan θ>sin θ;当θ∈⎝ ⎛⎭⎪⎫π2,π时,总有sin θ>0,tan θ<0,cos θ<0;当θ∈⎝⎛⎭⎪⎫π,3π2时,tan θ>0,sin θ<0.故当输出的结果是sin θ时,θ的取值范围是⎝ ⎛⎭⎪⎫π2,π.结合几何概型公式,得输出sin θ的概率为π-π232π-0=13.故选A. 11.解:(1)∵125°,278°角分别为第二、四象限角, ∴tan 125°<0,sin 278°<0. 因此tan 125°·sin 278°>0.(2)∵π2<7π12<π,3π2<23π12<2π,π2<11π12<π,∴cos 7π12<0,tan 23π12<0,sin 11π12>0.因此cos 7π12tan23π12sin11π12>0.12.解:设扇形半径为R ,圆心角为θ,θ所对的弧长为l .(1)依题意,得⎩⎪⎨⎪⎧12θR 2=4,θR +2R =10.∴2θ2-17θ+8=0.解得θ=8或12.∵8>2π(舍去),∴θ=12rad.(2)扇形的周长为40,即θR +2R =40, S =12lR =12θR 2=14θR ·2R ≤14⎝ ⎛⎭⎪⎫θR +2R 22=100. 当且仅当θR =2R ,即R =10,θ=2时,扇形面积取得最大值,最大值为100.第2讲 同角三角函数的基本关系式与诱导公式1.B 解析:sin 2013°=sin(5×360°+213°)=sin 213°=sin(180°+33°)=-sin 33°<-12.故选B.2.C 解析:∵sin 168°=sin(180°-12°)=sin 12°,cos 10°=cos(90°-80°)=sin 80°.由于正弦函数y =sin x 在区间[0°,90°]上为递增函数,因此sin 11°<sin 12°<sin 80°,即sin 11°<sin 168°<cos 10°.3.A 解析:由⎩⎨⎧sin α-cos α=2,sin 2α+cos 2α=1,消去sin α,得2cos 2α+22cos α+1=0,即(2cos α+1)2=0.∴cos α=-22.又α∈(0,π),∴α=3π4.∴tan α=tan 3π4=-1.4.C 解析:c =tan 35°>b =cos 55°=sin 35°>a =sin 33°.故选C.5.B 解析:由题知,tan θ=2,cos 2θ=cos 2 θ-sin 2 θcos 2 θ+sin 2 θ=1-tan 2θ1+tan 2θ=-35.故选B.6.D 解析:cos ⎝ ⎛⎭⎪⎫-7π4=cos π4>0,cos ⎝ ⎛⎭⎪⎫-23π5=cos 3π5<0.故选D.7.A 解析:sin α+cos α=33,两边平方可得1+sin 2α=13⇒sin 2α=-23.∵α是第二象限角,因此sin α>0,cos α<0.所以cos α-sin α=-α-sin α2=-1+23=-153.∴cos 2α=cos 2 α-sin 2α=(cos α+sin α)(cos α-sin α)=-53. 8.A 解析:由题设知(sin α+cos α)2=125,则2sin αcos α=-2425,故(sin α-cos α)2=1+2425=4925.所以sin α-cos α=75,与sin α+cos α=15联立解之可得sin α=45,cos α=-35,故tan α=-43.故选A.9.-105 解析:tan ⎝⎛⎭⎪⎫θ+π4=12,tan θ+11-tan θ=12,tan θ=-13,sin θcos θ=-13,cos θ=-3sin θ,代入sin 2θ+cos 2θ=1,得⎩⎪⎨⎪⎧sin θ=1010,cos θ=-31010.sin θ+cosθ=-105. 10.B 解析: 因为sin θ+cos θ=43(0<θ<π4),两边平方可得1+2sin θ·cosθ=169,即2sin θ·cos θ=79,所以(sin θ-cos θ)2=1-2sin θcos θ=1-79=29.又因为0<θ<π4,所以sin θ<cos θ.所以sin θ-cos θ<0.所以sin θ-cos θ=-23.故选B. 11.解:(1)函数f (x )要有意义,需满足cos x ≠0,解得x ≠π2+k π,k ∈Z ,即函数f (x )的定义域为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x ≠π2+k π,k ∈Z. (2)f (x )=1-2sin ⎝⎛⎭⎪⎫2x -π4cos x=1-2⎝ ⎛⎭⎪⎫22sin 2x -22cos 2x cos x =1+cos 2x -sin 2xcos x=2cos 2x -2sin x cos x cos x=2(cos x -sin x ).由tan α=-43,得sin α=-43cos α.又sin 2α+cos 2α=1,∴cos 2α=925.∵α是第四象限的角,∴cos α=35,sin α=-45.∴f (α)=2(cos α-sin α)=145.12.解:(1)tan ⎝⎛⎭⎪⎫α+π4=tan α+tanπ41-tan αtanπ4=tan α+11-tan α =2+11-2=-3. (2)sin 2αsin α+sin αcos α-cos 2α-1=2sin αcos αsin 2α+sin αcos α-2α--1=2sin αcos αsin 2α+sin αcos α-2cos 2α=2tan αtan 2α+tan α-2 =2×222+2-2 =1.第3讲 三角函数的图象与性质1.C 解析:将x =π12代入选项A ,B ,C ,D 中,只有选项C 取得最大值y =sin ⎝ ⎛⎭⎪⎫2×π12+π3=sin π2=1,所以关于直线x =π12对称,且T =2π2=π.2.A 解析:依题意,得f (x )=32sin ωx -12cos ωx =sin ⎝⎛⎭⎪⎫ωx -π6的图象相邻两个对称中心之间的距离为π2,于是有T =2πω=2×π2=π,ω=2,f (x )=sin ⎝⎛⎭⎪⎫2x -π6.当2k π-π2≤2x -π6≤2k π+π2,即k π-π6≤x ≤k π+π3,k ∈Z 时,f (x )=sin ⎝⎛⎭⎪⎫2x -π6单调递增.结合各选项知f (x )=sin ⎝ ⎛⎭⎪⎫2x -π6的一个单调递增区间为⎝ ⎛⎭⎪⎫-π6,π3.故选A. 3.A 解析:由图知,A =2,周期T =2⎣⎢⎡⎦⎥⎤π3-⎝ ⎛⎭⎪⎫-π6=π,所以ω=2ππ=2.所以y =2sin(2x +φ).因为图象过点⎝ ⎛⎭⎪⎫π3,2,所以2=2sin ⎝ ⎛⎭⎪⎫2×π3+φ.所以sin ⎝ ⎛⎭⎪⎫2π3+φ=1.所以2π3+φ=2k π+π2(k ∈Z ).令k =0,得φ=-π6.所以y =2sin ⎝⎛⎭⎪⎫2x -π6.故选A. 4.D 解析:因为函数f (x )和g (x )的图象的对称轴完全相同,故f (x )和g (x )的周期相同,所以ω =2,f (x )=3cos ⎝ ⎛⎭⎪⎫2x +π3.由x ∈⎣⎢⎡⎦⎥⎤0,π3,得2x +π3∈⎣⎢⎡⎦⎥⎤π3,π.根据余弦函数的单调性,当2x +π3=π,即x =π3时,f (x )min =-3;当2x +π3=π3,即x =0时,f (x )max =32.所以f (x )的取值范围是⎣⎢⎡⎦⎥⎤-3,32.故选D. 5.B 解析:设函数的最小正周期为T ,由题图可知T 2=⎝ ⎛⎭⎪⎫x 0+π4-x 0=π4,所以T =π2.又因为T =2πω,可解得ω=4.6.C 解析:方法一,y =|sin x |·cos x|cos x |,分类讨论.方法二,y =|tan x |cos x 的符号与cos x 相同.故选C.7.D 解析:函数的最小正周期为T =2π1=2π,则周期为2k π()k ∈Z .所以f (x )的一个周期为-2π.故选项A 正确;将x =8π3代入f (x )=cos ⎝ ⎛⎭⎪⎫x +π3,得f ⎝ ⎛⎭⎪⎫8π3=cos3π=-1为最小值.因此直线x =8π3为对称轴.故选项B 正确;将x =π6代入f (x +π),得cos 3π2=0.故选项C 正确;由x ∈⎝ ⎛⎭⎪⎫π2,π,得x +π3∈⎝ ⎛⎭⎪⎫5π6,4π3.函数在该区间显然不单调.故选项D 错误.故选D.8.7 解析:由sin 2x =cos x ⇒cos x =0或sin x =12.因为x ∈[0,3π],所以x =π2,3π2,5π2,π6,5π6,13π6,17π6,共7个. 9.A 解析:因为f (x )=2sin ⎝⎛⎭⎪⎫ωx -π3,T 2=π2,所以T =2πω=π.则ω=2.故f (x )=2sin ⎝ ⎛⎭⎪⎫2x -π3.故g (x )=2sin ⎣⎢⎡⎦⎥⎤2⎝⎛⎭⎪⎫x +π6-π3=2sin 2x ,故其单调递减区间为2k π+π2≤2x ≤2k π+3π2(k ∈Z ),即k π+π4≤x ≤k π+3π4(k ∈Z ),当k =0时,区间⎣⎢⎡⎦⎥⎤π4,3π4为函数g (x )的一个单调递减区间,又⎝ ⎛⎭⎪⎫π4,π3⊆⎣⎢⎡⎦⎥⎤π4,3π4.故选A.10.A 解析:方法一,ω=2⇒⎝⎛⎭⎪⎫ωx +π4∈⎣⎢⎡⎦⎥⎤5π4,9π4不合题意,排除D ;ω=1⇒⎝ ⎛⎭⎪⎫ωx +π4∈⎣⎢⎡⎦⎥⎤3π4,5π4合题意,排除B ,C.故选A. 方法二,由π2<x <π,得π2ω+π4<ωx +π4<πω+π4.由题意知,⎝ ⎛⎭⎪⎫π2ω+π4,πω+π4⊆⎣⎢⎡⎦⎥⎤π2,3π2.∴⎩⎪⎨⎪⎧π2ω+π4≥π2,πω+π4≤3π2.∴12≤ω≤54.故选A. 11.解:(1)因为f (x )=sin 2x +cos 2x +2sin x cos x +cos 2x=1+sin 2x +cos 2x =2sin ⎝⎛⎭⎪⎫2x +π4+1, 所以函数f (x )的最小正周期为T =2π2=π.(2)由(1)知,f (x )=2sin ⎝⎛⎭⎪⎫2x +π4+1. 当x ∈⎣⎢⎡⎦⎥⎤0,π2时,2x +π4∈⎣⎢⎡⎦⎥⎤π4,5π4.由正弦函数y =sin x 在⎣⎢⎡⎦⎥⎤π4,5π4上的图象知,当2x +π4=π2,即x =π8时,f (x )取最大值2+1;当2x +π4=5π4,即x =π2时,f (x )取最小值0.综上所述,f (x )在区间⎣⎢⎡⎦⎥⎤0,π2上的最大值为2+1,最小值为0.12.解:y =-⎝⎛⎭⎪⎫cos x -12a 2+a 24+58a -12, 当0≤x ≤π2时,0≤cos x ≤1.令t =cos x ,则0≤t ≤1.∴y =-⎝ ⎛⎭⎪⎫t -12a 2+a 24+58a -12,0≤t ≤1. 当0≤a 2≤1,即0≤a ≤2时,则当t =a 2,即cos x =a2时.y max =a 24+58a -12=1,解得a =32或a =-4(舍去).当a2<0,即a <0时,则当t =0,即cos x =0时, y max =58a -12=1,解得a =125(舍去).当a2>1,即a >2时,则当t =1,即cos x =1时, y max =a +58a -32=1,解得a =2013(舍去).综上所述,存在a =32符合题意.第4讲 函数y =A sin (ωx +φ)的图象1.C 解析:∵T 4=3-1=2,∴T =8,∴ω=2πT =π4.令π4×1+φ=π2,得φ=π4.故选C.2.A 解析:由于y =sin 3x +cos 3x =2sin ⎝⎛⎭⎪⎫3x +π4,y =2cos 3x =2sin ⎝⎛⎭⎪⎫3x +π2,因此只需将y =2cos 3x 的图象向右平移π12个单位长度,即可得到y =2sin ⎣⎢⎡⎦⎥⎤3⎝ ⎛⎭⎪⎫x -π12+π2= sin ⎝ ⎛⎭⎪⎫3x +π4的图象. 3.B 解析:f (x )=3sin ⎝⎛⎭⎪⎫2x +π3的图象向右平移π2个单位长度所得图象对应的函数为f (x )=3sin ⎣⎢⎡⎦⎥⎤2⎝⎛⎭⎪⎫x -π2+π3=-3sin ⎝ ⎛⎭⎪⎫2x +π3,其对称轴方程为2x +π3=π2+k π(k ∈Z ),即x =π12+k π2(k ∈Z ),排除A.当x =π12+k π(k ∈Z ),得-3sin ⎝⎛⎭⎪⎫2k π+π2=-3.故C 错误.由π2+2k π≤2x +π3≤3π2+2k π(k ∈Z ),得π12+k π≤x ≤7π12+k π(k ∈Z ),即f (x )的增区间为⎣⎢⎡⎦⎥⎤π12+k π,7π12+k π(k ∈Z ).故选B. 4.D 解析:向右平移φ个单位长度后,得到g (x )=sin(2x -2φ),∵|f (x 1)-g (x 2)|=2,∴不妨令2x 1=π2+2k π(k ∈Z ),2x 2-2φ=-π2+2m π(m ∈Z ).∴x 1-x 2=π2-φ+(k -m )π.又∵|x 1-x 2|min =π3,∴π2-φ=π3⇒φ=π6.故选D.5.B 解析:由已知,得ω=2,则f (x )=sin(2x +φ).设平移后的函数为g (x ),则g (x )=sin ⎝ ⎛⎭⎪⎫2x +π3+φ ⎝ ⎛⎭⎪⎫-π2<φ<π2,且为奇函数,所以φ=-π3,f (x )=sin ⎝⎛⎭⎪⎫2x -π3.令2x -π3=k π+π2(k ∈Z ),易得f (x )的图象关于直线x =5π12对称.故选B.6.[2,+∞) 解析:f (x )=3sin 3x +cos 3x =2sin ⎝⎛⎭⎪⎫3x +π6,|f (x )|max =2,∴a ≥2. 7.⎣⎢⎡⎦⎥⎤-12,1 ⎣⎢⎡⎦⎥⎤π6,π2 解析:当a =π3时,x ∈⎣⎢⎡⎦⎥⎤-π6,π3,2x +π6∈⎣⎢⎡⎦⎥⎤-π6,5π6,f (x )的值域是⎣⎢⎡⎦⎥⎤-12,1;若f (x )的值域是⎣⎢⎡⎦⎥⎤-12,1,π2≤2a +π6≤7π6,解得π6≤a ≤π2.8.π2 解析:根据三角函数图象与性质可得交点坐标为⎝ ⎛⎭⎪⎫1ω⎝ ⎛⎭⎪⎫2k 1π+π4,2,⎝ ⎛⎭⎪⎫1ω⎝ ⎛⎭⎪⎫2k 2π+5π4,-2,k 1,k 2∈Z +,距离最短的两个交点一定在同一个周期内,∴()2 32=1ω2⎝ ⎛⎭⎪⎫5π4-π42+(-2-2)2.∴ω=π2. 9.π2解析:由f (x )在区间(-ω,ω)内单调递增,且f (x )的图象关于直线x =ω对称,可得2ω≤πω,且f (ω)=sin ω2+cos ω2=2⇒sin ⎝⎛⎭⎪⎫ω2+π4=1,所以ω2+π4=π2⇒ω=π2. 10.解:(1)f (x )的最小正周期为π,x 0=7π6,y 0=3.(2)因为x ∈⎣⎢⎡⎦⎥⎤-π2,-π12,所以2x +π6∈⎣⎢⎡⎦⎥⎤-5π6,0.于是,当2x +π6=0,即x =-π12时,f (x )取得最大值0;当2x +π6=-π2,即x =-π3时,f (x )取得最小值-3.11.解:(1)因为f (x )=sin ⎝ ⎛⎭⎪⎫ωx -π6+sin ⎝⎛⎭⎪⎫ωx -π2,所以f (x )=32sin ωx -12cos ωx -cos ωx =32sin ωx -32cos ωx =3⎝ ⎛⎭⎪⎫12sin ωx -32cos ωx=3sin ⎝⎛⎭⎪⎫ωx -π3. 由题设知,f ⎝ ⎛⎭⎪⎫π6=0,所以ωπ6-π3=k π,k ∈Z . 故ω=6k +2,k ∈Z .又0<ω<3,所以ω=2.(2)由(1),得f (x )=3sin ⎝⎛⎭⎪⎫2x -π3. 所以g (x )=3sin ⎝ ⎛⎭⎪⎫x +π4-π3=3sin ⎝ ⎛⎭⎪⎫x -π12.根据x ∈⎣⎢⎡⎦⎥⎤-π4,3π4得到x -π12∈⎣⎢⎡⎦⎥⎤-π3,2π3,当x -π12=-π3,即x =-π4时,g (x )取得最小值-32.第5讲 两角和与差及二倍角的三角函数公式1.D 解析:cos ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫π4-α=2cos 2⎝ ⎛⎭⎪⎫π4-α-1=2×⎝ ⎛⎭⎪⎫352-1=-725,且cos ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫π4-α=cos ⎝ ⎛⎭⎪⎫π2-2α=sin 2α.故选D. 2.C 解析:原式=4sin 40°-sin 40°cos 40°=4cos 40°sin 40°-sin 40°cos 40°=2sin 80°-sin 40°cos 40°=--sin 40°cos 40°=3cos 40°+sin 40°-sin 40°cos 40°=3cos 40°cos 40°= 3.故选C.3.A 解析:由y =2cos 2⎝ ⎛⎭⎪⎫x -π4-1=cos ⎝ ⎛⎭⎪⎫2x -π2=sin2x ,∴T =π,且y =sin 2x 是奇函数,即函数y =2cos 2⎝⎛⎭⎪⎫x -π4-1是奇函数.故选A. 4.D 解析:设直线OA 的倾斜角为α,B (m ,n )(m >0,n >0),则直线OB 的倾斜角为π3+α.因为A (4 3,1),所以tan α=14 3,tan ⎝ ⎛⎭⎪⎫π3+α=n m ,nm =3+14 31-3·14 3=133 3,即m 2=27169n 2.因为m 2+n 2=(4 3)2+12=49,所以n 2+27169n 2=49.所以n =132或n=-132(舍去).所以点B 的纵坐标为132.5.75 解析:tan α=tan ⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫α-π4+π4=tan ⎝ ⎛⎭⎪⎫α-π4+tan π41-tan ⎝⎛⎭⎪⎫α-π4tanπ4=16+11-16=75.6.-79解析:因为角α与角β它们的终边关于y 轴对称,所以α+β=2k π+π()k ∈Z ,sin α=sin β=13,cos α=-cos β,cos(α-β)=cos αcos β+sinαsin β=-cos 2α+sin 2α=2sin 2α-1=-79.7.π3 解析:因为y =sin x -3cos x =2sin ⎝ ⎛⎭⎪⎫x -π3,所以函数y =sin x -3cos x的图象可由函数y =2sin x 的图象至少向右平移π3个单位长度得到.8.±3 解析:f (x )=16+a 2sin(x +φ),其中tan φ=a4,故函数f (x )的最大值为16+a 2,由已知,得16+a 2=5,解得a =±3.9.π6或5π6解析:3sin x =1+cos 2x ,即3sin x =2-2sin 2x ,所以2sin 2x +3sin x -2=0.解得sin x =12或sin x =-2(舍).所以方程在区间[0,2π]上的解为π6或5π6.10.π 3-22 ⎣⎢⎡⎦⎥⎤3π8+k π,7π8+k π,k ∈Z解析:f (x )=sin 2x +sin x cos x +1=12sin 2x +1-cos 2x 2+1=12sin 2x -12cos 2x+32=22·sin ⎝⎛⎭⎪⎫2x -π4+32,所以T =2π2=π,f (x )min =32-22.单调递减区间为⎣⎢⎡⎦⎥⎤3π8+k π,7π8+k π,k ∈Z . 11.解:(1)因为α∈⎝ ⎛⎭⎪⎫π2,π,sin α=55,所以cos α=-1-sin 2α=-2 55.故sin ⎝ ⎛⎭⎪⎫π4+α=sin π4cos α+cos π4sin α =22×⎝ ⎛⎭⎪⎫-2 55+22×55=-1010. (2)由(1),得sin 2α=2sin αcos α=-45,cos 2α=2cos 2α-1=35.所以cos ⎝ ⎛⎭⎪⎫5π6-2α=cos 5π6cos 2α+sin 5π6sin 2α =-32×35+12×⎝ ⎛⎭⎪⎫-45=-3 3+410.12.(1)解:f (x )=32cos 2x +32sin 2x -sin 2x =12sin 2x +32cos 2x =sin ⎝ ⎛⎭⎪⎫2x +π3.所以f (x )的最小正周期T =2π2=π.(2)证明:因为-π4≤x ≤π4,所以-π6≤2x +π3≤5π6.所以sin ⎝ ⎛⎭⎪⎫2x +π3≥sin ⎝ ⎛⎭⎪⎫-π6=-12. 所以当x ∈⎣⎢⎡⎦⎥⎤-π4,π4时,f (x )≥-12. 第6讲 简单的三角恒等变换1.C2.B 解析:f (x )=2sin ⎝ ⎛⎭⎪⎫x +π6×2cos ⎝ ⎛⎭⎪⎫x +π6=2sin ⎝⎛⎭⎪⎫2x +π3,故最小正周期T =2π2=π.故选B.3.D 解析:f (x )=2sin ⎝⎛⎭⎪⎫ωx +φ+π4,因为函数为奇函数且0<φ<π,所以φ+π4=π,即φ=3π4.所以f (x )=-2sin ωx .又2πω=π2,所以ω=4,f (x )=-2sin 4x ,其一个单调递增区间为⎝ ⎛⎭⎪⎫π8,3π8.4.D 解析:由题图可得A =2,最小正周期T =4⎝ ⎛⎭⎪⎫7π12-π3=π,则ω=2πT =2.又f ⎝ ⎛⎭⎪⎫7π12=2sin ⎝ ⎛⎭⎪⎫7π6+φ=-2,解得φ=-5π3+2k π(k ∈Z ).即k =1,φ=π3.则f (x )=2sin ⎝ ⎛⎭⎪⎫2x +π3.则f ⎝ ⎛⎭⎪⎫11π24=2sin ⎝ ⎛⎭⎪⎫11π12+π3=2sin 5π4=-1.故选D.5.D 解析:函数y =tan ⎝⎛⎭⎪⎫ωx +π4的图象向右平移π6个单位后得到函数y =tan ⎣⎢⎡⎦⎥⎤ω⎝⎛⎭⎪⎫x -π6+π4=tan ⎝ ⎛⎭⎪⎫ωx -ωπ6+π4的图象.又因为y =tan ⎝ ⎛⎭⎪⎫ωx +π6,依题意可得-ωπ6+π4=π6+k π,k ∈Z ,∴ω=12-6k ,()k ∈Z .由ω>0,得ω的最小值为12.6.B 解析:依题意,得T =2πω=4⎝ ⎛⎭⎪⎫7π12-π3=π,ω=2,f ⎝ ⎛⎭⎪⎫π3=cos ⎝⎛⎭⎪⎫φ+π6=1.又|φ|<π2,因此φ=-π6.所以f (x )=cos ⎝ ⎛⎭⎪⎫2x -2π3.当f ⎝ ⎛⎭⎪⎫x +π6=cos ⎝⎛⎭⎪⎫2x -π3取得最小值时,2x -π3=2k π-π,k ∈Z ,即x =k π-π3,k ∈Z .故选B.7.C 解析:∵sin α+2cos α=102, ∴sin 2α+4sin αcos α+4cos 2α=52.化简,得4sin 2α=-3cos 2α.∴tan 2α=sin 2αcos 2α=-34.故选C.8.5π6 解析:y =sin x-3cos x =2sin ⎝⎛⎭⎪⎫x -π3,由0≤x <2π⇔-π3≤x -π3<5π3,可知-2≤2sin ⎝⎛⎭⎪⎫x -π3≤2.当且仅当x -π3=π2,即x =5π6时,函数取得最大值.9.-1 解析:sin 235°-12cos10°cos80°=1-cos70°2-12cos10°sin10°=-12cos70°12sin20°=-1.10.(-2,-1] 解析:由题意可知,y =2sin ⎝ ⎛⎭⎪⎫2x +π6+a ,该函数在⎣⎢⎡⎦⎥⎤0,π2上有两个不同的零点,即y =-a ,y =2sin ⎝ ⎛⎭⎪⎫2x +π6的图象在⎣⎢⎡⎦⎥⎤0,π2上有两个不同的交点.结合函数的图象D104可知1≤-a <2,所以-2<a ≤-1.图D10411.解:(1)-π2+2k π≤3x +π4≤π2+2k π⇒-π4+23k π≤x ≤π12+23k π(k ∈Z ).(2)由已知,有sin ⎝ ⎛⎭⎪⎫α+π4=45cos ⎝ ⎛⎭⎪⎫α+π4cos 2α, 即sin α+cos α=45(cos α-sin α)(cos α-sin α)(sin α+cos α).若sin α+cos α=0,则cos α-sin α=- 2. 若sin α+cos α≠0,则1=45(cos α-sin α)2⇒cos α-sin α=-52.综上所述,cos α-sin α的值为-2或-52. 12.解:(1)f ⎝⎛⎭⎪⎫2π3=⎝ ⎛⎭⎪⎫322-⎝ ⎛⎭⎪⎫-122-2 3×32×⎝ ⎛⎭⎪⎫-12=2.(2)由cos 2x =cos 2x -sin 2x 与sin 2x =2sin x cos x ,得f (x )=-cos 2x -3sin 2x =-2sin ⎝⎛⎭⎪⎫2x +π6. 所以f (x )的最小正周期是π.由正弦函数的性质,得π2+2k π≤2x +π6≤3π2+2k π,k ∈Z .解得π6+k π≤x ≤2π3+k π,k ∈Z .所以f (x )的单调递增区间是⎣⎢⎡⎦⎥⎤π6+k π,2π3+k π,k ∈Z . 第7讲 正弦定理和余弦定理1.B 解析:方法一,由已知,得2sin A cos B =sin C =sin(A +B )=sin A cos B +cos A sin B ,即sin(A -B )=0.因为-π<A -B <π,所以A =B .方法二,由正弦定理,得2a cos B =c ,再由余弦定理,得2a ·a 2+c 2-b 22ac=c ⇒a 2=b2⇒a =b .2.A 解析:sin(A +C )+2sin B cos C =2sin A cos C +cos A sin C ,所以2sin B cos C =sin A cos C ⇒2sin B =sin A ⇒2b =a .故选A.3.D 解析:设BC 边上的高线为AD ,则BC =3AD ,DC =2AD .所以AC =AD 2+DC 2=5AD .由正弦定理知,AC sin B =BC sin A ,即5AD 22=3AD sin A.解得sin A =31010.故选D.4.A 解析:由正弦定理a sin A =b sin B =csin C及(b -c )·(sin B +sin C )=(a -3c )sin A ,得(b -c )(b +c )=(a -3c )a ,即b 2-c 2=a 2-3ac .∴a 2+c 2-b 2=3ac .∵cos B =a 2+c 2-b 22ac ,∴cos B =32.∴B =30°.5.D 解析:23cos 2A +cos 2A =25cos 2A -1=0,cos A =15或cos A =-15(舍),a 2=b 2+c 2-2bc cos A,49=b 2+36-12b ×15,5b 2-12b -65=0,(5b +13)(b -5)=0,且b >0,所以b =5.6.C 解析:由正弦定理,得AB sin C =AC sin B .解得sin C =32.由题意知C 有两解.当C =π3时,A =π2,此时S △ABC =12AB ·AC ·sin A =32;当C =2π3时,A =π6,此时S △ABC =12AB ·AC ·sin A =34.故选C. 7.3 解析:依题意有S △ABC =12AB ×BC ×sin B =12×2 3×3sin B =3 2,sin B =63.又角B 为锐角,所以cos B =33.所以AC =AB 2+BC 2-2AB ×BC ×cos B =12+9-2×2 3×3×33=3. 8. 6 解析:由正弦定理,得ABsin ∠ADB =ADsin B,即2sin ∠ADB =3sin 120°.解得sin∠ADB =22,∠ADB =45°.从而∠BAD =15°=∠DAC .所以C =180°-120°-30°=30°,AC =2AB cos 30°= 6.9.解:(1)在△ABC 中,∠A =60°,c =37a .sin C =c sin A a =3 314. (2)因为a =7,c =37a =3,由余弦定理,得a 2=b 2+c 2-2bc cos A ,即72=b 2+32-2×b ×3×12.解得b =8或b =-5(舍).所以S △ABC =12bc sin A =12×8×3×32=6 3.10.解:(1)由A +C =π-B ,sin(A +C )=sin B =8sin 2B2=4(1-cos B ),两边平方,整理得17cos 2B -32cos B +15=0.解得cos B =1(舍)或cos B =1517.(2)由cos B =1517,得sin B =817.故S △ABC =12ac sin B =417ac =2.∴ac =172.由余弦定理,得b 2=a 2+c 2-2ac cos B =(a +c )2-2ac (1+cos B )=36-2×172×⎝ ⎛⎭⎪⎫1+1517=4. 所以b =2.第8讲 解三角形应用举例1.C 解析:如图D105,在△ABC 中,AC =3,BC =3,∠ABC =30°.由余弦定理,得AC 2=AB 2+BC 2-2AB ·BC ·cos ∠ABC .∴3=x 2+9-6x ·cos 30°,解得x =3或2 3.图D105 图D1062.D 解析:如图D106,依题意,得∠ACB =120°.由余弦定理,得AB 2=AC 2+BC2-2AC ·BC cos 120°=a 2+a 2-2a 2·⎝ ⎛⎭⎪⎫-12=3a 2,∴AB =3a km.故选D.3.A 解析:在△ABC 中,∠BAC =50°-20°=30°,∠ABC =40°+65°=105°,AB =40×0.5=20(海里),则∠ACB =45°.由正弦定理,得BC sin 30°=20sin 45°.解得BC=10 2(海里).故选A.4.60 解析:根据已知的图形可得AB =46sin 67°.在△ABC 中,∠BCA =30°,∠BAC=37°,由正弦定理,得AB sin 30°=BC sin 37°.所以BC ≈2×460.92×0.60=60(m).5.40 解析:设两船在B 处碰头,设舰艇到达渔船的最短时间是x 小时,则AC =10,AB =21x ,BC =9x ,∠ACB =120°,由余弦定理,知(21x )2=100+(9x )2-2×10×9x ×cos120°,整理,得36x 2-9x -10=0.解得x =23或x =-512(舍).故舰艇到达渔船的最短时间是40分钟.6.152 104解析:取BC 中点E ,DC 中点F ,连接AE ,BF .由题意知AE ⊥BC ,BF⊥CD .在△ABE 中,cos ∠ABC =BE AB =14,∴cos ∠DBC =-14,sin ∠DBC =1-116=154.∴。
2019年《南方新课堂·高考总复习》数学(理科)作业及测试:课时作业 第六章不等式 Word版含解析
第六章 不等式第1讲 不等式的概念与性质1.(2017年河北承德实验中学统测)若a ,b ,c ∈R ,且a >b ,则下列不等式正确的个数是( )①1a <1b ;②a 2>b 2;③ac 4>bc 4;④a c 2+1>b c 2+1. A .1 B .2 C .3 D .42.(2016年北京)已知x ,y ∈R ,且x >y >0,则( ) A.1x -1y>0 B .sin x -sin y >0 C.⎝⎛⎭⎫12x -⎝⎛⎭⎫12y <0 D .ln x +ln y >03.已知下列不等式:①x 2+3>2x ;②a 3+b 3≥a 2b +ab 2(a ,b ∈R +);③a 2+b 2≥2(a -b -1).其中正确的个数是( )A .0B .1C .2D .34.(2015年湖北)将离心率为e 1的双曲线C 1的实半轴长a 和虚半轴长b (a ≠b )同时增加m (m >0)个单位长度,得到离心率为e 2的双曲线C 2,则( )A .对任意的a ,b ,e 1<e 2B .当a >b 时,e 1<e 2;当a <b 时,e 1>e 2C .对任意的a ,b ,e 1>e 2D .当a >b 时,e 1>e 2;当a <b 时,e 1<e 25.(2015年上海)记方程①:x 2+a 1x +1=0,方程②:x 2+a 2x +2=0,方程③:x 2+a 3x +4=0,其中a 1,a 2,a 3是正实数.当a 1,a 2,a 3成等比数列时,下列选项中,能推出方程③无实根的是( )A .方程①有实根,且②有实根B .方程①有实根,且②无实根C .方程①无实根,且②有实根D .方程①无实根,且②无实根6.已知函数f (x )=ax 2+bx +c 满足f (1)=0,且a >b >c ,则ca的取值范围为__________.7.(2016年山东滨州模拟)A 杯中有浓度为a 的盐水x g ,B 杯中有浓度为b 的盐水y g ,其中A 杯中的盐水更咸一些.若将A ,B 两杯盐水混合在一起,其浓度可用不等式表示为______________.8.用若干辆载重为8吨的汽车运一批货物,若每辆汽车只装4吨,则剩下20吨货物;若每辆汽车装8吨,则最后一辆汽车不满也不空.则有汽车________辆.9.设a ,b 为正实数.现有下列命题: ①若a 2-b 2=1,则a -b <1;②若1b -1a=1,则a -b <1;③若|a -b |=1,则|a -b |<1; ④若|a 3-b |=1,则|a -b |<1.其中的真命题有__________.(写出所有真命题的编号)10.(2016年湖南怀化模拟)某单位组织职工去某地参观学习需包车前往.甲车队说:“如领队买全票一张,其余人可享受7.5折优惠”,乙车队说:“你们属团体票,按原价的8折优惠”.这两车队的原价、车型都是一样的,试根据单位的人数,比较两车队的收费哪家更优惠.11.已知a >0,b >0,求证:⎝⎛⎭⎫a 2b 12+⎝⎛⎭⎫b 2a 12≥a 12+b 12.12.已知α∈(0,π),比较2sin 2α与sin α1-cos α的大小.第2讲 一元二次不等式及其解法1.(2016年湖北模拟)若关于x 的不等式ax -b >0的解集是(-∞,1),则关于x 的不等式(ax +b )(x -3)>0的解集是( )A .(-∞,-1)∪(3,+∞)B .(-1,3)C .(1,3)D .(-∞,1)∪(3,+∞)2.如果kx 2+2kx -(k +2)<0恒成立,那么实数k 的取值范围是( ) A .-1≤k ≤0 B .-1≤k <0 C .-1<k ≤0 D .-1<k <03.已知函数f (x )=⎩⎪⎨⎪⎧x +2,x ≤0,-x +2,x >0,则不等式f (x )≥x 2的解集是( )A .[-1,1]B .[-2,2]C .[-2,1]D .[-1,2]4.(2016年江西九江一模)若关于x 的不等式x 2-4x -2-a >0在区间(1,4)内有解,则实数a 的取值范围是( )A .(-∞,-2)B .(-2,+∞)C .(-6,+∞)D .(-∞,-6)5.已知不等式x 2-2x -3<0的解集为A ,不等式x 2+x -6<0的解集为B ,不等式x 2+ax +b <0的解集是A ∩B ,则a +b =( )A .-3B .1C .-1D .36.已知f (x )是定义域为R 的偶函数,当x ≤0时,f (x )=x 2+2x ,则不等式f (x +2)<3的解集是_________.7.已知a ∈Z ,关于x 的一元二次不等式x 2-6x +a ≤0的解集中有且仅有3个整数,则所有符合条件的a 的值之和是________.8.不等式ax 2+bx +c >0的解集为⎝⎛⎭⎫-13,2,对于系数a ,b ,c ,有如下结论:①a <0;②b >0;③c >0;④a +b +c >0;⑤a -b +c >0.其中正确的结论的序号是________.9.(2016年北京朝阳统一考试)已知函数f (x )=x 2-2ax -1+a ,a ∈R .(1)若a =2,试求函数y =f (x )x(x >0)的最小值;(2)对于任意的x ∈[0,2],不等式f (x )≤a 成立,试求a 的取值范围.10.设f (x )=ax 2+bx +c ,若f (1)=72,问是否存在a ,b ,c ∈R ,使得不等式x 2+12≤f (x )≤2x 2+2x +32对一切实数x 都成立?证明你的结论.第3讲 算术平均数与几何平均数1.下列命题正确的是( )A .函数y =x +1x 的最小值为2B .函数y =x 2+3x 2+2的最小值为2C .函数y =2-3x -4x (x >0)的最小值为2-4 3D .函数y =2-3x -4x (x >0)的最大值为2-4 32.若函数f (x )=x +1x -2(x >2)在x =a 处取得最小值,则a =( )A .1+ 2B .1+ 3C .3D .43.设正实数x ,y ,z 满足x 2-3xy +4y 2-z =0,则当zxy取得最小值时,x +2y -z 的最大值为( )A .0 B.98 C .2 D.944.若log 4(3a +4b )=log 2ab ,则a +b 的最小值是( ) A .6+2 3 B .7+2 3 C .6+4 3 D .7+4 35.(2015年湖南)若实数a ,b 满足1a +2b=ab ,则ab 的最小值为( )A. 2 B .2 C .2 2 D .46.(2015年陕西)设f (x )=ln x,0<a <b ,若p =f (ab ),q =f ⎝⎛⎭⎫a +b 2,r =12[f (a )+f (b )],则下列关系式正确的是( )A .q =r <pB .q =r >pC .p =r <qD .p =r >q7.已知正数x ,y 满足x +2y -xy =0,则x +2y 的最小值为( ) A .8 B .4 C .2 D .08.(2017年河南郑州第二次质量预测)已知正数x ,y 满足x 2+2xy -3=0,则2x +y 的最小值是__________.9.(1)设x >-1,则函数y =(x +5)(x +2)x +1的最小值为________.(2)已知x <54,则f (x )=4x -2+14x -5的最大值为________;10.(1)(2016年湖北七市联考)已知a >0,b >0,且2a +b =1,若不等式2a +1b≥m 恒成立,则m 的最大值等于( )A .10B .9C .8D .7(2)已知x >0,y >0,x +3y +xy =9,则x +3y 的最小值为________.第4讲 简单的线性规划1.(2017年北京)若x ,y 满足⎩⎪⎨⎪⎧x ≤3,x +y ≥2y ≤x ,,则x +2y 的最大值为( )A .1B .3C .5D .92.(2017年新课标Ⅲ)设x ,y 满足约束条件⎩⎪⎨⎪⎧3x +2y -6≤0,x ≥0,y ≥0,则z =x -y 的取值范围是( )A .[-3,0]B .[-3,2]C .[0,2]D .[0,3]3.已知实数x ,y 满足不等式组⎩⎪⎨⎪⎧0≤x ≤3,2x -3y ≤6,3x +4y ≤12,则z =x +y -2x +1的取值范围是( )A.⎣⎡⎦⎤-4,716 B .[-4,1] C.⎣⎡⎦⎤14,716 D.⎣⎡⎦⎤14,1 4.(2014年新课标Ⅰ)设x ,y 满足约束条件⎩⎪⎨⎪⎧x +y ≥a ,x -y ≤-1,且z =x +ay 的最小值为7,则a =( )A .-5B .3C .-5或3D .5或-35.设二元一次不等式组⎩⎪⎨⎪⎧2x +y -19≥0,x -y -8≤0,x +2y -14≤0所表示的平面区域为M ,则使函数y =log a x (a >0,a ≠1)的图象过区域M 的a 的取值范围是( )A .[1,3]B .[2,10]C .[2,9]D .[10,9]6.x ,y 满足约束条件⎩⎪⎨⎪⎧x +y -2≤0,x -2y -2≤0,2x -y +2≥0.若z =y -ax 取得最大值的最优解不唯一,则实数a 的值为( )A.12或-1 B .2或12 C .2或1 D .2或-17.在平面直角坐标系中,不等式组⎩⎪⎨⎪⎧x ≥1,x +y ≤0,x -y -4≤0表示的平面区域的面积是________.8.(2016年江苏) 已知实数x ,y 满足⎩⎪⎨⎪⎧x -2y +4≥0,2x +y -2≥0,3x -y -3≤0,则x 2+y 2的取值范围是________.9.变量x ,y 满足⎩⎪⎨⎪⎧x -4y +3≤0,3x +5y -25≤0,x ≥1.(1)设z =yx,求z 的最小值;(2)设z =x 2+y 2,求z 的取值范围;(3)设z =x 2+y 2+6x -4y +13,求z 的取值范围.10.已知函数g (x )=x 2+(a +1)x +a +b +1,两个零点可分别作为一个椭圆和一个双曲线的离心率.求ba的取值范围.第5讲 不等式的应用1.某汽车运输公司购买了一批豪华大客车投入营运,据市场分析:每辆客车营运的总利润y (单位:10万元)与营运年数x 的函数关系为y =-(x -6)2+11(x ∈N *),要使每辆客车运营的年平均利润最大,则每辆客车营运的最佳年数为( )A .3年B .4年C .5年D .6年2.(2017年广东惠州三模)设z =4x ·2y ,变量x ,y 满足条件⎩⎪⎨⎪⎧x -4y ≤-3,3x +5y ≤25,x ≥1,则z 的最小值为( )A .2B .4C .8D .163.某单位用2160万元购得一块空地,计划在该地块上建造一栋至少10层、每层2000平方米的楼房.经测算,若将楼房建为x (x ≥10)层,则每平方米的平均建筑费用为560+48x (单位:元).为了使楼房每平方米的平均综合费用最少,则楼房应建为( )A .10层B .15层C .20层D .30层4.(2016年山东烟台诊断)已知在等比数列{a n }中,a 2=1,则其前3项的和S 3的取值范围是( )A .(-∞,-1]B .(-∞,-1)∪(1,+∞)C .[3,+∞)D .(-∞,-1]∪[3,+∞)5.某农户计划种植黄瓜和韭菜,种植面积不超过50亩(1亩≈666.7平方米),投入资金不超过54植面积(单位:亩)分别为( )A .50,0B .30,20C .20,30D .0,506.某旅行社租用A ,B 两种型号的客车安排900名客人旅行,A ,B 两种车辆的载客量分别为36人和60人,租金分别为1600元/辆和2400元/辆,旅行社要求租车总数不超过21辆,且B 型车不多于A 型车7辆,则租金最少为( )A .31 200元B .36 000元C .36 800元D .38 400元7.(2017年江苏)某公司一年购买某种货物600吨,每次购买x 吨,运费为6万元/次,一年的总存储费用为4x 万元,要使一年的总运费与总存储之和最小,则x 的值是__________.8.某项研究表明,在考虑行车安全的情况下,某路段车流量F (单位时间内测量点的车辆数,单位:辆/时)与车流速度v (假设车辆以相同速度v 行驶,单位:米/秒),平均车长l (单位:米)的值有关,其关系式为F =76 000vv 2+18v +20l.(1)如果不限定车型,l =6.05,那么最大车流量为______辆/时;(2)如果限定车型,l =5,那么最大车流量比(1)中的最大车流量增加______辆/时.9.(2017年湖北孝感一模)经测算,某型号汽车在匀速行驶过程中每小时耗油量y (单位:升)与速度x (单位:千米/时)(50≤x ≤120)的关系可近似表示为:y =⎩⎨⎧175(x 2-130x +4900),x ∈[50,80),12-x60,x ∈[80,120].(1)该型号汽车速度为多少时,可使得每小时耗油量最低?(2)已知A,B两地相距120千米,假定该型号汽车匀速从A地驶向B地,则汽车速度为多少时总耗油量最少?10.(2017年天津)电视台播放甲、乙两套连续剧,每次播放连续剧时,需要播放广告.已不少于30分钟,且甲连续剧播放的次数不多于乙连续剧播放次数的2倍.分别用x,y表示每周计划播出的甲、乙两套连续剧的次数.(1)用x,y列出满足题目条件的数学关系式,并画出相应的平面区域;(2)问电视台每周播出甲、乙两套连续剧各多少次,才能使收视人次最多?第六章 不等式第1讲 不等式的概念与性质1.A 解析:①a =1,b =-1,1a <1b不成立;②a =1,b =-1,a 2>b 2不成立; ③c =0,ac 4>bc 4 不成立;④因为c 2+1>0,a >b ,所以a c 2+1>bc 2+1成立.2.C 解析:由x >y >0,得1x <1y ,即1x -1y<0,A 不正确;由x >y >0及函数y =sin x 的单调性,可知sin x -sin y >0不一定正确,B 不正确;由0<12<1,x >y >0,得⎝⎛⎭⎫12x <⎝⎛⎭⎫12y ,即⎝⎛⎭⎫12x-⎝⎛⎭⎫12y <0,C 正确;由x >y >0,得xy >0,但不一定大于1,故ln x +ln y =ln xy >0不一定成立,D 不正确.3.D 解析:∵x 2-2x +3=(x -1)2+2>0,∴x 2+3>2x .∵a 3+b 3-a 2b -ab 2=(a -b )(a 2-b 2)=(a +b )(a -b )2≥0,∴a 3+b 3≥a 2b +ab 2.∵a 2+b 2-2(a -b -1)=(a -1)2+(b +1)2≥0,∴a 2+b 2≥2(a -b -1).4.B 解析:e 1=1+b 2a 2,e 2=1+(b +m )2(a +m )2.不妨令e 1<e 2,化简,得b a <b +ma +m (m >0),得bm <am ,得b <a .所以当b >a 时,有b a >b +m a +m ,即e 1>e 2;当b <a 时,有b a <b +ma +m,即e 1<e 2.故选B.5.B 解析:当方程①有实根,且②无实根时,a 21≥4,a 22<8,从而a 3=a 22a 1<82=4,∴a 23<16,即方程③:x 2+a 3x +4=0无实根.故选B.而A ,D 由于不等式方向不一致,不可推;C 推出③有实根.6.⎝⎛⎭⎫-2,-12 解析:因为f (1)=0,所以a +b +c =0.所以b =-(a +c ). 又a >b >c ,所以a >-(a +c )>c ,且a >0,c <0.所以1>-a +c a >c a ,即1>-1-c a >ca .所以⎩⎨⎧2ca <-1,ca>-2,解得-2<c a <-12.7.b <ax +by x +y <a 解析:依题意,知a >b ,将A ,B 两杯盐水混合后,盐水的浓度变为ax +by x +y .则有ax +by x +y >bx +by x +y =b ,ax +by x +y <ax +ay x +y =a .故有b <ax +by x +y <a .8.6 解析:设有x 辆汽车,则货物重为(4x +20)吨.由题意,得⎩⎪⎨⎪⎧8(x -1)<4x +20,8x >4x +20,x ∈N *.解得5<x <7,且x ∈N *.故只有x =6才满足要求.9.①④ 解析:①中,∵a 2-b 2=1,∴a -b =1a +b.∵a >0,b >0,又a 2=b 2+1>1,∴a >1.从而1a +b<1,即a -b <1.∴①正确.②中,取a =5,b =56,验证知②错误.③中,取a =4,b =1,验证知③错误. ④∵a ,b 是正实数,不妨设a >b >0, ∴a 3-b 3=(a -b )(a 2+b 2+ab ).∴a -b =a 3-b 3a 2+ab +b 2=1a 2+ab +b 2. ∵a 3=1+b 3>1,∴a 2>1.∴a 2+ab +b 2>1.∴0<1a 2+ab +b 2<1.∴0<a -b =1a 2+ab +b 2<1.即|a -b |<1.同理,设0<a <b ,也能得到|a -b |<1的结论.故④正确. 10.解:设该单位职工有n 人(n ∈N *),全票价为x 元, 坐甲车需花y 1元,坐乙车需花y 2元.则y 1=x +34x ·(n -1)=14x +34nx ,y 2=45nx .因为y 1-y 2=14x +34nx -45nx=14x -120nx =14x ⎝⎛⎭⎫1-n 5. 当n =5时,y 1=y 2; 当n >5时,y 1<y 2; 当n <5时,y 1>y 2.因此当单位去的人数为5人时,两车队收费相同;多于5人时,选甲车更优惠;少于5人时,选乙车队更优惠.11.证明:方法一,左边-右边=(a )3+(b )3ab-(a +b )=(a +b )(a -ab +b )-ab (a +b )ab=(a +b )(a -2 ab +b )ab =(a +b )(a -b )2ab≥0.∴原不等式成立.方法二,左边>0,右边>0. 左边右边=(a +b )(a -ab +b )ab (a +b ) =a -ab +b ab ≥2 ab -ab ab=1.∴原不等式成立.12.解:2sin 2α-sin α1-cos α=4sin αcos α(1-cos α)-sin α1-cos α=sin α1-cos α(-4cos 2α+4cos α-1)=-sin α1-cos α(2cos α-1)2.∵α∈(0,π),∴sin α>0,1-cos α>0,(2cos α-1)2≥0.∴-sin α1-cos α(2cos α-1)2≤0,即2sin 2α-sin α1-cos α≤0.∴2sin 2α≤sin α1-cos α,当且仅当α=π3时取等号.第2讲 一元二次不等式及其解法1.B 解析:由题意关于x 的不等式ax -b >0的解集是(-∞,1),可得ba=1,且a <0.则(ax +b )(x -3)>0可变形为(x -3)⎝⎛⎭⎫x +ba <0,即得(x -3)(x +1)<0.所以-1<x <3.所以不等式的解集是(-1,3).故选B.2.C 解析:当k =0时,原不等式等价于-2<0,显然恒成立,∴k =0符合题意.当k ≠0时,由题意,得⎩⎪⎨⎪⎧k <0,(2k )2-4k ·[-(k +2)]<0.解得-1<k <0.∴-1<k ≤0. 3.A 解析:依题意,得⎩⎪⎨⎪⎧ x ≤0,x +2≥x 2或⎩⎪⎨⎪⎧x >0,-x +2≥x 2⇒-1≤x ≤0或0<x ≤1⇒-1≤x ≤1. 4.A 解析:不等式x 2-4x -2-a >0在区间(1,4)内有解等价于a <(x 2-4x -2)max .令g (x )=x 2-4x -2,x ∈(1,4),∴g (x )<g (4)=-2.∴a <-2.5.A 解析:由题意,得A ={x |-1<x <3},B ={x |-3<x <2}.A ∩B ={x |-1<x <2},由根与系数的关系可知,a =-1,b =-2.∴a +b =-3.6.{x |-5<x <1} 解析:设x ≥0,因为f (x )是定义域为R 的偶函数,所以f (x )=f (-x )=x 2-2x .又f (x +2)=f (|x +2|),所以f (x +2)<3⇔f (|x +2|)=(|x +2|)2-2|x +2|<3.所以(|x +2|-3)(|x +2|+1)<0.所以0≤|x +2|<3,解得-5<x <1.所以原不等式的解集为{x |-5<x <1}.7.21 解析:设f (x )=x 2-6x +a ,其图象是开口向上,对称轴是x =3的抛物线,图象如图D115.图D115关于x 的一元二次不等式x 2-6x +a ≤0的解集中有且仅有3个整数,则⎩⎪⎨⎪⎧f (2)≤0,f (1)>0即⎩⎪⎨⎪⎧f (2)=4-12+a ≤0,f (1)=1-6+a >0, 解得5<a ≤8.又a ∈Z ,所以a =6,7,8,则所有符合条件的a 的值之和是6+7+8=21.8.①②③④ 解析:∵不等式ax 2+bx +c >0的解集为⎝⎛⎭⎫-13,2,∴a <0;-13,2是方程ax 2+bx +c =0的两根,-13+2=-ba>0,∴b >0;f (0)=c >0,f (1)=a +b +c >0,f (-1)=a-b +c <0.故正确结论的序号为①②③④.9.解:(1)依题意,得y =f (x )x =x 2-4x +1x =x +1x-4.因为x >0,所以x +1x ≥2,当且仅当x =1x,即x =1时,等号成立,所以y ≥-2.所以当x =1时,y =f (x )x 的最小值为-2.(2)因为f (x )-a =x 2-2ax -1,所以要使得“∀x ∈[0,2],不等式f (x )≤a 成立”只要“x 2-2ax -1≤0在[0,2]上恒成立”.不妨设g (x )=x 2-2ax -1,则只要g (x )≤0在[0,2]上恒成立即可.所以⎩⎪⎨⎪⎧ g (0)≤0,g (2)≤0.即⎩⎪⎨⎪⎧0-0-1≤0,4-4a -1≤0. 解得a ≥34.故a 的取值范围为⎣⎡⎭⎫34,+∞. 10.解:由f (1)=72,得a +b +c =72.令x 2+12=2x 2+2x +32⇒x =-1.由f (x )≤2x 2+2x +32推得f (-1)≤32.由f (x )≥x 2+12推得f (-1)≥32.∴f (-1)=32.∴a -b +c =32.故a +c =52,且b =1.∴f (x )=ax 2+x +52-a .依题意ax 2+x +52-a ≥x 2+12对一切x ∈R 都成立,∴a ≠1,且Δ=1-4(a -1)(2-a )≤0.由a -1>0,得a =32.∴f (x )=32x 2+x +1.证明如下: ∵32x 2+x +1-2x 2-2x -32 =-12x 2-x -12=-12(x +1)2≤0.∴32x 2+x +1≤2x 2+2x +32对x ∈R 都成立. ∴存在实数a =32,b =1,c =1,使得不等式x 2+12≤f (x )≤2x 2+2x +32对一切x ∈R 都成立.第3讲 算术平均数与几何平均数1.D 解析:y =x +1x的定义域为{x |x ≠0},当x >0时,有最小值2,当x <0时,有最大值-2.故A 项不正确;y =x 2+3x 2+2=x 2+2+1x 2+2≥2,∵x 2+2≥2,∴取不到“=”.故B 项不正确;∵当x >0时,3x +4x ≥2·3x ·4x =4 3,当且仅当3x =4x ,即x =2 33时取“=”.∴y =2-⎝⎛⎭⎫3x +4x 有最大值2-4 3.故C 项不正确,D 项正确. 2.C 解析:∵x >2,∴f (x )=x +1x -2=(x -2)+1x -2+2≥2 (x -2)·1x -2+2=4,当且仅当x -2=1x -2,即x =3时取等号.3.C 解析:z =x 2-3xy +4y 2,z xy =x 2-3xy +4y 2xy ≥2x ·2y -3xy xy =xy xy=1. 当且仅当x =2y 时,zxy取最小值,此时z =2y 2.x +2y -z =4y -2y 2=-2(y 2-2y )=-2(y -1)2+2,最大值为2.故选C.4.D 解析:由题意知,ab >0,且3a +4b >0,所以a >0,b >0.又log 4(3a +4b )=log 2ab ,所以3a +4b =ab .所以4a +3b =1.所以a +b =(a +b )·⎝⎛⎭⎫4a +3b =7+4b a +3a b ≥7+2 4b a ·3a b =7+4 3.当且仅当4b a =3ab,即a =4+2 3,b =3+2 3时,等号成立.故选D.5.C 解析:∵1a +2b =ab ,∴a >0,b >0.∵ab =1a +2b ≥2 1a ·2b =2 2ab,∴ab ≥22(当且仅当b =2a 时取等号),∴ab 的最小值为2 2.故选C.6.C 解析:p =f (ab )=ln ab =12ln(ab ),q =f ⎝⎛⎭⎫a +b 2=ln a +b 2,r =12[f (a )+f (b )]=12ln(ab ).因为a +b 2>ab ,由f (x )=ln x 在区间(0,+∞)内是增函数,可知f ⎝⎛⎭⎫a +b 2>f (ab ),所以q >p =r .故选C.7.A 解析:方法一,由x +2y -xy =0,得2x +1y=1,且x >0,y >0.∴x +2y =(x +2y )·⎝⎛⎭⎫2x +1y =4y x +xy+4≥4+4=8(当且仅当x =4,y =2等号成立). 方法二,由x +2y =xy =12x ·2y ≤12⎝⎛⎭⎫x +2y 22=()x +2y 28,∴x +2y ≥8(当且仅当x =2y 时取等号).8.3 解析:由x 2+2xy -3=0,得y =3-x 22x =32x -12x .则2x +y =2x +32x -12x =3x 2+32x ≥2 3x 2·32x=3,当且仅当x =1时,等号成立.所以(2x+y )min =3.9.(1)9 (2)1解析:(1)因为x >-1,所以x +1>0,所以y =(x +5)(x +2)x +1=x 2+7x +10x +1=(x +1)2+5(x +1)+4x +1=(x +1)+4x +1+5≥2 (x +1)·4x +1+5=9.当且仅当x +1=4x +1,即x =1时等号成立.故函数y =(x +5)(x +2)x +1的最小值为9.(2)因为x <54,所以5-4x >0.则f (x )=4x -2+14x -5=-⎝⎛⎭⎫5-4x +15-4x +3≤-2+3=1.当且仅当5-4x =15-4x ,即x =1时,等号成立.故f (x )=4x -2+14x -5的最大值为1.10.(1)B (2)6解析:2a +1b =2(2a +b )a +2a +b b =4+2b a +2a b +1=5+2⎝⎛⎭⎫b a +a b ≥5+2×2 b a ·a b=9. 当且仅当a =b =13时取等号.∵2a +1b ≥m ,∴m ≤9,即m 的最大值等于9.故选B.(2)由已知,得x =9-3y1+y.方法一,(消元法)∵x >0,y >0,∴0<y <3.∴x +3y =9-3y 1+y +3y =121+y +(3y +3)-6≥2 121+y ·(3y +3)-6=6.当且仅当121+y=3y +3,即y =1,x =3时,取等号,故(x +3y )min =6.方法二,∵x >0,y >0,9-(x +3y )=xy =13x ·(3y )≤13·⎝⎛⎭⎫x +3y 22,当且仅当x =3y 时等号成立.设x +3y =t >0,则t 2+12t -108≥0. ∴(t -6)(t +18)≥0. 又t >0,∴t ≥6.故当x =3,y =1时,(x +3y )min =6.第4讲 简单的线性规划1.D 解析:如图D116,画出可行域.图D116z =x +2y 表示斜率为-12的一组平行线,当过点C (3,3)时,目标函数取得最大值z max=3+2×3=9.2.B 解析:将点(0,0),(2,0),(0,3)代入z =x -y 解得0,2,-3.所以z =x -y 的取值范围是[-3,2].故选B.3.B 解析:作出不等式组表示的平面区域(如图D117),因为z =x +y -2x +1=y -3x +1+1表示平面区域内的点与点(-1,3)之间连线的斜率k 与1的和.由图知,当x =0,y =-2时,k 取得最小值k min =-2-30+1=-5;当x =0,y =3时,k 取得最大值k max =3-30+1=0.所以z ∈[-4,1].故选B.图D1174.B 解析:根据题中约束条件可画出可行域如图D118.两直线交点坐标为A ⎝⎛⎭⎫a -12,a +12.又由z =x +ay 知,当a =0时,A ⎝⎛⎭⎫-12,12,z 的最小值为-12,不合题意;当a ≥1时,y =-1a x +za 过点A 时,z 有最小值,即z =a -12+a ×a +12=a 2+2a -12=7,解得a =3或a =-5(舍去);当a <1时,z 无最小值.故选B.图D1185.C 解析:区域M 是一个三角形区域,三个顶点的坐标分别是(8,3),(10,2),(9,1),结合图形检验,可知:当a ∈[2,9]时,符合题目要求.6.D 解析:如图D119,由y =ax +z 知z 的几何意义是直线在y 轴上的截距,故当a >0时,要使z =y -ax 取得最大值的最优解不唯一,则a =2;当a <0时,要使z =y -ax 取得最大值的最优解不唯一,则a =-1.图D1197.1 解析:不等式组表示的区域如图D120所示的阴影部分,图D120由x =1,x +y =0,得A (1,-1); 由x =1,x -y -4=0,得B (1,-3); 由x +y =0,x -y -4=0,得C (2,-2).∴|AB |=2.∴S △ABC =12×2×1=1.8.⎣⎡⎦⎤45,13 解析:由图D121知,原点到直线2x +y -2=0的距离平方为x 2+y 2的最小值,为⎝⎛⎭⎫ 252=45;原点到点(2,3)距离平方为x 2+y 2的最大值,为13.因此x 2+y 2的取值范围为⎣⎡⎦⎤45,13.图D1219.解:由约束条件⎩⎪⎨⎪⎧x -4y +3≤0,3x +5y -25≤0,x ≥1,作出(x ,y )的可行域如图D122所示的阴影部分.图D122由⎩⎪⎨⎪⎧ x =1,3x +5y -25=0,解得A ⎝⎛⎭⎫1,225. 由⎩⎪⎨⎪⎧x =1,x -4y +3=0,解得C (1,1). 由⎩⎪⎨⎪⎧x -4y +3=0,3x +5y -25=0,解得B (5,2). (1)∵z =y x =y -0x -0,∴z 的值即是可行域中的点与原点O 连线的斜率.观察图形可知z min=k OB =25.(2)z =x 2+y 2的几何意义是可行域上的点到原点O 的距离的平方. 结合图形可知,可行域上的点到原点的距离中, d min =|OC |=2,d max =|OB |=29. 故z 的取值范围是[2,29].(3)z =x 2+y 2+6x -4y +13=(x +3)2+(y -2)2的几何意义是可行域上的点到点(-3,2)的距离的平方.结合图形可知,可行域上的点到(-3,2)的距离中, d min =1-(-3)=4,d max =(-3-5)2+(2-2)2=8. 故z 的取值范围是[16,64].10.解:g (x )=x 2+(a +1)x +a +b +1,两个零点为方程x 2+(a +1)x +a +b +1=0的两根,且一根大于1,另一根大于0且小于1,由根的分布画图,得⎩⎪⎨⎪⎧ g (0)>0,g (1)<0,即⎩⎪⎨⎪⎧a +b +1>0,2a +b +3<0.作出可行域如图D123.图D123而b a =b -0a -0表示可行域中的点(a ,b )与原点连线的斜率k ,直线OA 的斜率k 1=-12,直线2a +b +3=0的斜率k 2=-2.所以k ∈⎝⎛⎭⎫-2,-12,即ba ∈⎝⎛⎭⎫-2,-12. 第5讲 不等式的应用1.C 解析:yx=-⎝⎛⎭⎫x +25x +12≤-2 x ×25x +12,当且仅当x =25x,即x =5时取等号.2.C 解析:作出不等式组对应的平面区域,由⎩⎪⎨⎪⎧ x -4y =-3,x =1解得⎩⎪⎨⎪⎧x =1,y =1,设A (1,1),由图可知,直线2x +y =m 经过点A 时,m 取最小值,同时z =4x ·2y =22x +y 取得最小值.所以z min =22×1+1=23=8.故选C.3.B 解析:设楼房每平方米的平均综合费用为f (x )元,则f (x )=(560+48x )+2160×10 0002000x=560+48x +10 800x=560+48⎝⎛⎭⎫x +225x ≥560+48×2 x ·225x=2000(x ≥10,x ∈N *).当且仅当x =225x,即x =15时,f (x )取得最小值为f (15)=2000.4.D 解析:设公比为q .因为a 2=1=a 1q ,所以S 3=a 1+1+a 1q 2=1q+q +1.当q >0时,1q +q ≥2;当q <0时,1q+q ≤-2.所以S 3≥3或S 3≤-1.故选D. 5.B 解析:设黄瓜和韭菜的种植面积分别为x ,y 亩,种植总利润为z 万元,则目标函数z =(0.55×4x -1.2x )+(0.3×6y -0.9y )=x +0.9y .作出约束条件如图D124所示的阴影部分.易求得点A (0,50),B (30,20),C (45,0).平移直线x +0.9y =0,当直线x +0.9y =0经过点B (30,20)时,z 取得最大值为48.故选B.图D124 图D1256.C 解析:设旅行社租用A 型客车x 辆,B 型客车y 辆,租金为z 元,则线性约束条件为⎩⎪⎨⎪⎧x +y ≤21,y -x ≤7,36x +60y ≥900,x ,y ∈N ,目标函数为z =1600x +2400y .画出可行域:如图D125所示的阴影部分,可知当目标函数过点(5,12)时,有最小值z min =36 800(元).7.30 解析:总费用4x +600x ×6=4⎝⎛⎭⎫x +900x ≥4×2900=240.当且仅当x =900x,即x =30时等号成立.8.(1)1900 (2)100解析:(1)当l =6.05时,F =76 000v v 2+18v +20l =76 000v +121v +18≤76 0002 v ·121v +18=76 00022+18=1900,当且仅当v =121v ,即v =11时,等号成立.(2)当l =5时,F =76 000v v 2+18v +20l =76 000v +100v +18≤76 0002 v ·100v +18=76 00020+18=2000,当且仅当v =100v ,即v =10时,等号成立.此时车流量比(1)中的最大车流量增加100辆/时. 9.解:(1)①当x ∈[50,80)时,y =175(x 2-130x +4900)=175[(x -65)2+675] 当x =65时,y 有最小值175×675=9.②当x ∈[80,120]时,函数单调递减,故当x =120时,y 有最小值10. 因为9<10,故当x =65时每小时耗油量最低.(2)设总耗油量为l ,由题意,可知l =y ·120x .①当x ∈[50,80)时,l =y ·120x =85⎝⎛⎭⎫x +4900x -130≥85⎝⎛⎭⎫2 x ×4900x -130=16. 当且仅当x =4900x ,即x =70时,l 取得最小值16.②当x ∈⎣⎢⎡⎦⎥⎤80120时,l =y ·120x =1440x -2为减函数,当x =120时,l 取得最小值10.因为10<16,所以当速度为120时,总耗油量最少.10.解:(1)由已知,x ,y满足的数学关系式为⎩⎪⎨⎪⎧70x +60y ≤600,5x +5y ≥30,x ≤2y ,x ≥0,y ≥0,即⎩⎪⎨⎪⎧7x +6y ≤60,x +y ≥6,x -2y ≤0,x ≥0,y ≥0,该二元一次不等式组所表示的平面区域为如图D126中的阴影部分.图D126 图D127 (2)设总收视人次为z 万, 则目标函数为z =60x +25y .考虑z =60x +25y ,将它变形为y =-125x +z 25,这是斜率为-125,随z 变化的一族平行直线.z 25为直线在y 轴上的截距,当z25取得最大值时,z 的值最大.又因为x ,y 满足约束条件,所以由图D127可知,当直线z =60x +25y 经过可行域上的点M 时,截距z25最大,即z最大.解方程组⎩⎪⎨⎪⎧7x +6y =60,x -2y =0得点M 的坐标为(6,3).所以,电视台每周播出甲连续剧6次、乙连续剧3次时才能使总收视人次最多。
2019年《·高考总复习》数学:第六章 第3讲 算术平均数与几何平均数
答案:8
2019年7月10日
你是我今生最美的相遇遇上你是我的缘
19
(2)已知 x>0,y>0,且1x+9y=1,则 x+y 的最小值为 __________.
解析:∵x>0,y>0,1x+9y=1,∴x+y=(x+y)1x+9y=yx+ 9yx+10≥6+10=16.当且仅当yx=9yx时,上式等号成立.由1x+9y= 1,得 x=4,y=12 时,(x+y)min=16.
答案:16
2019年7月10日
你是我今生最美的相遇遇上你是我的缘
20
(3)已知正数 a,b 满足 a+2b=1,则1a+1b的最小值是 _____________.
解析:1a+1b=a+a2b+a+b2b=3+2ab+ab≥3+2 2ab·ab=3 +2 2.当且仅当2ab=ab时等号成立,又 a+2b=1,得 a= 2-1, b=2-2 2时,1a+1bmin=3+2 2.
2019年7月10日
你是我今生最美的相遇遇上你是我的缘
18
考点 3 利用逆代法求最值 例 3:(1)(2017 年山东)若直线ax+by=1(a>0,b>0)过点(1,2), 则 2a+b 的最小值为____________.
解析:直线ax+by=1(a>0,b>0)过点(1,2),有1a+2b=1.则 2a+b=(2a+b)1a+2b=2+4ba+ba+2≥4+2 4ba·ba=8,当且 仅当4ba=ba时,上式等式成立.由1a+2b=1,得 a=2,b=4 时, (2a+b)min=8.
10 5
时,2x+y
取最大值2
10 5.
2019年7月10日
你是我今生最美的相遇遇上你是我的缘
27
(3)a+2 b叫做算术平均数, ab叫做几何平均数,基本不等 式可叙述为两个正数的算术平均数不小于它们的几何平均数.
2019年《南方新课堂·高考总复习》数学(理科)作业及测试阶段检测卷(六) Word版含解析
阶段检测卷(六)(立体几何)时间:分钟满分:分一、选择题:本大题共小题,每小题分,共分,有且只有一个正确答案,请将正确选项填入题后的括号中..已知,,是三条不同的直线,命题“∥且⊥⇒⊥”是正确的,如果把,,中的两个或三个换成平面,在所得的命题中,真命题有( ).个.个.个.个.如图-,在四面体-中,截面是正方形,则在下列命题中,错误的是( )图-.⊥.∥截面.=.异面直线与所成的角为°.如图-,在正方体-′′′′中,与′成°角的面对角线条数是( )图-.条.条.条.条.在如图-所示的空间直角坐标系-中,一个四面体的顶点坐标分别是(),(),(),(),给出编号①②③④的四个图,则该四面体的正视图和俯视图分别为( )图-.①和②.③和①.④和③.④和②.如图-,在四边形中,∥,=,∠=°,∠=°,将△沿折起,使平面⊥平面,构成三棱锥-,则在三棱锥-中,下列命题正确的是( )图-.平面⊥平面.平面⊥平面.平面⊥平面.平面⊥平面.如图-,四棱锥-的底面为正方形,⊥底面,则下列结论中不正确的是( )图-.⊥.∥平面.与平面所成的角等于与平面所成的角.与所成的角等于与所成的角.(年广东深圳二模)一个长方体被一平面截去一部分后,所剩几何体的三视图如图-,则该几何体的体积为()图-.....(年贵州贵阳二模)如图-,在正方形中,,分别是,的中点,沿,,把正方形折成一个四面体,使,,三点重合,重合后的点记为,点在△内的射影为,则下列说法正确的是( )图-.是△的垂心.是△的内心.是△的外心.是△的重心二、填空题:本大题共小题,每小题分,共分,把答案填在题中横线上..圆柱形容器内部盛有高度为的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图-),则球的半径是 .。
2019年《南方新课堂·高考总复习》数学(理科)作业及测试:课时作业 第一章集合与逻辑用语 Word版含解析
第一章 集合与逻辑用语第1讲 集合的含义与基本关系1.(2017年北京)若集合A ={x |-2<x <1},B ={x |x <-1,或x >3},则A ∩B =( ) A .{x |-2<x <-1} B .{x |-2<x <3} C .{x |-1<x <1} D .{x |1<x <3}2.(2017年天津)设集合A ={1,2,6},B ={2,4},C ={1,2,3,4},则(A ∪B )∩C =( ) A .{2} B .{1,2,4}C .{1,2,4,6}D .{1,2,3,4,6}3.(2016年浙江)已知集合P ={x ∈R |1≤x ≤3},Q ={x ∈R |x 2≥4}, 则P ∪(∁R Q )=( ) A .[2,3] B .(-2,3 ]C .[1,2)D .(-∞,-2]∪[1,+∞)4.设集合A =⎩⎨⎧⎭⎬⎫5,b a ,a -b ,B ={b ,a +b ,-1},若A ∩B ={2,-1},则A ∪B =( )A .{2,3}B .{-1,2,5}C .{2,3,5}D .{-1,2,3,5}5.已知集合A ={(x ,y )|y =log 2x },B ={(x ,y )|y =x 2-2x },则A ∩B 的元素有( ) A .1个 B .2个 C .3个 D .4个6.对任意两个正整数m ,n ,定义某种运算⊕:m ⊕n =⎩⎪⎨⎪⎧m +n ,m 与n 奇偶性相同,mn ,m 与n 奇偶性不同,则集合P ={(a ,b )|a ⊕b =8,a ,b ∈N *}中元素的个数为( )A .5个B .7个C .9个D .11个 7.若集合A 具有以下性质: (1)0∈A,1∈A ;(2)若x ∈A ,y ∈A ,则x -y ∈A ,且x ≠0时,1x∈A .则称集合A 是“好集”.下列命题正确的个数是( ) ①集合B ={-1,0,1}是“好集”; ②有理数集Q 是“好集”;③设集合A 是“好集”,若x ∈A ,y ∈A ,则x +y ∈A . A .0个 B .1个 C .2个 D .3个8.对于集合M ,N ,定义M -N ={x |x ∈M ,且x ∉N },M ⊕N =(M -N )∪(N -M ).设A ={y |y =3x ,x ∈R },B ={y |y =-(x -1)2+2,x ∈R },则A ⊕B =( )A .[0,2)B .(0,2]C .(-∞,0]∪(2,+∞)D .(-∞,0)∪[2,+∞)9.某校高三(1)班50名学生选择选修模块课程,他们在A ,B ,C 3个模块中进行选择,则3A .7人 B .6人 C .5人 D .4人10.已知集合A={x|x2+x-2=0},B={x|ax=1},若A∩B=B,则a=______________.11.已知集合A={x∈R|ax2-3x+2=0,a∈R}.(1)若A是空集,求实数a的取值范围;(2)若A中只有一个元素,求a的值,并写出A中的元素;(3)若A中至多有一个元素,求实数a的取值范围.12.已知集合P={x|a+1≤x≤2a+1},Q={x|x2-3x≤10}.(1)若a=3,求(∁R P)∩Q;(2)若P∪Q=Q,求实数a的取值范围.第2讲 命题、量词与简单的逻辑联结词1.(2015年浙江)命题“∀n ∈N *,f (n )∈N *,且f (n )≤n ”的否定形式是( ) A .∀n ∈N *,f (n )∈N *,且f (n )>n B .∀n ∈N *,f (n )∈N *,或f (n )>n C .∃n 0∈N *,f (n 0)∈N *,且f (n 0)>n 0 D .∃n 0∈N *,f (n 0)∉N *,或f (n 0)>n 02.(2017年山东)已知命题p :∃x 0∈R ,x 20-x 0+1≥0;命题q :若a 2<b 2,则a <b .下列命题为真命题的是( )A .p ∧qB .p ∧綈qC .綈p ∧qD .綈p ∧綈q3.命题“和为偶数的两个整数都为偶数”的否定是( ) A .和不为偶数的两个整数都为偶数 B .和为偶数的两个整数都不为偶数 C .和不为偶数的两个整数不都为偶数 D .和为偶数的两个整数不都为偶数4.已知命题p :“∀x ∈[0,1],a ≥e x ”,命题q :“∃x 0∈R ,x 20+4x 0+a =0”.若命题“p ∧q ”是真命题,则实数a 的取值范围是( )A .(4,+∞)B .[1,4]C .[e,4]D .(-∞,1]5.(2016年广东广州一模)已知下列四个命题:p 1:若直线l 和平面α内的无数条直线垂直,则l ⊥α;p 2:若f (x )=2x -2-x ,则∀x ∈R ,f (-x )=-f (x );p 3:若f (x )=x +1x +1,则∃x 0∈(0,+∞),f (x 0)=1;p 4:在△ABC 中,若A >B ,则sin A >sin B . 其中真命题的个数是( )A .1个B .2个C .3个D .4个6.(2017年广东汕头一模)若命题“ax 2-2ax +3>0恒成立”是假命题,则实数a 的取值范围是( )A .0<a <3B .a <0,或a ≥3C .a <0,或a >3D .a ≤0,或a ≥3 7.(2017年山东)已知命题p :∀x >0,ln(x +1)>0;命题q :若a >b ,则a 2>b 2,下列命题为真命题的是( )A .p ∧qB .p ∧綈qC .綈p ∧qD .綈p ∧綈q8.(2016年河南郑州质量预测)已知函数f (x )=x +4x ,g (x )=2x +a ,若∀x 1∈⎣⎡⎦⎤12,1,∃x 2∈[2,3],使得f (x 1)≥g (x 2),则实数a 的取值范围是( )A .a ≤1B .a ≥1C .a ≤2D .a ≥29.(2015年山东)若“∀x ∈⎣⎡⎦⎤0,π4,tan x ≤m ”是真命题,则实数m 的最小值为________. 10.(2017年湖南长沙质检)已知下面四个命题:①“若x 2-x =0,则x =0或x =1”的逆否命题为“若x ≠0,且x ≠1,则x 2-x ≠0”;②“x<1”是“x2-3x+2>0”的充分不必要条件;③命题p:∃x0∈R,使得x20+x0+1<0,则綈p:∀x∈R,都有x2+x+1≥0;④若p且q为假命题,则p,q均为假命题.其中为真命题的是________.(填序号)11.设函数f(x)=x2-2x+m.(1)若∀x∈[0,3],f(x)≥0恒成立,求m的取值范围;(2)若∃x0∈[0,3],f(x0)≥0成立,求m的取值范围.12.设命题p:函数y=kx+1在R上是增函数,命题q:∃x0∈R,x20+(2k-3)x0+1=0,如果p∧q是假命题,p∨q是真命题,求k的取值范围.第3讲充分条件与必要条件1.(2015年天津)设x∈R,则“1<x<2”是“|x-2|<1”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件2.(2016年四川)设p:实数x,y满足x>1,且y>1,q:实数x,y满足x+y>2,则p 是q的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件3.(2016年天津)设{a n}是首项为正数的等比数列,公比为q,则“q<0”是“对任意的正整数n,a2n-1+a2n<0”的()A.充要条件B.充分不必要条件C.必要不充分条件D.既不充分也不必要条件4.(2015年福建)若l,m是两条不同的直线,m垂直于平面α,则“l⊥m”是“l∥α”的()A.充分不必要条件B.必要不充分条件C .充要条件D .既不充分也不必要条件5.(2016年山东)已知直线a ,b 分别在两个不同的平面α,β内,则“直线a 和直线b 相交”是“平面α和平面β相交”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件6.(2015年陕西)“sin α=cos α”是“cos 2α=0”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件7.(2017年北京)设m ,n 为非零向量,则“存在负数λ,使得m =λn ”是“m·n <0”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件8.(2014年江西)下列叙述中正确的是( )A .若a ,b ,c ∈R ,则“ax 2+bx +c ≥0”的充分条件是“b 2-4ac ≤0”B .若a ,b ,c ∈R ,则“ab 2>cb 2”的充要条件是“a >c ”C .命题“对任意x ∈R ,有x 2≥0”的否定是“存在x 0∈R ,有x 20≥0”D .l 是一条直线,α,β是两个不同的平面,若l ⊥α,l ⊥β,则α∥β9.设α,β是两个不同的平面,m 是直线且m ⊂α,则“m ∥β” 是“α∥β”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件10.(2015年重庆)“x >1”是“log 12(x +2)<0”的( )A .充要条件B .充分不必要条件C .必要不充分条件D .既不充分也不必要条件11.已知(x +1)(2-x )≥0的解为条件p ,关于x 的不等式x 2+mx -2m 2-3m -1<0⎝⎛⎭⎫m >-23的解为条件q .(1)若p 是q 的充分不必要条件,求实数m 的取值范围; (2)若綈p 是綈q 的充分不必要条件,求实数m 的取值范围.12.在平面直角坐标系xOy 中,直线l 与抛物线y 2=2x 相交于A ,B 两点.(1)求证:命题“如果直线l 过点T (3,0),那么OA →·OB →=3”是真命题; (2)写出(1)中命题的逆命题,判断它是真命题还是假命题,并说明理由.习题集部分第一章 集合与逻辑用语 第1讲 集合的含义与基本关系1.A 解析:利用数轴可知A ∩B ={x |-2<x <-1}.故选A. 2.B 解析:(A ∪B )∩C ={1,2,4,6}∩{1,2,3,4}={1,2,4}.故选B.3.B 解析:∁R Q ={x ∈R |x 2<4}={x ∈R |-2<x <2},P ∪(∁R Q )=[1,3]∪(-2,2)=(-2,3].故选B.4.D 解析:由A ∩B ={2,-1},可得⎩⎪⎨⎪⎧b a =2,a -b =-1,或⎩⎪⎨⎪⎧b a =-1,a -b =2.当⎩⎪⎨⎪⎧b a =2,a -b =-1时,⎩⎪⎨⎪⎧a =1,b =2,此时B ={2,3,-1},则A ∪B ={-1,2,3,5};当⎩⎪⎨⎪⎧b a =-1,a -b =2时,⎩⎪⎨⎪⎧a =1,b =-1,不符合题意,舍去.故A ∪B ={-1,2,3,5}.5.B 解析:在同一平面直角坐标系中画出函数y =log 2x 与y =x 2-2x 的图象,如图D87,由图可知y =log 2x 与y =x 2-2x 的图象有2个交点,则A ∩B 的元素有2个.图D876.C 解析:当a ,b 奇偶性相同时,a ⊕b =a +b =1+7=2+6=3+5=4+4;当a ,b 奇偶性不同时,a ⊕b =ab =1×8.由于(a ,b )有序,故共有元素4×2+1=9(个).7.C 解析:(1)集合B 不是“好集”,假设集合B 是“好集”,因为-1∈B,1∈B ,所以-1-1=-2∈B ,这与-2∉B 矛盾.(2)有理数集Q 是“好集”,因为0∈Q ,1∈Q ,对任意的x ∈Q ,y ∈Q ,有x -y ∈Q ,且x ≠0时,1x ∈Q ,所以有理数集Q 是“好集”.(3)因为集合A 是“好集”,所以0∈A ,若x ∈A ,y ∈A ,则0-y ∈A ,即-y ∈A ,所以x -(-y )∈A ,即x +y ∈A .8.C 解析:由题意知,集合A ={y |y >0},B ={y |y ≤2}. 所以A -B ={y |y >2},B -A ={y |y ≤0}. 所以A ⊕B =(2,+∞)∪(-∞,0].故选C.9.B 解析:方法一,设三个模块都选择的学生人数为x ,由韦恩图D88,得5+x +2+x +1+x +11-x +12-x +13-x +x =50.得x =6.图D88方法二,由题意,得28+26+26-11-12-13+x =50.得x =6.10.-12或1或0 解析:依题意,可得A ∩B =B ⇔B ⊆A.集合A ={x |x 2+x -2=0}={-2,1},当x =-2时,-2a =1,解得a =-12;当x =1时,a =1;又B 是空集时也符合题意,这时a =0.11.解:集合A 是方程ax 2-3x +2=0在实数范围内的解组成的集合.(1)若A 是空集,即方程ax 2-3x +2=0无解,当a =0时,x =23,不合题意;则⎩⎪⎨⎪⎧a ≠0,Δ=(-3)2-8a <0.∴a >98,即实数a 的取值范围是⎝⎛⎭⎫98,+∞. (2)当a =0时,方程只有一个解23,此时A 中只有一个元素23;当a ≠0时,应有Δ=0,∴a =98.此时方程有两个相等的实数根.当a =98时,解得x 1=x 2=43,A 中只有一个元素43.∴当a =0或a =98时,A 中只有一个元素,分别是23或43.(3)A 中至多有一个元素,包括A 是空集和A 中只有一个元素两种情况,根据(1)(2)的结果,得a =0或a ≥98,即实数a 的取值范围是⎩⎨⎧⎭⎬⎫a |a =0,或a ≥98.12.解:(1)因为a =3,所以P ={x |4≤x ≤7}, ∁R P ={x |x <4,或x >7}.又Q ={x |x 2-3x -10≤0}={x |-2≤x ≤5},所以(∁R P )∩Q ={x |x <4,或x >7}∩{x |-2≤x ≤5}={x |-2≤x <4}. (2)当P ≠∅时,由P ∪Q =Q ,得P ⊆Q . 所以⎩⎪⎨⎪⎧a +1≥-2,2a +1≤5,2a +1≥a +1.解得0≤a ≤2.当P =∅,即2a +1<a +1时,有P ⊆Q ,得a <0. 综上所述,实数a 的取值范围是(-∞,2].第2讲 命题、量词与简单的逻辑联结词1.D 解析:根据全称命题的否定是特称命题.故选D.2.B 解析:显然命题p 为真命题, 命题q 为假命题, 即p ,綈q 均是真命题, p ∧綈q 为真命题.故选B.3.D 解析:命题“和为偶数的两个整数都为偶数”的否定是:和为偶数的两个整数不都为偶数.故选D.4.C 解析:∀x ∈[0,1],a ≥e x ,即a ≥(e x )max =e 1=e ;∃x 0∈R ,x 20+4x 0+a =0,即Δ=16-4a ≥0,a ≤4.命题“p ∧q ”是真命题,即p 真q 真.故选C.5.B 解析:若直线l 和平面α内的无数条直线垂直,则l ⊥α,或l ∥α,或l ⊂α,或l 与α相交,所以p 1是假命题;f (-x )=2-x -2x =-(2x -2-x )=-f (x ),所以p 2是真命题;由x +1x +1=1,得x =0.所以p 3是假命题;Α>Β⇒a >b ⇒2R sin Α>2R sin Β⇒sin Α>sin Β,所以p 4是真命题.故选B.6.B 解析:命题“ax 2-2ax +3>0恒成立”是假命题,即∃x 0∈R ,使ax 20-2ax 0+3≤0,当a =0时,不符合题意;当a <0时,符合题意;当a >0时,Δ=4a 2-12a ≥0⇒a ≥3.综上所述,实数a 的取值范围是a <0,或a ≥3.故选B.7.B 解析:当x >0时,x +1>1,ln(x +1)>0,即p 为真命题;当-1>-2时,而(-1)2<(-2)2,即q 为假命题,即p ,綈q 均是真命题, p ∧綈q 为真命题.故选B.8.A 解析:由题意知,f (x )min ⎝ ⎛⎭⎪⎪⎫x ∈⎣⎢⎢⎡⎦⎥⎥⎤121≥g (x )min (x ∈[2,3]),因为f (x )min =5,g (x )min =4+a ,所以5≥4+a ,即a ≤1.故选A.9.1 解析:若“∀x ∈⎣⎡⎦⎤0,π4,tan x ≤m ”是真命题,则实数m 大于或等于函数y =tan x 在⎣⎡⎦⎤0,π4上的最大值.因为函数y =tan x 在⎣⎡⎦⎤0,π4上为增函数,所以函数y =tan x 在⎣⎡⎦⎤0,π4上的最大值为tan π4=1.所以m ≥1.则实数m 的最小值为1.10.①②③ 解析:①正确.②中,x 2-3x +2>0⇔x >2或x <1,所以“x <1”是“x 2-3x +2>0”的充分不必要条件,②正确.由于特称命题的否定为全称命题,所以③正确.若p 且q 为假命题,则p ,q 至少有一个是假命题,所以④的推断不正确.11.解:(1)若对∀x ∈[0,3],f (x )≥0恒成立,即f (x )min ≥0. f (x )=x 2-2x +m =(x -1)2+m -1, f (x )min =f (1)=m -1≥0,即m ≥1.(2)若∃x 0∈[0,3],f (x 0)≥0成立,即f (x )max ≥0. f (x )=x 2-2x +m =(x -1)2+m -1, f (x )max =f (3)=m +3≥0,即m ≥-3.12.解:∵函数y =kx +1在R 上是增函数,∴k >0.由∃x 0∈R ,x 20+(2k -3)x 0+1=0,得关于x 的方程x 2+(2k -3)x +1=0有解,∴Δ=(2k -3)2-4≥0.解得k ≤12或k ≥52.∵p ∧q 是假命题,p ∨q 是真命题, ∴命题p ,q 一真一假.①若p 真q 假,则⎩⎪⎨⎪⎧k >0,12<k <52.∴12<k <52; ②若p 假q 真,则⎩⎪⎨⎪⎧k ≤0,k ≤12或k ≥52.∴k ≤0.综上所述,k 的取值范围为(-∞,0]∪⎝ ⎛⎭⎪⎫12,52.第3讲 充分条件与必要条件1.A 解析:由|x -2|<1⇒-1<x -2<1⇒1<x <3,可知“1<x <2”是“|x -2|<1”的充分不必要条件.故选A.2.A 解析:由x >1,且y >1,得x +y >2,而当x +y >2时,不能得出x >1且y >1.故p 是q 的充分不必要条件.故选A.3.C 解析:由a 2n -1+a 2n <0⇒a 1(q 2n -2+q 2n -1)<0⇒q 2(n -1)(q +1)<0⇒q ∈(-∞,-1),故是必要不充分条件.故选C.4.B 解析:若l ⊥m ,因为m 垂直于平面α,则l ∥α,或l ⊂α;若l ∥α,又m 垂直于平面α,则l ⊥m ,所以“ l ⊥m ”是“l ∥α”的必要不充分条件.故选B.5.A 解析:直线a 与直线b 相交,则α,β一定相交,若α,β相交,则a ,b 可能相交,也可能平行或异面.故选A.6.A 解析:cos 2α=0⇒cos 2α-sin 2α=0⇒(cos α-sin α)·(cos α+sin α)=0,所以sin α=cos α或sin α=-cos α.故选A.7.A 解析:若∃λ<0,使m =λn ,即两向量反向,夹角是180°,那么m ·n =|m ||n |cos 180°=-|m ||n |<0,若m ·n <0,那么两向量的夹角为(90°,180°],并不一定反向,即不一定存在负数λ,使得m =λn ,所以是充分不必要条件.故选A.8.D 解析:当a <0时,由“b 2-4ac ≤0”推不出“ax 2+bx +c ≥0”,A 错误;当b =0时,由“a >c ”推不出“ab 2>cb 2”,B 错误;命题“对任意x ∈R ,有x 2≥0”的否定是“存在x 0∈R ,有x 20<0”,C 错误;因为与同一条直线垂直的两个平面平行,所以D 正确.9.B 解析:由m ⊂α,m ∥β,得不到α∥β,因为α,β可能是相交的,只要m 和α,β的交线平行即可得到m ∥β;∵α∥β,m ⊂α,∴m 和β没有公共点.∴m ∥α,即由α∥β可推得m ∥β.∴m ∥β是α∥β的必要不充分条件.10.B 解析:log 12(x +2)<0⇔x +2>1⇔x >-1.故选B.11.解:(1)设条件p 的解集为集合A , 则A ={x |-1≤x ≤2}.设条件q 的解集为集合B , 则B ={x |-2m -1<x <m +1}. 若p 是q 的充分不必要条件,则A B . ⎩⎪⎨⎪⎧ m +1>2,-2m -1<-1,m >-23.解得m >1.(2)若綈p 是綈q 的充分不必要条件,则B A . ⎩⎪⎨⎪⎧m +1≤2,-2m -1≥-1,m >-23.解得-23<m ≤0.12.(1)证明:设过点T (3,0)的直线l 交抛物线y 2=2x 于点A (x 1,y 1),B (x 2,y 2). 当直线l 的斜率不存在时,直线l 的方程为x =3, 此时,直线l 与抛物线相交于点A (3,6),B (3,-6). ∴OA →·OB →=3. 当直线l 的斜率存在时,设直线l 的方程为y =k (x -3),其中k ≠0.由⎩⎪⎨⎪⎧y 2=2x ,y =k (x -3)得ky 2-2y -6k =0.则y 1y 2=-6. 又x 1=12y 21,x 2=12y 22,∴OA →·OB →=x 1x 2+y 1y 2=14(y 1y 2)2+y 1y 2=3.综上所述,命题“如果直线l 过点T (3,0),那么OA →·OB →=3”是真命题.(2)解:逆命题:如果OA →·OB →=3,那么直线l 过点T (3,0). 该命题是假命题,理由如下:例如:取抛物线上的点A (2,2),B ⎝ ⎛⎭⎪⎪⎫121,此时OA →·OB →=3,直线AB 的方程为y =23(x +1),而T (3,0)不在直线AB 上.则逆命题是假命题.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六章 不等式第1讲 不等式的概念与性质1.(2017年河北承德实验中学统测)若a ,b ,c ∈R ,且a >b ,则下列不等式正确的个数是( )①1a <1b ;②a 2>b 2;③ac 4>bc 4;④a c 2+1>b c 2+1. A .1 B .2 C .3 D .42.(2016年北京)已知x ,y ∈R ,且x >y >0,则( ) A.1x -1y>0 B .sin x -sin y >0 C.⎝⎛⎭⎫12x -⎝⎛⎭⎫12y <0 D .ln x +ln y >03.已知下列不等式:①x 2+3>2x ;②a 3+b 3≥a 2b +ab 2(a ,b ∈R +);③a 2+b 2≥2(a -b -1).其中正确的个数是( )A .0B .1C .2D .34.(2015年湖北)将离心率为e 1的双曲线C 1的实半轴长a 和虚半轴长b (a ≠b )同时增加m (m >0)个单位长度,得到离心率为e 2的双曲线C 2,则( )A .对任意的a ,b ,e 1<e 2B .当a >b 时,e 1<e 2;当a <b 时,e 1>e 2C .对任意的a ,b ,e 1>e 2D .当a >b 时,e 1>e 2;当a <b 时,e 1<e 25.(2015年上海)记方程①:x 2+a 1x +1=0,方程②:x 2+a 2x +2=0,方程③:x 2+a 3x +4=0,其中a 1,a 2,a 3是正实数.当a 1,a 2,a 3成等比数列时,下列选项中,能推出方程③无实根的是( )A .方程①有实根,且②有实根B .方程①有实根,且②无实根C .方程①无实根,且②有实根D .方程①无实根,且②无实根6.已知函数f (x )=ax 2+bx +c 满足f (1)=0,且a >b >c ,则ca的取值范围为__________.7.(2016年山东滨州模拟)A 杯中有浓度为a 的盐水x g ,B 杯中有浓度为b 的盐水y g ,其中A 杯中的盐水更咸一些.若将A ,B 两杯盐水混合在一起,其浓度可用不等式表示为______________.8.用若干辆载重为8吨的汽车运一批货物,若每辆汽车只装4吨,则剩下20吨货物;若每辆汽车装8吨,则最后一辆汽车不满也不空.则有汽车________辆.9.设a ,b 为正实数.现有下列命题: ①若a 2-b 2=1,则a -b <1;②若1b -1a=1,则a -b <1;③若|a -b |=1,则|a -b |<1; ④若|a 3-b 3|=1,则|a -b |<1.其中的真命题有__________.(写出所有真命题的编号)10.(2016年湖南怀化模拟)某单位组织职工去某地参观学习需包车前往.甲车队说:“如领队买全票一张,其余人可享受7.5折优惠”,乙车队说:“你们属团体票,按原价的8折优惠”.这两车队的原价、车型都是一样的,试根据单位的人数,比较两车队的收费哪家更优惠.11.已知a >0,b >0,求证:⎝⎛⎭⎫a 2b 12+⎝⎛⎭⎫b 2a 12≥a 12+b 12.12.已知α∈(0,π),比较2sin 2α与sin α1-cos α的大小.第2讲 一元二次不等式及其解法1.(2016年湖北模拟)若关于x 的不等式ax -b >0的解集是(-∞,1),则关于x 的不等式(ax +b )(x -3)>0的解集是( )A .(-∞,-1)∪(3,+∞)B .(-1,3)C .(1,3)D .(-∞,1)∪(3,+∞)2.如果kx 2+2kx -(k +2)<0恒成立,那么实数k 的取值范围是( ) A .-1≤k ≤0 B .-1≤k <0 C .-1<k ≤0 D .-1<k <03.已知函数f (x )=⎩⎪⎨⎪⎧x +2,x ≤0,-x +2,x >0,则不等式f (x )≥x 2的解集是( )A .[-1,1]B .[-2,2]C .[-2,1]D .[-1,2]4.(2016年江西九江一模)若关于x 的不等式x 2-4x -2-a >0在区间(1,4)内有解,则实数a 的取值范围是( )A .(-∞,-2)B .(-2,+∞)C .(-6,+∞)D .(-∞,-6)5.已知不等式x 2-2x -3<0的解集为A ,不等式x 2+x -6<0的解集为B ,不等式x 2+ax +b <0的解集是A ∩B ,则a +b =( )A .-3B .1C .-1D .36.已知f (x )是定义域为R 的偶函数,当x ≤0时,f (x )=x 2+2x ,则不等式f (x +2)<3的解集是_________.7.已知a ∈Z ,关于x 的一元二次不等式x 2-6x +a ≤0的解集中有且仅有3个整数,则所有符合条件的a 的值之和是________.8.不等式ax 2+bx +c >0的解集为⎝⎛⎭⎫-13,2,对于系数a ,b ,c ,有如下结论:①a <0;②b >0;③c >0;④a +b +c >0;⑤a -b +c >0.其中正确的结论的序号是________.9.(2016年北京朝阳统一考试)已知函数f (x )=x 2-2ax -1+a ,a ∈R .(1)若a =2,试求函数y =f (x )x(x >0)的最小值;(2)对于任意的x ∈[0,2],不等式f (x )≤a 成立,试求a 的取值范围.10.设f (x )=ax 2+bx +c ,若f (1)=72,问是否存在a ,b ,c ∈R ,使得不等式x 2+12≤f (x )≤2x 2+2x +32对一切实数x 都成立?证明你的结论.第3讲 算术平均数与几何平均数1.下列命题正确的是( )A .函数y =x +1x 的最小值为2B .函数y =x 2+3x 2+2的最小值为2C .函数y =2-3x -4x (x >0)的最小值为2-4 3D .函数y =2-3x -4x (x >0)的最大值为2-4 32.若函数f (x )=x +1x -2(x >2)在x =a 处取得最小值,则a =( )A .1+ 2B .1+ 3C .3D .43.设正实数x ,y ,z 满足x 2-3xy +4y 2-z =0,则当zxy取得最小值时,x +2y -z 的最大值为( )A .0 B.98 C .2 D.944.若log 4(3a +4b )=log 2ab ,则a +b 的最小值是( ) A .6+2 3 B .7+2 3 C .6+4 3 D .7+4 35.(2015年湖南)若实数a ,b 满足1a +2b=ab ,则ab 的最小值为( )A. 2 B .2 C .2 2 D .46.(2015年陕西)设f (x )=ln x,0<a <b ,若p =f (ab ),q =f ⎝⎛⎭⎫a +b 2,r =12[f (a )+f (b )],则下列关系式正确的是( )A .q =r <pB .q =r >pC .p =r <qD .p =r >q7.已知正数x ,y 满足x +2y -xy =0,则x +2y 的最小值为( ) A .8 B .4 C .2 D .08.(2017年河南郑州第二次质量预测)已知正数x ,y 满足x 2+2xy -3=0,则2x +y 的最小值是__________.9.(1)设x >-1,则函数y =(x +5)(x +2)x +1的最小值为________.(2)已知x <54,则f (x )=4x -2+14x -5的最大值为________;10.(1)(2016年湖北七市联考)已知a >0,b >0,且2a +b =1,若不等式2a +1b≥m 恒成立,则m 的最大值等于( )A .10B .9C .8D .7(2)已知x >0,y >0,x +3y +xy =9,则x +3y 的最小值为________.第4讲 简单的线性规划1.(2017年北京)若x ,y 满足⎩⎪⎨⎪⎧x ≤3,x +y ≥2y ≤x ,,则x +2y 的最大值为( )A .1B .3C .5D .92.(2017年新课标Ⅲ)设x ,y 满足约束条件⎩⎪⎨⎪⎧3x +2y -6≤0,x ≥0,y ≥0,则z =x -y 的取值范围是( )A .[-3,0]B .[-3,2]C .[0,2]D .[0,3]3.已知实数x ,y 满足不等式组⎩⎪⎨⎪⎧0≤x ≤3,2x -3y ≤6,3x +4y ≤12,则z =x +y -2x +1的取值范围是( )A.⎣⎡⎦⎤-4,716 B .[-4,1] C.⎣⎡⎦⎤14,716 D.⎣⎡⎦⎤14,1 4.(2014年新课标Ⅰ)设x ,y 满足约束条件⎩⎪⎨⎪⎧x +y ≥a ,x -y ≤-1,且z =x +ay 的最小值为7,则a =( )A .-5B .3C .-5或3D .5或-35.设二元一次不等式组⎩⎪⎨⎪⎧2x +y -19≥0,x -y -8≤0,x +2y -14≤0所表示的平面区域为M ,则使函数y =log a x (a >0,a ≠1)的图象过区域M 的a 的取值范围是( )A .[1,3]B .[2,10]C .[2,9]D .[10,9]6.x ,y 满足约束条件⎩⎪⎨⎪⎧x +y -2≤0,x -2y -2≤0,2x -y +2≥0.若z =y -ax 取得最大值的最优解不唯一,则实数a 的值为( )A.12或-1 B .2或12 C .2或1 D .2或-17.在平面直角坐标系中,不等式组⎩⎪⎨⎪⎧x ≥1,x +y ≤0,x -y -4≤0表示的平面区域的面积是________.8.(2016年江苏) 已知实数x ,y 满足⎩⎪⎨⎪⎧x -2y +4≥0,2x +y -2≥0,3x -y -3≤0,则x 2+y 2的取值范围是________.9.变量x ,y 满足⎩⎪⎨⎪⎧x -4y +3≤0,3x +5y -25≤0,x ≥1.(1)设z =yx,求z 的最小值;(2)设z =x 2+y 2,求z 的取值范围;(3)设z =x 2+y 2+6x -4y +13,求z 的取值范围.10.已知函数g (x )=x 2+(a +1)x +a +b +1,两个零点可分别作为一个椭圆和一个双曲线的离心率.求ba的取值范围.第5讲 不等式的应用1.某汽车运输公司购买了一批豪华大客车投入营运,据市场分析:每辆客车营运的总利润y (单位:10万元)与营运年数x 的函数关系为y =-(x -6)2+11(x ∈N *),要使每辆客车运营的年平均利润最大,则每辆客车营运的最佳年数为( )A .3年B .4年C .5年D .6年2.(2017年广东惠州三模)设z =4x ·2y ,变量x ,y 满足条件⎩⎪⎨⎪⎧x -4y ≤-3,3x +5y ≤25,x ≥1,则z 的最小值为( )A .2B .4C .8D .163.某单位用2160万元购得一块空地,计划在该地块上建造一栋至少10层、每层2000平方米的楼房.经测算,若将楼房建为x (x ≥10)层,则每平方米的平均建筑费用为560+48x (单位:元).为了使楼房每平方米的平均综合费用最少,则楼房应建为( )A .10层B .15层C .20层D .30层4.(2016年山东烟台诊断)已知在等比数列{a n }中,a 2=1,则其前3项的和S 3的取值范围是( )A .(-∞,-1]B .(-∞,-1)∪(1,+∞)C .[3,+∞)D .(-∞,-1]∪[3,+∞)5.某农户计划种植黄瓜和韭菜,种植面积不超过50亩(1亩≈666.7平方米),投入资金不超过54项目 年产量/亩 年种植成本/亩 每吨售价 黄瓜 4吨 1.2万元 0.55万元 韭菜 6吨 0.9万元 0.3万元植面积(单位:亩)分别为( )A .50,0B .30,20C .20,30D .0,506.某旅行社租用A ,B 两种型号的客车安排900名客人旅行,A ,B 两种车辆的载客量分别为36人和60人,租金分别为1600元/辆和2400元/辆,旅行社要求租车总数不超过21辆,且B 型车不多于A 型车7辆,则租金最少为( )A .31 200元B .36 000元C .36 800元D .38 400元7.(2017年江苏)某公司一年购买某种货物600吨,每次购买x 吨,运费为6万元/次,一年的总存储费用为4x 万元,要使一年的总运费与总存储之和最小,则x 的值是__________.8.某项研究表明,在考虑行车安全的情况下,某路段车流量F (单位时间内测量点的车辆数,单位:辆/时)与车流速度v (假设车辆以相同速度v 行驶,单位:米/秒),平均车长l (单位:米)的值有关,其关系式为F =76 000vv 2+18v +20l.(1)如果不限定车型,l =6.05,那么最大车流量为______辆/时;(2)如果限定车型,l =5,那么最大车流量比(1)中的最大车流量增加______辆/时.9.(2017年湖北孝感一模)经测算,某型号汽车在匀速行驶过程中每小时耗油量y (单位:升)与速度x (单位:千米/时)(50≤x ≤120)的关系可近似表示为:y =⎩⎨⎧175(x 2-130x +4900),x ∈[50,80),12-x60,x ∈[80,120].(1)该型号汽车速度为多少时,可使得每小时耗油量最低?(2)已知A,B两地相距120千米,假定该型号汽车匀速从A地驶向B地,则汽车速度为多少时总耗油量最少?10.(2017年天津)电视台播放甲、乙两套连续剧,每次播放连续剧时,需要播放广告.已不少于30分钟,且甲连续剧播放的次数不多于乙连续剧播放次数的2倍.分别用x,y表示每周计划播出的甲、乙两套连续剧的次数.(1)用x,y列出满足题目条件的数学关系式,并画出相应的平面区域;(2)问电视台每周播出甲、乙两套连续剧各多少次,才能使收视人次最多?第六章 不等式第1讲 不等式的概念与性质1.A 解析:①a =1,b =-1,1a <1b不成立;②a =1,b =-1,a 2>b 2不成立; ③c =0,ac 4>bc 4 不成立;④因为c 2+1>0,a >b ,所以a c 2+1>bc 2+1成立.2.C 解析:由x >y >0,得1x <1y ,即1x -1y<0,A 不正确;由x >y >0及函数y =sin x 的单调性,可知sin x -sin y >0不一定正确,B 不正确;由0<12<1,x >y >0,得⎝⎛⎭⎫12x <⎝⎛⎭⎫12y ,即⎝⎛⎭⎫12x-⎝⎛⎭⎫12y <0,C 正确;由x >y >0,得xy >0,但不一定大于1,故ln x +ln y =ln xy >0不一定成立,D 不正确.3.D 解析:∵x 2-2x +3=(x -1)2+2>0,∴x 2+3>2x .∵a 3+b 3-a 2b -ab 2=(a -b )(a 2-b 2)=(a +b )(a -b )2≥0,∴a 3+b 3≥a 2b +ab 2.∵a 2+b 2-2(a -b -1)=(a -1)2+(b +1)2≥0,∴a 2+b 2≥2(a -b -1).4.B 解析:e 1=1+b 2a 2,e 2=1+(b +m )2(a +m )2.不妨令e 1<e 2,化简,得b a <b +ma +m (m >0),得bm <am ,得b <a .所以当b >a 时,有b a >b +m a +m ,即e 1>e 2;当b <a 时,有b a <b +ma +m,即e 1<e 2.故选B.5.B 解析:当方程①有实根,且②无实根时,a 21≥4,a 22<8,从而a 3=a 22a 1<82=4,∴a 23<16,即方程③:x 2+a 3x +4=0无实根.故选B.而A ,D 由于不等式方向不一致,不可推;C 推出③有实根.6.⎝⎛⎭⎫-2,-12 解析:因为f (1)=0,所以a +b +c =0.所以b =-(a +c ). 又a >b >c ,所以a >-(a +c )>c ,且a >0,c <0.所以1>-a +c a >c a ,即1>-1-c a >ca .所以⎩⎨⎧2ca <-1,ca>-2,解得-2<c a <-12.7.b <ax +by x +y <a 解析:依题意,知a >b ,将A ,B 两杯盐水混合后,盐水的浓度变为ax +by x +y .则有ax +by x +y >bx +by x +y =b ,ax +by x +y <ax +ay x +y =a .故有b <ax +by x +y <a .8.6 解析:设有x 辆汽车,则货物重为(4x +20)吨.由题意,得⎩⎪⎨⎪⎧8(x -1)<4x +20,8x >4x +20,x ∈N *.解得5<x <7,且x ∈N *.故只有x =6才满足要求.9.①④ 解析:①中,∵a 2-b 2=1,∴a -b =1a +b.∵a >0,b >0,又a 2=b 2+1>1,∴a >1.从而1a +b<1,即a -b <1.∴①正确.②中,取a =5,b =56,验证知②错误.③中,取a =4,b =1,验证知③错误. ④∵a ,b 是正实数,不妨设a >b >0, ∴a 3-b 3=(a -b )(a 2+b 2+ab ).∴a -b =a 3-b 3a 2+ab +b 2=1a 2+ab +b 2. ∵a 3=1+b 3>1,∴a 2>1.∴a 2+ab +b 2>1.∴0<1a 2+ab +b 2<1.∴0<a -b =1a 2+ab +b 2<1.即|a -b |<1.同理,设0<a <b ,也能得到|a -b |<1的结论.故④正确. 10.解:设该单位职工有n 人(n ∈N *),全票价为x 元, 坐甲车需花y 1元,坐乙车需花y 2元.则y 1=x +34x ·(n -1)=14x +34nx ,y 2=45nx .因为y 1-y 2=14x +34nx -45nx=14x -120nx =14x ⎝⎛⎭⎫1-n 5. 当n =5时,y 1=y 2; 当n >5时,y 1<y 2; 当n <5时,y 1>y 2.因此当单位去的人数为5人时,两车队收费相同;多于5人时,选甲车更优惠;少于5人时,选乙车队更优惠.11.证明:方法一,左边-右边=(a )3+(b )3ab-(a +b )=(a +b )(a -ab +b )-ab (a +b )ab=(a +b )(a -2 ab +b )ab =(a +b )(a -b )2ab≥0.∴原不等式成立.方法二,左边>0,右边>0. 左边右边=(a +b )(a -ab +b )ab (a +b ) =a -ab +b ab ≥2 ab -ab ab=1.∴原不等式成立.12.解:2sin 2α-sin α1-cos α=4sin αcos α(1-cos α)-sin α1-cos α=sin α1-cos α(-4cos 2α+4cos α-1)=-sin α1-cos α(2cos α-1)2.∵α∈(0,π),∴sin α>0,1-cos α>0,(2cos α-1)2≥0.∴-sin α1-cos α(2cos α-1)2≤0,即2sin 2α-sin α1-cos α≤0.∴2sin 2α≤sin α1-cos α,当且仅当α=π3时取等号.第2讲 一元二次不等式及其解法1.B 解析:由题意关于x 的不等式ax -b >0的解集是(-∞,1),可得ba=1,且a <0.则(ax +b )(x -3)>0可变形为(x -3)⎝⎛⎭⎫x +ba <0,即得(x -3)(x +1)<0.所以-1<x <3.所以不等式的解集是(-1,3).故选B.2.C 解析:当k =0时,原不等式等价于-2<0,显然恒成立,∴k =0符合题意.当k ≠0时,由题意,得⎩⎪⎨⎪⎧k <0,(2k )2-4k ·[-(k +2)]<0.解得-1<k <0.∴-1<k ≤0. 3.A 解析:依题意,得⎩⎪⎨⎪⎧ x ≤0,x +2≥x 2或⎩⎪⎨⎪⎧x >0,-x +2≥x 2⇒-1≤x ≤0或0<x ≤1⇒-1≤x ≤1. 4.A 解析:不等式x 2-4x -2-a >0在区间(1,4)内有解等价于a <(x 2-4x -2)max .令g (x )=x 2-4x -2,x ∈(1,4),∴g (x )<g (4)=-2.∴a <-2.5.A 解析:由题意,得A ={x |-1<x <3},B ={x |-3<x <2}.A ∩B ={x |-1<x <2},由根与系数的关系可知,a =-1,b =-2.∴a +b =-3.6.{x |-5<x <1} 解析:设x ≥0,因为f (x )是定义域为R 的偶函数,所以f (x )=f (-x )=x 2-2x .又f (x +2)=f (|x +2|),所以f (x +2)<3⇔f (|x +2|)=(|x +2|)2-2|x +2|<3.所以(|x +2|-3)(|x +2|+1)<0.所以0≤|x +2|<3,解得-5<x <1.所以原不等式的解集为{x |-5<x <1}.7.21 解析:设f (x )=x 2-6x +a ,其图象是开口向上,对称轴是x =3的抛物线,图象如图D115.图D115关于x 的一元二次不等式x 2-6x +a ≤0的解集中有且仅有3个整数,则⎩⎪⎨⎪⎧f (2)≤0,f (1)>0即⎩⎪⎨⎪⎧f (2)=4-12+a ≤0,f (1)=1-6+a >0, 解得5<a ≤8.又a ∈Z ,所以a =6,7,8,则所有符合条件的a 的值之和是6+7+8=21.8.①②③④ 解析:∵不等式ax 2+bx +c >0的解集为⎝⎛⎭⎫-13,2,∴a <0;-13,2是方程ax 2+bx +c =0的两根,-13+2=-ba>0,∴b >0;f (0)=c >0,f (1)=a +b +c >0,f (-1)=a-b +c <0.故正确结论的序号为①②③④.9.解:(1)依题意,得y =f (x )x =x 2-4x +1x =x +1x-4.因为x >0,所以x +1x ≥2,当且仅当x =1x,即x =1时,等号成立,所以y ≥-2.所以当x =1时,y =f (x )x 的最小值为-2.(2)因为f (x )-a =x 2-2ax -1,所以要使得“∀x ∈[0,2],不等式f (x )≤a 成立”只要“x 2-2ax -1≤0在[0,2]上恒成立”.不妨设g (x )=x 2-2ax -1,则只要g (x )≤0在[0,2]上恒成立即可.所以⎩⎪⎨⎪⎧ g (0)≤0,g (2)≤0.即⎩⎪⎨⎪⎧0-0-1≤0,4-4a -1≤0. 解得a ≥34.故a 的取值范围为⎣⎡⎭⎫34,+∞. 10.解:由f (1)=72,得a +b +c =72.令x 2+12=2x 2+2x +32⇒x =-1.由f (x )≤2x 2+2x +32推得f (-1)≤32.由f (x )≥x 2+12推得f (-1)≥32.∴f (-1)=32.∴a -b +c =32.故a +c =52,且b =1.∴f (x )=ax 2+x +52-a .依题意ax 2+x +52-a ≥x 2+12对一切x ∈R 都成立,∴a ≠1,且Δ=1-4(a -1)(2-a )≤0.由a -1>0,得a =32.∴f (x )=32x 2+x +1.证明如下: ∵32x 2+x +1-2x 2-2x -32 =-12x 2-x -12=-12(x +1)2≤0.∴32x 2+x +1≤2x 2+2x +32对x ∈R 都成立. ∴存在实数a =32,b =1,c =1,使得不等式x 2+12≤f (x )≤2x 2+2x +32对一切x ∈R 都成立.第3讲 算术平均数与几何平均数1.D 解析:y =x +1x的定义域为{x |x ≠0},当x >0时,有最小值2,当x <0时,有最大值-2.故A 项不正确;y =x 2+3x 2+2=x 2+2+1x 2+2≥2,∵x 2+2≥2,∴取不到“=”.故B 项不正确;∵当x >0时,3x +4x ≥2·3x ·4x =4 3,当且仅当3x =4x ,即x =2 33时取“=”.∴y =2-⎝⎛⎭⎫3x +4x 有最大值2-4 3.故C 项不正确,D 项正确. 2.C 解析:∵x >2,∴f (x )=x +1x -2=(x -2)+1x -2+2≥2 (x -2)·1x -2+2=4,当且仅当x -2=1x -2,即x =3时取等号.3.C 解析:z =x 2-3xy +4y 2,z xy =x 2-3xy +4y 2xy ≥2x ·2y -3xy xy =xy xy=1. 当且仅当x =2y 时,zxy取最小值,此时z =2y 2.x +2y -z =4y -2y 2=-2(y 2-2y )=-2(y -1)2+2,最大值为2.故选C.4.D 解析:由题意知,ab >0,且3a +4b >0,所以a >0,b >0.又log 4(3a +4b )=log 2ab ,所以3a +4b =ab .所以4a +3b =1.所以a +b =(a +b )·⎝⎛⎭⎫4a +3b =7+4b a +3a b ≥7+2 4b a ·3a b =7+4 3.当且仅当4b a =3ab,即a =4+2 3,b =3+2 3时,等号成立.故选D.5.C 解析:∵1a +2b =ab ,∴a >0,b >0.∵ab =1a +2b ≥2 1a ·2b =2 2ab,∴ab ≥22(当且仅当b =2a 时取等号),∴ab 的最小值为2 2.故选C.6.C 解析:p =f (ab )=ln ab =12ln(ab ),q =f ⎝⎛⎭⎫a +b 2=ln a +b 2,r =12[f (a )+f (b )]=12ln(ab ).因为a +b 2>ab ,由f (x )=ln x 在区间(0,+∞)内是增函数,可知f ⎝⎛⎭⎫a +b 2>f (ab ),所以q >p =r .故选C.7.A 解析:方法一,由x +2y -xy =0,得2x +1y=1,且x >0,y >0.∴x +2y =(x +2y )·⎝⎛⎭⎫2x +1y =4y x +xy+4≥4+4=8(当且仅当x =4,y =2等号成立). 方法二,由x +2y =xy =12x ·2y ≤12⎝⎛⎭⎫x +2y 22=()x +2y 28,∴x +2y ≥8(当且仅当x =2y 时取等号).8.3 解析:由x 2+2xy -3=0,得y =3-x 22x =32x -12x .则2x +y =2x +32x -12x =3x 2+32x ≥2 3x 2·32x=3,当且仅当x =1时,等号成立.所以(2x+y )min =3.9.(1)9 (2)1解析:(1)因为x >-1,所以x +1>0,所以y =(x +5)(x +2)x +1=x 2+7x +10x +1=(x +1)2+5(x +1)+4x +1=(x +1)+4x +1+5≥2 (x +1)·4x +1+5=9.当且仅当x +1=4x +1,即x =1时等号成立.故函数y =(x +5)(x +2)x +1的最小值为9.(2)因为x <54,所以5-4x >0.则f (x )=4x -2+14x -5=-⎝⎛⎭⎫5-4x +15-4x +3≤-2+3=1.当且仅当5-4x =15-4x ,即x =1时,等号成立.故f (x )=4x -2+14x -5的最大值为1.10.(1)B (2)6解析:2a +1b =2(2a +b )a +2a +b b =4+2b a +2a b +1=5+2⎝⎛⎭⎫b a +a b ≥5+2×2 b a ·a b=9. 当且仅当a =b =13时取等号.∵2a +1b ≥m ,∴m ≤9,即m 的最大值等于9.故选B.(2)由已知,得x =9-3y1+y.方法一,(消元法)∵x >0,y >0,∴0<y <3.∴x +3y =9-3y 1+y +3y =121+y +(3y +3)-6≥2 121+y ·(3y +3)-6=6.当且仅当121+y=3y +3,即y =1,x =3时,取等号,故(x +3y )min =6.方法二,∵x >0,y >0,9-(x +3y )=xy =13x ·(3y )≤13·⎝⎛⎭⎫x +3y 22,当且仅当x =3y 时等号成立.设x +3y =t >0,则t 2+12t -108≥0. ∴(t -6)(t +18)≥0. 又t >0,∴t ≥6.故当x =3,y =1时,(x +3y )min =6.第4讲 简单的线性规划1.D 解析:如图D116,画出可行域.图D116z =x +2y 表示斜率为-12的一组平行线,当过点C (3,3)时,目标函数取得最大值z max=3+2×3=9.2.B 解析:将点(0,0),(2,0),(0,3)代入z =x -y 解得0,2,-3.所以z =x -y 的取值范围是[-3,2].故选B.3.B 解析:作出不等式组表示的平面区域(如图D117),因为z =x +y -2x +1=y -3x +1+1表示平面区域内的点与点(-1,3)之间连线的斜率k 与1的和.由图知,当x =0,y =-2时,k 取得最小值k min =-2-30+1=-5;当x =0,y =3时,k 取得最大值k max =3-30+1=0.所以z ∈[-4,1].故选B.图D1174.B 解析:根据题中约束条件可画出可行域如图D118.两直线交点坐标为A ⎝⎛⎭⎫a -12,a +12.又由z =x +ay 知,当a =0时,A ⎝⎛⎭⎫-12,12,z 的最小值为-12,不合题意;当a ≥1时,y =-1a x +za 过点A 时,z 有最小值,即z =a -12+a ×a +12=a 2+2a -12=7,解得a =3或a =-5(舍去);当a <1时,z 无最小值.故选B.图D1185.C 解析:区域M 是一个三角形区域,三个顶点的坐标分别是(8,3),(10,2),(9,1),结合图形检验,可知:当a ∈[2,9]时,符合题目要求.6.D 解析:如图D119,由y =ax +z 知z 的几何意义是直线在y 轴上的截距,故当a >0时,要使z =y -ax 取得最大值的最优解不唯一,则a =2;当a <0时,要使z =y -ax 取得最大值的最优解不唯一,则a =-1.图D1197.1 解析:不等式组表示的区域如图D120所示的阴影部分,图D120由x =1,x +y =0,得A (1,-1); 由x =1,x -y -4=0,得B (1,-3); 由x +y =0,x -y -4=0,得C (2,-2).∴|AB |=2.∴S △ABC =12×2×1=1.8.⎣⎡⎦⎤45,13 解析:由图D121知,原点到直线2x +y -2=0的距离平方为x 2+y 2的最小值,为⎝⎛⎭⎫ 252=45;原点到点(2,3)距离平方为x 2+y 2的最大值,为13.因此x 2+y 2的取值范围为⎣⎡⎦⎤45,13.图D1219.解:由约束条件⎩⎪⎨⎪⎧x -4y +3≤0,3x +5y -25≤0,x ≥1,作出(x ,y )的可行域如图D122所示的阴影部分.图D122由⎩⎪⎨⎪⎧ x =1,3x +5y -25=0,解得A ⎝⎛⎭⎫1,225. 由⎩⎪⎨⎪⎧x =1,x -4y +3=0,解得C (1,1). 由⎩⎪⎨⎪⎧x -4y +3=0,3x +5y -25=0,解得B (5,2). (1)∵z =y x =y -0x -0,∴z 的值即是可行域中的点与原点O 连线的斜率.观察图形可知z min=k OB =25.(2)z =x 2+y 2的几何意义是可行域上的点到原点O 的距离的平方. 结合图形可知,可行域上的点到原点的距离中, d min =|OC |=2,d max =|OB |=29. 故z 的取值范围是[2,29].(3)z =x 2+y 2+6x -4y +13=(x +3)2+(y -2)2的几何意义是可行域上的点到点(-3,2)的距离的平方.结合图形可知,可行域上的点到(-3,2)的距离中, d min =1-(-3)=4,d max =(-3-5)2+(2-2)2=8. 故z 的取值范围是[16,64].10.解:g (x )=x 2+(a +1)x +a +b +1,两个零点为方程x 2+(a +1)x +a +b +1=0的两根,且一根大于1,另一根大于0且小于1,由根的分布画图,得⎩⎪⎨⎪⎧ g (0)>0,g (1)<0,即⎩⎪⎨⎪⎧a +b +1>0,2a +b +3<0.作出可行域如图D123.图D123而b a =b -0a -0表示可行域中的点(a ,b )与原点连线的斜率k ,直线OA 的斜率k 1=-12,直线2a +b +3=0的斜率k 2=-2.所以k ∈⎝⎛⎭⎫-2,-12,即ba ∈⎝⎛⎭⎫-2,-12. 第5讲 不等式的应用1.C 解析:yx=-⎝⎛⎭⎫x +25x +12≤-2 x ×25x +12,当且仅当x =25x,即x =5时取等号.2.C 解析:作出不等式组对应的平面区域,由⎩⎪⎨⎪⎧ x -4y =-3,x =1解得⎩⎪⎨⎪⎧x =1,y =1,设A (1,1),由图可知,直线2x +y =m 经过点A 时,m 取最小值,同时z =4x ·2y =22x +y 取得最小值.所以z min =22×1+1=23=8.故选C.3.B 解析:设楼房每平方米的平均综合费用为f (x )元,则f (x )=(560+48x )+2160×10 0002000x=560+48x +10 800x=560+48⎝⎛⎭⎫x +225x ≥560+48×2 x ·225x=2000(x ≥10,x ∈N *).当且仅当x =225x,即x =15时,f (x )取得最小值为f (15)=2000.4.D 解析:设公比为q .因为a 2=1=a 1q ,所以S 3=a 1+1+a 1q 2=1q+q +1.当q >0时,1q +q ≥2;当q <0时,1q+q ≤-2.所以S 3≥3或S 3≤-1.故选D. 5.B 解析:设黄瓜和韭菜的种植面积分别为x ,y 亩,种植总利润为z 万元,则目标函数z =(0.55×4x -1.2x )+(0.3×6y -0.9y )=x +0.9y .作出约束条件如图D124所示的阴影部分.易求得点A (0,50),B (30,20),C (45,0).平移直线x +0.9y =0,当直线x +0.9y =0经过点B (30,20)时,z 取得最大值为48.故选B.图D124 图D1256.C 解析:设旅行社租用A 型客车x 辆,B 型客车y 辆,租金为z 元,则线性约束条件为⎩⎪⎨⎪⎧x +y ≤21,y -x ≤7,36x +60y ≥900,x ,y ∈N ,目标函数为z =1600x +2400y .画出可行域:如图D125所示的阴影部分,可知当目标函数过点(5,12)时,有最小值z min =36 800(元).7.30 解析:总费用4x +600x ×6=4⎝⎛⎭⎫x +900x ≥4×2900=240.当且仅当x =900x,即x =30时等号成立.8.(1)1900 (2)100解析:(1)当l =6.05时,F =76 000v v 2+18v +20l =76 000v +121v +18≤76 0002 v ·121v +18=76 00022+18=1900,当且仅当v =121v ,即v =11时,等号成立.(2)当l =5时,F =76 000v v 2+18v +20l =76 000v +100v +18≤76 0002 v ·100v +18=76 00020+18=2000,当且仅当v =100v ,即v =10时,等号成立.此时车流量比(1)中的最大车流量增加100辆/时. 9.解:(1)①当x ∈[50,80)时,y =175(x 2-130x +4900)=175[(x -65)2+675] 当x =65时,y 有最小值175×675=9.②当x ∈[80,120]时,函数单调递减,故当x =120时,y 有最小值10. 因为9<10,故当x =65时每小时耗油量最低.(2)设总耗油量为l ,由题意,可知l =y ·120x .①当x ∈[50,80)时,l =y ·120x =85⎝⎛⎭⎫x +4900x -130≥85⎝⎛⎭⎫2 x ×4900x -130=16. 当且仅当x =4900x ,即x =70时,l 取得最小值16.②当x ∈⎣⎢⎡⎦⎥⎤80120时,l =y ·120x =1440x -2为减函数,当x =120时,l 取得最小值10.因为10<16,所以当速度为120时,总耗油量最少.10.解:(1)由已知,x ,y满足的数学关系式为⎩⎪⎨⎪⎧70x +60y ≤600,5x +5y ≥30,x ≤2y ,x ≥0,y ≥0,即⎩⎪⎨⎪⎧7x +6y ≤60,x +y ≥6,x -2y ≤0,x ≥0,y ≥0,该二元一次不等式组所表示的平面区域为如图D126中的阴影部分.图D126 图D127 (2)设总收视人次为z 万, 则目标函数为z =60x +25y .考虑z =60x +25y ,将它变形为y =-125x +z 25,这是斜率为-125,随z 变化的一族平行直线.z 25为直线在y 轴上的截距,当z25取得最大值时,z 的值最大.又因为x ,y 满足约束条件,所以由图D127可知,当直线z =60x +25y 经过可行域上的点M 时,截距z25最大,即z最大.解方程组⎩⎪⎨⎪⎧7x +6y =60,x -2y =0得点M 的坐标为(6,3).所以,电视台每周播出甲连续剧6次、乙连续剧3次时才能使总收视人次最多。
