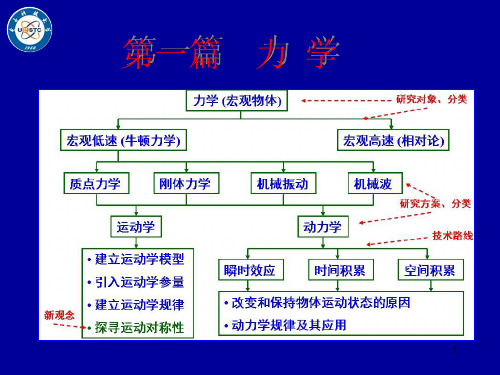
第一篇力学第一章 质点运动学
大学物理质点力学第一章 质点运动学 PPT

方向:
cosa
=
x r
cosβ=
y r
cosγ=
z r
路程:质点所经路径得总长度。
三、速度
描述位置矢量随时间变化快慢得物理量
1、平均速度
在移质为点r由)A,到单B的位过时程间中内(的所平用均时位间移为称为t该,质所点发在生该的过位
程中的平均速度。
v
=
Δ Δ
r t
=
Δx Δt
i
+ΔΔ
y t
j
+
Δ Δ
0
Δx
Δ t —割线斜率(平均速度)
dx —切线斜率(瞬时速度) dt
x~t图
t tt
1
2
2、 v ~ t 图
v ~ t图
割线斜率:
Δv Δt = a
v v2
切线斜率:
dv dt
=a
v1
v ~ t 图线下得面积(位移):
0 t1
t2
x2
dt dx x2 x1 x
t1
x1
t2 t
3、 a ~ t 图
=
dθ
dt
B
Δθ A
θ
0
x
(3)、角加速度
β =ΔΔωt
β
=
lim
Δt
Δω
0Δ t
=ddωt
=ddθt2 2
(4)、匀变速率圆周运动
0
t
1 2
t2
0 t
2
2 0
2
(5)、线量与角量得关系
Δ s = rΔθ
lim Δ s
Δt 0Δ t
=
lim
Δt 0
r
Δθ
第一章 质点力学ppt课件

6.加速度
a lim v dv v d2r r
t 0 t dt
dt2
加速度一定指向轨道的凹侧.
§1.2 速度、加速度的分量表示式
1. 直角坐标系
vr
r x&i
r y&j
r z&k
rrr
vxi vy j vzk
ar
r v&x i
v&y
r j
r v&z k
rr r
&x&i &y&j &z&k
切向加速度
法向加速度
a
set
s2
en
内禀方程
在自然坐标描述中, 需要已知质点运动的轨道, 而对
轨道的数学描述又需要一个坐标系, 所以必须掌握自
然的在坐不联标同系描的.a建述描立中述这方的个法物联理中系量有的不与基其同本他的依表坐据标达是系形: 中式速的,度但物它和理们加量的速之v大度间
小和方向是惟一确定的.
质点的位置由坐标量 和r确定, 要明确极角 的正
方向 (即 的增加方向)!
vd drtd drterrddetr
de rlie m r(t t)e r(t)
dt t 0
t
lt i0 m e tr lt i0 m te e
径向速度
横向速度
v r e rr e
a d dv td dt(r e rr e )
(2)牛顿第二定律
质点所获得的加速度的大小, 与它所受作用力的大
小成正比, 与它的质量成反比; 加速度的方向与所受作
用力的方向相同.
m rF mv F
d
(mv)
F
第1章-质点运动学
z A.
(t )
.B
的变化情况,定义:质点
的平均加速度为
(t t )
O
a t
y
24
x
质点的(瞬时)加速度定义为:
d d r a lim 2 t 0 t dt dt
2
即:质点在某时刻或某位置的(瞬时)加速度等于
速度矢量 对时间的一阶导数,或等于矢径 r 对时
第一篇 力 学
1
内容提要
第一章 运动学 第二章 质点动力学(牛顿运动定律) 第三章 刚体力学
第四章 振动学基础
第五章 第六章 波动学基础
狭义相对论
2
第1章 质点运动学
§1-1 参考系、坐标系和理想模型
运动的可认知性——绝对运动与相对静止的辩证统一
案例讨论:关于物质运动属性的两种哲学论断 赫拉克利特:“人不能两次踏进同一条河流”
y
y
位置矢量 r 的大小(即质点P到原点o的距离)为
2 2 2 r r x y z
方向余弦: cos=x/r, cos=y/r, cos=z/r 式中 , , 取小于180°的值。
z
r
P(x,y,z)
z
C
cos2 + cos2 + cos2 =1
x
A
运动方程
—— 轨道方程。
11
消去时间t得:x2+y2=62
§1-3 位移 速 度
一.位移和路程
如图所示,质点沿曲线C运动。时刻t在A点,时 刻t+t在B点。 从起点A到终点B的有向线 段AB=r,称为质点在时间t内 的位移。 而A到B的路径长度S为 路程。
第1章-质点运动学

位移
rrrBArxBxBAii
rA
yA
yB
j j
y
yB A r
r y A A
rB
B
yB yA
(xB xA)i ( yB yA) j
xi yj
o
xA
xB x
xB xA
若质点r 在 (三x维B 空x间A中)i运动( yB
yA)
j
(zB
z A )k
位移的大小为 r x2 y2 z2
23
1-2 求解运动学问题举例
例3 有 一个球体在某液体中竖直下落, 其初速度
为 v0 10 j , 它的加速度为 a 1.0v j. 问:(1)经
过多少时间后可以认为小球已停止运动, (2)此球体
在停止运动前经历的路程有多长?
解:由加速度定义
v dv 1.0
t
dt
,
v v0
0
a dv 1.0v dt
v v2
位矢量
t
0,
t 0
0,
tv
rv
a
dv dt
v2 r
en
2ren
法向单 位矢量
vB
r
o
en
v
vB
vA et r
vA
31
1-3 圆周运动
三alitlami tm 变00速litdmdv圆vvvt0tt周nt运vtavt动dvdttrev2ttleeit切mntv向a0nn加aaevn速tntneen度t 和法向v加2v速tove度2vnrevtv1vn1
一 圆周运动的角速度和角加速度
角坐标 (t)
角速度 (t) d (t)
dt
速率
力学舒幼生第一章质点运动学

通过积分,可以得到轨道方程 r r()
33
例 狐狸沿圆周跑,狗从圆心出发,速度都 为v,圆心、狗、狐狸始终连成一直线。
求狗的速度、加速度和轨道方程。
狐狸的角速度 d v
dt R
狗有横向和纵向速度
v r,vr v2v2
狗的横向和纵向加速度
a2d dd d r t trd d2 2t,ard d22 rtr d d t2
A (r ,,t) A re r A e
与直角坐标系的变换
xrco ,syrsin
27
正交基矢与极坐标的微分关系
正交基矢只依赖 ,与 r 无关
当θ变化时,正交基矢同时改变方向 满足微分关系
der
de
de de r
e
er
d r(t)
参考空间:沿左右、前后、上下三对方向无限扩展, 构成三维平直空间
参考系:参考空间+测量时间的时钟
z 坐标系:在参考空间中任选一点作为原点, 可建立各种坐标系。
时间的零点也可任选
O
y
x
相对运动的参考系
两个参考系之间若有相对运动,
他们观测同一个运动物体 是否会得到相同的距离和时间?
v
z
O
y
x
质点
由繁到简 将物体模型化为一个点——质点
dt dt
加速度
v(t)
dR
d
R
⊙k
a d v d R d R R v d td t d t a 心 v , a 切 R
22
曲线的曲率和曲率半径
曲率 d dl
第一章 质点运动学

物理学
已知:x(t ) 1.0t 2.0,y(t ) 0.25t 2 2.0, 解 (1) 由题意可得
dx dy vx 1.0, vy 0.5t dt dt t 3s 时速度为 v 1.0i 1.5 j
速度 v 与
x 轴之间的夹角
第一章 质点运动学
第一章 质点运动学
14
物理学
讨论 一运动质点在某瞬 y 时位于矢径 r ( x, y ) 的 y 端点处,其速度大小为
dr ( A) dt dr ( C) dt
注意
dr (B) dt
r (t )
x
o
x
dx 2 dy 2 ( D) ( ) ( ) dt dt
dr dr dt dt
1.5 0 arctan 56.3 1.0
17
物理学
x(t ) 1.0t 2.0, (2)运动方程 2 y(t ) 0.25t 2.0,
消去参数 t 可得轨迹方程为
y 0.25x x 3.0
2
轨迹图 t 4s
y/m
6 2
t 4s
t 2s 4
-6 -4 -2 0
dx B v A v x i i vi dt l dy vB v y j j o dt 2 2 2 x y l dx dy 两边求导得 2 x 2y 0 dt dt
第一章 质点运动学
解
y
A
v
x
20
物理学
dy x dx y 即 dt y dt B x dx vB j y dt dx o v dt vB vtan j
第一章 质点运动学

z
r rA rB
B
y
平均速度的方向与t时间内位移的方向一致。
§1-2 质点运动的描述
第1章 质点运动学
A
2. 瞬时速度(速度) 能精细地描述 z 质点在某时刻的运动情况。 r dr v lim O t d t t 0 x 速度的方向为轨道上质点所在
处的切线方向。
r rA rB
B
dr dx dy dz v i j k dt dt dt dt
v
r
2 z
y
A
B
v vx i v y j vz k
速度的大小: v v
dx dy dz vx , v y , vz dt dt dt
§1-2 质点运动的描述
第1章 质点运动学
速度(speed)----描述质点运动的快慢和方向。
定义:单位时间内质点所发生的位移。 1. 平均速度(mean speed) 设质点:
A
t 时刻: A, rA t t 时刻: B, rB O 位移: r x r 平均速度: v 单位:ms-1 t
大小: r
单位矢量:i , j , k
2 2
r
x y z
2
x y z 方向: cos cos cos r r r
cos cos cos 1
2 2 2
特性:矢量性、 瞬时性、相对性
§1-2 质点运动的描述
第1章 质点运动学
2. 运动方程(equation of motion): 质点运动时位置随时 间变化的规律。 z
ax 0 (2) x : vx 5 y : v y 15 10t a y 10 g
大学工程物理 第一章质点力学

例 题
质点作直线运动,运动方程为( ): 质点作直线运动,运动方程为(SI):
x = 12t − 6t
2
时质点的位置、 求 (1)t=4s时质点的位置、速度和加速度; ) 时质点的位置 速度和加速度; (2)质点通过原点时的速度和加速度; )质点通过原点时的速度和加速度; (3)质点速度为零时所在的位置。 )质点速度为零时所在的位置。 解:(1)由运动方程可得速度及加速度表达式为: )由运动方程可得速度及加速度表达式为: dx υ = = 12 − 12t dt dυ a= = −12 dt 时质点的位置、 在t=4s时质点的位置、速度和加速度分别为: 时质点的位置 速度和加速度分别为: -48m、-36m/s和-12m/s2。 、 和
dr = 2i − 2t j 解: v = dt
t = 0 v0 = 2i
t = 2 v2 = 2i − 4 j
−4 = −63 26′ 2
大小: v2 = 22 + 42 = 4.47m / s 大小: 方向: θ = arctan 方向:
v θ为 2与x轴的夹角
轴作直线运动,其位置坐标 坐标与时间的 例 一质点沿x轴作直线运动,其位置坐标与时间的 题 关系为 x=10+8t-4t2,求: x=10+8t质点在第一秒、第二秒内的平均速度。 (1)质点在第一秒、第二秒内的平均速度。 =0、 秒时的速度。 (2)质点在t=0、1、2秒时的速度。 解:() 时刻 1 t
= ∆xi + ∆yj + ∆zk
注 意 a) b)
位移是矢量, 位移是矢量,有大小和方向
Δr r1 o z A r2
∆ r 与∆r 的区别
为标量, ∆r为标量,∆r 为矢量
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一篇力 学 第一章质点运动学1-1-1选择题:1、用来描写质点运动状态的物理量是:(A )位置和速度。
(B )位置、速度和加速度。
(C )位置和位移。
(D )位置、位移、速度和加速度。
2、.一质点在平面上运动,已知质点位置矢量的表达式为 j bt iat r ˆˆ22+=ρ(其中a 、b 为常量), 则该质点作: (A) 匀速直线运动。
(B) 变速直线运动。
(C) 抛物线运动。
(D) 一般曲线运动.3、质点在XOY 平面内作曲线运动,则对与质点速率有关的下列式子中:(1) dtdrv = (2) dt rd v ρ= (3)dt r d v ρ=(4) dt ds v = (5) 22⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛=dt dy dt dx v正确的是:(A )(1),(2)和(3)。
(B )(2),(3)和(4)。
(C )(3),(4)和(5)。
(D )(2),(4)和(5)。
4、一小球沿斜面向上运动,其运动方程为:245t t s -+=(SI )。
小球运动到最高点 的时刻是:(A )t = 4 s (B )t = 2 s (C ) t = 8 s (D) t = 6 s5、在质点的下列运动中,说法正确的是: (A )匀加速运动一定是直线运动。
(B )在直线运动中,加速度为负,质点必作减速运动。
(C )在圆周运动中,加速度方向总指向圆心。
(D )在曲线运动过程中,法向加速度必不为零(拐点除外)。
6、质点作半径为R 的变速圆周运动时加速度大小为 (v 表示任一时刻质点的速率):(A)dt dv(B) R v 2(C)Rv dt dv 2+ (D) 242R v dt dv +⎪⎭⎫⎝⎛7、下列各种情况中,说法错误的是:(A)一物体具有恒定的速率,但仍有变化的速度。
(B)一物体具有恒定的速度,但仍有变化的速率。
(C)一物体具有加速度,而其速度可以为零。
(D)一物体速率减小,但其加速度可以增大。
8、一个质点作圆周运动时,下列说法中正确的是: (A)切向加速度一定改变,法向加速度也改变。
(B)切向加速度可能不变,法向加速度一定改变。
(C)切向加速度可能不变,法向加速度不变。
(D)切向加速度一定改变,法向加速度不变。
9、质点作曲线运动,r ρ表示位置矢量,v ρ表示速度,a ρ表示加速度,t a 表示切向加速度,s表示路程。
下列表达式正确的是:(A)a dt dv = (B)v dt dr = (C)t a dtdv= (D)t a dt v d =ρ10、一运动质点某瞬时位于位置矢量),(y x r ρ的端点处,对其速度大小有四种意见:(1)dt dr ; (2)dt r d ρ; (3)dt ds ; (4)22⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛dt dy dt dx下述判断正确的是:(A )只有(1),(2)正确。
(B )只有(2),(3)正确。
(C )只有(3),(4)正确。
(D)只有(1),(3)正确。
11、一质点在平面上作一般曲线运动,其瞬时速度为v ρ,瞬时速率为v ,某一段时间内的平均速度为><v ρ,平均速率为><v ,它们之间的关系必定有(A) >=<><=v v v v ρρ, (B) >=<><≠v v v v ρρ, (C) >≠<><≠v v vv ρρ,(D) >≠<><=v v v v ρρ,12、质点作以坐标原点为中心的匀速率圆周运动,下列各量:(1)t r t ∆∆→∆0lim (2)t r t ∆∆→∆ρ0lim (3)t v t ∆∆→∆ρ0lim (4)tvt ∆∆→∆0lim在运动中保持中恒定不变的量是:(A )(1)和(2)。
(B )(2)和(3)。
(C )(2)和(4)。
(D )(1)和(4)。
13、一个质点作简谐振动,振幅为A,在t=0的时刻质点离开平衡位置的位移为:-A/2,且向X轴的正方向运动。
下面四个图中代表此简谐振动的旋转矢量为:(A)(B)(C)(D)14、已知某质点作简谐振动,在t=0时质点的位置位于X轴负方向距平衡位置为0.5A处(这里A为振幅)且向X轴的负方向运动。
若质点振动的圆频率为ω。
该质点的运动方程为:(A))32cos(πω-=t A x (B))32cos(πω+=t A x (C))31cos(πω-=t A x (D))31cos(πω+=t A x15、对平面简谐波,下面说法正确的是: (A)波长大,波的速度就大。
(B)频率大,波的速度就大。
(C)波长大,频率也大,波的速度就大。
(D)波的速度只与传播波的媒质的情况有关,与波的波长和频率无关。
1-1-2填空题:1、一质点的运动方程为2219,2t y tx -==(均为国际单位)。
则质点的轨迹方程为: ;t=2s时的位置矢量为:=r ρ。
2、一质点的运动方程为2219,2t y tx -==(均为国际单位)。
t=2s时的速度为:=v ρ;前两秒内的平均速度为:>=<v ρ。
3、一质点作半径为R的圆周运动,在t=0时经过P点,此后其速率按Bt A v +=变化。
其中A和B均为常量,则该质点走过的路程随时间变化的关系为=s 。
该质点沿园运动一周再经过P点时的切向加速度为:=t a 。
4、一质点沿半径为R的圆周运动,其所转过的角度与时间的函数关系为:22110t t ππθ+=。
则质点的角速度为ω= ,角加速度为β= 。
5、一质点沿半径为R的圆周运动,其所转过的角度与时间的函数关系为:22110t t ππθ+=。
该质点的切向加速度为=t a ;法向加速度=n a 。
6、路程是指质点沿 走过的距离,它是一个 量。
7、质点在t 到t + Δt 时间段内的位移是:连接其在t 时刻的位置和t+Δt 时刻的位置的 线段。
方向由 时刻的位置指向 时刻的位置。
8、用Δs 和r ρ∆分别表示质点在t 到t + Δt 时间段内的路程和位移,它们之间的区别是:路程是 量,而位移是 量 。
它们之间的联系是: 。
9、某质点的运动方程是:26t t x -=(SI ),在t 由0至4秒的时间段内,质点位移的大小为 ;质点走过的路程为 。
10、一质点沿X 轴作直线运动运动方程为3225.4t t x +=(SI )其在1~2秒内的平均速度为 ;其沿X 轴正方向运动时做减速运动的时间间隔是Δt = 。
11、某质点作平面运动,其运动方程为:)(t r r ρρ=,速度为:)(t v v ρρ=。
如果其在运动中有:0=dt dr 而0≠dtrd ρ,则该质点的运动为 运动。
如果其在运动中有:0=dt dv 而0≠dtvd ρ,则该质点的运动为 运动。
12、某质点的运动方程为:t A y t A x ωωsin ,cos ==,其中A 和ω为常量,该质点所作的运动为运动,它的轨迹方程为 。
13、某质点以角速度为ω作半径为R 的圆周运动,角加速度为β。
该质点的运动速率为 ;其法向加速度的大小为 ,切向加速度的大小为 。
14、简谐振动的运动学特征是:质点运动的加速度的大小与其离开 位移的大小成正比,方向与该位移的方向 。
15、一个沿X 轴正方向传播的平面简谐波,其波动方程可写为:⎪⎭⎫⎝⎛+-=0)(cos φωu x t A y式中的u 表示的是 ,而φ0表示的是坐标原点处质点振动的 。
1-1-3计算题:1、一质点沿X 轴作直线运动,其运动方程为:3225.4t t x -=(SI )。
试求: (1)第二秒末的即时速度。
(2)第二秒内的路程。
2、已知质点的运动方程为:j t A i t A r ˆsin ˆcos 21ωω+=ρ(SI ),其中A 1、A 2、ω均为正常数,且A 1>A 2 。
试证明:(1)质点的运动轨迹为椭圆。
(2)质点运动的加速度恒指向椭圆的中心。
3、某质点作速率为 v ,半径为R其由计算3题图中的A 点运动到B (1)位移 。
(2)路程s.(3)速度增量 。
(4)速度增量的大小 。
(5)速度大小的增量 。
4、一质点沿X 轴运动,其速度与时间的关系为24t v +=(SI )当t=3s 时质点位于x=9m 处。
求: (1)质点运动的加速度。
(2)质点的运动方程。
5、质点沿X 轴作直线运动,其速度与坐标的关系为 v = 1 + 2x (SI )初始时刻质点位于坐标原点。
试求:质点的位置、速度、加速度随时间变化的关系。
6、已知质点沿X 轴运动,其加速度和坐标的关系为262x a +=(SI )且质点在x = 0处的速率为10 m/s 。
求:该质点的速度v 与坐标x 的关系。
7、质点作半径为R=0.10m 的圆周运动,其角位置与时间的关系为:342t +=θ(SI )。
试求:(1)当t = 2s 时的角速度、角加速度,切向加速度和法向加速度。
(2)角位置等于多少时,切向加速度的大小恰为总加速度的大小的一半r ρ∆v ρ∆v ρ∆v ∆计算3题图8、质点作半径为R = 3 m 的圆周运动,切向加速度为2ms 3-=t a 在t = 0 时质点的速度为零。
试求:(1)t = 1 s 时的速度与加速度。
(2)第2秒内质点所通过的路程。
9、物体沿X 轴作简谐振动。
在t = 0 时,其坐标x (0) = - 8.5 cm ,速度v (0) = - 0.92 m/s ,加速度a (0) = 47.0 m/s 2 。
试求:(1)弹簧振子的周期和频率。
(2)弹簧振子的初位相和振幅。
10、已知平面简谐波的波动方程为:)cos(bx at A y -=。
其中a 与b 均为正值。
求: 该波的波长、频率、周期、和波速。
参考答案:1-1-1选择题:1、用来描写质点运动状态的物理量是:(A )位置和速度。
(B )位置、速度和加速度。
(C )位置和位移。
(D )位置、位移、速度和加速度。
答案:(A )2、.一质点在平面上运动,已知质点位置矢量的表达式为 j bt iat r ˆˆ22+=ρ(其中a 、b 为常量), 则该质点作: (B) 匀速直线运动。
(B) 变速直线运动。
(C) 抛物线运动。
(D) 一般曲线运动. 答案:(B )3、质点在XOY 平面内作曲线运动,则对与质点速率有关的下列式子中:(1) dtdrv = (2) dt rd v ρ= (3)dt r d v ρ=(4) dt ds v = (5) 22⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛=dt dy dt dx v正确的是:(A )(1),(2)和(3)。
(B )(2),(3)和(4)。
(C )(3),(4)和(5)。
(D )(2),(4)和(5)。
