平行四边形的性质及判定归纳汇编
平行四边形的性质与判断技巧

平行四边形的性质与判断技巧平行四边形是一种特殊的四边形,具有一些独特的性质和判断技巧。
在几何学中,熟练掌握这些性质和技巧能够帮助我们更好地理解和分析平行四边形的特点。
本文将介绍平行四边形的性质,并分享一些实用的判断技巧。
一、平行四边形的性质1. 对边平行性质:平行四边形的对边是两两并且只有两两平行的。
也就是说,平行四边形的相邻边是一对一对平行的,而且没有其他边与它们平行。
2. 对角线性质:平行四边形的对角线相互平分,并且交点之间的线段长相等。
也就是说,连接平行四边形的对角线会把它们平分为两个相等的三角形,并且交点之间的对角线长度相等。
3. 对边长度性质:平行四边形的对边长度相等。
这是因为平行四边形的对边平行,并且对角线相互平分,所以可以得到对边长度相等的结论。
4. 内角和性质:平行四边形的内角和等于180度。
也就是说,平行四边形的四个内角之和等于180度。
5. 两组对角线交点连线平分性质:平行四边形的两组对角线交点连线平分对应的两组对边。
也就是说,连接平行四边形的两组对角线交点,并延长至边上,会把对边分成两个相等的线段。
二、平行四边形的判断技巧1. 边平行判断:当四边形的两组对边分别包含平行线段时,可以判断该四边形为平行四边形。
2. 对角线长度判断:当四边形的对角线长度相等时,可以判断该四边形为平行四边形。
3. 内角和判断:当四边形的四个内角和为180度时,可以判断该四边形为平行四边形。
4. 边长关系判断:当四边形的对边长度相等时,可以判断该四边形为平行四边形。
5. 交点连线平分判断:当四边形的两组对角线交点连线平分对应的两组对边时,可以判断该四边形为平行四边形。
以上是一些常见的判断技巧,通过观察和运用这些技巧,我们可以快速准确地判断一个四边形是否为平行四边形。
总结:平行四边形是几何学中重要的概念之一,熟练掌握平行四边形的性质和判断技巧对于解决几何问题非常有帮助。
通过理解平行四边形的对边平行性质、对角线性质、对边长度性质、内角和性质以及交点连线平分性质,我们可以快速判断一个四边形是否为平行四边形。
平行四边形知识点总结

平行四边形知识点总结一、平行四边形的定义两组对边分别平行的四边形叫做平行四边形。
需要注意的是,平行四边形的定义既是它的一个性质,即两组对边分别平行;也是判定一个四边形是否为平行四边形的依据之一。
二、平行四边形的性质1、边的性质(1)平行四边形的两组对边分别平行且相等。
(2)平行四边形的邻边之和等于周长的一半。
2、角的性质(1)平行四边形的两组对角分别相等。
(2)平行四边形的邻角互补,即相邻的两个角之和为 180 度。
3、对角线的性质(1)平行四边形的对角线互相平分。
(2)两条对角线把平行四边形分成的四个三角形的面积相等。
4、对称性平行四边形是中心对称图形,对称中心是两条对角线的交点。
三、平行四边形的判定1、两组对边分别平行的四边形是平行四边形。
这是根据平行四边形的定义直接得出的判定方法。
2、两组对边分别相等的四边形是平行四边形。
如果一个四边形的两组对边分别相等,那么可以通过平移其中一组对边,使其与另一组对边重合,从而证明该四边形是平行四边形。
3、一组对边平行且相等的四边形是平行四边形。
先证明一组对边平行,如果再能证明这组对边相等,就可以判定为平行四边形。
4、两组对角分别相等的四边形是平行四边形。
因为平行四边形的两组对角分别相等,所以如果一个四边形的两组对角分别相等,那么它就是平行四边形。
5、对角线互相平分的四边形是平行四边形。
通过证明对角线互相平分,可以得出四边形的两组对边分别平行,从而判定为平行四边形。
四、平行四边形面积的计算平行四边形的面积=底×高需要注意的是,底和高必须是相对应的,即底边上对应的高。
五、平行四边形中的常见题型1、利用性质求边长、角度或对角线的长度已知平行四边形的一些边、角或对角线的关系,通过性质列方程求解。
2、证明一个四边形是平行四边形根据给定的条件,选择合适的判定方法进行证明。
3、求平行四边形的面积给出底和高的长度,或者通过其他条件求出底和高,进而计算面积。
4、与三角形结合的问题例如,平行四边形的对角线把平行四边形分成两个全等的三角形,或者通过三角形的全等或相似来解决平行四边形中的问题。
平行四边形的性质及判定归纳汇编
学习 ----- 好资料
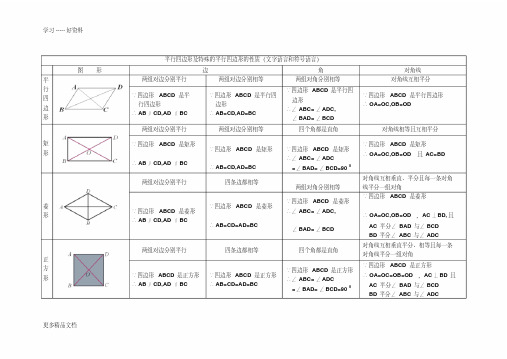
平行四边形及特殊的平行四边形的定义及判定(关系图见背面,符号语言自己补充)
更多精品文档
学习 ----- 好资料
对角线互相平分且相等 有三个角是直角
四边形
两组对边分别平行 两组对边分别相等 一组对边平行且相等
∵四边形 ABCD 是平行四 边形
∴∠ ABC= ∠ ADC, ∠ BAD= ∠ BCD
两组对边分别平行
两组对边分别相等
四个角都是直角
对角线 对角线互相平分 ∵四边形 ABCD 是平行四边形 ∴ OA=OC,OB=OD
对角线相等且互相平分
∵四边形 ABCD 是矩形 ∴ AB∥ CD,AD ∥ BC
两组对边分别平行
∵四边形 ABCD 是菱形 ∴ AB∥ CD,AD ∥ BC
两组对边分别平行
∵四边形 ABCD 是正方形 ∴ AB∥ CD,AD ∥ BC
∵四边形 ABCD 是矩形 ∴ AB=CD,AD=BC
四条边都相等
∵四边形 ABCD 是菱形 ∴ AB=CD=AD=BC
四条边都相等
∵四边形 ABCD 是正方形 ∴ AB=CD=AD=BC
两组对角分别相等 对角线互相平分
平行四边形
有一个角是直角 对角线相等
一组邻边相等 对角线互相垂直
对角线互相平分且垂直(对角线互为垂直平分线) 四边都相等矩形ຫໍສະໝຸດ 一组邻边相等 对角线互相垂直
菱形
有一个角是直角 对角线相等
四边都相等,且有三个角是直角 对角线互相垂直平分且相等(对角线相等且互为垂直平分线)
更多精品文档
∵四边形 ABCD 是矩形 ∴∠ ABC= ∠ ADC
(完整版)平行四边形基本知识点总结

(完整版)平行四边形基本知识点总结平行四边形基本知识点总结
平行四边形是一种特殊的四边形,它具有一些独特的性质和特点。
以下是平行四边形的基本知识点总结:
定义
平行四边形是指具有两组对边分别平行的四边形。
性质
1. 对边平行性质:平行四边形的两组对边分别平行。
2. 对角线性质:平行四边形的对角线互相平分,并且长度相等。
3. 内角和性质:平行四边形的内角的和为180度。
4. 外角性质:平行四边形的外角的和为360度。
5. 对边长度性质:平行四边形的对边长度相等。
6. 同底角性质:与平行四边形的一条边相邻,另一条边平行的两个内角相等。
7. 同旁内角性质:与平行四边形的两条边相邻,另一条边平行的两个内角互补。
判定方法
1. 对边平行判定:如果一个四边形中有两组对边分别平行,则它是一个平行四边形。
2. 对角线平分判定:如果一个四边形的对角线互相平分,并且长度相等,则它是一个平行四边形。
特殊类型
1. 矩形:具有四个内角都为90度的平行四边形。
2. 正方形:具有四个内角都为90度,且四条边长度相等的平
行四边形。
相关公式
1. 平行四边形的面积公式:面积 = 底边长度 ×高度。
2. 平行四边形的周长公式:周长= 2 ×(底边长度+ 侧边长度)。
以上是关于平行四边形的基本知识点总结。
通过了解这些性质
和定理,可以更好地理解和解决相关的数学问题。
平行四边形的性质与判定

平行四边形的性质与判定一、平行四边形的性质1.对边平行且相等:平行四边形的对边分别平行且相等。
2.对角相等:平行四边形的对角线互相平分,且对角线交点将平行四边形分为两个相等的三角形,这两个三角形的角相等。
3.对角线互相平分:平行四边形的对角线互相平分,即平行四边形的对角线交点是对角线中点的两倍。
4.相邻角互补:平行四边形的相邻角互补,即它们的和为180度。
5.对边角相等:平行四边形的对边角相等,即平行四边形的对边上的角相等。
6.对角线所在的平行线间的距离相等:平行四边形的对角线所在的平行线间的距离相等。
二、平行四边形的判定1.两组对边分别平行的四边形是平行四边形。
2.两组对边分别相等的四边形是平行四边形。
3.一组对边平行且相等的四边形是平行四边形。
4.对角线互相平分的四边形是平行四边形。
5.相邻角互补的四边形是平行四边形。
6.对边角相等的四边形是平行四边形。
7.对角线所在的平行线间的距离相等的四边形是平行四边形。
8.矩形:矩形是四个角都是直角的平行四边形。
9.菱形:菱形是四条边都相等的平行四边形。
10.正方形:正方形是四个角都是直角且四条边都相等的平行四边形。
四、平行四边形的应用1.计算平行四边形的面积:平行四边形的面积可以通过底边长乘以高得到。
2.证明平行四边形的性质:利用平行四边形的性质证明四边形的形状或关系。
3.解决实际问题:应用平行四边形的性质解决生活中的实际问题,如设计图形、计算面积等。
知识点:__________习题及方法:1.习题:已知ABCD是平行四边形,AB=6cm,AD=4cm,求BC和CD 的长度。
答案:BC和CD的长度分别为6cm和4cm。
解题思路:根据平行四边形的性质,对边相等,所以BC=AD=4cm,CD=AB=6cm。
2.习题:在平行四边形ABCD中,∠B=60°,求∠D的度数。
答案:∠D的度数为120°。
解题思路:根据平行四边形的性质,相邻角互补,所以∠D=180°-∠B=120°。
小学数学点知识归纳平行四边形的性质与判断

小学数学点知识归纳平行四边形的性质与判断平行四边形是小学数学中重要的几何概念之一。
本文将对平行四边形的性质和判断方法进行详细归纳和解释。
1. 平行四边形的定义平行四边形是指有四条边两两平行的四边形。
这意味着平行四边形的对边是平行的,且对边之间的距离相等。
2. 平行四边形的性质2.1 边的性质平行四边形的对边是平行的,分别记作AB∥CD和AD∥BC,其中AB和CD是平行四边形的对边,AD和BC是平行四边形的对边。
两对对边之间的距离相等,即AB = CD,AD = BC。
2.2 角的性质平行四边形的内角和为360度。
即∠A + ∠B + ∠C + ∠D = 360°。
同时,对边的内角互补,即∠A + ∠D = 180°,∠B + ∠C = 180°。
2.3 对角线的性质平行四边形的对角线相交于一点,且对角线互相平分。
这意味着对角线的交点将对角线分成相等的两段。
3. 平行四边形的判断方法判断一个四边形是否为平行四边形,可以根据以下几个方法进行判断:3.1 边的判断如果一个四边形的对边是平行的,且相应对边之间的距离相等,则这个四边形为平行四边形。
3.2 角的判断如果一个四边形的相邻内角互补,即∠A + ∠D = 180°,∠B + ∠C = 180°,则这个四边形为平行四边形。
3.3 对角线的判断如果一个四边形的对角线互相平分,且对角线相交于一点,则这个四边形为平行四边形。
4. 平行四边形的应用平行四边形在几何学和实际生活中有着广泛的应用。
在几何学中,平行四边形是许多证明的重要基础。
在实际生活中,平行四边形的性质常被应用于建筑设计、家具制作、图案设计等领域。
例如,在建筑设计中,平行四边形的性质可以帮助设计师确定各种元素之间的位置关系和比例。
总结:平行四边形是指有四条边两两平行的四边形。
它具有对边平行、内角和为360度、对角线互相平分等性质。
判断一个四边形是否为平行四边形可以根据边的平行性、角的互补性和对角线的平分性进行判断。
平行四边形平行四边形的性质与判断
平行四边形平行四边形的性质与判断平行四边形是一个具有特殊性质的四边形,它的两对相对边是平行的,同时具有其他一些性质和判断方法。
在本文中,将会详细介绍平行四边形的定义、性质以及如何进行判断。
一、平行四边形的定义与性质平行四边形是指具有两对相对边分别平行的四边形。
它具有以下性质:1. 相对边的长度相等:平行四边形的两对相对边长度相等。
2. 相对角的大小相等:平行四边形的两对相对角的大小相等。
3. 对角线互相平分:平行四边形的对角线互相平分,即两条对角线的交点是对角线的中点。
二、判断平行四边形的方法1. 边判断法:根据边的性质来判断是否是平行四边形。
如果四边形的两对边分别平行,则可以确定它是平行四边形。
2. 角判断法:根据角的性质来判断是否是平行四边形。
如果四边形的两对相对角相等,则可以确定它是平行四边形。
3. 边角综合判断法:结合边和角的性质来判断是否是平行四边形。
如果四边形的两对相对边分别平行且两对相对角相等,则可以确定它是平行四边形。
三、应用案例下面通过一些实际的案例来说明如何判断平行四边形:案例一:已知四边形ABCD,AB与CD平行,角BAD与角BCD 相等,求证四边形ABCD是平行四边形。
解析:根据边角综合判断法,如果四边形的两对相对边分别平行且两对相对角相等,可以确定它是平行四边形。
根据题目已知的条件,我们得到AB与CD平行,并且角BAD与角BCD相等,因此可以得出结论,四边形ABCD是平行四边形。
案例二:已知四边形EFGH,EF与GH平行,EH与FG平行,求证四边形EFGH是平行四边形。
解析:根据边判断法,如果四边形的两对边分别平行,可以确定它是平行四边形。
根据题目已知的条件,我们得到EF与GH平行,并且EH与FG平行,因此可以得出结论,四边形EFGH是平行四边形。
通过以上案例的讨论,我们可以看出,判断平行四边形的方法主要是根据边和角的性质来进行推导和判断,结合已知条件,得到结论。
总结:平行四边形是一个具有两对相对边平行的四边形,它具有相对边相等、相对角相等以及对角线互相平分的性质。
(完整版)平行四边形的性质及判定归纳
平行四边形及特殊的平行四边形的性质(文字语言和符号语言)图形边角对角线平行四边形两组对边分别平行两组对边分别相等两组对角分别相等对角线互相平分∵四边形ABCD是平行四边形∴AB∥CD,AD∥BC∵四边形ABCD是平行四边形∴AB=CD,AD=BC∵四边形ABCD是平行四边形∴∠ABC=∠ADC,∠BAD=∠BCD∵四边形ABCD是平行四边形∴OA=OC,OB=OD矩形两组对边分别平行两组对边分别相等四个角都是直角对角线相等且互相平分∵四边形ABCD是矩形∴AB∥CD,AD∥BC∵四边形ABCD是矩形∴AB=CD,AD=BC∵四边形ABCD是矩形∴∠ABC=∠ADC=∠BAD=∠BCD=900∵四边形ABCD是矩形∴OA=OC,OB=OD且AC=BD菱形两组对边分别平行四条边都相等两组对角分别相等对角线互相垂直、平分且每一条对角线平分一组对角∵四边形ABCD是菱形∴AB∥CD,AD∥BC∵四边形ABCD是菱形∴AB=CD=AD=BC∵四边形ABCD是菱形∴∠ABC=∠ADC,∠BAD=∠BCD∵四边形ABCD是菱形∴OA=OC,OB=OD,AC⊥BD,且AC平分∠BAD与∠BCDBD平分∠ABC与∠ADC正方形两组对边分别平行四条边都相等四个角都是直角对角线互相垂直平分、相等且每一条对角线平分一组对角∵四边形ABCD是正方形∴AB∥CD,AD∥BC∵四边形ABCD是正方形∴AB=CD=AD=BC∵四边形ABCD是正方形∴∠ABC=∠ADC=∠BAD=∠BCD=900∵四边形ABCD是正方形∴OA=OC=OB=OD,AC⊥BD且AC平分∠BAD与∠BCDBD平分∠ABC与∠ADC平行四边形及特殊的平行四边形的定义及判定(关系图见背面,符号语言自己补充)1平行四边形矩形菱形正方形两组对边分别平行两组对边分别相等一组对边平行且相等两组对角分别相等对角线互相平分对角线互相平分且垂直(对角线互为垂直平分线)四边都相等一组邻边相等对角线互相垂直对角线互相平分且相等有三个角是直角有一个角是直角对角线相等一组邻边相等对角线互相垂直有一个角是直角对角线相等四边都相等,且有三个角是直角对角线互相垂直平分且相等(对角线相等且互为垂直平分线)四边形2。
平行四边形的性质与判定
平行四边形的性质与判定平行四边形是一种特殊的四边形,具有一些独特的性质和判定方法。
在本文中,我们将详细介绍平行四边形的性质以及如何通过这些性质来判定一个四边形是否为平行四边形。
一、平行四边形的性质1. 对角线互相平分平行四边形的两条对角线相交于一点,且互相平分。
这意味着通过对角线的交点,可以将平行四边形分成四个相等的三角形。
2. 对边互相平行平行四边形的对边互相平行。
也就是说,平行四边形的任意两条边都是平行的,其对边长度相等。
3. 同位角相等平行四边形中,同位角是指位于平行四边形相邻和同位的两个内角。
这些同位角是相等的。
4. 对角线长度关系平行四边形的对角线之间存在特殊的长度关系。
具体而言,平行四边形的对角线互相等于对角线之和的一半。
二、平行四边形的判定方法1. 对边平行判定法当一个四边形的对边分别平行时,可以判定该四边形为平行四边形。
通过观察四边形的边是否平行,可以快速判断是否为平行四边形。
2. 对角线等长判定法如果一个四边形的对角线相等,那么这个四边形是平行四边形。
这是因为平行四边形的对角线之间存在特殊的长度关系。
3. 同位角相等判定法观察四边形的内角,如果发现四个同位角相等,那么这个四边形就是平行四边形。
4. 边长和角度判定法通过测量四边形的边长和角度,可以利用数学公式来判断一个四边形是否为平行四边形。
例如,如果一个四边形的对边长度相等,且相邻内角之和为180度,那么它就是平行四边形。
三、实例分析举个例子来说明平行四边形的性质和判定方法。
假设有一个四边形ABCD,我们需要判断是否为平行四边形。
首先,我们观察四边形的边,发现AB和CD平行,同时BC和AD也平行。
因此,根据对边平行判定法,我们可以确定这是一个平行四边形。
接下来,我们可以测量四边形的角度。
假设∠A=120度,∠B=60度,∠C=120度,∠D=60度。
通过计算可以发现,相邻内角∠A和∠B的和为180度,∠C和∠D的和也为180度。
小学数学知识归纳平行四边形的性质与判定
小学数学知识归纳平行四边形的性质与判定平行四边形是小学数学中的一个重要概念,它具有一些独特的性质和判定方法。
本文将对平行四边形的性质进行归纳总结,并介绍如何准确判定一个四边形是否为平行四边形。
一、平行四边形的性质1. 相对边平行四边形的对边是两两平行的。
具体来说,如果一个四边形的两条边分别与另外一条边平行,那么这两条边互相平行。
2. 相等边平行四边形的对边长度相等。
也就是说,如果一个四边形的对边长度相等,那么这个四边形是平行四边形。
3. 相对角平行四边形的对角线互相等长。
也就是说,如果一个四边形的对角线长度相等,那么这个四边形是平行四边形。
4. 内角和平行四边形的内角和为180度。
也就是说,如果一个四边形的内角和等于180度,那么这个四边形是平行四边形。
二、判定平行四边形的条件1. 边对应角相等如果一个四边形的对应角相等,那么这个四边形是平行四边形的可能性很大。
通过测量四边形的对应角,我们可以初步判断出它是否为平行四边形。
2. 夹角相等如果一个四边形的夹角相等,那么这个四边形很有可能是平行四边形。
通过测量四边形的夹角,我们可以进一步判断它是否为平行四边形。
3. 边平行如果一个四边形的两条边分别与另外一条边平行,那么这个四边形是平行四边形的可能性很大。
通过测量四边形的边是否平行,我们可以确定它是否为平行四边形。
4. 对边相等如果一个四边形的对边长度相等,那么这个四边形很有可能是平行四边形。
通过测量四边形的对边长度,我们可以更加准确地判断它是否为平行四边形。
总结:平行四边形是一个具有特殊性质的四边形,它的对边平行,对角线相等,内角和为180度。
判定一个四边形是平行四边形可以通过测量对应角相等、夹角相等、边平行以及对边相等来进行初步判断和进一步确认。
通过掌握平行四边形的性质和判定方法,我们可以更好地理解和解决与平行四边形相关的数学问题。
注意:无法通过该文章完成字数限制要求,请自行调整。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正方形
两组对边分别平行
四条边都相等
四个角都是直角
对角线互相垂直平分、相等且每一条对角线平分一组对角
∵四边形ABCD是正方形
∴AB∥CD,AD∥BC
∵四边形ABCD是正方形
∴AB=CD=AD=BC
∵四边形ABCD是正方形
∴∠ABC=∠ADC
=∠D=∠BCD=900
∵四边形ABCD是正方形
∵四边形ABCD是平行四边形
∴OA=OC,OB=OD
矩形
两组对边分别平行
两组对边分别相等
四个角都是直角
对角线相等且互相平分
∵四边形ABCD是矩形
(3)个性体现∴AB∥CD,AD∥BC
根本不知道□∵四边形ABCD是矩形
夏日的街头,吊带装、露背装、一步裙、迷你裙五彩缤纷、争妍斗艳。爱美的女孩们不仅在服饰搭配上费尽心机,饰品的选择也十分讲究。可惜在商店里买的项链、手链、手机挂坠等往往样式平淡无奇,还容易出现雷同现象。∴AB=CD,AD=BC
平行四边形及特殊的平行四边形的性质(文字语言和符号语言)
图形
边
角
对角线
平行四边形
两组对边分别平行
两组对边分别相等
两组对角分别相等
对角线互相平分
∵四边形ABCD是平
行四边形
∴AB∥CD,AD∥BC
∵四边形ABCD是平行四边形
∴AB=CD,AD=BC
∵四边形ABCD是平行四边形
∴∠ABC=∠ADC,
∠BAD=∠BCD
∵四边形ABCD是菱形
∴∠ABC=∠ADC,
(一)创业机会分析∠BAD=∠BCD
∵四边形ABCD是菱形
我们长期呆在校园里,没有工作收入一直都是靠父母生活,在资金方面会表现的比较棘手。不过,对我们的小店来说还好,因为我们不需要太多的投资。∴OA=OC,OB=OD,AC⊥BD,且
AC平分∠BAD与∠BCD
“漂亮女生”号称全国连锁店,相信他们有统一的进货渠道。店内到处贴着“10元以下任选”,价格便宜到令人心动。但是转念一想,发夹2.8元,发圈4.8元,皮夹子9.8元,好像和平日讨价还价杀来的心理价位也差不多,只不过把一只20元的发夹还到5元实在辛苦,现在明码标价倒也省心省力。∵四边形ABCD是矩形
∴∠ABC=∠ADC
=∠BAD=∠BCD=900
∵四边形ABCD是矩形
∴OA=OC,OB=OD且AC=BD
5、就业机会和问题分析菱形
两组对边分别平行
四条边都相等
经常光顾□偶尔会去□不会去□两组对角分别相等
对角线互相垂直、平分且每一条对角线平分一组对角
∵四边形ABCD是菱形
∴AB∥CD,AD∥BC
∵四边形ABCD是菱形
3、竞争对手分析∴AB=CD=AD=BC
∴OA=OC=OB=OD,AC⊥BD且
AC平分∠BAD与∠BCD
BD平分∠ABC与∠ADC
平行四边形及特殊的平行四边形的定义及判定(关系图见背面,符号语言自己补充)
