种群模型-微分方程模型
微分方程数值解(生物种群的相互竞争模型)
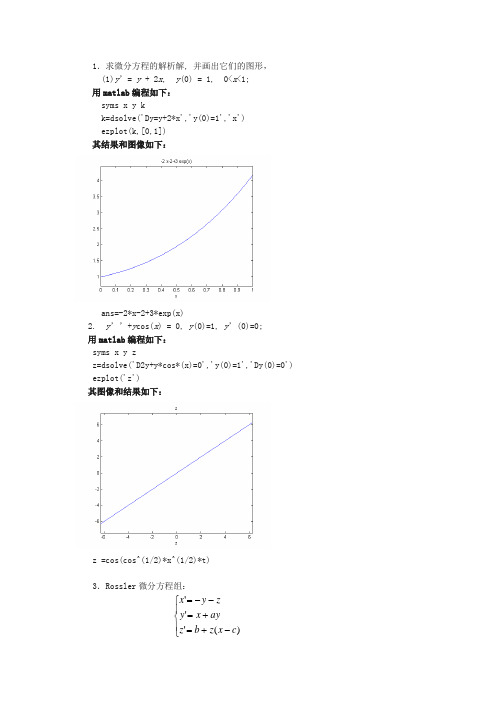
1.求微分方程的解析解, 并画出它们的图形, (1)y ’= y + 2x , y (0) = 1, 0<x <1;用matlab 编程如下: syms x y kk=dsolve('Dy=y+2*x','y(0)=1','x') ezplot(k,[0,1]) 其结果和图像如下:ans=-2*x-2+3*exp(x)2. y ’’+y cos(x ) = 0, y (0)=1, y ’(0)=0; 用matlab 编程如下: syms x y zz=dsolve('D2y+y*cos*(x)=0','y(0)=1','Dy(0)=0') ezplot('z')其图像和结果如下:z =cos(cos^(1/2)*x^(1/2)*t)3.Rossler 微分方程组:⎪⎩⎪⎨⎧-+=+=--=)('''c x z b z ay x y z y x当固定参数b=2, c=4时,试讨论随参数a 由小到大变化(如a ∈(0,0.65))而方程解的变化情况,并且画出空间曲线图形,观察空间曲线是否形成混沌状? 用matlab 编程建立rossler.m 文件: function r=rossler(t,x) global a; global b; global c;r=[-x(2)-x(3);x(1)+a*x(2);b+x(3)*(x(1)-c)]; 建立exp4-3.m 如下: global a; global b; global c; b=2; c=4;t0=[0,200];for a=0:0.03:0.65[t,x]=ode45('rossler',t0,[0,0,0]); subplot(1,2,1);plot(t,x(:,1),'r',t,x(:,2),'g',t,x(:,3),'b');title('x(红色),y(绿色),z(蓝色)随t 变化情况');xlabel('t'); subplot(1,2,2);plot3(x(:,1),x(:,2),x(:,3))title('相图');xlabel('x');ylabel('y');zlabel('z'); end(1)当a=0时,图像如下:所以当a=0时,(x,y,z)收敛于(0,0.5,0.5) (2)当a=0.12时,图像如下:x(红色),y(绿色),z(篮色)随t 变化情况t相图z当a=0.27时,(x,y,z)仍然收敛,但是收敛速度大大降低。
微分方程模型介绍

微分方程模型介绍在研究实际问题时,常常会联系到某些变量的变化率或导数,这样所得到变量之间的关系式就是微分方模型。
微分方程模型反映的是变量之间的间接关系,因此,要得到直接关系,就得求微分方程。
求解微分方程有三种方法:1)求解析解;2)求数值解(近似解);3)定性理论方法。
建立微分方程模型的方法:1)利用数学、力学、物理、化学等学科中的定理或经过实验检验的规律等来建立微分方程模型。
2)微元分析法利用已知的定理与规律寻找微元之间的关系式,与第一种方法不同的是对微元而不是直接对函数及其导数应用规律3)模拟近似法在生物、经济等学科的实际问题中,许多现象的规律性不很清楚,即使有所了解也是极其复杂的,建模时在不同的假设下去模拟实际的现象,建立能近似反映问题的微分方程,然后从数学上求解或分析所建方程及其解的性质,再去同实际情况对比,检验此模型能否刻画、模拟某些实际现象。
下面我们以生态学模型为例介绍微分方程模型的建立过程: 一. 单种群模型1. 马尔萨斯(Malthus)模型假定只有一个种群,()N t 表示t 时刻生物总数,r 表示出生率,0t 表示初始时刻,则生物总数增长的数学模型为()()()00d ,d (1)t t N t rN t t N t N =⎧=⎪⎨⎪=⎩不难得到其解为()0()0r t t N t N e-=.2. 密度制约模型由马尔萨斯模型知,种群总数将以几何级数增长,显然与实际不符,因为种群密度增大时,由于食物有限,生物将产生竞争,或因为传染病不再按照增长率r 增长,因而有必要修改,在(1)式右端增加一项竞争项。
()()()d (1)(2)d N t N t rN t tK=-其中K 为最大容纳量,可以看出当()N t K =时,种群的规模不再增大。
这个模型就是著名的Logistic 模型,可以给出如下解释:由于资源最多仅能维持K 个个体,故每个个体平均需要的资源为总资源的1K,在t 时刻个体共消耗了总资源的()N t K此时资源剩余()1N t K-,因此Logistic 模型表明:种群规模的相对增长率与当时所剩余的资源份量成正比,这种种群密度对种群规模增长的抑制作用。
数学建模生物种群模型

( t) c e c te x 11 12 y t t 1 1 t) c e c te ( 21 22
2019/2/27
t 1
t 1
p ( a d ), q ad bc
2 p p 4 q 1 ,2 2
f ( x0 , y0 ) 0 g( x0 , y0 ) 0
记为
P 0 (x 0, y 0)
2019/2/27
稳定与不稳定:如果存在某个邻域,使系统(1)的 解 (x 从这个邻域内的某一初值 (x (t),y (t)) ( 0 ),y ( 0 ))
出发,满足
lim x ( t ) x , lim y ( t ) y 0 0
的数学模型(Volterra模型)
(1)两个食饵种群A,B,一个捕食者种群C 。
( t ),x ( t ), x ( t ) 设 A,B,C t 时刻的密度分别为 x 1 2 3
假设:C 种群主要以A,B种群为食饵, A,B不 存在时,C 要逐渐绝灭,C 不是密度制约的; A, B种群不靠本系统为生,它们为密度制约且相互
N 表示 t 时刻的种群数量,r 称
为内禀增长率。
r ( t t ) 0
N ( t ) N ( t ) e 0
2) 罗杰斯特(Logistic)模型
dN N r( 1 )N K表示该种群的最大容纳量。 dt K K N ( t) K N ( t) r ( t t) 1 N e ( t)
x ,y ), g ( x ,y ) , 在平面区 假定方程组(1)的右端函数 f( 域 G 满足解的存在唯一的条件,则过相平面中任一点 有唯一的轨线。
2019/2/27
数学建模 种群模型

若 F ( p ) 0 ,则p* 是稳定平衡点。 若 F ( p )模型
16
回到我们的问题,由于 F( p0 ) k r F( p1) r k 所以, • 当k < r 时, F ( p0 ) 0 F ( p1) 0
p0 是稳定平衡点, p1 不是 ; • 当k > r 时, F ( p0 ) 0 F ( p1) 0
弱肉强食模型,生态学
上称为食饵(Prey)—捕食 者(Predater)系统,简称 为P—P系统。
二十世纪20年代中期, 意大利生物学家D’Ancona研究鱼类种群间的制约关系。 在研究过程中,他偶然注意到了在第一次世界大战时期, 地中海各个港口的捕鱼资料中,鲨鱼等(捕食者)鱼类 的比例有明显的提高(见下表)。
数学建模
种群模型
11
模型建立
记
F ( p) f ( p) h( p) ,
则在有捕捞条件下渔场鱼量的增长模型为
dp dt
F( p)
rp 1
p N
kp
(7)
数学建模
种群模型
12
模型讨论 由本问题的目标出发,我们关心的是渔场中鱼 量达到稳定的平衡状态时的情形,而不必知道每一 时刻的鱼量变化情况,故不需要解出方程,只需要 讨论方程 (7) 的平衡点并分析其稳定性。
当初值p(t0)=p0给定时,(3)的解为
p(t)
bp0
(r
rp0 bp0 )er (tt0 )
(4)
其变化曲线见下图。
数学建模
种群模型
7
注意到
p(t) r b
(t )
于是,不论初值怎样,群体规模总是小于并且趋于
极限值 r/b, 这个极限值的实际意义是环境资源对该
生物种群演化中的偏微分方程模型

生物种群演化中的偏微分方程模型引言:生物种群演化是生物学中一个重要的研究领域,它关注的是物种在时间和空间中的变化。
为了理解和预测物种的演化过程,科学家们提出了一种被称为偏微分方程模型的数学工具。
本文将介绍这一模型的基本原理和应用,并探讨其对生物种群演化研究的意义。
一、偏微分方程模型的基本原理偏微分方程模型是一种描述物种在时间和空间中变化的数学工具。
它基于物种数量与时间和空间的连续性假设,通过建立方程来描述物种数量的变化规律。
具体而言,偏微分方程模型可以分为两类:扩散方程模型和反应扩散方程模型。
1. 扩散方程模型扩散方程模型描述的是物种在空间中的扩散过程。
它假设物种的扩散速度与其数量密度成正比,即物种数量密度的变化满足扩散方程。
扩散方程模型的基本形式为:∂N/∂t = D∇²N其中,N表示物种数量密度,t表示时间,D表示扩散系数,∇²表示拉普拉斯算子。
这个方程表明物种数量密度随时间的变化速率等于扩散系数乘以物种数量密度的二阶空间导数。
2. 反应扩散方程模型反应扩散方程模型描述的是物种在空间中的扩散和繁殖过程。
它假设物种的数量密度变化既受扩散影响,也受繁殖影响,即物种数量密度的变化满足反应扩散方程。
反应扩散方程模型的基本形式为:∂N/∂t = D∇²N + f(N)其中,N表示物种数量密度,t表示时间,D表示扩散系数,∇²表示拉普拉斯算子,f(N)表示与物种数量密度相关的繁殖函数。
这个方程表明物种数量密度随时间的变化速率等于扩散项和繁殖项之和。
二、偏微分方程模型在生物种群演化研究中的应用偏微分方程模型在生物种群演化研究中具有广泛的应用。
它可以帮助科学家们理解和预测物种的演化过程,揭示物种数量分布和演化的规律。
以下是偏微分方程模型在生物种群演化研究中的几个典型应用:1. 种群扩散模型扩散方程模型可以用来描述物种在地理空间中的扩散过程。
科学家们可以根据实际观测数据,通过拟合扩散方程模型的参数,预测物种在不同环境条件下的扩散速度和范围。
种群连续增长模型积分式推导

种群连续增长模型积分式推导种群连续增长模型积分式推导1.引言在生物学和生态学中,种群的规模是一个关键的研究对象。
种群连续增长模型是一种数学模型,用于描述种群规模随时间的变化。
本文将介绍一种常见的种群连续增长模型,即基于微分方程的种群增长模型,同时将使用积分式对其进行推导和解释。
2.微分方程描述的种群增长模型在种群生态学中,常用的描述种群增长的微分方程模型是Verhulst模型,也称为Logistic增长模型。
Verhulst模型考虑了种群的内部和外部因素对种群规模的影响,并具有以下形式:dN/dt = rN(1 - N/K)其中,dN/dt表示时间t上种群规模N的变化率,r代表种群的固有增长率,K是种群的环境容量。
3.积分式推导为了求解Verhulst模型,我们将其转化为积分式,并对其进行推导。
我们可以将上述微分方程稍作改写,得到:dN / N(1 - N/K) = rdt。
对上式两边同时进行积分操作,得到∫dN / N(1 - N/K) = ∫rdt此时,我们需要使用换元法,设u = 1 - N/K,则有dN = -Kdu,并将其代入原方程,得到:∫du / (u(1 - u)) = -∫rKdt上述第一个积分可以通过分解为部分分式的形式进行解,最后得到:ln|u| - ln|1 - u| = -rt + C其中,C是积分常数。
将u的值替换回原来的变量N,得到:ln|N/ (K - N)| = rt + C4.模型解释和个人观点从上述推导可以看出,种群的规模随时间的变化是通过积分式来描述的。
这种积分式的推导不仅使我们能够理解种群连续增长模型的基本原理,还可以提供一种更全面、深刻和灵活的理解方式。
对于Verhulst模型,我们可以从几个方面来解释和理解它。
模型中的固有增长率r表示种群在没有外部限制或干扰的情况下的增长速率。
当种群规模逼近环境容量K时,种群的增长速率将逐渐减缓,直至趋于稳定状态。
这种饱和增长模式在实际生态系统中是非常普遍的。
种群增长模型

具密度效应旳种群离散增长最简朴旳模型是:
Nt+1=[1.0-B(Nt-Neq)]Nt
模型旳行为特征,用变化参数值旳措施来检验:
设Neq=100,B=0.011,N0=10, N1=[1.0-0.011(10-100)]10=19.9 N2=[1.0-0.011(19.9-100)]19.9=37.4 N3=63.1 N4=88.7 N5=99.7
与密度有关
种群离散增长模型 种群连续增长模型
(一)与密度无关旳种群增长模型 1、种群离散增长模型(差分方程)
假设:①种群在无限环境中增长,增长率不变 ②世代之间不重叠,增长不连续 ③种群没有迁入、迁出 ④种群没有年龄构造
N t+1=λNt 或
Nt=N0 λt lgNt=lgN0+(lgλ)t
式中:N —— 种群大小; t —— 时间; λ—— 种群旳周限增长率。
§1、种群旳概念
§2、种群动态 种群统计学
密度 初级种群参数 次级种群参数 生命表和存活曲线 种群增长率
三、种群增长模型
研究种群旳目旳:阐明自然种群动态 规律及调整机制。
归纳法(搜集资料、解释、归纳)
措施
自然种群
演绎法(假设、搜集资料、检验)
试验种群
种群 增长 模型
与密度无关
种群离散增长模型 种群连续增长模型
按此方程,种群增长将不再是“J”字型, 而是“S”型。“S”型曲线有两个特点:
①曲线渐近于K值,即平衡密度; ② 曲线上升是平滑旳。
草履虫(Paramecium caudatum)种群旳S型增长(Gause,1934)
逻缉斯谛曲线常划分为5个时期: ① 开始期,种群个体数极少,密度增长缓慢; ② 加速期,随个体数增长,密度增长逐渐加紧; ③ 转折期,当个体数到达饱和密度旳二分之一 (即 K/2时),密度增长最快; ④ 减速期,个体超出 K/2 后来,增长变慢; ⑤ 饱和期,种群个体数到达 K 值而饱和。
种群增长

或译为非密度制约性增长。
与密度无关的增长模型又可分为两类。 1、离散种群的增长模型 离散种群:种群的各个世代彼此不相重叠。
如一年生植物和许多一生生殖一次的昆虫,
第二节 种群增长模型及其应用
种群增长模型是指在一定空间里,随着时间
推移,种群数量表现出来的变化形式。
数学模型:是用来描述现实系统性质的抽象、
简化的数学结构。
利用数学模型可以揭露系统的内在机制, 对系统的行为进行预测。
本节只涉及单种种群模型。
种群增长模型的学习要点: 1 模型的假设及其构建 2 模型中参数的生物学意义
NMSY的数值通过对方程
dN/dt= rN(1 - N/K)求导数,令一阶 导数=0 求得:
NMSY=K/2 当NMSY=K/2 时,
MSY=rK/4
当 NMSY=K/2 时,MSY=rK/4 只要知道某一种群的环境容纳量K值和瞬时 增长率r两个参数值,就能从理论上求出最大 持续产量MSY和提供MSY的种群数量NMSY。
由此产生的最重要的问题是: 什么样的种群水平能保证最大的产量? 最大产量是多少?
英国鱼类学家格雷厄姆(Graham,1935)
用Logistic 增长理论来解决最大持续产量问题。
Logistic 模型为:
现假设K=200,种群的r=1.0,种群增长率与种群 大小的关系就如下表
在这个例子中,
当种群数量 N=50 时,
即一年种群数量增长20倍。 若种群在无限环境下,以这个速率年复一年的 增长, 即 N (t+1) =λN (t) 或 N t =N0〃λt。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 2 3 4 5 6
1000 450 200 50 10 0
550 250 150 40 10
1 0.45 0.2 0.05 0.01 0
0.55 0.556 0.75 0.8 1
725 325 125 30 5
1210 485 160 35 5
Rhum岛上赤鹿的特定时间(静态)生命表(1957年)
内禀增长率(rm) 种群在不受外界环境限制情况下的增长率。
三、种群的增长模型 (一)与密度无关的种群增长模型 种群的空间、食物等资源是无限的情况下呈指数增长,此时 可以称为密度无关的增长(density-independence growth) 种群离散增长模型(种群的各个世代不相重叠) 种群连续增长模型(种群的各个世代重叠) (二)与密度有关的种群增长模型 相对于无密度模型增加的2点假设: 环境容纳量(K);增长率随密度上升而降低 逻辑斯谛方程(Logistic equation) 逻辑斯谛曲线的5个时期
四、 自然种群的数量变动 (一)种群增长 “J”型增长;“S”型增长 (二)季节消长 (三)不规则波动(蝗虫) (四)周期波动 (五)种群的暴发 (六)种群平衡 (七)种群的衰落和灭亡 (八)生态入侵(水葫芦、米草、龙虾)
第三节 种群的空间格局 种群空间分布的3种格局 均匀分布、随机分布、成群分布 第四节 种群调节(阅读) 一、气候调节 二、生物学派 三、食物因素 四、自动调节学说
第三章 种群及其基本特征
第一节 种群的概念 种群(population)是在一定空间中同种个体的组 合。 种群生态研究种群的数量、分布以及种群与其栖息 环境中的非生物因素和其他生物种群的相互作用 第二节 种群的动态 种群动态是种群生态学研究的核心问题,其主要包 括种群的数量、种群的分布、种群数量变动和扩散 迁移、种群调节
一个假设的生命表
nx
x
年龄组
本年龄 组开始 时存活 个数
Dx
本年龄 组死亡 个体数
lx
年龄组 开始时 存活个 体数
qx
本年龄 组期间 的死亡 率
Lx
本年龄 组期间 平均个 体数
Tx
种群全 部个体 平均寿 命和
ex
本年龄 组开始 时存活 个体的 平均生 命期望 1.21 1.08 0.8 0.7 0.5
二、种群统计学
种群统计的指标 种群密度;初级种群参数(出生率、死亡率、迁入和迁出 率);次级种群参数(性别比例、年龄分布、种群增长等) 种群结构和性别比例 年龄锥体图 生命表的编制 生命表的一般构成 特定时间(静态)生命表和特定年龄(动态)生命表 综合生命表 综合生命表是在简单生命表的基础上添加了mx,即各年龄 的出生率
种群增长率和内禀增长率 种群增长率 由于各种生物的平均世代时间不同导致R0的可比性不强, 因此做种间比较时通常使用种群增长率(r)来代替R0, r=lnR0/T 其中,T表示种群中子代从母体出生到子代再产子的平均时 间,用生命表估算为T=(∑xlxmx)/(∑lxmx)
根据上式可以提出控制种群数量的方法
加拿大山猫种群数量与雪兔种群数量的关系
x 1 2
nx
100000qx 282 9.8
ex
5.81 6.89
3
4 5 6 7 8 9 10 11 12 13
711
704 697 690 684 502 249 92 78 64 50
7
7 7 7 182 253 157 14 14 14 14
9.8
9.9 10 10.1 266 504 630.6 152.1 179.4 218.7 279.9
x/a 0
lx
0.99
lg(1000lx) 3
kx
0
mx
0
lxmx
0
xlxmx 0
1
2 3 4
0.99
0.97 0.89 0.87
3
2.99 2.95 2.94
0.07
0.275 0.07 0
0
0 0 0.134
0
0 0 0.134
0
0 0 0.536
5
0.87
2.94
0.04
0.349
0.349
0.745
5.95
5.01 4.05 3.09 2.11 1.7 1.91 3.31 2.81 2.31 1.82
14
15 16
36
22 8
14
14 8
388.9
636.3 1000
1.33
0.86 0.5
藤壶(Balanus glandula)的特定年龄(动态)生命表
x/a 0
nx
142
dx
80
qx
0.563
122 74
47 29.25 16 7.25 3 1 0
1.97 2.18
2.35 1.89 1.45 1.12 1.5 0.5
0.472 0.239
0.141 0.109 0.077 0.046 0.014 0.014 0
利用新添加的mx可以计算该种群的世代净增殖率R0, R0=∑lxmx kx表示年龄组死亡率的指标
1. 开始期种群个体少增长缓慢2. 加速期个体数目增加增长变快 3. 转 折期个体数量达到K值一半时增长最快4. 减速期数目增长变缓5. 饱和 期,种群趋向稳定
美国加州西南部的莫哈韦沙漠中的灌木丛(larrea tridentata)
1910年4头雄性驯鹿和24头雌性驯鹿被引入到美国阿拉斯 加,30年后,驯鹿的数量增长到2000头,1950年由于食 物的极度匮乏驯鹿种群减少到8头。
一、种群的密度和分布
(一)数量统计 直接统计某一地区内物种的数量 标志重捕法(动物) 在调查样地上捕获一部分个体进行标志后释放,经 一定期限进行重捕,根据公式计算 N:M=n:m M-标志数 n-重捕个体数 m-重捕中标记数 N-样地上个体总数
标志重捕法成立必须满足:重捕取样中标志 比例与样地总数中标志比例相等(假设); 种群数量没有增加或减少,标志没有丢失 对濒危动物种群数量的调查 (二)单体生物和构件生物 单体生物个体很清楚,个体保持基本一致的 形态结构;构件生物由一套构件组成 对单体生物和构件生物必须从不同的层次进 行种群统计
Lx 102
Tx 224
ex
1.58
lx
1
1 2
3 4 5 6 7 8 9
62 34
20 15.5 11 6.5 2 2 0
28 14
4.5 4.5 4.5 4.5 0 2 0
0.452 0.412
0.225 0.29 0.409 0.692 0 1
48 27
17.75 13.25 8.75 4.25 2 1 0
