3. 随机信号分析_随机信号的频域分析
第3章随机信号的频域分析
1 2 GX ( ) lim E X T ( ) T 2T 1 2 GX ( ) lim X T ( , e) T 2T
随机信号分析
第三章 随机信号的频域分析
9 /30
（2）实随机过程功率谱密度的性质
第三章 随机信号的频域分析
5 /30
（3）能量谱密度
2 E s 信号s(t)的总能量为 (t )dt
根据帕塞瓦尔定理：对能量有限信号，时域内信 号的能量等于频域内信号的能量。即 2 1 2 E s (t )dt S ( ) d 2
S ( ) 称为s(t)的能量谱密度（能谱密度）。
随机信号分析
第三章 随机信号的频域分析
23 /30
（2）噪声的分类
从噪声与电子系统的关系来看： 内部噪声：系统本身的元器件及电路产生的 外部噪声：包括电子系统之外的所有噪声 根据噪声的分布： 高斯噪声：具有高斯分布的噪声 均匀噪声：具有均匀分布的噪声 从功率谱的角度来看： 白噪声：随机过程的功率谱为常数（无论是 什么分布）。 色噪声：功率谱中各种频率分量的大小不同。
2
随机信号分析
第三章 随机信号的频域分析
21 /30
例3.5：设两个随机过程X(t)和Y(t)联合平稳，其互相 关函数为： 9e 3 0 RXY ( ) 0 0 求互相关函数 GXY () 和 GYX () 解：G ( ) XY RXY ( )e
j
GXY () GYX () 0
随机信号分析
第三章 随机信号的频域分析
20 /30
性质4：若X(t),Y(t)是互不相关的两个随机过程，且数 学期望不为零，则有
随机信号分析
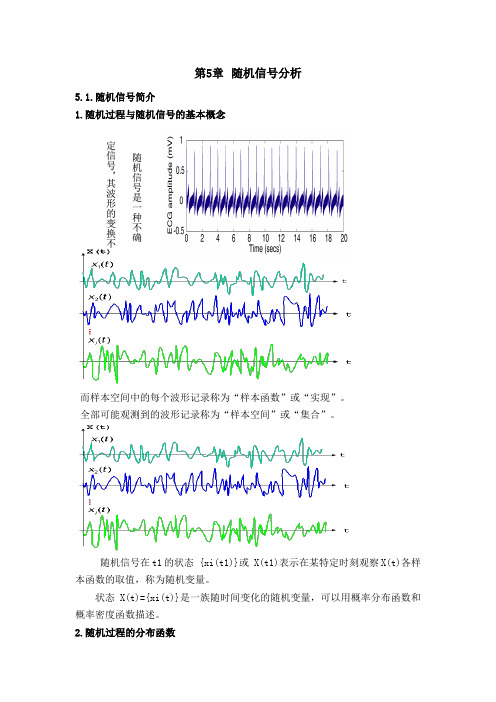
第5章 随机信号分析5.1.随机信号简介1.随机过程与随机信号的基本概念而样本空间中的每个波形记录称为“样本函数”或“实现”。
全部可能观测到的波形记录称为“样本空间”或“集合”。
随机信号在t1的状态 {xi(t1)}或 X(t1)表示在某特定时刻观察X(t)各样本函数的取值，称为随机变量。
状态X(t)={xi(t)}是一族随时间变化的随机变量，可以用概率分布函数和概率密度函数描述。
2.随机过程的分布函数随机信号是一种不确定信号，其波形的变换不存在。
任何确定的规律。
因而无法准确预测未来值{X[k], k ∈Z}表示一个随机过程一维分布函数 )][();(x k X P k x F ≤=二维分布函数 )][,][(),;,(22112121x k X x k X P k k x x F ≤≤= 三维分布函数 ),,;,,,(2121N N k k k x x x F)][,][(11N N x k X x k X P ≤≤=3.随机信号的数字特征均值 ]}[{][k X E k m x =方差 ]}[][{}])[][{(][2222k m k X E k m k X E k x x x-=-=σ 自相关函数 ]}[][{],[2121k X k X E k k R x =互相关函数 ]}[][{],[2121k Y k X E k k R xy = 4.平稳各态遍历随机信号的时域描述 （1） 平稳随机序列指统计特性不随时间的平移而变化的那一类随机序列 严平稳随机序列：),,;,,,(),,;,,,(21212121n k n k n k x x x F k k k x x x F N N N N +++=宽平稳随机序列：x m k X E =]}[{ ][]}[][{n R n k X k X E x =+平稳随机信号自相关函数特性：1）对称性 ][][n R n R x x -=2）极限值 0=n ]}[{]0[2k X E R x =∞→n 2][xx m R =∞ 3）不等式 ][]0[n R R x x ≥（2）各态遍历随机信号:时间平均等于统计平均 ∑-=∞→+==NNk N xk x N k X E m ][121lim ]}[{ ∑-=∞→-+=-=NNk x N x xm k x N m k X E 222]][[121lim }]][{[σ][][121lim ]}[][{][n k x k x N n k X k X E n R NNk N x ++=+==∑-=∞→ 5.平稳各态遍历随机信号的频域描述 随机信号的平均功率定义为][121lim 2k x N P NNk N x ∑-=∞→+= 对平稳、各态遍历的随机过程上式可写为]0[x x R P = 随机信号的功率谱定义为(维纳—辛钦定理)]}[{DTFT )(n R P x x =Ω由IDTFT 可得：ΩΩ==⎰-d )(π21]0[ππx x x P P R5.2、经典功率谱估计1.谱估计的质量估计量的偏差 θθθ-=}ˆ{}ˆ{bia E 估计量的方差 })}ˆ{ˆ({}ˆvar{2θθθE E -= 的一致估计为ˆ则称,0}ˆvar{lim ,0}ˆ{bia 若θθθθ==∞→N2.相关法(间接法)进行功率谱估计 相关法的理论基础维纳—辛钦定理 )(][DTFTΩ−−−−→←x x P n R 估计的方法：1) 由随机序列一个样本的N 个观测值计算自相关函数的估计][ˆn R x 2) 对][ˆn Rx 进行DTFT 即得该随机序列的功率谱估计 （2） 自相关函数的估计X[k]是宽平稳各态遍历随机信号，x[k]是其一个样本∑-=∞→++=N Nk N x n k x k x N n R ][][121lim ][ 已知x[k]的N 个观测值x[0],x[1],⋯,x[N-1]，则自相关函数的估计为][][1][ˆ1n k x k x Nn RN kx +=∑-=][*][1n x n x N-=1)1(-≤≤--N n N][ˆn Rx 的计算过程：10-≤≤N n][][1][ˆ10n k x k x Nn RnN kx +=∑--=)1(≤≤--n N∑--=+=1][][1][ˆN nk x n k x k x Nn R∑+-=-=n N ln l x l x N10][][11][][1][10-≤+=∑--=N n n k x k x Nn R nN kx（3） 相关法进行功率谱估计∑-=∧+=10][][1][N kx n k x k x Nn RΩ--=∑=Ωn LLn x x n R P j e ][ˆ)(ˆ}e ][ˆRe{2]0[ˆj 11Ω--=∑+=n N n n R R(4） 相关法功率谱估计的质量功率谱估计的质量与自相关函数估计的质量密切相关][]}[{bia n R Nn n R x x -=∧])[][][(1]}[ˆvar{2n r R n r R r R Nn R r-++≈∑∞-∞=][ˆ),(ˆDFT DTFT,][ˆ估计][m P P n R k x x x x Ω−−−−−−→−−−−−→−N →∞，偏差、方差趋于零，是一致估计。
《随机信号分析》课件
方差
均值
自相关函数描述了随机信号在不同时间点之间的相关性。
自相关函数可以用于分析信号的周期性和趋势性。
谱密度函数描述了随机信号的频率成分。
通过谱密度函数，可以了解信号在不同频率下的强度和分布。
04
CHAPTER
随机信号的频域分析
傅立叶变换是信号处理中的基本工具，用于将时间域的信号转换为频域的表示。通过傅立叶变换，我们可以分析信号的频率成分和频率特性。
02
时间变化特性
由于随机信号的取值是随机的，因此其时间变化特性也是随机的，表现为信号的幅度、频率和相位都是随机的。
在通信领域，随机信号可以用于扩频通信、信道编码等，以提高通信的可靠性和抗干扰能力。
通信
在雷达领域，随机信号可以用于雷达测距、目标跟踪等，以提高雷达的抗干扰能力和探测精度。
雷达
在地球物理学领域，随机信号可以用于地震勘探、矿产资源探测等，以提高探测的精度和可靠性。
线性系统的输出信号的统计特性与输入信号的统计特性和系统的传递函数有关。通过分析线性系统对随机信号的作用，我们可以了解系统对信号的影响和信号经过系统后的变化情况。
05
CHAPTER
随机信号的变换域分析
总结词
拉普拉斯变换是一种将时域信号转换为复平面上的函数的方法，用于分析信号的稳定性和可预测性。
详细描述
详细描述
06
CHAPTER
随机信号处理的应用
信号传输
随机信号分析在通信系统中用于信号传输的调制和解调过程，通过对信号的随机性进行编码和解码，实现可靠的信息传输。
目标检测
01
随机信号分析在雷达系统中用于目标检测和跟踪，通过对接收到的回波信号进行分析和处理，实现高精度和高可靠性的目标定位和识别。
随机信号分析课件
密度函数
连续型随机变量
？
连续取值而非连续型或混合
型随机变量
分布函数定义：设(S，F ，P)是一概率空间，X(s)是定义在其上的 随机变量，R1={x:-∞<x< ∞}，对于任意x∈R1，令
FX(x)=P[X≤x] 称FX(x)为随机变量X的分布函数。
按分布函数的定义，当a<b时， P[a＜X≤b]如何用分布函数表示？
P[B|A]=P[B] P[A∩B]=P[A]P[B]
两个事件的独立性 具有相互对称性质
P[A|B]=P[A]
在概率独立性的定义中，一般是使用乘积公式，即 概率范畴的
P[A∩B]=P[A]P[B] 注意：互斥事件与统计独立的区别。
统计独立---- P[A∩B]=P[A]P[B]
概念 集合范畴的
概念
互斥----A∩B=φ ，P[A∩B]=P[φ]
几何概率的基本性质：
1 0P[A]1
2
P[S] 1
3
Pkn1
Ak
n k1
P
Ak
1.1.3 统计概率
f (n) A
nA n
事件频率的性质：
1Leabharlann 0f (n) A1
2
f (n) S
1
n
3
(n )
(n )
f f n Ai
Ai i 1
i 1
几种概率共有的基本性质：
P { X 2 } 1 P { X 2 } 1 P { X 0 } P { X 1 } 1 0 . 9 4- 4 0 8 0 0 0 3 . 0 9 0 . 9 0 ， 98 2
随机信号分析简化
地球物理学中的随机信号处理
地震信号处理
利用随机信号处理技术对地震数据进行处理和分析，提取地震特 征，进行地震勘探和资源探测。
地球磁场和重力场测量
通过随机信号处理技术实现地球磁场和重力场测量，研究地球物理 特性和地质构造。
PART 04
随机信号的频域分析
傅里叶变换
01
将时间域信号转换为频域信号，通过分析频谱特性来理解信号 的频率组成和变化规律。
02
傅里叶变换的公式为：X(f) = ∫x(t)e^(-j2πft)dt，其中X(f)表示
频域信号，x(t)表示时域信号，f表示频率。
傅里叶变换具有线性、时移、频移、尺度变换等性质，这些性
概率质量函数（PMF）
定义
01
描述随机信号取各个离散值时的概率。
作用
02
用于分析随机信号的离散概率分布特性。
计算方法
03
直接统计随机信号各个离散取值的出现次数。
累积分布函数（CDF）
01
02
03
定义
描述随机信号小于或等于 某个值的概率。
作用
用于分析随机信号的分布 范围和概率覆盖。
计算方法
通过累加概率质量函数得 到。
线性合成
通过线性组合多个随机信号来生成新的随机信号。
非线性合成
利用非线性函数对随机信号进行处理，生成非线 性随机信号。
PART 06
随机信号处理的应用
通信系统中的随机信号处理
信号调制与解调
利用随机信号处理技术对信号进行调制和解调，提高通信系统的 抗干扰能力和传输效率。
信道编码与解码
随机信号分析PPT课件
RY ( )
N0 (bebu)(beb(u))du 20
N0b2 eb e2budu N 0b e b
2
0
4
相关函数为偶函数，τ<0时
R Y ( )
输出自相关函数为
N 0b e b 4
RY()
N0beb 4
a
25
输出的平均功率为
E[Y 2 (t)] RY (0)
N 0b 4
b为时间常数的倒数
a
2
4.1 线性系统的基本理论 4.1.1 线性时不变系统
x(t)
y(t)
L[ ·]
y(t)L[x(t)]
连续时间系统 双侧系统
离散时间系统
单侧系统
a
双侧信号 单侧信号
3
线性系统
L [ a 1 ( t ) x b 2 ( t ) x a ][ x 1 ( t L ) b ][ x 2 ( L t )]
RXY()0 h(u)RX(u)du
输出自相关R 函YX数(为)0 h(u)RX(u)du
RY()h(u)h(v)RX(uv)dudv
0
R Y()0 h(u)RXY(u)du
R Y()0 h(u)R Y aX(u)du
18
输出的均方值（总平均功率）
E[Y2(t)]h(u)h(v)RX(uv)dudv
(
)
N 0b 4
eb
与白噪声输入时 情况相同
a
31
例4.3中的相关函数可以进一步表示为
R Y()4 N 0e b 1 b 1 2/ 2 1be ( b)
二、双侧随机信号
K X(t)
Y(t) h(t)
Y(t)0h(u)X (tu)U (tu)du
使用Matlab技术进行随机信号分析的基本步骤
使用Matlab技术进行随机信号分析的基本步骤随机信号分析是信号与系统领域中的一个重要研究课题，它主要涉及到信号的时间特性、频率特性、概率特性等方面的分析。
而使用Matlab技术进行随机信号分析，则是一种十分高效且常见的方法。
在本文中，我们将向您介绍使用Matlab 技术进行随机信号分析的基本步骤。
第一步：信号生成随机信号的分析首先需要产生实验信号。
Matlab提供了丰富的信号生成函数，例如rand、randn等，可以生成均匀分布的随机信号、高斯分布的随机信号等。
根据所需要分析的信号类型和特性，我们可以选择适合的函数进行信号生成。
第二步：采样和量化分析随机信号之前，我们需要对其进行采样和量化。
采样是将连续信号转化为离散信号的过程，而量化则是将连续信号的振幅值转化为离散信号的过程。
Matlab 提供了相应的函数，例如downsample和quantize，可以实现信号的采样和量化操作。
第三步：时域分析时域分析是对信号在时间域上的特性进行分析。
常用的时域分析方法包括信号的均值、方差、自相关函数、互相关函数等。
在Matlab中，我们可以使用mean、var、xcorr等函数，对随机信号的时域特性进行计算和分析。
第四步：频域分析频域分析是对信号在频率域上的特性进行分析。
通过对随机信号进行傅里叶变换，我们可以得到信号的频谱特性。
Matlab中提供了fft函数，可以用于实现傅里叶变换。
通过对傅里叶变换结果进行幅度谱和相位谱的计算，我们可以更全面地了解信号在频率域上的特性。
第五步：概率分布分析概率分布分析是对信号的概率特性进行分析。
在随机信号分析中，常见的概率分布包括均匀分布、高斯分布、泊松分布等。
Matlab中提供了相应的概率分布函数，我们可以使用这些函数计算信号的概率密度函数、累积分布函数等。
第六步：建立模型和拟合通过对信号进行分析，我们可以建立信号的数学模型，并利用拟合技术将实际信号与模型进行比较。
Matlab中提供了polyfit、lsqcurvefit等函数，可以用于信号的模型建立和拟合。
3. 随机信号分析_随机信号的频域分析
1 s (t ) 2
S ( )e jt d F 1 [ S ( )]....... （反变换）
其中S(w)称为信号s(t)的频谱，它反映了s(t)中各种频率成分 的分布状况。 可以证明：对一般实信号s(t)，其频谱是w的复函数， 即
S ( ) S ( ) ，（“*”表示复共轭）。
(3). 功率谱密度是 的偶函数
G X ( ) G X ( )
根据傅立叶变换的性质，当
xiT (t) 为 t 的实函数时，其频谱满足
X iT ( ) X iT ( ) X iT ( ) X iT ( ) 则随机过程截断后的频谱为 X T ( ) X T ( ) X T ( ) X T ( )
a .s
4、各态历经过程的功率谱密度 若过程 X(t) 的平均功率和 其样本函数的平均功率
a .s
1 P GX ( )d 2 － 1 P Gk ( )d k 2 －
由X(t)的各态历经性，P Pk 因此有
a.s
1 2 GX () Gk () lim X kT () T 2T
| s (t ) |dt
（绝对可积）
或
2 | s ( t ) | dt （信号的总能量有限）
若s(t)满足上述条件，则其傅立叶变换对存在。
S ( ) s (t )e jt dt F [ s (t )].................. （正变换）
即各态历经过程 X(t) 的功率谱密度 GX ( )与其样本函数的功率 谱密度 Gk ( ) 以概率1 相等。
5 、实随机过程功率谱密度的性质 功率谱密度是随机过程在频域中主要的统计特征。 (1). 功率谱密度为非负值 由定义式3-12
随机信号分析
随机信号分析随机信号是在时间或空间上具有随机性质的信号，其数学模型采用随机过程来描述。
随机信号的分析是信号与系统理论中的重要内容，其应用广泛涉及通信、控制、电力系统等领域。
本文将从随机信号的基本特性、常见的随机过程以及随机信号分析的方法等方面进行阐述。
随机信号的基本特性包括：平均性、相关性和功率谱密度。
首先，平均性是指随机信号的统计平均等于其数学期望值。
随机信号的平均性是通过计算信号在一定时间或空间范围内的平均值来描述的。
其次，相关性是指随机信号在不同时刻或不同空间位置上的取值之间存在一定程度的相关性。
相关性可以描述信号之间的相似度和相关程度，常用相关函数来表示。
最后，功率谱密度是用来描述信号在频域上的分布特性，它表示了随机信号在不同频率上所占的功率份额。
随机信号的常见模型主要有白噪声、随机行走、随机震荡等。
其中，白噪声是指功率谱密度在整个频率范围内均匀分布的信号，其在通信领域中应用广泛。
随机行走模型是一种随机过程，它描述了随机信号在不同时刻之间的步长是独立同分布的。
随机震荡模型是一种具有振荡特性的随机过程，常用于描述具有周期性或周期性变化的信号。
对于随机信号的分析方法，主要包括时间域分析和频域分析两种。
时间域分析是通过观察信号在时间上的波形和变化规律来分析随机信号的特性，常用的方法有自相关函数和互相关函数等。
频域分析是将信号转换为频率域上的功率谱密度来分析信号的频谱特性，常用的方法有傅里叶变换和功率谱估计等。
在实际应用中，随机信号的分析对于信号处理和系统设计具有重要意义。
在通信系统中，随机信号的噪声特性是衡量系统性能的关键因素之一，因此通过对随机信号的分析可以有效地优化通信系统的传输质量。
此外，在控制系统和电力系统中，随机信号的分析也能帮助我们进行系统建模和性能预测，从而实现系统的稳定性和可靠性。
综上所述，随机信号的分析是信号与系统理论中的重要内容，其对于各个领域的应用具有重要的意义。
通过对随机信号的基本特性、常见的随机过程以及分析方法的了解，可以为我们深入理解和应用随机信号提供帮助。
《随机信号分析》课件
连续随机信号
连续时间和连续幅度的随机信号，如噪声信号。
高斯随机信号
服从高斯分布的随机信号，常用于描述自然界 的随机现象。
非高斯随机信号
不服从高斯分布的随机信号，如脉冲信号和干 扰信号。
常见的随机信号分析方法
自相关分析
用于分析信号的自身相关性和 平稳性。
频谱分析
通过对信号进行频域分析，得 到信号的频谱特性。
统计特性分析
对信号的均值、方差等统计特 性进行分析。
使用MATLAB进行随机信号分析的步骤
1
准备据
收集并整理所需信号的数据。
2
数据预处理
对数据进行去噪、归一化等预处理操作。
3
信号分析
运用MATLAB提供的工具进行信号分析和特征提取。
随机信号分析的应用领域
通信系统
用于优化信道传输和抗干扰能力的研究。
金融市场
用于分析股票价格、汇率等随机变动的特性。
生物医学
用于分析心电图、脑电图等生物信号。
气象预报
用于分析天气数据，提高气象预报的准确性。
总结
通过本课件，您了解了随机信号的定义、特性、分类以及分析方法，以及其在不同领域的应用。
《随机信号分析》PPT课 件
本课件将介绍随机信号分析的基本概念和方法，包括随机信号的定义、特性、 分类以及常见的分析方法。
分析随机信号的定义
1 随机信号
随机信号是不确定的信号，具有随机性和不可预测性。
2 随机过程
随机信号可以看作是随时间变化的随机过程。
3 概率论基础
随机信号的定义和性质可以通过概率论进行分析和描述。
随机信号的特性
1 均值和方差
随机信号的均值和方差是 表征其平均值和离散程度 的重要特性。
通信原理-第三章 随机信号分析
第三章随机信号分析随机过程平稳随机过程噪声随机过程通过系统3.1 随机过程通信过程就是信号和噪声通过系统的过程。
通信中信号特点：具有不可预知性——随机信号。
通信中噪声特点：具有不确定性——随机噪声。
统计学上：随机过程。
一、基本概念二、统计特性一、基本概念随机变量定义分布函数概率密度函数二维随机变量随机变量的数字特征数学期望方差协方差矩基本概念（续）随机过程设E是随机试验，S={e}是其样本空间，如果对于每一个e∈S，有一个时间t的实函数ξ(e,t) t ∈T与之对应，于是对于所有的e∈S，得到时间t的函数族。
该族时间t的函数称为随机过程，族中每个函数称为这个随机过程的样本函数。
ξ(t)={x(t),x2(t),……,x n(t),……}1x1(t),x2(t),……为样本函数基本概念（续）随机过程的一个实现每一个实现都是一个确定的时间函数，即样本。
随机过程其随机性体现在出现哪一个样本是不确定的。
随机过程没有确定的时间函数，只能从统计角度，用概率分布和数字特征来描述。
基本概念（续）二、统计特性概率分布数学期望方差协方差函数相关函数1.概率分布2.数学期望1[()](,)()E t xf x t dx a t ξ∞−∞==∫物理意义：表示随机过程的n 个样本函数曲线的摆动中心（平均值）3. 方差D(ξ (t )] = E{ξ (t ) − E[ξ (t )]} = σ (t )2 2物理意义：表示随机过程在某时刻t的取 值（随机变量）相对于该时刻的期望a(t) 的偏离程度4. 自相关函数R(t1 , t2 ) = E[ξ (t1 )ξ (t2 )] = ∫∞ −∞ −∞ 1 2 2∫∞x x f ( x1 , x2 ; t1 , t2 )dx1dx2物理意义：表示随机过程在两个时刻的 取值的关联程度， ξ(t)变化越平缓， 两个时刻取值的相关性越大，R值越大5.自协方差函数B(t1 , t2 ) = E{[ξ (t1 ) − a(t1 )][ξ (t2 ) − a(t2 )]} =∫ ∫−∞∞f 2 ( x1 , x2 ; t1 , t2 ) dx1dx2 x1 − a ( t1 ) ⎤ x2 − a ( t2 ) ⎤ ⎡ ⎡ ⎣ ⎦ ⎣ ⎦ −∞∞物理意义：表示随机过程在两个时刻间 的线性依从关系6.互协方差及互相关函数Bξη (t1 , t2 ) = E{[ξ (t1 ) − a (t1 )][η (t2 ) − a (t2 )]}Rξη (t1 , t2 ) = E[ξ (t1 )η (t2 )] = ∫∞−∞ −∞∫∞x1 y 2 f 2 ( x1 , y 2 ; t1 , t2 )dx1dy 23.2 平稳随机过程 定义 各态历经性 自相关函数 功率谱密度一、定义若随机过程的n维概率分布函数Fn ()和n维概 率密度函数fn ()与时间起点无关，则为平稳随 机过程 严平稳过程，狭义平稳过程f n ( x1 , x2 ,..., xn ; t1 , t2 ,..., tn ) = f n ( x1 , x2 ,..., xn ; t1 + τ , t2 + τ ,..., tn + τ )定义（续）a (t)Æa; σ2(t)Æ σ2; R(t1,t2)ÆR(τ) 一维分布与t无关： 二维分布只与τ有关 统计特性与时间起点无关 依据数字特征定义宽平稳过程，广义平稳过程二、各态历经性设x (t)是ξ(t)的任一实现，ξ(t)的统计平均= x (t)的 1 T2 时间平均 a=a = x (t ) dtlim T ∫T →∞−T2σ =σ22=lim ∫T →∞T →∞1 TT2 2−T[ x (t ) − a ] 2 dtR (τ ) = R (τ ) = lim1 T∫2 −T 2Tx (t ) x (t + τ ) dt意义 ： 随机过程中的任一实现都经历了随机过程的所有可能 状态。
第3章 随机信号的频域分析
RY (τ )dτ =∫
∞
3.2． 联合平稳信号互功率谱密度与互相关函数之间的关系
若 X (t ) ，Y (t ) 联合平稳，则 RXY (t , t + τ ) ↔ G XY (ω )
3‐ 3 / 4
∞ ⎧ ⎪ ⎪ G ω RXY (τ ) e − jωτ dτ = ( ) XY ∫ ⎪ −∞ 即⎪ ⎨ 1 ∞ ⎪ ⎪ R G XY (ω ) e jωτ dω τ = ( ) XY ⎪ ∫ −∞ ⎪ π 2 ⎩
2. 低通带限白噪声：
⎧ ⎪N 0 2 ω ≤ Ω / 2 功率谱密度：GX (ω ) = ⎪ ⎨ ⎪ ω >Ω/ 2 ⎪ ⎩0 1 ∞ ΩN 0 G X (ω ) e jωτ dω = ⋅ Sa (Ωτ / 2) 自相关函数： RX (τ ) = ∫ 2π −∞ 4π 3. 带通带限白噪声：
⎧ N ⎪ ⎪ 0 功率谱密度为G Y (ω ) = ⎪ ⎨ 2 ⎪ ⎪ ⎪ ⎩ 0
第三章 随机信号的频域分析
3.1 随机信号功率谱密度
1. 确知信号 f (t ) ：
f (t ) 傅氏变换---Æ频域 F (ω )
时间相关函数 R (τ ) 傅氏变换--Æ功率谱 Ps (ω ) （注：能量有限信号的时间相关函数 R (τ ) = ∫ 信号能量为：
E =∫
∞
∞ −∞
x (t )x * (t + τ )dt ）
RY (τ ) = E {Y (t )Y (t + τ )} = E {X (t )X (t + τ ) cos(ω0t + ω0τ + Θ) cos(ω0t + Θ)} ⎧1 ⎫ 1 = E {X (t )X (t + τ )} E ⎪ ⎨ cos(ω0τ ) + cos(2ω0t + ω0τ + 2Θ)⎪ ⎬ ⎪ ⎪ 2 ⎪2 ⎪ ⎩ ⎭ 1 = RX (τ ) cos(ω0τ ) 2
随机信号分析期末总复习提纲重点知识点
第 一 章1.1不考 条件部分不考△雅柯比变换 （随机变量函数的变换 P34） △随机变量之间的“不相关、正交、独立” P51 （各自定义、相关系数定义相互关系：两个随机变量相互独立必定互不相关，反之不一定成立 正交与不相关、独立没有明显关系 结合高斯情况）△随机变量的特征函数及基本性质 （一维的 P53 n 维的 P58）△ 多维高斯随机变量的概率密度和特征函数的矩阵形式、三点性质 P61()()()()()()()221()211222211,,exp 22exp ,,exp 22TTx m XX X X X n n XTT jUX X X X X n X MX M f x f x x U U u Q u j m Q u u E e jM U σπσμ---⎡⎤--⎢⎥==-⎢⎥⎢⎥⎣⎦⎡⎤⎡⎤⎡⎤⎢⎥=-==-⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦⎣⎦C C C另外一些性质： []()20XY XY X YX C R m m D X E X m ⎡⎤=-=-≥⎣⎦第二章 随机过程的时域分析1、随机过程的定义从三个方面来理解①随机过程(),X t ζ是,t ζ两个变量的函数②(),X t ζ是随时间t 变化的随机变量③(),X t ζ可看成无穷多维随机矢量在0,t n ∆→→∞的推广 2、什么是随机过程的样本函数？什么是过程的状态？随机过程与随机变量、样本函数之间的关系？3、随机过程的概率密度P74、特征函数P81。
（连续、离散）一维概率密度、一维特征函数 二元函数4、随机过程的期望、方差、自相关函数。
（连续、离散）5、严平稳、宽平稳的定义 P836、平稳随机过程自相关函数的性质：0点值，偶函数，周期函数（周期分量），均值 7、自相关系数、相关时间的定义 P88222()()()()()(0)()X X XX X X X X XXC R m R R R R τττρτσσ--∞==-∞=非周期相关时间用此定义（00()d τρττ∞=⎰）8、两个随机过程之间的“正交”、“不相关”、“独立”。
随机信号分析基础图文 (4)
(4-6)
第四章 随机信号的频域分析
4.1.2
1. 能量信号s(t)的自相关函数的定义为
Rs
s
t
s
t
dt
,
(4-7)
第四章 随机信号的频域分析
自相关函数反映了一个信号与时间延迟τ后的同一信号 间的相关程度。 自相关函数Rs(τ)与时间t无关， 只和时间差 τ有关。 当τ=0时， 能量信号的自相关函数Rs(0)等于信号的 能量E：
第四章 随机信号的频域分析
同样， 两个能量信号的互相关函数 Rs1s2 与其互能量
谱密度 Es1s2 f 也构成一对傅里叶变换， 即满足：
Es1s2
R s1s2
e j d S1*
S2
(4-27)
Rs1s2
1 2π
E s1s2
ej d
(4-28)
第四章 随机信号的频域分析
若我们仍希望用连续的功率谱密度来表示周期信号的功
率， 可以引入δ函数将式（4-35）表示为
第四章 随机信号的频域分析
P 1
T0
T0 2 s2 (t)dt
T0 2
1 2π
n =-
Cn
2
n0
d
因此， 定义周期信号s(t)的功率谱密度为
(4-37)
Ps
1 2π
n =-
Cn
2
n0
第四章 随机信号的频域分析
第四章 随机信号的频域分析
4.1 确知信号分析 4.2 随机信号的功率谱密度 4.3 互功率谱密度 4.4 随机信号的带宽 4.5 高斯白噪声与带限白噪声
第四章 随机信号的频域分析
4.1 确知信号分析
4.1.1
对于确知信号， 根据能量是否有限， 可将其分为能量 信号和功率信号两类。 在通信理论中， 通常把信号功率定 义为电流或电压信号在单位电阻(1 Ω)上消耗的功率， 即归 一化功率P。 因此， 功率就等于电流或电压的平方：
随机信号分析第一章
02
随机信号的统计描
述
概率密度函数
定义
概率密度函数（PDF） 是描述随机信号在各个 时刻取值概率分布的函 数。
性质
概率密度函数具有非负 性、归一化性质，即概 率密度函数在全域上的 积分等于1。
计算方法
可以通过直方图法、核 密度估计法等方法计算 概率密度函数。
概率分布函数
定义
概率分布函数（CDF）是描述随机信号取值小于或等 于某个值的概率的函数。
随机信号的特性
统计特性
随机信号的统计特性包括均值、 方差、概率分布等，这些特性描 述了信号的平均行为和不确定性 。
时间特性
随机信号的时间特性包括自相关 函数、互相关函数、功率谱密度 等，这些特性描述了信号在不同 时间点的相关性以及频率成分。
随机信号的应用
通信
在通信领域，随机信号可用 于扩频通信、无线通信等领 域，以提高通信的抗干扰能 力和保密性。
05
随机信号的采样定
理
采样定理的内容
采样定理定义
对于一个时间连续的模拟信号，如果以不高于其最高频率分量的频 率进行采样，则可以无失真地恢复原始信号。
采样定理的数学表达式
如果信号的最高频率为Fmax，则采样频率应不小于2Fmax。
采样定理的意义
采样定理是数字信号处理的基础，它确保了从离散样本中能够准确 重建原始信号。
雷达与声呐
在雷达与声呐领域，随机信 号可用于目标检测、测距、 定位等方面，以提高探测的 精度和可靠性。
地球物理学
在地球物理学领域，随机信 号可用于地震勘探、矿产资 源探测等方面，以揭示地球 内部结构和物质分布。
金融与经济
在金融与经济领域，随机信 号可用于股票价格分析、市 场预测等方面，以揭示市场 动态和经济发展趋势。
随机信号分析课件
谱密度函数
谱密度函数描述了随机信号的频率成分。
通过谱密度函数，可以了解信号在不同频率下的强度分布。
04
随机信号的频域分析
傅里叶变换
傅里叶变换的定义
傅里叶变换是一种将时间域信号转换为频域信号的方法， 通过将信号分解为不同频率的正弦波和余弦波的线性组合， 可以更好地理解信号的频率成分。
功率谱密度的计算
功率谱密度可以通过傅里叶变换的模平方得到， 也可以通过相关函数得到。
功率谱密度的应用
功率谱密度在信号处理中用于频域滤波、噪声抑 制、频率估计等方面。
滤波器设计
滤波器的分类
滤波器可以分为低通滤波器、高通滤波器、带通滤波器和带阻滤波 器等类型，不同类型的滤波器具有不同的频率响应特性。
滤波器的设计方法
傅里叶变换的性质
傅里叶变换具有线性性、时移性、频移性、共轭性、对称 性等性质，这些性质有助于简化信号处理和分析的过程。
傅里叶变换的应用
傅里叶变换在信号处理、通信、图像处理等领域有着广泛 的应用，例如频谱分析、滤波器设计、调制解调等。
功率谱密度
功率谱密度的定义
功率谱密度是描述随机信号频域特性的重要参数， 它表示信号功率随频率的分布情况。
04
通信
在通信领域中，随机信号分析 用于信道容量评估、信噪比估
计、误码率分析等方面。
雷达
在雷达领域中，随机信号分析 用于目标检测、跟踪和成像等
方面。
地球物理学
在地球物理学领域中，随机信 号分析用于地震勘探、矿产资
源评估等方面。
金融
在金融领域中，随机信号分析 用于股票价格波动分析、风险
评估等方面。
02
第三章_随机信号的频域分析
G ( ) R ( )e j d X X 换对，即 1 RX ( ) GX ( )e j d 2
维纳—辛钦定理给出了平稳随机信号 X t 的时域特性和频域特性之间的联系，也是分 析平稳随机信号的一个最重要最基本的公式。 由于平稳随机信号 X t 的自相关函数 RX
《随机信号分析基础》第三章：随机信号的频域分析
第1页
共 10 页
第三章
随机信号的频域分析(4 课时)
对确定信号可以采用傅立叶变换工具来实现确定信号的频域分析， 得到频谱分布。 对随 机信号是否也能应用傅立叶变换呢？随机信号也有频谱概念？在一般意义下， 信号持续时间 无限，故能量无限，因此多考虑单位时间内的能量即功率(功率有限)，因此主要考虑平均功 率在频域上的分布 功率谱密度(Power Spectral Density, PSD)。功率谱密度指“单位带 宽上的平均功率”。 3.1实随机信号（分析）的功率谱密度 【确知信号频域分析补充】★ 1．信号分析中信号的分类 信号 s t 的能量 E
是 的偶函数 RX RX
所以 GX GX —— GX 也是 的偶函数。
G ( ) 2 R ( ) cos d 0 X X 因此维纳—辛钦公式（定理）又可写成 1 RX ( ) GX ( ) cos d 0
W
rad / s 或 P f lim
T
1 2 ST ( f ) 2T
W
Hz
其中 ST ( ) 或 ST ( f ) 为功率信号 s t 的截短（断）信号 ST (t ) 的傅里叶变换。 【说明】 ①功率谱密度用 P 或者 P f 更为通用，但课本采用 G 或者 G ( f ) 来表示。 ②信号的功率谱密度函数是指这样的频率函数： 对其在整个频率范围内进行积分以后， 就是 信号的总功率；它描述了信号功率在各个不同频率上分布的情况。
通信原理(第二版)第2章确知信号与随机信号分析
信号分析
目录
• 确知信号分析 • 随机信号分析 • 确知信号与随机信号的应用 • 信号分析的现代方法
01
确知信号分析
定义与分类
定义
确知信号是指在任何时刻都已知 其全部信息的信号，如正弦波、 方波等。
分类
连续信号和离散信号，周期信号 和非周期信号，实信号和复信号 等。
小波变换具有多分辨率分析的 特点，能够适应不同频率的信 号处理需求。
小波变换在信号降噪、特征提 取、模式识别等领域有着广泛 的应用。
神经网络在信号分析中的应用
神经网络能够通过学习自动提取信号 中的特征，具有很强的自适应性。
神经网络在语音识别、图像处理、雷 达信号处理等领域有着广泛的应用。
神经网络可以处理非线性信号，对于 一些难以用传统方法处理的复杂信号 非常有效。
随机信号的时域分析
自相关函数
描述随机信号取值在时间上的相关性。
互相关函数
描述两个随机信号在时间上的相关性。
谱估计
通过时域数据估计随机信ห้องสมุดไป่ตู้的功率谱密度的方法。
03
确知信号与随机信号的应 用
确知信号在通信中的应用
载波信号
用于调制信息信号，实现信息的 传输。
脉冲信号
用于数字通信中表示二进制状态， 如脉冲编码调制（PCM）。
确知信号的频域分析
01
02
03
傅里叶级数
将确知信号表示为无穷多 个正弦波的叠加，每个正 弦波具有不同的幅度、频 率和相位。
频谱密度函数
描述信号中各频率分量的 强度，通常用图形表示， 即频谱图。
频谱分析
通过频谱图分析信号中各 频率分量的特性，如频率 范围、幅度和相位等。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1 GX ( ) lim E[| X T ( ) |2 ] T 2T
故而 GX 的实函数 X ( ) G X ( )
由式3-12也可以看到， | X T ( ) | 是 的实函数，
2
故 G X ( ) 也必定为 的实函数。
2 m a 2 m2 2 m2 ... a0 G X ( ) G0 2 n b2 n 2 2 n 2 ... b0
则必定满足：
G0 0 ①由性质(1)要求： ②由性质(4)要求：式中分母无实根(即在实轴上无极点)，且 n m。
例3.1 判断下列函数中，哪些能是平稳过程的功率谱密度？
当
当
[ s (t )]2 dt 时， s(t)是 能量有限信号，
x 2 (t ) dt 时，X(t)是 能量无限信号。 X(t)能量在频
1 lim T 2T
域上的分布(能量谱)不存在，但是：
T
T
x 2 (t ) dt
X (t) 的平均功率是有限的，可以讨论X (t) 平均功率在频域上分布。
f 3 ( )
3.1.2 平稳过程的功率谱密度与自相关函数的关系 一、维纳—辛钦定理 对于一般随机过程X(t)： G X ( )
R X (t , t )e j d
若 X(t)是平稳过程 则有： R X (t , t ) R X ( )
R X (t , t ) R X ( ) R X ( )
2
即有：
1 [s(t )] dt 2
2
2 | S ( ) | d ←帕赛瓦尔定理
2
由于左边是：s(t)在时间 ( , ) 上的总能量＝ | S ( ) | 在整 2 个频域上的积分。因此 | S ( ) | ←表示 s(t) 在不同频率上总 能量的分布密度，称为：能量谱密度。
第三章 随机信号的频域分析
§3.1 实随机信号的功率谱密度 确定信号的频谱（回顾） 首先对确定性时间信号的傅立叶变换作一下简单回顾。 设s(t)是时间(0~T)上的“非周期”信号，其傅立叶变换存在的 条件是： ⑴. s(t)在 ( , ) 范围内满足狄利赫利条件。 (s(t)只有有限个极值点和有限个第一类间段点。) ⑵.
a .s
4、各态历经过程的功率谱密度 若过程 X(t) 的平均功率和 其样本函数的平均功率
a .s
1 P GX ( )d 2 － 1 P Gk ( )d k 2 －
由X(t)的各态历经性，P Pk 因此有
a.s
1 2 GX () Gk () lim X kT () T 2T
k 不同由于样本函数 xk (t)不同， Pk 也不同。
相对所有试验结果 来讲，所有样本的平均功率 Pk 的总体
P 就是一个随机变量。
2 1 T 2 1 P X (t )dt lim XT ( ) d lim T 2T －T T 4 T 其中X(t)是随机过程，XT () XT (, )是随机过程的截取函数的频谱
f 1 ( ) cos 3
1 f 2 ( ) ( 1) 2 2
2 1 f 3 ( ) 4 2 5 6
解：因为
2 4 f 4 ( ) 4 4 2 3
f 1 ( ) 0
f 2 ( )
f 4 ( )
所以只有
非偶 在实数轴上有极点， 满足平稳过程功率谱密度的性质。
| s (t ) |dt
（绝对可积）
或
2 | s ( t ) | dt （信号的总能量有限）
若s(t)满足上述条件，则其傅立叶变换对存在。
S ( ) s (t )e jt dt F [ s (t )].................. （正变换）
(3). 功率谱密度是 的偶函数
G X ( ) G X ( )
根据傅立叶变换的性质，当
xiT (t) 为 t 的实函数时，其频谱满足
X iT ( ) X iT ( ) X iT ( ) X iT ( ) 则随机过程截断后的频谱为 X T ( ) X T ( ) X T ( ) X T ( )
xkT (t )
xk (t ),| t | T xkT (t ) 0,| t | T
称 xkT (t ) 为 满足绝对可积条件， 其傅立叶变换存在。
T
0 T
t
x(t ) 的截断函数。当T为有限值时，截断函数 xkT (t )
xkT (t ) dt
T
T
xkT (t ) dt
即各态历经过程 X(t) 的功率谱密度 GX ( )与其样本函数的功率 谱密度 Gk ( ) 以概率1 相等。
5 、实随机过程功率谱密度的性质 功率谱密度是随机过程在频域中主要的统计特征。 (1). 功率谱密度为非负值 由定义式3-12
2 | X ( ) | 0 因为 T
G X ( ) 0
二、实随机信号的平均功率 随机过程的任意一个样本函数，都不满足傅立叶变换的绝对 可积条件，直接对随机过程进行傅立叶变换不可能。但是对其样 本函数作某些限制后，其傅立叶变换存在。 最简单的是应用截断函数。如右图所示： x 在 xk (t) x(t, k ) 中任意截取长为2T的一段
k (t )
2 x 若 x (t ) 代表一噪声电压（或电流），则 －T k (t )dt 表示噪 k
1 2 2 － xkT (t )dt －T xk (t )dt 2
T
X kT ( ) d
T
2
声的一个样本在时间（-T,T）内消耗在1欧姆电阻上的总能量。 若对此总能量在(-T,T)上求时间平均，并求极限
1 T 1 2 2 P E[P E[ X (t )]dt lim E[ XT ( ) ]d ] lim T 2T －T T 4 T
若对 P 取统计平均，得确定值：
P ←通常称为随机过程X(t)的平均功率。
三、功率谱密度 1 、实随机过程的功率谱密度 由于随机过程X(t)的平均功率：
2、平稳过程的平均功率
GX ( )d
2 E [ X (t )] R (0)与“t”无关， 若X(t)为平稳过程，其均方值
则其时间平均 P E[ X 2 (t )] R (0) R (0) 所以平稳过程的平均功率：
P R (0)
3、各态历经过程的平均功率 由于各态历经过程X(t)的每个样本函数的时间平均都以概率1 相 同，与 无关，则可推出：
1 s (t ) 2
S ( )e jt d F 1 [ S ( )]....... （反变换）
其中S(w)称为信号s(t)的频谱，它反映了s(t)中各种频率成分 的分布状况。 可以证明：对一般实信号s(t)，其频谱是w的复函数， 即
S ( ) S ( ) ，（“*”表示复共轭）。
由于s(t)是 (0~T)上的“非周期”信号， s ( t ) dt 绝对可积，所以频谱存在。
T
0
s ( t ) dt
而随机过程样本函数持续的时间是无限的，因为 t→∞， 若：
x (t ) dt ←非绝对可积
则样本函数的频谱不存在。此时随机过程的频谱不存在。
(4)、平稳过程功率谱密度绝对可积：
G X ( )d
证明：因为平稳过程有 R (0) E[ X 2 (t )]
1 且平稳过程有 P E[ X (t )] 2
2
GX ( )d
所以功率谱密度函数绝对可积。 (5)、若平稳过程的功率谱密度可以表示为 的有理函数形式
G ( ) R ( )e j d F R ( ) X X X 有： 1 j 1 RX ( ) G ( ) e d F GX ( ) X 2 因为X(t) 平稳 R X ( )，G X ( )是偶函数。 G ( ) 2 R ( ) cos d X X 0 则有： 1 R X ( ) 0 G X ( ) cos d
P lim
k T
T
－T
xk 2 (t )dt 2T
Pk 表示随机过程的样本函数 xk (t) 消耗在1欧姆电阻上的平均功率
2 1 lim X kT ( ) d T 4 T
Pk 称为随机过程样本函数 xk (t ) 的平均功率（时间平均） 。
由于对一次试验结果 k 来讲， 对应的样本函数xk (t ) 是个确定函 数，因此这个平均功率 Pk 仅是一个确定值。 对于不同 K，由于
1 P lim T 2T
1 －T X (t, )dt Tlim 2T
T 2 a. s
T
－T
xk 2 (t )dt Pk 常数
P E [ P ] E [ Pk ] Pk 即各态历经过程 X(t) 的平均功率 P 与其样本函数的平均功率 Pk
以概率1 相等。
1 1 2 GX ( ) lim E | X ( ) | lim E X T T ( ) X T ( ) T 2T T 2T 1 lim E X ( ) X T T ( ) G X ( ) T 2T
1 T 1 1 2 2 P lim E[ X (t )]dt lim E[ XT ( ) ]d T 2T T 2 T 2T 1 GX ( )d 2 是 GX ( ) 在整个频域上的积分，则被积函数 GX ( ) 表示随机过程