数学物理方法仿真
数学物理方法之计算机仿真示例
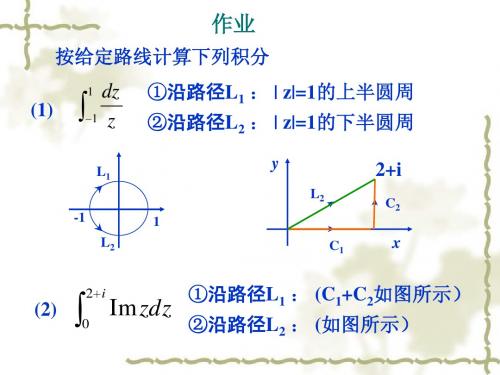
(1)
x 2y
2
1 2 0
y : 0 1
2 2 2 2 2
l
z dz (4 y y )d (2 y) 4 y dy i[4 y d (2 y) (4 y y )dy]
(2 11i ) / 3
例2:计算积分
z
l
2
2
dz
y
i
O
A
分别沿路径(1)和(2) )
x
2 2
z x y i 2 xy
2 2
2 2 l
(2) B 2
z dz
( x y )dx 2 xydy i[2 xydx ( x y )dy]
y0
2 2
(2) OB :
2
x:0 2
1
BA :
1
x2
2
y : 0 1
z dz x dx (4 y)dy i (4 y )dy
C
( u iv )( dx idy )
C
C
( udx vdy ) i ( vdx udy )
C
即一个复积分等价于两个二元的实的曲线积分
2.复积分的计算
方法: ①按定义,分割,作和,取极限
②将积分化为实积分 【例1】求积分
I
Re
L
zdz
y ①直线: 0—(1,1) 1+i L1 ②折线:0—(1,0) —(1,1) 0 L3 x
2 2
W1 z W2 z
1/ 2
[cos(
2
) i sin(
2
)]
物理仿真计算方法及实践

物理仿真计算方法及实践随着科技的进步,计算机模拟和仿真已经成为现代科学研究不可缺少的工具,涉及的领域包括物理、生物、化学、工程学等,广泛应用于科研、工业制造、医疗等领域。
而在其中,物理仿真计算技术显得尤为重要,能够精确模拟和解决一系列问题,同时还可以节省大量的时间和经费。
物理仿真计算方法的原则是模拟现实世界中的物理规律和现象,将其转化为数学模型,再通过计算机程序运算来求解。
最终得到的结果可以为科学家、工程师和其他专业人士提供有价值的信息和指导。
在实际应用中,物理仿真计算可以包括多个计算领域,例如流体力学、结构力学、电磁学、动力学等,并且可以应用于多个设备平台,例如计算机、移动设备和云计算。
物理仿真计算方法的实践正在不断推进和发展,目前已经有了许多成熟的模拟和计算工具,例如有限元方法(FEM)、有限体积法(FVM)、元胞自动机模拟(CA)等。
其中,有限元方法是目前最常使用的一种仿真计算工具,主要应用于工程设计和建筑施工领域。
该方法采用数学方程和物理方程,可以对各种复杂的力学问题进行计算,例如材料力学、热力学、电场和磁场问题等。
有限体积法则是最常见的流体力学计算方法之一,主要应用于气流风格、水流、火焰燃料等流体的模拟和计算。
此外,元胞自动机模拟工具则主要应用于自然界的生态系统、社会网络和生物学等领域,可以将一个大系统看成一个个细胞,并对其进行计算、处理和模拟。
物理仿真计算方法的实践应用已经得到了广泛的应用,例如在制造业方面,可以利用物理仿真计算模拟零部件的生产、运输和装配过程,从而得出最佳的生产方案,并实现生产线的自动化;在医疗方面,物理仿真计算可以帮助医生做出更为准确的诊断结果和手术方案,同时还可以节省手术时间和风险;在城市规划方面,物理仿真计算可以帮助规划者了解城市的运行情况、能源利用和环境影响情况,从而制定出最佳的城市规划和发展策略。
总的来说,物理仿真计算方法在当今各个领域的发展应用是不可避免的。
数学物理方程三维可视化仿真——《数学物理方法》课程实践

义。 二、 光 子 晶体 电磁理 论 基础
在倒 易 空 间 中 , r、 T 、 N 、 x 和M 等点 为 布里 渊 区 的高对 称点 , 它们所构成 的多边形区域 ( 深灰色部分)称为不可 约 布里 渊 区。 不可 约布 里 渊 区是 倒 易空 间 中最 小 的 、可 重 复 的 区域 ,可 以 映射 出 电磁 波 在整 个 光 子 晶 体 中 的传 输 特 性 。 对 称 点 坐 标 分 别 为 : r= ( 0 , 0 ) , T = 卫 ( 1 ,
【 探 索与实践 】
数学物理 方程三维 可视化仿真
— —
《 数 学物理方法》 课程 实践
萍, 杨华军 , 何文森 , 罗志华
物理 电子 学 院 , 四川 成都 6 1 0 0 5 4 )
江
( 电子科 技 大学
摘 要 :数 学 物理 方 程 三 维 可视 化仿 真 及 创 新 实践 训 练是 《 数 学 物 理 方 法》教 学模 式 改 革 中的 重 要 内容 。本 文通 过 MA T L A B 程 序 求解 二 维 菱形 晶格 光 子 晶体 的 电磁 场本 征值 方程 , 绘 制 出二 维 能 带 曲线 , 并将 结 果 三 维可视 化 , 体 现 出复杂 数 学 物理 问题 的物 理 图像 , 解 决 大学 生在课 程 学 习过程 中理解 困难 的教 学 问题 , 加 强 大 学生 编程 实践 能 力和 创新 能 力 的培
e c t g 0 e y. b : e 。
改革 中的重要 内容 。利用M A T L A B 数值求解数学物理方 程, 将传统教学手段 与计算机仿真教学相结合 改变只用 公式符号教学 的模式【 l l , 令学生对复杂 、 抽象 、 烦琐的数学 物 理 问题具 有更 深 刻 的理解 。 本论 文 旨在 进行 数 学物 理方 程仿 真 求解 实 践训 练 , 着 力培 养 大学 生应 用 数学 物 理思 想 解决 实 际 问题 的能 力 。 本着“ 重 理论 、 强实 践 、 突 创新 ” 的教 育理念 , 结合科技前沿 , 以光子 晶体 的电磁场理论作为实 践 内容 , 利用 M A T L A B 对 复 杂 的 电磁 场本 征 值 问题 进 行 计 算 机 仿 真 求解 , 将 结 果 三维 可 视 化 , 以 此来 展 现 复 杂 电 磁
电子课件 [数学物理方法与仿真(第3版)][杨华军][电子教案(PPT版本)]chapter22
![电子课件 [数学物理方法与仿真(第3版)][杨华军][电子教案(PPT版本)]chapter22](https://img.taocdn.com/s3/m/abb24fad31126edb6e1a105c.png)
凡是 “%”后的语句为解释语句,MATLAB不执行)
(1)题目定义
g='squareg';
% 定义单位方形区域
b='squareb3';
% 左右零边界条件,顶底零导数边界条件
c=1;a=0;f=0;d=1;
(2)初始的粗糙网格化
[p,e,t]=initmesh('squareg');
(3)初始条件
22.1 用偏微分方程工具箱求解微分方程
直接使用图形用户界面(Graphical User Interface,简记作GUI)求解.
例 22.1.1 解热传导方程 ut u f
边界条件是齐次类型,定解区域自定。
计算机仿真
【解】 第一步:启动MATLAB,键入命令pdetool并回
车,就进入GUI.在Options菜单下选择Grid命 令,打开栅格.栅格使用户容易确定所绘图形的 大小. 第二步:选定定解区域 本题为自定区域 :自拟定解区域如图22.1所 示:E1-E2+R1-E3.具体用快捷工具分别画椭 圆E1、圆E2、矩形R1、圆E3.然后在Set formula栏中进行编辑并用算术运算符将图形对 象名称连接起来. (或删去默认的表达式,直接键入E1-E2+R1-E3)
2.动画图形显示 为了将所得的解形象地表示出来,还要通过一些动画图形命 令.为了加速绘图,首先把三角形网格转化成矩形网格.调用形 式如下: (1)uxy=tri2grid(p,t,u1,x,y) p、t是描述三角形网格的矩阵,x、y是求解区域中矩形网格的坐 标点(矩阵x、y必须都是递增顺序),u1是各时刻三角形网格中 的解.输出矩阵uxy是用线性插值法在矩形网格点上得出的相应u 值. (2) [uxy,tn,a2,a3]=tri2grid(p,t,u,x,y) uxy、p、t、u、x、y意义同上,tn是格点的指针矩阵,a2、a3是内 插法的系数. (3) uxy=tri2grid(p,t,u,tn,a2,a3) 用此命令之前,应先用一个tri2grid命令得出矩阵tn、a2、a3.用此 方法可以加快速度.
二、《数学物理方法与计算机仿真》习题解答

(2) uxx − 2uxy − 3uyy + 2ux + 6uy = 0
(3) uxx + 4uxy + 5uyy + ux + 2uy = 0
【答案
(1) ξ
=
x−
y,η
=
x, uηη
+
c
− a
b
uξ
+
b a
uη
+
1u=0 a
(2)ξ = x − y,η = 3x + y; 4uξη − uξ + 3uη = 0
0,ux (l,t)
=
F0
sin ωt Ys
;u(x, 0)
=
0,ut (x, 0)
=
0】
9.6 有一均匀细杆,一端固定,另一端沿杆的轴线方向被拉长 ε 而静止(设拉长在弹性限
度内).突然放手任其振动,试推导其其纵振动方程与定解条件.
【答案
utt
− a2uxx
=
0; u (0, t )
=
0=
ux (l,t);u(x, 0)
【答案 取 x 沿槽的长度方向, u 为水的质点的 x 方向位移,则 utt = ghuxx 】 9.11. 有一长为 l 的均匀细弦,一端固定,另一端为弹性支撑,设弦上各点受有垂直于平衡位置
的外力,外力线密度已知,开始时.弦 1 处受到冲量 I 作用,试写出其定解问题. 2
⎧ ∂ 2u
⎪ ⎪
∂t
2
【答案(1)
u
=
−α
e2
x− β 2
y
v,
v xx
+ v yy
+ (γ
物理实验技术中的数据模拟与仿真方法

物理实验技术中的数据模拟与仿真方法概述:物理实验技术是科学研究中不可或缺的一环,而数据模拟与仿真方法是实验技术中的重要工具。
本文将介绍物理实验技术中的数据模拟与仿真方法,并探讨其在实验设计、数据分析和结果验证等方面的应用。
一、数据模拟方法数据模拟是指通过建立数学模型,使用计算机程序生成与实际实验相似的数据。
数据模拟方法基于物理原理和统计学理论,能够帮助研究人员预测实验结果、设计实验方案和优化实验条件。
1. 数学模型建立在数据模拟中,首先需要根据实验对象和研究目的建立相应的数学模型。
数学模型可以是物理模型、化学模型或统计模型等,通过对现象和过程进行抽象和描述,可以量化实验中的因变量和自变量关系。
2. 计算机程序设计建立数学模型后,需要编写计算机程序来实现模拟过程。
计算机程序可以通过数值计算、数学推理或随机抽样等方法,基于模型的输入变量生成对应的输出值。
3. 参数调节与模型验证在数据模拟过程中,需要通过逐步调整模型中的参数,以使模拟结果更好地符合实际实验数据。
同时,还需要进行模型验证,即将模拟结果与实际实验数据进行比较,评估模型的准确性和可靠性。
二、数据仿真方法数据仿真是指通过计算机模拟物理实验过程,生成与实际实验相似的数据。
与数据模拟不同,数据仿真是通过模拟整个实验过程中的影响因素和变化规律,从而得到实验数据。
1. 数值计算方法数值计算方法是数据仿真中常用的一种方法。
它通过运用数值计算算法和数学模型,模拟实验对象在不同环境和条件下的物理行为,从而得到与实际实验相一致的数据。
2. 实验设备模拟对于一些复杂的实验设备,数据仿真可以通过建立设备的物理模型和运动模型,模拟实验设备在不同状态下的行为,进而生成实验过程中的相关数据。
3. 条件优化和结果分析通过数据仿真,研究人员可以对实验条件进行优化,找到最佳的实验参数和操作策略。
此外,还可以通过对实验数据的分析,得出实验结果的统计规律和趋势,为实验设计和结果验证提供支持。
电子课件 [数学物理方法与仿真(第3版)][杨华军][电子教案(PPT版本)]chapter11
11.3.2 达朗贝尔公式的物理意义 由上面的讨论我们得到了自由弦振动泛定方程 的通解(11.3.4)为
u(x,t) F1(x at) F2(x at)
即定解问题的解可以表示为两个函数 F1(x at), F2(x at) 之 和,而这两个函数的具体形式完全由初始条件来确 定.为了阐述达朗贝尔公式的物理意义, 实际上只需 阐明这两个函数 F1(x at), F2(x at) 的物理意义就行了.
u(x,t) 1 [(x at) (x at)] 1
xat
( )d
2
2a xat
(11.3.9)
当函数(x) 是二次连续函数,函数 (x) 是一次连续可微
的函数时,(11.3.9)式即为无界弦自由振动定解问题的
解,表达式(11.3.9)称为达朗贝尔(D.Alembert)公式.
无界弦自由振动定解问题的解称为达朗贝尔解.
uut(t
a x,0)
2u
xx
0, 0 x x,ut x,0
x,
0
x
u0,t 0
(13.4.4) (13.4.5) (13.4.6)
由于端点固定,所以有u(0,t) 0. 为了使用无界的达
朗贝尔公式,故需要把半无界问题延拓为无界问题来
处理,即必须把 u(x,t) 、 (x) 和(x) 延拓到整个无界区
假设方程的行波解具有下列形式
u(x, y) F(y x)
(11.2.2)
代入方程即得
a2F(y x) bF(y x) cF(y x) 0
需要求方程的非零解,故
F(x x) 0
a2 b c 0
(11.2.3)
(i) b2 4ac 0,对应于双曲型方程,式(11.2.3)有两
电子课件 [数学物理方法与仿真(第3版)][杨华军][电子教案(PPT版本)]chapter13
(l 2m) a1
将它们代入解的表达式中,得到勒让德方程解的形式
y(x)
a0[1
l(l 1) 2!
x2
l(l
2)(l 1)(l 4!
3)
x4
]
a1[ x
(l
1)(l 3!
2)
x3
(l
1)(l
3)(l 5!
2)(l
4)
x5
=pl (x) ql (x)
] (13.1.7)
其中 pl (x) , ql (x) 分别是偶次项和奇次项组成的级数,当 l 不是整数 时, pl (x) , ql (x) 都是无穷级数,容易求得其收敛半径均为 1,而且
关于线性二阶常微分方程在常点邻域上的级数解,有 下面的定理.
定理 13.1.1 若方程(13.1.1)的系数 p(z) 和 q(z) 为点 z0 的
邻域 z z0 R 中的解析函数,则方程在这圆中存在唯一的
解析解w(z) 满足初始条件w (z0 ) C0 ,w(z0 ) C1 ,其中 C0 、
(即要求在有界解的情况下)求解,则勒让德方程的解 只有第一类勒让德函数即勒让德多项式 Pn (x) .因为第
二类勒让德函数 Qn (x) 在闭区间[1,1] 上是无界的.
13.1.3 奇点邻域的级数解法:贝塞尔方程的求解
前一章分离变量法中,我们引出了贝塞尔方程,本节
我们来讨论这个方程的幂级数解法.按惯例,仍以 x
C1 是任意给定的复常数.
15.1.2 常点邻域上的幂级数解法 勒让德方程的求解
(注明:推导解的过程仅供了解求解的方法,读者可直接参考其结论)
由分离变量法得到了勒让德方程,下面讨论在 x0 0 邻域上求解 l 阶勒让德方程
物理仿真技术的使用教程
物理仿真技术的使用教程物理仿真技术是一种基于物理规律的数值计算方法,它可以模拟真实世界中的各种物理现象和行为,在科学研究、工程设计和教育培训等领域具有广泛的应用。
本文将为您介绍物理仿真技术的使用教程,帮助您快速上手并运用到自己的工作中。
一、了解物理仿真技术的基础知识在开始使用物理仿真技术之前,我们需要了解一些基础知识。
首先是物理规律的理解,包括牛顿力学、电磁学、热力学等方面的知识。
这些知识将帮助您理解物体的运动规律、相互作用以及能量转化等基本原理。
其次是学习一种常见的物理仿真软件,比如Ansys、COMSOL Multiphysics等。
这些软件提供了丰富的模型库和工具,能够帮助您进行复杂的物理仿真计算。
选择一款适合您领域需求的软件,并学习其使用方法是非常重要的。
二、准备数据和模型在进行物理仿真之前,需要准备相应的数据和模型。
数据包括材料性质、初始条件、外部边界条件等。
模型是指构建物体的几何结构和属性。
根据所需仿真目标的不同,您可以选择使用已有的模型进行修改,或者自己从头开始构建模型。
对于材料性质,您需要收集相关的物理参数,比如密度、弹性模量、热导率等。
对于初始条件和边界条件,您需要确定物体的初始状态和与外界的交互方式。
这些条件将直接影响到仿真结果的准确性和可信度。
三、进行仿真计算在准备好数据和模型之后,就可以开始进行物理仿真计算了。
具体的操作步骤如下:1. 导入模型:将准备好的模型导入到物理仿真软件中,确保模型的几何结构和属性正确。
2. 网格划分:对模型进行网格划分,将模型划分为一系列小的单元。
网格的划分需要根据模型的复杂程度和仿真要求进行选择,一般来说,细致的网格划分可以提高仿真计算的精度,但同时也会增加计算的时间和资源消耗。
3. 设置物理属性:对模型的材料性质、初始条件和边界条件进行设置。
确保这些参数的准确性和合理性,以保证仿真结果的可靠性。
4. 运行仿真计算:根据所选择的仿真软件提供的方法和算法,运行仿真计算。
电子课件 [数学物理方法与仿真(第3版)][杨华军][电子教案(PPT版本)]chapter18
sech(x) 是钟形的正割双曲函数,其图形与浅水槽中观察到 的孤立波的形状相同.上述 KdV 方程的行波解(18.2.8)称为孤立 波解,从而在数学上证实了孤立波的存在.20 世纪 70 年代两 位美国科学家(Zabusky 和 Kruskal)用数值模拟证实了:两个相 对运动的孤立波在碰撞之后仍为两个稳定的,形状与碰撞前相 同的孤立波,仅仅相位发生了变化,也就是说两个孤立波的碰 撞类似于粒子之间的碰撞.这种孤立波具有类似粒子的性能, 因而这两位科学家将孤立波命名为“孤立子”(Solition).
3du d u 3c u
查积分表,可解得
(18.2.6)
Au
3du
3c u
1 ln c
3c 3c
3c u 3c u
(18.2.7)
其中 A 为积分常数.不妨设 A=0 (否则对 作平移), 则(18.2.7) 式可化简为
c
c
u 3c sech2 ( c ) 3c (e 2 e 2 )2 ,
现在来寻求方程(18.2.1)的平面前进波(简称行波)
解,令
x ct,u(x,t) u( )
(18.2.2)
其中c 是常数,将(18.2.2)式代入(18.2.1),得
cu uu u 0
对 积分一次得
cu
2
u2
u
A
( A 为任意常数)
用u 乘(18.2.3)式两边,并对 积分,得
的解为
u(
x,
y)
_____________________
.
uy (x, 0) 0
二.试用行波法求解右行波的初值问题 (20 分)
uut (x,a0u)x
0, ( (x)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
仿真实验
第一部分:计算机仿真在复变函数中的应用
仿真实验1: 绘出对数函数Ln z 的图形.
【Matlab 源程序】
z=cplxgrid(20); w=log(z); for k=0:3 w=w+i*2*pi;
surf(real(z),imag(z),imag(w),real(w)); hold on title('Lnz')
end
view(-75,30)
仿真实验2:若 (1,2,,)k z k n =⋅⋅⋅对应为10n
z -=的根,其中2n ≥且取整数.试用计算机
仿真编程验证下列数学恒等式 1
1()
1
0,
()
n
n
k k m m m k z z ==≠=-∑
∏
成立.
【Matlab 源程序】
n=round(1000*random('beta',1,1))+1 % n=input('please enter n=') su=1; sum=0; for s=1:n
N(s)=exp(i*2*s*pi/n); end
for k=1:n for s=1:n if s~=k
su=1/(N(k)-N(s))*su; end end
sum=sum+su; su=1; end sum
%仿真验证结果为:n =735 sum =2.2335e-016 -5.1707e-016i
仿真实验3: 对于复变函数sin ()z f z z
=
,用Mtlab 仿真计算极限0lim ()z f z →,1lim ()
z i f z →+.
【Matlab 源程序】
clear syms z
f=sin(z)/z; limit(f,z,0)
%仿真结果为ans=1 limit(f,z,1+i) %仿真结果为
ans=1/2*sin(1)*cosh(1)-1/2*i*sin(1)*cosh(1)+1/2*i*cos(1)*sinh(1)+1/2*cos(1)*sinh(1)
仿真实验5: 研究电偶极子(Diploe)所产生的电势和电场强度
【2】
.设在(,)a b 处有电荷q +,
在(,)a b --处有电荷q -.则在电荷所在平面上任何一点的电势为
011()
2πq V r r ε+
-
=
-,
其中
9
1,,910,
4πr r ε+-=
=
=⨯6
210
, 1.5, 1.5q a b -=⨯==-
【Matlab 源程序】
根据解析函数理论中求复势的方法,可由等势线求出电力线方程.
下面给出计算机仿真方法求解:仿真(MATLAB)程序和仿真结果
clear ;
clf;q=2e-6;k=9e9;a=1.5;b=-1.5;x=-6:0.6:6;y=x; [X,Y]=meshgrid(x,y);
rp=sqrt((X-a).^2+(Y-b).^2); rm=sqrt((X+a).^2+(Y+b).^2);
V=q*k*(1./rp-1./rm); % 计算电势 [Ex,Ey]=gradient(-V); %计算电场强度
AE=sqrt(Ex.^2+Ey.^2);Ex=Ex./AE;Ey=Ey./AE; %场强归一化
cv=linspace(min(min(V)),max(max(V)),49); %用黑
实线绘等势线
contour (X,Y,V,cv,'k-') %axis('square')
title('\fontname{宋体}\fontsize{22}电偶极子的场和等势线'),hold on quiver(X,Y,Ex,Ey,0.7) plot(a,b,'wo',a,b,'w+') plot(-a,-b,'wo',-a,-b,'w-')
xlabel('x'); ylabel('y'),hold off
说明:图21.5中黑实线代表等势线,箭头构成电力线.根据题中电荷的位置,不难看出图中右下方为正电荷,左上方为负电荷. 仿真实验6: 求积分 π6
i i
x1=ch3zdz; x2(1)d z
z e z
-=
-⎰⎰
.
【Matlab 源程序】
syms z
x1=int(cosh(3*z),z,pi/6*i,0) x2=int((z-1)*exp(-z),z,0,i) %仿真结果为:
x1 = -1/3*i x2 = -i/exp(i)
仿真实验7:求函数11
2
++z z 在奇点处的留数. 【Matlab 源程序】
[R,P,K]= residue ([1,0,1],[1,1])
%仿真结果为: R= 2 P = -1 K = 1 -1
图 21.5电偶极子的场和等势线
仿真实验8:求函数
22
2
(,)(2)x y xy
z f x y x x e---
==-在原点(0,0),以及(1,a)点处的
Taylor展式.
【Matlab源程序】
syms x y; f=(x^2-2*x)*exp(-x^2-y^2-x*y);
F=maple('mtaylor',f,'[x,y]',8) %在(0,0)点处的泰勒级数展开latex(collect(F,x))
syms a;
F=maple('mtaylor',f,'[x=1,y=a]',3); %在(1,a)点处的泰勒级数展开F=maple('mtaylor',f,'[x=a]',3); %对单变量展开, 且x=a
仿真实验8:求
1
()
f t
t
=
的Fourier变换.
【Matlab源程序】
syms t v
fourier(1/t)
%仿真结果为: ans = i*pi*(1-2*heaviside(w))
仿真实验9:求
3w
(w)w heaviside(w)
F e-
=的Fourier逆变换.
【Matlab源程序】
syms t u w
ifourier(w*exp(-3*w)*sym('Heaviside(w)'))
%仿真结果为: ans =1/2/(-3+i*x)^2/pi
仿真实验10:求
1
()
1
F s
s
=
-的Laplace逆变换.
【Matlab源程序】
syms s t w
F=ilaplace(1/(s-1))
%仿真结果为: F=exp(t)。
