空间角及其计算
空间角总结
空间角总结什么是空间角？空间角是几何学中的一个重要概念，用来描述两个向量之间的夹角。
空间角通常用希腊字母θ（theta）表示，其单位是弧度（rad）。
空间角的概念可以扩展到三维空间中，帮助我们描述物体之间的方向关系和位置关系。
空间角的特征空间角具有以下几个重要特征：1.空间角是无向角：空间角没有方向之分，只关注两个向量之间夹角的大小，与向量的起点和终点无关。
2.空间角的大小范围：空间角的取值范围是0到π（也就是0到180度）。
3.水平角和垂直角：当两个向量在同一平面内，夹角为水平角；当两个向量互相垂直，夹角为垂直角。
4.空间角的计算方法：可以使用余弦定理或向量的点积来计算空间角的大小。
空间角的计算方法余弦定理余弦定理是计算空间角的常用方法之一。
设有两个向量A和B，它们之间的夹角θ满足以下关系：cos(θ) = (A·B) / (|A| * |B|)其中，A·B表示向量A和向量B的点积，|A|和|B|表示向量A和向量B的模。
通过余弦定理，我们可以根据向量的数值计算出它们之间的夹角。
向量的点积另一种计算空间角的方法是使用向量的点积。
向量A·B的点积可以通过以下公式计算得到：A·B = |A| * |B| * cos(θ)其中，θ表示向量A和向量B的夹角。
通过这个公式，我们可以根据两个向量的点积来计算它们之间的夹角。
球面角与立体角除了空间角之外，还有两个相关概念：球面角和立体角。
球面角球面角是指由球心发出的射线与球面上两个端点所夹的角。
球面角的单位是球面度（sr），1球面度是球面上的一个单位面积所占的立体角。
球面角可以通过球面面积和球半径来计算。
立体角立体角用来描述三维空间中的角度，是由空间中一点发出的射线与空间中的两个向量所夹的角。
立体角的单位是立体度（steradian，sr），1立体度表示空间中的一个单位面积所占的立体角。
立体角可以通过空间角和距离来计算。
空间的角
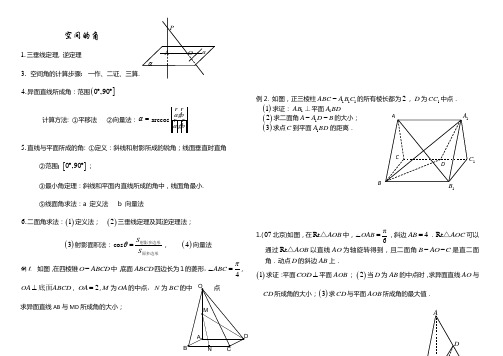
空间的角1.三垂线定理, 逆定理3. 空间角的计算步骤 一作、二证、三算.4.异面直线所成角：范围(]0,90︒︒计算方法: ①平移法 ②向量法：α=arccos a ba b5.直线与平面所成的角: ①定义：斜线和射影所成的锐角；线面垂直时直角②范围 []0,90︒︒；③最小角定理：斜线和平面内直线所成的角中，线面角最小. ⑤线面角求法：a 定义法 b 向量法6.二面角求法：()1定义法； ()2三垂线定理及其逆定理法；()3射影面积法：cos S S θ=射影多边形原多边形， ()4向量法例1. 如图，在四棱锥O ABCD -中，底面ABCD 四边长为1的菱形，4ABC π∠=,OA ABCD ⊥底面, 2OA =,M 为OA 的中点，N 为BC 的中点求异面直线AB 与MD 所成角的大小；例2. 如图，正三棱柱111ABC A B C -的所有棱长都为2，D 为1CC 中点．()1求证：1AB ⊥平面1A BD()2求二面角1A A D B --的大小； ()3求点C 到平面1A BD 的距离．1.(07北京)如图，在Rt AOB △中，π6OAB ∠=，斜边4AB =．Rt AOC △可以通过Rt AOB △以直线AO 为轴旋转得到，且二面角B AO C --是直二面角．动点D 的斜边AB 上．()1求证：平面COD ⊥平面AOB ； ()2当D 为AB 的中点时，求异面直线AO 与CD 所成角的大小；()3求CD 与平面AOB 所成角的最大值．αAPO aABCD1A1C1BOCADB。
空间角度
空间角度在机械零件加工中经常可以遇到具有空间角度的斜孔、斜面，在加工这些零件或设计这些零件夹具时，常常需要进行空间角度的计算。
因此，在这里就对空间角度的计算及应用进行讨论。
一、关于双斜线的空间角度计算在机械制图中我们把和三个投影面的位置都倾斜的直线叫做一般位置直线，在这我们称一般位置直线为双斜线。
1、双斜线的空间角度某斜孔零件如图所示，立体图剖切图从图中可以看到：斜孔和三个基本投影面都是倾斜的，但斜孔倾斜的方向和角度大小完全可以由斜孔轴线来表示，而斜孔轴线可看成是一般直线及双斜线，因此倾斜孔的空间角度问题就简化为双斜线的空间角度问题。
下面我们就来讨论双斜线的角度及角度代号。
1）、方向角为便于讨论，可把空间直线和三个投影面的关系抽象成一个长方体，双斜线就作为对角线，如图。
从图中可看出红色直线的方向可以由与投影轴之间的角度来确定。
直线与X轴、Y轴、Z轴的夹角通常用α、β、γ表示，称为方向角。
α表示双斜线与X投影轴之间的夹角。
β表示双斜线与Y投影轴之间的夹角。
γ表示双斜线与Z投影轴之间的夹角。
注意在这里所讨论的夹角都是双斜线与投影轴之间所夹的正锐角。
如图如果双斜线不通过原点，可以在直线上的任意点作三条线分别平行于X、Y、Z轴，这三条线与双斜线的夹角也是方向角。
如图2）、真实倾角从双斜线和三个投影面之间的几何关系看，双斜线和三个投影面之间存在着倾角，即线和面之间的倾角。
双斜线对投影面的倾角是可用双斜线和它在该投影面上投影之间的夹角表示。
双斜线与W （yz）面、V（xz）面、H（xy）面的夹角通常用α0、β0、γ0表示，称为真实倾角。
α0表示双斜线与W（yz）面的夹角。
β0表示双斜线与V（xz）面的夹角。
γ0表示双斜线与H（xy）面的夹角。
由下图可看出方向角和真实倾角之间的关系：α+α0=90°、β+β0=90°、γ+γ0=90°3）、投影角如图所示双斜线在三个投影面上的投影与投影轴之间的夹角也可反应空间直线的方向，我们把这些夹角称为投影角。
11.2.3 空间角的概念及其求法
11.2.3 空间角的概念及其求法
高考总复习· 数学
一．异面直线所成的角： （1）.定义 （2）.异面直线所成的角的范围： （3）．求异面直线所成的角的方法：（1）几何法；（2）向量法。
高考总复习· 数学
二．直线和平面所成角
（1）定义：平面的一条斜线和它在平面上的射影所成 的锐角叫做这条斜线和这个平面所成的角。
高考总复习· 数学
设EC1与FD1所成的角为
，则:
高考总复习· 数学
EC1 FD1 1 (4) 3 2 2 2 21 cos 2 2 2 2 2 2 14 EC1 FD1 1 3 2 (4) 2 2
2
GE , BA1
或
GE , BA1 2
高考总复习· 数学 求二面角的大小
1.几何法：将二面角问题转化求为其平面角的大小问题， 要掌握以下三种基本做法： ①直接利用定义，图4(1). ②利用三垂线定理及其逆定理，图4(2).最常用。 ③作棱的垂面，图4(3). A
的大小为
60
高考总复习· 数学
[点评与感悟]在处理二面角问题时，可能会遇到二面角的具体
3 3 ,1, ) 时，会算得 大小问题，如本题中若取n2 ( 2 2 1 cos BB1 , n2 从而所求二面角为120 2
但依题意只为60 。因为二面角的大小有时为锐角、直角， 有时也为钝角。所以在计算之前不妨先依题意判断一下所求二 面角的大小，然后根据计算取“相等角”或取“补角”。
3 BB1 0, （ 3 ,0） 2
高考总复习· 数学 设 平面 AB1 D 的法向量为
空间角
② 由①知 B1O 平面MAC 所以B1O是平面MAC的一个法向量 z 且B1O (1， 1， 2) C1 设平面B1MA的一个法向量为n ( x，y，z ) D1 由A(2，0) M (0，1) B1 (2， 2)得 0，， 0，， 2， A1 B1 M MA (2， 1)， 1 (2，1) 0， MB 2， 所以n MA 0，n MB1 0
质疑：空间向量的夹角与异面直线的夹角有什么
区别？
例1、如图，正三棱柱ABC—A1B1C1的底面边长为a,侧棱长为 2a 求AC1和CB1的夹角， 分析：求异面直线的夹角 解法步骤：1、写出异面直线的方向 向量的坐标。 2、利用空间两个向量的 夹角公式求出夹角。
Z
A1
C1
B1
3 1 3 1 AC1 ( a, a, 2a) CB1 ( a, a, 2a) 2 2 2 2
C1
B1
D1
A1
C
所以： 1 ( 1 , 0,1), BD1 ( 1 , 1 ,1) AF A 2 2 2 1 x 1 AF1 BD1 30 4 cos AF1 , BD1 10 | AF1 || BD1 | 5 3 4 2 30 所以 BD1与 AF1 所成角的余弦值为 10
①证明：以 DA、 、 1 DC DD为正交基底， A1 建立空间直角坐标系如图。则可得 所以MA (2， 1)， (0， 1)， 0， MC 2， B1O ( 1， 1， 2)
M
B1
C1
D O B
空间几何角度计算公式
空间几何角度计算公式在空间几何中，角度是一个重要的概念，用于描述两条线、平面或多个向量之间的夹角。
计算空间几何角度的公式可以根据具体情况而变化，下面将介绍几种常见的计算公式。
1. 点和直线的夹角设直线L上有一点A，过点A引一直线与直线L相交于点B，计算点A和直线L之间的夹角，可使用以下公式：cosθ = |AB| / |OB|其中θ表示点A和直线L的夹角，|AB|表示线段AB的长度，|OB|表示向量OB的长度。
2. 直线与直线的夹角设两条直线L1和L2，如果它们的方向向量分别为a和b，计算直线L1和直线L2之间的夹角，可使用以下公式：cosθ = |a·b| / (|a| |b|)其中θ表示直线L1和直线L2的夹角，|a·b|表示向量a与向量b的点乘的绝对值，|a|和|b|表示向量a和向量b的长度。
3. 平面和平面的夹角设两个平面α和β，它们的法线向量分别为n1和n2，计算平面α和平面β之间的夹角，可使用以下公式：cosθ = |n1·n2| / (|n1| |n2|)其中θ表示平面α和平面β的夹角，|n1·n2|表示向量n1与向量n2的点乘的绝对值，|n1|和|n2|表示向量n1和向量n2的长度。
4. 空间向量的夹角设两个非零向量a和b，计算向量a和向量b之间的夹角，可使用以下公式：cosθ = (a·b) / (|a| |b|)其中θ表示向量a和向量b的夹角，a·b表示向量a与向量b的点乘，|a|和|b|表示向量a和向量b的长度。
以上就是在空间几何中常用的几种角度计算公式。
根据具体情况，选择适合的公式进行计算，可以帮助我们解决空间几何问题。
空间角及其计算
建筑学中的应用
建筑设计
空间角在建筑设计中具有重要应用，如确定建筑物的朝向、布局和采光等。通 过合理利用空间角，可以优化建筑物的空间布局和采光效果，提高居住和使用 质量。
室内设计
在室内设计中，空间角的应用同样重要。通过合理调整室内家具和装饰品的摆 放角度，可以营造出更加舒适和美观的室内环境。
物理学中的应用
物理学
在物理学的力学、电磁学和光学等 领域，空间角也具有重要应用，如 描述带电粒子的运动轨迹、光的折 射和反射等。
02
空间角的计算方法
几何法
定义
几何法是利用空间几何知识，通 过作垂线、平行线、中线等手段， 将空间角转化为平面角或线线角，
然后进行计算的方法。
步骤
1. 作出相关垂线、平行线或中线； 2. 将空间角转化为平面角或线线 角；3. 利用平面几何知识计算角
空间角在其他领域的应用拓展
航天工程
利用空间角计算，优化航天器的轨道设计和姿态控制，提高航天 任务的可靠性和成功率。
机器人技术
通过空间角的计算，实现机器人的精准定位和自主导航，拓展机器 人在工业、医疗等领域的应用。
虚拟现实与游戏设计
利用空间角技术，提升虚拟环境的真实感和沉浸感，为游戏玩家和 设计师提供更加丰富的体验。
空间角及其计算
• 空间角的基本概念 • 空间角的计算方法 • 空间角的应用实例 • 空间角与空间几何的关系 • 空间角的未来发展与展望
01
空间角的基本概念
定义与性质
定义
空间角是指两个非平行直线或平 面在三维空间中形成的角度。
性质
空间角具有方向性，其大小和方 向可以通过几何学和三角函数来 描述。
光学研究
在光学研究中，空间角是描述光线传播方向和角度的重要参数。通过测量和计算 空间角，可以研究光线的反射、折射和散射等现象，进一步探索光与物质之间的 相互作用。
第60讲 空间角及其计算
第65讲 空间的角及计算【考点解读】了解空间三种角的概念，并会求三种角的大小.【知识扫描】1、异面直线,a b 所成的角：范围(0,]2π① 平移法：过空间上一点（注意取图形中的特殊点）作1//a a 、1//b b ，则1a 与1b 所成的锐角或直角就是异面直线,a b 所成的角；（书写时要分三步：作— 指— 求） ② 证明a b ⊥，则a 与b 的夹角为2π； ③ 向量法：求a < ，b >（[0,]π∈)，再确定异面直线a 与b 所成的角((0,]2πα∈)。
2、直线与平面所成的角：范围[0,)π① 定义法：找出直线PA 在平面α内的射影AO （射影AO 怎么找），则锐角PAO ∠就是直线PA 与平面α所成的角；（书写时要分三步：作— 证— 求） ② 证明a α⊥(或//a α)，则直线a 与平面α所成的角2π（或0）； ③ 向量法：求a 与α的法向量n 所成的角,a n <> ，则直线a 与平面α所成的角θ为,2a n π-<>或,2a n π<>- ，总之有||sin |cos ,|||||a n a n a n θ⋅=<>=⨯。
3、二面角① 直接法：直接作出二面角AB αβ--的平面角（书写时要分三步：作—证— 求）；② 向量法：设平面α的法向量1n 与平面β的法向量2n所成的角为θ，则所求的二面角为θ或πθ-（要依图形确定是取θ，还是取θπ-）。
【考计点拨】牛刀小试：1．在正三棱柱ABC-A 1B 1C 1中，若AB=2，A A 1=1，则点A 到平面A 1BC 的距离为（B ）A ．43B ．23 C ．433 D ．32．在正三棱柱ABC-A 1B 1C 1中，若AB=2BB 1,则AB 1与C 1B 所成的角的大小为 （B ）A.60ºB. 90ºC.105ºD. 75º3．正方体ABCD —A 1B 1C 1D 1中，E 、F 分别是AA 1与CC 1的中点，则直线ED 与D 1F 所成角的大小是（A）A ．15 B 。
高中数学空间的角的计算
面-线-面
0，2
语言叙述
二面角 半平面-线-半平面
0，
语言叙述或符号表示
要点三：直线和平面的夹角 1. 有关概念 斜线：一条直线和一个平面相交，但不和这个平面垂直，这条直线叫作平面的斜．线．，斜 线和平面的交点叫作斜．足．. 射影：过斜线上斜足以外的一点向平面引垂线，过垂足和斜足的直线叫作斜线在这个平 面上的射影. 斜线与平面的夹角：平面的一条斜线与它在该平面内的射影的夹角叫作该直线与此平面 的夹角. 如图， l 是平面 的一条斜线，斜足为 O ， OA 是 l 在平面 内的射影， POA 就是直 线 l 与平面 的夹角.
3. “平面间的夹角”不同于“二面角” （1）二面角的有关概念 半平面：一个平面内的一条直线，把这个平面分成两部分，其中的每一部分都叫半平面. 二面角：从一条直线出发的两个半平面所组成的图形叫二面角. 如图，可记作二面角 -a- 或 - AB - .
2
（2）区别： 构成 范围
表示法
平面间的夹角
2
5
举一反三：
【变式 1】 如图，在四棱锥 P ABCD 中，底面 ABCD 是正方形，侧棱 PD ⊥底面 ABCD ， PD DC ，点 E 是 PC 的中点，作 EF ⊥ PB 交 PB 于点 F ．
（1）求证： PB ⊥平面 EFD ；
（2）求平面 与平面 的夹角的大小．
【变式 2】在四棱锥 P ABCD 中，侧面 PCD ⊥底面 ABCD ，PD ⊥ CD ，E 为 PC 中点， 底面 ABCD 是直角梯形， AB ∥ CD ， ADC=90 ， AB AD PD 1， CD 2 . 设 Q 为侧
11
一、选择题
S
C
B
D
A
空间几何中的角度与距离计算
空间几何中的角度与距离计算在空间几何中，角度与距离的计算是非常重要的。
通过正确计算角度和距离，我们能够准确描述和分析物体的位置、运动以及相互关系。
本文将介绍空间几何中常用的角度计算方法和距离计算方法。
一、角度计算在空间几何中，角度是表示物体之间相对方向关系的重要指标。
常见的角度计算方法有以下几种：1. 余弦定理余弦定理是计算三角形内角的常用方法之一。
在空间几何中，如果已知三点的坐标，可以通过余弦定理计算出这三个点所形成的夹角。
余弦定理的公式如下：cos A = (b² + c² - a²) / (2bc)其中，A为夹角的大小，a、b、c为夹角对应的边长。
2. 矢量法矢量法是一种基于向量运算的角度计算方法。
通过将空间中的两个向量进行运算，可以得到它们之间的夹角。
常见的向量法角度计算包括点乘法和叉乘法。
（1）点乘法：两个向量的点乘结果等于它们的模长相乘再乘以它们之间的夹角的余弦值。
可以通过点乘法计算向量之间的夹角。
（2）叉乘法：两个向量的叉乘结果等于它们的模长相乘再乘以它们之间的夹角的正弦值。
可以通过叉乘法计算向量之间的夹角。
3. 三角函数在空间几何中，三角函数也是用于角度计算的常用方法之一。
通过正弦、余弦和正切等三角函数的运算，可以计算出角度的大小。
三角函数的计算方法需要先将坐标系进行转换，然后根据坐标的数值，利用相应的三角函数公式进行计算。
二、距离计算在空间几何中，距离是表示物体之间远近程度的重要指标。
常见的距离计算方法有以下几种：1. 欧几里得距离欧几里得距离是空间几何中最常用的距离计算方法。
对于二维或三维空间中的两个点，欧几里得距离可以通过计算它们在各坐标轴上的差值的平方和再开方的方式得到。
欧几里得距离的公式如下：d = √[(x₂-x₁)² + (y₂-y₁)² + (z₂-z₁)²]其中，d为距离，(x₁, y₁, z₁)和(x₂, y₂, z₂)分别为两个点的坐标。
高中空间几何求各种角的公式
在高中的空间几何学习中，常见的几何形状包括点、线、面、体等，涉及到各种角的计算。
以下是一些常见的角的公式：
1. 平面内的角：
-顶点在圆心的圆心角和半圆角：圆心角等于对应的圆周角，半圆角为180度。
-对顶角：对顶角相等。
-同位角：同位角相等。
-内错角和内错角互补：内错角之和等于180度，内错角互补。
2. 空间内的角：
-平行线与截线：平行线与截线的对应角相等。
-直线与平面：直线与平面的夹角等于其倾斜角。
-平面与平面：两平面的夹角等于它们法向量的夹角。
3. 立体几何中的角：
-直线与立体的交角：直线与平面或立体的夹角等于90度减去它们的夹角余补角。
-两平面之间的夹角：两平面的夹角是它们的法线之间的夹角。
这些公式是空间几何中常见的角度计算原则，通过理解和掌握这些规律，可以更好地解决空间几何题目中涉及到的各种角度问题。
空间角的求法
PCDBA 空间角的求法空间角，能比较集中反映空间想象能力的要求，历来为高考命题者垂青，几乎年年必考。
空间角是异面直线所成的角、直线与平面所成的角及二面角总称。
空间角的计算思想主要是转化：即把空间角转化为平面角，把角的计算转化到三角形边角关系或是转化为空间向量的坐标运算来解。
空间角的求法一般是：一找、二证、三计算。
异面直线所成的角的范围：090θ<≤ （一）平移法【例1】已知四边形ABCD 为直角梯形，//AD BC ，90ABC ∠=，PA ⊥平面AC ，且2BC =，1PA AD AB ===，求异面直线PC 与BD 所成角的余弦值的大小。
【解】过点C 作//CE BD 交AD 的延长线于E ，连结PE，则PC 与BD 所成的角为PCE ∠或它的补角。
CEBD ==PE=∴由余弦定理得 222cos 2PC CE PE PCE PC CE +-∠==⋅∴PC 与BD 所成角的余弦值为63 （二）补形法【变式练习】已知正三棱柱111ABC A B C -的底面边长为8，侧棱长为6，D 为AC 中点。
求异面直线1AB与1BC 所成角的余弦值。
【答案】125A 1C 1CBAB 1 DCP二、直线与平面所成角直线与平面所成角的范围：090θ≤≤ 方法：射影转化法（关键是作垂线，找射影）【例2】如图，在三棱锥P ABC -中，90APB ∠=，60PAB ∠=，AB BC CA ==，点P 在平面ABC内的射影O 在AB 上，求直线PC 与平面ABC 所成的角的大小。
【解】连接OC ，由已知，OCP ∠为直线PC 与平面ABC 所成角设AB 的中点为D ，连接,PD CD 。
AB BC CA ==，所以CD AB ⊥90,60APB PAB ∠=∠=，所以PAD ∆为等边三角形。
不妨设2PA =，则1,3,4OD OP AB ===2223,13CD OC OD CD ∴==+=在Rt OCP ∆中，339tan 13OP OCP OC ∠===【变式练习1】如图，四棱锥S ABCD -中，//AB CD ，BC CD ⊥，侧面SAB 为等边三角形。
《空间角的计算》课件
计算示例
通过具体的示例来理解空间角的计算方法。例如，在已知两个向量的情况下， 我们可以求解它们之间的夹角；又或者在已知三个点的坐标时，我们可以计 算它们围成的空间角。
总结
通过比较不同的计算方法，我们可以了解空间角的重要性和不同计算方法的优缺点。学习空间角对于提高相关 领域的数学能力具有重要意义。
《空间角的计算》PPT课 件
这是一份关于《空间角的计算》的PPT课件，旨在通过生动的图片和清晰的解 释，向大家介绍空间角的定义、计算方式、关系以及其在物理和工程中的应 用。
什么是空间角
空间角是三维空间中两个向量之间的夹角称为空间角。它可以通过向量的内积或两度和空间角之间存在着密切的关系。角度通常使用度数或弧度来表示，并且可以与空间角进行转换。此外， 定向角度和不定向角度也有着不同的概念和用途。
空间角的应用
空间角在物理学和工程中有着广泛的应用。在物理学中，它可以描述物体的 运动和力的方向。在工程中，它可以用于测量和设计三维结构。
空间角的计算方法
空间角的计算可以使用空间直角坐标系的方法、三点坐标法或两向量夹角法。每种方法都有其适用的场景和计 算方式。
高中数学中的立体几何空间角与空间距离计算方法
高中数学中的立体几何空间角与空间距离计算方法立体几何是数学中的一个分支，其重点研究的是三维空间中点、线、面和体之间的关系。
在立体几何中，空间角和空间距离是非常关键的概念。
本文将详细探讨高中数学中的立体几何空间角与空间距离计算方法。
一、空间角的概念与计算方法1. 空间角的概念空间角指的是由两个非共面向量所张成的角度，在立体几何中具有重要的意义。
空间角的大小是依据两个向量的夹角计算得来的。
2. 空间角的计算方法在计算空间角时，我们首先需要求出两个向量的点积。
设向量a=(a1,a2,a3)和向量b=(b1,b2,b3)，则它们的点积为a*b=a1b1+a2b2+a3b3。
接下来，我们可以利用余弦定理来计算角度，即cosθ=(a*b)/(|a||b|)，其中|a|和|b|分别表示向量a和向量b的模长，θ表示向量a和向量b之间的夹角。
二、空间距离的概念与计算方法1. 空间距离的概念空间距离指的是三维空间中两个点之间的距离，也是立体几何中经常涉及到的一个概念。
2. 空间距离的计算方法我们可以借助勾股定理来计算空间距离。
设点A(x1,y1,z1)和点B(x2,y2,z2)是三维空间中的两个点，它们之间的距离为d，则d=sqrt((x2-x1)^2+(y2-y1)^2+(z2-z1)^2)。
三、空间角和空间距离的应用空间角和空间距离在立体几何中的应用非常广泛，例如在计算棱台的侧面积、计算四面体内切圆半径、求解圆锥截面面积等问题中，我们都需要用到空间角和空间距离的知识。
比如，在计算棱台的侧面积时，我们需要首先求出两条棱所在的平面之间的空间角，然后根据棱长和计算出的角度，就可以快速计算出棱台的侧面积。
在计算四面体内切圆半径时，我们需要先计算出四面体各面的法线向量，然后根据法线向量计算面上的角度，最后用勾股定理求出四面体内切圆的半径。
在求解圆锥截面面积时，我们需要用到空间角和空间距离的知识，以找出圆锥截面的边界和计算截面的面积。
空间角的概念与计算
空间角的概念与计算在几何学中，角是一个基本的概念，用于描述物体之间的相对方向。
而空间角则是在三维空间中描述物体之间方向关系的重要指标。
本文将介绍空间角的概念及其计算方法。
一、空间角的概念空间角是用来描述三维空间中两个矢量之间的夹角关系。
在二维空间中，我们可以通过一条射线和一条直线之间的夹角来描述角度，而在三维空间中，空间角则需要考虑更多的因素。
具体而言，对于任意两个非零矢量a和b，它们之间的空间角被定义为它们的夹角θ，满足0 ≤ θ ≤ π。
其中，θ=0时表示a和b共线，θ=π/2时表示a和b正交，θ=π时表示a和b反向。
二、空间角的计算1. 余弦定理计算空间角余弦定理是空间角计算中常用的方法之一。
对于两个非零矢量a和b，它们之间的空间角θ满足以下关系：cosθ = (a·b) / (|a|·|b|)其中，·表示矢量的点积，|a|和|b|分别表示矢量a和b的模长。
通过求解上式，我们可以得到空间角θ的值。
2. 向量叉积计算空间角另一种常用的空间角计算方法是利用向量的叉积。
对于两个非零矢量a和b，它们之间的空间角θ满足以下关系：sinθ = |a×b| / (|a|·|b|)其中，×表示矢量的叉积。
通过求解上式，我们可以得到空间角θ的正弦值，进而计算出空间角的值。
三、实例演示下面通过一个实例来演示如何计算空间角。
假设有两个矢量a = (1, 2, 3)和b = (4, 5, 6)。
我们希望计算出它们之间的空间角θ。
首先，我们可以通过求解余弦定理来计算空间角的余弦值：cosθ = (1×4 + 2×5 + 3×6) / √(1² + 2² + 3²) × √(4² + 5² + 6²)= (4 + 10 + 18) / √14 × √77= 32 / √1078 ≈ 0.979然后，通过反余弦函数可以求得空间角的弧度值：θ = arccos(0.979) ≈ 0.199 rad最后，将弧度值转换为度数，即可得到空间角的度数表示：θ ≈ 0.199 × (180/π) ≈ 11.4°因此，矢量a和b之间的空间角约为11.4°。
空间中的角度计算与应用
空间中的角度计算与应用角度是空间中一种重要的几何概念，可以用来描述物体之间的相对位置和方向关系。
在工程、物理、建筑、航天等领域中，角度计算和应用都扮演着重要的角色。
本文将介绍空间中角度的计算方法和几个相关应用。
一、空间中的角度计算方法在二维平面中，我们可以使用直尺和量角器等工具来测量角度。
但在空间中，由于有长度、高度和深度三个方向的变化，所以需要使用更高级的工具和方法来计算角度。
1. 三维空间中的角度计算方法在三维空间中，我们通常使用向量来表示方向和位置。
一个向量可以用起点和终点来表示，这两个点在三维坐标系中分别有三个坐标值。
设两个向量A和B，它们的坐标分别为(Ax, Ay, Az)和(Bx, By, Bz)。
我们可以使用向量的点积和模长计算它们之间的夹角θ。
点积的计算公式为：A·B = Ax·Bx + Ay·By + Az·Bz向量的模长计算公式为：|A| = √(Ax^2 + Ay^2 + Az^2)两个向量的夹角θ的余弦值可表示为：cosθ = (A·B) / (|A|·|B|)通过反余弦函数可求得夹角θ的值，即θ = arccos(cosθ)2. 四元数计算法四元数是一种用于表示旋转的数学工具，它可以用一个实部和三个虚部来表示。
四元数既可以描述物体的姿态和旋转角度，也可以用来计算两个物体之间的旋转或夹角。
具体计算步骤如下：1）定义两个四元数q1和q2，分别表示两个物体的姿态；2）求解它们的乘积p = q1 * q2的实部，得到一个新的四元数；3）通过arccos函数计算p的实部的绝对值，得到两个物体之间的夹角。
二、空间中角度的应用在物理和工程领域，空间中的角度计算和应用非常广泛，下面介绍几个常见的应用场景。
1. 机械设计与运动控制在机械设计和运动控制领域，角度的计算和控制是非常重要的。
例如，在机器人运动控制中，需要根据机器人末端执行器的位置和姿态，计算出各个关节的角度，以实现期望的运动轨迹。
空间角的求法方法归纳
空间角的求法方法归纳
空间角的求法方法归纳
在数学和物理学中，空间角是一种非常重要的概念。
物体在空间中的角度关系经常被用到各种计算和分析中。
因此，求解空间角的方法也变得尤为重要。
本文将按类划分，总结空间角的求法方法。
立体角的求法
立体角是三维空间中用来描述四面体的角度大小的量，并且与其各个顶点相对应。
求解四面体的立体角可以通过以下公式进行计算：
V5 = 1/3(arccos(A1) + arccos(A2) + arccos(A3) - π )
其中V5指四面体的立体角，A1、A2、A3为三个向量的夹角余弦，pi 为圆周率。
平面角的求法
平面角是在二维平面中两个射线之间的角度大小，于是端点重合，两条射线叫做角的顶点，并记为O。
平面角的计算公式如下：
cosθ = a·b / |a||b|
其中，a和b分别表示两个向量，|a|和|b|表示向量的模，lala和lblb都为0，则cosθ没有定义。
球面角的求法
球面角是指在球面上相互靠近的两条弧（或线）之间的角度大小。
求解球面角需要先计算其对应的球面扇形的面积，然后进行换算即可，具体公式如下：
S = R²θ
其中R表示球体半径，θ表示对应的球面角。
总结
空间角的求法方法主要包括立体角、平面角和球面角三种。
其中立体角的求解需要根据四面体的三个向量夹角余弦值计算，平面角的计算需要先计算两个向量的点积并除以其模，而球面角的求解则需要先计算出对应的球面扇形面积。
这些空间角的求法方法可以帮助我们更准确地分析并解决各类问题。
空间角的计算方法
空间角的计算方法当建立空间直角坐标系后，空间图形顶点的坐标容易得出且比较简单时，三类空间角的计算可利用空间向量来处理.但是，当用空间向量处理起来比较困难时，我们还要学会用其它方式来处理.三类空间角的计算有别于平面几何中计算，它要充分地“说理”.因为空间图形不可能像平面图形那样明确、直接，有时看起来是“锐角”或“钝角”的图形，实际上是直角.因此，在立体几何中实施角的计算时，要认真做好三步工作“作——证——算”.“作”——即作出符合要求的平面角；“证”——即证明所作平面角是所求的角；“算”——通过解三角形求出该平面角的大小.本单元我们重点讨论用常规方法，来处理三类空间角的计算问题.【异面直线所成的角】求两异面直线所成角的问题是立体几何中常见且重要的计算之一，其方法通常是在其中一条直线上取一个特殊点通过三角形中位线或平行四边形引另一条直线的平行线来实现平行移动，然后通过余弦定理或解直角三角形来求解；对不易平移的问题可通过补形的方式来求解，也可考虑利用三余弦公式求解.两异面直线所成角θ的取值范围为θ∈(0，π2]. 例1.在正四面体ABCD 中，E 、F 分别是BC 、AD 的中点，求DE 和BF 所成角的余弦值. 解法1(平移).如图2.5—1.联结AE ，取AE 的中点M ，联结MF 、MB ， ∵ M 、F 分别为AE 、AD 的中点，∴ M F ∥DE ，故∠MFB 为DE 和BF 所成的角或补角. 设正四面体ABCD 的棱长为a ，则由平面几何知识易知BF=√3a 2，MF=√3a4. 在Rt ∆BEM 中，MB=.47)43()2(22a a a =+由余弦定理可得，.324323216716343cos 222=⋅⋅-+=∠aa aa a MFB 解法2(补形). 如图2.5—2.将原正四面体补形为三棱柱.取AC 1的中点M ，联结D 1M 、BM ，BD 1，易知F 是空间角的求法异面直线所成的角 ①利用中位线或平行四边形平移. ③三余弦公式. 直线与平面所成的角二面角①直接法. ②等积转换法. ③三余弦公式法.①直接法——利用三垂线定理或棱的垂面. ②利用等腰三角形底边上的中线. ③利用面积的射影定理.②补形.A BCDF E图2.5—1 M ABCDF E 图2.5—2C 1D 1MBD 1的中点，MD 1∥DE ，∴∠MD 1B 为DE 和BF 所成的角或补角. 设正四面体ABCD的棱长为a.易求得，MD 1=√3a 2，BD 1=√3a ，BM=√7a2(可由余弦定理求得).再由余弦定理可得 cos ∠MD 1B= 23.例2.如图2.5—3.在正方体ABCD—A 1B 1C 1D 1中，M 、N 分别是BB 1与C 1C 的中点，设DM与A 1N 所成的角为θ，求cosθ的值. 解：在原正方体ABCD—A 1B 1C 1D 1的前面补一个相同的正方体，如图2.5—3.联结A 2M 、A 2D ，易知A 2M ∥A 1N ， ∴ ∠A 2MD 为DM 与A 1N 所成的角θ或补角. 设正方体棱长为a. ∵ DM=A 2M=√(√2a)2+(a2)2=3a 2，A 2D=a a a 5)2(22=+.由余弦定理可得cos ∠A 2MD = - 19. ∴ cosθ= 19.说明：①由于两异面直线所成角的取值范围为θ∈(0，π2]，所以cosθ不可能为负值，当计算得出角的余弦值为“—”时，应将最后结果改为“+”.这是因为在平移时，所得的平面角可能是两异面直线所成角的补角，而互为补角的两角的余弦值互为相反数.②当我们试图在原图形的表面或其中作“平移”较困难时，可考虑“补形”.一般补形方式为：①三棱锥补形为三棱柱；②三棱柱补形为四棱柱；③四棱柱可在某一个侧面或底面“拼”一个相同的四棱柱.三余弦公式：平面α的斜线a 与α内一直线b 相交成θ角，a 与α相交成ϕc 与b 相交成ϕ2角，则有θϕϕcos cos cos 21=证明：设点P 在平面α上的射影为O ，过点O 作O B ⊥b 于B ，连接PB ， 由三垂线定理知AB ⊥PB.如图2.5—4. ∴ θϕϕcos cos cos 21==⋅=APAB AOAB APAO .在此公式中，直线a 和b 可以是相交直线，也可以是异面直线. 我们不妨把ϕ1叫做线 面角，θ叫做线线角，ϕ2叫做线影角.很明显，线线角是这三个角中最大的一个角.例3.(1)如图2.5—5(1)，MA ⊥平面ABCD ，四边形ABCD 是正方形，且MA=AB=a ，试求异面直线MB 与AC 所成的角.(2)如图2.5—5(2).在立体图形P -ABCD 中，底面ABCD 是一个直角梯形.∠BAD=900，AD//BC ，AB=BC=a ，AD=2a ，且PA ⊥底面ABCD ，PD 与底面成300角，AE ⊥PD 于D.求异面直线AE 与CD 所成角的余弦值.解:(1)由图2.5—5(1)可知，直线MB 在平面ABCD 内的射影为AB ，直线MB 与平面ABCD所成的角为450，直线AC 与直线MB 的射影AB 所成的角为450，所以直线AC 与直MB 所成的角为θ，满足cosθ=cos45°· cos45°= 12，∴ 直线AC 与MB 所成的角为600.ACDA 1B 1C 1D 1 NM BA 2 图2.5—3图2.5—4ϕ2ϕ1cba θP αO AB(2)如图2.5—5(2)，过E 作PA 的平行线EF 交AD 于F ，由PA ⊥底面ABCD 可知，直线AE 在平面ABCD 内的射影为AD ，直线AE 与平面ABCD 所成的角为∠DAE ，其大小为600，射影AD 与直线CD 所成的角为∠CDA ，其大小为450，∴ 直线AE 与直线CD 所成的角θ满足：cosθ=cos60°· cos45°= √24. 即AE 与CD 所成角的余弦值 √24.想一想①:1.正四面体SABC 的棱长为a ，E ，F 分别是SC 和AB 的中点． 求异面直线SA 和EF 所成角．2.如图2.5—6.A 1B 1C 1—ABC 是直三棱柱，∠BCA=900，点D 1、F 1 分别是A 1B 1、A 1C 1的中点，若BC=CA=CC 1，求BD 1与AF 1所成 角的余弦值.【直线与平面所成的角】直线与平面所成的角也是立体几何中常见且重要的计算问题之一.它一般可通过解Rt △ 来求解.其解法通常有①直接法；②三棱锥体积等积变形法；③三余弦公式法——此法主要用于解选填题，若用于解答题，则要给出三余弦公式的简略证明.例4.如图2.5—7.在正方体AC 1中.(1)求BC 1与平面ACC 1A 1所成的角.(2)求A 1B 1与平面A 1BC 1所成的角的余弦值.解:(1)联结BD 交AC 于O ，∵ BO ⊥AC ，BO ⊥A 1A ，由线面垂直的判定定理可得BO ⊥平面ACC 1A 1， ∴ ∠OC 1B 为BC 1与平面ACC 1A 1所成的角. 在Rt ∆BOC 1中，∵ sin ∠OC 1B=OB BC 1=12，且∠OC 1B 为锐角，∴ BC 1与平面ACC 1A 1所成的角为300. (2)法1.如图1.6—7. 联结BC 1、B 1C 交于点E. 易知BC 1⊥平面A 1B 1C.又∵ BC 1⊂平面A 1BC 1，∴ 平面A 1BC 1⊥平面A 1B 1C. 过B 1作B 1H ⊥A 1E 于H ，联结A 1H ，∵ 平面A 1BC 1∩平面A 1B 1C=AE, ∴ B 1H ⊥平面A 1BC 1,因此，∠B 1A 1E 是A 1B 1与平面A 1C 1B 所成的角. ∵ tan ∠B 1A 1E= B 1EA 1B 1=√22，∴ cos ∠B 1A 1E=√63.法2.过B 1作B 1H ⊥平面A 1BC 1于H ，联结A 1H ，∴∠B 1A 1H 是A 1B 1与平面A 1C 1B 所成的角.∵ △A 1BC 1是正三角形，且A 1B 1=B 1C 1=BB 1. ∴ 棱锥B 1—A 1BC 1是正三棱锥. 可得点H 是△A 1B 1C 1的外心.设A 1B 1=a,则A 1B=√2a ,得A 1H= √63a. ∴ cos ∠B 1A 1H=A 1H A 1B 1=√63，即所求角的余弦值为√63.说明：F 1 A B D 1C 1A 1B 1图2.5—6C 图2.5—7 PE DFA B C图2.5—5(2)图2.5—5(1) A B C D M1.当题设条件中或由已知可推出两个平面互相垂直时，要作出线面角， 可利用两平面垂直的性质，在一个平面内作交线的垂线即可.2.在求线面角时，很多时候垂线位置的确定，是很费“周折”的.而利用三棱锥体积等积变形可简化此不必要的麻烦. 其思路和原理如下：如图2.5—8.设PA 是平面α的斜线，PB 为平面α的垂线段，其长为h ，则θ为PA 与平面α所成的角.由于sin θ= hPA .一般地PA 之长往往是已知的，因此要求出sin θ就只需要求出点P 到平面α的距离h 即可.这里的h 值可通过三棱锥体积等积变形得到.例5.如图2.5—9所示，在四棱锥P —ABCD 中，底面ABCD 是一直角梯形，∠BAD=900.AD ∥BC ，PA=AB=BC=a ，AD=2a ，PA ⊥底面ABCD. (1)求证：CD ⊥平面PAC.(2)求直线AD 与平面PCD 所成角的正弦值. 解:(1)在直角梯形ABCD 中，∵ ∠BAD=900，AD ∥BC ，AB=BC ， 取AD 的中点E ，联结CE ，知四边形ABCE 是正方形，又∵ AD=2a ，∴ CE=ED ，即∠ECD=450，∴ AC ⊥CD. ∵ PA ⊥底面ABCD ，CD ⊂底面ABCD ，∴ CD ⊥PA ，又∵ PA∩AC=C ， PA 、AC ⊂平面PAC ，∴ CD ⊥平面PAC. (2)法1.设点A 到平面PCD 的距离为h ，直线AD 与平面PCD 所成角为θ，则有ADh =θsin .∵ .36,21312131a h CD AC PA CD PC h V V ACD P PCD A =⇒⨯⋅⋅⋅=⨯⋅⋅⋅⇒=，——又∵ AD=2a ，∴66sin ==AD h θ.即直线AD 与平面PCD 所成角的正弦值为66.法2.由(1)知，平面PAC ⊥平面PDC ，平面PA C ∩平面PDC=PC ，过点A 作AH ⊥PC 于H ，则AH ⊥平面PDC ，联结DH ，知∠ADH 为直线AD 与平面PCD 所成角. 在Rt △PAC 中，AC=,2a PA=a ，PC=,3a 由Rt △PAC 的面积等积变形得， AH=36a . 又∵ AD=2a ，∴ 66sin ==AD h θ.即AD 与面PCD 所成角的正弦值为66.【一个结论的应用】结论：若平面α的一条斜线PA 与平面α内∠BAC 的两边BA 、BC 所成的角相等，则PA 在平面α上的射影为∠BAC 的角平分线 .例6.(1)有一东西方向的河流，离河岸若干米处有一探照灯，照着岸边的某点B ，探照灯在点B 的东北方向.灯光与地面成600角，求灯光与岸边所成角的余弦值.(2)在正方体ABCD —A 1B 1C 1D 1中，E 、F 分别是AB ，C 1D 1的中点，求直线A 1B 1与平面A 1ECF 所成角的余弦值.解:(1)如图2.5—10(1).由已知，∠DBA=ϕ1=600， ∠ABC=ϕ2=450，∠DBC=θ，由三余弦公式得，cosθ=cos450·cos600= √24， ∴ 灯光与岸边所成角的余弦值为 √24.图2.5—9B P ACD EHPA θB 图2.5—8αD BCA东图2.5—10(1)ABC DB 1C 1D 1A 1FE图2.5—10(2)(2) 如图2.5—10(2).∵ A 1B 1与A 1E 、A 1F 所成角∠B 1A 1E=∠B 1A 1F ，∴ 直线A 1B 1在平面A 1ECF 上的射影为∠FA 1E 的平分线. 又由已知可推得四边形A 1ECF 为菱形，∴∠FA 1E 的平分线为A 1C. ∵ cos ∠B 1A 1E=sin ∠AA 1E= AEA1E=√55，由余弦定理可得cos ∠CA 1E=√155. 设直线A 1B 1与平面A 1ECF 所成的角为ϕ1，由三余弦公式得cos ϕ1= √33. ∴ 直线A 1B 1与平面A 1ECF 所成的角的余弦值为 √33.注：(2)也可以联结B 1C ，由上述分析知，直线A 1B 1与平面A 1ECF 所成角为∠B 1A 1C ，在Rt △A 1B 1C 中，易求得cos ∠B 1A 1C = √33.想一想②:1.在正方体ABCD －A 1B 1C 1D 1中，E 、F 分别为AA 1、AB 的中点，则EF 与平面AA 1C 1C 所成的角为( ). 2.如图2.5—11.空间四边形PABC 中，PA 、PB 、PC 两两相互垂直， ∠PBA=450,∠PBC=600.则cos ∠ABC=( ).3.正方体ABCD ﹣A 1B 1C 1D 1中，若E 为棱AB 的中点，则直线C 1E 与平面ACC 1A 1所成角的正弦值为( ).4.求例5中PB 与平面PCD 所成角的正弦值.【二面角】二面角的计算是三类空间角计算中的难点，解决它的关键在于合理、有效地找出二面角的平面角，常用的方法有如下几种：1.直接法——⎪⎩⎪⎨⎧.)(中线作出平面角利用等腰三角形底边的面角；利用作棱的垂面作出平定理作出平面角；或逆利用三垂线 2.间接法——利用面积的射影定理. 对于无棱的二面角(只给出了两个半平面的一个公共点)，则要先确定棱的位置. 二面角的取值范围为θ∈[0，π].例7.(1)如图2.5—12(1). PC ⊥平面ABC ，AB ＝BC=CA ＝PC=a ，求二面角B －PA －C 的平面角的正切值.(2)如图2.5—12(2).已知二面角α－AB －β为1200，AC ⊂α，BD ⊂β，且AC ⊥AB ，BD ⊥AB ，AB ＝AC ＝BD ＝a ，求CD 的长为.解:(1)法1(三垂线定理法).∵ PC ⊥平面ABC, ∴ 平面PAC ⊥平面ABC ，交线为AC.作BD ⊥AC 于点D ，据面面垂直性质定理知BD ⊥平面PAC ，作DE ⊥PA 于E ，连BE ，由三垂线定理，得BE ⊥PA ，从而∠BED 是二面角B －PA －C 的平面角.设PC ＝a ，依题意知三角形ABC 是边长为aPA BC图2.5—11 图2.5—12(1)P ABCDE图2.5—12(2)的正三角形，∴ D 是AC 的中点且BD=√32a ，∵ PC =CA=a ，∠PCA=900， ∴ ∠PAC ＝450. 在Rt △DEA 中，ED=ADsin450= √24a ， ∴ tan ∠BED= BD ED =√6， 即二面角B －PA －C 的平面角的正切值为√6. 法2.(面积的射影定理法).同法1，作BD ⊥AC 于点D ，可知BD ⊥平面PAC ，∴ 三角形ABP 在平面PAC 上的射影为三角形PDA.设所求二面角为θ，则cos θ=S∆PAD S ∆PBA . 由已知易求得PB=PA=√2a ， AB=a ，PC=PA=a ，∴ S ∆PDC =12S ∆PAC =14a 2，S ∆PAB =√74a 2，因此cos θ=S ∆PAD S ∆PBA= √77，从而可得二面角B －PA －C 的平面角的正切值为√6.(2)在平面β内，作AD′∥BD ，连DD′，则DD′∥AB. ∵ AC ⊥AB ，D′A ⊥AB ，∴ ∠D′AC 为二面角α－AB －β的平面角， 即∠D′AC ＝120°.∵ AB ＝AC ＝BD ＝a ，∴ CD′＝3a ，又AB ⊥平面ACD′，DD′∥AB ， ∴ DD′⊥平面ACD′，∴ DD′⊥D′C ，又 DD′＝a ，∴ CD ＝DD′2＋D′C 2＝2a.例8.(1)如图2.5—13(1).在600二面角M －a －N 内有一点P ，P 到平面M 、N 的距离分别为1和2，求点P 到直线a 的距离.(2)如图2.5—13(2).正方体AC 1的棱长为a ，求二面角D —A1B —C 的余弦值.解:(1)设PA 、PB 分别为点P 到平面M 、N 的距离，过PA 、PB 作平面α，分别交M 、N于AQ 、BQ.(相当于作棱的垂面). ∵ PA ⊥M ，a ⊂M ，∴ PA ⊥a. 同理，有PB ⊥a ， ∵ PA∩PB=P ，PA 、PB ⊂平面PAQB ， ∴ a ⊥平面PAQB 于Q.又 AQ 、BQ ⊂平面PAQB ，∴ a ⊥AQ ，a ⊥BQ. 即 ∠AQB 是二面角M －a －N 的平面角. ∴ ∠AQB ＝60°.联结PQ ，则PQ 是P 到a 的距离，在平面图形PAQB 中，有∠PAQ ＝∠PBQ=90°，∴ P 、A 、Q 、B 四点共圆，且PQ 是四边形PAQB 的外接圆的直径2R. 在△PAB 中，∵ PA=1，PB=2，∠BPA ＝120°，由余弦定理得，AB=√7. 由正弦定理：PQ=2R=.3212237sin ==∠APBAB(2)取A 1B 的中点E ，过点E 作EF ∥BC 交A 1C 与F ，联结DF 、DE.在正方体AC 1中易知 BC ⊥A 1B ，∵ EF ∥BC ∴ EF ⊥A 1B ，又∵A 1D=DB ，E 为A 1B 的中点，∴ EF ⊥A 1B ，因此∠DEF 为二面角D —A 1B —C 的平面角. ∵ DE= √32A 1B = √6a2，EF= BC 2=a2，DF=A 1C 2=√32a.由余弦定理可得，cos ∠DEF=√63.即二面角D —A1B —C 的余弦值为√63.想一想③:1.在正四面体ABCD 中，求相邻两个平面所成二面角的平面角的余弦值PN ABQMa 图2.5—13(1)A BC DA 1B 1C 1D 1图2.5—13(2) EF2.自二面角内的一点到两个平面的距离都是6cm ，两个垂足间的距离也是6cm ，求此二面角的度数.3.在四面体ABCD 中，AC=AB=BC=1，CD=BD=√132，AD=3.求二面角A—BC—D 的余弦值.例9.长方体ADCD—A 1B 1C 1D 1中，底面ABCD 是正方形，过对角线AC 1的一个截面是锐角为α的菱形，若底面与截面AEC 1F 成θ角，求证：cos θ=tan α2.证法1:如图2.5—14.联结AC 、BD. ∵ 过对角线AC 1的一个截面是菱形，由长方体的特性知， BD ∥EF ，且EF=BD. 由线面平行的判定定理知BD ∥截面AEC 1F ，再由线面 平行的性质定理知BD ∥过点A 的直线l . 其中l 为平面ABCD 与截面AEC 1F 的交线，即下底面与截面所成二面角的棱为直线l .∵ AC 1⊥EF ，AC ⊥BD ，∴ AC ⊥l ，AC 1⊥l ，即∠C 1AC 为底面与截面AEC 1F 所成角，即 ∠C 1AC=θ，∵ cos θ= ACA 1C ，tan α2=EF AC 1=BD AC 1=ACAC 1，∴ cos θ=tan α2.证法2.设底面与截面AEC 1F 成θ角，由面积射影定理知，cosθ=S ∆BCDS ∆EC 1E=BD×AC EF×AC 1=AC AC 1. 下同法1.略.例10.如图2.5—15.在△ABC 中，AB ⊥BC ，S 为平面ABC 外的一点，SA ⊥平面ABC ，∠ACB ＝600，SA ＝AC ＝a.求二面角A －SC －B 的余弦值. 解: ∵ SA ⊥平面ABC ，SA 平面SAC ，∴ 平面SAC ⊥平面ABC. 过点B 作BD ⊥AC 于D ，平面SAC 平面∩ABC=AC ， ∴ BD ⊥平面SAC ，联结SD. 设二面角A －SC －B=θ， ∵ SA ＝AC ＝a ，∠ACB ＝600，BC ⊥SB ，∴ BC=a2，CD =BC 2=a4，SB=√7a2，∴ cos θ=S ∆SDC S ∆SBC=SA×CD SB×BC=√77. 即二面角A －SC －B的余弦值为√77.想一想④:如图2.5—16所示.在四棱锥P—ABCD 中，底面ABCD 是一直角梯形，∠BAD=900，AD ∥BC ，PA=AB=BC=a ，AD=2a ，PA ⊥底面ABCD. 求:(1)二面角P—CD—A 的余弦值.(2)平面PCD 与平面PAB 所成二面角的余弦值.【线面角、二面角的一个统一求法】如图2.5—17，设平面α的斜线PA 与平面α所成的角为θ，点P 到平面α的距离为h ，则 有， sin θ=hPA . 其中h 可利用三棱锥体积等积变形求得.图2.5—16BPA C DABCS图2.5—15D 图2.5—14 A BC A 1B 1C 1D 1DFE l如图2.5—18.在平面β内取一点P ，过点P 作PA ⊥平面α于A ，过点A 作AB ⊥l 于B ，联结PB ，由三垂线定理易知∠PBA =θ为二面角α—l —β的平面角(或补角)，设点P 到平面α的距离为h ，则有，sin θ=hPB . 其中h 可利用三棱锥体积等积变形求得，PB 为点P 到棱l 的距离，可通过三角形面积等积变形求得.这样一来，求线面角和二面角的问题可统一为，先利用三棱锥的体积等积变形求出点面距h ，再由已知或利用三角形面积等积变形求出点线距，从而易得所成角的正弦值.例11.如图2.5—19.在四棱锥P —ABCD 中，PA ⊥平面ABCD ，底面ABCD 是菱形，PA=4，AC=2√3，BD=2.又点E 在侧棱PC 上，且PC ⊥平面BDE. (1)求线段CE 的长.(2)且二面角A —PD —C 的余弦值.解:(1)设AC ∩BD =O ，联结OE ，由已知条件易得PC=2√7.∵ PC ⊥平面BDE ，∴ OE ⊥PC.在Rt ∆PAC 和Rt∆OEC 中， cos ∠OCE=ECOC =ACPC ，⇒EC =3√77.(2)由已知可求得菱形的边长为2，PD=2√5. 设点A 到平面PDC 的距离为h ，点A 到二面角A —PD —C 的棱PD 距离为d ，二面角A —PD —C 的平面角(或补角)为θ，则sin θ=hd . 在∆PDC 中，S ∆PDC =12DP ×DC ×sin∠PDC =12DP ×DC ×√1−cos 2∠PDC =√19，∵ V A—PDC = V P—ADC ，可求得h=4√5719，又在∆PAD 中利用面积等积变形可得d=4√55， ∴ sin θ=hd =√15√19，∵ 二面角A —PD —C 是钝二面角，故二面角A —PD —C 的余弦值为-2√1919.例12.如图2.5—20.四棱锥P —ABCD 的底面是一个边长为4的菱形，其中∠ADC=600，顶点在底面上的射影恰好为AD 的中点E ，若PA=√7. (1)求直线PB 与平面PAD 所成角的正弦值.(2)求平面PBC 与平面PAD 所成二面角的余弦值.解:(1)设点B 到平面PAD 的距离为h ，直线PB 与平面PAD 所成角为θ，则sin θ=hPB ..∵ PE ⊥平面ABCD ，且E 为AD 的中点，由PA=√7，AD=4，∴ PE=√3. 又∵ V B—PAD = V P—BAD ，得 h =PE×S ∆ABDS ∆APD=2√3，在∆AEB 中，由余弦定理得EB=2√7，再由勾股定理得PB=√31， ∴ sin θ=hPB =2√3√31=2√9331. 即直线PB 与平面PAD 所成角的正弦值为2√9331. (2)设平面PBC 与平面PAD 所成二面角为α，点C 到平面PAD 的距离为h ，点C 到二面角的棱l 的距离为h 1，则 ，sin α=hh 1. ∵ BC ∥AD ，由线面平行的判定和性质知，平面PBC 与平面PAD 的交线l ∥BC ，∴ h 1为∆P CB 的底边BC 边上的高.由AD ⊥平面PEC ，知AD ⊥PC ，又∵ AD ∥BC ，∴ BC ⊥PC ，即h 1=PC.联结CE 、AC 由已知易得∆ACD 为αP A Bθh图2.5—17αP A h 图2.5—18Bθ βlP AEBCD l图2.5—20.PDECBA 图2.5—19.O正三角形，∴ PC=√PE 2+EC 2=√15，由BC ∥平面PAD 和(1)知h=2√3， ∴ sin α=h h 1=2√55，故平面PBC 与平面PAD 所成二面角的余弦值为2√55.例13.如图2.5—21，在四棱锥P —ABCD 中，底面ABCD 是边长为2的正方形，侧面PAD ⊥ 底面ABCD ，且PA=PD=√22AD ，在线段AB 上是否存在一点G ，使二面角C —PD —G 的正弦值为2√23，说明理由. 解：取AD 的中点E ，联结PE 、CE ，∵ 侧面PAD ⊥底面ABCD ，底面ABCD 是边长为2的正方形，且PA=PD= √22AD ， ∴ PD ⊥AB ，DP ⊥平面PAB ，从而可得，DP ⊥P G ，EC=√5， PC=√6， PA =PD =√2，PE =1.设AG=a ，点G 到平面PDC 的距离为h ，二面角C —PD —G 的平面角(或补角)为θ，则sin θ=h PG.由V G—PDC = V P—DGC ，得 h =S ∆DGCS ∆PDC=√2，又∵ PG=√2+a 2，∴ sin θ=hPG =√2√2+a 2=2√23，⇒a =12. 故存在点G 满足题设条件，且AG= 12.想一想⑤:在正方体ABCD —A 1B 1C 1D 1中，点M 、N 、O 分别在棱CD 、BC 、CC 1上，且CM=CN=OC 1， 当OM 与平面ABCD 所成角的余弦值为√22时，求二面角N —MO —C 的余弦值.(请用多种方法)习题2.51.四面体ABCD 中，AC ⊥BD ，且AC ＝4，BD ＝3，M 、N 分别是AB 、CD 的中点，则MN 和BD 所成角的正切值为( ).2.在四面体ABCD 中，AB ⊥BC ，AB ⊥BD ，BC ⊥CD ，且AB ＝BC ＝6，BD ＝8，E 是AD 中点，则BE 与CD 所成角的余弦值是( ).3.正三棱柱的九条棱都相等，M 、N 分别是BC 和A 1C 1的中点. 则MN 与CC 1所成角的余弦值是( ).4.不共面的三条射线OA 、O1B 、OC 两两成600的角，则OC 与平面AOB 所成角的余弦值为( ).5.正四棱柱ABCD ﹣A 1B 1C 1D 1中，对角线BD 1=8，BD 1与侧面BC 1所成的角为30°，则BD 1和底面ABCD 所成的角为( ). A.30°. B.60°. C.45°. D.90°.6.设P 是边长为1的正△ABC 所在平面外一点，且PA=PB=PC= 23，那么PC 与平面ABC 所成的角为( ). A.30°. B.45°. C.60° D.90°.7.长方体ABCD －A 1B 1C 1D 1中，AB=AA 1=2cm ，AD=1cm ，求异面直线A 1C 1与BD 1所成角的余弦值.(要求用三种不同的方法).8.已知ABCD 是正方形，PB 平面ABCD ，PB=AB=1，求二面角A —PD —C 的大小.9.如图2.5—22.空间三条射线CA 、CP 、CB ，∠PCA=∠PCB=60o ， ∠ACB=90o，求二面角B -PC -A 的余弦值.10.在四棱锥P -ABCD 中，ABCD 为正方形，PA ⊥平面ABCD ，PA ＝AB ＝a ，求平面PBA 与PBα CAE F D图2.5—22 图2.5—21PDAB ECG平面PDC 所成二面角的大小.11.设M 为正方体ABCD -A 1B 1C 1D 1的棱CC 1的中点，求平面BMD 1与底面ABCD 所成的二面角的余弦值. 12.AC ⊂α，BD ⊂β，α与β所成的角为600，AC ⊥l 于C ，BD ⊥l 于B ，AC ＝3，BD ＝4，CD ＝2，求A 、B 两点间的距离.【参考答案】想一想①:1. 45°.2.1015.提示，法1.联结D 1F 1，过F 1作F 1M ∥BD 1角BC 与M.法2.在左侧面“拼”一个相同的三棱柱. 3..2222222cb a b a b a ++⋅+-利用三余弦公式，联结AC 、BD 交于O ，其中AC C 11∠=ϕ，COB ∠=2ϕ. 想一想②:1.300.提示，相当于求A 1B 平面AA 1C 1C 所成的角.2.√24.换个角度画图.由已知知CP ⊥平面PBA.∠ABC=θ,∠PBA=450=φ1,∠PBC=600=φ2.由三余弦公式可得.3.√26.直接法或等积变形. V E—ACC 1= V C 1—ACE . 4. √26.等积变形. V B—PCD = V P—BCD .想一想③:1.13.法1.过一个顶点作对面的垂线，由三垂线定理得到二面角的平面角，再求之. 法2.利用等腰三角形的特性作出二面角的平面角. 法3.利用面积的射影定理亦可求解. 2.1200.仿例8(1)作棱的垂面求解. 3.−√74. 利用等腰三角形的特性作出二面角的平面角.想一想④:(1) √63.法1.联结AC ，先证CD ⊥平面PAC.可知∠PCA 为平面角，再计算. 法2.利用面积的射影定理求.(cos θ=S∆ACD S ∆PCD).(2) √66.法1.延长DC 交AB 于点E ，则PE 为二面角的棱.再用直接法求之.法2. 利用面积的射影定理求. (cos θ=S∆PAB S ∆PCD).想一想⑤: √33. 习题2.51. 43.. 2. √75. 3.2√55. 4. √33.利用三余弦公式. 5.C. 6.A. 7. √558.1200.注意到∆PCD ≌∆PAD ，过点C 作CE ⊥PD,联结AE,则AE ⊥PD ，∴ ∠AEC 为二面角 A —PD —C 的平面角，利用直角三角形PCD 面积等积变形可求得CE=AE=√63下略.9.13.提示：在射线CP上取点D，作平面DEF ⊥CP.即棱的垂面.10.450.法1.∵ CD∥AB,由线面平行的判断和性质可推得二面角的棱为过点P且平行于AB的直线，又∵ AB⊥平面PAD，可知∠APD为二面角的平面角.法2.利用面积的射影定理. cosθ=S∆PABS∆PCD11.√63.利用面面平行的性质可知过三点B、M、D1的截面如图D2.5—1所示.此二面角的棱l为过点B且MN∥l∥AC的直线.也可用面积的射影定理求.12.√17.仿例7(2)的方法求解.A BCDA1B1C1D1图D2.5—1NM11。
空间角公式
空间角公式空间角公式是三维空间中两个向量之间的夹角，也称为向量夹角。
在三维空间中，向量的方向和大小都很重要，因此空间角公式是非常重要的数学工具。
空间角公式可以用余弦定理来表示。
假设有两个向量a和b，它们的夹角为θ，那么它们的余弦值可以表示为：cosθ = (a·b) / (|a|·|b|)其中，a·b表示向量a和向量b的点积，|a|和|b|分别表示向量a和向量b的模长。
这个公式可以用来计算任意两个向量之间的夹角。
空间角公式还可以用向量的坐标表示。
假设有两个向量a和b，它们的坐标分别为(a1, a2, a3)和(b1, b2, b3)，那么它们的夹角可以表示为：cosθ = (a1b1 + a2b2 + a3b3) / (sqrt(a1^2 + a2^2 + a3^2)·sqrt(b1^2 + b2^2 + b3^2))其中，sqrt表示平方根。
这个公式可以用来计算任意两个向量之间的夹角，只需要知道它们的坐标。
空间角公式在三维计算机图形学中有广泛的应用。
例如，在计算机游戏中，需要计算物体之间的碰撞，就需要用到空间角公式来计算它们之间的夹角。
在计算机辅助设计中，也需要用到空间角公式来计算物体之间的相对位置和方向。
除了空间角公式，还有一些其他的向量公式也非常重要。
例如，向量的叉积公式可以用来计算两个向量的垂直向量，向量的投影公式可以用来计算一个向量在另一个向量上的投影长度。
这些公式都是三维空间中向量计算的基础，对于理解和应用三维计算机图形学非常重要。
空间角公式是三维空间中向量计算的重要工具，它可以用来计算任意两个向量之间的夹角。
在三维计算机图形学中，空间角公式是非常重要的数学工具，它可以用来计算物体之间的相对位置和方向，对于计算机游戏和计算机辅助设计等领域都有广泛的应用。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第52讲 空间角及其计算
1．在正方体ABCD -A 1B 1C 1D 1中，BC 1与平面BDD 1B 1所成的角为(A)
A ．30°
B ．45°
C ．60°
D ．90°
取B 1D 1的中点E ，连接C 1E ，BE ，
因为C 1E ⊥平面BDD 1B 1，所以∠C 1BE 即为所求角θ. 因为sin θ＝2
22＝1
2
，所以θ＝30°，选A.
2．正四棱锥的侧棱长为23，侧棱与底面所成的角为60°，则该棱锥的体积为(B) A ．3 B ．6
C ．9
D ．18
棱锥的底面对角线长为2×23cos 60°＝23，高为23sin 60°＝3，设底面边长为
a ，则2a ＝23，所以a ＝6，
所以底面面积为a 2＝6，
所以其体积V ＝1
3
×6×3＝6，所以选B.
3．已知二面角α-l -β的大小为60°，m ，n 为异面直线，且m ⊥α，n ⊥β，则m ，n 所成
的角为(B)
A ．30°
B ．60°
C ．90°
D ．120°
4．如图，平面α⊥平面β，A ∈α，B ∈β，AB 与平面α、β所成的角分别为π4和π
6
.过A 、B
分别作两平面交线的垂线，垂足为A ′、B ′，若AB ＝12，则A ′B ′＝(B)
A. 4 B ．6 C
．8 D ．9
连接AB ′，设AB ＝a ，可得AB 与平面α所成的角为∠BAB ′＝π
4
，在Rt △BAB ′
中，有AB ′＝2
2
a .
同理可得AB 与平面β所成的角为∠ABA ′＝π
6
，
所以A ′A ＝1
2
a .
因此在Rt △AA ′B ′中，A ′B ′＝
(
22a )2－(12a )2＝12
a ， 因为AB ＝12，所以A ′B ′＝6，故选B.
5．长为2a 的线段AB 在平面α内的射影线段A 1
B 1的长为a ，则直线AB 与平面α所成
的角的大小为 60° .
设直线AB 与平面α所成的角为θ，则cos θ＝a 2a ＝1
2
，则θ＝60°.
6．已知正三棱锥的侧棱长是底面边长的2倍，则侧棱与底面所成角的余弦值等于 36
.
如图，O 为底面正△ABC 的中心，则OP ⊥平面ABC ，∠PCO 即为所求角，
设AB ＝1，
则PC ＝2，OC ＝
33， 所以cos ∠PCO ＝OC PC ＝3
6.
7．(2017·天津卷)如图，在四棱锥P -ABCD 中，AD ⊥平面PDC ，AD ∥BC ，PD ⊥PB ，AD ＝1，BC ＝3，CD ＝4，PD ＝2.
(1)求异面直线AP 与BC (2)求证：PD ⊥平面PBC ；
(3)求直线AB 与平面PBC 所成角的正弦值．
(1)如图，由已知AD ∥BC ，故∠DAP 或其补角即为异面直线AP 与BC 所成的角．
因为AD ⊥平面PDC ，直线PD ⊂平面PDC ， 所以AD ⊥PD .
在Rt △PDA 中，由已知，得AP ＝AD 2＋PD 2＝5，
故cos ∠DAP ＝AD AP ＝5
5
.
所以异面直线AP 与BC 所成角的余弦值为
55
. (2)证明：由(1)知AD ⊥PD .又因为BC ∥AD ，所以PD ⊥BC . 又PD ⊥PB ，PB ∩BC ＝B ，所以PD ⊥平面PBC .
(3)过点D 作DF ∥AB ，交BC 于点F ，连接PF ，则DF 与平面PBC 所成的角等于AB 与平面PBC 所成的角．
因为PD ⊥平面PBC ，所以PF 为DF 在平面PBC 上的射影，所以∠DFP 为直线DF 和平面PBC 所成的角．
由于AD ∥BC ，DF ∥AB ，故BF ＝AD ＝1. 由已知，得CF ＝BC －BF ＝2. 又AD ⊥DC ，所以BC ⊥DC . 在Rt △DCF 中，可得DF ＝
CD 2＋CF 2＝25，
在Rt △DPF 中，可得sin ∠DFP ＝PD DF ＝5
5
.
所以直线AB 与平面PBC 所成角的正弦值为55
.
8．(2014·新课程卷Ⅱ)直三棱柱ABC -A 1B 1C 1中，∠BCA ＝90°，M ，N 分别是A 1B 1，A 1C 1
的中点，BC ＝CA ＝CC 1，则BM 与AN 所成的角的余弦值为(C)
A. 110
B. 25
C. 3010
D. 22
取BC 的中点D ，连接MN ，ND ，AD ，
由于MN 綊1
2
B 1
C 1綊B
D ，因此ND 綊BM ，
则ND 与NA 所成的角即为异面直线BM 与AN 所成的角． 设BC ＝2，则BM ＝ND ＝6，AN ＝5，AD ＝5， 因此，cos ∠AND ＝ND 2＋NA 2－AD 22ND ·NA ＝30
10.
9．已知正四面体A -BCD 的棱长为a .
(1)AC 与平面 BCD 所成角的余弦值为
3
3 ； (2)二面角A -BD -C 的平面角的余弦值为 1
3 .
设A 在底面BCD 上的射影为O ，连接OA ，连接OC 并延长与BD 相交于E ，连
接AE .
(1)因为AO ⊥平面BCD ，所以∠ACO 就是AC 与平面BCD 所成的角． 因为△BCD 是正三角形， 所以O 是△BCD 的中心．
在Rt △AOC 中，OC ＝23×32a ＝3
3a ，
所以cos ∠ACO ＝OC AC ＝3
3.
所以AC 与平面BCD 所成角的余弦值为33
. (2)因为四面体A -BCD 为正四面体， 所以△BCD 和△ABD 都为正三角形， 所以OE ⊥BD 且AE ⊥BD ，
所以∠AEO 为二面角A -BD -C 的平面角，
所以OE ＝13×32a ＝3a 6，AE ＝3
2
a ，
所以cos ∠AEO ＝OE AE ＝1
3.
所以二面角A -BD -C 的平面角的余弦值为1
3
.
10．如图，已知菱形ABCD 的边长为a ，∠ABC ＝60°，PC ⊥平面ABCD ，且PC ＝a ，E 为P A 的中点．
(1)求证：平面BED ⊥平面ABCD ； (2)求PB 与平面P AC 所成角的正弦值； (3)求二面角D -P A -B 的平面角的余弦值．
(1)证明：设AC 交BD 于O ，连接OE ，因为O 是AC 的中点，E 是P A 的中点，
所以OE ∥PC ，又PC ⊥平面ABCD ， 所以OE ⊥平面ABCD ，
因为OE ⊂平面BED ，所以平面BED ⊥平面ABCD . (2)连接OP ，因为ABCD 是菱形，所以BD ⊥AC ， 又PC ⊥平面ABCD ，所以BD ⊥PC ， PC ∩AC ＝C ，所以BD ⊥平面P AC ， 所以OP 是BP 在平面P AC 上的射影， 所以∠BPO 即为所求角．
在Rt △BPO 中，OB ＝
3
2a ，PB ＝2a ， 所以sin ∠BPO ＝OB PB ＝6
4.
所以PB 与平面P AC 所成角的正弦值为
64
. (3)过D 作DF ⊥P A 于F ，连接BF ，由(2)知BD ⊥P A ， DF ∩BD ＝D ，所以P A ⊥平面BFD ，BF ⊂平面BFD ， 所以P A ⊥BF ，
所以∠DFB 即是所求二面角的平面角． 在△DFB 中，可考虑用余弦定理求∠DFB . 因为PD ＝P A ＝2a ，
取AD 的中点G ，连接PG ，则PG ⊥AD ， PG ＝
PD 2－DG 2＝
72
a ， 由等面积法知AD ×PG ＝P A ×DF ， 得DF ＝a ×72a
2a
＝14
4a ，
BF ＝DF ＝14
4
a ，BD ＝3a ，
所以cos ∠DFB ＝1416a 2＋1416a 2
－3a 22×1416a 2
＝－5
7.
所以二面角D -P A -B 的平面角的余弦值为－5
7
.。