南邮数电-第5章习题答案
数电各章复习题及答案(DOC)

数电各章复习题及答案(DOC)第1章逻辑代数基础一、选择题(多选题)1.以下代码中为无权码的为A.8421BCD码B.5421BCD码C.余三码D.格雷码2.一位十六进制数可以用位二进制数来表示。
A.1B.2C.4D.163.十进制数25用8421BCD码表示为A.10101B.00100101C.100101D.101014.与十进制数(53.5)10等值的数或代码为A.(01010011.0101)8421BCDB.(35.8)16C.(110101.1)2D.(65.4)85.与八进制数(47.3)8等值的数为:A.(100111.011)2B.(27.6)16C.(27.3)16D.(100111.11)26.常用的BCD码有A.奇偶校验码B.格雷码C.8421码D.余三码7.与模拟电路相比,数字电路主要的优点有A.容易设计B.通用性强C.保密性好D.抗干扰能力强8.逻辑变量的取值1和0可以表示:A.开关的闭合、断开B.电位的高、低C.真与假D.电流的有、无9.求一个逻辑函数F的对偶式,可将F中的A.“·”换成“+”,“+”换成“·”B.原变量换成反变量,反变量换成原变量C.变量不变D.常数中“0”换成“1”,“1”换成“0”E.常数不变10.A+BC=A.A+BB.A+CC.(A+B)(A+C)D.B+C11.在何种输入情况下,“与非”运算的结果是逻辑0。
A.全部输入是0B.任一输入是0C.仅一输入是0D.全部输入是112.在何种输入情况下,“或非”运算的结果是逻辑0。
A.全部输入是0B.全部输入是1C.任一输入为0,其他输入为1D.任一输入为113.以下表达式中符合逻辑运算法则的是2A.C·C=CB.1+1=10C.0<1D.A+1=114.当逻辑函数有n个变量时,共有个变量取值组合?2nA.nB.2nC.nD.215.逻辑函数的表示方法中具有唯一性的是A.真值表B.表达式C.逻辑图D.卡诺图16.F=AB+BD+CDE+AD=A.ABDB.(AB)DC.(AD)(BD)D.(AD)(BD)17.逻辑函数F=A(AB)=A.BB.AC.ABD.AB二、判断题(正确打√,错误的打某)1.8421码1001比0001大。
数电第五版(阎石)第五章课后习题及答案pptx

03
习题三答案ຫໍສະໝຸດ 习题三第1题答案1.1 逻辑函数的表示方法 1.1答案:逻辑函数有多种表示方法, 如真值表、逻辑表达式、波形图和卡
诺图等。
1.2 逻辑函数的化简方法
1.2答案:逻辑函数的化简方法包括代 数法、公式法和卡诺图法等。
1.3 逻辑函数的运算规则
1.3答案:逻辑函数的运算规则包括与、 或、非等基本运算,以及与或、与非、 或非等复合运算。
习题一第3题答案
总结词
卡诺图化简
答案
通过卡诺图化简,我们得到最简的逻 辑表达式为(F = A'B + A'C + BC)。
02
习题二答案
习题二第1题答案
总结词
逻辑函数的表示方法
详细描述
逻辑函数的表示方法有真值表、逻辑表达式、逻辑图和波形图等。这些表示方法各有特 点,可以根据具体需求选择使用。真值表可以清晰地表示输入和输出之间的逻辑关系; 逻辑表达式简化了函数表示,便于分析和计算;逻辑图能够直观地展示逻辑函数的结构
习题三第2题答案
在此添加您的文本17字
2.1 逻辑函数的化简步骤
在此添加您的文本16字
2.1答案:逻辑函数的化简步骤包括合并项、消去项和简 化表达式等。
在此添加您的文本16字
2.2 逻辑函数的化简技巧
在此添加您的文本16字
2.2答案:逻辑函数的化简技巧包括利用运算规则、消去 项和合并项等。
在此添加您的文本16字
和功能;波形图则可以反映函数在时间序列上的动态变化。
习题二第2题答案
总结词
逻辑函数的化简方法
详细描述
逻辑函数的化简方法有多种,包括公式化简法、卡诺 图化简法和布尔代数化简法等。公式化简法基于逻辑 代数的基本公式和规则,通过简化表达式得到最简结 果;卡诺图化简法利用卡诺图的性质,通过图形直观 地找出最小项的组合,从而得到最简逻辑函数表达式 ;布尔代数化简法则通过代数运算简化逻辑函数。这 些化简方法各有优缺点,应根据具体情况选择使用。
南邮数电第5章6序列信号发生器.ppt

Q3 Q2 Q1 状态转移路线 模数 1 01
0 10 1 00 0 00
M=4 ×
0 01
0 10
需增加一个触发器! 取n=4,重新列状态转移表
Q4 Q3 Q2 Q1 状态转移路线 模数
101 0
010 0 100 0
M=6
000 1
√
001 0
010 1
101 0
(3) 求激励函数
Qn4 Qn3 Qn2 Qn1 Qn4+1 Qn3+1 Qn2+1 Qn+11 D1
解:方法一:用小规模器件实现 (1)设计M=8的计数器,方法同前面的同 步(异步)计数器的设计。 本解取n=3 的异步二进制加法计数器 (2)设计组合电路
组合电路真值表为:
Q3
Q2
Q1 F
0
0
01
0
0
11
0
1
01
0
1
11
1
0
00
1
0
11
1
1
00
1
1
11
用卡诺图化简得到:F=Q3+Q1
逻辑图为:
5
的n位码就是起跳状态。
表 2-4线译码器的真值表
Q2
Q1
Y0
Y1
Y2
Y3
0
0
1
0
0
0
0
1
0
1
0
0
1
0
0
0
1
0
1
1
0
0
0
1
Q2
Q1
1J
1J
C1
C1
1K
1K
数电第五章习题答案 .doc
自我检查题5.1 时序电路和组合电路的根本区别是什么?同步时序电路与异步时序电路有何不同?解答:从功能上看,时序电路任何时刻的稳态输出不仅和该时刻的输入相关,而且还决定于该时刻电路的状态,从电路结构上讲,时序电路一定含有记忆和表示电路状态的存储器。
而组合电路任何时刻的稳态输出只决定于该时刻各个输入信号的取值,由常用门电路组成则是其电路结构的特点。
在同步时序电路中,各个触发器的时钟信号是相同的,都是输入CP 脉冲,异步时序电路则不同,其中有的触发器的时钟信号是输入cp 脉冲,有的则是其他触发器的输出,前者触发器的状态更新时同步的,后者触发器状态更新有先有后,是异步的。
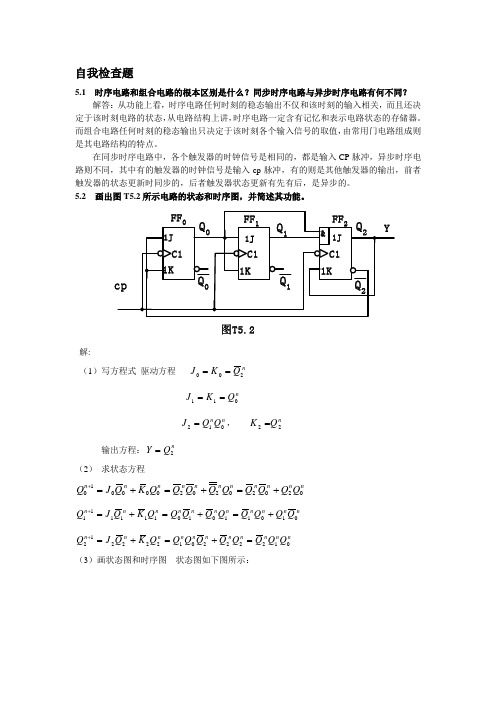
5.2 画出图T5.2所示电路的状态和时序图,并简述其功能。
图T5.2解:(1)写方程式 驱动方程 nQ K J 200==n Q K J 011==n n Q Q J 012=, n Q K 22=输出方程:nQ Y 2= (2) 求状态方程nn n n n n n n n n n Q Q Q Q Q Q Q Q Q K Q J Q 02020202000010+=+=+=+ n n n n n n n n n n n Q Q Q Q Q Q Q Q Q K Q J Q 01011010111111+=+=+=+ n n n n n n n n n n n Q Q Q Q Q Q Q Q Q K Q J Q 01222201222212=+=+=+(3)画状态图和时序图 状态图如下图所示:101时序图如下图所示:CP Q 0Q 1Q 25.3 试用边沿JK 触发器和门电路设计一个按自然态序进行计数的七进制同步加法计数器。
解:(1)状态图如下图:(2)求状态方程、输出方程CQ Q Q n n n /101112+++的卡诺图如下图所示:输出方程为nn Q Q C 12=状态方程:n n n n n Q Q Q Q Q 120112+=+ n n n n n n Q Q Q Q Q Q 0120111+=+ n n n n n Q Q Q Q Q 120110+=+驱动方程:n n n n n n n n n n n n n n n Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q 0122120121220112)(++=++=+n n n n n n Q Q Q Q Q Q 1021011+=+n n n n n Q Q Q Q Q 0012101)(++=+与JK 触发器的特性方程 比较,可以得到驱动方程 n n Q Q J 012= 、 n Q K 12=n Q J 01= 、n n Q Q K 021=n n n n Q Q Q Q J 12120=+= 10=K(4) 无效状态转换情况 111/1000 能自启动(5) 逻辑图如下图所示:5.4 画出用时钟脉冲上升沿触发的边沿D 触发器组成的4位二进制异步加法计数器和减法计数器的逻辑电路图。
数电第五章习题解答2

1 第五章习题解答2
5.10解:要周期性的输出00101101脉冲序列,分析题意可得如下时序图:
可看出输出信号Y 的周期为8个CP 周期,即电路应该有8个状态,联想到3位二进制同步加法计数器,可以把Y 看成210Q Q Q
的函数,可得Y 的卡洛图:
n n Y 的卡诺图
2110n n n n Y Q Q Q Q =+ 逻辑图(略)
5.13解:因为74290是异步清零和异步置9,所以:
(a )0101N S =,为5进制计数器;
(b )这种接法可参照教材P333图5.2.45,且其中1100为过渡状态,所以N=9;
(c )因为是异步置9,所以当计数器计到0110时计数器置为1001,而0110为过渡状态,所以计数器的实际进制为7进制;其状态图为:
000000010010001101000101
−−→−−→−−→−−→−−→3210
n n n n Q Q Q Q 1001
5.14解:
(a )因为74163是同步清零,所以有:11100N S -=,N=13
(b )因为74161是同步置数,所以有:11100N S -=,N=13。
南邮信号与系统答案第5章

信号与系统 · 习题解答
第11页
5-8 试用单位阶跃序列表示图示离散信号。 (b) f (k)
2
3
2
1 −2 −1 0 1 2 3
4 5
6
−1
k
解:f 2 (k ) = ε (k + 2) + ε (k ) + ε (k − 2) − 4ε (k − 4) + ε (k − 6)
信号与系统 · 习题解答
10 5
k<0 k =0 k ≥1
∴ f1 (k − 1) + f 2 (k + 1) 0 k <0 ⎧ ⎪ =⎨ 1 k =0 ⎪2 k + k − 1 k ≥ 1 ⎩
2
1
−1 0 1 2
L
3 k
信号与系统 · 习题解答
第5页
*(4) f1 (k − 1) ⋅ f 2 (k + 1) 解:
f1 (k − 1) ⋅ f 2 (k + 1) ⎧ 0 ⎪ =⎨ 0 ⎪2 k (k − 1) ⎩ ⎧ 0 =⎨ k ⎩2 (k − 1) k <0 k =0 k ≥1 k <1 k ≥1
⎧C1 = 0 解得 C1 = 0 , ⎪ 2 ⎨ 2 2 C2 = ⎪2[C1 cos 3 π + C2 sin 3 π ] = 2 3 ⎩
2 2 sin kπ 所以 yzi (k ) = 2 ⋅ 3 3
k
k ≥0
信号与系统 · 习题解答
第19页
5-15 试求下列差分方程的单位函数响应 (1) y (k + 2) + 3 y (k + 1) + 2 y (k ) = x(k + 1) + x(k )
南邮计算机网络课后答案第五章资料

第五章传输层5—01 试说明运输层在协议栈中的地位和作用,运输层的通信和网络层的通信有什么重要区别?为什么运输层是必不可少的?答:运输层处于面向通信部分的最高层,同时也是用户功能中的最低层,向它上面的应用层提供服务运输层为应用进程之间提供端到端的逻辑通信,但网络层是为主机之间提供逻辑通信(面向主机,承担路由功能,即主机寻址及有效的分组交换)。
各种应用进程之间通信需要“可靠或尽力而为”的两类服务质量,必须由运输层以复用和分用的形式加载到网络层。
5—02 网络层提供数据报或虚电路服务对上面的运输层有何影响?答:网络层提供数据报或虚电路服务不影响上面的运输层的运行机制。
但提供不同的服务质量。
5—03 当应用程序使用面向连接的TCP和无连接的IP时,这种传输是面向连接的还是面向无连接的?答:都是。
这要在不同层次来看,在运输层是面向连接的,在网络层则是无连接的。
5—04 试用画图解释运输层的复用。
画图说明许多个运输用户复用到一条运输连接上,而这条运输连接有复用到IP数据报上。
5—05 试举例说明有些应用程序愿意采用不可靠的UDP,而不用采用可靠的TCP。
答:VOIP:由于语音信息具有一定的冗余度,人耳对VOIP数据报损失由一定的承受度,但对传输时延的变化较敏感。
有差错的UDP数据报在接收端被直接抛弃,TCP数据报出错则会引起重传,可能带来较大的时延扰动。
因此VOIP宁可采用不可靠的UDP,而不愿意采用可靠的TCP。
5—06 接收方收到有差错的UDP用户数据报时应如何处理?答:丢弃5—07 如果应用程序愿意使用UDP来完成可靠的传输,这可能吗?请说明理由答:可能,但应用程序中必须额外提供与TCP相同的功能。
5—08 为什么说UDP是面向报文的,而TCP是面向字节流的?答:发送方UDP 对应用程序交下来的报文,在添加首部后就向下交付IP 层。
UDP 对应用层交下来的报文,既不合并,也不拆分,而是保留这些报文的边界。
南邮数电-第5章习题答案

南邮数电-第5章习题答案5.1 基本触发器的逻辑符号与输入波形如图P5.1所示。
试作出 Q 、Q 的波形。
图 P5.15.2 图P5.2电路,在开关S 由A 点拨到B点,再由B 点拨回A 点过程中,A 、B 两点电压波形如图中所示。
试作出 Q 和 Q 端的波形。
图 P5.2S D R D QQ345TitleNumSize B Date:24-Ma File:E:\DesS RQQS R D DAB C D6543TitleNumber RevisionSize B Date:24-Mar-2002Sheet ofSRRRS+5VBAQQU AtU BtQttQ5.3 分析图P5.3的逻辑功能:列出真值表,导出特征方程并说明 S D 、R D 的有效电平。
解:(1)列真值表如下 (2)求特征方程5.4 对于图P5.4电路,试导出其特征方程并说明对A 、B 的取值有无约束条件。
Ø1 111 000 1Qn0 0Q n+1S D R D Ø00100Ø11100101011S DR D Q nS D R D =0Q n+1=S D +R D Q n QRD≥1G ≥1G 2Q S D图解:(1)列真值表如下 (2)求特征方程5.5 试写出图P5.5触发器电路的特征方程。
QA&G ≥1G 2Q B图 11 1Qn1 010 110 0Qn+1A B 101100111011111001A BQ nQn+1=A+B+Qn 对A 、B 的取值时,Q n+1=S+RQ nSR=0CP=1图Q≥1≥1Q&&CP=0时,5.11 画出图P5.11电路Q 端的波形。
设初态为“0”。
解:特征方程为: 而且 ,Q 端波形如图P5.11所示。
图P5.115.125.12 画出图P5.12电路中Q 1、Q 2 的波形。
解:特征方程为: ,Q 端波形如图P5.12所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5.4 对于图P5.4电路,试导出其特征方程并说明对A、B的取值有无约束条件。
Q
图P5.11
P5.12
5.12 画出图P5.12电路中Q 1、Q 2 的波形。
解:特征方程为: ,Q 端波形如图P5.12所示。
=[D]·CP 1,Q 1n+1
Q 2n+1= Q 1n
[]·CP 2
图P5.14 图P5.15
5.15 画出图P5.15电路中Q 端的波形。
解:Q 端波形如图P5.15所示。
5.16 试作出图P5.16电路中Q A 、Q B 的波形。
解:特征方程为: , ,Q 端波形如图P5.16所示。
Q A n+1= Q B n
[]·A Q B n+1= Q A n []·B
A R D
B Q A Q B
R D CP CP ⊕Q 2
Q 1Q 2
图P5.16 图P5.17
5.17 试作出图P5.17电路中Q 1、Q 2 的波形。
解:特征方程为: , ,Q 端波形如图P5.17所示。
5.18 试作出图P5.18电路中Q 1和Q 2的波形(设Q 1和Q 2的初态均为“0”),并说明Q 1和 Q 2对于CP 2各为多少分频。
解:特征方程为: , ,Q 端波形如图P5.18所示。
Q 1和Q 2对于CP 2都是4分频,即
图P5.18 图P5.19
5.19 已知电路如图P5.19,试作出Q 端的波形。
设Q 的初态为“0”。
解:特征方程为: ,Q 端波形如图P5.19所示。
5.20 已知输入u I 、输出u O 波形分别如图P5.20所示,试用两个D 触发器将该输入波形u I 转换成输出波形u O 。
解:输出u O 是对输入u I 的4分频,而采用1个DFF 可实现2分频,故实现电路如图P5.20所示。
图P5.20
5.21 试分别用公式法和列表图解法将主从SR 触发器转换成JK 触发器。
解1:
Q 1n+1= Q 1n []·(CP ⊕Q 2)Q 2n+1
= Q 2n []·Q 1?)?,(2
2
21==CP
Q CP Q f f f f Q 1n+1= Q 1n []·
CP 1
Q 2n+1= ·Q 2n []·CP 2Q 1n CP 2CP 1Q 1Q 2
4
1
,412
221==CP Q CP Q f f f f Q n+1
= [ A ]·CP CP A Q
u I
u O
Q n+1=S+RQ n SR =0
Q n+1=JQ n +KQ
n
令新老触发器的次态方程相等,则有S=JQ n ,R=K
但不满足约束条件SR =0。
改为:
解2: (1)列综合表,如下所示: (2)作卡诺图,如下图所示
(3)电路图如下:
图P5.21
S=JQ n
,R=KQ n
=JQ (因为Q n+1=JQ n +KQ n n +KQ n Q n )01 101 010 100 0Q n+1K Q n
S R
0 1 Ø0 ØØ0 0 0 0 0 0 J 0
1 1
11 010 110 0 1 1
Ø0 0 0 0 1 1 1 1 1
S=JQ
n
R=KQ n
J K。
