行为博弈理论
博弈论

2.2.1 博弈论的定义现代经济学的最新发展有一个特别引人注目的特点,那就是博弈论在经济学中越来越受到重视。
博弈论,又称为对策论,它是研究决策主体的行为发生直接相互作用时候的决策以及这种决策的均衡问题。
也就是说,当一个主体,好比说一个人或一个企业的选择受到其他人、其他企业选择的影响,而且反过来影响到其他人、其他企业选择时的决策问题和均衡问题①。
简单地说,就是研究决策主体的行为在发生直接相互作用时,他们如何进行决策,以及这种决策的均衡问题。
1944 年冯·诺依曼和摩根斯特恩(Morgenstern)合作出版了《博弈论与经济行为》(The Theory of Games and Economic Behavior),开始将博弈论引入经济学,成为现代经济博弈论研究的开端。
20 世纪50 年代纳什(John F. Nash)、塔克(Tucker)等人的研究,奠定了现代博弈论的基石。
在其后的几十年里,许多经济学家致力于博弈论的研究,1965 年泽尔腾(Reinhard Selten)将纳什均衡的概念引入了动态分析;1967-1968 年,海萨尼(John C. Harsanyi)把不完全信息分析引入博弈论的研究;1982 年克瑞普斯(David M. Kreps)和威尔逊(RobertWilson)分析了动态不完全信息条件下的博弈问题。
1994 年诺贝尔经济学奖授予了纳什、泽尔腾和海萨尼三位博弈论专家,此后在2001 年诺贝尔经济学奖同样授予了三位博弈论的专家②。
博弈论是一种关于行为主体策略相互作用的理论,它已形成了一套完整的理论体系和方法论体系。
它具有基本假设的合理性、研究对象的普遍性、研究结论的真实性、方法论的实证性等特点。
正是因为这些特点,博弈论的产生和发展引发了一场深刻的经济学革命,使得现代经济学从方法论,到概念和分析的方法体系,都发生了很大的变化。
正如克瑞普斯(Kreps)在《博弈论与经济模型》一书中指出“在过去一二十年中,经济学在方法论,以及语言、概念等等方面,经历了一场温和的革命,非合作博弈已经成为范式的中心……在经济学或者与经济学原理相关的金融、会计、营销和政治科学等学科中,现在人们已经很难找到不①懂纳什均衡能够‘消化’近代文献的领域。
博弈论完整版PPT课件

2-阶理性: C相信R相信C是理性的,C会将R4从R的战略空间中剔除, 所以 C不会选择C1;
3-阶理性: R相信C相信R相信C是理性的, R会将C1从C的战略空间中剔 除, R不会选择R1;
基本假设:完全竞争,完美信息
个人决策是在给定一个价格参数和收入的条 件下最大化自己的效用,个人的效用与其他人 无涉,所有其他人的行为都被总结在“价格”参数 之中
一般均衡理论是整个经济学的理论基石 和道义基础,市场机制是完美的,帕累托 最优成立,平等与效率可以兼顾。
.
3
然而在以下情况,上述结论不成立:
.
19
理性共识
0-阶理性共识:每个人都是理性的,但不知道其 他人是否是理性的;
1-阶理性共识:每个人都是理性的,并且知道其 他人也是理性的,但不知道其他人是否知道自己 是理性的;
2-阶理性共识:每个人都是理性的,并且知道其
他人也是理性的,同时知道其他人也知道自己是
理性的;但不知道其他人是否知道自己知道他们
如果你预期我会选择X,我就真的会选择X。
如果参与人事前达成一个协议,在不存在外部强 制的情况下,每个人都有积极性遵守这个协议,这 个协议就是纳什均衡。
.
28
应用1——古诺的双寡头垄断模型(1938)
假定:
只有两个厂商 面对相同的线形需求曲线,P(Q)=a-Q, Q=q1+q2 两厂商同时做决策; 假定成本函数为C(qi)=ciqi
劣策略:如果一个博弈中,某个参与人有占优策略,那么
该参与人的其他可选择策略就被称为“劣策略”。
基于博弈理论的市场参与者行为分析

基于博弈理论的市场参与者行为分析市场是一个复杂的生态系统,各种不同类型的参与者在其中争夺资源和利益。
为了更好地理解市场参与者的行为,我们可以借助博弈理论来进行分析。
博弈理论将参与者视为理性的决策者,通过分析他们的策略和互动,揭示了市场行为背后的深层规律。
在市场中,参与者的行为可以被视为一场博弈,参与者的目标是追求自身的利益最大化。
博弈理论将市场行为分为合作和竞争两种模式,每种模式对应不同的策略和结果。
接下来,我们将分别探讨这两种模式下的市场参与者行为。
在合作模式下,市场参与者倾向于通过合作与其他参与者互利共赢。
这种合作可以体现为企业之间的联盟合作、供应链的协同以及跨国公司的国际合作等。
在这种情况下,博弈理论中的合作博弈成为分析参与者行为的重要工具。
合作博弈通过定义参与者之间的合作程度,分析他们之间的收益分配和行为策略。
例如,在确定如何分配合作利益时,参与者可以采用合作博弈中的谈判和合同机制。
通过这种方式,他们可以协商出合适的方案,并维持长期的合作关系。
然而,在市场中,并非所有的参与者都能够达成合作。
竞争模式下,各参与者之间追求的是自身利益的最大化,而非与他人的合作。
这种竞争博弈反映出市场中的竞争与合作两种力量的较量。
在竞争模式下,参与者为了获得更多的市场份额和利润,采取了各种策略来击败竞争对手。
博弈理论中的非合作博弈技巧和理论工具被广泛应用于分析这种情况下的市场参与者行为。
非合作博弈模型中的核心概念是“纳什均衡”,即在参与者之间不存在更好的策略选择。
纳什均衡是指在参与者选择最优策略的前提下,任何一方都没有动机改变自己的策略。
通过分析纳什均衡点,我们可以揭示市场中不同参与者之间的互动和竞争策略。
例如,在定价竞争中,参与者可以通过建立价格反应模型和分析竞争对手的价格策略,找到纳什均衡点,从而制定出最优的定价策略。
市场参与者的行为分析还可以从博弈理论的其他角度进行深入研究。
例如,“重复博弈”模型可以用来分析市场参与者在长期竞争中的行为。
【国家社会科学基金】_行为博弈理论_基金支持热词逐年推荐_【万方软件创新助手】_20140813
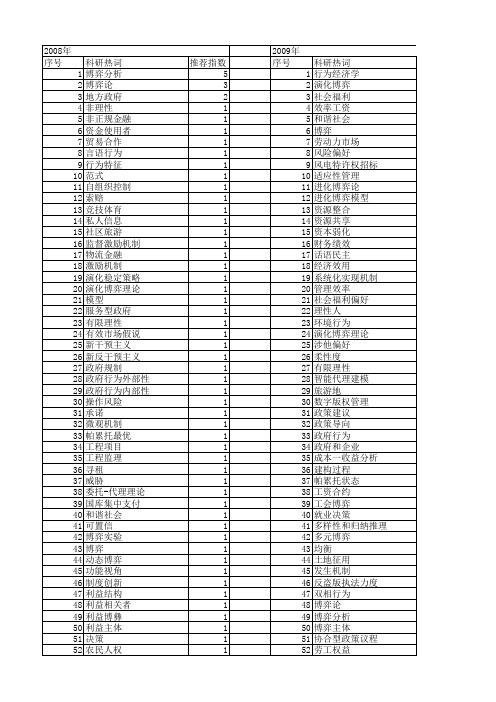
科研热词 博弈分析 博弈论 地方政府 非理性 非正规金融 资金使用者 贸易合作 言语行为 行为特征 范式 自组织控制 索赔 竞技体育 私人信息 社区旅游 监督激励机制 物流金融 激励机制 演化稳定策略 演化博弈理论 模型 服务型政府 有限理性 有效市场假说 新干预主义 新反干预主义 政府规制 政府行为外部性 政府行为内部性 操作风险 承诺 微观机制 帕累托最优 工程项目 工程监理 寻租 威胁 委托-代理理论 国库集中支付 和谐社会 可置信 博弈实验 博弈 动态博弈 功能视角 制度创新 利益结构 利益相关者 利益博彝 利益主体 决策 农民人权
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80
2011年 科研热词 演化博弈 激励理论 金融监管 行为经济学 博弈 分析 互惠 隐性契约治理 随机稳定 道德距离 逆向选择 违规行为 越界迁移 计算主义 西部农村金融机构 西藏民族文化 衍生产品 行为合约 行为博弈理论 自动机博弈 联合操纵 社会距离 社会偏好 研究进展 知识转移 知识联盟 知识共享 监管套利 理性经济人 激励约束政策 激励 沟通 污染密集型企业 次贷危机 模型 期货市场 期货交易 显性契约治理 旅游资源 旅游区域合作 意向性 惩罚 心理契约 微观主体 家族企业 实验经济学 多元动态博弈模型 外资零售业 复制动态 均衡选择 均衡博弈 地方政府 推荐指数 6 3 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
博弈论与经济行为

博弈论与经济行为引言博弈论是研究决策制定者在不确定环境中作出选择时的数学工具和框架。
它不仅仅应用于数学和理论经济学领域,也在实际的经济行为中发挥了重要的作用。
本文将探讨博弈论如何与经济行为相关,并分析其在经济学中的应用。
博弈论的根本概念博弈论主要研究多个决策制定者之间的相互作用和决策选择。
它涉及到参与者的利益、行动和信息。
博弈论中的根本概念包括博弈参与者、策略、支付和收益等。
在博弈论中,参与者根据自身的利益和目标选择策略,并希望通过决策获得最大的支付或收益。
参与者的决策会受到其他参与者的决策影响,因此博弈论研究参与者之间的相互作用和相互影响。
博弈论与经济学之间的联系博弈论与经济学密切相关,因为经济行为往往涉及到多个经济主体之间的相互作用和选择。
一些经典的经济学问题可以通过博弈论的方法来研究和解决。
例如,在市场经济中,供应者和需求者之间的交互可以看作是一个博弈过程。
供应者希望以尽可能高的价格出售产品,而需求者那么希望以尽可能低的价格购置产品。
供应者和需求者的策略选择将会直接影响产品的价格和销售量。
通过博弈论的分析,可以确定供应者和需求者的最优策略,从而实现市场均衡。
博弈论还可以应用于其他经济学领域,如产业组织、拍卖、博弈模型和战略行为等。
通过博弈论的分析,可以研究市场的竞争结构、企业的策略选择以及市场参与者之间的合作和冲突。
实际案例分析为了更好地理解博弈论在经济行为中的应用,我们将通过一个实际案例来进行分析。
假设有两家咖啡店A和B在同一区域竞争。
研究说明,如果一家店的价格比另一家低,它将吸引更多的顾客。
两家店之间的竞争导致它们都希望降低自己的价格以吸引更多的顾客。
但是,如果两家店都降低价格,它们的利润都会下降。
这个案例可以用博弈论中的囚徒困境来解释。
店A和店B都希望通过降低价格获得更多的顾客,但如果两家店都降低价格,它们的利润将受损。
由于缺乏合作机制,两家店很可能会陷入囚徒困境,最终导致利润的下降。
博弈论与经济行为

博弈论与经济行为博弈论,作为一门研究决策者在面对不确定环境时进行决策的数学工具,在经济学领域具有重要的地位。
通过博弈论的分析,我们可以更好地理解和预测经济行为背后的决策动机和结果。
本文将探讨博弈论对经济行为的影响,并深入分析其中的一些重要概念和理论。
博弈论的核心思想是理性决策。
在博弈论中,个体被认为是理性的,并在面对不确定性时尽力追求自身的利益最大化。
在经济领域,这一理念被广泛应用于分析企业的市场竞争、投资者的资产配置以及政府的政策制定等方面。
一个重要的博弈论概念是“纳什均衡”。
纳什均衡是指在一个博弈中,每个参与者选择的策略都是相互协调的,没有任何一个参与者可以通过单方面改变策略而达到更好的结果。
这个概念对解释市场行为和竞争具有重要意义。
在市场中,企业之间相互竞争,为了争夺市场份额,它们需要考虑对手可能的反应,从而选择最优的策略。
纳什均衡理论帮助我们预测市场行为和竞争结果,为企业决策提供有力支持。
除了纳什均衡,博弈论还包含了许多其他的重要理论和概念。
例如,博弈矩阵是博弈论中常用的分析工具之一。
博弈矩阵将参与者的策略以及可能的结果呈现为一个矩阵,通过分析矩阵中不同策略的组合对参与者的影响,我们可以得出关于决策者策略选择的结论。
这种分析方法可以应用于许多经济领域,如竞价拍卖和合作博弈等。
此外,还有一些博弈论模型和理论被广泛应用于解释和预测现实世界中的经济行为。
例如,囚徒困境是一个经典的博弈模型,用于解释为什么在某些情况下,个体往往会为了追求自身利益而最终导致双方都得不到最佳结果。
这个模型可以解释为什么在一些市场中,企业往往无法达到理想的竞争结果,以及为什么国家之间在某些问题上很难达成合作。
对于个体和国家来说,面临的困境是如何在追求自身利益的同时尽可能达到最佳结果。
博弈论在经济学领域的应用还包括博弈策略的设计和调整。
在现实世界中,参与者可能会根据他们的利益和对手的动作不断调整自己的策略。
通过博弈论的分析,我们可以研究这种策略调整的动态过程,并预测参与者最终可能选择的策略。
经济学中的博弈理论
经济学中的博弈理论导言博弈理论,作为经济学中的一个关键分支,研究了人们在决策过程中相互作用的情况下所面临的策略选择。
本文将探讨博弈理论的基本概念、应用领域以及对经济学的影响。
一、博弈理论的基本概念博弈理论涉及参与者之间的相互作用和决策过程。
下面是博弈理论中的一些关键概念:1.1 参与者在博弈理论中,参与者是指在决策过程中采取行动的个体或组织。
他们的决策将在相互作用中彼此影响。
1.2 策略策略是参与者为达到特定目标而采取的行动计划。
博弈理论通过分析不同策略的优劣势来推断参与者的最佳选择。
1.3 支付支付是参与博弈的参与者所获得或损失的效用。
博弈理论通过对支付的分析来评估参与者采取特定策略的激励和决策。
1.4 博弈形式博弈形式确定了参与者之间的规则和限制。
它定义了参与者可采取的策略集合,以及每种策略组合的结果。
1.5 均衡博弈均衡是指在博弈中参与者达到的一种稳定状态,其中没有参与者有动机单方面改变其策略。
二、博弈理论的应用领域博弈理论在许多领域中得到广泛应用,包括经济学、政治学、战略管理等。
以下是一些典型的应用领域:2.1 经济学博弈理论在经济学中的应用是最为重要和广泛的。
它研究了在市场、公司决策和资源分配等方面的决策制定过程,并分析了个体和组织之间的相互作用。
2.2 政治学政治学家运用博弈理论来研究选举、立法和国际关系等政治过程。
博弈理论的工具为研究者提供了一种分析决策制定者之间相互作用的方式。
2.3 战略管理战略管理是博弈理论的一个重要应用领域。
企业通过运用博弈理论,制定合适的竞争策略,从而在市场竞争中取得优势。
三、博弈理论对经济学的影响博弈理论对经济学产生了深远的影响,尤其是在以下方面:3.1 市场分析博弈理论提供了一种有效的工具,用于分析市场中不同参与者的策略选择和相互作用。
基于博弈理论的分析,可以预测市场行为和价格的变化。
3.2 合作与竞争博弈理论研究了合作和竞争之间的相互作用。
通过博弈理论的研究,经济学家可以理解参与者之间的合作动机和竞争策略,并为政策制定者提供有关如何促进合作或竞争的建议。
博弈论的十大定律
博弈论,作为现代经济学、政治学、社会学等领域的重要理论基础,研究的是在信息不完全、相互依赖的决策环境中,理性个体如何进行策略选择以实现自身利益最大化。
以下是博弈论的十大定律,这些定律帮助我们更好地理解和预测个体或群体在博弈中的行为。
一、零和博弈定律零和博弈定律指出,在博弈中,一方所获得的收益等于另一方所付出的成本,整个博弈的收益总和为零。
这意味着一方得益的同时,另一方必然受损。
这一定律在经济学中广泛应用,如股市、竞争市场等。
二、纳什均衡定律纳什均衡定律认为,在博弈中,每个参与者都选择了自己的最优策略,而且这种策略组合是不可改变的,即没有任何参与者愿意单独改变自己的策略。
纳什均衡是博弈论中最重要的概念之一,为研究个体或群体在博弈中的行为提供了理论依据。
三、囚徒困境定律囚徒困境定律描述了一个典型的非合作博弈,其中两个理性的囚徒在面临选择时,如果都选择合作,则会获得较好的结果;但如果一方选择背叛,另一方选择合作,背叛者将获得更好的结果,而被背叛者将遭受损失。
在这种情况下,囚徒们往往会选择背叛,导致双方都受损。
四、合作博弈定律合作博弈定律认为,在博弈中,参与者可以通过合作实现共赢。
合作博弈强调个体或群体之间的相互依赖和利益共享,以实现整体利益的最大化。
在合作博弈中,参与者通常会寻求制定合作策略,以实现共同目标。
五、承诺定律承诺定律指出,在博弈中,承诺是一种有效的策略。
承诺可以降低博弈中的不确定性,使其他参与者相信你的决策是可信的。
在承诺博弈中,承诺可以促使其他参与者采取合作策略,从而实现共赢。
六、声誉定律声誉定律认为,个体在博弈中的声誉对其决策具有重要影响。
在长期博弈中,个体会努力维护自己的声誉,以获取其他参与者的信任。
声誉良好的个体在博弈中更容易获得合作机会,从而实现自身利益最大化。
七、风险规避定律风险规避定律指出,在博弈中,个体往往倾向于规避风险。
当面临不确定性时,个体会选择保守策略,以降低损失。
这一定律在金融、保险等领域具有重要意义。
行为经济学博弈论
行为经济学博弈论
行为经济学是经济学的一个分支,它将心理学和经济学原理结合起来,研究人们在经济决策中的行为和心理过程。
博弈论则是一种数学工具,用于分析竞争环境中参与者的策略和决策。
在行为经济学中,博弈论可以用于分析人们在竞争环境中的决策行为。
例如,在囚徒困境中,两个犯罪嫌疑人被逮捕并分别审讯。
如果他们都保持沉默,他们将被判处较轻的刑期;如果他们都认罪,他们将被判处较重的刑期;如果一个认罪而另一个保持沉默,认罪的人将被释放,而保持沉默的人将被判处较重的刑期。
在这个例子中,每个犯罪嫌疑人都面临着一个决策:是保持沉默还是认罪。
如果他们都考虑自己的利益,他们可能会认罪,因为这样他们可以获得最短的刑期。
然而,如果他们考虑到对方的行为,他们可能会意识到保持沉默是更好的选择,因为这样他们可以共同获得较轻的刑期。
通过使用博弈论,行为经济学家可以分析人们在这种竞争环境中的决策,并研究影响这些决策的因素,例如信任、合作、竞争等。
这些研究可以帮助我们更好地理解人们在经济决策中的行为,并为政策制定者提供有价值的建议。
动物行为学中的博弈理论及其应用
动物行为学中的博弈理论及其应用动物行为学是生物学中一个重要的分支,研究动物的行为模式、社会行为和进化心理学。
其中,博弈理论是动物行为学中的重要概念,它帮助我们更好的理解动物之间复杂的相互作用。
一、博弈理论简介博弈理论主要是研究决策行为的数学方法,它源于人类社会中的赌博游戏,但逐渐被应用于动物行为学中。
博弈理论主要关注参与者之间的相互作用和选择下的结果。
在动物世界中,博弈理论意味着动物之间的交互可以被看做是一个博弈过程。
例如,两个动物之间的相互作用可以被看做一个“博弈”,其中每个动物都根据自身的行为做出最优选择,以期达到最有利的结果。
二、博弈策略与动物行为在动物行为学中,博弈策略是指在博弈过程中动物会采取的行为方式。
动物选择的行为方式可能会受到种群中其它动物的影响。
例如,雄性砂地鸫通过多次展示作为求偶行为的“翅膀舞”来吸引雌性的注意,这个过程可以被视为一种“博弈”的过程。
如果雄性表现得不佳,雌性就会失去兴趣,随后的结局将是他们分手。
对于这个问题,雄性可以选择认输或更改策略。
还有一种经典的策略称为“策略稳定性”。
它描述的是当所有参与者都执行同样的策略时,这个策略产生的结果是无法被改变并被所有动物接受的。
基于这个策略,许多动物在决策中选择跟从常规行为而不是尝试新的策略。
例如,狒狒群体中,所有动物都更喜欢尝试每天都能获得的果实,而不是冒险去争夺新的水果。
三、博弈理论的应用博弈理论在动物行为学中的应用非常广泛。
其中一个应用就是研究动物之间的斗争。
斗争是许多动物之间的常见行为。
许多生物通过斗争来争夺资源,例如食物、水源和繁殖机会。
博弈模型可以用来描述这些斗争过程中动物之间的策略和结果。
博弈模型还可以应用于社会生物学中,这是一门研究动物社会行为的学科。
例如,当新加入一个动物到已有群体中,这个动物需要做出的选择可能影响整个群体。
当新加入的动物采取了不同的行为方式时,群体中的其它动物可能会做出不同的选择,结果可能会导致大部分动物获得更少的资源。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
行为博弈理论
在“菜鸟”上看到一篇非常有意思的文章,讲的是行为博弈理论,真的是很有意思。
我们有很多人都学过数学,但是大都把数学当作一门科学上的工具,实际生活中用到的数学原理好像并不多见,能把数学思想来指导个人学习生活的例子就更少了,所以能看到这样一篇用数学来剖析大众在生活中可以遇见的事例的文章,实在是弥足珍贵。
不过美中不足的是文章中的分析并不是完全正确的,这是非常可惜的一件事情。
我们还是把文章引出来吧:下面要讲到的例子与美国1970年代的一个电视节目有关,其中的概率计算困扰着成千上万的大众。
在节目中,节目参与者将在3扇门之间选择其中一扇。
这3扇门中有且仅有一扇门的后面装着奖品,另外两扇门则装着讽刺性礼品比如鸡崽(chicken)或者笨驴(donkey) 。
当节目参与者选定一扇门之后,主持人就会打开另外两扇门中没有奖品的一扇。
然后在剩下的两扇关闭的门中,主持人会问参与者要不要改变最初的选择。
这里的问题就是:参与人希望获得奖品,而不是获得讽刺性礼品,那么现在仍关闭的两扇门中,他应当坚持最初的选择呢?还是改变主意选择另外一扇门?
大多数人凭直觉认为,剩下的两扇门中,每扇门后有奖品或没有奖品的概率各占50%。
因此,改变主意选择另外一扇门和坚持最初的选择不改变,预期的赢利是一样的。
的确,这种思路看来是没有什么错。
因为在做最初的选择时,选择正确的概率是1/3;而一旦选择之后,剩下两扇门,参与者从主持人的行为中所能得到的信息就只是将信念修正为自己选择正确的概率为1/2,选择失误的概率也是1/2。
此外没有任何其他的信息改善。
因此,他坚持原来的选择似乎可以说得过去。
但是,上述看法不符合真实的情况。
真实的情况是,如果参与者改变自己最初的选择,那么获得奖品的概率是2/3,而不改变最初选择则获得奖品的概率仅为1/3。
也就是他应该改变自己最初的选择。
奇怪的是,将这个结果告诉给参与者后,他们也常常还难以理解为什么会这样。
一种比较浅显的解释是这样的:在最初的选择中,选择了错误的门的概率是2/3。
如果参与人一开始的确选择了错误的门,那么主持人随后必然打开空门,而没有被打开的那一扇就必然有奖品,此时参与人显然应该改变主意转换到自己没选择也没有被打开的那扇门。
如果最初的选择中参与人的确选正确了(概率为1/3),那么他显然应该坚持,并因此获得奖品。
也就是说,如果参与人一开始就选错了则参与人应该换门并一定获得奖金,如果参与人一开始就选对了则应该坚持并一定获得奖金——于是,转换门获得奖金的概率与不转换门获得奖金的概率实际上就是最初选择是正确和错误的概率。
而一开始,选择出现错误的概率是2/3,为正确的概率是1/3。
因此,在不知自己选择是正是误的情况下,在第二阶段改变主意转换到另一扇门,的确增加了获得奖品的概率。
对于有些读者,可能仍难以明白上述道理。
那么我建议你可以做这样一个游戏:准备三张扑克和一枚硬币,让你的朋友来当节目主持人将三张牌铺在桌面上(并将那枚硬币放在其中一张之下);然后你来选择一张牌;你的朋友将你没选取的牌中拿走没有硬币的一张,再问你是否改变你当初选的牌。
为了证明转换选择不不转换选择将更有可能获得奖品,你可以尝试以“转换选择”为策略进行数十次(比如50次),再以“不转换选择”为策略进行同样多的次数(比如50次)。
结果你会发现什么?你将发现“转换选择”的策略中,得到硬币的次数基本上是“不转换选择”策略中得到硬币的次数的两倍,而两种策略中硬币出现的频率也基本上分别接近2/3和1/3。
当然,在一次性节目中,并不允许这样的重复实验。
而且大多数人的确也不明智地选择了“不转换选择”。
我曾在学生中做这个实验,结果32人中有20人坚持“不转换选择”。
说明大多数人是不清楚这样复杂的概率思考的。
更有意思的是,我跟我太太(一个没有修过高等数学的文学士、教育学硕士)玩这个游戏时,她也是坚持“不转换选择”。
当我告诉她如果转换则可以成倍提高获奖概率时,她却说:如果我开始选对了,改变了结果错了就会后悔,所以心理素质好的就不应该改变。
当然,她说的已经不是纯粹的概率计算,但也不是没有道理的。
人们的行为的确不仅受制于各种精心的算计,也往往受制于某些心理因素(比如后悔)。
不过,我对她的答案疑问在于:“如果开始选择对了,那么后来改变了选择会令人后悔。
但是,如果后来你知道开始的选择错了,而你又没有转换选择,你就不后悔没有转换吗?”太太的回答更
经典:“一开始选择错了,我就只认为运气不好,没什么可后悔的;如果开始对了,后来改变错了,才是后悔的。
”这让我理解想到人们日常生活中常提到的道理:从没得到的东西,也就不会有失去它痛苦,而已得到的失去了,就会深感创伤。
从太太的回答中,我突然明白了为什么行为博弈理论(behavioral game theory)现在大行其道。
好了,文章引完了,大家也应该看完了,大家的第一感觉差不多都是“啧,原来数学还可以这样用”,然后就是“好像有点不对头,似乎明明最有把握的机会怎么一下子变小了”,不要紧,自己也来开动大脑分析一下不就行了?
三扇门,只有一扇门背后有Bonus,很显然如果只选一次的话,大家都只有1/3的机会,现在节目给我们加了一个障眼法,一次机会变成了两次机会,结果会如何呢?我们可以知道,如果参与者最终赢得了Bonus,无非只有两种可能性:
A.第一次就选择正确且第二次没有更改选择(概率为1/3×1/2=1/6)
B.第一次选择错误而在第二次更改了选择(概率为2/3×1/2=1/3)
很显然,真的如作者所说的那样,在第二次改变选择的话,赢的机会会更大一些,不过可惜就可惜在作者的的分析在结论上成立(两种方案的成功比为1:2)却在数学上过程错误。
为什么会错呢?作者其实在论证过程中否定了第二次选择为一次选择,将其当作一个必然的没有选择的选择。
这是事后诸葛亮的处事方式——没有人可以预见自己在第一次猜中与否。
因此,在面临第二次选择的时候,选与不选也是要经过参与者的鱼与熊掌的心理斗争的,这恰恰是被作者所忽略的那个1/2,事实上大多数人只是在第一种方案时否定了第二次选择而造成困惑。
PS:两次选择,选与不选,实际上是有四种可能的
A:第一次就选择正确且第二次没有更改选择(概率为1/3×1/2=1/6)结果:成功
B:第一次选择错误而在第二次更改了选择(概率为2/3×1/2=1/3)结果:成功
C:第一次就选择正确而第二次更改了选择(概率为1/3×1/2=1/6)结果:失败
D:第一次选择错误而在第二次没有更改选择(概率为2/3×1/2=1/3)结果:失败
可以看到,在第二次更改选择的话,成功机会要比失败的可能性大(与此相对的是不改变选择,失败的可能性比成功的可能性要高),而且考虑到第一次猜错的可能性比较大,在第二次改变选择是值得一试的!本来就是Gambol嘛。
