静电场习题与解答
大学物理静电场练习题带标准答案
大学物理静电场练习题带答案————————————————————————————————作者：————————————————————————————————日期：大物练习题（一）1、如图，在电荷体密度为ρ的均匀带电球体中，存在一个球形空腔，若将带电体球心O 指向球形空腔球心O '的矢量用a 表示。
试证明球形空腔中任一点电场强度为 . A 、03ρεa B 、0ρεa C 、02ρεa D 、3ρεa2、如图所示的绝缘细线上均匀分布着线密度为λ的正电荷,两直导线的长度和半圆环的半径都等于R ．试求环中心O 点处的场强A 、02πR λε-B 、0πRλε- C 、00ln 22π4λλεε+ D 、00ln 2π2λλεε+3、 如图所示，一导体球半径为1R ,外罩一半径为2R 的同心薄导体球壳, 外球壳所带总电荷为Q ,而内球的电势为0V ，求导体球和球壳之间的电势差 （填写A 、B 、C 或D ，从下面的选项中选取）。
A 、1020214R Q V R R πε⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭ B 、102024R Q V R R πε⎛⎫- ⎪⎝⎭C 、0024Q V R πε- D 、1020214R Q V R R πε⎛⎫⎛⎫+-⎪ ⎪⎝⎭⎝⎭4.如图所示，电荷面密度为1σ的带电无限大板A 旁边有一带电导体B ，今测得导体表面靠近P 点处的电荷面密度为2σ。
求：（1）P 点处的场强 ；（2）导体表面靠近P 点处的电荷元S ∆2σ所受的电场力 。
A 、20σεB 、202σεC 、2202S σε∆D 、220S σε∆5．如图，在一带电量为Q 的导体球外，同心地包有一各向同性均匀电介质球壳，其相对电容率为r ε，壳外是真空，则在壳外P 点处(OP r =)的场强和电位移的大小分别为［ ］Q Opr)（A ）2200,44r Q QE D rr εεε==ππ； （B ）22,44r Q QE D r r ε==ππ； （C ）220,44Q QE D r r ε==ππ； （D ）2200,44Q QE D r r εε==ππ。
高中物理静电场经典习题30道--带答案
高中物理静电场经典习题30道--带答案1.如图，在光滑绝缘水平面上，三个带电小球a、b和c 分别位于边长为l的正三角形的三个顶点上；a、b带正电，电荷量均为q，c带负电．整个系统置于方向水平的匀强电场中．已知静电力常量为k．若三个小球均处于静止状态，则匀强电场场强的大小为（）A．$\frac{kq}{l^2}$。
B．$\frac{\sqrt{3}kq}{l^2}$。
C．$\frac{2kq}{l^2}$。
D．$\frac{3kq}{l^2}$2.如图，一半径为R的圆盘上均匀分布着电荷量为Q的电荷，在垂直于圆盘且过圆心c的轴线上有a、b、d三个点，a和b、b和c、c和d间的距离均为R，在a点处有一电荷量为q（q＞）的固定点电荷．已知b点处的场强为零，则d点处场强的大小为（k为静电力常量）A．$\frac{kQ}{4R^2}$。
B．$\frac{\sqrt{2}kQ}{4R^2}$。
C．$\frac{kQ}{2R^2}$。
D．$\frac{\sqrt{2}kQ}{R^2}$3.如图所示，在光滑绝缘水平面上放置3个电荷量均为q （q＞）的相同小球，小球之间用劲度系数均为k的轻质弹簧绝缘连接．当3个小球处在静止状态时，每根弹簧长度为l．已知静电力常量为k，若不考虑弹簧的静电感应，则每根弹簧的原长为A．$l+\frac{2q^2}{kl}$。
B．$l-\frac{2q^2}{kl}$。
C．$l-\frac{q^2}{kl}$。
D．$l+\frac{q^2}{kl}$4.如图所示，在光滑的绝缘水平面上，由两个质量均为m 带电量分别为+q和﹣q的甲、乙两个小球，在力F的作用下匀加速直线运动，则甲、乙两球之间的距离r为A．$\frac{F}{2kq^2}$。
B．$\frac{F}{kq^2}$。
C．$\frac{F}{4kq^2}$。
D．$\frac{2F}{kq^2}$5.一带负电荷的质点，在电场力作用下沿曲线abc从a运动到c，已知质点的速率是递减的．关于b点电场强度E的方向，下列图示中可能正确的是（虚线是曲线在b点的切线）A．。
静电场习题及解析
静电场习题及解析（1）电荷Q 均匀地分布在长为L 的细棒上。
求证：（1）在棒的延长线，且离棒中心为r处的电场强度为22041Lr QE -=πε（2）在棒的垂直平分线上，离棒为r 处的电场强度为22421Lr r Q E +=πε若棒为无限长（即∞→L ），试将结果与无限长均匀带电直线的电场强度相比较。
分析：这是计算连续分布电荷的电场强度。
此时棒的长度不能忽略，因而不能将棒当作点电荷处理。
但带电细棒上的电荷可看作均匀分布在一维的长直线上。
如图所示，在长直线上任意取一线元，其电荷为d q = Q d x /L ，它在点P 的电场强度为rr q e E 2d 41d '=πε整个带电体在点P 的电场强度⎰=E E d接着针对具体问题来处理这个矢量积分。
（1） 若点P 在棒的延长线上，带电棒上各电荷元在点P 的电场强度方向相同，⎰=LiE E d（2） 若点P 在棒的垂直平分线上，则电场强度E 沿x 轴方向的分量因对称性叠加为零，因此，点P 的电场强度就是⎰⎰==LLj j E E E d sin d y α证：（1）延长线上一点P 的电场强度⎰'=Lr qE 204d πε，利用几何关系xr r -='统一积分变量，则2200222-041212141)(d 41L r QL r L r L x r L x Q E L L P -=⎥⎦⎤⎢⎣⎡+--=-=⎰πεπεπε电场强度的方向沿x 轴。
（3） 根据以上分析，中垂线上一点P 的电场强度E 的方向沿y 轴，大小为⎰'=Lr qE 204d sin πεα利用几何关系22,sin xr r r r +=''=α统一积分变量，则220232222-0412)(d 41rL rQ r x L x rQ E L L +=+=⎰πεπε当棒长∞→L时，若棒单位长度所带电荷为λ常量，则P 点电场强度rLrL Q rE L 022024121limπελπε=+=∞→此结果与无限长带电直线周围的电场强度分布相同。
大学物理静电场练习题带答案
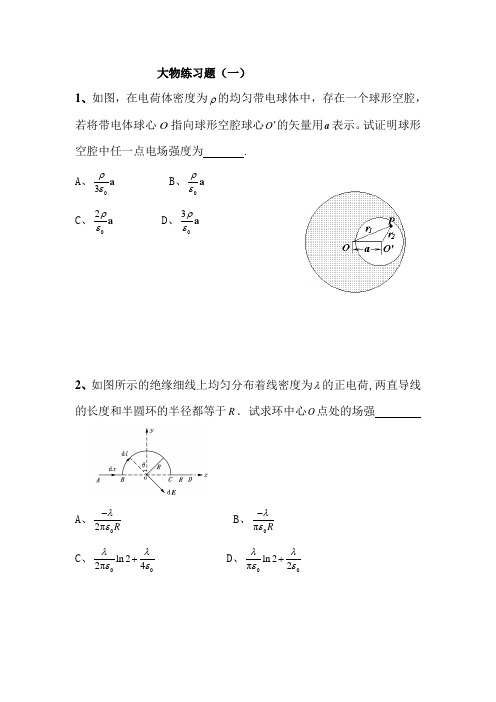
大物练习题（一）1、如图，在电荷体密度为ρ的均匀带电球体中，存在一个球形空腔，若将带电体球心O指向球形空腔球心O'的矢量用a表示。
试证明球形空腔中任一点电场强度为 .A、3ρεa B、ρεaC、2ρεa D、3ρεa2、如图所示的绝缘细线上均匀分布着线密度为λ的正电荷,两直导线的长度和半圆环的半径都等于R．试求环中心O点处的场强A、2πRλε- B、πRλε-C、00ln22π4λλεε+ D、00ln2π2λλεε+3、 如图所示，一导体球半径为1R ,外罩一半径为2R 的同心薄导体球壳, 外球壳所带总电荷为Q ,而内球的电势为0V ，求导体球和球壳之间的电势差 （填写A 、B 、C 或D ，从下面的选项中选取）。
A 、1020214R Q V R R πε⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭ B 、102024R Q V R R πε⎛⎫- ⎪⎝⎭C 、0024Q V R πε- D 、1020214R Q V R R πε⎛⎫⎛⎫+-⎪ ⎪⎝⎭⎝⎭4.如图所示，电荷面密度为1σ的带电无限大板A 旁边有一带电导体B ，今测得导体表面靠近P 点处的电荷面密度为2σ。
求：（1）P 点处的场强 ；（2）导体表面靠近P 点处的电荷元S ∆2σ所受的电场力 。
A 、20σεB 、202σεC 、2202S σε∆D 、220S σε∆5．如图，在一带电量为Q 的导体球外，同心地包有一各向同性均匀电介质球壳，其相对电容率为r ε，壳外是真空，则在壳外P 点处(OP r =)的场强和电位移的大小分别为［ ］Q Opr（A ）2200,44r Q QE D rr εεε==ππ； （B ）22,44r Q QE D r r ε==ππ； （C ）220,44Q QE D r r ε==ππ； （D ）2200,44Q QE D r r εε==ππ。
6、在一点电荷产生的静电场中，一块电介质如图放置，以点电荷所在处为球心作一球形闭合面，则对此球形闭合面： （A ）高斯定理成立，且可用它求出闭合面上各点的场强；（B ）高斯定理成立，但不能用它求出闭合面上各点的场强； （C ）由于电介质不对称分布，高斯定理不成立； （D ）即使电介质对称分布，高斯定理也不成立。
高中物理静电场练习题(含解析)
高中物理静电场练习题学校:___________姓名：___________班级：___________一、单选题1．2022年的诺贝尔物理学奖同时授予给了法国物理学家阿兰•阿斯佩、美国物理学家约翰•克劳泽及奥地利物理学家安东•蔡林格，以表彰他们在“纠缠光子实验、验证违反贝尔不等式和开创量子信息科学”方面所做出的杰出贡献。
许多科学家相信量子科技将改变我们未来的生活，下列物理量为量子化的是（ ）A ．一个物体带的电荷量B ．一段导体的电阻C ．电场中两点间的电势差D ．一个可变电容器的电容2．如图所示，+Q 为固定的正电荷，在它的电场中，一电荷量为+q 的粒子，从a 点以沿ab 方向的初速度v 0开始运动．若粒子只受电场力作用，则它的运动轨迹可能是图中的（ ）A ．ab 直线B ．ac 曲线C ．ad 曲线D ．ae 曲线 3．电荷量之比为1∶7的带异种电荷的两个完全相同的金属球A 和B ，相距为r 。
两者接触一下放到相距2r 的位置，则稳定后两小球之间的静电力大小与原来之比是（ ） A ．4∶7B ．3∶7C ．36∶7D ．54∶74．描述电场强弱的物理量是（ ）A ．电荷量B ．电场力C ．电场强度D ．电流强度 5．人体的细胞膜模型图如图a 所示，由磷脂双分子层组成，双分子层之间存在电压（医学上称为膜电位），现研究某小块均匀的细胞膜，厚度为d ，膜内的电场可看作匀强电场，简化模型如图b 所示，初速度可视为零的一价正钠离子仅在静电力的作用下，从图中的A 点运动到B 点，下列说法正确的是（ ）A ．A 点电势等于B 点电势B．钠离子的电势能增大C．若膜电位越小，钠离子进入细胞内的速度越大D．若膜电位增加，钠离子进入细胞内的速度更大6．如图所示为真空中正点电荷的电场线和等势面，实线为电场线，虚线为等势面，电场中有a、b、c三点。
下列关于各点电场强度E的大小和电势φ的高低说法正确的是（）A．Ea＝Eb B．Ea＞Ec C．φb＞φc D．φa＝φc7．两个较大的平行金属板A、B相距为d，分别接在电压为U的电源正、负极上，这时质量为m、带电荷量为-q的油滴恰好静止在两板之间，如图所示。
静电场练习题及答案解析
静电场练习题及答案解析练习1一、选择题1. 一带电体可作为点电荷处理的条件是( )A. 电荷必须呈球形分布；B. 带电体的线度与其它有关长度相比可忽略不计；C. 电量很小；D. 带电体的线度很小。
2. 试验点和q0在电场中受力为F⃗，其电场强度的大小为F，以下说法正确的( )q0A. 电场强度的大小E是由产生电场的电荷所决定的，不以试验电荷q0及其受力的大小决定；B. 电场强度的大小E正比于F且反比与q0；C. 电场强度的大小E反比与q0；D. 电场强度的大小E正比于F。
3. 如果通过闭合面S的电通量Φe为零，则可以肯定( )A. 面S内没有电荷；B. 面S内没有净电荷；C. 面S上每一点的场强都等于零；D. 面S上每一点的场强都不等于零。
4. 如图所示为一具有球对称性分布的静电场的E~r关系曲线，产生该静电场的带电体是( ) A 半径为R的均匀带电球面；B半径为R的均匀带电球体；C半径为R的、电荷体密度为ρ=Ar（A为常数）的非均匀带电球体；D半径为R的、电荷体密度为ρ=A r⁄（A为常数）的非均匀带电球体。
5. 在匀强电场中，将一负电荷从A移动B，如图所示，则( )A. 电场力做负功，负电荷的电荷能增加；B. 电场力做负功，负电荷的电势能减少；C. 电场力做正功，负电荷的电势能增加；D. 电场力做正功，负电荷的电势能减少。
二、填空题1. 点电荷q1、q2、q3和q4在真空中的分布如图所示，图中S为闭合曲面，则通过该闭合曲面的电通量∮E⃗⃗∙dS⃗=，式中E⃗⃗是点电荷在闭合曲面上任一点产生的场强的矢量和。
2. 真空环境中正电荷q均匀地分布在半径为R的细圆环上.在环环心O处电场强度为，环心的电势为。
=0，这表3. 在静电场中，场强沿任意闭合路径的线积分等于零，即∮E⃗⃗∙dl⃗L明静电场中的电场线。
4. 一半径为R的均匀带电球面，其电荷面密度为σ，该球面内、外的场强分布为（r⃗表示从球心引出的矢径）：E⃗⃗r=(r<R)；E⃗⃗r=(r>R)。
09静电场习题解答
第九章 静电场一 选择题1. 在坐标原点放一正+Q ，它在P 点（x =+1，y =0）产生的电场为E 。
现在，另外有一个负电荷-2Q ，试问应将它放在什么位置才能使P 点的电场强度为零？（ ）Ａ. x 轴上x >1。
B. x 轴上x <0。
C. x 轴上0<x <1。
Ｄ. y 轴上y >0。
E. y 轴上y <0。
解：根据电场叠加原理，应选（Ｂ）。
2. 下列说法中哪一个是正确的？A.电场中某点场强的方向，就是将点电荷放在该点所受的电场力的方向。
B.在以点电荷为中心的球面上，该电荷产生的场强处处相同。
C.场强方向可由定出，其中q 为试验电荷的电量，q 可正可负，ＦqFE =为试验电荷所受的电场力。
D.以上说法都不正确。
( )解：根据电场强度的定义应选(C)。
3. 如图，电量为Q 的点电荷被曲面S 所包围，从无穷远处引另一电量为q 的点电荷至曲面外一点，则： （ ）Ａ．曲面S 的E 通量不变，曲面上各点场强不变Ｂ．曲面S 的E 通量变化，曲面上各点场强不变Ｃ．曲面S 的E 通量变化，曲面上各点场强变化Ｄ．曲面S 的E 通量不变，曲面上各点场强变化解：根据高斯定理，应选(D)。
4. 两个同心均匀带电球面，半径分别为R a 和R b （R a <R b ），所带电量分别为Q a 和Q b ，设某点与球心相距r ，当R a <r< R b 时，该点的电场强度的大小为：（ ）202202020π41D.π41C.π41B.π41A.r Q .) R Q r Q (r Q Q .r Q Q .abb a b a b a εεεε+-+解：外球面上的电荷在其内部产生的场强为零，两球面间的场强仅由内球面电荷产生，故选（D ）。
5. 图示为一具有球对称性分布的静电场的E -r 关系曲线，请指出该静电场是由下列哪种带电体产生的。
（ ）S ．Q．q 选择题3图A ．半径为R 的均匀带电球面 B. 半径为R 的均匀带电球体C. 半径为R 、电荷体密度ρ =Ar （A 为常数）的非均匀带电球体D.半径为R 、电荷体密度ρ =A/r （A 为常数）的非均匀带电球体解：根据计算可知，该电场为半径为R 、电荷体密度ρ =A/r （A 为常数）的非均匀带电球体所产生，故选（D ）。
静电场练习题专题复习及答案
静电场练习题专题一、单项选择题：（每题只有一个选项正确，每题 4 分）1、以下说法正确的选项是：（）A．只有体积很小的带电体，才能看做点电荷B．电子、质子所带电量最小，因此它们都是元电荷C．电场中A、B两点的电势差是恒定的，不随零电势点的不一样而改变，因此U AB＝ U BA D．电场线与等势面必定互相垂直，在等势面上挪动电荷电场力不做功2、在真空中同向来线上的A、B 处罚别固定电量分别为＋2Q、－ Q的两电荷。
如下图，若在 A、 B 所在直线上放入第三个电荷C，只在电场力作用下三个电荷都处于均衡状态，则C 的电性及地点是 ()A ．正电，在、B 之间AB ．正电，在B点右边C．负电，在B点右边D．负电，在A点左边3、如下图，实线为不知方向的三条电场线，从电场中点以同样速度飞出、两个带电M a b粒子，仅在电场力作用下的运动轨迹如图中虚线所示。
则（）A．a必定带正电，b必定带负电B．a的速度将减小，b的速度将增添C．a的加快度将减小，b的加快度将增添D．两个粒子的电势能一个增添一个减小4、某静电场的电场线散布如下图，图中P、 Q 两点的电场强度的大小分别为P QE和 E，电势分别为φP 和φQ，则()A．P< Q，φP <φQE EPQ P QB．E >E，φ<φC．P< Q，φP>φQE ED．E P>E Q，φP>φQ5、一个点电荷，从静电场中的 a 点移到 b 点，其电势能的变化为零，则（）A、 a、 b 两点的场强必定相等；B、该点电荷必定沿等势面挪动；C、作用于该点电荷的电场力与其挪动方向老是垂直的；D、 a、 b 两点电势必定相等。
6、在点电荷 Q 形成的电场中有一点 A，当一个－ q 的查验电荷从电场的无穷远处被移到电场中的A 点时，电场力做的功为 W，则查验电荷在 A 点的电势能及电场中 A 点的电势分别为（规定无穷远处电势能为 0）：A．C．AAW，W，WB．AqWD．AqAW，AWqAW，AWq7、如下图，圆滑绝缘水平面上带异号电荷的小球A、B，它们一同在水平向右的匀强电场中向右做匀加快运动，且保持相对静止。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
静电场1、在正方形的两个相对的角上各放置一点电荷Q ，在其它两个相对的角上各置一点电荷q ，如果作用在Q 上的力为零，求Q 与q 的关系。
分析：若使Q 所受合力为零，如图所示，两种电荷符号必然相反，大小关系有Qq QQ F F 2=。
设正方形边长为a 。
解：222222a Qqk F a Q k F QqQQ === 得 q Q 22-=2、在直角三角形ABC 的A 点放置点电荷q 108.1⨯=C Q 9108.4-⨯-=，已知BC = 4cm ，AC = 3cm ，试求直角顶点C 处的场强。
分析：如图，C 点场强为两电荷激发电场的合场强。
解：r q E AC q 8.11091085.814.34108.141412920=⨯⨯⨯⨯⨯⨯==---πε m V r Q E AC Q /107.210161085.814.34108.4414412920⨯=⨯⨯⨯⨯⨯⨯==---πε m V E E E q Q /1024.3422⨯=+=5.18.17.2tan ===qQ E E θ 则 ︒=34θ 3、一均匀带电细棒，长为L ，带电量Q 。
求在棒的延长线上与棒的近端相距为R 的A 点的场强。
分析：如图建立坐标系，取棒上一小段dx ，电量为dq ，与A 点距离为L-x+R ，在A 点激发的场强为dE 。
则A 点的总场强只需对dE 积分即可。
解：由分析得)(41)(41)(41002020L R R Q x R L dx L Q x R L dq dE E L+=-+=-+==⎰⎰⎰πεπεπε 4、一半圆形带电线，半径为R ，电荷线密度为η，求圆心O 处的电场强度。
分析：如图建立坐标系，取线上一小段d l ，电量为dq ， 有dq = ηd l = ηRd θ。
在O 点激发的场强为dE 。
由于电线轴 对称，dE y= 0则dE = dE x ，则O 点的总场强只需对dE 积分即 可。
解：由分析得RR Rd RdqdE dE dE E x 02220202cos 41cos 41cos πεηθθηπεθπεθππ======⎰⎰⎰⎰⎰-5、在一个半径为R 的球体内，分布着电荷体密度ρ= k r ，式中r 为径向距离，k 是常数，求空间的场强分布，并画出E ——r 的关系曲线。
分析：用高斯定理对球内和球外分别求解。
由于电荷分布是球对称的，电场分布必然也是球对称的，则各点电场方向与同心球面方向垂直。
球内半径为r 的球体总电荷可如下计算，取半径为x ，厚度为dx 的球壳，设其电荷为dq ，则4024kr dx x kx dq Q rππ===⎰⎰。
解：当r<R 时，取同心球面为高斯面，则40214επεπkr Qr E d ===⋅⎰⎰S E 得 0214εkr E =当r>R 时，也取同心球面为高斯面，则40224επεπkR Qr E d ===⋅⎰⎰S E 得 02424εr kR E = E —— r 的关系曲线如右图。
6、一无限长半径为R 的圆柱体上电荷均匀分布，圆柱体单位长度上的电荷为λ，用高斯定理求（1）圆柱体内距轴线距离为r 处的电场强度；（2）圆柱体外距轴线距离为r 处的电场强度。
分析：无限长圆柱体的电荷具有轴对称分布，电场强度也为轴对称分布，且沿矢径方向。
取同轴圆柱面为高斯面，电场强度在圆柱侧面上大小相等，且与柱面正交。
在圆柱的两个底面上，电场强度与底面平行，0=⋅S E d 。
整个高斯面的电场强度通量为⎰⎰=⋅rl E d π2S E由于电荷均匀分布，电荷的体密度2Rπλρ=。
用高斯定理可解得圆柱体内外的电场强度。
解：（1）取r<R 的同轴圆柱面为高斯面，则l r RV rl E d 2200112ππλερεπ===⋅⎰⎰S E 202R rE πελ=（2）取r>R 的同轴圆柱面为高斯面，则l rl E d λεπ012==⋅⎰⎰S ErE 02πελ=7、一个内外半径分别为1R 和2R 的均匀带电球壳，总电量为1Q ，球壳外同心罩一个半径为3R 的均带电球面，球面电荷为2Q ，求其电场的分布？分析：以球心O 为原点，球心至场点的距离r 为半径，作同心球面为高斯面。
由于电荷呈球对称分布，电场强度也为球对称分布，高斯面上的电场强度沿径矢方向，且大小相等。
因而⎰⎰⋅=⋅24r E d πS E 。
在确定高斯面内的电荷∑q 后，利用高斯定理⎰⎰∑=⋅0/εq d S E 即可求出电场强度的分布。
解：取半径r 为的同心球面为高斯面，由上述分析 02/4επ∑=⋅q r E1R r <，该高斯面内无电荷，0=∑q ，故01=E21R r R <<，高斯面内电荷31323131)(RR R r Q q --=∑，故23132031312)(4)(rR R R r Q E --=πε 32R r R <<，高斯面内电荷为1Q ，故20134rQ E πε=3R r >高斯面内电荷为21Q Q +，故202144r Q Q E πε+=8、点电荷1q 、2q 、3q 、4q 的电量各为C 9104-⨯，放置在一正方形的四个顶点上，各顶点距正方形中心的距离均为5cm ，求：（1）、计算O 点的场强和电势；（2）、将一试探电荷0q =C 910-从无穷远移到O 点，电场力作功多少？（3）、（2）中所述过程中0q的电势能改图7变多少？ 分析：（1）由于四个点电荷对O 点是对称的，且电量相等，符号相同，根据场强的叠加原理，总场强为零。
而根据电势的叠加原理，总电势V = 4V q =RQ 044πε（取无穷远处电势为零）。
（2）正电荷周围的电势为正，而一正的试探电荷从无穷远处移至O 点电场力作负功，大小为A = 0q V 。
（3）A = - W 。
解：由分析得 （1） E = 0V = 4V q =R Q044πεV 321291088.21051085.814.341044⨯=⨯⨯⨯⨯⨯⨯=--- （2） A = 0q -V = J 6391088.21088.210--⨯-=⨯⨯- （3） W J A 61088.2-⨯=-=9、四个点电荷对称地分布在x 轴上，电量及其坐标位置如图，其中（a 、b>0）。
证明：以a为半径的球面（球心在圆心）是电势为0分析：因为空间是轴对称的，我们只需 证明xy 平面上即可。
设平面上一点的坐标为（x ，y ），以a 为半径的球面（球心在圆心） 在xy 平面的投影为圆，且圆上一点满足 x 2 + y 2 = a 2。
证明：由电势叠加原理，该点电势 V = V 1+V 2+V 3+V 4 =22202202202220)(4)(4)(4)(4y ba x qb a y b x q y b x q yba x qb a +--+-++++++-πεπεπεπε将 y 2 = a 2-x 2代入上式222202220222022220)(4)(4)(4)(4x a ba x qb a x a b x q x a b x q xa ba x qb a V -+---+-+-+++-++-=πεπεπεπεx ba ab a q babx a b qbx a b qx b a a b a q ba 22220220220222202)(424242)(4-+--+++++++-=πεπεπεπεbxa b qbxa b qbxa b qbxa b q24242424220220220220-+--+++++++-=πεπεπεπε = 010、在一次典型的闪电中，两个放电点间的电势差约为910V ，被迁移的电荷约为30C ，如果释放出的能量都用来使0℃的冰融化为0℃的水，则可融化多少冰？（冰的融化热151034.3-⋅⨯=Kg J L ）解：闪电中释放出的能量为冰所吸收，故可融化冰的质量 Kg LqUL E m 41098.8⨯==∆=即可融化约90吨冰。
11、两个同心球面的半径分别为R 1和R 2，各自带电荷Q 1和Q 2，求各区域电势的分布及两球面上的电势差。
分析：一个均匀带电的球面，在球面外产生的电势为rQ V 04πε=，在球内电势处处相等，等于球面的电势RQ V 04πε=。
本题可利用电势叠加原理求得空间电势分布。
解：当r ≤R 1时， 202101144R Q R Q V πεπε+=当R 1≤r ≤R 2时， 20201244R Q rQ V πεπε+=当r ≥R 2时， rQ Q V 02134πε+=两球面间的电势差201101211244|2R Q R Q V V U R r πεπε-=-==12、电场中有A 、B 、C 三个点，把电量为C 8105-⨯-的电荷从A 点移到B 点，电场力作功，把这个电荷从B 移到C 点，电势能增加J 5106-⨯，求U AB 和U BC ，如果取U A = 0，则U B 和U C 各是多大？ 解：V q A U AB AB80010510485-=⨯-⨯==-- V q W U BC BC120010510685=⨯-⨯-==--V U U U AB BA B 800=-==V U U U U BA CB CA C 4008001200-=+-=+==13、一长为L 的细棒均匀带电，线密度为η，求其在左端正上方距左端距离为z 的P 点的电势。
分析：如图建立坐标系，取棒上一小段dx ，设其电量为dq ，dq =ηdx 。
若dq 在z 点的电势为du ，则根据电势叠加原理，U =⎰du 。
解：U =z z L L x z dxr dq du L22002200ln 44141++=+==⎰⎰⎰πεηηπεπε。