《信号与系统》郑君里第二章习题解答
合集下载
《信号与系统》第二版课后答案_(郑君里)_高等教育出版社

解题过程: (1)方法一:
f (t)
1
f (t − 2)
1
→
-2
-1
f (3t − 2)
0
1
→
1
2
f (−3t − 2)
1
→
3
2/3 1
-1 -2/3
方法二:
f (t)
f (3t )
1
1
→
→
-2
-1
f (3t − 2)
0
1
-2/3
→
1/3
f (−3t − 2)
2/3 1 方法三:
-1 -2/3
1
f (t)
解题过程:
fe
(t)
=
1 2
⎡⎣
f
(t ) +
f
(−t )⎤⎦
fo
(t)
=
1 2
⎡⎣
f
(t)
−
f
(−t )⎤⎦
(a-1)
(a-2)
(a-3)
(a-4)
4
(b) f (t ) 为偶函数,故只有偶分量,为其本身
(c-1)
(c-2)
(c-3)
(c-4)
(d-1)
(d-2)
(d-3)
(d-4)
1-20 分析过程:本题为判断系统性质:线性、时不变性、因果性 (1)线性(Linearity):基本含义为叠加性和均匀性
7
t
(7) r (t ) = ∫ e(τ ) dτ −∞
t
t
线性:设 r1 (t ) = ∫ e1 (τ ) dτ 、 r2 (t ) = ∫ e2 (τ ) dτ ,
−∞
−∞
信号与系统课后题解第二章

⑺
对⑺式求一阶导,有:
de(t ) d 2 i 2 (t ) di (t ) du (t ) =2 +2 2 + c 2 dt dt dt dt de(t ) d 2 i2 (t ) di (t ) =2 + 2 2 + 2i1 (t ) + 2i 2 (t ) 2 dt dt dt
⑻
将⑸式代入⑻式中,有:
λ 2 + 2λ + 1 = 0
可解得特征根为 微分方程齐次解为
λ1, 2 = −1
y h (t ) = C1e −t + C2 te− t
由初始状态为 y (0 ) = 1, y ' (0 ) = 0 ,则有:
C1 = 1 − C 1 + C 2 = 0
由联立方程可得 故系统的零输入响应为:
由联立方程可得 故系统的零输入响应为:
A1 = 2, A2 = −1
y zi (t ) = 2e − t − e −2 t
(2)由原微分方程可得其特征方程为
λ 2 + 2λ + 2 = 0
可解得特征根为 微分方程齐次解为
λ1, 2 = −1 ± i
y h (t ) = e −t (C1 cos t + C2 sin t )
(− 3C1 + 3C2 )δ (t ) + (C1 + C2 )δ ' (t ) − (− 2C1 + C 2 )δ (t ) = δ (t )
(
(
( + C e )δ (t ) + (C e
2 1
)
−2 t
+ C2 e t δ ' (t )
信号与系统(郑君里)习题答案

2 j2 3
− 1t
h(t) = e 2 (cos
3 t + 1 sin
3 t)u(t)
2 32
∫ ∫ g(t) = t h(τ )dτ = t h(τ )dτ
∴
−∞
0
− 1t
= [e 2 (− cos
3 t + 1 sin
3 t) + 1]u(t)
2 32
d r(t) + 2r(t) = d 2 e(t) + 3 d e(t) + 3e(t)
零输入响应: r(t) = ( A1t + A2 )e−t
代入初始条件, ⇒ A1 = 3 A2 = 1
r(t) = (3t + 1)e−t
d 3 r(t) + 2 d 2 r(t) + d r(t) = 0
(3)dt 3
dt 2
dt
给定:r(0+ ) = r ' (0+ ) = 0, r " (0+ ) = 1
信号与系统习题答案(注:教材---郑君里编) 习题二
2-1 对下图所示电路图分别列写求电压的微分方程表示。
图(a):微分方程:
2i1
(t
)
+
1∗
di1 (t dt
)
+
uc
(t
)
=
e(t
)
u20d(itd2)(t=t)2+di2id2((ttt))= uc (t)
⇒
duc (t) dt
=
i1 (t )
r(t) = −eα1t + 2eα2t = e−t (cos t − 3sin t)
郑君里《信号与系统》(第3版)笔记和课后习题(含考研真题)详解-第2章 连续时间系统的时域分析【圣才

Ri(t) v1(t) e(t)
Ri(t)
1 C
t
i(
)d
v1 (t )
e(t)
vo (t) v1(t)
消元可得微分方程:
6 / 59
圣才电子书
十万种考研考证电子书、题库视频学习平
1
台
C
d
dt
vo (t)
1 R
vo (t)
R
e(t)
2-2 图 2-2-2 所示为理想火箭推动器模型。火箭质量为 m1,荷载舱质量为 m2,两 者中间用刚度系数为 k 的弹簧相连接。火箭和荷载舱各自受到摩擦力的作用,摩擦系数分 别为 f1 和 f2。求火箭推进力 e(t)与荷载舱运动速度 v2(t)之间的微分方程表示。
M
di1 (t ) dt
Ri2 (t)
0
化简方程组可得微分方程:
(L2
M
2
)
d4 dt 4
vo
(t)
2RL
d3 dt 3
vo
(t)
2L C
R2
d2 dt 2
vo
(t)
2R C
d dt
vo
(t)
1 C2
vo
(t)
MR
d2 dt 2
e(t)
(3)由图 2-2-1(c)所示列写电路方程,得:
C
dv1 (t ) dt
b.自由响应由两部分组成,其中,一部分由起始状态决定,另一部分由激励信号决 定,二者都与系统的自身参数有关;当系统 0-状态为零,则零输入响应为零,但自由响应 可以不为零。
c.零输入响应在 0-时刻到 0+时刻不跳变,此时刻若发生跳变,可能为零状态响应分 量。
郑君里的信号与系统的第二三章习题参考解

郑君⾥的信号与系统的第⼆三章习题参考解B 第⼆章习题参考解2-2,试画出下列信号波形,从中可得出何结论。
其中t -∞<<∞t1=0:1/200:8;>> y1=sin(0.5*pi*t1);>> subplot(4,1,1),plot(t1,y1),title('sin(0.5*pi*t1)u(t1)的⼀段'),grid >> t2=1:1/200:8;>> y2=sin(0.5*pi*t2);>> subplot(4,1,2),plot(t2,y2),title('sin(0.5*pi*t)u(t2-1)的⼀段'),grid >> y3=sin(0.5*pi*(t1-1));>> subplot(4,1,3),plot(t1,y3),title('sin(0.5*pi*(t1-1))u(t)的⼀段'),grid >> y4=sin(0.5*pi*(t2-1));>> subplot(4,1,4),plot(t2,y4),title('sin(0.5*pi*(t2-1))u(t2-1)的⼀段'),grid 解:⽤MA TLAB 作图如上。
从中可看出:1,周期信号Sin 与单位阶跃信号相乘,得到⾮周期信号。
2,1sin()()2t u t π与1sin[(1)](1)2t u t π--是向右移动1。
⽽1sin[(1)]()2t u t π-与1sin()()2t u t π只是sin 的起始相位不同。
2-12,⼰知序列(0.8)2302,3(){k k k k x k -≤≤<>=1,⽤阶跃信号的截取特性表⽰X (k );解:()(0.8)[(2)4()]kx k u k u k =+--2,⽤加权单位脉冲序列表⽰X(k)。
清华大学信号与系统(郑君里)课后答案

(4) f ( at ) 右移
故(4)运算可以得到正确结果。 注:1-4、1-5 题考察信号时域运算:1-4 题说明采用不同的运算次序可以得到一致的结果; 1-5 题提醒所有的运算是针对自变量 t 进行的。如果先进行尺度变换或者反转变换,再进行 移位变换,一定要注意移位量和移位的方向。 1-9 解题过程: (1) f ( t ) = 2 − e
解题过程:
(a-1)
(a-2)
(a-3)
4
(a-4)
(b) f ( t ) 为偶函数,故只有偶分量,为其本身
(c-1)
(c-2)
(c-3)
(c-4)
(d-1)
(d-2)
(d-3)
(d-4)
1-20 分析过程:本题为判断系统性质:线性、时不变性、因果性 (1)线性(Linearity) :基本含义为叠加性和均匀性
1 2 2
−∞
5t 5t
t
t
则
∫
5t
−∞
⎡ ⎣ c1e1 (τ ) + c2 e2 (τ ) ⎤ ⎦ dτ = r1 ( t ) = c1 ∫−∞ e1 (τ ) dτ + c2 ∫−∞ e2 (τ ) dτ = c1r1 ( t ) + c2 r2 ( t )
时变:输入 e ( t − t0 ) ,输出 非因果: t = 1 时, r (1) =
∫
5t
−∞
e (τ − t0 ) dτ =
τ − t0 = x
∫
5t − t0
−∞
e ( x ) dx ≠ ∫
5( t − t0 )
−∞
e ( x ) dx = r ( t − t0 )
∫ e (τ ) dτ , r (1) 与 ( −∞,5] 内的输入有关。
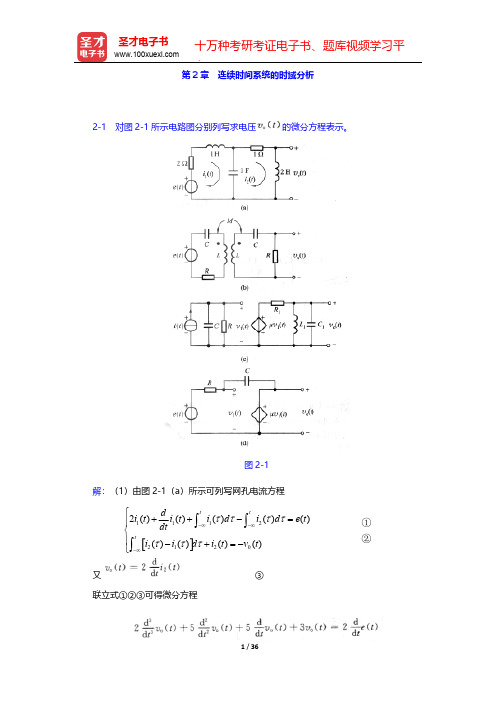
郑君里《信号与系统》(第3版)(上册)(课后习题 连续时间系统的时域分析)【圣才出品】
3 / 36
圣才电子书
十万种考研考证电子书、题库视频学习平 台
解:对汽车底盘进行受力分析。
图 2-4
图 2-5
设汽车底盘运动速度为 v(t) ,方向向上; Fk 为弹簧对汽车底盘的拉力,方向向下; Ff 为减震器阻尼力,方向向下。
汽车底盘的加速度:
a(t)
dv(t) dt
d dt
[ dy(t)] dt
d
2 y(t) dt 2
①
因弹簧的位移量为 x(t) y(t) ,所以拉力: Fk (t) k[ y(t) x(t)]
②
减震器对汽车底盘的作用力: Ff
(t)
f
d [ y(t) x(t)] dt
③
由牛顿第二定律知: Fk (t) Ff (t) ma(t)
将式①②③代入上式,可得微分方程
2-6 给定系统微分方程
若激励信号和起始状态为: 试求它的完全响应,并指出其零输入响应、零状态响应,自由响应、强迫响应各分量。
解:方程的特征方程为
特征根为
(1)设零输入响应
①
6 / 36
圣才电子书
由已知条件可得
十万种考研考证电子书、题库视频学习平 台
rzi (0 ) rzi (0 ) r(0 ) 1
台
(2)
d dt
r
t
2r
t
3
d dt
et
,r
0
0,et
ut
。
试判断在起始点是否发生跳变,据此对(1)(2)分别写出其 r0 值。
解:当微分方程右端包含 (t) 及其各阶导数时,系统从 0 状态到 0 状态发生跳变。
(1)将 e(t) u(t) 代入原方程得:
圣才电子书
十万种考研考证电子书、题库视频学习平 台
解:对汽车底盘进行受力分析。
图 2-4
图 2-5
设汽车底盘运动速度为 v(t) ,方向向上; Fk 为弹簧对汽车底盘的拉力,方向向下; Ff 为减震器阻尼力,方向向下。
汽车底盘的加速度:
a(t)
dv(t) dt
d dt
[ dy(t)] dt
d
2 y(t) dt 2
①
因弹簧的位移量为 x(t) y(t) ,所以拉力: Fk (t) k[ y(t) x(t)]
②
减震器对汽车底盘的作用力: Ff
(t)
f
d [ y(t) x(t)] dt
③
由牛顿第二定律知: Fk (t) Ff (t) ma(t)
将式①②③代入上式,可得微分方程
2-6 给定系统微分方程
若激励信号和起始状态为: 试求它的完全响应,并指出其零输入响应、零状态响应,自由响应、强迫响应各分量。
解:方程的特征方程为
特征根为
(1)设零输入响应
①
6 / 36
圣才电子书
由已知条件可得
十万种考研考证电子书、题库视频学习平 台
rzi (0 ) rzi (0 ) r(0 ) 1
台
(2)
d dt
r
t
2r
t
3
d dt
et
,r
0
0,et
ut
。
试判断在起始点是否发生跳变,据此对(1)(2)分别写出其 r0 值。
解:当微分方程右端包含 (t) 及其各阶导数时,系统从 0 状态到 0 状态发生跳变。
(1)将 e(t) u(t) 代入原方程得:
《信号与系统》第二版 (郑君里) 高等教育出版社课后答案

2
后
e2 ( t ) = e1 ( t − 0.5 ) = u ( t − 0.5 ) − u ( t − 2 ) ,则 r2 ( t ) = u ( t + 1) − u ( t − 0.5 ) ≠ r1 ( t − 0.5 )
时不变:输入 e ( t − t0 ) ,输出 e
因果: r ( t ) 仅与此时刻 e ( t ) 有关
课
) u (t )
后
t0 ⎡ ⎛ t ⎞⎤ : f ⎢ a ⎜ t + 0 ⎟ ⎥ = f ( at + t0 ) ≠ f ( t0 − at ) a ⎣ ⎝ a ⎠⎦
答
案 网
(1) f ( − at ) 左移 t0 : f ⎡ ⎣ − a ( t + t0 ) ⎤ ⎦ = f ( −at − at0 ) ≠ f ( t0 − at )
线性系统是指系统的全响应可以分解为零输入响应和零状态响应, 并且二者均分别具有 线性性质。 本题未说明初始条件,可认为系统起始状态为零( “松弛”的) ,故零输入响应为零,只 需判断系统的输入——输出是否满足线性。 (2)时不变性(Time-Invariblity) :是指当激励延迟一段时间 t0 时,其响应也同样延迟 t0 ,
(d-2)
பைடு நூலகம்
课后答案网
即 输 入 x1 ( t ) , x2 ( t ) 得 到 的 输 出 分 别 为 y1 ( t ) , y2 ( t ) , T ⎡ ⎣ x1 ( t ) ⎤ ⎦ = y1 ( t ) ,
T⎡ 。 ⎣ x2 ( t ) ⎤ ⎦ = y2 ( t ) ,则 T ⎡ ⎣ c1 x1 ( t ) + c2 x2 ( t ) ⎤ ⎦ = c1 y1 ( t ) + c2 y2 ( t ) ( c1 , c2 为常数)
后
e2 ( t ) = e1 ( t − 0.5 ) = u ( t − 0.5 ) − u ( t − 2 ) ,则 r2 ( t ) = u ( t + 1) − u ( t − 0.5 ) ≠ r1 ( t − 0.5 )
时不变:输入 e ( t − t0 ) ,输出 e
因果: r ( t ) 仅与此时刻 e ( t ) 有关
课
) u (t )
后
t0 ⎡ ⎛ t ⎞⎤ : f ⎢ a ⎜ t + 0 ⎟ ⎥ = f ( at + t0 ) ≠ f ( t0 − at ) a ⎣ ⎝ a ⎠⎦
答
案 网
(1) f ( − at ) 左移 t0 : f ⎡ ⎣ − a ( t + t0 ) ⎤ ⎦ = f ( −at − at0 ) ≠ f ( t0 − at )
线性系统是指系统的全响应可以分解为零输入响应和零状态响应, 并且二者均分别具有 线性性质。 本题未说明初始条件,可认为系统起始状态为零( “松弛”的) ,故零输入响应为零,只 需判断系统的输入——输出是否满足线性。 (2)时不变性(Time-Invariblity) :是指当激励延迟一段时间 t0 时,其响应也同样延迟 t0 ,
(d-2)
பைடு நூலகம்
课后答案网
即 输 入 x1 ( t ) , x2 ( t ) 得 到 的 输 出 分 别 为 y1 ( t ) , y2 ( t ) , T ⎡ ⎣ x1 ( t ) ⎤ ⎦ = y1 ( t ) ,
T⎡ 。 ⎣ x2 ( t ) ⎤ ⎦ = y2 ( t ) ,则 T ⎡ ⎣ c1 x1 ( t ) + c2 x2 ( t ) ⎤ ⎦ = c1 y1 ( t ) + c2 y2 ( t ) ( c1 , c2 为常数)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2
rZi ( t ) 的求法与经典时域法一致, rZi ( t ) = ( 4e− t − 3e−2t ) u ( t )
再求 rZs ( t ) :e ( t ) = u ( t ) ,r ( t ) =
p+3 u ( t ) = ( p + 3) ⎡ e − t u ( t ) ∗ e −2t u ( t ) ∗ u ( t ) ⎤ ⎣ ⎦ ( p + 1)( p + 2 )
∴ s (t ) = f (t ) ∗ f (t ) = u (t ) ∗ ⎡ ⎣δ ( t ) − δ ( t − 1) ⎤ ⎦ ∗ u (t ) ∗ ⎡ ⎣δ ( t ) − δ ( t − 1) ⎤ ⎦ =⎡ ⎣u ( t ) ∗ u ( t ) ⎤ ⎦∗⎡ ⎣δ ( t ) − 2δ ( t − 1) + δ ( t − 2 ) ⎤ ⎦ = tu ( t ) ∗ ⎡ ⎣δ ( t ) − 2δ ( t − 1) + δ ( t − 2 ) ⎤ ⎦ = tu ( t ) − 2 ( t − 1) u ( t − 1) + ( t − 2 ) u ( t − 2 )
−t
1 2
⎛ ⎝
1 −2t 3 ⎞ e + ⎟ u (t ) 2 2⎠ ⎛ ⎝
−t
③全响应: r ( t ) = rZi ( t ) + rZs ( t ) = ⎜ 2e −
5 −2t 3 ⎞ e + ⎟ u (t ) 2 2⎠
自由响应: ⎜ 2e −
⎛ ⎝
−t
5 −2t ⎞ e ⎟ u (t ) 2 ⎠
−t
(
−2 t
) u (t )
'' '
②求 rZs : 将 e ( t ) = u ( t ) 代入原方程,有 rZs ( t ) + 3rZs ( t ) + 2rZs ( t ) = δ ( t ) + 3u ( t )
⎧rZs '' ( t ) = aδ ( t ) + bΔu ( t ) ⎪ ⎪ ' 用冲激函数匹配法,设 ⎨rZs ( t ) = aΔu ( t ) ⎪ ⎪ ⎩rZs ( t ) = at Δu ( t )
∫
+∞
−∞
x1 (τ ) x2 ( t − τ ) dτ ,但是这种依靠定义的基本方
法可能不是最简便的。更应该注意灵活运用卷积的性质(卷积的交换律、结合律、分配律; 卷积的微分与积分;与冲激函数或阶跃函数的卷积)对表达式进一步的化简,甚至直接得到 结果。 解题过程: (1) f ( t ) = u ( t ) − u ( t − 1) = u ( t ) ∗ ⎡ ⎣δ ( t ) − δ ( t − 1) ⎤ ⎦
引入微分算子 p , ( ∗) 式变成:
( p + 5) h ( t ) =
1 δ ( t ) + 2δ ( t ) p +1
3
1 ⎞ ⎛ 1 ⎜ −4 ⎟ 1 1 2 2 δ (t ) + δ (t ) = ⎜ δ (t ) ⇒ h (t ) = ⋅ + 4 ⎟δ (t ) + p + 5 p +1 p+5 p 5 p 1 p 5 + + + ⎜ ⎟ ⎝ ⎠
2-6 解题过程: (1) e ( t ) = u ( t ) , r ( 0 − ) = 1 , r ( 0 − ) = 2
'
方法一:经典时域法:
⎧rZi '' ( t ) + 3rZi ' ( t ) + 2rZi ( t ) = 0 ⎪ ⎪ ' ' ①求 rZi :由已知条件,有 ⎨rZi ( 0+ ) = rZi ( 0− ) = 2 ⎪ ' ' ⎪ ⎩rZi ( 0+ ) = rZi ( 0− ) = 1
其中 e u ( t ) ∗ e
−t
−2 t
t 1 ⎛1 ⎞ u ( t ) ∗ u ( t ) = ∫ ( e−τ − e−2τ ) dτ = ⎜ − e− t + e−2t ⎟ u ( t ) 0 2 ⎝2 ⎠
1 1 3⎞ ⎛1 ⎞ ⎛ ∴ rZs ( t ) = ( p + 3) ⎜ − e− t + e−2t ⎟ u ( t ) = ⎜ −2e− t + e −2t + ⎟ u ( t ) 2 2 2⎠ ⎝2 ⎠ ⎝ 5 3⎞ ⎛ ∴ 全响应 r ( t ) = rZi ( t ) + rZs ( t ) = ⎜ 2e − t − e−2t + ⎟ u ( t ) 2 2⎠ ⎝
利用冲激函数匹配法,在 ( 0− , 0+ ) 时间段内
⎧d ⎪ h1 ( t ) = aδ ( t ) + bΔu ( t ) ⎨ dx ⎪h1 ( t ) = aΔu ( t ) ⎩
( 0− < t < 0+ )
⇒ aδ ( t ) + bΔu ( t ) + 5aΔu ( t ) = δ ( t ) ⇒ a = 1, b = −5 ⇒ h1 ( 0+ ) = a + h ( 0− ) = A = 1 ⇒ h1 ( t ) = e −5t u ( t )
−t
d h ( t ) + 5h ( t ) = e − t u ( t ) + 2δ ( t ) dt
对于因果系统 h ( 0− ) = 0 先求满足
( ∗)
d h1 ( t ) + 5h1 ( t ) = δ ( t ) 的 h1 ( t ) : h1 ( t ) = Ae −5t u ( t ) dt
3 2
因为 e ( t ) = u ( t ) 故设特解为 rZsp ( t ) = C ⋅ u ( t ) ,代入原方程得 C = 故 rZs ( t ) = rZsh ( t ) + rZsp ( t ) = ⎜ B1e + B2 e
−t
'
⎛ ⎝
−2 t
3⎞ + ⎟ u (t ) 2⎠
代入 rZs ( 0+ ) , rZs ( 0+ ) 得 B1 = −2 , B2 = 故 rZs ( t ) = ⎜ −2e +
1 ⎞ ⎛7 ⇒ h ( t ) = ⎜ e −5t + e− t ⎟ u ( t ) 4 ⎠ ⎝4
注:由本例再次看到,相比经典法, p 算子法形式简洁,易算易记。 2-14 分析:求解两个信号的卷积,可以直接用定义,依照“反转 → 平移 → 相乘 → 求和” 的顺序来求,积分式为 x1 ( t ) ∗ x2 ( t ) =
1
受迫响应:
3 u (t ) 2
方法二: p 算子法
d2 d d r t + 3 r ( t ) + 2r ( t ) = e ( t ) + 3e ( t ) 2 ( ) dt dt dt
化为算子形式为: p + 3 p + 2 r ( t ) = ( p + 3) e ( t )
2
(
)
特征方程: α + 3α + 2 = 0 特征根为: α1 = −1 , α 2 = −2
方法二: p 算子法 (常用关系式:①
dx ( t ) 1 = px ( t ) ,② e− λt u ( t ) = δ (t ) dt p+λ
③
⎡ 1 ⎤ 1 1 x (t ) = δ ( t ) ∗ x (t )⎤ δ ( t ) ⎥ ∗ x ( t ) = e− λt u ( t ) ∗ x ( t ) ) =⎢ ⎡ ⎣ ⎦ p+λ p+λ ⎣ p+λ ⎦
4
= f1 ( t ) ∗ ⎡ ⎣δ ( t + 10 ) + 2δ ( t ) + δ ( t − 10 ) ⎤ ⎦
= f1 ( t + 10 ) + 2 f1 ( t ) + f1 ( t − 10 )
(3) s3 ( t ) = ⎡ ⎣ f1 ( t ) ∗ f 2 ( t ) ⎤ ⎦⎡ ⎣u ( t + 5 ) − u ( t − 5 ) ⎤ ⎦ ∗ f2 (t ) 由(1)得 f1 ( t ) ∗ f 2 ( t ) = s1 ( t ) , ⎡ ,保留 ( −5,5 ) ⎣u ( t + 5 ) − u ( t − 5 ) ⎤ ⎦ 相当于一个“时间窗” 内的信号,其它范围内的信号为 0。 (4) s4 ( t ) = f1 ( t ) ∗ f 3 ( t ) 发生时域信号的叠加
特征方程: α + 3α + 2 = 0 特征根为: α1 = −1 , α 2 = −2
2
故 rZi ( t ) = A1e + A2 e
−t
(
−2 t
) u ( t ) ,代入 r ( 0 ) , r ( 0 ) 得 A = 4 , A
'
Zi
+
Zi
+
1
2
= −3
故 rZi (单位冲激响应 h ( t ) 为“输入——输出”对,故 e ( t ) = δ ( t ) 时,
r ( t ) = h ( t ) 。类似上题,也可以用经典法和算子法两种思路求解该微分方程。
解题过程:方法一:经典法 代入 e ( t ) = δ ( t ) , f ( t ) = e u ( t ) + 3δ ( t ) 得到
2.15 分析:利用卷积的性质: f ( t ) ∗ ⎡ ⎣δ ( t + t0 ) + δ ( t − t0 ) ⎤ ⎦ = f ( t + t0 ) + f ( t − t0 ) 可画出 如下波形: (1) s1 ( t ) = f1 ( t ) ∗ f 2 ( t ) = f1 ( t ) ∗ ⎡ ⎣δ ( t + 5 ) + δ ( t − 5 ) ⎤ ⎦ = f1 ( t + 5 ) + f 2 ( t − 5 ) (2) s2 ( t ) = f1 ( t ) ∗ f 2 ( t ) ∗ f 2 ( t ) = f1 ( t ) ∗ ⎡ ⎣δ ( t + 5 ) + δ ( t − 5 ) ⎤ ⎦⎡ ⎣δ ( t + 5 ) + δ ( t − 5 ) ⎤ ⎦
rZi ( t ) 的求法与经典时域法一致, rZi ( t ) = ( 4e− t − 3e−2t ) u ( t )
再求 rZs ( t ) :e ( t ) = u ( t ) ,r ( t ) =
p+3 u ( t ) = ( p + 3) ⎡ e − t u ( t ) ∗ e −2t u ( t ) ∗ u ( t ) ⎤ ⎣ ⎦ ( p + 1)( p + 2 )
∴ s (t ) = f (t ) ∗ f (t ) = u (t ) ∗ ⎡ ⎣δ ( t ) − δ ( t − 1) ⎤ ⎦ ∗ u (t ) ∗ ⎡ ⎣δ ( t ) − δ ( t − 1) ⎤ ⎦ =⎡ ⎣u ( t ) ∗ u ( t ) ⎤ ⎦∗⎡ ⎣δ ( t ) − 2δ ( t − 1) + δ ( t − 2 ) ⎤ ⎦ = tu ( t ) ∗ ⎡ ⎣δ ( t ) − 2δ ( t − 1) + δ ( t − 2 ) ⎤ ⎦ = tu ( t ) − 2 ( t − 1) u ( t − 1) + ( t − 2 ) u ( t − 2 )
−t
1 2
⎛ ⎝
1 −2t 3 ⎞ e + ⎟ u (t ) 2 2⎠ ⎛ ⎝
−t
③全响应: r ( t ) = rZi ( t ) + rZs ( t ) = ⎜ 2e −
5 −2t 3 ⎞ e + ⎟ u (t ) 2 2⎠
自由响应: ⎜ 2e −
⎛ ⎝
−t
5 −2t ⎞ e ⎟ u (t ) 2 ⎠
−t
(
−2 t
) u (t )
'' '
②求 rZs : 将 e ( t ) = u ( t ) 代入原方程,有 rZs ( t ) + 3rZs ( t ) + 2rZs ( t ) = δ ( t ) + 3u ( t )
⎧rZs '' ( t ) = aδ ( t ) + bΔu ( t ) ⎪ ⎪ ' 用冲激函数匹配法,设 ⎨rZs ( t ) = aΔu ( t ) ⎪ ⎪ ⎩rZs ( t ) = at Δu ( t )
∫
+∞
−∞
x1 (τ ) x2 ( t − τ ) dτ ,但是这种依靠定义的基本方
法可能不是最简便的。更应该注意灵活运用卷积的性质(卷积的交换律、结合律、分配律; 卷积的微分与积分;与冲激函数或阶跃函数的卷积)对表达式进一步的化简,甚至直接得到 结果。 解题过程: (1) f ( t ) = u ( t ) − u ( t − 1) = u ( t ) ∗ ⎡ ⎣δ ( t ) − δ ( t − 1) ⎤ ⎦
引入微分算子 p , ( ∗) 式变成:
( p + 5) h ( t ) =
1 δ ( t ) + 2δ ( t ) p +1
3
1 ⎞ ⎛ 1 ⎜ −4 ⎟ 1 1 2 2 δ (t ) + δ (t ) = ⎜ δ (t ) ⇒ h (t ) = ⋅ + 4 ⎟δ (t ) + p + 5 p +1 p+5 p 5 p 1 p 5 + + + ⎜ ⎟ ⎝ ⎠
2-6 解题过程: (1) e ( t ) = u ( t ) , r ( 0 − ) = 1 , r ( 0 − ) = 2
'
方法一:经典时域法:
⎧rZi '' ( t ) + 3rZi ' ( t ) + 2rZi ( t ) = 0 ⎪ ⎪ ' ' ①求 rZi :由已知条件,有 ⎨rZi ( 0+ ) = rZi ( 0− ) = 2 ⎪ ' ' ⎪ ⎩rZi ( 0+ ) = rZi ( 0− ) = 1
其中 e u ( t ) ∗ e
−t
−2 t
t 1 ⎛1 ⎞ u ( t ) ∗ u ( t ) = ∫ ( e−τ − e−2τ ) dτ = ⎜ − e− t + e−2t ⎟ u ( t ) 0 2 ⎝2 ⎠
1 1 3⎞ ⎛1 ⎞ ⎛ ∴ rZs ( t ) = ( p + 3) ⎜ − e− t + e−2t ⎟ u ( t ) = ⎜ −2e− t + e −2t + ⎟ u ( t ) 2 2 2⎠ ⎝2 ⎠ ⎝ 5 3⎞ ⎛ ∴ 全响应 r ( t ) = rZi ( t ) + rZs ( t ) = ⎜ 2e − t − e−2t + ⎟ u ( t ) 2 2⎠ ⎝
利用冲激函数匹配法,在 ( 0− , 0+ ) 时间段内
⎧d ⎪ h1 ( t ) = aδ ( t ) + bΔu ( t ) ⎨ dx ⎪h1 ( t ) = aΔu ( t ) ⎩
( 0− < t < 0+ )
⇒ aδ ( t ) + bΔu ( t ) + 5aΔu ( t ) = δ ( t ) ⇒ a = 1, b = −5 ⇒ h1 ( 0+ ) = a + h ( 0− ) = A = 1 ⇒ h1 ( t ) = e −5t u ( t )
−t
d h ( t ) + 5h ( t ) = e − t u ( t ) + 2δ ( t ) dt
对于因果系统 h ( 0− ) = 0 先求满足
( ∗)
d h1 ( t ) + 5h1 ( t ) = δ ( t ) 的 h1 ( t ) : h1 ( t ) = Ae −5t u ( t ) dt
3 2
因为 e ( t ) = u ( t ) 故设特解为 rZsp ( t ) = C ⋅ u ( t ) ,代入原方程得 C = 故 rZs ( t ) = rZsh ( t ) + rZsp ( t ) = ⎜ B1e + B2 e
−t
'
⎛ ⎝
−2 t
3⎞ + ⎟ u (t ) 2⎠
代入 rZs ( 0+ ) , rZs ( 0+ ) 得 B1 = −2 , B2 = 故 rZs ( t ) = ⎜ −2e +
1 ⎞ ⎛7 ⇒ h ( t ) = ⎜ e −5t + e− t ⎟ u ( t ) 4 ⎠ ⎝4
注:由本例再次看到,相比经典法, p 算子法形式简洁,易算易记。 2-14 分析:求解两个信号的卷积,可以直接用定义,依照“反转 → 平移 → 相乘 → 求和” 的顺序来求,积分式为 x1 ( t ) ∗ x2 ( t ) =
1
受迫响应:
3 u (t ) 2
方法二: p 算子法
d2 d d r t + 3 r ( t ) + 2r ( t ) = e ( t ) + 3e ( t ) 2 ( ) dt dt dt
化为算子形式为: p + 3 p + 2 r ( t ) = ( p + 3) e ( t )
2
(
)
特征方程: α + 3α + 2 = 0 特征根为: α1 = −1 , α 2 = −2
方法二: p 算子法 (常用关系式:①
dx ( t ) 1 = px ( t ) ,② e− λt u ( t ) = δ (t ) dt p+λ
③
⎡ 1 ⎤ 1 1 x (t ) = δ ( t ) ∗ x (t )⎤ δ ( t ) ⎥ ∗ x ( t ) = e− λt u ( t ) ∗ x ( t ) ) =⎢ ⎡ ⎣ ⎦ p+λ p+λ ⎣ p+λ ⎦
4
= f1 ( t ) ∗ ⎡ ⎣δ ( t + 10 ) + 2δ ( t ) + δ ( t − 10 ) ⎤ ⎦
= f1 ( t + 10 ) + 2 f1 ( t ) + f1 ( t − 10 )
(3) s3 ( t ) = ⎡ ⎣ f1 ( t ) ∗ f 2 ( t ) ⎤ ⎦⎡ ⎣u ( t + 5 ) − u ( t − 5 ) ⎤ ⎦ ∗ f2 (t ) 由(1)得 f1 ( t ) ∗ f 2 ( t ) = s1 ( t ) , ⎡ ,保留 ( −5,5 ) ⎣u ( t + 5 ) − u ( t − 5 ) ⎤ ⎦ 相当于一个“时间窗” 内的信号,其它范围内的信号为 0。 (4) s4 ( t ) = f1 ( t ) ∗ f 3 ( t ) 发生时域信号的叠加
特征方程: α + 3α + 2 = 0 特征根为: α1 = −1 , α 2 = −2
2
故 rZi ( t ) = A1e + A2 e
−t
(
−2 t
) u ( t ) ,代入 r ( 0 ) , r ( 0 ) 得 A = 4 , A
'
Zi
+
Zi
+
1
2
= −3
故 rZi (单位冲激响应 h ( t ) 为“输入——输出”对,故 e ( t ) = δ ( t ) 时,
r ( t ) = h ( t ) 。类似上题,也可以用经典法和算子法两种思路求解该微分方程。
解题过程:方法一:经典法 代入 e ( t ) = δ ( t ) , f ( t ) = e u ( t ) + 3δ ( t ) 得到
2.15 分析:利用卷积的性质: f ( t ) ∗ ⎡ ⎣δ ( t + t0 ) + δ ( t − t0 ) ⎤ ⎦ = f ( t + t0 ) + f ( t − t0 ) 可画出 如下波形: (1) s1 ( t ) = f1 ( t ) ∗ f 2 ( t ) = f1 ( t ) ∗ ⎡ ⎣δ ( t + 5 ) + δ ( t − 5 ) ⎤ ⎦ = f1 ( t + 5 ) + f 2 ( t − 5 ) (2) s2 ( t ) = f1 ( t ) ∗ f 2 ( t ) ∗ f 2 ( t ) = f1 ( t ) ∗ ⎡ ⎣δ ( t + 5 ) + δ ( t − 5 ) ⎤ ⎦⎡ ⎣δ ( t + 5 ) + δ ( t − 5 ) ⎤ ⎦
