六年级下奥数 巧求面积
六年级奥数讲义-巧求周长及面积(附答案)

数学学科教师辅导教案知识精讲知识点一(长方形、正方形的周长)【知识梳理】同学们都知道,长方形的周长=(长+宽)×2,正方形的周长=边长×4。
长方形、正方形的周长公式只能用来计算标准的长方形和正方形的周长。
如何应用所学知识巧求表面上看起来不是长方形或正方形的图形的周长,还需同学们灵活应用已学知识,掌握转化的思考方法,把复杂的问题转化为标准的图形,以便计算它们的周长。
【典型例题】例1 有5张同样大小的纸如下图(a)重叠着,每张纸都是边长6厘米的正方形,重叠的部分为边长的一半,求重叠后图形的周长。
答案:72课堂练习一:1.下图由8个边长都是2厘米的正方形组成,求这个图形的周长。
答案:18*2=36厘米2.下图由1个正方形和2个长方形组成,求这个图形的周长。
答案:178厘米45cm3.有6块边长是1厘米的正方形,如例题中所说的这样重叠着,求重叠后图形的周长。
答案:14厘米例2 一块长方形木板,沿着它的长度不同的两条边各截去4厘米,截掉的面积为192平方厘米。
现在这块木板的周长是多少厘米?答案:192-4*4=176平方厘米176/4=44厘米44*2=88厘米课堂练习二:1.有一个长方形,如果长减少4米,宽减少2米,面积就比原来减少44平方米,且剩下部分正好是一个正方形。
求这个正方形的周长。
答案:6*4=24米2.有两个相同的长方形,长是8厘米,宽是3厘米,如果按下图叠放在一起,这个图形的周长是多少?答案:4*8=32厘米3.有一块长方形广场,沿着它不同的两条边各划出2米做绿化带,剩下的部分仍是长方形,且周长为280米。
求划去的绿化带的面积是多少平方米?答案:280/2*2+2*2=284平方米例3 已知下图中,甲是正方形,乙是长方形,整个图形的周长是多少?答案:2a+4b课堂练习三:1.有一张长40厘米,宽30厘米的硬纸板,在四个角上各剪去一个同样大小的正方形后准备做一个长方体纸盒,求被剪后硬纸板的周长。
济南六年级奥数题及答案

济南六年级奥数题及答案:面积1.一半模型如下图,长方形AFEB和长方形FDCE拼成了长方形ABCD ,长方形 ABCD的长是20,宽是12,则它内部阴影部分的面积是.2.直线型面积如图,边长为10的正方形中有一等宽的十字,其面积(阴影部分)为36,则十字中央的小正方形面积为________.1.分百应用题小明到商店买红、黑两种笔共66支.红笔每支定价5元,黑笔每支定价9元.由于买的数量较多,商店就给予优惠,红笔按定价85%付钱,黑笔按定价80%付钱,如果他付的钱比按定价少付了18%,那么他买了红笔多少支?2.列方程解应用题有一个敞口的立方体水箱,在其侧面一条高线的三等分处开两个排水孔A和B ,已知两孔的排水速度相同且保持不变,现在从水箱上面匀速注水,如果打开A孔,关闭B孔,那么经过20分钟可将水箱注满,如果关闭A孔,打开B孔,则需要 22分钟才能将水箱注满,那么两孔都打开,经过分钟才能将水箱注满.济南六年级奥数题及答案:质数和合数1.质数和合数一个三角形的三条边的边长都是质数,三条边长之和是16。
那么最长边与最短边的差是____。
2.数阵、数表下列数表的最后一个数的个位数是_____。
1 2 3 4 5……97 98 99 1003 5 7 9 …… 195 197 1998 12 16 …… 392 39620 28 (788)…… ……1.行程问题四、五、六3个年级各有100名学生去春游,都分成2列(竖排)并列行进.四、五、六年级的学生相邻两行之间的距离分别是1米、2米、3米,年级之间相距5米.他们每分钟都行走90米,整个队伍通过某座桥用4分钟,那么这座桥长米.2.行程问题已知甲车速度为每小时90千米,乙车速度为每小时60千米,甲、乙两车分别从A ,B 两地同时出发相向而行,在途经C地时乙车比甲车早到10分钟;第二天甲、乙分别从B ,A 两地出发同时返回原来出发地,在途经C地时甲车比乙车早到1个半小时,那么A ,B 两地的距离是多少?济南六年级奥数题及答案:数论综合1.数论综合已知四位数的个位数与千位数之和为10,个位数既是偶数又是质数,百位数与十位数组成两位数是个质数,又知这个四位数能被36整除,则所有满足条件的四位数中最大的是.2.数论综合有一个小于2000的四位数,它恰有14个正约数(包括1和本身),其中有一个质因数的末位数字是1,求这个四位数.1.计算与巧算11×19+12×18+13×17+14×16=2.计算与巧算济南六年级奥数题及答案:乘法原理1.乘法原理,分类讨论现有1角币1张,2角币1张,5角币1张,1元币4张,5元币2张。
六年级奥数1.1表面积与体积

六年级奥数1,1表面积与体积(tǐjī)六年级奥数1,1专题(zhuāntí)简析;小学阶段(jiēduàn)所学的立体图形主要有四种长方体·正方体·圆柱体和圆锥体。
从平面图形(túxíng)到立体图形是认识上的一个飞跃,需要有更高水平的空间想象能力。
因此,要牢固掌握这些几何图形的特征和有关的计算方法,能将公式作适当的变形,养成“数·形”结合(jiéhé)的好习惯,解题时要认真细致观察,合理大胆想象,正确灵活地计算。
在解答立体图形的表面积问题时,要注意以下几点;(1)充分利用正方体六个面的面积都相等,每个面都是正方形的特点。
(2)把一个立体图形切成两部分,新增加的表面积等于切面面积的两倍。
反之,把两个立体图形粘合到一起,减少的表面积等于粘合面积的两倍。
(3)若把几个长方体拼成一个表面积最大的长方体,应把它们最小的面拼合起来。
若把几个长方体拼成一个表面积最小的长方体,应把它们最大的面拼合起来。
例1,从一个棱长为10里面的正方体上挖去一个长10厘米·宽2厘米·高2厘米的小长方体,剩下部分的表面积是多少?〔思路导航〕这是一道开放题,方法有多种;1)沿一条棱挖,剩下部分的表面积为592平方厘米。
2)在某个面挖,剩下部分的表面积为632平方厘米。
3)挖通某两个对面,剩下部分的表面积为672平方厘米。
练习1,1,把一个长为12分米·宽为6分米·高为9分米的长方体木块锯成两个相同的小长方体木块,这两个小长方体的表面积之和比原来长方体的表面积增加了多少平方米?2,在一个棱长是4厘米的立方体上挖一个棱长是1厘米的小正方体后,表面机会发生怎样的变化?例2,把19个棱长为3厘米的正方体重叠起来,拼成一个立体图形(t úx íng),求这个立体图形的表面积。
〔思路(s īl ù)导航〕要求(y āoqi ú)这个复杂形体的表面积,必须从整体入手,从上·左·前三个方向(f āngxi àng)观察,每个方向上的小正方体各面就组合成了如下图形。
奥数第4讲-巧求周长与面积

巧求周长与面积掌握巧求周长与面积的基本方法;1. 理解并掌握割补、平移等数学思想方法。
【例1】 (2007年“希望杯”第一试)右图中的阴影部分BCGF 是正方形,线段FH 长18厘米,线段AC 长24厘米,则长方形ADHE 的周长是__________厘米。
【分析】 由于图中阴影部分BCGF 是个正方形,其四条边的边长都相等,且等于长方形ADHE 的宽。
FH AC +的和应为长方形ADHE 的长加上正方形BCGF 的边长,所以等于长方形ADHE 的长与宽之和。
所以长方形ADHE 的周长为:(1824)284+⨯=厘米。
【例2】 如右图所示,在一个正方形内画中、小两个正方形,使三个正方形具有公共顶点,这样大正方形被分割成了正方形区域甲,和L 形区域乙和丙。
甲的边长为4厘米,乙的边长是甲的边长的1.5倍,丙的边长是乙的边长的1.5倍,那么丙的周长为多少厘米?EF 长多少厘米?【分析】 乙的周长实际上是正方形AHJE 的周长(我们可将乙与甲重合的两条线段分别向左、向下平移),同样的,丙的周长也就是正方形ABCD 的周长。
由于4 1.56AE =⨯=,6 1.59AD =⨯=,所以丙的周长为9436⨯=厘米,642EF AE AF =-=-=(厘米)。
【例3】 用若干个边长都是2厘米的平行四边形与三角形(如右图)拼接成一个大的平行四边形,已知大平行四边形的周长是244厘米,那么平行四边形和三角形各有多少个?【分析】 大平行四边形上、下两边的长为(24422)2120-⨯÷=厘米,观察上边,每6厘米有两个平行四边形的边,所以共有小平行四边形1206240÷⨯=个,三角形的数量与小平行四边形的数量相等,也是40个。
[拓展] 用若干个边长都是2厘米的平行四边形与三角形(如右图)拼接成一个大的平行四边形,已知大平行四边形的周长是236厘米,那么平行四边形和三角形各有多少个?[分析] 大平行四边形上、下两边的长为(23622)2116-⨯÷=厘米,观察上边,每6厘米有两个平行四边形的边,1166192÷=,所以有三角形19238⨯=个,小平行四边形38139+=个。
(完整版)六年级奥数--体积、表面积

六年级奥数——体积、表面积一、知识要点解答立体图形的体积问题时,要注意以下几点:(1)物体沉入水中,水面上升部分的体积等于物体的体积。
把物体从水中取出,水面下降部分的体积等于物体的体积。
这是物体全部浸没在水中的情况。
如果物体不全部浸在水中,那么派开水的体积就等于浸在水中的那部分物体的体积。
(2)把一种形状的物体变为另一种形状的物体后,形状变了,但它的体积保持不变。
(3)求一些不规则形体体积时,可以通过变形的方法求体积。
(4)求与体积相关的最大、最小值时,要大胆想象,多思考、多尝试,防止思维定。
二、精讲精练【例题1】有大、中、小三个正方体水池,它们的内边长分别为6米、3米、2米。
把两堆碎石分别沉在中、小水池里,两个水池水面分别升高了6厘米和4厘米。
如果将这两堆碎石都沉在大水池里,大水池的水面升高多少厘米?中、小水池升高部分是一个长方体,它的体积就等同于碎石的体积。
两个水池水面分别升高了6厘米和4厘米,两堆碎石的体积就是3×3×0.06+2×2×0.04=0.7(立方米)。
把它沉到大水池里,水面升高部分的体积也就是0.7立方米,再除以它的底面积就能求得升高了多少厘米。
3×3×0.06+2×2×0.04=0.7(立方米)0.7÷6的平方=7/360(米)=1又17/18(厘米)答:大水池的水面升高了1又17/18厘米。
练习1:1、有大、中、小三个正方体水池,它们的内边长分别为4米、3米、2米。
把两堆碎石分别沉没在中、小水池的水中,两个水池的水面分别升高了4厘米和11厘米,如果将这两堆碎石都沉没在大水池中,那么大水池水面将升高多少厘米?2、用直径为20厘米的圆钢,锻造成长、宽、高分别为30厘米、20厘米、5厘米的长方体钢板,应截取圆钢多长(精确到0.1厘米)?3、将表面积为54平方厘米、96平方厘米、150平方厘米的三个铁质正方体熔铸成一个大正方体(不计损耗),求这个大正方体的体积。
奥数-巧求面积
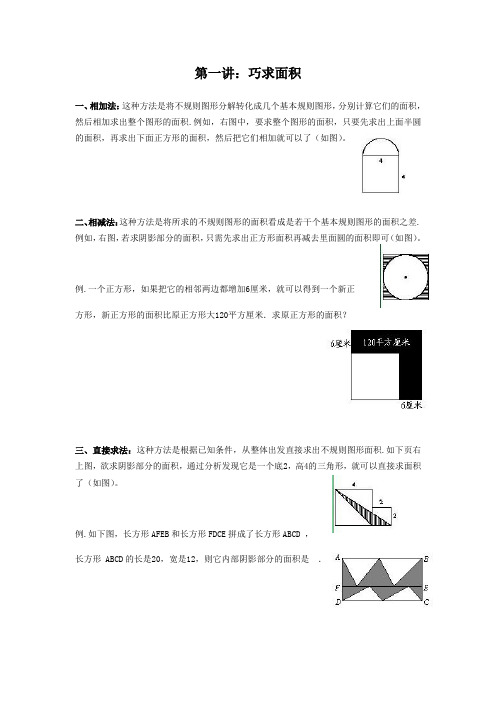
第一讲:巧求面积一、相加法:这种方法是将不规则图形分解转化成几个基本规则图形,分别计算它们的面积,然后相加求出整个图形的面积.例如,右图中,要求整个图形的面积,只要先求出上面半圆的面积,再求出下面正方形的面积,然后把它们相加就可以了(如图)。
二、相减法:这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差.例如,右图,若求阴影部分的面积,只需先求出正方形面积再减去里面圆的面积即可(如图)。
例.一个正方形,如果把它的相邻两边都增加6厘米,就可以得到一个新正方形,新正方形的面积比原正方形大120平方厘米.求原正方形的面积?三、直接求法:这种方法是根据已知条件,从整体出发直接求出不规则图形面积.如下页右上图,欲求阴影部分的面积,通过分析发现它是一个底2,高4的三角形,就可以直接求面积了(如图)。
例.如下图,长方形AFEB和长方形FDCE拼成了长方形ABCD ,长方形 ABCD的长是20,宽是12,则它内部阴影部分的面积是.四、重新组合法:这种方法是将不规则图形拆开,根据具体情况和计算上的需要,重新组合成一个新的图形,设法求出这个新图形面积即可.例如,欲求右图中阴影部分面积,可以把它拆开使阴影部分分布在正方形的4个角处,这时采用相减法就可求出其面积了(如图)。
例.已知大正方形边长是7厘米,小正方形边长5厘米,求阴影部分的面积。
五、辅助线法:这种方法是根据具体情况在图形中添一条或若干条辅助线,使不规则图形转化成若干个基本规则图形,然后再采用相加、相减法解决即可.如右图,求两个正方形中阴影部分的面积.此题虽然可以用相减法解决,但不如添加一条辅助线后用直接法作更简便(如图)。
六、割补法:这种方法是把原图形的一部分切割下来补在图形中的另一部分使之成为基本规则图形,从而使问题得到解决.例如,如右图,欲求阴影部分的面积,只需把右边弓形切割下来补在左边,这样整个阴影部分面积恰是正方形面积的一半(如图).例.求阴影部分的面积。
小学六年级奥数课件:巧求面积
例7. 如图,已知长方形ABCD的面积是54平方厘
米,BE=2AE,CF=2BF,则四边形ACFE的面
积是多少平方厘米?
A
E
B
F
D
C
解析
S△ABC=54÷ 2=27
连接CE。因为AE:EB=1:2,所以:S△ACE:S△BCE=1:2,
S△ACE=27÷ 3=9(平方厘米),S△BCE=27-9=18(平方厘米)
S△BPC的=S△BCE÷ 2=16(平方厘米) S△CDE=8× 4÷ 2=16(平方厘米) S△PDC 的面积=S△CDE÷ 2=8(平方厘米)
S阴=S正÷2-16-8=8(平方厘米)
例6.如图△ABC是一个等腰直角三角形,AB=BC=10,求图中阴 影部分的面积。(单位:分米)
解析
我们做辅助线。做AE垂直AB,EC平行AB,得到正 方形ABCE。 S半圆=5× 5× 3.14÷ 2=39.25(平方厘米) S正=10× 10=100(平方厘米) S△ADE=10× 15÷ 2=75(平方厘米) S阴=(39.25+100-75)÷2=32.125(平方厘米)
D
F
E
G
C
例4.在三角形ABC中,三角形AEO的面积是1,三角形ABO面积 是2,三角形BOD的面积是3,则四边形DCEO的面积是多少?
解析
连接OC,把DCEO分成两个三角形ECO和DCO 设ECO面积为x,DCO面积为y 由条件知,EO:OB=1:2, AO:OD=2:3
A E
则(AEO+ECO):DCO=2 :3
O
ECO:(DCO+BOD)=1:2
即: x:(y+3)=1:2
B
C
六年级奥数专题圆的面积
平面图形面积————圆的面积在正方形里的最大圆的面积占所在正方形的面积的3.144 ,而在圆内的最大正方形占所在圆的面积的23.14例题1。
求图中阴影部分的面积(单位:厘米)。
. 练习11.求下面各个图形中阴影部分的面积(单位:厘米)。
2.求下面各个图形中阴影部分的面积(单位:厘米)。
答1、计算下面图形中阴影部分的面积(单位:厘米,正方形边长4)。
答2、计算下面图形中阴影部分的面积(单位:厘米,正方形边长4)。
答1 2. 练习41、如图所示,三角形ABC是直角三角形,AC长4厘米,BC长2厘米。
以AC、BC为直径画半圆,两个半圆的交点在AB边上。
求图中阴影部分的面积。
答例题5。
在图中,正方形的边长是10厘米,求图中阴影部分的面积。
.1、求下面各图形中阴影部分的面积(单位:厘米)。
答2、求右面各图形中阴影部分的面积(单位:厘米)。
答3、求右面各图形中阴影部分的面积(单位:厘米)。
答.例题6。
在图的扇形中,正方形的面积是30平方厘米。
求阴影部分的面积。
练习61、如图所示,平行四边形的面积是100平方厘米,求阴影部分的面积。
答圆的面积与组合圆积专题训练一、填空题1.算出下面圆内正方形的面积为 .2.右下图是一个直角等腰三角形,直角边长2厘米,图中阴影部分面积是平方厘米.3.一个扇形圆心角120,以扇形的半径为边长画一个正方形,这个正方形的面积是120平方厘米.这个扇形面积是 .4.如图所示,以B 、C 为圆心的两个半圆的直径都是2厘米,则阴影部分的周长是 厘米.(保留两位小数)5.左下图三角形ABC 是直角三角形,阴影部分①的面积比阴影部分②的面积小28平方厘米. AB 长40厘米, BC 长 厘米6.如右下图,阴影部分的面积为2平方厘米,7.157平方厘米,这个扇形的圆心角是 .度。
8.图中扇形的半径OA=OB=6厘米.45=∠AOB , AC 垂直OB 于C,那么图中阴影部分的面积是 平方厘米.)14.3(=π9.在右图中(单位:厘米),两个阴影部分面积的和是 平方厘米.10.大圆的半径比小圆的半径长6厘米,且大圆半径是小圆半径的4倍.大圆的面积比小圆的面积大 平方厘米.11.左下图在一个半径是4.5厘米的圆中挖去两个直径都是2厘米的圆.剩下的图形的面积是 平方厘米.(π取3.14,结果精确到1平方厘米)12.右上图中三角形是等腰直角三角形,阴影部分的面积是 (平方厘米).13.如左下图所示,圆的周长是16.4厘米,圆的面积与长方形的面积正好相等.图中阴影部分的周长是 厘米.)14.3(=π14.如右下图,151=∠的圆的周长为62.8厘米,平行四边形的面积为100平方厘米.阴影部分的面积是 .15. 如左下图已知:ABCD 是正方形, ED=DA=AF=2厘米,阴影部分的面积是 .16.右下图中,扇形BAC 的面积是半圆ADB 的面积的311倍,那么,CAB 是 度.。
小学奥数第九讲-图形的面积(二)
【若缺失公式、图片现象属于系统读取不成功,文档内容齐全完整,请放心下载。
】第九讲图形的面积(二)阅读与思考上讲里我们学习了几何图形中一些面积计算的相关知识和方法。
本讲我们继续探讨平面几何图形面积的计算问题。
对于较为复杂的组合图形的面积问题,要注意观察图形的特点,寻找图形中的内在联系,灵活运用典型的数学思想方法、技巧解题。
1、利用弦图分割拼补求面积:如图1 弦图是由四个相同的长方形拼成一个大正方形,大正方形的边长等于长方形的长和宽的和,小正方形的边长等于长方形的长和宽的差。
根据大小正方形的边长和长方形的长与宽之间的关系可以巧妙地解决许多面积问题。
2、利用等量代换的思想计算有部分图形重叠的组合图形面积计算问题。
这类问题需要我们认真观察图形的特点,从组合图形中重叠的部分出发,寻找图形中的内在联系,巧妙地利用已知图形面积的和与差之间的关系建立等式,等量代换。
从而巧妙地求出组合图形的面积。
3、添加合适的辅助线构造成特殊图形如平行四边形、正方形、等腰直角三角形或等积形等。
添加辅助线的一般技巧有“见中点连中线,见中线延长一半”;“四十五度旁边想直角,分割拼补成等腰”等等。
典型例题|例①|如图2 从一个正方形木板上锯下宽0.5米的一个长方形木条后,剩下的长方形面积为5平方米。
问锯下的长方形木条面积是多少?分析与解这类题可以巧妙地运用弦图来求面积。
如图2 可以看出剩下的长方形的长是原正方形的边长,它的宽比长少0.5米。
根据弦图的启发,我们可以假设有四个与剩下的长方形一样的长方形,把它们拼成如图 3 的大正方形,这个大正方形的边长是长方形的长和宽的和,阴影小正方形的边长是长方形长和宽的差,正好等于0.5米,问题迎刃而解了。
大正方形的面积=0.5×0.5+4×5=20.25,大正方形的边长为4.5米,于是剩下的长方形中长+宽=4.5,长-宽=0.5,长=(4.5+0.5)÷2=2.5(米)。
六年级下册奥数专题练习-立体图形的计算(含答案) 全国通用
立体图形的计算【表面积的计算】例1 一个正方体木块,棱长1米,沿水平方向将它锯成3片,每片又锯成4长条,每条又锯成5小块,共得到大小不等的长方体60块(如图5.69)。
那么,这60块长方体的表面积的和是平方米。
(1988年北京小学数学奥林匹克邀请赛试题)讲析:不管每次锯的长方体大小如何,横着锯2次一共增加了4个正方形面;前后竖直方向锯3次共增加了6个正方形面;左右竖直方向锯4次共增加了8个正方形面。
原来大正方体有6个正方形面,所以一共有24个正方形面。
所以,60块长方体的表面积之和是(1×1)×24=24(平方米)。
例2 图5.70是由19个边长都是2厘米的正方体重叠而成的。
求这个立体图形的外表面积。
(北京市第一届“迎春杯”小学数学竞赛试题)讲析:如果按每一层有多少个正方体,然后再数出每层共有多少个外表面正方形,则很麻烦。
于是,我们可采用按不同的方向来观察的方法去计算。
俯视,看到9个小正方形面;正视,看到10个小正方形面;侧视,看到8个小正方形面。
所以,这个立体图形的表面积是(2×2)×[(9+10+8)×2]=216(平方厘米)。
【体积的计算】例1 一个正方体的纸盒中恰好能放入一个体积为628立方厘米的圆柱体,如图5.71,纸盒的容积有多大?(π取3.14)(全国第四届“华杯赛”复赛试题)讲析:因圆柱体的高、底面直径以及正方体的棱长都相等。
故可设正方即:正方体纸盒的容积是800立方厘米。
例2 在一个棱长4厘米的正方体的上面、右面、前面这三个面的中心分别挖一个边长1厘米的正方形小孔(如图5. 72所示),并通过对面,求打孔后剩下部分的体积。
(北京市第二届“迎春杯”小学数学竞赛试题)。
讲析:打完孔之后,在大正方体正中央就有一个1×1×1的空心小正方体。
三个孔的体积是(1×1×4)×3-(1×1×1)×2=10(立方厘米)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
教育讲义:巧求面积
一、课题名称:巧求面积(二)
二、学习目标
1、掌握常见图形面积的公式,能够解决一些简单的实际问题。
2、利用等量代换、割补法、重新组合法、添辅助线等方法来求面积。
三、教学过程
知识回顾
【典型例题】
例1.如图,在边长为6厘米的等边三角形中挖去三个同样的扇形,求阴影部分的面积。
例2.正方形边长为2厘米,求阴影部分的面积。
例3.图中四个圆的半径都是1厘米,求阴影部分的面积。
例4.如图,四个扇形的半径相等,求阴影部分的面积。
(单位:厘米)
例5.如图,正方形ABCD的对角线AC=2厘米,扇形ACB是以AC为直径的半圆,扇形DAC是以D为圆心,AD为半径的圆的一部分,求阴影部分的面积。
例6.求阴影部分的面积。
(单位:厘米)
例7.如图,三角形ABC是直角三角形,阴影部分甲比阴影部分乙面积大28平方厘米,AB=40厘米。
求BC的长度。
例8.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)
归纳总结
组合图形阴影部分面积计算的解题思路
组合图形阴影部分面积计算是小学平面几何知识的综合运用,在小学数学中是一个重点,由于小学生只学习过三角形、正方形、长方形、平行四边形、梯形、圆、扇形面积的计算,但没有具体地学习线、面、图形相互关系方面的知识联系,因此,这些几何知识对于小学生来是零碎的;再说,小学生的空间思维发展滞后,于是组合图形阴影部分面积的计算在小学教育教学中成为了难点。
我总结了一点经验,概括了几种求组合图形阴影部分面积的解题思路,从思维上帮助学生清晰了解题思路,引导小学生走上正确地解决组合图形阴影部分面积的解题思路。
方法一:移拼、割补的思路
移拼、割补的思路是把不规则的阴影面积通过学习割补,使之变为一个面积大小不变且能实施计算成面积相同的规则图形。
方法二:重叠、分层的思路
重叠、分层思路是图形中不规则的阴影部分看作几个规则图形用不同的方法重叠的结果,利用分层把重叠部分分出来,组成重叠图形各项个规则图形的面积总和减去分掉的那面积,就是剩下所求那部分面积。
方法三:加法、分割的思路
加法分割思路是把所求阴影部分面积分割成几块能用公式计算的规则图形(三角形、正方形、长方形、平行四边形、梯形、圆、扇形),分别计算出面积,并相加得出阴影部分的面积。
方法四:减法、拓展的思路
减法拓展思路是把不规则图形阴影部分面积拓展到包含阴影部分的规则图形中进行分析,通过计算这个规则图形的面积和规则图形中除阴影部分面积之外多余的面积,运用“总的”减去“部分的”方法解得答案。
课后作业
1、求阴影部分的周长和面积。
(单位:厘米)
二、已知阴影部分的面积是8平方厘米,求圆的面积。
三、能力拓展题。
1.求下图正方形内阴影部分的面积。
(正方形边长是4厘米)
家长签名:
年月日。
