高中数学北师大版必修5 第一章1.2 数列的函数特性 作业2 Word版含解析
2020-2019学年北师大版数学必修5学案:1.1.2 数列的函数特性 Word版含解析
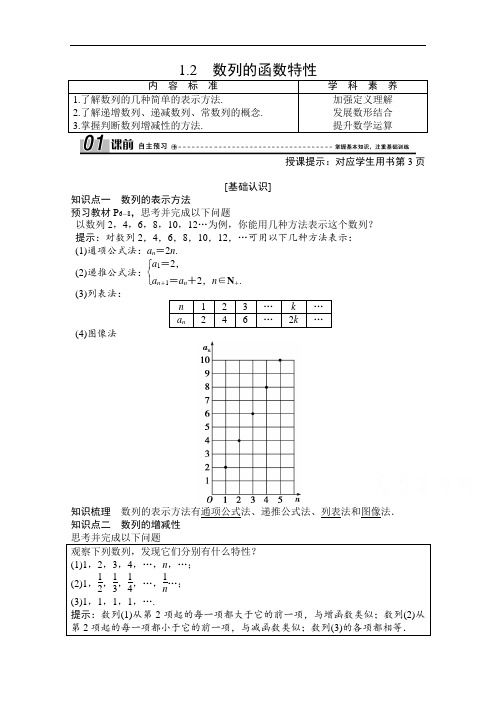
1.2数列的函数特性内容标准学科素养1.了解数列的几种简单的表示方法.2.了解递增数列、递减数列、常数列的概念.3.掌握判断数列增减性的方法.加强定义理解发展数形结合提升数学运算授课提示:对应学生用书第3页[基础认识]知识点一数列的表示方法预习教材P6-8,思考并完成以下问题以数列2,4,6,8,10,12…为例,你能用几种方法表示这个数列?提示:对数列2,4,6,8,10,12,…可用以下几种方法表示:(1)通项公式法:a n=2n.(2)递推公式法:⎩⎨⎧a1=2,a n+1=a n+2,n∈N+.(3)列表法:n 123…k …a n246…2k …(4)图像法知识梳理数列的表示方法有通项公式法、递推公式法、列表法和图像法.知识点二数列的增减性观察下列数列,发现它们分别有什么特性?(1)1,2,3,4,…,n,…;(2)1,12,13,14,…,1n…;(3)1,1,1,1,….提示:数列(1)从第2项起的每一项都大于它的前一项,与增函数类似;数列(2)从第2项起的每一项都小于它的前一项,与减函数类似;数列(3)的各项都相等.分类 定义 表达式 递增数列 从第2项起,每一项都大于它前面的一项 a n +1>a n 递减数列 从第2项起,每一项都小于它前面的一项 a n +1<a n 常数列 各项都相等 a n +1=a n1.已知数列{a n }的通项公式a n =n ·⎝ ⎛⎭⎪⎫34n,n ∈N +,则数列{a n }是( ) A .递增数列 B .递减数列 C .摆动数列 D .先递增再递减的数列 答案:D2.已知a n =3n -2,则数列{a n }的图像是( ) A .一条直线 B .一条抛物线 C .一个圆 D .一群孤立的点 答案:D3.若数列{a n }为递减数列,则{a n }的通项公式可能为________(填序号).①a n =-2n +3;②a n =-n 2+3n +1;③a n =12n ;④a n =(-1)n . 答案:①③授课提示:对应学生用书第4页探究一 数列的表示法[阅读教材P8练习1]在1984年到2004年的6届夏季奥运会上,我国获得的金牌数依次排成数列:15,5,16,16,28,32,试画出该数列的图像.解析:用横坐标表示年数,纵坐标表示获得的金牌数,得到该数列的图像如图.[例1] 图中的三角形图案称为谢宾斯基三角形,在四个三角形图案中,着色的小三角形的个数依次构成一个数列的前4项,请写出这个数列的递推公式和一个通项公式,并在直角坐标系中画出它的图像.[解析]如题图,这四个三角形图案中着色的小三角形第(2)个是第(1)个的3倍,第(3)个是第(2)个的3倍,故有递推公式a1=1,a n+1=3a n,n∈N+,个数依次为1,3,9,27.则所求数列的前4项都是3的指数幂,指数为序号减1.所以,这个数列的一个通项公式是a n=3n-1,n∈N+.在直角坐标系中的图像为一些孤立的点(如图所示).方法技巧求数列的递推公式注重观察数列项与项的关系,求通项公式注重观察项与序号的关系,图像法则一如既往地直观.跟踪探究 1.某种练习本单价5元,小王买了n本(n∈N+,n≤5)该练习本,记a n 为买n本的总价,试用三种方法来表示数列{a n}.解析:通项公式法:a n=5n(n∈N+,n≤5).列表法:n 1234 5a n510152025图像法:探究二数列的单调性[阅读教材P7例3及解答]判断下列无穷数列的增减性.(1)2,1,0,-1,…,3-n,…(2)12,23,34,…,nn+1,…题型:定义法判断数列的增减性.方法步骤:①设出数列通项公式a n.②作差并化简a n+1-a n.③判断符号得出结论.[例2] 已知函数f (x )=x -1x ,设a n =f (n )(n ∈N +). (1)求证:a n <1.(2){a n }是递增数列还是递减数列?为什么? [解题指南] a n =n -1n →判断a n <1→由a n +1-a n 的符号,判断是递增数列还是递减数列[解析] (1)证明:因为a n =n -1n =1-1n ,且n ∈N +,所以a n <1.(2)a n +1-a n =n n +1-n -1n =n 2-(n 2-1)n (n +1)=1n (n +1)>0,所以a n +1>a n ,因此{a n }为递增数列.方法技巧 判断数列的增减性,一般是将其转化为比较相邻两项的大小,常用的方法有作差法、作商法,作差法判断数列增减性的步骤为(1)作差;(2)变形;(3)定号;(4)结论.作商法适用于各项都是同号的数列,且应比较比值与1的大小关系.跟踪探究 2.已知数列{a n }的通项公式为a n =nn 2+9(n ∈N +),写出其前5项,并判断数列{a n }的单调性.解析:当n =1,2,3,4,5时,a n 依次为110,213,16,425,534,a n +1-a n =n +1(n +1)2+9-nn 2+9=-n 2-n +9[(n +1)2+9](n 2+9).∵函数f (x )=-x 2-x +9=-⎝ ⎛⎭⎪⎫x +122+374.在[1,+∞)上是递减的,又f (1)=7>0,f (2)=3>0,f (3)=-3<0, ∴当n =1,2时,a n +1>a n ,当n ≥3,n ∈N +时,a n +1<a n ,即a 1<a 2<a 3>a 4>a 5>…. ∴数列{a n }的前3项是递增的,从第3项往后是递减的.[例3] 已知数列{a n }的通项公式a n =n 2+kn (n ∈N +),若数列{a n }是递增数列,求实数k 的取值范围.[解析] 由{a n }是递增数列,得a n +1-a n =(n +1)2+k (n +1)-(n 2+kn )=2n +1+k >0对于任意n ∈N +恒成立.∵f (x )=2x +1+k 在[1,+∞)上为增函数,∴2n +1+k >0对任意n ∈N +恒成立等价于2×1+1+k >0,∴k >-3,∴实数k 的取值范围是(-3,+∞).方法技巧 实际上,当-3<k <-2时,函数y =x 2+kx 在[1,+∞)上不是单调函数,但数列a n =n 2+kn 是单调的,由此可知函数y =f (x )在[1,+∞)上单调,则数列a n =f (n )一定单调,反之则不一定.究其原因,是数列与函数定义域不同造成的差别.跟踪探究 3.已知递增数列{a n }的通项公式为a n =2kn +1,则实数k 的取值范围是________.解析:由于数列{a n }是递增数列,所以a n +1-a n >0,即[2k (n +1)+1]-(2kn +1)=2k >0,解得k >0. 答案:(0,+∞)[阅读教材P7例4及解答] 作出数列-12,14,-18,116,…,⎝ ⎛⎭⎪⎫-12n,…的图像,并分析数列的增减性.题型:图像法判断数列的增减性. 方法步骤:①作出数列的图像; ②根据图像判断数列的增减性. [例4] 在数列{a n }中,a n =n 2-8n . (1)画出{a n }的图像;(2)根据图像写出数列{a n }的增减性. [解析] (1)列表1 2 3 4 5 6 7 8 9 … -7 -12 -15 -16 -15 -12 -7 0 9 …n ,-12),(3,-15),(4,-16),(5,-15),(6,-12),(7,-7),(8,0),(9,9),…,图像如图所示.(2)当1≤n ≤4(n ∈N +)时,数列{a n }为递减数列;当n >4(n ∈N +)时,数列{a n }为递增数列.方法技巧 数列是自变量为正整数的一种特殊的函数,因此也可以用图像来表示,以位置序号n 为横坐标,相应的项为纵坐标,即坐标为(n ,a n )描点画图,就可以得到数列的图像.因为它的定义域是正整数集N +(或它的有限子集{1,2,3,…,n }),所以其图像是一群孤立的点,这些点的个数可以是有限的,也可以是无限的.跟踪探究 4.已知数列{a n }的通项公式为a n =22n -9,画出它的图像,并判断增、减性.解析:图像如图所示,该数列在{1,2,3,4}上是递减的,在{5,6,…}上也是递减的.探究三求数列的最大(小)项[例5]已知数列{a n}满足a n=22n-5,此数列有无最大项?若有,是第几项?[解题指南]假设存在最大项→作差a n-a n-1→讨论差的符号→下结论,或利用数列的函数特性作图像求解.[解析]法一:假设数列{a n}中存在最大项,因为a n=22n-5=1n-52,所以a n-a n-1=1n-52-1(n-1)-52=⎝⎛⎭⎪⎫n-72-⎝⎛⎭⎪⎫n-52⎝⎛⎭⎪⎫n-52⎝⎛⎭⎪⎫n-72=-1⎝⎛⎭⎪⎫n-52⎝⎛⎭⎪⎫n-72(n≥2,n∈N+),当n<3时,n-52<0,n-72<0,所以a n-a n-1<0,有a n<a n-1,将n=1,2代入a n知:a2<a1<0;当n=3时,n-52>0,n-72<0,所以a n-a n-1>0,有a n>a n-1,将n=3代入a n知:0<a3=2;当n>3时,n-52>0,n-72>0,所以a n-a n-1<0,有a n<a n-1,将n=4,5,6,…代入a n知:23=a4>a5>a6> 0由以上分析知,第三项a3=2是数列的最大值.法二:作出函数f(x)=22x-5的图像.由图像知,此数列有最大项,是第3项.延伸探究 本例中,条件不变,求“此数列有无最小项”?解析:由以上分析知,a 2<a 1<0,a 3>a 4>a 5>a 6>…>0,所以数列的最小项是第二项a 2=-2.方法技巧 求数列的最大(小)项的方法 (1)利用数列的单调性→作差a n +1-a n →分析差与0的关系,得出数列的单调性→求最值(2)函数思想的应用→确定与数列对应的函数→化简,找到基本函数→分析函数的单调性→求函数最值 (3)不等式思想的应用→设出最大(小)项为第k 项→列不等式组⎩⎨⎧a k ≥(≤)a k +1a k ≥(≤)a k -1→解出k 的取值范围→确定k 的值跟踪探究 5.在数列{a n }中,a n =(n +1)⎝ ⎛⎭⎪⎫1011n(n ∈N +).(1)求证:数列{a n }先递增,后递减; (2)求数列a n 的最大项.解析:(1)证明:令a na n -1>1(n ≥2),即(n +1)·⎝ ⎛⎭⎪⎫1011n n ·⎝ ⎛⎭⎪⎫1011n -1>1,整理得n +1n >1110,解得n<10.令a na n +1>1,即(n +1)·⎝ ⎛⎭⎪⎫1011n (n +2)·⎝ ⎛⎭⎪⎫1011n +1>1,整理得n +1n +2>1011,解得n >9.所以数列{a n }从第1项到第9项递增,从第10项起递减,即数列{a n }先增后减.(2)由(1)知,a 9=a 10=1010119最大.授课提示:对应学生用书第5页[课后小结](1){a n }与a n 是不同的两种表示,{a n }表示数列a 1,a 2,…,a n ,…,是数列的一种简记形式.而a n 只表示数列{a n }的第n 项,a n 与{a n }是“个体”与“整体”的从属关系.(2)数列的表示方法:①图像法;②列表法;③通项公式法;④递推公式法.(3)数列的单调性是通过比较{a n }中任意相邻两项a n 和a n +1的大小来判定的.某些数列的最大项或最小项问题,可以通过研究数列的单调性加以解决. (4)数列是特殊函数,一定要注意其定义域是N +(或它的有限子集).[素养培优]忽略数列中项数的特殊性致误在数列{a n }中,a n =3n 2-14n -8,求该数列的最小项.易错分析 解决数列问题时可以借鉴函数的方法,但必须注意数列相对函数的特殊性,尤其是数列中项数n 只能取正整数;在求解此题时容易忽略这一点而得到错误的结论-733.自我纠正 a n =3n 2-14n -8=3⎝ ⎛⎭⎪⎫n -732-733,因为73∈(2,3),所以当n 取距离73最近的整数时,a n 最小,而a 2=-24,a 3=-23,所以该数列中的最小项为a 2=-24.。
高中数学北师大版必修5习题:第一章数列1.1.2含解析

所以 a9<a 10.故选 C.
答案 :C
4.在下列图像中给定函数 y=f (x)的图像 ,且对任意 an∈(0,1),由关系式 an+ 1=f (an)得到的数
列 { an} 满足 an+1>a n(n∈N+ ),则该函数的图像是 ( )
A.
B.
C. 1
D. 解析 :由 an+1>a n可知数列 { an} 为递增数列 .
θ=
(3n-2)S,
∴ = = , ??△ ??????????
??△ ???2???2
12× ?? × ????sin??(3??-2)??
12× 2× 2??sin??
4??
∴ ??2
4
=
3??- 2
4 ,∴ x=√3??-2,即
an= √3??-2(n≥3),经验证知
an=√3??-2(n∈N+ ).
x1= 1 代入
1
xn+1= ????+1 -1,得
1
x2=- 2 ,再将
x2 代入
1
xn+ 1=
????+1
-1,得
x3= 1,则数列 { xn} 的周
期为 2,x2 017=x1= 1.
答案 :D
3.数列 { an} 满足
a1= 1,a2= 1,an+2= (1
+
sin 2
??
π
) an
+
4cos2??
k 项,则 k=
.
解析 :已知数列最大项为第
2 ??
2 ??+1
k 项 ,则有 {
??(??+
高中数学必修五北师大版 1.2 数列的函数特性 作业(含答案)2

2.已知数列{an}满足a1=1,a2=1,an+1=|an-an-1|(n≥2),则该数列前2 008项的和S2 008等于()
A.670 B.669
C.1 338 D.1 339
解析:∵a1=a2=1,∴a3=0,a4=1,a5=1,a6=0.
∴{an}是周期为3的周期数列.∴S2 008=669(a1+a2+a3)+a2 008=669×2+a1=1 338+1=1 339.
A.1B.2
C.D.2-987
解析:由已知,得a1=1,a2=2,a3=2,a4=1,a5=,a6=,a7=1,a8=2,a9=2,a10=1,a11=,a12=,即an的值以6为周期重复出现,故a17=.
答案:C
3.已知数列{an}的通项公式是an=n2+kn+2,若对于n∈N*,都有an+1>an成立,则实数k的取值范围是()
答案:4
10.已知函数f(x)=2x-2-x,数列{an}满足f(log2an)=-2n.
(1)求数列{an}的通项公式;
(2)证明数列{an}是递减数列.
解析:(1)∵f(x)=2x-2-x,f(log2an)=-2n,
∴2log2an-2-log2an=-2n,an-=-2n,
∴a+2nan-1=0,解得an=-n±.
解析:设n-1=t∈(0,1],则5·2n-2-4·n-1=5t2-4t,∴t=1,即n=1时,取最大值,t=,n=2时,取最小值,即x=1,y=2.∴x+y=3.
答案:3
5.在数列{an}中,an=(n+1)n(n∈N+).
(1)求证:数列{an}先递增,后递减;
(2)求数列{an}的最大项.
解析:(1)证明:令≥1(n≥2),即≥1.整理得≥,解得n≤10.令≥1,即≥1.
2022_2022学年高中数学第一章数列1.1.2数列的函数特性课时作业含解析北师大版必修5

课时作业 2 数列的函数特性时,a n 最小,且最小项a 3=a 4=-20.法二:设a n 为数列{a n }的最小项,则⎩⎪⎨⎪⎧ a n ≤a n -1a n ≤a n +1,(n ≥2) 即{n 2-7n -8≤(n -1)2-7(n -1)-8,n 2-7n -8≤(n +1)2-7(n +1)-8, 解得3≤n ≤4,故当n =3或n =4时,a 3=a 4是数列中的最小项,且最小项a 3=a 4=-20. |能力提升|(20分钟,40分)11.数列{a n }满足a n +1=⎩⎨⎧ 2a n ,0≤a n <122a n -1,12≤a n <1.若a 1=35,则a 2018=( ) A.15 B.25C.35D.45 解析:∵a 1=35>12,∴a 2=2a 1-1=15<12,a 3=2a 2=25<12,a 4=2a 3=45>12,a 5=2a 4-1=35>12, ∴a n +4=a n ,∴a 2018=a 4×504+2=a 2=15.故选A. 答案:A12.设数列{a n }的通项公式为a n =n 2+λn ,且{a n }满足a 1<a 2<a 3<…<a n <a n +1<…,则实数λ的取值范围是________.解析:方法一:因为a n =n 2+λn ,其图象的对称轴为n =-λ2,显然,当-λ2≤1,即λ≥-2时,数列{a n }是单调递增数列.如图所示,当⎩⎪⎨⎪⎧1<-λ2<2a 1<a 2时,数列{a n }也是单调递增的,此时-3<λ<-2. 故实数λ的取值范围为{λ|λ≥-2}∪{λ|-3<λ<-2}={λ|λ>-3},即实数λ的取值范围是(-3,+∞).方法二:直接根据定义来处理.∵数列{a n }是单调递增数列,∴a n +1-a n >0,又a n =n 2+λn ,∴(n +1)2+λ(n +1)-n 2-λn >0,∴2n +1+λ>0,λ>-(2n +1),又n ∈N *,∴λ>-3,即实数λ的取值范围是(-3,+∞).答案:(-3,+∞)13.(1)已知数列{a n }中,a 1=1,a n +1=a n +2,求数列{a n }的通项公式;(2)已知数列{a n }满足a 1=23,a n +1=n n +1a n ,求数列{a n }的通项公式.。
2019高中数学北师大版高二必修5_第一章1.2_数列的函数特性_作业2_word版含解析.doc

,[学生用书单独成册])[A.基础达标]1.已知a n +1-a n -3=0,则数列{a n }是( ) A .递增数列 B .递减数列 C .常数列D .不能确定解析:选A.因为a n +1-a n =3>0,故数列{a n }是递增数列. 2.已知数列{a n }的通项公式为a n =nn +1,则这个数列是( )A .递增数列B .递减数列C .常数列D .摆动数列解析:选A.因为a n +1-a n =n +1n +2-n n +1=(n +1)2-n (n +2)(n +1)(n +2)=1(n +1)(n +2)>0.故选A.3.数列{a n }中,a n =-2n 2+29n +3,则此数列最大项的值是( ) A .109 B .10818C .108D .107解析:选C.a n =-2n 2+29n +3=-2(n 2-292n )+3=-2·(n -294)2+3+2928,当n =7时,a n最大且等于108,故选C.4.已知数列{a n }满足a n =n -1na n -1(n ≥2),则数列{a n }为( ) A .递增数列 B .递减数列 C .常数列D .以上都有可能解析:选D.若a 1>0,则a n <a n -1(n ≥2),{a n }为递减数列;若a 1=0,则a n =0(n ∈N +),{a n }为常数列;若a 1<0,则a n >a n -1(n ≥2),{a n }为递增数列,故选D.5.已知数列{a n }的通项公式是a n =n -1n +1,则a n 与a n +1间的大小关系是( ) A .a n >a n +1 B .a n <a n +1 C .a n =a n +1D .不能确定解析:选B.因为a n +1-a n =nn +2-n -1n +1= n (n +1)-(n -1)(n +2)(n +2)(n +1)=n 2+n -(n 2+n -2)(n +2)(n +1)=2(n +2)(n +1)>0,所以a n <a n +1,选B.6.已知下列数列:①2 010,2 014,2 018,2 022; ②0,12,23,…,n -1n ,…;③1,12,14,…,12n -1,…;④1,-23,35,…,(-1)n -1·n 2n -1,…;⑤6,6,6,6,6,6.其中,有穷数列是________,无穷数列是________,递增数列是______,递减数列是______,常数列是________,摆动数列是______.(将符合条件的数列的序号填在横线上)解析:①是有穷递增数列; ②是无穷递增数列; ③是无穷递减数列;④是摆动数列,也是无穷数列; ⑤是常数列,也是有穷数列.答案:①⑤ ②③④ ①② ③ ⑤ ④7.已知数列{a n }的通项公式a n =n 2-4n -12(n ∈N +),则这个数列从第________项起各项为正数.解析:令a n =n 2-4n -12>0,解得n >6或n <-2(舍去).故从第7项起各项为正数. 答案:78.已知数列{a n }为单调递增数列,通项公式为a n =n +λn,则λ的取值范围是________.解析:由于数列{a n }为单调递增数列,a n =n +λn ,所以a n +1-a n =[(n +1)+λn +1]-(n +λn )=1-λn (n +1)>0,即λ<n (n +1)(n ∈N +),所以λ<2.答案:(-∞,2)9.已知函数f (x )=x -x 2+1,数列{a n }满足a n =f (n )(n ∈N +),试判断数列{a n }的增减性. 解:因为a n +1-a n =(n +1)-(n +1)2+1-(n -n 2+1) =1-[(n +1)2+1-n 2+1] =1-2n +1(n +1)2+1+n 2+1>1-2n +1(n +1)+n=0,所以a n +1>a n .所以数列{a n }是递增数列.10.已知数列{a n }的通项公式为a n =n 2-5n +4, (1)数列中有多少项为负数?(2)n 为何值时,a n 有最小值?并求此最小值. 解:(1)由n 2-5n +4<0得1<n <4,n ∈N +, 所以n =2或3.所以数列中有2项为负数.(2)因为a n =n 2-5n +4=⎝ ⎛⎭⎪⎫n -522-94,又因为n ∈N +,所以n =2或3时,a n 有最小值-2.[B.能力提升]1.一给定函数y =f (x )的图像在下列各图中,并且对任意a n ∈(0,1),由关系式a n +1=f (a n )得到的数列{a n }满足a n +1>a n (n ∈N +),则该函数的图像是( )解析:选A.由a n +1=f (a n ),a n +1>a n 知f (a n )>a n .可以知道x ∈(0,1)时f (x )>x ,即f (x )的图像在y =x 图像的上方,由选项中所给的图像可以看出,A 符合条件.2.已知数列{a n }的通项公式a n =anbn +1(a ,b 为正常数),那么a n 与a n +1的关系是( ) A .a n >a n +1 B .a n <a n +1 C .a n =a n +1D .以上都不对解析:选B.考虑函数y =axbx +1=a b (bx +1)-a b bx +1=a b +-a bbx +1=ab +-a b 2x +1b,其图像可由y =-ab 2x 先向左平移1b 个单位长度,再向上平移ab个单位长度得到,如图.由图像不难得知y =ax bx +1在[1,+∞)上单调递增,所以a n =anbn +1的值随n 的变大而变大. 所以数列{a n }是递增数列,即a n <a n +1,故选B. 3.已知数列{a n }的通项公式a n =n -96n -98,n ∈N +,则数列{a n }的最大项为________,最小项为________.解析:将数列{a n }的通项公式变形为a n =1+98-96n -98,考察函数f (x )=1+98-96x -98,画出图像(图略),数列{a n }的图像即为曲线上横坐标为正整数的孤立的点,易知n =10时,a n 取得最大值,为10-9610-98;n =9时,a n 取得最小值,为9-969-98.所以,数列{a n }中最大项为a 10=10-9610-98,最小项为a 9=9-969-98 .答案:10-9610-98 9-969-984.已知通项公式为a n =(m 2-2m )(n 3-2n )的数列是递减数列,则实数m 的取值范围为____________.解析:因为数列{a n }为递减数列,所以a n +1<a n .所以a n +1-a n =(m 2-2m )[(n +1)3-2(n +1)-n 3+2n ]=(m 2-2m )(3n 2+3n -1)<0. 因为n ∈N +,所以3n 2+3n -1=3⎝ ⎛⎭⎪⎫n +122-74≥5>0.所以m 2-2m <0,解得0<m <2. 故m ∈(0,2). 答案:(0,2)5.已知数列{a n }的通项公式为a n =(n +2)⎝ ⎛⎭⎪⎫910n,试问n 取何值时,a n 取最大值?试求出a n 的最大值.解:因为a n +1a n =(n +3)⎝ ⎛⎭⎪⎫910n +1(n +2)⎝ ⎛⎭⎪⎫910n =9(n +3)10(n +2)=910+910·1n +2,由a n +1a n =1,解得n =7,则当n=7时,a 8a 7=1,即a 7=a 8.当n <7时,a n +1a n>1,即a n +1>a n . 当n ≥8时,a n +1a n<1,即a n +1<a n . 则当n =7或n =8时,a n 取最大值, 最大值为a 7=a 8=98107.6.设f (x )=log 2x -log x 4(0<x <1),又知数列{a n }的通项a n 满足f (2a n )=2n . (1)求数列{a n }的通项公式; (2)试判断数列{a n }的增减性.解:(1)因为f (x )=log 2x -log x 4(0<x <1),f (2 an )=2n , 所以log 22an -log 2 an 4=2n ,由换底公式,得log 22 an -log 24log 22a n=2n , 即a n -2a n=2n ,所以a 2n -2na n -2=0, 所以a n =n ±n 2+2.① 由0<x <1,有0<2an <1, 所以a n <0.②由①②得a n =n -n 2+2,此即为数列{a n }的通项公式.(2)a n +1a n =(n +1)-(n +1)2+2n -n 2+2 =n +n 2+2(n +1)+(n +1)2+2<1, 因为a n <0,所以a n +1>a n , 所以数列{a n }是递增数列.。
新高中数学(北师大版)必修五同步练习:1-1-2数列的函数特性(含答案解析)

1.2 数列的函数特性双基达标限时20分钟1.已知a n =3n -2,则数列{a n }的图像是( ).A .一条直线B .一条抛物线C .一个圆D .一群孤立的点解析 ∵a n =3n -2,n ∈N +,∴数列{a n }的图像是一群孤立的点. 答案 D2.在数列{a n }中,a n =n ,则{a n }是 ( ).A .递增数列B .递减数列C .常数列D .以上都不是解析 ∵a n +1-a n =(n +1)-n =1>0,∴数列{a n }是递增数列.答案 A 3.在递减数列{a n }中,a n =kn(k 为常数),则实数k 的取值范围是( ).A .RB .(0,+∞)C .(-∞,0)D .(-∞,0]解析 ∵{a n }是递减数列,∴a n +1-a n =k(n +1)-kn =k<0.答案 C4.若数列{a n }为递减数列,则{a n }的通项公式可能为________(填写序号). ①a n =-2n +1; ②a n =-n 2+3n +1;③a n =12n ; ④a n =(-1)n . 解析 可以通过画函数的图像一一判断.②有增有减,④是摆动数列. 答案 ①③5.数列{-2n 2+9n +3}的最大项是第________项,最大项为________.解析 由已知a n =-2n 2+9n +3=-2⎝⎛⎭⎫n -942+1058.∵n ∈N +,故当n =2时,a n 取到最大 值13.答案 2 136.已知数列{a n }是递减数列,且a n =(m 2-2m)(n 3-2n),求实数m 的取值范围. 解 ∵数列为递减数列,∴a n +1<a n ,∴a n +1-a n =(m 2-2m)[(n +1)3-2(n +1)-n 3+2n]=(m 2-2m)(3n 2+3n -1)<0.∵n ∈N +,∴3n 2+3n -1=3⎝⎛⎭⎫n +122-74≥5>0, ∴m 2-2m<0,解得0<m<2.故实数m 的取值范围为0<m<2.综合提高(限时25分钟)7.已知a n =32n -11(n ∈N +),记数列{a n }的前n 项和为S n ,则使S n >0的n 的最小值为 ( ).A .10B .11C .12D .13 解析 ∵-a 1=a 10,-a 2=a 9,-a 3=a 8,-a 4=a 7,-a 5=a 6,∴S 11>0,则当n≥11时, S n >0,故n 最小为11.答案 B8.函数f(x)定义如下表,数列{x n }满足x 0=5,且对任意的自然数均有x n +1=f(x n ),则x 2 011=( ).A.1 解析 ∵x 0=5,x 1=f(x 0)=f(5)=2,x 2=f(x 1)=f(2)=1,x 3=f(x 2)=f(1)=5,x 4=f(x 3)=f(5)=2,…,∴x n 的值周期出现,且周期T =3,则x 2 011=x 670×3+1=x 1=2. 答案 B9.已知数列{a n }满足a 1>0,a n +1a n =12(n ∈N +),则数列{a n }是________数列(填“递增”或“递减”). 解析 由已知a 1>0,a n +1=12a n (n ∈N +),得a n >0(n ∈N +).又a n +1-a n =12a n -a n =-12a n <0, 所以{a n }是递减数列. 答案 递减10.已知数列{a n }的通项公式是a n =an bn +1,其中a ,b 均为正常数,那么a n +1与a n 的大小关系是________.解析 ∵a n +1-a n =+++1-an bn +1= a+++>0.∴a n +1-a n >0,即a n +1>a n . 答案 a n +1>a n11.已知数列{a n }的通项公式为a n =n 2-5n +4.(1)数列中有多少项是负数?(2)n 为何值时,a n 有最小值?并求出最小值. 解 (1)由n 2-5n +4<0,解得1<n<4. 因为n ∈N +,故n =2,3,所以该数列中有两项是负数.(2)因为a n =n 2-5n +4=⎝⎛⎭⎫n -522-94,可知对称轴方程为n =52=2.5.又n ∈N +,故n =2或3时,a n 有最小值,其最小值为22-5×2+4=-2.12.(创新拓展)已知函数f(x)=2x -2-x ,数列{a n }满足f(log 2a n )=-2n. (1)求数列{a n }的通项公式;(2)证明数列{a n }是递减数列.(1)解 ∵f(x)=2x -2-x ,f(log 2a n )=-2n , ∴2log 2a n -2-log 2a n =-2n ,a n -1a n=-2n , ∴a n 2+2na n -1=0,解得a n =-n±n 2+1. ∵a n >0,∴a n =n 2+1-n ,n ∈N +.(2)证明 a n +1a n =+2+1-+n 2+1-n =n 2+1+n+2+1++<1. ∵a n >0,∴a n +1<a n ,∴数列{a n }是递减数列.。
北师大版高中数学必修五课时作业2 数列的函数特性.doc
高中数学学习材料马鸣风萧萧*整理制作课时作业2 数列的函数特性时间:45分钟 满分:100分一、选择题(每小题5分,共35分)1.数列{a n },a n =f (n )是一个函数,则它的定义域为( ) A .非负整数集 B .正整数集 C .正整数集或其子集D .正整数集或{1,2,3,4,…,n } 【答案】 D【解析】 根据数列的定义可以得出.2.数列53,108,17a +b ,a -b 24,…中,有序数对(a ,b )可以是( )A .(21,-5)B .(16,-1)C .(-412,112)D .(412,-112)【答案】 D【解析】 通项公式为(n +1)2+1n (n +2),故⎩⎪⎨⎪⎧a +b =15,a -b =26. ∴a =412,b =-112.3.数列{a n }中,a n =-2n 2+29n +3,则此数列最大项的值是( ) A .107 B .108 C .10818 D .109【答案】 B【解析】 a n =-2n 2+29n +3 =-2(n 2-292n )+3=-2(n -294)2+3+2928. 当n =7时,a n 最大且a 7=108.4.已知数列{a n }的通项公式a n =n 2+kn +2,若对于n ∈N +,都有a n +1>a n 成立,则实数k 的取值范围是( )A .k >0B .k >-1C .k >-2D .k >-3【答案】 D【解析】 ∵a n +1>a n , ∴a n +1-a n >0. 又a n =n 2+kn +2,∴(n +1)2+k (n +1)+2-(n 2+kn +2)>0. ∴k >-2n -1.又-2n -1(n ∈N +)的最大值为-3, ∴k >-3.5.已知数列{a n },{b n }的通项公式分别为a n =an +2,b n =bn +1(a ,b 为常数),且a >b ,那么两个数列中序号与数值均相同的项的个数是( )A .0B .1C .2D .3【答案】 A【解析】 设an +2=bn +1, ∴(a -b )n +1=0, ∵a >b ,n >0,∴(a -b )n +1=0不成立,故选A.6.在数列1,1,2,3,5,8,13,x,34,55,…中x 的值是( ) A .21 B .20 C .18 D .5【答案】 A【解析】 由题意知:从第3项起,每一项都等于它的前面相邻两项的和,所以x =8+13=21.7.已知数列{a n }的通项公式为a n =⎝ ⎛⎭⎪⎫34n -1⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫34n -1-1,则关于a n的最大项,最小项叙述正确的是( )A .最大项为a 1,最小项为a 3B .最大项为a 1,最小项不存在C .最大项不存在,最小项为a 3D .最大项为a 1,最小项为a 4 【答案】 A【解析】 令t =⎝ ⎛⎭⎪⎫34n -1,则它在N +上递减且0<t ≤1,而a n =t 2-t ,在0<t ≤12时递减,在t ≥12时递增,且n =1时,t =1,n =2时,t =34,n =3时,t =916,n =4时,t =2764,且a 4>a 3,故选A.二、填空题(每小题5分,共15分)8.数列{a n }的前n 项和S n =n 2-2n +5,则它的通项公式为________.【答案】 a n =⎩⎪⎨⎪⎧4 (n =1)2n -3 (n ≥2)【解析】 n ≥2时,a n =S n -S n -1=n 2-2n +5-(n -1)2+2(n -1)-5=2n -3,n =1时,a 1=S 1=4,不适合上式,∴a n =⎩⎪⎨⎪⎧4 (n =1)2n -3 (n ≥2).9.已知数列{a n }中,a n =b n +m (b <0,n ∈N +)满足a 1=2,a 2=4,则a 3=________.【答案】 2【解析】 a 1=2,a 2=4,∴⎩⎪⎨⎪⎧ 2=b +m 4=b 2+m ,∴⎩⎪⎨⎪⎧ b =2m =0(舍去)或⎩⎪⎨⎪⎧b =-1m =3, ∴a 3=(-1)3+3=2.10.若数列{a n }的通项公式为a n =-2n 2+13n ,关于该数列,有以下四种说法:(1)该数列有无限多个正数项;(2)该数列有无限多个负数项;(3)该数列的最大项就是函数f (x )=-2x 2+13x 的最大值;(4)-70是该数列中的一项.其中正确的说法有________.(把所有正确的序号都填上) 【答案】 (2)(4)【解析】 令-2n 2+13n >0,得0<n <132,故数列{a n }有6项是正数项,有无限个负数项.当n =3时,数列{a n }取到最大值,而当x =3.25时函数f (x )取到最大值.令-2n 2+13n =-70,得n =10,或n =-72(舍去).即-70是该数列的第10项.三、解答题(共50分,解答应写出必要的文字说明、证明过程或演算步骤)11.(15分)已知数列{a n }的前n 项和S n =-n 2+24n (n ∈N +). (1)求{a n }的通项公式.(2)当n 为何值时,S n 达到最大?最大值是多少? 【解析】 (1)a n =-2n +25(n ∈N +). (2)当n =12时,S n 最大,S 12=144.12.(15分)已知数列{a n }的通项公式为a n =n 2-8n +7. (1)数列中有多少项是负数?(2)n 为何值时,a n 有最小值?并求出最小值.【解析】 数列的通项a n 与n 之间构成二次函数关系,可结合二次函数知识去进行探求,同时要注意n 的取值范围.(1)由n 2-8n +7<0,得1<n <7,∵n ∈N +, ∴n =2,3,4,5,6, ∴{a n }有5项是负数.(2)∵a n =n 2-8n +7=(n -4)2-9, ∴n =4时,a n 取最小值,其最小值为9.13.(20分)数列{a n }中,a n =9n 2-9n +29n 2-1.(1)求这个数列的第10项; (2)99100是否为该数列的项,为什么? (3)求证:a n ∈(0,1);(4)在区间(13,23)内有无数列{a n }的项,若有,有几项?若无,说明理由.【解析】 (1)∵a n =9n 2-9n +29n 2-1=3n -23n +1,∴a 10=2831.(2)假设99100是数列{a n }中的项,则 3n -23n +1=99100⇒3n =299, 此方程无整数解, ∴99100不是该数列的项.(3)证明:∵a n =3n -23n +1=1-33n +1,n ∈N +,∴0<33n +1<1,∴a n ∈(0,1). (4)由13<a n <23, 得13<3n -23n +1<23.∴⎩⎪⎨⎪⎧3n +1<9n -69n -6<6n +2⇒76<n <83, ∴当且仅当n =2时,在区间(13,23)内有数列{a n }的项.。
高中数学北师大版必修5同步精练1.1.2数列的函数特性 Word版含答案
基础巩固已知数列{}是递增数列,则当∈+时,有( ).+≥.+≤.+>.+<已知数列{}的图像是上升的,则{}是( ).递增数列.递减数列.常数列.以上均有可能=-+(为常数),数列{}是递减数列,则有 ( ).>.<.≠.∈=-,则数列{}的图像是( ).一条直线.一条抛物线.一个圆.一群孤立的点求数列{-++}中的最大项.是否是数列{-++}中的一项?综合过关若数列{}的通项公式为=-+(∈+),画出它在轴上方的图像,并根据图像求出的最大值,并在同一坐标系中画出函数()=-+的图像,根据图像求出()的最大值.若用函数来求=-+的最大值,应如何处理.已知数列{}的通项公式是=(∈+),求数列{}中的最大项.能力提升一辆邮车每天从地往地运送邮件,沿途(包括、)共有站,从地出发时,装上发往后面站的邮件各一个,到达后面各站后卸下前面各站发往该站的一个邮件,同时装上该站发往下面各站的邮件各一个,试写出邮车在各站装卸完毕后剩余邮件个数所成的数列,画出该数列的图像,并判断该数列的增减性.参考答案答案:答案:答案:答案:分析:由通项公式可以看出:是的二次函数,求二次函数的最值可采用配方法,此时要注意其中自变量为正整数.解:由已知=-++=-(-)+,由于为正整数,故当取时,取到最大值为.∴数列{-++}的最大项为=.解:令-++=,解得=或=.由于∈+,则方程-++=无正整数解,所以不是数列{-++}中的一项.分析:由=()可知,的图像应该为函数=()图像上横坐标为正整数的点.求{}的最大值既可用图像来解决,也可用函数的相关知识解决.解:由-+>,可得<<.又因为∈+,所以=、、、、、,分别代入通项公式,可得=,=,=,=,=,=,图像如图所示,为个点.最大值为.函数()=-+的图像如图所示(图中曲线).()=-+=-(-)+,当=时,()=.因为<<,且离较近,所以最大值=.解:令()=(∈+).设<<≤,∈+,∈+,则()-()=-==.又<<≤,∈+,∈+,则-<,->,(+)(+)>.所以<.所以()<().所以当≤时,()是增函数.同理可证,当>时,()是减函数,所以当=时,()取最大值()=,即{}中的最大项为=.解:将、之间所有站按序编号,通过计算,上面各站剩余邮件数依次排成数列:。
2020-2021学年高二数学北师大版必修5作业:1.1.2数列的函数特性
11.数列{an}满足an+1= a2n,an为偶数, 3an+1,an为奇数,
解析:数列{an}的图像为直线y=2x-7上满足x∈N+的一系列 孤立的点.
2.已知点(n,an)(n∈N*)在函数f(x)=
1-2x,x<2 016 x-2 015,x≥2 016
的图像上,则a1+a2 016=( A )
A.0
B.1
C.2 016
D.2 017
解析:由题意知an=
1-2n,n<2 016, n-2 015,n≥2 016
其中,有穷数列是 ①⑤ ,无穷数列是 ②③④ ,递增数 列是 ①② ,递减数列是 ③ ,常数列是 ⑤ ,摆动 数列是 ④ .(将符合条件的数列的序号填在横线上)
解析:①是有穷递增数列;②是无穷递增数列;③是无穷递 减数列;④是摆动数列,也是无穷数列;⑤是常数列,也是有穷 数列.
10.设数列{an}满足an=2n2-an+2(n∈N+),且数列{an}是 递增数列,则实数a的取值范围是 a<6 .
C.C20,C21
D.C21,C20
解析:由Cn=
19.2-n 20.2-n
=1+
1 n-20.2
可知点(n,Cn)在函数y=1
+x-120.2的图像上,如图.
注意到n∈N+,故{Cn}的最小项为C20=-4,{Cn}的最大项为 C21=2.25,故选C.
(教参):第一章1.2数列的函数特性Word版含解析
1.2 数列的函数特性学习目标1.了解递增数列、递减数列、常数列的概念(数学抽象)2.数列的图像表示(直观想象)3.会判断数列的增减性并能简单应用(逻辑推理)必备知识·自主学习导思1. 如何判断数列的单调性?2.若函数f(x)在[1,+∞)上单调递增,那么数列a n=f(n)也单调递增吗?反之成立吗?1.数列的三种表示法(1)列表法.(2)图像法.(3)通项公式法.2.数列的增减性(1)递增数列:一个数列{a n},如果从第2项起,每一项都大于它前面的一项,即a n+1>a n(n∈N+),那么这个数列叫作递增数列.(2)递减数列:一个数列{a n},如果从第2项起,每一项都小于它前面的项,即a n+1<a n(n∈N+),那么这个数列叫作递减数列.(3)常数列:如果数列{a n}的各项都相等,那么这个数列叫作常数列.(4)一个数列{a n},如果从第2项起,有些项大于它的前一项,有些项小于它的前一项,这样的数列叫摆动数列.1.辨析记忆(对的打“√”,错的打“×”).(1)数列的图像可以分布在坐标系内的任意象限. ( )(2)递增数列没有最大项. ( )(3)递减数列的最大项一定是当n=1时取得. ( )提示:(1)×.数列的定义域决定了数列的图像只可能在y轴右侧,不可能在第二、三象限.(2)×.递增数列是有穷数列时必有最大项.(3)√.由递减数列的概念可知.2.数列{a n}满足a n+1=a n+1,则数列{a n}是( )A.递增数列B.递减数列C.常数列D.摆动数列【解析】选A.因为a n+1-a n=1>0,所以{a n}为递增数列.3.数列{a n}中,a n=-n2+11n,则此数列最大项的值是( )A. B.30 C.31 D.32【解析】选B.a n=-n2+11n=-+,因为n∈N+,所以当n=5或6时,a n取最大值30.关键能力·合作学习类型一数列的表示方法(直观想象)【典例】在数列{a n}中,a n=n2-8n,(1)画出{a n}的图像.(2)根据图像判定数列{a n}的增减性.【思路导引】列表、描点画图像,再判断增减性.【解析】(1)列表n 1 2 3 4 5 6 7 8 9 …a n-7 -12 -15 -16 -15 -12 -7 0 9 …描点:在平面直角坐标系中描出下列各点即得数列{a n}的图像:(1,-7),(2,-12),(3,-15),(4,-16),(5,-15),(6,-12),(7,-7),(8,0),(9,9),…图像如图所示.(2)数列{a n}的图像既不是上升的,也不是下降的,则{a n}既不是递增的,也不是递减的.画数列的图像的方法数列是一个特殊的函数,因此也可以用图像来表示,以位置序号n 为横坐标,相应的项为纵坐标,即坐标为(n,a n)描点画图,就可以得到数列的图像.因为它的定义域是正整数集N+(或它的有限子集{1,2,3,…,n}),所以其图像是一群孤立的点,这些点的个数可以是有限的,也可以是无限的.根据数列的通项公式,写出数列的前5项,并用图像表示出来.(1)a n=(-1)n+2;(2)a n=.【解析】(1)a1=1,a2=3,a3=1,a4=3,a5=1.图像如图.(2)a1=-,a2=-,a3=-,a4=-2,a5=2.图像如图所示.类型二数列的增减性(逻辑推理)角度1 数列增减性的判断【典例】1.已知数列{a n}的通项公式为a n=,按项的变化趋势,该数列是( )A.递增数列B.递减数列C.摆动数列D.常数列2.已知函数f(x)=(x≥1),构造数列a n=f(n)(n∈N+).(1)求证:a n>-2.(2)数列{a n}是递增数列,还是递减数列?为什么?【思路导引】通过计算a n+1-a n,判断差的符号确定增减性.【解析】1.选B.因为a n+1-a n=-=<0,所以a n+1<a n.故该数列是递减数列.2.(1)由题意得a n=f(n)===-2+.因为n∈N+,所以>0. 所以a n=-2+>-2.(2)数列{a n}是递减数列,证明如下:因为a n=,a n+1==,所以a n+1-a n=-===<0,所以a n+1<a n,所以数列{a n}是递减数列.如果{a n}为递增数列,则{a n}的通项公式可以为( )A.a n=-2n+3B.a n=-n2-3n+1C.a n=D.a n=log2 n【解析】选D.A选项是n的一次函数,一次项系数为-2,所以为递减数列;B选项是n的二次函数,图像开口向下,且对称轴为n=-,所以为递减数列;C选项是n的指数函数,且底数为,是递减数列;D选项是n的对数函数,且底数为2,是递增数列.角度2 数列增减性的应用【典例】(2020·贵阳高一检测)若数列的通项公式是a n=(n+1)·0.9n,对于任意的正整数n都有a n≤a N成立,则N为( )A.6或7B.7或8C.8或9D.9或10【思路导引】作差判断数列的单调性,得到当n<8时,a n+1>a n,数列单调递增;当n>8时,a n+1<a n,数列单调递减,当n=8时,a9=a8,由此可判断数列的最大项.【解析】选C.a n+1-a n=(n+2)·0.9n+1-(n+1)·0.9n=0.9n=0.9n,当n=8时,a n+1-a n=0,当n<8时,a n+1-a n>0,当n>8时,a n+1-a n<0.所以当n<8时,a n+1>a n,数列单调递增;当n>8时,a n+1<a n,数列单调递减,所以当n=8时,a 9=a8为数列的最大项.数列增减性两方面的应用(1)利用数列的增减性可以求参数范围:数列的增减性揭示了项之间的大小关系,可以据此列出不等式(组),求某些参数的范围.(2)利用数列的增减性求数列的最大或最小项:如果数列先增后减或先减后增,则存在最大(小)项,递增(减)数列中首项是最小(大)项.1.已知数列{a n}的通项公式为a n=n2-21n+20.(1)n为何值时,a n有最小值?并求出最小值;(2)数列{a n}有没有最大项?若有,求出最大项,若没有,说明理由.【解析】(1)因为a n=n2-21n+20=-,可知对称轴方程为n==10.5.又因n∈N+,所以n=10或n=11时,a n有最小值,其最小值为102-21×10+20=-90.(2)由(1)知,a1>a2>…>a10=a11<a12<…,所以数列{a n}没有最大项.2.已知数列{a n}的通项公式为a n=2n×0.9n,求数列{a n}中的最大项. 【解析】设a n是数列{a n}中的最大项,则即所以所以即9≤n≤10,所以当n=9或n=10时,a n最大,最大项a9=a10=2×10×0.910=20×0.910.3.在数列{a n}中,a n=(n+1)(n∈N+).(1)求证:数列{a n}先递增,后递减;(2)求数列{a n}的最大项.【解析】(1)因为a n+1-a n=(n+2)-(n+1)=·, 当n<9时,a n+1-a n>0,即a n+1>a n;当n=9时,a n+1-a n=0,即a n+1=a n;当n>9时,a n+1-a n<0,即a n+1<a n.所以a1<a2<a3<…<a9=a10>a11>a12>…,所以数列{a n}先递增,后递减.(2)由(1)可知数列中有最大项,最大项为第9,10项,即a9=a10=.课堂检测·素养达标1.下列数列中,既是无穷数列又是递增数列的是 ( )A.1,,,,…B.sin ,sin ,sin,sin ,…C.-1,-,-,-,…D.1,2,3,4,…,30【解析】选C.数列1,,,,…是无穷数列,但它不是递增数列,而是递减数列;数列sin ,sin ,sin ,sin ,…是无穷数列,但它既不是递增数列,又不是递减数列;数列-1,-,-,-,…是无穷数列,也是递增数列;数列1,2,3,4,…,30是递增数列,但不是无穷数列.2.已知数列{a n}的通项公式是a n=,则这个数列是( )A.递增数列B.递减数列C.常数列D.摆动数列【解析】选B.数列{a n}的通项公式是a n===1+,则当n∈N+时为递减数列.3.数列{a n}的通项公式为a n=n2-6n,则它的最小值是.【解析】a n=n2-6n=(n-3)2-9,所以当n=3时,a n取得最小值-9.答案:-94.已知递增数列{a n}的通项公式为a n=2kn+1,则实数k的取值范围是.【解析】因为{a n}单调递增,所以a n+1-a n=[2k(n+1)+1]-(2kn+1)=2k>0,所以k>0.答案:(0,+∞)5.(教材二次开发:习题改编)数列{a n}满足a n+1=-2a n,若{a n}单调递增,则首项a1的范围是.【解题指南】先表示出a n+1-a n,再结合{a n}单调递增可求首项a1的范围. 【解析】因为a n+1=-2a n,所以a n+1-a n=-3a n>0,解得a n>3或a n<0,则有a1>3或a1<0.由于a 2=-2a1,所以-2a1>3或-2a1<0,解得a1>3或a1<-1(0<a1<2舍去).答案:(-∞,-1)∪(3,+∞)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
, [学生用书单独成册])[A.基础达标]1.已知a n +1-a n -3=0,则数列{a n }是( ) A .递增数列 B .递减数列 C .常数列 D .不能确定解析:选A.因为a n +1-a n =3>0,故数列{a n }是递增数列.2.已知数列{a n }的通项公式为a n =nn +1,则这个数列是( )A .递增数列B .递减数列C .常数列D .摆动数列解析:选A.因为a n +1-a n =n +1n +2-n n +1=(n +1)2-n (n +2)(n +1)(n +2)=1(n +1)(n +2)>0.故选A.3.数列{a n }中,a n =-2n 2+29n +3,则此数列最大项的值是( )A .109B .10818C .108D .107解析:选C.a n =-2n 2+29n +3=-2(n 2-292n )+3=-2·(n -294)2+3+2928,当n =7时,a n 最大且等于108,故选C.4.已知数列{a n }满足a n =n -1n a n -1(n ≥2),则数列{a n }为( )A .递增数列B .递减数列C .常数列D .以上都有可能解析:选D.若a 1>0,则a n <a n -1(n ≥2),{a n }为递减数列;若a 1=0,则a n =0(n ∈N +),{a n }为常数列;若a 1<0,则a n >a n -1(n ≥2),{a n }为递增数列,故选D.5.已知数列{a n }的通项公式是a n =n -1n +1,则a n 与a n +1间的大小关系是( )A .a n >a n +1B .a n <a n +1C .a n =a n +1D .不能确定解析:选B.因为a n +1-a n =nn +2-n -1n +1= n (n +1)-(n -1)(n +2)(n +2)(n +1)=n 2+n -(n 2+n -2)(n +2)(n +1)=2(n +2)(n +1)>0,所以a n <a n +1,选B. 6.已知下列数列:①2 010,2 014,2 018,2 022;②0,12,23,…,n -1n ,…;③1,12,14,…,12n -1,…;④1,-23,35,…,(-1)n -1·n 2n -1,…;⑤6,6,6,6,6,6.其中,有穷数列是________,无穷数列是________,递增数列是______,递减数列是______,常数列是________,摆动数列是______.(将符合条件的数列的序号填在横线上)解析:①是有穷递增数列; ②是无穷递增数列; ③是无穷递减数列;④是摆动数列,也是无穷数列;⑤是常数列,也是有穷数列.答案:①⑤ ②③④ ①② ③ ⑤ ④7.已知数列{a n }的通项公式a n =n 2-4n -12(n ∈N +),则这个数列从第________项起各项为正数.解析:令a n =n 2-4n -12>0,解得n >6或n <-2(舍去).故从第7项起各项为正数. 答案:78.已知数列{a n }为单调递增数列,通项公式为a n =n +λn ,则λ的取值范围是________.解析:由于数列{a n }为单调递增数列,a n =n +λn ,所以a n +1-a n =[(n +1)+λn +1]-(n +λn )=1-λn (n +1)>0,即λ<n (n +1)(n ∈N +),所以λ<2. 答案:(-∞,2)9.已知函数f (x )=x -x 2+1,数列{a n }满足a n =f (n )(n ∈N +),试判断数列{a n }的增减性.解:因为a n +1-a n =(n +1)-(n +1)2+1-(n -n 2+1)=1-[(n +1)2+1-n 2+1]=1-2n +1(n +1)2+1+n 2+1>1-2n +1(n +1)+n =0,所以a n +1>a n .所以数列{a n }是递增数列.10.已知数列{a n }的通项公式为a n =n 2-5n +4, (1)数列中有多少项为负数?(2)n 为何值时,a n 有最小值?并求此最小值.解:(1)由n 2-5n +4<0得1<n <4,n ∈N +, 所以n =2或3.所以数列中有2项为负数.(2)因为a n =n 2-5n +4=⎝⎛⎭⎫n -522-94,又因为n ∈N +,所以n =2或3时,a n 有最小值-2.[B.能力提升]1.一给定函数y =f (x )的图像在下列各图中,并且对任意a n ∈(0,1),由关系式a n +1=f (a n )得到的数列{a n }满足a n +1>a n (n ∈N +),则该函数的图像是()解析:选A.由a n +1=f (a n ),a n +1>a n 知f (a n )>a n .可以知道x ∈(0,1)时f (x )>x ,即f (x )的图像在y =x 图像的上方,由选项中所给的图像可以看出,A 符合条件.2.已知数列{a n }的通项公式a n =anbn +1(a ,b 为正常数),那么a n 与a n +1的关系是( )A .a n >a n +1B .a n <a n +1C .a n =a n +1D .以上都不对解析:选B.考虑函数y =axbx +1=a b (bx +1)-a b bx +1=ab +-a b bx +1=a b +-a b 2x +1b , 其图像可由y =-a b 2x 先向左平移1b 个单位长度,再向上平移ab个单位长度得到,如图.由图像不难得知y =ax bx +1在[1,+∞)上单调递增,所以a n =anbn +1的值随n 的变大而变大.所以数列{a n }是递增数列,即a n <a n +1,故选B.3.已知数列{a n }的通项公式a n =n -96n -98,n ∈N +,则数列{a n }的最大项为________,最小项为________.解析:将数列{a n }的通项公式变形为a n =1+98-96n -98,考察函数f (x )=1+98-96x -98,画出图像(图略),数列{a n }的图像即为曲线上横坐标为正整数的孤立的点,易知n =10时,a n 取得最大值,为10-9610-98;n =9时,a n 取得最小值,为9-969-98.所以,数列{a n }中最大项为a 10=10-9610-98,最小项为a 9=9-969-98.答案:10-9610-98 9-969-984.已知通项公式为a n =(m 2-2m )(n 3-2n )的数列是递减数列,则实数m 的取值范围为____________.解析:因为数列{a n }为递减数列,所以a n +1<a n .所以a n +1-a n =(m 2-2m )[(n +1)3-2(n +1)-n 3+2n ]=(m 2-2m )(3n 2+3n -1)<0. 因为n ∈N +,所以3n 2+3n -1=3⎝⎛⎭⎫n +122-74≥5>0. 所以m 2-2m <0,解得0<m <2. 故m ∈(0,2).答案:(0,2)5.已知数列{a n }的通项公式为a n =(n +2)⎝⎛⎭⎫910n,试问n 取何值时,a n 取最大值?试求出a n 的最大值.解:因为a n +1a n =(n +3)⎝⎛⎭⎫910n +1(n +2)⎝⎛⎭⎫910n =9(n +3)10(n +2)=910+910·1n +2,由a n +1a n =1,解得n =7,则当n =7时,a 8a 7=1,即a 7=a 8.当n <7时,a n +1a n >1,即a n +1>a n .当n ≥8时,a n +1a n <1,即a n +1<a n .则当n =7或n =8时,a n 取最大值,最大值为a 7=a 8=98107.6.设f (x )=log 2x -log x 4(0<x <1),又知数列{a n }的通项a n 满足f (2a n )=2n . (1)求数列{a n }的通项公式; (2)试判断数列{a n }的增减性.解:(1)因为f (x )=log 2x -log x 4(0<x <1),f (2 a n )=2n , 所以log 22a n -log 2 a n 4=2n ,由换底公式,得log 22 a n -log 24log 22a n=2n , 即a n -2a n=2n ,所以a 2n -2na n -2=0, 所以a n =n ±n 2+2.①由0<x <1,有0<2an <1,所以a n <0.② 由①②得a n =n -n 2+2,此即为数列{a n }的通项公式.(2)a n +1a n =(n +1)-(n +1)2+2n -n 2+2=n +n 2+2(n +1)+(n +1)2+2<1,因为a n <0,所以a n +1>a n , 所以数列{a n }是递增数列.。
