力学量与算符
第三章 力学量的算符汇总
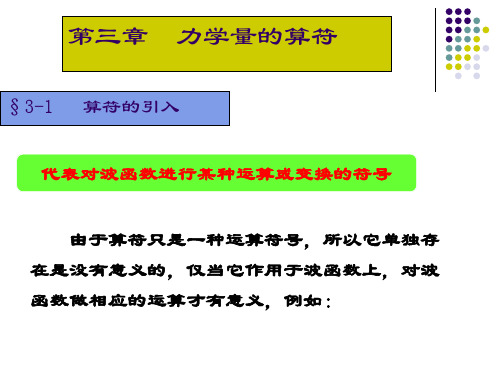
其中Fn, ψn 分别称为算符 F的本征值和相应的本征态, 上式即是算符F的本征方程。求解时,ψ 作为力学量 的本征态或本征函数还要满足物理上对波函数的要求 即波函数的标准条件。
问题:本征值、本征态、本征方程
§3-3 算符的运算规则 线性厄米算符
(1)线性算符
满足如下运算规律的 算符 Ô 称为线性算符
第三章 力学量的算符
§3-1 算符的引入
代表对波函数进行某种运算或变换的符号
由于算符只是一种运算符号,所以它单独存 在是没有意义的,仅当它作用于波函数上,对波 函数做相应的运算才有意义,例如:
Ôu
换的算符。
1)du / dx = v , d / dx
n
综上所述,量子力学作如下假定:
就是算符,其作用 是对函数 u 微商, 故称为微商算符。
2)x u = v, x
也是算符。 它对 u 作用 是使 u 变成 v。
体系状态用坐标表象中的波函数 ψ(r) 描 写时,坐标 x 的算符就是其自身,即
xˆ x
说明力学量在自身表象中的算符形式最简单。
而动量 px 在坐标表象(非自身表象)中的形式 必须改造成动量算符形式:
(12) 厄米算符
满足如右关系的算符 称为厄密算符.
d *Oˆ d (Oˆ )*
或 Oˆ Oˆ
性质 I: 两个厄密算符之和 仍是厄密算符。
Ô + = Ô , Û+ = Û (Ô +Û)+ = Ô + + Û+ = (Ô +Û)
问题:厄米算符
性质 II: 两个厄密算符之积一般 不是厄密算符, 除非二算符对易。 因为
注意,算符运算没有相减,因为减可用加来代替。 Ô - Û = Ô + (-Û)。
第二章算符

2. 算符的对易: ˆB ˆ , 则称算符 A ˆ 与B ˆB ˆA ˆ 对易; 反之为非对易。 若A 一般情况下 , 算符的乘法不对易。 ˆ, B ˆB ˆ ˆ] A ˆ B ˆA 算符的对易关系式定义 为 : [ A 例如 : [ , x ] 1 x 证明 : [ , x ] f ( x ) [ xf ( x )] x f ( x) f ( x) x x x x f ( x) x f ( x ) f ( x ),即: [ , x] 1 x x x
将动量算符的形式代入上式, 得到动能算符为: 2 2 ˆx ˆ2 ˆ p p p 1 2 2 2 y z ˆ K {( i ) ( i ) ( i ) } 2m 2m x y z
2 2 2 2 2 2 ( 2 2 2) 2m x y z 2m
ˆ 是厄米算符 . 因此 , A
定理 1:厄米算符的本征值是 实数。 ˆ 是厄米算符, g为它的本征函数, 证明:若 A ˆ g ag, ˆ g )* a * g *, 本征值为 a,即: A (A 根据厄米算符的定义, 可以得到: ˆ gd g ( A ˆ g ) * d , 即: g *A
i
j
j
i
a j i * j d ai j i *d , (注意 ai * ai ) ( a j ai ) j i *d 0, j i *d 0 因此, i 和 j 相互正交。
厄米算符属于不同本征 值的两个本征函 数一定互相正交。具有 相同本征值的本征函 数如何保证它们正交呢 ?这需要运用施米特 (Schmidt)正交化方法。 ˆ , 若存在函数 F和G满足下列 例如 , 对算符 A ˆ F aF, A ˆ G aG, 则F和G具有相同的本 关系 : A 征值 , 令 : 1 F , 2 G cF , 要求 1和 2 正交, 可以求出常数 c。
量子力学基本假设
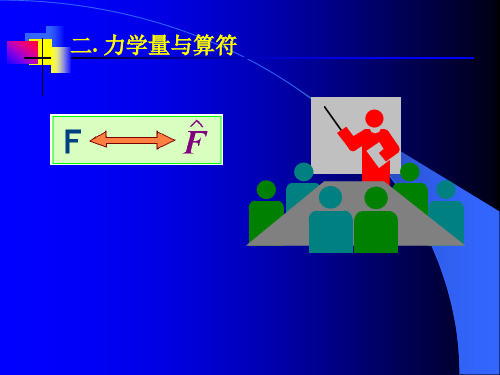
(注:乘法交换律不一定满足)
③算符相等 若Aˆ f Bˆf ,则Aˆ Bˆ。
④算符的平方
Aˆ 2 Aˆ Aˆ, Aˆ 2 f Aˆ Aˆ f ,Aˆ n Aˆ Aˆ ……Aˆ (共n个)
2.力学量与算符关系假设
pˆ x i
d, dx
pˆ y
i
d, dy
pˆ z
i
d
dz 其中,
h
2
构造力学量算符的方法
先将力学量写成作标、时间和动量的函数,然后进行如下代换:
A x, y, z, px, py , pz ,t
Aˆ x, y, z, i
, i x
, i y
一质量为m的粒子围绕点O运动,其角动量 M r p
按照矢量积的定义展开之:
i jk
M x y z ypz zpy i zpx xpz j xpy ypx k
px py pz
则角动量在三个坐标轴上的分量 Mx, My , Mz以及角动量平方M 2 的经典表达式应为:
注: 运算顺序是从右到左。 BˆAˆ f 不一定等于 Aˆ Bˆf ,二者不相等时则不对易。 若二者对易,则 Aˆ,Bˆ 所代表的物理量可以同时测定。
⑤ 厄米(Hermite)算符
若有算符 Aˆ 满足 u*Aˆ vd v
Aˆ u
*
d
,则称
Aˆ 为厄米算符。
例:
Aˆ i d ,设u v eix ,则有: dx
能量算符(哈密顿算符)
E T V , E 总能量,T 动能,V 势能
粒子的能量算符——哈密顿算符 Hˆ ,Hˆ Tˆ Vˆ
算符与力学量的关系

7
§3-6-2 力学量的可能值和相应几率
在一般状态 ψ(x) 中测量力学量F,将会得到哪些值? 即测量的可能值及其每一可能值对应的几率? 量子力学假定, 量子力学假定,测力学量 F 得到的可能值必是力学量算符 F的 本征值 λn (n = 1,2,…) 之一, 该本征值由本征方程确定: 该本征值由本征方程确定: ˆ φ n ( x ) = λ nφ n ( x ) F n = 1, 2 , L |cn|2具有几率的意义, 而每一本征值λn各以一定几率出现。 各以一定几率出现。 cn 称为几率振幅 称为几率振幅 那末这些几率究竟是多少呢? 那末这些几率究竟是多少呢? 如前所述, 如前所述,如果φn(x)组成完备系, ψ ( x) = ∑cnφn ( x) n 体系任一状态 体系任一状态Ψ(x)可按其展开: 可按其展开: 量子力学基本假定: 量子力学基本假定: ˆ 的本征函数φn(x)组成正交归一完备系, 任何力学量算符 F 组成正交归一完备系, 在任意已归一态ψ (x)中测量力学量 F 得到本征值 λn的几率等 于ψ (x)按φn(x)展式中φn(x) 前的系数cn的平方|cn|2 , ˆ 取λ 的几率. 即|cn|2则表示 F n 8
ψ ( x) = ∑cnφn ( x)
n
量子力学基本假定: 量子力学基本假定: ˆ 的本征函数φn(x)组成正交归一完备系, 任何力学量算符 F 组成正交归一完备系, 在任意已归一态ψ (x)中测量力学量 F 得到本征值 λn的几率等 于ψ (x)按φn(x)展式中φn(x) 前的系数cn的平方|cn|2 , ˆ 取λ 的几率. 即|cn|2则表示 F n 9
展开系数
* c( p) = ∫ Ψp ( x)Ψ( x, t )dx
25 力学量的平均值、算符表示 平均值
§2.5 力学量的平均值、算符表示—算符表示
Cartesian coordinates
Spherical coordinates
( x, y, z )
(r , , )
x r sin cos y r sin sin z r cos
r x2 y 2 z 2 z arccos x2 y 2 z 2 y arctan x
i
p r
d
( p, t )
2
表示平面波
e
pr
的所占的比重,即粒子动量取为 p 的概率。
(p,符表示—平均值
所以,动量的平均值
p
p ( p, t ) dp * ( p, t ) p ( p, t )dp
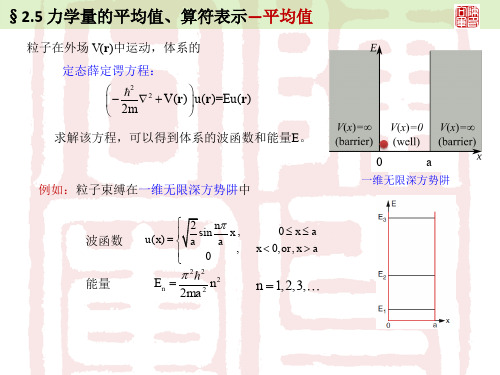
定态薛定谔方程:
2 2 V (r ) u (r )=Eu (r ) 2m
ˆ (r)=Eu(r) Hu
§2.5 力学量的平均值、算符表示—算符表示
量子力学中,描述微观粒子的力学量均有对应的算符
(1) 位矢 r r (2) 势能 V(r) V(r) (3) 动量 p
r x2 y 2 z 2 z arccos x2 y 2 z 2 y arctan x
§2.6 单电子(H)原子—中心力场薛定谔方程
From
求解中心力场中的薛定谔方程,球坐标系是自然的选择
ˆ ˆ z zp ˆ y i Lx yp ˆ ˆ x xp ˆ z i Ly zp ˆz xp ˆ y yp ˆ x i L
y z y z z x z x x y x y
力学量和算符

第三章力学量和算符内容简介:在上一章中,我们系统地介绍了波动力学,它的着眼点是波函数。
用波函数描述粒子的运动状态。
本章将介绍量子力学的另一种表述,它的着眼点是力学量和力学量的测量,并证实了量子力学中的力学量必须用线性厄米算符表示。
然后进一步讨论力学量的测量,它的可能值、平均值以及具有确定值的条件。
我们将证实算符的运动方程中含有对易子,出现。
§3.1 力学量算符的引入§3.2 算符的运算规则§3.3 厄米算符的本征值和本征函数§3.4 连续谱本征函数§3.5 量子力学中力学量的测量§3.6 不确定关系§3.7 守恒与对称在量子力学中。
微观粒子的运动状态用波函数描述。
一旦给出了波函数,就确定了微观粒子的运动状态。
在本章中我们将看到:所谓“确定”,是在能给出概率以及能求得平均值意义下说的。
一般说来。
当微观粒子处在某一运动状态时,它的力学量,如坐标、动量、角动量、能量等,不同时具有确定的数值,而具有一系列可能值,每一可能值、均以一定的概率出现。
当给定描述这一运动状态的波函数后,力学量出现各种可能值的相应的概率就完全确定。
利用统计平均的方法,可以算出该力学量的平均值,进而与实验的观测值相比较。
既然一切力学量的平均值原则上可由给出,而且这些平均值就是在所描述的状态下相应的力学量的观测结果,在这种意义下认为,波函数描写了粒子的运动状态。
力学量的平均值对以波函数(,)r t ψ描述的状态,按照波函数的统计解释,2(,)r t ψ表示在t 时刻在 r r d r →+中找到粒子的几率,因此坐标的平均值显然是:()2*(,)(,)(,) 3.1.1r r t rdr r t r r t dr ψψψ∞∞-∞-∞==⎰⎰坐标r 的函数()f r 的平均值是:()()()*(,)(,) 3.1.2f r r t f r r t dr ψψ∞-∞=⎰现在讨论动量的平均值。
3.6算符与力学量的关系
1 x xdx c c xn xdx c c
m n mn
cn 称为概率振幅。
二.展开假定 量子力学中表示力学量的算符都是厄米算符,它们的本 征函数组成完全系。当体系处于 x cnn x 所描写
ˆ 的状态时,测量力学量F所得的数值,必定是算符 F
s x e dx, s 0
s 1 x 0
,
5
,
0
x n e ax dx
n! a n 1
当s=1时, 递推公式
1 e dx 1
x 0
2 x e x dx 1 1
0
s 1 ss , s 0
x x dx c n m xn xdx cn mn cm m n n
即
cn n ( x) x dx
(3.6.2)
由 x 的归一化条件,可得出 cn
m n m n n
2
1 。
cn (3.6.3)
§3.6算符与力学量的关系
ˆ 是满足一定条件的厄米算符, 一.数学中已证明:如果 F 它的正交归一本征函数是 n x ,对应的本征值是
n ,则任意函数 x 可以按 n x 展开为级数:
x cnn , x (3.6.1)
n
本征函数的这种性质称为完全性。或者说 n x 组成完全系。展开系数
x cnn x c x d
n
(3.6.7)
(3.6.8)
c x dx
代替(3.6.3)式:有
cn
2
ቤተ መጻሕፍቲ ባይዱc
4. 力学量与算符
ˆ ) d F ˆ )d ( F ˆ )d ˆG ˆ (G ˆ ) (G 证明: ( F
ˆ F ˆF ˆF ˆ d (G ˆ ) d [( G ˆ )] d G
力学量—表示一个体系力学性质的量。 微观体系的力学量与经典系统的力学量有着重要的区别的:
经典力学体系中假定力学量都是可以连续变化的,任何两个 力学量(如: x, p x )可同时具有确定值,即存在轨道的概念;
微观体系的一些量却往往只取分立值(如势阱中粒子的能 量,线性谐振子的能量,原子的能量及角动量等) ,也有些量根 本不可能同时具有确定值(如: x和p x ;T和U ) 。微观体系的 这些特点源于它的波动性(无轨道问题) 。
ˆ 之和仍是线性算符 ˆ,G <2 >线性算符F
ˆ (c u c u ) ˆ (c u c u ) G ˆ )(c u c u ) F ˆ G (F 1 1 2 2 1 1 2 2 1 1 2 2
ˆ 线性 ˆ ,G F
和定义
ˆ ˆ ˆu c F ˆ c1 F 1 2 u 2 c 1 Gu 1 c 2 Gu 2
3. 算符相乘 ˆ 之 ˆ (F ˆ u) M ˆ u , 则称算符 M ˆ F ˆ为 与 G u ,有G 若对任意的函数
ˆF ˆ 不一定等于 ˆF ˆ ) ˆ G ˆ (注意:G ˆG F 积。记为 M 。
ˆ 相继作用在 ˆ n 表示,即: u 上 n 次,则可用 F F 如一个算符
ˆF ˆ F ˆu F ˆ nu ˆ (F ˆ u) F ˆ 2u ; F F ˆ m和F ˆ n 可以交换顺序,n, m 均为正整数。 ˆ nF ˆm F ˆ mF ˆ n ,即 F 即有F
量子力学算符和力学量的关系
r[e
r a0
i
pr
e
r a0
i
pr
]dr
0
2i p(2a 0)3 / 2
2i p(2a 0)3 / 2
1i
1i
[
re
( a0
p)r
dr
re ( a0 p)r dr]
0
0
[1
1
]
(1 a0
i
p) 2
(1 a0
i
p) 2
2i p(2a 0)3/ 2
( 1 i p)2 ( 1 i p)2
1
e 2
r a0
i
e prx r 2drdxd
0 1 0
(积分次序是先对 ,再 x ,再对 r )
2 (2a 0)3/ 2
r
r e
1
2
a0
0 1
i
e
prx
drdx
2 (2a 0)3/ 2
r
r 2ea0 dr
0
1 ipr
/
[e
i
pr
e
i
pr
]dr
2i p(2a 0)3 / 2
其中:Cn n dx ; C dx ;
Cn
2
C
2
d
1
;
n
Cn 为2 在 (态x)中测 得 F 旳几n率;
C 2 为d在 态(中x)测 得 F 在 范围 内d旳 几率;
平均值公式: F
n
Cn
2
; C
2
d
n
阐明:当 Cn 0 时为连续谱情况;C 0 时为分立 谱旳情况;Cn 0 ,C 0 时为一般情况。
量子力学中表示力学量的算符 Fˆ 都是线性厄米算符,它们
力学量和算符
第三章 力学量和算符内容简介:在上一章中,我们系统地介绍了波动力学,它的着眼点是波函数 。
用波函数描述粒子的运动状态。
本章将介绍量子力学的另一种表述,它的着眼点是力学量和力学量的测量,并证实了量子力学中的力学量必须用线性厄米算符表示。
然后进一步讨论力学量的测量,它的可能值、平均值以及具有确定值的条件。
我们将证实算符的运动方程中含有对易子,出现 。
§ 3.1 力学量算符的引入 § 3.2 算符的运算规则§ 3.3 厄米算符的本征值和本征函数 § 3.4 连续谱本征函数§ 3.5 量子力学中力学量的测量 § 3.6 不确定关系 § 3.7 守恒与对称在量子力学中。
微观粒子的运动状态用波函数描述。
一旦给出了波函数,就确定了微观粒子的运动状态。
在本章中我们将看到:所谓“确定”,是在能给出概率以及能求得平均值意义下说的。
一般说来。
当微观粒子处在某一运动状态时,它的力学量,如坐标、动量、角动量、能量等,不同时具有确定的数值,而具有一系列可能值,每一可能值、均以一定的概率出现。
当给定描述这一运动状态的波函数 后,力学量出现各种可能值的相应的概率就完全确定。
利用统计平均的方法,可以算出该力学量的平均值,进而与实验的观测值相比较。
既然一切力学量的平均值原则上可由 给出,而且这些平均值就是在 所描述的状态下相应的力学量的观测结果,在这种意义下认为,波函数描写了粒子的运动状态。
力学量的平均值对以波函数(,)r t ψ 描述的状态,按照波函数的统计解释,2(,)r t ψ表示在t 时刻在 r r d r →+中找到粒子的几率,因此坐标的平均值显然是:()2*(,)(,)(,) 3.1.1r r t rdr r t r r t dr ψψψ∞∞-∞-∞==⎰⎰坐标r 的函数()f r的平均值是:()()()*(,)(,) 3.1.2f r r t f r r t dr ψψ∞-∞=⎰现在讨论动量的平均值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
令本征值 令本征值
′h2 上式可写为: λ = λ 上式可写为:
该微分方程被称为球谐方程。 该微分方程被称为球谐方程。在数学物理方法中 有专门的讲述
ˆ Aunj =anunj
j =12,3,⋅⋅⋅g ,
g 为简并度
ˆ = −ih d 的本征值及本征波函数。 的本征值及本征波函数。 例1:求解算符 Lz : dϕ
解:首先写出该算符的本征值方程为: 首先写出该算符的本征值方程为:
ˆ Φ(ϕ) =−ih d Φ(ϕ) = L Φ(ϕ) Lz z dϕ i 求解此方程: 求解此方程: dΦ i Lzϕ = Lzdϕ ⇒Φ(ϕ) =ceh Φ h
i Lz 2π eh
Φ(ϕ) =Φ(ϕ +2π)
=1
2 Lz π +isin 2πLz =1 cos h h 2πLz 2 Lz π =m2π m=0,±1±2,±3⋅⋅⋅ cos =1⇒ , h h
则本征值及本征波函数为: 则本征值及本征波函数为:
Lz = mh m=0,±1±2,±3⋅⋅⋅ , Φ(ϕ) =ceimϕ 积分常数c 利用归一化条件来确定积分常数 : 2π 1 2 2 ∫0 Φ(ϕ) dϕ = c 2π =1⇒c = 2π 最后结果: 最后结果: Lz = mh m=0,±1±2,±3⋅⋅⋅ , 1 imϕ Φ(ϕ) = e 2π
§2、力学量的测得值与平均值
问题: 问题 如何确定在一定的微观状态下, 如何确定在一定的微观状态下 微观粒子各力学量的取值呢? 微观粒子各力学量的取值呢
对微观粒子进行力学量的测量, 对微观粒子进行力学量的测量 每次测得的结果只能是该力学量算 符的所有本征值中的一个. 符的所有本征值中的一个
2011-1-3
ˆ Aψ = φ
2) 算符的表示 算符的表示:
r ˆ p = −ih∇
r r ˆ r =r
对该算符的表示: 对该算符的表示
力学量算符
Hale Waihona Puke 同一个力学量的算符可以有多种不同的表示. 同一个力学量的算符可以有多种不同的表示 3) 量子力学中的“态”与“力学量”是截然分开的 这是 量子力学中的“ 力学量”是截然分开的, 与经典力学的一个根本不同之处. 与经典力学的一个根本不同之处 力学量: 用算符来描写. 用波函数来描写. 力学量 用算符来描写 态: 用波函数来描写 4) 线性算符 线性算符: ˆ ˆ ψ =φ Aψ 2 = φ 2 A 1 1 若有: 若有 对线性算符总有: 对线性算符总有
ˆ Iψ =ψ 则称算符 I为单位算符 为单位算符. 为单位算符
ˆ ˆ 则称算符A与 相等 相等. Aψ = Bψ 则称算符 与B相等 ˆ ˆ ˆ Mψ = ( A + B)ψ
ˆ ˆ ˆ ˆ ˆ ˆ A + ( B + C ) = ( A + B) + C
则称算符M=A+B 则称算符 算符的加法满足交换律与结合律, 即有: 算符的加法满足交换律与结合律 即有
1 ∂ ∂ 1 ∂2 Y(θ,ϕ) = −λ′Y(θ,ϕ) sinθ + 2 2 ∂θ sin θ ∂ϕ sinθ ∂θ
结论: 为使方程在整个空间内有有限解 结论: 为使方程在整个空间内有有限解 ① +1)的值 λ’只能取=l(l +1)的值
λ =λl =l(l +1 h2 l =0,12,3⋅⋅⋅ ) ,
ˆ ˆ ˆ ˆ A+ B = B + A
4) 算符的乘法 算符的乘法:
ˆˆ ˆ ˆ ˆ Mψ = ABψ = A( Bψ )
若对任意函数ψ 若对任意函数ψ有: 任意函数 则称算符M=AB 则称算符
注意: 一般说来算符的乘法并不满足交换律. 注意 一般说来算符的乘法并不满足交换律 即: AB = BA 以动量算符为例: 以动量算符为例
9
一、厄米算符: 厄米算符:
1) 本征值与本征函数 本征值与本征函数: A) 若有 若有:
ˆ Aun =anun
an为常数
则 an为算符A的本征值 为算符 的本征值, 的本征值 为对应于该本征值的本征函数. 而un为对应于该本征值的本征函数 B) 分立本征值与连续本征值. 分立本征值与连续本征值 有限多个, 无限多个本征值. 有限多个 无限多个本征值 C) 力学量的本征值都应为实数 力学量的本征值都应为实数. D) 简并与非简并 简并度 简并度:
(φ,ψ) = φ ψdτ
*
(φ,ψ
① ②
+∞ * ) = ∫ −∞ (x, y,z)
φ
ψ(x, y,z)dxdydz
2
内积的性质: 内积的性质
( ,ψ) = ∫ψ ψdτ = ∫ψ dτ ≥0 ψ
*
(φ,ψ) = ∫φ* dτ =(∫ψ* dτ )*=( ,φ)* ψ φ ψ
B) 厄米算符 厄米算符: 若对任意函数ψ 算符A满足 满足: 若对任意函数ψ与ϕ算符 满足
例2:求解算符 :
1 ∂ ∂ ∂2 1 ˆ L2 = −h2 sinθ + 2 2 ∂θ sin θ ∂ϕ sinθ ∂θ
的本征值及本征波函数。 的本征值及本征波函数。 首先写出该算符的本征值方程为: 解:首先写出该算符的本征值方程为: ˆ L2Y(θ,ϕ) =
m m m
ˆ (um, Aun) = an(um,un) * am =am
am(um,un) = an(um,un)
(am −an)(um,un) =0
所以必有: 但m≠n 即an≠am 所以必有
* (um,un) = ∫ umund * (un,un) = ∫ umund
其中c为积分常数。后面把它作为归一化系数来处理。 其中 为积分常数。后面把它作为归一化系数来处理。 为积分常数 由标准化条件:单值,连续,有限来确定本征值。 由标准化条件:单值,连续,有限来确定本征值。 要求Φ 要求Φ有限 单值条件要求
i Lzϕ ceh i Lz (ϕ+2π ) =ceh
Lz只能取实数
ˆ ˆ ˆ A(c1ψ 1 + c2ψ 2 ) = Ac1ψ 1 + Ac2ψ 2 = c1φ1 + c2φ2
表示开方, 如:表示开方 乘方等运算的算符 就不是线性算符 表示开方 乘方等运算的算符, 就不是线性算符.
二、线性算符的性质: 线性算符的性质:
1) 单位算符 单位算符: 若对任意函数 任意函数ψ 若对任意函数ψ有: 2) 算符的相等 算符的相等: 若对任意函数ψ 若对任意函数ψ有: 任意函数 3) 算符的加法 算符的加法: 若对任意函数ψ 若对任意函数ψ有: 任意函数
α = x, y, z. β = x, y, z.
这是量子力学的基本对易关系. 这是量子力学的基本对易关系
三、力学量算符的具体表示形式: 力学量算符的具体表示形式:
1) 两类力学量 两类力学量: A) 可以在经典力学中找到相应的对应量的力学量 可以在经典力学中找到相应的对应量的力学量. 找到相应的对应量的力学量 动量, 角动量, 如: 动量 角动量 …... B) 在经典力学中找不到相应的对应量的力学量. 在经典力学中找不到相应的对应量的力学量 找不到相应的对应量的力学量 自旋, 宇称, 如: 自旋 宇称 …...
∫ ∫
0
π
2π
0
Ylm(θ,ϕ) sin θdθdϕ =1
2
Nlm
=(−1 m )
2l +1(l −m)! 4 (l +m)! π
2) 厄米算符 厄米算符: A) 内积 或称标量积 内积(或称标量积 或称标量积):
∫ 定义: 函数ψ 内积为: 定义 函数ψ与ϕ的内积为 这里∫...dτ指对体系的全部空间坐标进行积分, 这里∫... τ指对体系的全部空间坐标进行积分 dτ是坐标空间的体积元 τ是坐标空间的体积元. 若有φ φ ψ=ψ(x, 则有: 如: 若有φ=φ(x,y,z) ψ=ψ y,z) 则有
n n n * ˆ (Aum,un) = am(um,un)
厄米算符函数的正交性 算符函数的正交性: ③ 厄米算符函数的正交性 为厄米算符 的对应于本征值为a 的本征函数, 算符A的对应于本征值为 设un为厄米算符 的对应于本征值为 n的本征函数 ˆ ˆ 则有: 则有 Au = a u Au =a u
②本征函数为球谐函数: 本征函数为球谐函数:
Ylm(θ,ϕ) = NlmPm(cosθ)eimϕ l
締合勒让德多项式(l 阶): 締合勒让德多项式(
m=0,±1±2⋅⋅⋅±l ,
l +m
Pm( l
1 2)m 2 d ζ ) = l (1−ζ (ζ 2 −1 l ) l +m 2 l! dζ
③归一化: 归一化:
ⅰ) 厄米算符的本征 值必为实数 量子力学中的所有力学 量算符都是厄米算符
ⅱ) 对微观粒子进行 力学量的测量, 每次测 力学量的测量 每次测 只能是该力 得的结果只能是该 得的结果只能是该力 学量算符的所有 的所有本征 学量算符的所有本征 中的一个. 值中的一个
讨论厄米算符的重要性 讨论厄米算符的重要性
问题: 量子力学中的力学量是如何表示的? 问题 量子力学中的力学量是如何表示的
量子力学中的力学量的取值也具有 不确定性吗? 不确定性吗 测不准关系与量子力学的基本原理 之间有什么样的联系? 之间有什么样的联系
在量子力学中描述物理系统的 每一个可观测的力学量都对应一个 线性算符. 线性算符
2011-1-3
∂ ∂ ˆ ˆ ( xpx − px x)ψ = (−ihx + ih x)ψ 即有: 即有 ∂x ∂x ∂ ∂ = −ihx( ψ ) + ih ( xψ ) ˆ ˆ xpx − px x = ih ∂x ∂x ∂ψ ∂ψ + ihψ = −ihx + ihx 量子力学中称算符x 量子力学中称算符 ∂x ∂x 与px不对易 = ihψ ≠ 0
