2014年秋期高二年级数学科12月月考试题
河北省衡水市第十四中学高二数学12月月考试题新人教版

河北省衡水市第十四中学2013-2014学年高二数学12月月考试题新人教版一、选择题(本大题共12个小题,每个5分,共60分。
) 1.复数11Z i =-(i 为虚数单位)的模为( ) (A )12 (B)2(C(D )2 2.观察下列等式,332123+=,33321236++=,33332123410+++=根据上述规律,333333123456+++++=( )A .219 B .220 C .221 D .222 3.若,,a b c R a c b ∈-<,且,则正确的是 ( ) A. a b c <+ B. a b c <- C. a b c >+ D. a b c >- 4.已知命题p :对任意x R ∈,有cos 1x ≤,则( )A.:p ⌝存在x R ∈,使cos 1x ≥B.:p ⌝对任意x R ∈,有cos 1x ≥C.:p ⌝存在x R ∈,使cos 1x >D.:p ⌝对任意x R ∈,有cos 1x > 5.已知{}n a 为等差数列,13518a a a ++=,24624a a a ++=,则20()a = A. 10B. 20C. 40D. 806.若i b i i a -=-)2(,其中,a b R ∈,i 是虚数单位,则22a b +=( ) A .0 B .2 C .25D .57.设实数y x ,满足不等式组1103300x y x y x +-≤⎧⎪-+≤⎨⎪≥⎩,则y x z +=2的最大值为(A )13 (B )19 (C )24 (D )298.已知命题:0318≤-≤xp ,命题2:log 1<q x ,则p ⌝是q ⌝的( )A .充分必要条件B .必要而不充分条件C .充分而不必要条件D .既不充分也不必要条件9.若关于x 的不等式2420x x a --->在区间(1,4)内有解,则实数a 的取值范围是( )A .2a <-B .2a >-C .6a >-D .6a <- 10.(文).若2()2'(1)f x xf x =+,则'(0)f 等于( ) A. 4- B. 2- C. 0 D. 2 (理)若11(2)3ln 2(1)ax dx a x+=+>⎰,则a 的值是( )A .2B .3C .4D .611.已知抛物线22y px =的焦点F 与双曲线22179x y -=的右焦点重合,抛物线的准线与x 轴的交点为K ,点A 在抛物线上且||2||AK AF =,则△AFK 的面积为( )(A ) 4 (B ) 8 (C ) 16 (D ) 32 12. 设的两个极值点分别是若(-1,0),则2a +b 的取值范围是A 、(1,7)B 、(2,7)C 、(1,5)D 、(2,5)第II 卷(非选择题)二、填空题本大题共4个小题,每个5分,共20分。
高二数学月考试题及答案-南充市2013_2014学年度下期高中二年级教学质量监测(理)
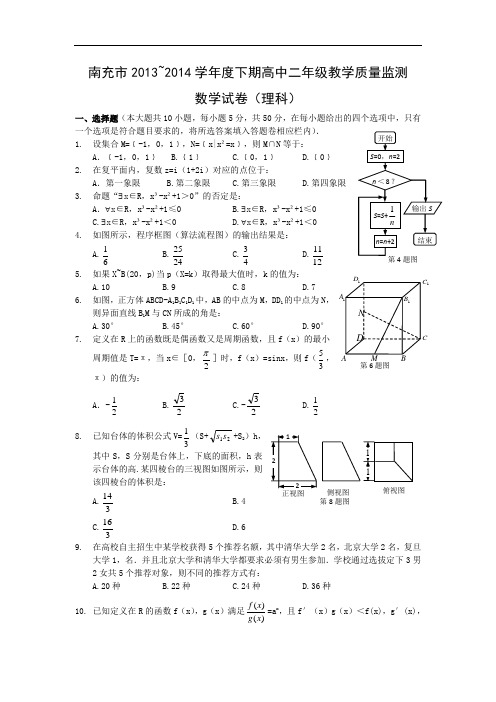
南充市2013~2014学年度下期高中二年级教学质量监测数学试卷(理科)一、选择题(本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一个选项是符合题目要求的,将所选答案填入答题卷相应栏内).1. 设集合M=﹛-1,0,1﹜,N=﹛x|x²=x﹜,则M∩N 等于:A .﹛-1,0,1﹜ B.﹛1﹜ C.﹛0,1﹜ D.﹛0﹜2. 在复平面内,复数z=i (1+2i )对应的点位于:A .第一象限 B.第二象限 C.第三象限 D.第四象限3. 命题“∃x ∈R,x³-x²+1>0”的否定是:A .∀x ∈R,x³-x²+1≤0 B.∃x ∈R,x³-x²+1≤0C.∃x ∈R,x³-x²+1<0D.∀x ∈R,x³-x²+1<0 4. 如图所示,程序框图(算法流程图)的输出结果是:A.61 B.2425 C.43D.1211 5. 如果X~B(20,p)当p (X=k )取得最大值时,k 的值为:A.10B.9C.8D.76. 如图,正方体ABCD-A 1B 1C 1D 1中,AB 的中点为M ,DD 1的中点为N ,则异面直线B 1M 与CN 所成的角是:A.30°B.45°C.60°D.90° 7. 定义在R 上的函数既是偶函数又是周期函数,且f (x )的最小周期值是T=π,当x∈[0,2]时,f (x )=sinx ,则f (35,π)的值为:A .-21B.23 C.-23 D.21 8. 已知台体的体积公式V=31(S+21s s +S 2)h ,其中S ,S 分别是台体上,下底的面积,h 表示台体的高.某四棱台的三视图如图所示,则该四棱台的体积是: A.314B.4C.316 D.6 9. 在高校自主招生中某学校获得5个推荐名额,其中清华大学2名,北京大学2名,复旦大学1,名.并且北京大学和清华大学都要求必须有男生参加.学校通过选拔定下3男2女共5个推荐对象,则不同的推荐方式有:A.20种B.22种C.24种D.36种10. 已知定义在R 的函数f (x ),g (x )满足)()(x g x f =a x,且f′(x )g (x )<f(x),g′(x),第8题图 侧视图 俯视图 ABC1C 1D 1A 1B DM N第6题图)1()1(g f +)1()1(--g f =25,若有穷数列{)()(n g n f }(n∈N *)的前n 项和为128127,则n=:A.4B.5C.6D.7二、填空题(本大题共5小题,每小题5分,共25分,把答案填在答题卷中相应的横线上).11. 在x (1+x )6的展开式中,含x 3项的系数为___________;12. 已知函数f (x )=e x-1,则f (x )=0处的切线方程为___________;13. 已知抛物线y ²=8x 准线过双曲线2222by -a x =1(a >0,b >0)的一个焦点,且双曲线的离心率为2,则双曲线的焦点到其渐近线的距离是___________;14. 设常数a >0,若9x +xa 2≥a ²-7对一切实数的正实数x 均成立,则a 的取值范围为___________; 15. 对于在D 上的函数f (x ),若存在的距离为d 的两条直线y =kx +m 1和y =kx +m 2使得对任意x ∈D 都有kx +m 1≤f (x )≤kx +m 2恒成立,则称函数f (x )(x ∈D )有一个宽度为d 的通道.给出下列函数:①f (x )=x 1;②f (x )=sinx ;③f (x )=12-x ;④f (x )=xx ln ,其中在区间[1,∞)上通道宽度可以为1的函数有___________(写出所有正确的序号). 三、解答题(本小题共6小题,共75分,解答应写出必要的文字说明、证明过程或演算步骤).16. (本大题共12小题)某项竞赛分为初赛,复赛,决赛三个阶段进行,每个阶段选手只需要回答一个问题,规定正确回答才能进入下一阶段,否则即遭淘汰,已知某选手通过初赛,复赛,决赛的概率分别是43,21,41,且各阶段通过与否相互独立.(1)求该选手在复赛阶段被淘汰的概率;(2)设该选手在竞赛中回答问题的个数为X ,求X 的分布列及数学期望.17. (本大题共12小题)已知向量)2s i n 3,(c o s ),1,cos 2(x x n x m ==,函数2012)(+⋅=x f .(1)化简)(x f 的解析式,求函数)(x f 的单调递增区间;(2)在△ABC 中,a 、b 、c 分别为角A 、B 、C 所对的边,若4,2014)(==a A f ,△ABC 的面积为34,试判断△ABC 的形状,并说明理由.18. (本大题共12小题)已知四棱锥P -ABCD 的底面ABCD 是菱形,PA ⊥平面ABCD ,PA =AD =AC ,点F 为PC 的中点. (1)求证:PA //平面BFD ;(2)求二面角C -BF -D 的余弦值. 19. (本大题共12小题)设等差数列{a n }的前n 项和为S n ,且a 3=6,S 10=110.(1)求数列{a n }的通项公式;BCDAF P(2)设数列{b n }的前n 项和为T n ,且na n T )22(1-=,令*)(N n b a c n n n ∈⋅=,求数列{c n }的前n 项和R n .20. (本大题共13小题)已知点P (4,4),圆C :)3(5)(22<=+-m y m x 与椭圆E :)0(12222>>=+b a b ya x 有一个公共点A (3,1),F 1、F 2分别是椭圆的左、右焦点,直线PF 1与圆C 相切. (1)求m 的值与椭圆E 的方程;(2)设Q 为椭圆E 上的一个动点,求⋅的取值范围. 21. (本大题共14小题)设函数2ln 83)(2++=x x x f ,x x g =)(.(1)求函数)(2)()(x g x f x F -=的极值点;(2)若函数)(2)()(x g x f x F -=在))(,[Z t e t ∈+∞上有零点,求t 的最大值; (3)若*)()()1(1N n n g b n g n ∈=+,试问数列}{n b 中是否存在)(n m b b m n ≠=?若存在,求出所有相等的两项;若不存在,请说明理由(e 为自然对数的底数).参考答案一、选择题:本大题共10小题,每小题5分,共50分。
2014年下期12月份月考高二数学试卷(文科)

2014年下期12月份月考 高二数学试卷(文科)时量:120分钟 分值:150分一.选择题(本大题共10小题,每小题5分,共50分)1.ABC ∆中,若︒===60,2,1B c a ,则ABC ∆的面积为 ( )A .21B .23 C.1D.32.不等式20(0)ax bx c a ++<≠的解集为R ,那么 ( ) A. 0,0a <∆< B. 0,0a <∆≤ C. 0,0a >∆≥ D. 0,0a >∆>3. 设a ∈R ,则a>1是a1<1 的( )A .充分但不必要条件B .必要但不充分条件C .充要条件D .既不充分也不必要条件4. 到两定点()0,31-F 、()0,32F 的距离之差的绝对值等于6的点M 的轨迹( )A .椭圆B .线段C .双曲线D .两条射线5.过椭圆125922=+y x 左焦点F 1 的弦AB 交椭圆于A 、B 两点,则△ABF 2的周长为 ( ) A .9 B .12 C .15 D .20 6. 若抛物线28y x =上一点P 到其焦点的距离为9,则点P 的坐标( )A .(7,B .(14,C .(7,±D .(7,-±7.函数 3y x x =+的递增区间是 ( )A .),0(+∞B .)1,(-∞C .),(+∞-∞D .),1(+∞8.32()32f x ax x =++,若'(1)4f -=,则a 的值等于 ( )A .319B .316C .313D .3109.函数()323922y x x x x =---<<有 ( ) A .极大值5,极小值27- B .极大值5, 极小值11- C .极大值5,无极小值 D .极小值27-,无极大值10.已知函数()()y f x x R =∈的图象如图所示,则不等式'()0xf x <的解集( )A .(-∞,12)∪(12,2)B .(-∞,0)∪(12,2) C .(-∞,12∪(12,+∞) D .(-∞,12)∪(2,+∞)二、填空题(本题共6小题,每小题5分,共30分)11. 命题“若△ABC 不是等腰三角形,则它的任何两个内角不相等”的逆否命题是 ;12.221916x y -=的焦点为 、焦距是 . 13.椭圆22189x y k +=+的离心率为12,则k 的值为______________; 14. 函数344+-=x x y 在区间[]2,3-上的最小值为______________; 15. 一个物体的运动方程为21t t s +-=其中s 的单位是米,t 的单位是秒, 求物体在3秒末的瞬时速度_______________。
【VIP专享】2014-2015高二数学第二次月考试题

乐东中学2014-2015学年第一学期高二数学第二次月考试题本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共120分考试时间120分钟 命题人:刘鸿鹄第I 卷(选择题 共48分)一、选择题(共12题,每题4分)1.命题“若a ∉A ,则b∈B”的逆命题是( ) A .若a ∉A ,则b ∉B B .若a∈A,则b ∉B C .若b∈B,则a ∉A D .若b ∉B ,则a ∉A 2.口袋内装有一些大小相同的红球、白球和黒球,从中摸出个球,摸出红球1的概率是,摸出白球的概率是,那么摸出黒球的概率是( )0.420.28A . B . C . D . 0.420.280.30.73.命题:“对任意的x ∈R ,x 3-x 2+1≤0”的否定是 ( )A.不存在x ∈R ,x 3-x 2+1≤0B.存在x 0∈R ,x -x +1≤03020C.存在x 0∈R ,x -x +1>03020D.对任意的x ∈R ,x 3-x 2+1>04.取一根长度为5 m 的绳子,拉直后在任意位置剪断,那么剪得两段的长都不小于2 m 的概率是.() A. B. C. D.不确定1514135.若抛物线的焦点与椭圆的右焦点重合,则的值为( 22y px =22162x y +=p )A . B . C . D .2-24-46、从装有2个红球和2个黑球的口袋内任取2个球,则恰好有一个红球的概率是( )A B C D 312132657.若一个椭圆长轴的长度、短轴的长度和焦距成等差数列,则该椭圆的离心率是( )A. B. C. D.453525158.两个事件对立是这两个事件互斥的( )A .充分但不是必要条件B .必要但不是充分条件C .充分必要条件D .既不充分又不必要条件9.双曲线的的渐近线方程是( )191622=-y x A . B . C . D . 034=±y x 043=±y x 0169=±y x 0916=±y x 10.若点P 是抛物线上的一个动点,则点P 到点(0,2)的距离与P 到该抛24y x =物线准线的距离之和的最小值为 ( )AB . CD .39211.已知△ABC 的顶点B 、C 在椭圆+y 2=1上,顶点A 是椭圆的一个焦点,且椭x 3圆的另外一个焦点在BC 边上,则△ABC 的周长是( ) B. 4 C.6 D.123312、函数f (x )=x|x+a|+b 是奇函数的充要条件是( )A.ab =0 B.a +b=0 C.a =b D.a 2+b 2=0乐东中学2014-2015学年第一学期高二数学第二次月考试题第Ⅱ卷(非选择题 共72分)命题人:刘鸿鹄二.填空题(每题4分,共16分)13.命题“若m>0,则方程x 2-x +m =0有实数根”的等价命题是______________________________________________.14.在一个边长为3 cm 的正方形内部画一个边长为2cm 的正方形,向大正方形内随机投点,则所投的点落入小正方形内的概率是_____________. 15.设p 、q 是两个命题,若p 是q 的充分不必要条件,则是的q ⌝p ⌝_________________条件.16、方程表示双曲线,则k 的取值范围是_____________________11122=-++k y k x ____三.解答题(共56分)17.(9分)求证:△ABC是等边三角形的充要条件是a 2+b 2+c 2=ab +ac +bc 。
高二年级上学期12月份数学月考试题含答案

21.(12分)21.如图,在四棱锥 中, 平面 ,
在直角梯形 中, , ,
, 为线段 的中点
(1)求证:平面 平面
(2)若 是 中点, , , ,求三棱锥 的体积.
22.(12分)22.如图倾斜角为 的直线与抛物线 相交于 、 两点.
(1)求抛物线 的焦点F的坐标及准线l的方程;
所以 ,设直线m与 的交点为E,
则 , ,
所以直线m的方程为: ,
令 得: ,所以 ,
因为 ,所以 ,
所以 ,
即 为定值,且定值为6;
由点 、 、 在一直线上,得 ,即 ,
由射影定理得 ,即 ,
把 代入 得: ( ).
21.(12分)
22.(12分)22【详解】
(1)由已知抛物线的方程可得: ,所以 ,
故抛物线的焦点F的坐标为: ,准线l的方程为: ;
(2)证明:由题意可知直线 斜率存在,设直线 的方程为: ,
联立方程 ,消去y可得: ,
C.两组数据的样本方差相同;D.两组数据的样本标准差不同.
4.(5分)4.某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分成6组:[40,50), [50,60), [60,70), [70,80), [80,90), [90,100]加以统计,得到如图所示的频率分布直方图.已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为
(2)
证明:若 的斜率不存在,则 , ,
此时 ,
若 的斜率存在,设 , , , ,
设 的方程为 ,
,得 ,
由韦达定理得 , ,
则 , ,
所以
,
综上 .
高二上12月月考数学试题(理)及答案

沈阳二中2013——2014学年度上学期12月份小班化学习成果 阶段验收高二( 15 届)数学试题(理)命题人:高二数学组 审校人: 高二数学组说明:1.测试时间:120分钟 总分:150分2.客观题涂在答题纸上,主观题答在答题纸的相应位置上第Ⅰ卷 (60分)一、选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1. 下列命题:①至少有一个x 使x 2+2x +1=0成立;②对任意的x 都有x 2+2x +1=0成立;③对任意的x 都有x 2+2x +1=0不成立;④存在x 使x 2+2x +1=0成立. 其中是全称命题的有( )A .1个B .2个C .3个D .0个2. 已知命题p :“∀x ∈[1,2],x 2-a ≥0”,命题q :“∃x ∈R ”,x 2+2ax +2-a =0,若命题“p ∧q ”是真命题,则实数a 的取值范围是( )A .a ≤-2或a =1B .a ≤-2或1≤a ≤2C .a ≥1D .-2≤a ≤13. P 为正六边形ABCDEF 外一点,O 为ABCDEF 的中心,则PA PB PC PD PE PF +++++等于( )A .POB .3POC .6POD .04. 对于空间任意一点O 和不共线的三点A 、B 、C ,有OP →=xOA →+yOB →+zOC →(x 、y 、z ∈R),则x +y +z =1是P 、A 、B 、C 四点共面的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件5. 已知△ABC 的顶点B 、C 在椭圆x 23+y 2=1上,顶点A 是椭圆的一个焦点,且椭圆的另外一个焦点在BC边上,则△ABC 的周长是 ( ) A .2 3B .6C .4 3D .126. 下列四个条件中,p 是q 的必要不充分.....条件的是 ( ) A .p :a >b q :a 2>b 2 B .p :a >b q :2a >2bC .p :ax 2+by 2=c 为双曲线 q :ab <0 D .p :ax 2+bx +c >0 q :c x 2+b x+a >0 7. 抛物线y 2=8x 的焦点到双曲线x 212-y 24=1的渐近线的距离为( )A .1 B. 3 C.33 D.368. 设椭圆x 2a 2+y 2b2=1和x 轴正半轴交点为A ,和y 轴正半轴的交点为B ,P 为第一象限内椭圆上的点,那么四边形OAPB 面积最大值为 ( )A.2abB.22abC.12ab D .2ab9. 已知双曲线的两个焦点为F 1(-10,0)、F 2(10,0),M 是此双曲线上的一点,且满足12120,||||2,MF MF MF MF ==则该双曲线的方程是( )A .2219x y -=B .2219y x -= C. 22137x y -= D. 22173x y -=10. 已知1F 、2F 是双曲线)0b ,0a (1by a x 2222>>=-的两焦点,以线段F 1F 2为边作正21F MF ∆,若边1MF 的中点在双曲线上,则双曲线的离心率是( )A. 324+B.13- C.213+ D. 13+ 11. 已知抛物线y 2=2px (p >0),过其焦点且斜率为1的直线交抛物线于A 、B 两点,若线段AB 的中点的纵坐标为2,则该抛物线的准线方程为( )A .x =1B .x =-1C .x =2D .x =-212. 已知椭圆x 23m 2+y 25n 2=1和双曲线x 22m 2-y 23n2=1有公共的焦点,那么双曲线的渐近线方程为( )A .x =±152y B .y =±152x C .x =±34y D .y =±34x 第Ⅱ卷 (90分)二、填空题 (本大题共4小题,每小题5分,共20分)13. 已知F 1、F 2是椭圆x 2a 2+y 2b2=1(a >b >0)的左右焦点,P 是椭圆上一点,∠F 1PF 2=90°,求椭圆离心率的最小值为14.过抛物线22y px =(0)p >焦点F 的弦AB ,过,A B 两点分别作其准线的垂线,AM BN ,垂足分别为,M N ,AB 倾斜角为α,若1122(,),(,)A x y B x y ,则①2124p x x =;221p y y -=.②||1cos p AF α=-,||1cos p BF α=+③||||2||||AF BF AF BF p+=∙, ④||AB =1222,sin p x x p α++=⑤0FM FN = 其中结论正确的序号为15. 若椭圆x 236+y 29=1的弦被点(4,2)平分,则此弦所在直线的斜率为________.16. 设有两个命题:①关于x 的不等式mx 2+1>0的解集是R ;②函数f (x )=log m x 是减函数,如果这两个命题中有且只有一个真命题,则实数m 的取值范围是________.三、解答题(本大题包括6小题,共70分,解答应写出文字说明,证明过程或演算步骤)17、(本小题满分10分)如右图,在空间四边形SABC 中,AC 、BS 为其对角线,O 为△ABC 的重心,试证:(1)OA 0OB OC ++=(;(2)1()3SO SA SB SC =++.18. (本小题满分12分)已知条件p :A ={x |2a ≤x ≤a 2+1},条件q :B={x |x 2-3(a +1)x +2(3a +1)≤0}.若条件p 是条件q 的充分条件,求实数a 的取值范围. 19. (本小题满分12分) 设直线y ax b =+与双曲线2231x y -=交于A 、B ,且以AB 为直径的圆过原点,求点(,)P a b 的轨迹方程.20. (本小题满分12分)在抛物线 y 2=4x 上恒有两点关于直线l :y =kx +3对称,求k 的范围. 21.(本小题满分12分)已知双曲线方程2x 2-y 2=2.(1)求以A (2,1)为中点的双曲线的弦所在的直线方程;(2)过点(1,1)能否作直线l ,使l 与双曲线交于Q 1,Q 2两点,且Q 1,Q 2两点的中点为(1,1)?如果存在,求出它的方程;如果不存在,说明理由.22. (本小题满分12分)已知椭圆C 1的方程为1422=+y x ,双曲线C 2的左、右焦点分别为C 1的左、右顶点,而C 2的左、右顶点分别是C 1的左、右焦点. (Ⅰ)求双曲线C 2的方程;(Ⅱ)若直线2:+=kx y l 与椭圆C 1及双曲线C 2都恒有两个不同的交点,且l 与C 2的两个交点A 和B 满足6<⋅(其中O 为原点),求k 的取值范围.沈阳二中2013——2014学年度上学期12月份小班化学习成果阶段验收高二( 15 届)(理)数学试题答案一、 选择题(每题5分,共60分) BACCC DABAD BD二、 填空题(每题5分共20分)13、22 14、①②③④⑤ 15、-1216、m ≥1或m =0 三、 解答题(共70分)17、证明:(1),①,② ,③①+②+③得. (2),④,⑤,⑥由(1)得:.④+⑤+⑥得3即SO =13().18. 解: A ={x |2a ≤x ≤a 2+1},B ={x |(x -2)[x -(3a +1)]≤0}.①当a ≥13时,B ={x |2≤x ≤3a +1};②当a <13时,B ={x |3a +1≤x ≤2}.因为p 是q 的充分条件,所以A ⊆B ,于是有⎩⎪⎨⎪⎧a ≥13,a 2+1≤3a +1,2a ≥2,解得1≤a ≤3.,或⎩⎪⎨⎪⎧a <13,a 2+1≤2,2a ≥3a +1,解得a =-1.故a 的取值范围是{a |1≤a ≤3或a =-1}.19. 解: 联立直线与双曲线方程得⎩⎪⎨⎪⎧y =ax +b3x 2-y 2=1,消去y 得:(a 2-3)x 2+2abx +b 2+1=0.∵直线与双曲线交于A 、B 两点,∴⎩⎨⎧a 2-3≠0Δ>0⇒a 2<3.设A (x 1,y 1),B (x 2,y 2)则x 1+x 2=2ab3-a 2,x 1·x 2=b 2+1a 2-3.由OA →⊥OB →得x 1x 2+y 1y 2=0,又y 1·y 2=(ax 1+b )(ax 2+b )=a 2x 1x 2+ab (x 1+x 2)+b 2, ∴有b 2+1a 2-3+a 2·b 2+1a 2-3-2a 2b 2a 2-3+b 2=0.化简得:a 2-2b 2=-1.故P 点(a ,b )的轨迹方程为2y 2-x 2=1(x 2<3).20. 解: 设B 、C 关于直线y =kx +3对称,直线BC 方程为x =-ky +m ,代入y 2=4x ,得y 2+4ky -4m=0,设B (x 1,y 1),C (x 2,y 2),BC 中点M (x 0,y 0), 则y 0=y 1+y 22=-2k ,x 0=2k 2+m .∵点M (x 0,y 0)在直线l 上,∴-2k =k (2k 2+m )+3, ∴m =-2k 3+2k +3k,因M (x 0,y 0)在抛物线y 2=4x 内部,则y 02<4x 0,把m 代入化简得k 3+2k +3k <0,即(k +1)(k 2-k +3)k<0,解得-1<k <0.21.解: (1)设A (2,1)是弦P 1P 2的中点,且P 1(x 1,y 1),P 2(x 2,y 2),则x 1+x 2=4,y 1+y 2=2.22. 解:(Ⅰ)设双曲线C 2的方程为12222=-b y a x ,则.1,31422222==+=-=b c b a a 得再由故C 2的方程为.1322=-y x(II )将.0428)41(1422222=+++=++=kx x k y x kx y 得代入由直线l 与椭圆C 1恒有两个不同的交点得,0)14(16)41(16)28(22221>-=+-=∆k k k即 .412>k ① 0926)31(1322222=---=-+=kx x k y x kx y 得代入将.由直线l 与双曲线C 2恒有两个不同的交点A ,B 得.131.0)1(36)31(36)26(,0312222222<≠⎪⎩⎪⎨⎧>-=-+-=∆≠-k k k k k k 且即)2)(2(,66319,3126),,(),,(22+++=+<+<⋅--=⋅-=+B A B A B A B A B A B A BA B A B B A A kx kx x x y y x x y y x x OB OA k x x k k x x y x B y x A 而得由则设.1373231262319)1(2)(2)1(222222-+=+-⋅+--⋅+=++++=k k kk k k k x x k x x k B A B A .0131315,613732222>--<-+k k k k 即于是解此不等式得.31151322<>k k 或 ③ 由①、②、③得.11513314122<<<<k k 或故k 的取值范围为)1,1513()33,21()21,33()1513,1( ----。
高二年级十二月月考数学试卷
仪 征 电 大 附 中高二年级十二月月考数学试卷2005.12一、选择题(每小题5分,共60分) 1、若直线过点)3,3(-,且倾斜角为o 30,则直线的方程为( ) )A (2x 33y +=)B (4x 33y -=)C (6x 3y -= )D (34x 3y +=2.两定点A (-2,-1),B (2,-1),动点P 在抛物线2x y =上移动,则△PAB 重 心G 的轨迹方程是( ) A .312-=x y B .3232-=x yC .3222-=x yD .41212-=x y3、直线x – 2y +2 = 0与直线3x – y + 7 = 0的夹角等于 ( ) A 4π-. B4π. C 43π. D arctan7. 4.参数方程⎪⎪⎩⎪⎪⎨⎧-=+=t t y t t x 11 )0(≠t 表示曲线的离心率为( )A .22B .21C .2D .25.右图是一个正方体的展开图,在原正方体中,有下列命题: ①AB 与CD 所在直线垂直; ②CD 与EF 所在直线平行③AB 与MN 所在直线成60°角;④MN 与EF 所在直线异面其中正确命题的序号是( )A .①③B .①④C .②③D .③④6.已知A (1,2)和B (3,—4)在直线)2(+=x k y 的同侧,则k 的取值范围是( )A .)54,32(B .),32()54,(+∞⋃--∞ C .)32,54(-D .]32,54[-7.已知椭圆的中心在原点,离心率21e =,且它的一个焦点与抛物线x 4y 2-=的 焦点重合,则此椭圆方程为 ( )A .1y 2x 22=+ B. 16y 8x 22=+ C. 13y 4x 22=+ D.1y 4x 22=+ 8.如果方程x 2+ky 2=2表示焦点在y 轴上的椭圆,那么实数k 的取值范围是( ) A .(0, +∞)B .(0, 2)C .(1, +∞)D .(0, 1) 9.直线y = x +1被椭圆x 2+2y 2=4所截得的弦的中点坐标是 ( )A .(31, -32) B ..(-32, 31) C .(21, -31) D .(-31,21) 10.一动圆与两圆:x 2+y 2=1和x 2+y 2-8x +12=0都外切,则动圆心的轨迹为 ( ) A .抛物线B .圆C .双曲线的一支D .椭圆11.过点(2,—2)且与1222=-y x 有相同渐近线的双曲线方程是( )A .12422=-y x B . 14222=-x y C .12422=-x y D . 14222=-y x12.直线a x y -=与抛物线ax y =2交于A 、B 两点,O 为原点,则△AOB 是( ) A .锐角三角形B .直角三角形C .钝角三角形D .其形状不能确定二、填空题(每空4分,共16分)13.以点(-2,3)为圆心且与y 轴相切的圆的方程是 . 14.若a >0, b >0,则)11)((ba b a ++ 的最小值是 .15、椭圆5522=+ky x 的一个焦点为(0,2),那么k=____________。
河北省邯郸市永年二中2014-2015学年高二数学上学期12月月考试卷 文(含解析)
河北省邯郸市永年二中2014-2015学年高二上学期12月月考数学试卷(文科)一、选择题:本大题共12题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)若集合A={0,4},B={2,a2},则“a=2”是“A∩B={4}”的()A.充分非必要条件B.必要非充分条件C.充要条件D.既不充分也不必要条件2.(5分)已知复数z1=1﹣2i,则的虚部是()A.i B.﹣i C.1 D.﹣13.(5分)若,且α是第二象限角,则tanα的值为()A.B.C.D.4.(5分)已知向量=(1,2),=(﹣3,2),若(k+)∥(﹣3),则实数k的取值为()A.﹣B.C.﹣3 D.35.(5分)已知函数f(x)=x3﹣2x2+2有唯一零点,则下列区间必存在零点的是()A.B.C.D.6.(5分)设x,y满足约束条件,则z=x+2y的最大值为()A.8 B.7 C.2 D.17.(5分)阅读程序框图,如果输出的函数值在区间内,则输入的实数x的取值范围是()A.(﹣∞,﹣2] B.[﹣2,﹣1] C.[﹣1,2] D.[2,+∞)8.(5分)下列命题正确的是()A.函数y=sin(2x+)在区间内单调递增B.函数y=cos4x﹣sin4x的最小正周期为2πC.函数y=cos(x+)的图象是关于点(,0)成中心对称的图形D.函数y=tan(x+)的图象是关于直线x=成轴对称的图形9.(5分)已知各项均为正数的等比数列{a n}中,a1a2a3=8,a3a4a5=,则a2a3a4=()A.512 B.64 C.1 D.10.(5分)若函数f(x)=kx﹣lnx在区间(1,+∞)单调递增,则k的取值范围是()A.(﹣∞,﹣2] B.(﹣∞,﹣1] C.[2,+∞)D.[1,+∞)11.(5分)已知S,A,B,C是球O表面上的点,SA⊥平面ABC,AB⊥BC,SA=AB=1,,则球O的表面积等于()A.4πB.3πC.2πD.π12.(5分)已知函数f(x)是定义在(﹣3,3)上的奇函数,当0<x<3时,f(x)的图象如图所示,则不等式f(﹣x)•x>0的解集是()A.(﹣1,0)∪(0,1)B.(﹣1,1)C.(﹣3,﹣1)∪(0,1)D.(﹣1,0)∪(1,3)二.填空题:本大题共4个小题,每小题5分.13.(5分)如图,若一个空间几何体的三视图中,直角三角形的直角边长均为1,则该几何体的体积为.14.(5分)已知数列{a n}为等差数列,其前n项和为S.若a1>0,S20=0,则使a n>0成立的n的最大值是.15.(5分)函数y=sin2x+cos2x的最小正周期为.16.(5分)已知函数f(x)=()x﹣lnx,a>b>c>0,且满足f(a)f(b)f(c)<0,若实数d是函数y=f(x)的一个零点,那么下列四个判断:①d<a;②d>b;③d<c;④d>c;其中有可能成立的判断的序号为.三、解答题:(本大题共6小题,共75分)17.(10分)已知{a n}是等差数列,满足a1=3,a4=12,数列{b n}满足b1=4,b4=20,且{b n﹣a n}为等比数列.(Ⅰ)求数列{a n}和{b n}的通项公式;(Ⅱ)求数列{b n}的前n项和.18.(12分)在△ABC中,角A、B、C的对边分别为a、b、c,且满足(2b﹣c)cosA﹣acosC=0,(Ⅰ)求角A的大小;(Ⅱ)若,,试判断△ABC的形状,并说明理由.19.(12分)如图所示,在四棱锥P﹣ABCD中,AB⊥平面PAD,AB∥CD,PD=AD,E是PB的中点,F是CD上的点且,PH为△PAD中AD边上的高.(Ⅰ)证明:PH⊥平面ABCD;(Ⅱ)若PH=1,,FC=1,求三棱锥E﹣BCF的体积.20.(12分)如图,四棱锥P﹣ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.(Ⅰ)证明:PB∥平面AEC;(Ⅱ)设AP=1,AD=,三棱锥P﹣ABD的体积V=,求A到平面PBC的距离.21.(12分)已知点A(﹣3,0),B(3,0),动点P满足|PA|=2|PB|,(1)若点P的轨迹为曲线C,求此曲线的方程(2)若点Q在直线l1:x+y+3=0上,直线l2经过点Q且与曲线C只有一个公共点M,求|QM|的最小值.22.(12分)设函数f(x)=x3+ax2﹣a2x+5(a>0)(1)当函数f(x)有两个零点时,求a的值;(2)若a∈[3,6],当x∈[﹣4,4]时,求函数f(x)的最大值.河北省邯郸市永年二中2014-2015学年高二上学期12月月考数学试卷(文科)参考答案与试题解析一、选择题:本大题共12题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)若集合A={0,4},B={2,a2},则“a=2”是“A∩B={4}”的()A.充分非必要条件B.必要非充分条件C.充要条件D.既不充分也不必要条件考点:必要条件、充分条件与充要条件的判断;交集及其运算.分析:判断“a=2”成立时是否有A∩B={4}成立;判断A∩B={4}成立时是否有“a=2”成立;利用充分、必要条件的定义判断出答案.解答:解:当“a=2”成立时,B={2,4},∴A∩B={4}成立反之,当A∩B={4}”成立时,∴4∈B∴a2=4∴a=±2即“a=2“不一定成立∴“a=2”是“A∩B={4}”的充分不必要条件故选A点评:本题考查如何判断一个命题是另一个命题的什么条件、考查利用交集的定义解决集合的交集运算.2.(5分)已知复数z1=1﹣2i,则的虚部是()A.i B.﹣i C.1 D.﹣1考点:复数代数形式的乘除运算;复数的基本概念.专题:计算题.分析:利用两个复数代数形式的乘除法,虚数单位i的幂运算性质化简,依据复数的虚部的定义求出其虚部.解答:解:∵复数z1=1﹣2i,则====1+i,虚部等于1,故选C.点评:本题考查两个复数代数形式的乘除法,虚数单位i的幂运算性质,两个复数相除,分子和分母同时乘以分母的共轭复数.复数的徐不得定义.3.(5分)若,且α是第二象限角,则tanα的值为()A.B.C.D.考点:同角三角函数间的基本关系.专题:计算题.分析:由α是第二象限角,得到sinα的值大于0,可由cosα的值,利用同角三角函数间的基本关系求出sinα的值,再由sinα及cosα的值,利用同角三角函数间的基本关系弦化切,即可求出tanα的值.解答:解:∵,且α是第二象限角,∴sinα==,则tanα==﹣.故选C点评:此题考查了同角三角函数间的基本关系,熟练掌握基本关系是解本题的关键,同时注意角度的范围.4.(5分)已知向量=(1,2),=(﹣3,2),若(k+)∥(﹣3),则实数k的取值为()A.﹣B.C.﹣3 D.3考点:平行向量与共线向量;平面向量坐标表示的应用.专题:平面向量及应用.分析:根据题目给出的两个向量的坐标,运用向量的数乘和加法运算求和,然后运用向量共线的坐标表示列式求k的值.解答:解:由=(1,2),=(﹣3,2),得=(k﹣3,2k+2),=(10,﹣4),则由,得(k﹣3)×(﹣4)﹣10×(2k+2)=0,所以k=﹣.故选A.点评:本题考查了平行向量及平面向量坐标表示的应用,解答的关键是掌握向量共线的坐标表示,即,,则⇔x1y2﹣x2y1=0.5.(5分)已知函数f(x)=x3﹣2x2+2有唯一零点,则下列区间必存在零点的是()A.B.C.D.考点:函数零点的判定定理.专题:计算题.分析:根据函数的解析式f(x)=x3﹣2x2+2,结合零点存在定理,我们可以分别判断四个答案中的四区间,如果区间(a,b)满足f(a)•f(b)<0,则函数在区间(a,b)有零点.解答:解:∵f(x)=x3﹣2x2+2∴f(﹣1)=(﹣1)3﹣2(﹣1)2+2=﹣1﹣2+2=﹣1<0f(﹣)=(﹣)3﹣2(﹣)2+2=﹣﹣+2=>0∴f(﹣1)•f(﹣)<0故函数f(x)=x3﹣2x2+2在区间必有零点故选:C点评:本题考查的知识点是函数零点的判定定理,其中连续函数在区间(a,b)满足f(a)•f(b)<0,则函数在区间(a,b)有零点,是判断函数零点存在最常用的方法.6.(5分)设x,y满足约束条件,则z=x+2y的最大值为()A.8 B.7 C.2 D.1考点:简单线性规划.专题:不等式的解法及应用.分析:作出不等式对应的平面区域,利用线性规划的知识,通过平移即可求z的最大值.解答:解:作出不等式对应的平面区域,由z=x+2y,得y=﹣,平移直线y=﹣,由图象可知当直线y=﹣经过点A时,直线y=﹣的截距最大,此时z最大.由,得,即A(3,2),此时z的最大值为z=3+2×2=7,故选:B.点评:本题主要考查线性规划的应用,利用数形结合是解决线性规划题目的常用方法.7.(5分)阅读程序框图,如果输出的函数值在区间内,则输入的实数x的取值范围是()A.(﹣∞,﹣2] B.[﹣2,﹣1] C.[﹣1,2] D.[2,+∞)考点:选择结构.专题:图表型.分析:分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是计算分段函数f(x)=的函数值.根据函数的解析式,结合输出的函数值在区间内,即可得到答案.解答:解:分析程序中各变量、各语句的作用再根据流程图所示的顺序,可知:该程序的作用是计算分段函数f(x)=的函数值.又∵输出的函数值在区间内,∴x∈[﹣2,﹣1]故选B点评:本题考查的知识点是选择结构,其中根据函数的流程图判断出程序的功能是解答本题的关键.8.(5分)下列命题正确的是()A.函数y=sin(2x+)在区间内单调递增B.函数y=cos4x﹣sin4x的最小正周期为2πC.函数y=cos(x+)的图象是关于点(,0)成中心对称的图形D.函数y=tan(x+)的图象是关于直线x=成轴对称的图形考点:函数y=Asin(ωx+φ)的图象变换;三角函数的周期性及其求法;余弦函数的对称性;正切函数的奇偶性与对称性.专题:分析法.分析:先根据x的范围求出2x+的范围,再由正弦函数的单调性可判断A;根据同角三角函数的基本关系和二倍角公式将y=cos4x﹣sin4x为y=Asin(wx+ρ)的形式,再由T=可判断B;根据对称中心的函数值等于0可判断C,从而确定答案.解答:解:∵x∈∴2x+∈(﹣,),∴y=sin(2x+)在区间内是先增后减,排除A;∵y=cos4x﹣sin4x=cos2x﹣sin2x=cos2x,T=,排除B;令x=代入得到cos(+)=cos=0,∴点(,0)是函数y=cos(x+)的图象的对称中心,满足条件.故选C.点评:本题主要考查正弦函数的单调性、二倍角公式和单调性的应用.三角函数部分公式比较多,要强化记忆.9.(5分)已知各项均为正数的等比数列{a n}中,a1a2a3=8,a3a4a5=,则a2a3a4=()A.512 B.64 C.1 D.考点:等比数列的性质.专题:计算题.分析:利用等比数列的性质可得a1a2a3,a2a3a4,a3a4a5成等比数列,利用等比数列的性质可求解答:解:∵数列{a n}中等比数列,a1a2a3=8,a3a4a5=,且a n>0由等比数列的性质可得,a1a2a3,a2a3a4,a3a4a5成等比数列∴a2a3a4==1故选C点评:本题主要考查了等比数列的性质的简单应用,属于基础试题10.(5分)若函数f(x)=kx﹣lnx在区间(1,+∞)单调递增,则k的取值范围是()A.(﹣∞,﹣2] B.(﹣∞,﹣1] C.[2,+∞)D.[1,+∞)考点:利用导数研究函数的单调性.专题:导数的综合应用.分析:f′(x)=k﹣,由于函数f(x)=kx﹣lnx在区间(1,+∞)单调递增,可得f′(x)≥0在区间(1,+∞)上恒成立.解出即可.解答:解:f′(x)=k﹣,∵函数f(x)=kx﹣lnx在区间(1,+∞)单调递增,∴f′(x)≥0在区间(1,+∞)上恒成立.∴,而y=在区间(1,+∞)上单调递减,∴k≥1.∴k的取值范围是[1,+∞).故选:D.点评:本题查克拉利用导数研究函数的单调性、恒成立问题的等价转化方法,属于基础题.11.(5分)已知S,A,B,C是球O表面上的点,SA⊥平面ABC,A B⊥BC,SA=AB=1,,则球O的表面积等于()A.4πB.3πC.2πD.π考点:直线与平面垂直的性质;球的体积和表面积.专题:压轴题.分析:先寻找球心,根据S,A,B,C是球O表面上的点,则OA=OB=OC=OS,根据直角三角形的性质可知O为SC的中点,则SC即为直径,根据球的面积公式求解即可.解答:解:∵已知S,A,B,C是球O表面上的点∴OA=OB=OC=OS=1又SA⊥平面ABC,AB⊥BC,SA=AB=1,,∴球O的直径为2R=SC=2,R=1,∴表面积为4πR2=4π.故选A.点评:本题主要考查了直线与平面垂直的性质,以及球的表面积等有关知识,考查空间想象能力、运算能力和推理论证能力,属于基础题.12.(5分)已知函数f(x)是定义在(﹣3,3)上的奇函数,当0<x<3时,f(x)的图象如图所示,则不等式f(﹣x)•x>0的解集是()A.(﹣1,0)∪(0,1)B.(﹣1,1)C.(﹣3,﹣1)∪(0,1)D.(﹣1,0)∪(1,3)考点:函数奇偶性的性质.专题:函数的性质及应用.分析:由f(﹣x)•x>0,得f(x)•x<0,由图象知,当x∈(0,3)时不等式的解,根据奇函数性质可得x∈(﹣3,0]时不等式的解.解答:解:f(﹣x)•x>0即﹣f(x)•x>0,所以f(x)•x<0,由图象知,当x∈(0,3)时,可得0<x<1,由奇函数性质得,当x∈(﹣3,0]时,可得﹣1<x<0,综上,不等式f(﹣x)•x>0的解集是(﹣1,0)∪(0,1),故选A.点评:本题考查函数奇偶性的应用,考查数形结合思想,属基础题.二.填空题:本大题共4个小题,每小题5分.13.(5分)如图,若一个空间几何体的三视图中,直角三角形的直角边长均为1,则该几何体的体积为.考点:由三视图求面积、体积.专题:计算题.分析:几何体是一个四棱锥,四棱锥的底面是一个边长是1的正方形,四棱锥的一条侧棱与底面垂直,且这条侧棱长是1,根据四棱锥的体积公式,写出四棱锥的体积.解答:解:由三视图知,几何体是一个四棱锥,四棱锥的底面是一个边长是1的正方形,四棱锥的一条侧棱与底面垂直,且这条侧棱长是1,∴四棱锥的体积是,故答案为:点评:本题考查由三视图求几何体的体积,本题是一个基础题,题目所给的图形和数字都比较简单,没有易错点.14.(5分)已知数列{a n}为等差数列,其前n项和为S.若a1>0,S20=0,则使a n>0成立的n的最大值是10.考点:等差数列的性质.分析:先由等差数列前n项和将转化为∴a1+a20=0,再由等差数列的性质求解.解答:解∵∴a1+a20=0由等差数列的性质得:∴a1+a20=a2+a19=…=a11+a10=0又∵a1>0∴a10>0,a11<0∴使a n>0成立的n的最大值是10故答案是10点评:本题主要考查等差数列的性质.15.(5分)函数y=sin2x+cos2x的最小正周期为π.考点:二倍角的余弦;两角和与差的正弦函数;三角函数的周期性及其求法.专题:三角函数的图像与性质.分析:利用两角和的正弦公式、二倍角的余弦公式化简函数的解析式为f(x)=sin(2x+),从而求得函数的最小正周期解答:解:∵函数y=sin2x+cos2x=sin2x+=sin(2x+)+,故函数的最小正周期的最小正周期为=π,故答案为:π.点评:本题主要考查两角和的正弦公式、二倍角的余弦公式,正弦函数的周期性,属于基础题.16.(5分)已知函数f(x)=()x﹣lnx,a>b>c>0,且满足f(a)f(b)f(c)<0,若实数d是函数y=f(x)的一个零点,那么下列四个判断:①d<a;②d>b;③d<c;④d>c;其中有可能成立的判断的序号为①②③④.考点:函数零点的判定定理.专题:计算题;压轴题.分析:利用函数f(x)=()x﹣lnx 在(0,+∞)上是减函数及已知条件,分 f(a)<0,f(c)>f(b)>0;或 f(a)<f(b)<f(c)<0 二种情况,分别求得可能成立选项,从而得到答案.解答:解:∵已知函数f(x)=()x﹣lnx 在(0,+∞)上是减函数,a>b>c>0,且f(a)f(b)f(c)<0,故f(a)、f(b)、f(c)中一项为负的两项为正的;或者三项都是负的.即 f(a)<0,0<f(b)<f(c);或 f(a)<f(b)<f(c)<0.由于实数d是函数y=f(x)的一个零点,当 f(a)<0,f(c)>f(b)>0 时,b<d<a,此时①②④成立.当 f(a)<f(b)<f(c)<0时,d<c,此时①③成立.综上可得,有可能成立的判断的序号为①②③④,故答案为①②③④.点评:本题主要考查函数的零点的定义,判断函数的零点所在的区间的方法,体现了分类讨论的数学思想,属于基础题.三、解答题:(本大题共6小题,共75分)17.(10分)已知{a n}是等差数列,满足a1=3,a4=12,数列{b n}满足b1=4,b4=20,且{b n﹣a n}为等比数列.(Ⅰ)求数列{a n}和{b n}的通项公式;(Ⅱ)求数列{b n}的前n项和.考点:数列的求和;等差数列的通项公式;等比数列的通项公式.专题:等差数列与等比数列.分析:(Ⅰ)利用等差数列、等比数列的通项公式先求得公差和公比,即得结论;(Ⅱ)利用分组求和法,有等差数列及等比数列的前n项和公式即可求得数列的和.解答:解:(Ⅰ)设等差数列{a n}的公差为d,由题意得d===3.∴a n=a1+(n﹣1)d=3n(n=1,2,…),设等比数列{b n﹣a n}的公比为q,则q3===8,∴q=2,∴b n﹣a n=(b1﹣a1)q n﹣1=2n﹣1,∴b n=3n+2n﹣1(n=1,2,…).(Ⅱ)由(Ⅰ)知b n=3n+2n﹣1(n=1,2,…).∵数列{a n}的前n项和为n(n+1),数列{2n﹣1}的前n项和为1×=2n﹣1,∴数列{b n}的前n项和为n(n+1)+2n﹣1.点评:本题主要考查学生对等差数列及等比数列的通项公式和前n项和公式的应用,考查学生的基本的运算能力,属基础题.18.(12分)在△ABC中,角A、B、C的对边分别为a、b、c,且满足(2b﹣c)cosA﹣acosC=0,(Ⅰ)求角A的大小;(Ⅱ)若,,试判断△ABC的形状,并说明理由.考点:正弦定理;余弦定理.专题:计算题.分析:(1)先利用正弦定理把(2b﹣c)cosA﹣acosC=0中的边转化成角的正弦,进而化简整理得sinB(2cosA﹣1)=0,求得cosA,进而求得A.(2)根据三角形面积公式求得bc,进而利用余弦定理求得b2+c2进而求得b和c,结果为a=b=c,进而判断出∴△ABC为等边三角形.解答:解:(Ⅰ)∵(2b﹣c)cosA﹣acosC=0,由正弦定理,得(2sinB﹣sinC)co sA﹣sinAcosC=0,∴2sinBcosA﹣sin(A+C)=0,sinB(2cosA﹣1)=0,∵0<B<π,∴sinB≠0,∴,∵0<A<π,∴.(Ⅱ)∵,即∴bc=3①由余弦定理可知cosA==∴b2+c2=6,②由①②得,∴△ABC为等边三角形.点评:本题主要考查了正弦定理和余弦定理的应用.考查了学生分析问题和灵活运用所学知识的能力.19.(12分)如图所示,在四棱锥P﹣ABCD中,AB⊥平面PAD,AB∥CD,PD=AD,E是PB的中点,F是CD上的点且,PH为△PAD中AD边上的高.(Ⅰ)证明:PH⊥平面ABCD;(Ⅱ)若PH=1,,FC=1,求三棱锥E﹣BCF的体积.考点:直线与平面垂直的判定;棱柱、棱锥、棱台的体积.专题:综合题;空间位置关系与距离.分析:(Ⅰ)因为AB⊥平面PAD,所以PH⊥AB,因为PH为△PAD中AD边上的高,所以PH⊥AD,由此能够证明PH⊥平面ABCD.(Ⅱ)连接BH,取BH中点G,连接EG,因为E是PB的中点,所以EG∥PH,因为PH⊥平面ABCD,所以EG⊥平面ABCD,由此能够求出三棱锥E﹣BCF的体积.解答:(Ⅰ)证明:∵AB⊥平面PAD,∴PH⊥AB,∵PH为△PAD中AD边上的高,∴PH⊥AD,又∵AB∩AD=A,∴PH⊥平面ABCD.(Ⅱ)解:如图,连接BH,取BH中点G,连接EG,∵E是PB的中点,∴EG∥PH,∵PH⊥平面ABCD,∴EG⊥平面ABCD,则EG=PH=,∴V E﹣BCF=S△BCF•EG=••FC•AD•EG=.点评:本题考查直线与平面垂直的证明,求三棱锥的体积,解题时要认真审题,注意合理地化立体几何问题为平面几何问题.20.(12分)如图,四棱锥P﹣ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.(Ⅰ)证明:PB∥平面AEC;(Ⅱ)设AP=1,AD=,三棱锥P﹣ABD的体积V=,求A到平面PBC的距离.考点:点、线、面间的距离计算;棱柱、棱锥、棱台的体积;直线与平面平行的判定.专题:空间位置关系与距离.分析:(Ⅰ)设BD与AC 的交点为O,连结EO,通过直线与平面平行的判定定理证明PB∥平面AEC;(Ⅱ)通过AP=1,AD=,三棱锥P﹣ABD的体积V=,求出AB,作AH⊥PB角PB于H,说明AH就是A到平面PBC的距离.通过解三角形求解即可.解答:解:(Ⅰ)证明:设BD与AC 的交点为O,连结EO,∵ABCD是矩形,∴O为BD的中点∵E为PD的中点,∴EO∥PB.EO⊂平面AEC,PB⊄平面AEC∴PB∥平面AEC;(Ⅱ)∵AP=1,AD=,三棱锥P﹣ABD的体积V=,∴V==,∴AB=,作AH⊥PB交PB于H,由题意可知BC⊥平面PAB∴BC⊥AH,故AH⊥平面PBC.又A到平面PBC的距离.点评:本题考查直线与平面垂直,点到平面的距离的求法,考查空间想象能力以及计算能力.21.(12分)已知点A(﹣3,0),B(3,0),动点P满足|PA|=2|PB|,(1)若点P的轨迹为曲线C,求此曲线的方程(2)若点Q在直线l1:x+y+3=0上,直线l2经过点Q且与曲线C只有一个公共点M,求|QM|的最小值.考点:直线和圆的方程的应用;轨迹方程.专题:计算题;综合题.分析:(1)设P点的坐标为(x,y),用坐标表示|PA|、|PB|,代入等式|PA|=2|PB|,整理即得点P的轨迹方程;(2)求出圆心坐标,圆的半径,结合题意,利用圆的到直线的距离,半径,|QM|满足勾股定理,求出|QM|就是最小值.解答:解:(1)设P点的坐标为(x,y),∵两定点A(﹣3,0),B(3,0),动点P满足|PA|=2|PB|,∴(x+3)2+y2=4[(x﹣3)2+y2],即(x﹣5)2+y2=16.所以此曲线的方程为(x﹣5)2+y2=16.(2)∵(x﹣5)2+y2=16的圆心坐标为M′(5,0),半径为4,则圆心M′到直线l1的距离为:=4,∵点Q在直线l1:x+y+3=0上,过点Q的直线l2与曲线C(x﹣5)2+y2=16只有一个公共点M,∴|QM|的最小值为:=4.点评:考查两点间距离公式及圆的性质,着重考查直线与圆的位置关系,勾股定理的应用,考查计算能力,转化思想的应用,属于难题.22.(12分)设函数f(x)=x3+ax2﹣a2x+5(a>0)(1)当函数f(x)有两个零点时,求a的值;(2)若a∈[3,6],当x∈[﹣4,4]时,求函数f(x)的最大值.考点:利用导数研究函数的极值;利用导数求闭区间上函数的最值.专题:计算题;分类讨论.分析:(1)由题意得f′(x)=3(x﹣)(x+a)(a>0),所以函数f(x)的增区间为(﹣∞,﹣a),(,+∞),减区间为(﹣a,),所以函数f(x)有两个零点,当且仅当f (﹣a)=0或f()=0,因为a>0所以a=3.(2)由题知﹣a∈[﹣6,﹣3],∈[1,2],当4≤a≤6时,因为函数f(x)在[﹣4,)上单调递减,在(,4]上单调递增,所以f(﹣4)﹣f(4)=8(a2﹣16)≥0,所以f(x)2+16a+69;max=f(﹣4)=4a2+16a﹣59,同理得当3≤a<4时,f(x)max=f(4)=﹣4a解答:解:(1)由题意得f′(x)=3x2+2ax﹣a2=3(x﹣)(x+a)(a>0),由f′(x)>0得x<﹣a,或x>,由f′(x)<0得﹣a<x<,所以函数f(x)的增区间为(﹣∞,﹣a),(,+∞),减区间为(﹣a,),即当x=﹣a时,函数取极大值f(﹣a)=a3+5,当x=时,函数取极小值f()=﹣+5,又f(﹣2a)=﹣2a3+5<f(),f(2a)=10a3+5>f(﹣a),所以函数f(x)有两个零点,当且仅当f(﹣a)=0或f()=0,注意到a>0,所以f()=﹣=0,即a=3.故a的值是3.(2)由题知﹣a∈[﹣6,﹣3],∈[1,2],当﹣a≤﹣4即4≤a≤6时,函数f(x)在[﹣4,)上单调递减,在(,4]上单调递增,注意到f(﹣4)﹣f(4)=8(a2﹣16)≥0,所以f(x)max=f(﹣4)=4a2+16a﹣59;当﹣a>﹣4即3≤a<4时,函数f(x)在[﹣4,﹣a)上单调增,在(﹣a,)上单调减,在(,4]上单调增,注意到f(﹣a)﹣f(4)=a3+4a2﹣16a﹣64=(a+4)2(a﹣4),所以f(x)max=f(4)=﹣4a2+16a+69;综上,f(x)max=.点评:本题考查利用导数解决极值问题通过极值求出参数,利用参数的范围与定义域的关系讨论函数的单调性,进而得到函数的最大值.本题利用了分类讨论的思想这是数学上的一个很主要的数学思想.。
江苏省宿迁市沭阳银河学校2014-2015学年高二12月月考试卷 数学
江苏省宿迁市沭阳银河学校2014-2015学年高二12月月考试卷 数学12月11日一、填空题:本大题共10小题,每小题4分,共计40分.请把答案填写在答题卡相应位置上......... 1. “1>x ”是“12>x ”的 ▲ 条件.(填“充分不必要”、“必要不充分”、“充分必要”、“既不充分也不必要”之一)2. 已知椭圆中心在原点,一个焦点为(3,0),且长轴长是短轴长的2倍,则该椭圆的标准方程是 ▲ .3. 底面边长为2,侧棱与底面成60︒的正四棱锥的侧面积为 ▲ .4. 在平面直角坐标系xOy中,已知y =是双曲线22221x y a b-=的一条渐近线方程,则此双曲线的离心率为 ▲ .5.已知空间四边形OABC 中,OA =a ,OB =b , OC =c , 点M 在OA 上,且OM =2MA ,N 为BC 的中点,则MN = ▲ .6. 过抛物线)0(2>=a ax y 的焦点F 作一条直线交抛物线于P Q 、两点,若线段PF 与FQ 的长分别是p 、q ,则=+qp 11 ▲ . 7. 已知A ,B ,C 的坐标分别为(0,1,0),(-1,0,-1),(2,1,1),点P 的坐标是(,0,)x y ,若PA ABC ⊥平面,则点P 的坐标是 ▲ .8. 如图边长为a 的等边三角形ABC 的中线AF 与中位线DE 交于点G ,已知△A 'DE 是△ADE 绕DE 旋转过程中的一个图形(点A '∉平面ABC ),则下列命题中正确的是 ▲ .①动点A ' 在平面ABC 上的射影在线段AF 上; ②BC ∥平面A 'DE ;③三棱锥A '-FED 的体积有最大值. 9. 设椭圆x 2a 2+y 2b 2 = 1(a >b >0)恒过定点A (1,2),则椭圆的中心到准线距离的最小值是 ▲ .10. 一个三棱柱恰好可放入一个正四棱柱的容体中,底面如图所示,其中三棱柱的底面AEF 是一个直角三角形,∠AEF = 90︒,AE = a ,EF = b ,三棱柱的高与正四棱柱的高均为1,则此正四棱柱的体积为 ▲ .作答,二、解答题:本大题共6小题,共计60分.请在答题卡指定区域.......内解答时应写出文字说明、证明过程或演算步骤. 11. (本题满分8分)FEDCBA抛物线的顶点在原点,对称轴为y 轴,它与圆229x y +=相交,公共弦MN的长为方程,并写出它的焦点坐标与准线方程.12. (本题满分8分) 已知12a >且1a ≠.条件p :函数(21)()l og a f x x -=在其定义域上是减函数;条件q :函数()g x =的定义域为R .如果p ∨q 为真,试求a 的取值范围.13. (本题满分10分)已知0a >,命题:0,2a p x x x ∀>+≥恒成立;命题:,q k R ∀∈直线20kx y -+=与椭圆2221y x a+=有公共点.是否存在正数a ,使得p q ∧为真命题,若存在,请求出a 的范围,若不存在,请说明理由.14. (本题满分10分)在如图所示的几何体中,四边形ABCD 是等腰梯形,AB ∥CD , ∠DAB=60°,FC ⊥平面ABCD ,AE ⊥BD ,CB=CD=CF . (Ⅰ)求证:BD ⊥平面AED ; (Ⅱ)求二面角F-BD-C 的余弦值.15.(本题满分12分)在直三棱柱ABC - A 1B 1C 1中,AB = AC = AA 1 = 3a , BC = 2a ,D 是BC 的中点,E ,F 分别是A 1A ,C 1C 上一点,且AE = CF = 2a .(1)求证:B 1F ⊥平面ADF ; (2)求三棱锥B 1 - ADF 的体积; (3)求证:BE ∥平面ADF .A FC B 1111 1 1.16. (本题满分12分)已知椭圆E :()222210x y a b a b=>>+的离心率为12,右焦点为F ,且椭圆E 上的点到点F 距离的最小值为2.(1)求椭圆E 的方程;(2)设椭圆E 的左、右顶点分别为A 、B ,过点A 的直线l 与椭圆E 及直线8x =分别相交于点M 、N . ① 当过A 、F 、N 三点的圆半径最小时,求这个圆的方程;② 若cos AMB ∠=ABM △的面积.2013年12月高二数学理科试题参考答案1.充分不必要 2.2214x y += 3. 4.2 5.23-a 12+b 12+c 6.4a 7.(1,0,2)- 8.①②③ 9. 2+5. 10.422()a a ab +-11.解:由题意,抛物线方程为22(0).x ay a =≠设公共弦MN 交y 轴于点A ,则3ON =,2,2).OA N ∴==∴±N 点在抛物线上,52(2),a ∴=⋅±即522a =±,故抛物线的方程为252x y =或25.2x y =-……………4分 抛物线252x y =的焦点坐标为5(0,),8准线方程为58y =-.抛物线252x y =-的焦点坐标为5(0,),8-准线方程为58y =.……………8分12.解:若p 为真,则0211a <-<,得112a <<.……………2分若q 为真,则20x x a +--≥对x R ∀∈恒成立.记()2f x x x a =+--,则22,,()2,,x a x af x a x a --≥⎧=⎨-<⎩所以()f x 的最小值为2a -,故q 为真即为20a -≥,即2a ≥.……………6分于是p q ∨为真,即为“112a <<或2a ≥”故a 的取值范围为[1(,1)2,)2+∞.……8分 13.解:对0x ∀>,a x x +≥,(0a >),所以要使2ax x+≥恒成立,应有2, 1.a ≥∴≥……………4分k R ∀∈,直线20kx y -+=恒过定点(0,2),要使直线20kx y -+=与椭圆2221y x a+=有公共点,应有222201a +≤,解得 2.a ≥若p q ∧为真命题,则p 与q 都为真命题,因此1,2a a ≥⎧⎨≥⎩所以 2.a ≥ ……………8分综上,存在 2.a ≥使得p q ∧为真命题.……………10分 14.解析:(Ⅰ)在等腰梯形ABCD 中,AB ∥CD ,∠DAB=60°,CB=CD, 由余弦定理可知202223)180cos(2CD DAB CB CD CB CD BD =∠-⋅⋅-+=, 即AD CD BD 33==,在ABD ∆中,∠DAB=60°,AD BD 3=,则ABD ∆为直角三角形,且DB AD ⊥.又AE ⊥BD ,⊂AD 平面AED ,⊂AE 平面AED ,且A AE AD = ,故BD ⊥平面AED ;……………5分(Ⅱ)由(Ⅰ)可知CB AC ⊥,设1=CB ,则3==BD CA ,建立如图所示的空间直角坐标系,)0,21,23(),0,1,0(),01,0(-D B F ,向量)1,0,0(=为平面BDC 的一个法向量. 设向量),,(z y x =为平面BDF 的法向量,则⎪⎩⎪⎨⎧=⋅=00m ,即⎪⎩⎪⎨⎧=-=-02323z y y x ,取1=y ,则1,3==z x ,则)1,1,3(=为平面BDF 的一个法向量.5551,cos ==>=<,而二面角F-BD-C 的平面角为锐角,则 二面角F-BD-C 的余弦值为55.……………10分 15.(1)证明:∵AB = AC ,D 为BC 中点,∴AD ⊥BC .在直三棱柱ABC - A 1B 1C 1中,∵B 1B ⊥底面ABC ,AD ⊂底面ABC ,∴AD ⊥B 1B . ∵BC B 1B = B ,∴AD ⊥平面B 1BCC 1.∵B 1F ⊂平面B 1BCC 1,∴AD ⊥B 1F .在矩形B 1BCC 1中,∵C 1F = CD = a ,B 1C 1 = CF = 2a , ∴Rt △DCF ≌ Rt △FC 1B 1.∴∠CFD = ∠C 1B 1F .∴∠B 1FD = 90°.∴B 1F ⊥FD . ∵AD FD = D ,∴B 1F ⊥平面AFD .……………6分 (2)∵B 1F ⊥平面AFD ,∴1113B ADF ADF V S B F -=⋅⋅△=11132AD DF B F ⨯⨯⨯⨯=(3)连EF ,EC ,设EC AF M =,连DM ,2AE CF a ==,∴四边形AEFC 为矩形,M ∴为EC 中点. D 为BC 中点,//MD BE ∴.M D ⊂平面ADF ,.BE ⊄平面ADF ,//BE ∴平面ADF ……………12分 16.解:⑴由已知,12c a =,且2a c -=,所以4a =,2c =,所以22212b a c =-=,所以椭圆E 的方程为2211612x y =+.………………………4分 ⑵(ⅰ)由⑴,(4,0)A -,(2,0)F ,设(8,)N t .设圆的方程为220x y dx ey f =++++,将点,,A F N 的坐标代入,得21640,420,6480,d f d f t d et f ⎧-=⎪=⎨⎪=⎩+++++++解得2,72,8,d e t t f =⎧⎪⎪=--⎨⎪=-⎪⎩…………………………6分 所以圆的方程为22722()80x y x t y t--=+++, 即222172172(1)[()]9()24x y t t t t-=+++++,因为2272()t t +≥,当且仅当72t t=±+故所求圆的方程为22280x y x ±-=++.……………………………8分 (ⅱ)由对称性不妨设直线l 的方程为(4)(0)y k x k =>+.由22(4),1,1612y k x x y =⎧⎪⎨=⎪⎩++得222121624(,)3434k k M k k -++,……………………………9分 所以222424(,)3434kMA k k--=++,2223224(,)3434k k MB k k -=++, A FCBDC B 111E1 1 1 AM所以cos 24MA MB AMB MA MB∠===, 化简,得42164090k k -+=,……………………………………10分解得214k =,或294k =,即12k =,或32k =, 此时总有3M y =,所以ABM △的面积为183122⨯⨯=.…………………………12分。
高二数学月考试题及答案-故城县高级中学2014-2015学年高二12月月考
一. 选择题1.命题“21cos ,≥∈∀x R x ”的否定是( )A 21cos ,≥∈∃x R x B 21cos ,>∈∃x R xC 21cos ≥∈∀x R , D 21cos ,>∈∀x R x2.若p 是真命题,q 是假命题,则( )A 是真命题q p ∧B 是假命题q p ∨C 真命题p ⌝D 真命题q ⌝3.椭圆 的焦距等于13610022=+y x ( )A 20B 8C 12D 164.双曲线的离心率为1222=-y x ( ) A 26B 2C 3D 225.“p 且q 是真命题”,是“非p 为假命题”的( )A 充分而不必要条件B 必要而不充分条件C 充要条件D 既不充分也不必要条件6.椭圆1422=+y m x 的焦距为2,则m 的值为( )A 6或2B 5C 3或5D 1或97.双曲线112422=-y x 的焦点到渐近线的距离为( )A 32B 2C 3D 18.两个正数a,b 的等差中项是25,一个等比中项是6,且a>b ,则椭圆等于的离心率e b y a x 12222=+( )A 313B 13C 35D 239.已知双曲线的渐近线方程为x y 3±=,焦点坐标为(-4,0),(4,0),则双曲线方程为( )A 124822=-y xB 1141222=-y xC 182422=-y xD 112422=-y x 10.已知双曲线C:116922=-y x 的左,右焦点分别为21,F F ,P 为C 右支上一点,且212F F PF =,则21F PF ∆的面积等于( )A 24B 36C 48D 9611.已知条件p :1>x ,条件q: 2-<x ,则的是q p ⌝⌝( )A 充分而不必要条件B 必要而不充分条C 充要条件D 既不充分也不必要条件12.设[]πα,0∈,则方程1cos sin 22=+ααy x 不能表示的曲线为( )A 椭圆B 双曲线C 抛物线D 圆13. 设11625,2221=+y x F F 分别是椭圆的左,右焦点,P 为椭圆上一点,M 是P F 1的中点, 3=OM ,则P 点到椭圆左焦点的距离为( )A 2 B 3 C 4 D 514.若点O 和点F 分别为椭圆 13422=+y x 的中心和左焦点,点P 位椭圆上的任意一点,则∙的最大值为( )A 2B 3C 6D 8卷II二.填空题15.命题P :若22,22<<-<x x 则.则P 的否命题是,命题非P 是 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2014年秋期高二年级数学科考试题
考试时间:120分钟,总分:150分
一、选择题(每题5分,12题,共60分):
1、若α是第四象限的角,则πα-是( )
A.第一象限的角
B.第二象限的角
C.第三象限的角
D.第四象限的角
2、等差数列32,12-,52-,92
-,…的一个通项公式是( ) A .122n - B .322n - C .722n - D .322
n + 3、已知4sin 5α=,并且α是第二象限的角,那么tan α的值等于( ) A.4
3- B.3
4- C.43
D.3
4
4、02120sin 等于( )
A .23±
B .23
C .23-
D .2
1 5、已知向量a ,b 满足1=a ,4=b ,且2⋅=a b ,则a 与b 的夹角为( ).
A .
6π B .4π C .3π D .2
π 6、在△ABC 中,若B a b sin 2=,则A 等于( )
A .006030或
B .006045或
C .0060120或
D .0015030或 7、在等差数列{}n a 中,若34567450a a a a a ++++=,则28a a +的值等于( )
A .45
B .75
C .180
D .300 8、C ∆AB 中,三内角A 、B 、C 成等差数列,则∠B =( )
A .30
B .60
C .90
D .120 9、2000是等差数列4,6,8,…的( )
A .第998项
B .第999项
C .第1001项
D .第1000项
10、在数列{}n a 中,S n =2n 2-3n(n ∈N *),则a 4等于 ( )
A .- 1
B .- 5
C .7
D .2
11、等比数列{}n a 中, ,243
,952==a a 则{}n a 的第4项为( ) A .81 B .243 C .27 D .192
12、在等差数列{}n a 中,2483=+a a ,则S 10等于 ( )
A .48 B.240 C.60 D.120
二、填空题(共4题,每小题5分,共20分):
13、一个等差数列1533a =,2566a =,则35a =___________
14、14、在等比数列{}n a 中,若101,a a 是方程06232=--x x 的两根则47a a ⋅=___________.
15、若数列{}n a 满足:111,2()n n a a a n N *+==∈,则5a =
16、在等比数列}{n a 中,已知为则公比q a a ,8,141==____________
三、解答题:(本大题共6小题,共70分。
解答过程应写出文字说明,证明过程或演算步骤。
)
17、(12分)在等差数列{}n a 中,已知510a =,12
31a =,求20a ,10s
18、(10分)在各项均为正数的等比数列{}n a 中,10,3312=+=a a a ,求n a
19、(10分)已知数列{n a }的前n 项和n S ,22+=n s n (n 为正整数),
求:数列{n a }的通项公式;
.
20、(10分)若等差数列{a n }中,S n 是{a n }的前n 项和,S 6=7,S 15=16,求a 11。
21、(14分)已知函数1cos sin 32cos 2)(2-+=x x x x f (R x ∈).
(1)化简函数)(x f 的表达式,并求函数)(x f 的最小正周期;
(2)当]2
,0[π∈x 时,求函数)(x f 的值域。
22、(14分)在ABC △中,5cos 13A =-,3cos 5
B =. (Ⅰ)求sin
C 的值;
(Ⅱ)设5BC =,求ABC △的面积.。
