2020届高三数学立体几何专项训练(文科)

2020届高三数学立体几何专题(文科)

吴丽康2019-11

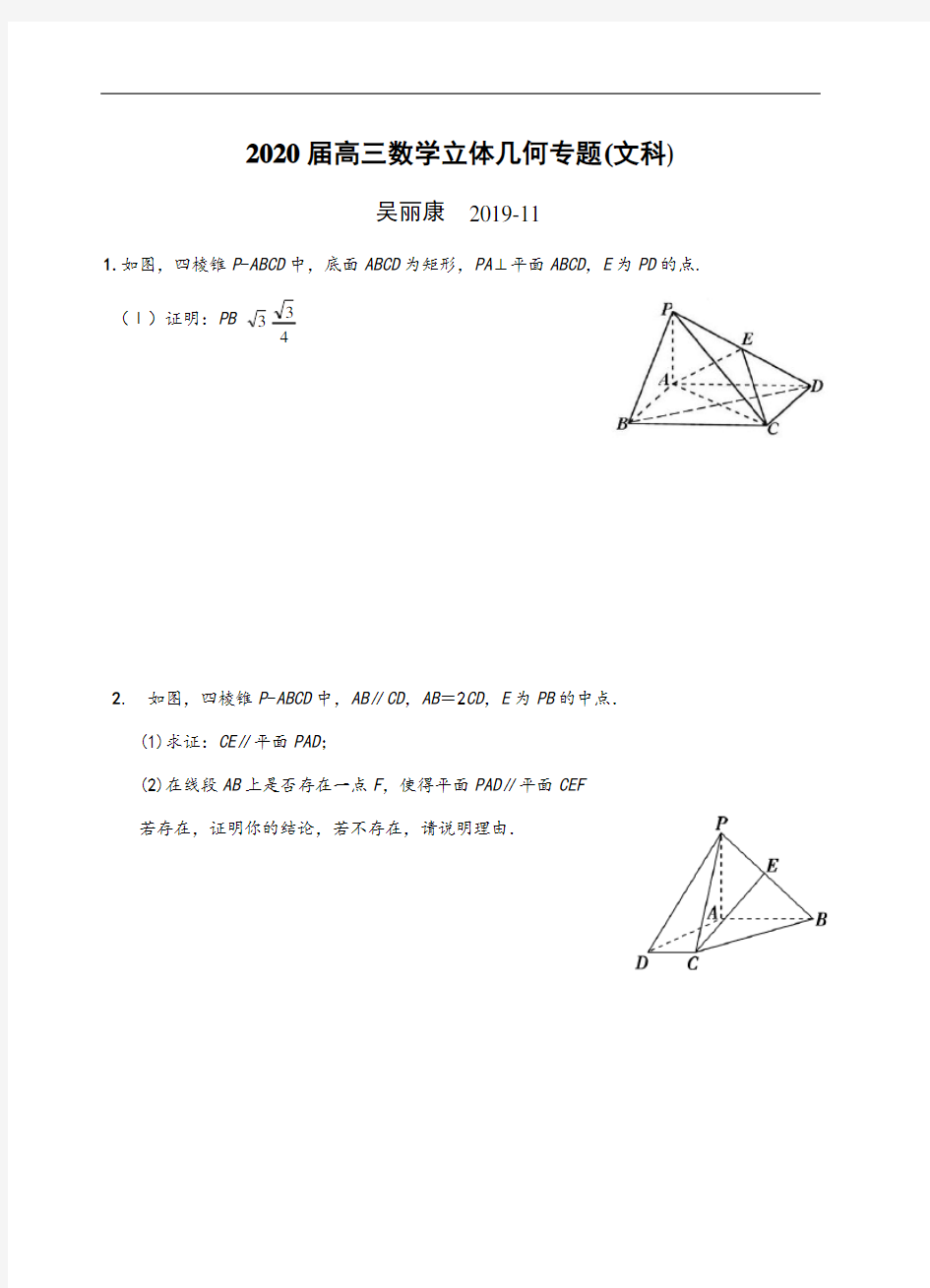
1.如图，四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD，E为PD的点.

（Ⅰ）证明：PB 3

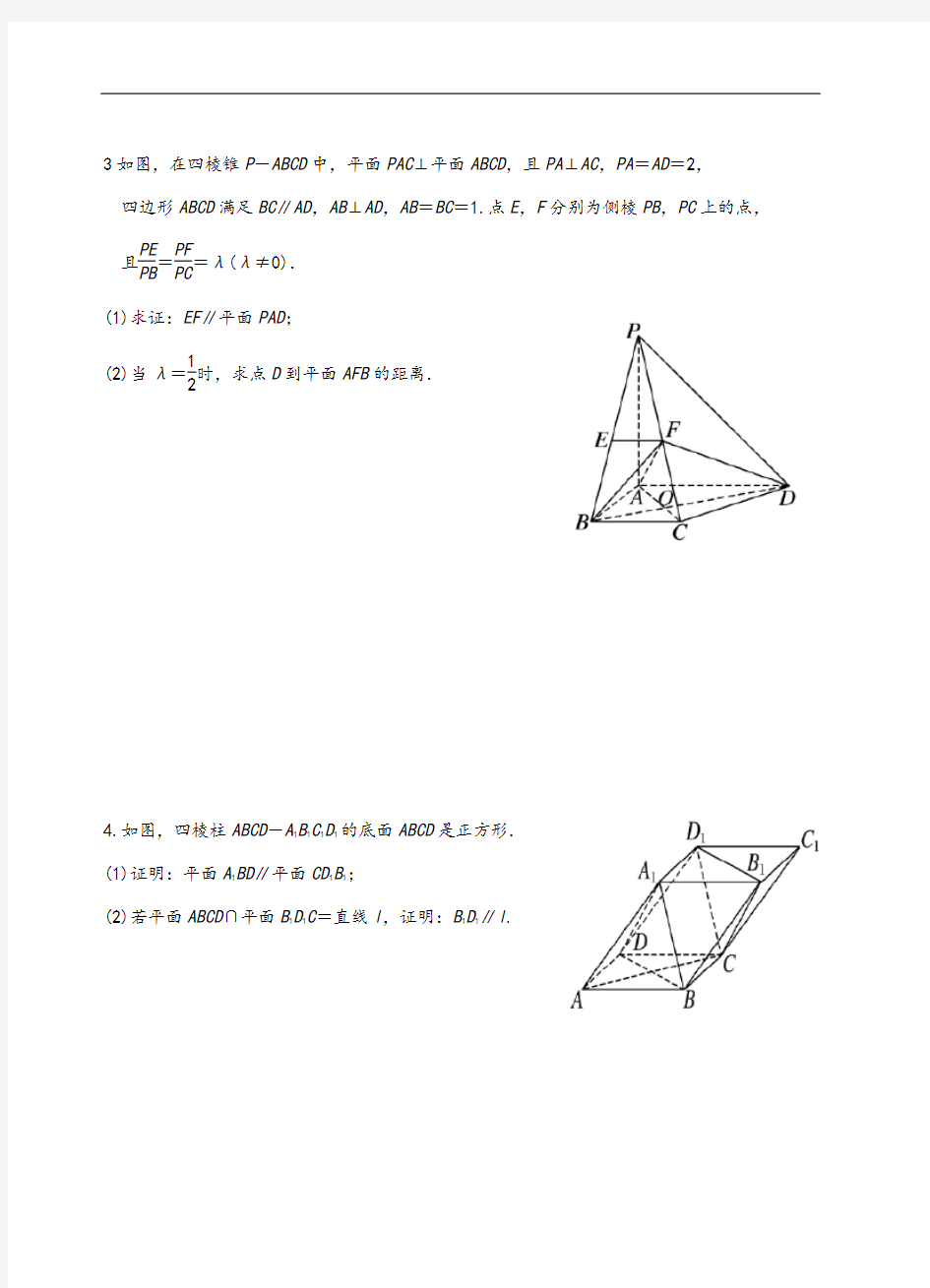
2. 如图，四棱锥P-ABCD中，AB∥CD，AB＝2CD，E为PB的中点．

(1)求证：CE∥平面PAD；

(2)在线段AB上是否存在一点F，使得平面PAD∥平面CEF

若存在，证明你的结论，若不存在，请说明理由．

3如图，在四棱锥P －ABCD 中，平面PAC ⊥平面ABCD ，且PA ⊥AC ，PA ＝AD ＝2，四边形ABCD 满足BC ∥AD ，AB ⊥AD ，AB ＝BC ＝1.点E ，F 分别为侧棱PB ，PC 上的点，且

PE PB ＝PF

＝λ(λ≠0)． (1)求证：EF ∥平面PAD ； (2)当λ＝1

2时，求点D 到平面AFB 的距离．

4.如图，四棱柱ABCD －A 1B 1C 1D 1的底面ABCD 是正方形． (1)证明：平面A 1BD ∥平面CD 1B 1；

(2)若平面ABCD ∩平面B 1D 1C ＝直线l ，证明：B 1D 1∥l .

5..如图，四边形ABCD是平行四边形，点P是平面ABCD外一点，

M是PC的中点，在DM上取一点G，过G和AP作平面交平面BDM于GH.求证：AP∥GH.

6.如图，在四棱锥P-ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，

∠ABC＝60°，PA＝AB＝BC，E是PC的中点．

证明：(1)CD⊥AE；(2)PD⊥平面ABE.

7.(2018北京通州三模,18)如图,在四棱锥P-ABCD中,平面PAB⊥平面ABCD,四边形ABCD

为正方形,△PAB为等边三角形,E是PB中点,平面AED与棱PC交于点F.

(1)求证:AD∥EF; (2)求证:PB⊥平面AEFD;

(3)记四棱锥P-AEFD的体积为V1,四棱锥P-ABCD的体积为V2,直接写出的值.

8...如图，在四棱锥P-ABCD中，底面ABCD是∠DAB＝60°且边长为a的菱形，

侧面PAD为正三角形，其所在平面垂直于底面ABCD，若G为AD的中点．

(1)求证：BG⊥平面PAD；

(2)求证：AD⊥PB；

(3)若E为BC边的中点，能否在棱PC上找到一点F，使平面DEF⊥平面ABCD

并证明你的结论．

9.(2016·高考北京卷)如图，在四棱锥P-ABCD中，PC⊥平面ABCD，AB∥DC，DC⊥AC.

(1)求证：DC⊥平面PAC；

(2)求证：平面PAB⊥平面PAC；

(3)设点E为AB的中点．在棱PB上是否存在点F，

使得PA∥平面CEF说明理由．

10..如图，在四棱锥P－ABCD中，底面ABCD是矩形，点E在棱PC上(异于点P，C)，

平面ABE 与棱PD 交于点F . (1)求证：AB ∥EF ；

(2)若AF ⊥EF ，求证：平面PAD ⊥平面ABCD .

11..如图，在四棱锥P －ABCD 中，PA ⊥平面ABCD ，PA ＝AB ＝BC ＝3，AD ＝CD ＝1， ∠ADC ＝120°，点M 是AC 与BD 的交点，点N 在线段PB 上，且PN ＝1

4PB .

(1)证明：MN ∥平面PDC ；

(2)求直线MN 与平面PAC 所成角的正弦值．

12..(2016·高考四川卷)如图，在四棱锥P ABCD 中，PA ⊥CD ，AD ∥BC ，

∠ADC ＝∠PAB ＝90°，BC ＝CD ＝1

AD ．

(1)在平面PAD 内找一点M ，使得直线CM ∥平面PAB ，并说明理由； (2)证明：平面PAB ⊥平面PBD ．

13．(2016·高考江苏卷)如图，在直三棱柱ABC

A 1

B 1

C 1中，

D ，

E 分别为AB ，BC

的中点，点F 在侧棱B 1B 上，且B 1D ⊥A 1F ，A 1C 1⊥A 1B 1. 求证：(1)直线DE ∥平面A 1C 1F ；

(2)平面B 1DE ⊥平面A 1C 1F .

14.【2014,19】如图，三棱柱111C B A ABC -中，

侧面C C BB 11为菱形，C B 1的中点为O ，且⊥AO 平面C C BB 11. （1）证明：;1AB C B ⊥

（2）若1AB AC ⊥,,1,601==∠BC CBB 求三棱柱111C B A ABC -的高.

15.(2017天津,文17)如图,在四棱锥P-ABCD 中,AD⊥平面PDC,AD ∥ BC, PD⊥PB, AD=1,BC=3,CD=4,PD=2. (1)求异面直线AP 与BC 所成角的余弦值; (2)求证:PD⊥平面PBC;

(3)求直线AB 与平面PBC 所成角的正弦值.

16.(2016·高考浙江卷)如图，在三棱台ABC DEF中，平面BCFE⊥平面ABC，∠ACB＝90°，BE＝EF＝FC＝1，BC＝2，AC＝3.

(1)求证：BF⊥平面ACFD；

(2)求直线BD与平面ACFD所成角的余弦值．

17..(2018·全国Ⅲ)如图，矩形ABCD所在平面与半圆弧CD所在平面垂直，

M是CD上异于C，D的点．

(1)证明：平面AMD⊥平面BMC.

(2)在线段AM上是否存在点P，使得MC∥平面PBD说明理由．

立体几何中的翻折问题

18...如图(1)，在直角梯形ABCD 中，AD ∥BC ，∠BAD ＝π2，AB ＝BC ＝1

AD ＝a ，

E 是AD 的中点，O 是AC 与BE 的交点．将△ABE 沿BE 折起到图(2)中△A 1BE 的位置，得到

四棱锥A 1-BCDE .

(1)证明：CD ⊥平面A 1OC ；

(2)当平面A 1BE ⊥平面BCDE 时，四棱锥A 1-BCDE 的体积为362，求a 的值．

19.．如图1，在直角梯形ABCD 中，∠ADC ＝90°，AB ∥CD ，AD ＝CD ＝1

AB ＝2，

E 为AC 的中点，将△ACD 沿AC 折起，使折起后的平面ACD 与平面ABC 垂直，

如图2.在图2所示的几何体D －ABC 中： (1)求证：BC ⊥平面ACD ；

(2)点F 在棱CD 上，且满足AD ∥平面BEF ，求几何体F －BCE 的体积．

20．如图，长方体ABCD -A 1B 1C 1D 1中，AB ＝16，BC ＝10，AA 1＝8.点E ，F 分别在A 1B 1，D 1C 1上，过点E 、F 的平面α与此长方体的面相交，交线围成一个正方形EFGH . (1)求证：A 1E ＝D 1F ；

(2)判断A 1D 与平面α的关系．

2020届高三数学立体几何专题(文科)

1解析：（Ⅰ）设AC 的中点为O ，连接EO . 在三角形PBD 中，中位线EO

（Ⅱ）∵AP =1，3AD =，-3

P ABD V =

， -11=32P ABD V PA AB AD ∴???33=

=64AB ，∴3

AB =，作AH ⊥PB 角PB 于H ，

由题意可知BC ⊥平面PAB ，∴BC ⊥AH ，故AH ⊥平面PBC ．又313

PA AB AH PB ?=

，故A 点到平面PBC 的距离313. 2.(1)证明：如图所示，取PA 的中点H ，连接EH ，DH ，

因为E 为PB 的中点，所以EH ∥AB ，EH ＝1

2AB ，

又AB ∥CD ，CD ＝1

2AB ．所以EH ∥CD ，EH ＝CD ，

因此四边形DCEH 是平行四边形，所以CE ∥DH ，又DH ?平面PAD ，CE ?平面PAD ，所以CE ∥平面PAD ．

(2)如图所示，取AB 的中点F ，连接CF ，EF ，所以AF ＝1

AB ，

又CD ＝1

2AB ，所以AF ＝CD ，又AF ∥CD ，所以四边形AFCD 为平行四边形，所以CF ∥AD ，

又CF ?平面PAD ，所以CF ∥平面PAD ，

由(1)可知CE ∥平面PAD ，又CE ∩CF ＝C ，故平面CEF ∥平面PAD ，故存在AB 的中点F 满足要求．

3.(1)证明 ∵PE PB ＝PF

＝λ(λ≠0)，∴EF ∥BC .∵BC ∥AD ，∴EF ∥AD .

又EF ?平面PAD ，AD ?平面PAD ，∴EF ∥平面PAD . (2)解 ∵λ＝1

，∴F 是PC 的中点，

在Rt△PAC 中，PA ＝2，AC ＝2，∴PC ＝PA 2

＋AC 2

＝6，

∴PF ＝12PC ＝6

.∵平面PAC ⊥平面ABCD ，且平面PAC ∩平面ABCD ＝AC ，

PA ⊥AC ，PA ?平面PAC ，∴PA ⊥平面ABCD ，∴PA ⊥BC .

又AB ⊥AD ，BC ∥AD ，∴BC ⊥AB ，又PA ∩AB ＝A ，PA ，AB ?平面PAB ， ∴BC ⊥平面PAB ， ∴BC ⊥PB ，∴在Rt△PBC 中，BF ＝12PC ＝6

连接BD ，DF ，设点D 到平面AFB 的距离为d ，在等腰三角形BAF 中，BF ＝AF ＝

，AB ＝1， ∴S △ABF ＝

，又S △ABD ＝1，点F 到平面ABD 的距离为1， ∴由V F －ABD ＝V D －AFB ，得13×1×1＝13×d ×54，解得d ＝455，即点D 到平面AFB 的距离为45

4.证明(1)由题设知BB1∥DD1且BB1＝DD1，

所以四边形BB1D1D是平行四边形，

所以BD∥B1D1.又BD?平面CD1B1，B1D1?平面CD1B1，

所以BD∥平面CD1B1.因为A1D1∥B1C1∥BC且A1D1＝B1C1＝BC，

所以四边形A1BCD1是平行四边形，所以A1B∥D1C.

又A1B?平面CD1B1，D1C?平面CD1B1，所以A1B∥平面CD1B1.

又因为BD∩A1B＝B，BD，A1B?平面A1BD，所以平面A1BD∥平面CD1B1.

(2)由(1)知平面A1BD∥平面CD1B1，又平面ABCD∩平面B1D1C＝直线l，

平面ABCD∩平面A1BD＝直线BD，所以直线l∥直线BD，

在四棱柱ABCD－A1B1C1D1中，四边形BDD1B1为平行四边形，

所以B1D1∥BD，所以B1D1∥l.

5.连接AC交BD于点O，连接MO，因为PM＝MC，AO＝OC，所以PA∥MO，

因为PA?平面MBD，MO?平面MBD，所以PA∥平面MBD．

因为平面PAHG∩平面MBD＝GH，所以AP∥GH.

6.[证明] (1)在四棱锥P-ABCD中，因为PA⊥底面ABCD，CD?平面ABCD，所以PA⊥CD，因为AC⊥CD，且PA∩AC＝A，

所以CD⊥平面PAC，而AE?平面PAC，所以CD⊥AE.

(2)由PA＝AB＝BC，∠ABC＝60°，可得AC＝PA.

因为E是PC的中点，所以AE⊥PC.

由(1)知AE⊥CD，且PC∩CD＝C，所以AE⊥平面PCD．

而PD?平面PCD，所以AE⊥PD．

因为PA⊥底面ABCD，所以PA⊥AB．

又因为AB⊥AD且PA∩AD＝A，

所以AB⊥平面PAD，而PD?平面PAD，所以AB⊥PD．

又因为AB∩AE＝A，所以PD⊥平面ABE.

7.(1)证明因为ABCD为正方形,所以AD∥BC.

因为AD?平面PBC,BC?平面PBC,所以AD∥平面PBC.

因为AD?平面AEFD,平面AEFD∩平面PBC=EF, 所以AD∥EF.

(2)证明因为四边形ABCD是正方形,所以AD⊥AB.

因为平面PAB⊥平面ABCD,平面PAB∩平面ABCD=AB,AD?平面ABCD,

所以AD⊥平面PAB.因为PB?平面PAB,所以AD⊥PB.

因为△PAB为等边三角形,E是PB中点,所以PB⊥AE.

因为AE?平面AEFD,AD?平面AEFD,AE∩AD=A,所以PB⊥平面AEFD.

(3)解由(1)知,V1=V C-AEFD,V E-ABC=V F-ADC=V C-AEFD=V1,

∴V BC-AEFD=V1,则V P-ABCD=V1+V1=V1, ∴.

8.[解] (1)证明：在菱形ABCD中，∠DAB＝60°，G为AD的中点，所以BG⊥AD．

又平面PAD⊥平面ABCD，平面PAD∩平面ABCD＝AD，

所以BG⊥平面PAD．

(2)证明：如图，连接PG.因为△PAD为正三角形，G为AD的中点，

所以PG⊥AD．

由(1)知，BG⊥AD，又PG∩BG＝G，所以AD⊥平面PGB．

因为PB?平面PGB，所以AD⊥PB．

(3)当F为PC的中点时，满足平面DEF⊥平面ABCD．

证明如下：取PC的中点F，连接DE、EF、DF.

在△PBC中，FE∥PB，在菱形ABCD中，GB∥DE.

而FE?平面DEF，DE?平面DEF，EF∩DE＝E，PB?平面PGB，GB?平面PGB，

PB∩GB＝B，所以平面DEF∥平面PGB．

因为BG⊥平面PAD，PG?平面PAD，所以BG⊥PG.

又因为PG⊥AD，AD∩BG＝G，所以PG⊥平面ABCD．

又PG?平面PGB，所以平面PGB⊥平面ABCD，

所以平面DEF⊥平面ABCD．

9.【解】(1)证明：因为PC⊥平面ABCD，所以PC⊥DC.

又因为DC⊥AC，且PC∩AC＝C，所以DC⊥平面PAC.

(2)证明：因为AB∥DC，DC⊥AC，所以AB⊥AC.

因为PC⊥平面ABCD，所以PC⊥AB．又因为PC∩AC＝C，

所以AB⊥平面PAC.又AB?平面PAB，所以平面PAB⊥平面PAC.

(3)棱PB上存在点F，使得PA∥平面CEF.

理由如下：

如图，取PB中点F，连接EF，CE，CF.又因为E为AB的中点，所以EF∥PA.

又因为PA?平面CEF，且EF?平面CEF，所以PA∥平面CEF.

10.证明(1)因为四边形ABCD是矩形，所以AB∥CD. 又AB?平面PDC，CD?平面PDC，所以AB∥平面PDC，

又因为AB?平面ABE，平面ABE∩平面PDC＝EF，所以AB∥EF.

(2)因为四边形ABCD 是矩形，所以AB ⊥AD . 因为AF ⊥EF ，(1)中已证AB ∥EF ，所以AB ⊥AF .

又AB ⊥AD ，由点E 在棱PC 上(异于点C )，所以点F 异于点D ，所以AF ∩AD ＝A ，AF ，AD ?平面PAD ，

所以AB ⊥平面PAD ，又AB ?平面ABCD ，所以平面PAD ⊥平面ABCD . 11.(1)证明因为AB ＝BC ，AD ＝CD ，所以BD 垂直平分线段AC . 又∠ADC ＝120°，所以MD ＝12AD ＝12，AM ＝3

2. 所以AC ＝

又AB ＝BC ＝3，所以△ABC 是等边三角形，

所以BM ＝32，所以BM MD ＝3，又因为PN ＝14PB ，所以BM MD ＝BN

NP ＝3，所以MN ∥PD .

又MN ?平面PDC ，PD ?平面PDC ，所以MN ∥平面PDC .

(2)解因为PA ⊥平面ABCD ，BD ?平面ABCD ，所以BD ⊥PA ，又BD ⊥AC ，PA ∩AC ＝A ，PA ，AC ?平面PAC ，所以BD ⊥平面PAC .

由(1)知MN ∥PD ，所以直线MN 与平面PAC 所成的角即直线PD 与平面PAC 所成的角，故∠DPM 即为所求的角．在Rt△PAD 中，PD ＝2，

所以sin∠DPM ＝DM DP ＝1

22＝14，所以直线MN 与平面PAC 所成角的正弦值为1

12.【解】 (1)取棱AD 的中点M (M ∈平面PAD )，点M 即为所求的一个点．理由如下：因为AD ∥BC ，BC ＝1

AD ，所以BC ∥AM ，且BC ＝AM ，

所以四边形AMCB 是平行四边形，从而CM ∥AB ．又AB ?平面PAB ，CM ?平面PAB ，所以CM ∥平面PAB ．

(说明：取棱PD 的中点N ，则所找的点可以是直线MN 上任意一点)

(2)证明：由已知，PA ⊥AB ，PA ⊥CD ，因为AD ∥BC ，BC ＝1

2AD ，所以直线AB 与CD 相交．

所以PA ⊥平面ABCD ，从而PA ⊥BD ．连接BM ，因为AD ∥BC ，BC ＝1

AD ，所以BC ∥MD ，且BC ＝MD ．

所以四边形BCDM 是平行四边形．所以BM ＝CD ＝1

2AD ，所以BD ⊥AB ．

又AB ∩AP ＝A ，所以BD ⊥平面PAB ．又BD ?平面PBD ，所以平面PAB ⊥平面PBD ． 13.[证明] (1)在直三棱柱ABC

A 1

B 1

C 1中，A 1C 1∥AC .

在△ABC 中，因为D ，E 分别为AB ，BC 的中点，所以DE ∥AC ，于是DE ∥A 1C 1. 又DE ?平面A 1C 1F ，A 1C 1?平面A 1C 1F ，所以直线DE ∥平面A 1C 1F . (2)在直三棱柱ABC

A 1

B 1

C 1中，A 1A ⊥平面A 1B 1C 1.

因为A 1C 1?平面A 1B 1C 1，所以A 1A ⊥A 1C 1.

又A 1C 1⊥A 1B 1，A 1A ?平面ABB 1A 1，A 1B 1?平面ABB 1A 1，A 1A ∩A 1B 1＝A 1，所以A 1C 1⊥平面ABB 1A 1.因为B 1D ?平面ABB 1A 1，

所以A 1C 1⊥B 1D ．又B 1D ⊥A 1F ，A 1C 1?平面A 1C 1F ，A 1F ?平面A 1C 1F ，A 1C 1∩A 1F ＝A 1，

所以B 1D ⊥平面A 1C 1F .

因为直线B 1D ?平面B 1DE ，所以平面B 1DE ⊥平面A 1C 1F

14.证明：(Ⅰ)连接 BC 1，则O 为B 1C 与BC 1的交点，

∵AO ⊥平面BB 1C 1C . ∴AO ⊥B 1C ， …2分因为侧面BB 1C 1C 为菱形，∴BC 1⊥B 1C ，…4分 ∴BC 1⊥平面ABC 1，∵AB ?平面ABC 1，故B 1C ⊥AB . …6分

(Ⅱ)作OD ⊥BC ，垂足为D ，连结AD ，∵AO ⊥BC ，∴BC ⊥平面AOD ，

又BC ?平面ABC ，∴平面ABC ⊥平面AOD ，交线为AD ，作OH ⊥AD ，垂足为H ，∴OH ⊥平面ABC . …9分 ∵∠CBB 1=60°，所以ΔCBB 1为等边三角形，又BC =1，可得OD =

，由于AC ⊥AB 1，∴11122

OA B C =

=，∴2274AD OD OA =+=，

由 OH·AD=OD·OA ，可得OH=

，又O 为B 1C 的中点，所以点B 1到平面ABC 的距离为

217

，所以三棱柱ABC-A 1B 1C 1的高高为

。 …12分另解(等体积法)：∵∠CBB 1=60°，所以ΔCBB 1为等边三角形，又BC =1，可得BO =

3，由于AC ⊥AB 1，∴11122

OA B C ==，∴AB =1，AC=2

2，…9分则等腰三角形ABC 的面积为221227

1()2248

??-=

，

设点B1到平面ABC的距离为d，由V B1-ABC=V A-BB1C得

73121

8427

d d

=?=

解得，

所以三棱柱ABC-A1B1C1的高高为21

。…12分

15.(1)解如图,由已知AD∥BC,故∠DAP或其补角即为异面直线AP与BC所成的角.因为AD⊥平面PDC, 所以AD⊥PD.

在Rt△PDA中,由已知,得AP=,

故cos∠DAP=.所以,异面直线AP与BC所成角的余弦值为.

(2)证明因为AD⊥平面PDC,直线PD?平面PDC, 所以AD⊥PD.

又因为BC∥AD,所以PD⊥BC.又PD⊥PB,所以PD⊥平面PBC.

(3)解过点D作AB的平行线交BC于点F,连接PF,

则DF与平面PBC所成的角等于AB与平面PBC所成的角.

因为PD⊥平面PBC,故PF为DF在平面PBC上的射影,

所以∠DFP为直线DF和平面PBC所成的角.由于AD∥BC,DF∥AB,故BF=AD=1,

由已知,得CF=BC-BF=2.又AD⊥DC,故BC⊥DC,

在Rt△DCF中,可得DF==2, 在Rt△DPF中,可得sin∠DFP=.

所以,直线AB与平面PBC所成角的正弦值为

16.【解】(1)证明：延长AD，BE，CF相交于一点K，如图所示．

因为平面BCFE⊥平面ABC，且AC⊥BC，所以AC⊥平面BCK，因此BF⊥AC.

又因为EF∥BC，BE＝EF＝FC＝1，BC＝2，

所以△BCK为等边三角形，且F为CK的中点，则BF⊥CK.

近五年高考数学(理科)立体几何题目汇总

高考真题集锦（立体几何部分） 1.(2016.理1）如图是由圆柱和圆锥组合而成的几何体的三视图，则该几何体的表面积是（） A 20π B24π C28π D.32π 2. βα，是两个平面，m,n 是两条直线，有下列四个命题：（1）如果m ⊥n,m ⊥α，n ∥β，那么βα⊥；（2）如果m ⊥α，n ∥α，那么m ⊥n. （3）如果αβα?m ，∥那么m ∥β。（4）如果m ∥n,βα∥，那么m 与α所成的角和n 与β所成的角相等。其中正确的命题有___________ 3.（2016年理1）如图，某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径．若该几何体的体积是π328，则它的表面积是 A 17π B.18π C.20π D.28π 4.平面α过正方体1111D C B A ABCD -的顶点A ，α//平面11D CB ，?α平面ABCD =m ， ?α平面11A ABB =n,则m,n 所成角的正弦值为（） A.23 B.22 C.33 D.3 1 5.（2016年理1）如图，在以A,B,C,D,E,F 为顶点的五面体中，面ABEF 为正方形，AF=2FD ，∠AFD=90°，且二面角D-AF-E 与二面角C-BE-F 都是60° .（12分）（Ⅰ）证明：平面ABEF ⊥平面EFDC ；（Ⅱ）求二面角E-BC-A 的余弦值.

6. (2015年理1）圆柱被一个平面截取一部分后与半球（半径为r ）组成一个几何体，该几何体三视图的正视图和俯视图如图所示，若该几何体的表面积是16+20π，则r=（） A.1 B.2 C.7 D.8 7.如图，四边形ABCD 为菱形，∠ABC=120°，E,F 是平面ABCD 同一侧的亮点，BE ⊥平面ABCD,DF ⊥平面ABCD,BE=2DF,AE ⊥EC. (1) 证明：平面AEC ⊥平面AFC; (2) 求直线AE 与直线CF 所成角的余弦值。 8.一个正方体被一个平面截去一部分后，剩余部分的三视图如下图，则截取部分体积和剩余部分体积的比值为（） 9.如图，长方体1111D C B A ABCD -中，AB = 16，BC = 10，AA1 = 8，点E ，F 分别在1111C D B A ，上，411==F D E A ，过点E,F 的平面α与此长方体的面相交，交线围成一个正方形。（1）在图中画出这个正方形（不必说明画法和理由）；（2）求直线AF 与平面α所成的角的正弦值 10.如图，菱形ABCD 的对角线AC 与BD 交于点O ，AB=5，AC=6，点E,F 分别在AD,CD 上，AE=CF=45 ，EF 交BD 于点H.将△DEF 沿EF 折到△DEF 的位置，OD ’=10 （1）证明：D ’H ⊥平面ABCD （2）求二面角B-D ’A-C 的正弦值

高三数学知识点总结：立体几何

2019年高三数学知识点总结：立体几何由查字典数学网高中频道提供，2019年高三数学知识点总结：立体几何，因此老师及家长请认真阅读，关注孩子的成长。立体几何初步 (1)棱柱：定义：有两个面互相平行，其余各面都是四边形，且每相邻两个四边形的公共边都互相平行，由这些面所围成的几何体。分类：以底面多边形的边数作为分类的标准分为三棱柱、四棱柱、五棱柱等。表示：用各顶点字母，如五棱柱或用对角线的端点字母，如五棱柱几何特征：两底面是对应边平行的全等多边形;侧面、对角面都是平行四边形;侧棱平行且相等;平行于底面的截面是与底面全等的多边形。 (2)棱锥定义：有一个面是多边形，其余各面都是有一个公共顶点的三角形，由这些面所围成的几何体分类：以底面多边形的边数作为分类的标准分为三棱锥、四棱锥、五棱锥等表示：用各顶点字母，如五棱锥几何特征：侧面、对角面都是三角形;平行于底面的截面与底面相似，其相似比等于顶点到截面距离与高的比的平方。 (3)棱台：

定义：用一个平行于棱锥底面的平面去截棱锥，截面和底面之间的部分分类：以底面多边形的边数作为分类的标准分为三棱态、四棱台、五棱台等表示：用各顶点字母，如五棱台几何特征：①上下底面是相似的平行多边形②侧面是梯形③侧棱交于原棱锥的顶点 (4)圆柱：定义：以矩形的一边所在的直线为轴旋转，其余三边旋转所成的曲面所围成的几何体几何特征：①底面是全等的圆;②母线与轴平行;③轴与底面圆的半径垂直;④侧面展开图是一个矩形。 (5)圆锥：定义：以直角三角形的一条直角边为旋转轴，旋转一周所成的曲面所围成的几何体几何特征：①底面是一个圆;②母线交于圆锥的顶点;③侧面展开图是一个扇形。 (6)圆台：定义：用一个平行于圆锥底面的平面去截圆锥，截面和底面之间的部分几何特征：①上下底面是两个圆;②侧面母线交于原圆锥的顶点;③侧面展开图是一个弓形。

立体几何经典大题(各个类型的典型题目)

1．如图，已知△ABC 是正三角形，EA ，CD 都垂直于平面ABC ，且EA ＝AB ＝2a ，DC ＝a ，F 是BE 的中点．（1）FD ∥平面ABC ；（2）AF ⊥平面EDB ． 2．已知线段PA ⊥矩形ABCD 所在平面，M 、N 分别是AB 、PC 的中点。（1）求证：MN //平面PAD ；（2）当∠PDA ＝45°时，求证：MN ⊥平面PCD ； F C B A E D

A B C D E F 3．如图，在四面体ABCD 中，CB=CD,BD AD ⊥，点E ，F 分别是AB,BD 的中点．求证：（1）直线EF// 面ACD ；（2）平面⊥EFC 面BCD ． 4．在斜三棱柱A 1B 1C 1—ABC 中，底面是等腰三角形，AB =AC ，侧面BB 1C 1C ⊥底面ABC （1）若D 是BC 的中点，求证AD ⊥CC 1；（2）过侧面BB 1C 1C 的对角线BC 1的平面交侧棱于M ，若AM =MA 1，求证截面MBC 1⊥侧面BB 1C 1C ；（3）AM =MA 1是截面MBC 1⊥平面BB 1C 1C 的充要条件吗？请你叙述判断理由 ] 立体几何大题训练(3) C 1

5. 如图，在正方体ABCD —A 1B 1C 1D 1中，M 、N 、G 分别是A 1A ，D 1C ，AD 的中点．求证：（1）MN//平面ABCD ；（2）MN ⊥平面B 1BG ． 6.如图，在正方体ABCD －A 1B 1C 1D 1中，E 、F 为棱AD 、AB 的中点．（1）求证：EF ∥平面CB 1D 1；（2）求证：平面CAA 1C 1⊥平面CB 1D 1．立体几何大题训练(4) 7、如图，在直四棱柱ABCD-A 1B 1C 1D 1中，底面ABCD 为等腰梯形，AB ∥CD ，AB=4，BC=CD=2，AA 1=2，_ G _ M _ D _1 _ C _1 _ B _1 _ A _1 _ N _ D _ C _ B _ A B A 1 F

2015届高三数学立体几何专题训练及详细答案

2015届高三数学立体几何专题训练 1．(2013·高考新课标全国卷Ⅰ)某几何体的三视图如图所示，则该几何体的体积为( ) A ．16＋8π B ．8＋8π C ．16＋16π D ．8＋16π 解析：选A. 原几何体为组合体：上面是长方体，下面是圆柱的一半(如图所示)，其体积为V ＝4×2×2＋1 2 π×22×4＝16＋8π. 2．(2013·高考新课标全国卷Ⅰ)如图，有一个水平放置的透明无盖的正方体容器，容器高8 cm ，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为6 cm ，如果不计容器厚度，则球的体积为( ) A.500π3 cm 3 B.866π3 cm 3 C.1 372π3 cm 3 D.2 048π3 cm 3 解析：选A. 如图，作出球的一个截面，则MC ＝8－6＝2(cm)， BM ＝12AB ＝1 2 ×8＝4(cm)．设球的半径为R cm ，则R 2＝OM 2＋MB 2＝(R －2)2＋42，∴R ＝5， ∴V 球＝43π×53＝500π 3 (cm 3)． 3．(2013·高考新课标全国卷Ⅱ)已知m ，n 为异面直线，m ⊥平面α，n ⊥平面β.直线l 满足l ⊥m ，l ⊥n ，l ?α，l ?β，则( ) A ．α∥β且l ∥α B ．α⊥β且l ⊥β

C ．α与β相交，且交线垂直于l D ．α与β相交，且交线平行于l 解析：选D. 根据所给的已知条件作图，如图所示．由图可知α与β相交，且交线平行于l ，故选D. 4．(2013·高考大纲全国卷)已知正四棱柱ABC D-A 1B 1C 1D 1中，AA 1＝2AB ，则C D 与平面B D C 1所成角的正弦值等于( ) A.23 B.33 C.23 D.13 解析：选A.法一：如图，连接AC ，交B D 于点O ，由正四棱柱的性质，有AC ⊥B D.因为CC 1⊥平面ABC D ，所以CC 1⊥B D.又CC 1∩AC ＝C ，所以B D ⊥平面CC 1O .在平面CC 1O 内作CH ⊥C 1O ，垂足为H ，则B D ⊥CH .又B D ∩C 1O ＝O ，所以CH ⊥平面B D C 1，连接D H ，则D H 为C D 在平面B D C 1上的射影，所以∠C D H 为C D 与平面B D C 1所成的角．设AA 1＝2AB ＝2.在Rt △COC 1中，由等面积变换易求得CH ＝23.在Rt △C D H 中，s in ∠C D H ＝CH CD ＝2 3 . 法二：以D 为坐标原点，建立空间直角坐标系，如图，设AA 1＝2AB ＝2，则D(0，0,0)，C (0,1,0)， B (1,1,0)， C 1(0,1,2)，则DC →＝(0,1,0)，DB →＝(1,1,0)，DC 1→ ＝(0,1,2)．设平面B D C 1的法向量为n ＝(x ，y ，z )，则 n ⊥DB →，n ⊥DC 1→ ，所以有????? x ＋y ＝0，y ＋2z ＝0，令y ＝－2，得平面B D C 1的一个法向量为n ＝(2，－2,1)．设C D 与平面B D C 1所成的角为θ，则s in θ＝|co s n ，DC → ＝???? ??n ·DC →|n ||DC →|＝23. 5．(2013·高考大纲全国卷)已知正四棱柱ABC D-A 1B 1C 1D 1中，AA 1＝2AB ，则C D 与平面B D C 1所成角的正弦值等于( ) A.23 B.33

2011—2017高考全国卷文科数学立体几何总结

新课标全国卷文科数学总结立体几何一、选择题【2017，6】如图，在下列四个正方体中，A ，B 为正方体的两个顶点，M ，N ，Q 为所在棱的中点，则在这四个正方体中，直接AB 与平面MNQ 不平行的是（）【2016，7】如图所示，某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径．若该几何体的体积是 28π 3 ，则它的表面积是（） A ．17π B ． 18π C ． 20π D ． 28π 【2016，11】平面α过正方体1111ABCD A BC D -的顶点 A ，α∥平面11C B D ，α平面ABCD m =， α 平面11ABB A n =，则,m n 所成角的正弦值为（） A ． 2 B ．2 C ．3 D ．13 【2015，6】《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有委米依垣内角，下周八尺，高五尺，问”积及为米几何？”其意思为：“在屋内墙角处堆放米（如图，米堆为一个圆锥的四分之一），米堆底部的弧长为8尺，米堆的高为5尺，米堆的体积和堆放的米各位多少？”已知1斛米的体积约为1．62立方尺，圆周率约为3，估算出堆放的米有( ) A ．14斛 B ．22斛 C ．36斛 D ．66斛【2015，11】圆柱被一个平面截去一部分后与半球（半径为r ）组成一个几何体，该几何体的三视图中的正视图和俯视图如图所示，若该几何体的表面积为16+20π，则r =( ) B A ．1 B ．2 C ．4 D ．8 【2015，11】【2014，8】【2013，11】【2012，7】【2014，8】如图，网格纸的各小格都是正方形，粗实线画出的一个几何体的三视图，则这个几何体是( ) A ．三棱锥 B ．三棱柱 C ．四棱锥 D ．四棱柱【2013，11】某几何体的三视图如图所示，则该几何体的体积为( )． A ．16＋8π B ．8＋8π C ．16＋16π D ．8＋16π 【2012，7】如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的体积为 A ．6 B ．9 C ．12 D ．15

高中数学立体几何专题

高中课程复习专题——数学立体几何一空间几何体㈠空间几何体的类型 1 多面体：由若干个平面多边形围成的几何体。围成多面体的各个多边形叫做多面体的面，相邻两个面的公共边叫做多面体的棱，棱与棱的公共点叫做多面体的顶点。 2 旋转体：把一个平面图形绕它所在的平面内的一条定直线旋转形成了封闭几何体。其中，这条直线称为旋转体的轴。㈡几种空间几何体的结构特征 1 棱柱的结构特征棱柱的定义：有两个面互相平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行，由这些面所围成的几何体叫做棱柱。棱柱的分类棱柱的性质 ⑴侧棱都相等，侧面是平行四边形； ⑵两个底面与平行于底面的截面是全等的多边形； ⑶过不相邻的两条侧棱的截面是平行四边形； ⑷直棱柱的侧棱长与高相等，侧面的对角面是矩形。长方体的性质 ⑴长方体的一条对角线的长的平方等于一个顶点上三条棱的平方和：AC12 = AB2 + AC2 + AA12 ⑵长方体的一条对角线AC1与过定点A的三条棱所成图1-2 长方体

的角分别是α、β、γ，那么： cos2α + cos2β + cos2γ = 1 sin2α + sin2β + sin2γ = 2 ⑶ 长方体的一条对角线AC1与过定点A的相邻三个面所组成的角分别为α、β、γ，则： cos2α + cos2β + cos2γ = 2 sin2α + sin2β + sin2γ = 1 棱柱的侧面展开图：正n棱柱的侧面展开图是由n个全等矩形组成的以底面周长和侧棱为邻边的矩形。棱柱的面积和体积公式 S直棱柱侧面 = c·h (c为底面周长，h为棱柱的高) S直棱柱全 = c·h+ 2S底 V棱柱 = S底·h 2 圆柱的结构特征 2-1 圆柱的定义：以矩形的一边所在的直线为旋转轴，其余各边旋转而形成的曲面所围成的几何体叫圆柱。图1-3 圆柱 2-2 圆柱的性质 ⑴上、下底及平行于底面的截面都是等圆； ⑵过轴的截面(轴截面)是全等的矩形。 2-3 圆柱的侧面展开图：圆柱的侧面展开图是以底面周长和母线长为邻边的矩形。 2-4 圆柱的面积和体积公式 S圆柱侧面= 2π·r·h (r为底面半径，h为圆柱的高) S圆柱全= 2π r h + 2π r2 V圆柱 = S底h = πr2h 3 棱锥的结构特征 3-1 棱锥的定义 ⑴棱锥：有一个面是多边形，其余各面是有一个公共顶点的三角形，由这些面所围成的几何体叫做棱锥。

高考立体几何大题经典例题.

N M P C B A <一 >常用结论 1.证明直线与直线的平行的思考途径:(1转化为判定共面二直线无交点; (2转化为二直线同与第三条直线平行; (3转化为线面平行; (4转化为线面垂直; (5转化为面面平行 . 2.证明直线与平面的平行的思考途径:(1转化为直线与平面无公共点; (2转化为线线平行; (3转化为面面平行 . 3. 证明平面与平面平行的思考途径:(1 转化为判定二平面无公共点; (2 转化为线面平行; (3转化为线面垂直 . 4.证明直线与直线的垂直的思考途径:(1转化为相交垂直; (2转化为线面垂直; (3转化为线与另一线的射影垂直; (4转化为线与形成射影的斜线垂直 . 5.证明直线与平面垂直的思考途径:(1转化为该直线与平面内任一直线垂直; (2转化为该直线

与平面内相交二直线垂直; (3转化为该直线与平面的一条垂线平行; (4转化为该直线垂直于另一个平行平面; (5转化为该直线与两个垂直平面的交线垂直 . 6.证明平面与平面的垂直的思考途径:(1转化为判断二面角是直二面角; (2转化为线面垂直 . 3、如图,在正方体 1111ABCD A B C D -中, E 是 1AA 的中点, 求证: 1//AC 平面BDE 。 5、已知正方体 1111ABCD A B C D -, O 是底 ABCD 对角线的交点 . 求证:(1 C1O ∥面 11AB D ; (21 AC ⊥面 11AB D . 9、如图 P 是ABC ?所在平面外一点, , PA PB CB =⊥平面 PAB , M 是 PC 的中点, N 是 AB 上的点, 3AN NB = A D 1 C B D C D D B A C 1

2020高考数学专题复习----立体几何专题

空间图形的计算与证明一、近几年高考试卷部分立几试题 1、（全国 8）正六棱柱 ABCDEF －A 1B 1C 1D 1E 1F 1 底面边长为 1，侧棱长为 2 ，则这个棱柱的侧面对角线 E 1D 与 BC 1 所成的角是（） A 、90° B 、60° C 、45° D 、30° [评注]主要考查正六棱柱的性质，以及异面直线所成角的求法。 2、（全国 18）如图，正方形ABCD 、ABEF 的边长都是 1，而且平面 ABCD 、ABEF 互相垂直，点 M 在 AC 上移动，点 N 在 BF C 上移动，若 CM=NB=a(0

的底面是边长为a的正方形，PB⊥面ABCD。（1）若面PAD与面ABCD所成的二面角为60°，求这个四棱锥的体积；（2）证明无论四棱锥的高怎样变化，面PAD与面 PCD所成的二面角恒大于90°。 [评注]考查线面关系和二面角概念，以及空间想象力和逻辑推理能力。 4、（02全国文22）（一）给出两块面积相同的正三角形纸片，要求用其中一块剪拼成一个正三棱锥模型，使它们的全面积都与原三角形面积相等，请设计一种剪拼法，分别用虚线标示在图（1）（2）中，并作简要说明。 (3) (1)(2) （二）试比较你剪拼的正三棱锥与正三棱柱的体积的大小。（三）如果给出的是一块任意三角形的纸片，如图（3）要求剪拼成一个直三棱柱模型，使它的全面积与给出的三角形面积相等，请设计一种剪拼方法，用虚线标出在图3中，并作简要说明。

高中文科数学立体几何知识点总结材料

立体几何知识点整理（文科）一．直线和平面的三种位置关系： 1. 线面平行 l 符号表示： 2. 线面相交符号表示： 3. 线在面内符号表示：二．平行关系： 1.线线平行：方法一：用线面平行实现。 m l m l l // // ? ? ? ? ? ? = ? ? β α β α 方法二：用面面平行实现。 m l m l// // ? ? ? ? ? ? = ? = ? β γ α γ β α 方法三：用线面垂直实现。若α α⊥ ⊥m l,，则m l//。方法四：用向量方法：若向量l和向量m共线且l、 m不重合，则m l//。 2.线面平行：方法一：用线线平行实现。 α α α// // l l m m l ? ? ? ? ? ? ? ? 方法二：用面面平行实现。 α β β α // // l l ? ? ? ? ? 方法三：用平面法向量实现。若n为平面α的一个法向量，l n⊥且α ? l,则 α // l。 3.面面平行：方法一：用线线平行实现。 β α α β // ' ,' , ' // ' // ? ? ? ? ? ? ? ? ? ? 且相交且相交 m l m l m m l l l

方法二：用线面平行实现。 βαβαα //,////??? ? ???且相交m l m l 三．垂直关系： 1. 线面垂直：方法一：用线线垂直实现。 αα⊥???? ? ??? ?=?⊥⊥l AB AC A AB AC AB l AC l , 方法二：用面面垂直实现。 αββαβα⊥??? ? ?? ?⊥=?⊥l l m l m , 2. 面面垂直：方法一：用线面垂直实现。 βαβα⊥?? ?? ?⊥l l 方法二：计算所成二面角为直角。 3. 线线垂直：方法一：用线面垂直实现。 m l m l ⊥?? ?? ?⊥αα 方法二：三垂线定理及其逆定理。 PO l OA l PA l αα⊥? ? ⊥?⊥???? 方法三：用向量方法：若向量l 和向量m 的数量积为0，则m l ⊥。三．夹角问题。 (一) 异面直线所成的角： (1) 范围：]90,0(?? (2)求法：方法一：定义法。步骤1：平移，使它们相交，找到夹角。

立体几何-2009-2017全国高中数学联赛分类汇编

2009-2017全国高中数学联赛分类汇编第09讲：立体几何 1、（2010一试7）正三棱柱111C B A ABC -的9条棱长都相等，P 是1CC 的中点，二面角α=--11B P A B ,则=αsin 【答案】4 【解析】 O E P 1B 1 A 1 C B A 设分别与平面P BA 1、平面P A B 11垂直的向量是),,(111z y x m =、),,(222z y x n =，则 ???? ?=++-=?=+-=?,03, 022111111z y x z x BA ???? ?=-+-=?=-=?, 03, 022221211z y x B x A B n 由此可设)3,1,0(),1,0,1(==，所以cos m n m n α?=? ，即 2cos cos αα=?= .所以4 10sin =α. 解法二：如图，PB PA PC PC ==11, . 设B A 1与1AB 交于点,O 则1111,,OA OB OA OB A B AB ==⊥ . 11,,PA PB PO AB =⊥因为所以从而⊥1AB 平面B PA 1 . 过O 在平面B PA 1上作P A OE 1⊥,垂足为E .

连结E B 1,则EO B 1∠为二面角11B P A B --的平面角.设21=AA ,则易求得 3,2,5111== ===PO O B O A PA PB . 在直角O PA 1?中，OE P A PO O A ?=?11,即5 6,532= ∴?= ?OE OE . 11B O B E =∴===又.4 10 5 542sin sin 111= ==∠=E B O B EO B α. 2、（2011一试6）在四面体ABCD 中，已知?=∠=∠=∠60CDA BDC ADB ，3==BD AD ，2=CD ，则四面体ABCD 的外接球的半径为【解析】因为?=∠=∠=∠60ADB CDB CDA ，设CD 与平面ABD 所成角为θ，可求得3 2sin ,3 1cos = = θθ．在△DMN 中，332 33232,121=??=?=== DP DN CD DM ．学科*网由余弦定理得231312)3(1222=? ??-+=MN ，故2=MN ．四边形DMON 的外接圆的直径 33 22sin === θ MN OD ．故球O 的半径3=R ． 3、（2012一试5）设同底的两个正三棱锥P ABC -和Q ABC -内接于同一个球．若正三棱锥P ABC -的

高考立体几何大题20题汇总

(2012XX省）（本小题满分12分）如图，在梯形ABCD中，AB∥CD，E，F是线段AB上的两点，且DE⊥AB，CF⊥AB，AB=12，AD=5，BC=42，DE=4.现将△ADE ，△CFB分别沿DE，CF折起，使A，B两点重合与点G，得到多面体CDEFG. （1）求证：平面DEG⊥平面CFG；（2)求多面体CDEFG的体积。 2012，(19)(本小题满分12分) 如图，几何体EABCD是四棱锥，△ABD为正三角形， CBCD,ECBD. (Ⅰ)求证：BEDE； (Ⅱ)若∠BCD120，M为线段AE的中点，求证：DM∥平面 BEC. BC 2012XX20．（本题满分15 分）如图，在侧棱锥垂直 A D 底面的四棱锥ABCDA1B1C1D1中，AD//BC,AD FE AB,AB2,AD2,BC4,AA2,E是DD的中点，F 11 是平面B C E 与直线AA1 的交点。 1 1 A1 B1 D1 ( 第20题图) C1 （Ⅰ）证明：（i ）E F//A1D1;（ii）BA1平面B1C1EF; （Ⅱ）求BC与平面B1C1EF所成的角的正弦值。 1 （2010）18、(本小题满分12分)已知正方体ABCDA'B'C'D'中，点M是棱AA' 的中点，点O是对角线BD'的中点，（Ⅰ）求证：OM为异面直线AA'与BD'的公垂线；

（Ⅱ）求二面角MBC'B'的大小； 2010XX文（19）（本小题满分12分）如图，棱柱 ABCA1B1C1的侧面BCC1B1是菱形，B1CA1B （Ⅰ）证明：平面A B C平面A1BC1； 11 （Ⅱ）设D 是A C上的点，且 11 AB1//平面BCD，求 1 A1D :DC1的值。 2012（18）(本小题满分12分) 如图，直三棱柱/// ABCABC，BAC90， ABAC2,AA′=1，点M，N分别为/ AB和// BC的中点。 (Ⅰ)证明：MN∥平面// AACC;

2021高考数学立体几何专题

专题09立体几何与空间向量选择填空题历年考题细目表题型年份考点试题位置单选题2019 表面积与体积2019年新课标1理科12 单选题2018 几何体的结构特征2018年新课标1理科07 单选题2018 表面积与体积2018年新课标1理科12 单选题2017 三视图与直观图2017年新课标1理科07 单选题2016 三视图与直观图2016年新课标1理科06 单选题2016 空间向量在立体几何中的应用2016年新课标1理科11 单选题2015 表面积与体积2015年新课标1理科06 单选题2015 三视图与直观图2015年新课标1理科11 单选题2014 三视图与直观图2014年新课标1理科12 单选题2013 表面积与体积2013年新课标1理科06 单选题2013 三视图与直观图2013年新课标1理科08 单选题2012 三视图与直观图2012年新课标1理科07 单选题2012 表面积与体积2012年新课标1理科11 单选题2011 三视图与直观图2011年新课标1理科06 单选题2010 表面积与体积2010年新课标1理科10 填空题2017 表面积与体积2017年新课标1理科16 填空题2011 表面积与体积2011年新课标1理科15 填空题2010 三视图与直观图2010年新课标1理科14 历年高考真题汇编 1．【2019年新课标1理科12】已知三棱锥P﹣ABC的四个顶点在球O的球面上，P A＝PB＝PC，△ABC是边长为2的正三角形，E，F分别是P A，AB的中点，∠CEF＝90°，则球O的体积为（） A．8πB．4πC．2πD．π 2．【2018年新课标1理科07】某圆柱的高为2，底面周长为16，其三视图如图．圆柱表面上的点M在正视图上的对应点为A，圆柱表面上的点N在左视图上的对应点为B，则在此圆柱侧面上，从M到N的路径中，最短路径的长度为（）

文科立体几何知识点方法总结高三复习

立体几何知识点整理（文科）一．直线和平面的三种位置关系： 1. 线面平行 l 符号表示： 2. 线面相交符号表示： 3. 线在面内符号表示：二．平行关系： 1.线线平行：方法一：用线面平行实现。方法二：用面面平行实现。方法用线直实现。若α α⊥ ⊥m l,，则m l//。方法四：用向量方法：若向量和向量共线且l、m不重合，则m l//。 2.线面平行：方法一：用线线平行实现。方法二：用面面平行实现。方法三：用平面法向量实现。若n为平面α的一个法向量，l n⊥且α ? l,则 α // l。 3.面面平行：方法一：用线线平行实现。 β α α β // ' ,' , ' // ' // ? ? ? ? ? ? ? ? ? ? 且相交且相交 m l m l m m l l 方法二：用线面平行实现。三．垂直关系： 1. 线面垂直：方法一：用线线垂直实现。方法二：用面面垂直实现。 2. 面面垂直：方法一：用线面垂直实现。方法二：计算所成二面角为直角。 3.线线垂直：方法一：用线面垂直实现。方法二：三垂线定理及其逆定理。方法三：用向量方法：若向量和向量的数量积为0，则m l⊥。三．夹角问题。 (一)异面直线所成的角： (1) 范围：] 90 , 0(? ? (2)求法：方法一：定义法。步骤1：平移，使它们相交，找到夹角。步骤2：解三角形求出角。(常用到余弦定理) 余弦定理： (计算结果可能是其补角 ) θ c b a l

方法二：向量法。转化为向量的夹角 (计算结果可能是其补角)： (二) 线面角 (1)定义：直线l 上任取一点P （交点除外），作PO ⊥α于O,连结AO ，则AO 为斜线PA 在面α内的射影，PAO ∠(图中θ)为直线l 与面α所成的角。 (2)范围：]90,0[?? 当?=0θ时，α?l 或α//l 当?=90θ时，α⊥l (3)求法：方法一：定义法。步骤1：作出线面角，并证明。步骤2：解三角形，求出线面角。 (三) 二面角及其平面角 (1)定义：在棱l 上取一点P ，两个半平面内分别作l 的垂线（射线）m 、n ，则射线m 和n 的夹角θ为二面角α—l —β的平面角。 (2)范围：]180,0[?? (3)求法：方法一：定义法。步骤1：作出二面角的平面角(三垂线定理)，并证明。步骤2：解三角形，求出二面角的平面角。方法二：截面法。步骤1：如图，若平面POA 同时垂直于平面βα和，则交线(射线)AP 和AO 的夹角就是二面角。步骤2：解三角形，求出二面角。方法三：坐标法(计算结果可能与二面角互补)。步骤一：计算121212 cos n n n n n n ?= ? 步骤二：判断θ与12n n 的关系，可能相等或者互补。四．距离问题。 1．点面距。方法一：几何法。步骤1：过点P 作PO ⊥α于O ，线段PO 即为所求。步骤2：计算线段PO 的长度。(直接解三角形；等体积法和等面积法；换点法) 2．线面距、面面距均可转化为点面距。 3．异面直线之间的距离方法一：转化为线面距离。如图，m 和n 为两条异面直线，α?n 且α//m ，则异面直线m 和n 之间的距离可转化为直线m 与平面α之间的距离。方法二：直接计算公垂线段的长度。方法三：公式法。如图，AD 是异面直线m 和n 的公垂线段， '//m m ，则异面直线m 和n 之间的距离为：高考题典例考点1 点到平面的距离例1如图，正三棱柱111ABC A B C -的所有棱长都为2，D 为1CC 中点．（Ⅰ）求证：1AB ⊥平面1A BD ；（Ⅱ）求二面角1A A D B --的大小；（Ⅲ）求点C 到平面1A BD 的距离．考点2 异面直线的距离 A B C D O F

高中数学立体几何知识点总结

高中数学之立体几何平面的基本性质公理1 如果一条直线上的两点在一个平面内，那么这条直线上所有的点都在这个平面内. 公理2 如果两个平面有一个公共点，那么它们有且只有一条通过这个点的公共直线. 公理3 经过不在同一直线上的三个点，有且只有一个平面. 根据上面的公理，可得以下推论. 推论1 经过一条直线和这条直线外一点，有且只有一个平面. 推论2 经过两条相交直线，有且只有一个平面. 推论3 经过两条平行直线，有且只有一个平面. 空间线面的位置关系共面平行—没有公共点 (1)直线与直线相交—有且只有一个公共点异面(既不平行，又不相交) 直线在平面内—有无数个公共点 (2)直线和平面直线不在平面内平行—没有公共点 (直线在平面外) 相交—有且只有一公共点 (3)平面与平面相交—有一条公共直线(无数个公共点) 平行—没有公共点异面直线的判定证明两条直线是异面直线通常采用反证法. 有时也可用定理“平面内一点与平面外一点的连线，与平面内不经过该点的直线是异面直线”. 线面平行与垂直的判定 (1)两直线平行的判定 ①定义：在同一个平面内，且没有公共点的两条直线平行. ②如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线和交线平行，即若a∥α,aβ，α∩β=b,则a∥b. ③平行于同一直线的两直线平行，即若a∥b,b∥c,则a∥c. ④垂直于同一平面的两直线平行，即若a⊥α，b⊥α，则a∥b ⑤两平行平面与同一个平面相交，那么两条交线平行，即若α∥β,α∩γ,β∩γ=b,则a∥b ⑥如果一条直线和两个相交平面都平行，那么这条直线与这两个平面的交线平行，即若α∩β=b,a∥α,a∥β，则a∥b. (2)两直线垂直的判定

立体几何典型例题精选(含答案)

F E D C B A 立体几何专题复习热点一：直线与平面所成的角例1．（2014，广二模理 18）如图，在五面体ABCDEF 中，四边形ABCD 是边长为2的正方形， EF ∥平面ABCD ， 1EF =，,90FB FC BFC ?=∠=，3AE =. （1）求证：AB ⊥平面BCF ；（2）求直线AE 与平面BDE 所成角的正切值. 变式1：（2013湖北8校联考）如左图，四边形ABCD 中，E 是BC 的中点，2,1,5,DB DC BC === 2.AB AD ==将左图沿直线BD 折起，使得二面角A BD C --为60,?如右图. （1）求证：AE ⊥平面;BDC （2）求直线AC 与平面ABD 所成角的余弦值. 变式2：[2014·福建卷] 在平面四边形ABCD 中，AB ＝BD ＝CD ＝1，AB ⊥BD ，CD ⊥BD .将△ABD 沿BD 折起，使得平面ABD ⊥平面BCD ，如图1-5所示． (1)求证：AB ⊥CD ； (2)若M 为AD 中点，求直线AD 与平面MBC 所成角的正弦值．

热点二：二面角例2．[2014·广东卷] 如图1-4，四边形ABCD为正方形，PD⊥平面ABCD，∠DPC＝30°，AF⊥PC于点F，FE∥CD，交PD于点E. (1)证明：CF⊥平面ADF；(2)求二面角D-AF-E的余弦值．变式3：[2014·浙江卷] 如图1-5，在四棱锥A-BCDE中，平面ABC⊥平面BCDE，∠CDE＝∠BED＝90°，AB＝CD＝2，DE＝BE＝1，AC＝ 2. (1)证明：DE⊥平面ACD；(2)求二面角B-AD-E的大小．变式4：[2014·全国19] 如图1-1所示，三棱柱ABC-A1B1C1中，点A1在平面ABC内的射影D在AC 上，∠ACB＝90°，BC＝1，AC＝CC1＝2. (1)证明：AC1⊥A1B; (2)设直线AA1与平面BCC1B1的距离为3，求二面角A1 -AB -C的大小．

高三数学立体几何专题复习课程

高三数学立体几何专题

专题三立体几何专题【命题趋向】高考对空间想象能力的考查集中体现在立体几何试题上，着重考查空间点、线、面的位置关系的判断及空间角等几何量的计算．既有以选择题、填空题形式出现的试题，也有以解答题形式出现的试题．选择题、填空题大多考查概念辨析、位置关系探究、空间几何量的简单计算求解，考查画图、识图、用图的能力；解答题一般以简单几何体为载体，考查直线与直线、直线与平面、平面与平面的位置关系，以及空间几何量的求解问题，综合考查空间想象能力、推理论证能力和运算求解能力．试题在突出对空间想象能力考查的同时，关注对平行、垂直关系的探究，关注对条件或结论不完备情形下的开放性问题的探究．【考点透析】立体几何主要考点是柱、锥、台、球及其简单组合体的结构特征、三视图、直观图，表面积体积的计算，空间点、直线、平面的位置关系判断与证明，（理科）空间向量在平行、垂直关系证明中的应用，空间向量在计算空间角中的应用等．【例题解析】题型1 空间几何体的三视图以及面积和体积计算例1（2008高考海南宁夏卷）某几何体的一条棱长为7，在该几何体的正视图中，这条棱的投影是长为6的线段，在该几何体的侧视图与俯视图中，这条棱的投影分别是长为a 和b 的线段，则a b +的最大值为 A ． 22 B ． 32 C ． 4 D ． 52 分析：想像投影方式，将问题归结到一个具体的空间几何体中解决．解析：结合长方体的对角线在三个面的投影来理解计算，如图设长方体的高宽高分别为,,m n k = =1n ?=， a = b =，所以22(1)(1)6a b -+-= 228a b ?+=，22222()282816a b a ab b ab a b +=++=+≤++=∴4 a b ?+≤当且仅当2a b ==时取等号．

立体几何-2019年高考理科数学解读考纲

05 立体几何（三）立体几何初步 1.空间几何体 (1)认识柱、锥、台、球及其简单组合体的结构特征,并能运用这些特征描述现实生活中简单物体的结构. (2)能画出简单空间图形(长方体、球、圆柱、圆锥、棱柱等的简易组合)的三视图,能识别上述三视图所表示的立体模型,会用斜二侧法画出它们的直观图. (3)会用平行投影与中心投影两种方法画出简单空间图形的三视图与直观图,了解空间图形的不同表示形式. (4)会画某些建筑物的视图与直观图(在不影响图形特征的基础上,尺寸、线条等不作严格要求). (5)了解球、棱柱、棱锥、台的表面积和体积的计算公式. 2.点、直线、平面之间的位置关系 (1)理解空间直线、平面位置关系的定义,并了解如下可以作为推理依据的公理和定理. ? 公理1：如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在此平面内. 公理2：过不在同一条直线上的三点,有且只有一个平面. 格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一部分后所得，则该几何体的体积为 A．90πB．63π C．42πD．36π 【答案】B 【名师点睛】在由三视图还原为空间几何体的实际形状时，要从三个视图综合考虑，根据三视图的规

则，空间几何体的可见轮廓线在三视图中为实线，不可见轮廓线在三视图中为虚线．在还原空间几何体实际形状时，一般是以正视图和俯视图为主，结合侧视图进行综合考虑．求解以三视图为载体的空间几何体的体积的关键是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系，利用相应体积公式求解．考向二球的组合体样题4 （2017新课标全国Ⅲ理科）已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为 A ．π B ． 3π4 C ． π2 D ． π4 【答案】B 【解析】绘制圆柱的轴截面如图所示：由题意可得：，结合勾股定理，底面半径，由圆柱的体积公式，可得圆柱的体积是，故选B. 【名师点睛】（1）求解空间几何体体积的关键是确定几何体的元素以及线面的位置关系和数量关系，利用相应体积公式求解；（2）若所给几何体的体积不能直接利用公式得出，则常用等积法、分割法、补形法等方法进行求解. 样题5 （2017江苏）如图，在圆柱12O O 内有一个球O ，该球与圆柱的上、下底面及母线均相切．记圆柱12 O O 的体积为1V ，球O 的体积为2V ，则 1 2 V V 的值是 .

历年高考立体几何大题试题(卷)

2015年高考立体几何大题试卷 1. 【2015高考新课标2，理19】如图，长方体ABCD -A1B1C1D1中,AB=16, BC=10, AA = 8，点E , F 分别在AB , C1D1上，A1E =4 .过点E , F的平面:-与此长方体的面相交，交线围成一个正方形. （1题图）（I ）在图中画出这个正方形（不必说出画法和理由）（n ）求直线AF与平面〉所成角的正弦值. 2. 【2015江苏高考，16】如图，在直三棱柱ABC—中，已知AC丄BC ,

BC =CC 1，设 AB 1 的中点为 D , BQ BC^ E .求证：（1） DE // 平面 AA 1C 1C ; (2) BC 1 _ AB 1 . （2题图）（3题图） C C 第的题图

3. 【2015高考安徽，理19】如图所示，在多面体 AEDQCBA ，四边形AABB , ADD 1A 1 ,ABCD 均为正方形，E 为Bp 的中点，过 A,D,E 的平面交CD ,于F. (I)证明：EF //BQ ； (□)求二面角E - A ,D - B i 余弦值. 4. 【2015江苏高考，22】如图，在四棱锥P-ABCD 中，已知PA _平面ABCD ，且四边形 ABCD 为直角梯形，.ABC =/BAD = —,PA 二 AD =2,AB 二 BC =1 2 (1)求平面PAB 与平面PCD 所成二面角的余弦值； (2)点Q 是线段BP 上的动点，当直线 CQ 与DP 所成角最小时，求线段 BQ 的长 (4题图) 5 .【2015高考福建，理17】如图，在几何体 ABCDE 中，四边形ABCD 是矩形，AB A 平面BEC , BE A EC , AB=BE=EC=2 , G , F 分别是线段 BE , DC 的中点. (I 求证：GF //平面ADE ; (^)求平面AEF 与平面BEC 所成锐二面角的余弦值. 6. 【2015高考浙江，理17】如图，在三棱柱 AB^A 1B 1C 1-中，.BAC =90；, AB = AC=2 , AA = 4 , A 在底面ABC 的射影为BC 的中点，D 为B 1C 1的中点. (5题图) D

高考数学专题立体几何专题

专题三立体几何专题【命题趋向】高考对空间想象能力的考查集中体现在立体几何试题上,着重考查空间点、线、面的位置关系的判断及空间角等几何量的计算.既有以选择题、填空题形式出现的试题,也有以解答题形式出现的试题.选择题、填空题大多考查概念辨析、位置关系探究、空间几何量的简单计算求解,考查画图、识图、用图的能力;解答题一般以简单几何体为载体,考查直线与直线、直线与平面、平面与平面的位置关系,以及空间几何量的求解问题,综合考查空间想象能力、推理论证能力与运算求解能力.试题在突出对空间想象能力考查的同时,关注对平行、垂直关系的探究,关注对条件或结论不完备情形下的开放性问题的探究. 【考点透析】立体几何主要考点就是柱、锥、台、球及其简单组合体的结构特征、三视图、直观图,表面积体积的计算,空间点、直线、平面的位置关系判断与证明,空间向量在平行、垂直关系证明中的应用,空间向量在计算空间角中的应用等.【例题解析】题型1 空间几何体的三视图以及面积与体积计算例 1 某几何体的一条棱长为7,在该几何体的正视图中,这条棱的投影就是长为6的线段,在该几何体的侧视图与俯视图中,这条棱的投影分别就是长为a 与b 的线段,则a b +的最大值为 A. 22 B. 32 C. 4 D. 5 2分析:想像投影方式,将问题归结到一个具体的空间几何体中解决. 解析:结合长方体的对角线在三个面的投影来理解计算,如图设长方体的高宽高分别为,,m n k ,由题意得2227m n k ++=,226m k +=1n ?=, 21k a +=,21m b +=,所以22(1)(1)6 a b -+-=228a b ?+=,22222()282816a b a ab b ab a b +=++=+≤++=∴4a b ?+≤当且仅当2a b ==时取等号. 点评:本题就是高考中考查三视图的试题中难度最大的一个,我们通过移动三个试图把问题归结为长方体的一条体对角线在三个面上的射影,使问题获得了圆满的解决. 例2下图就是一个几何体的三视图,根据图中数据,可得该几何体的表面积就是 A.9π B.10π C.11π D.12π