振型分解反应谱法
五、计算水平地震作用的振型分解反应谱法(共22张PPT)
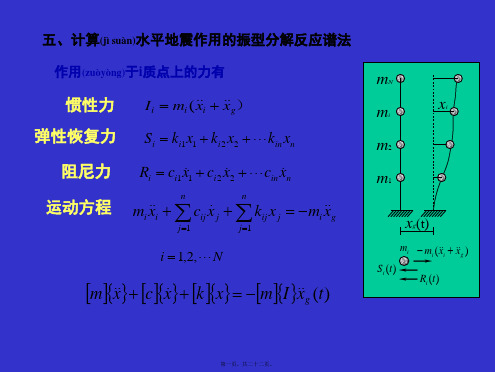
第七页,共二十二页。
Fji j x ji jGi
---体系j振型i质点水平地震作用标准值计算公式
j ---相应于j振型自振周期的地震影响系数; x ji --- j振型i质点的水平相对位移; j --- j振型的振型参与系数; Gi --- i质点的重力荷载代表值。
F1n
F2n
Fjn
Fnn
地震特征周期分组的特征周期值(s)
场地类别 Ⅰ
Ⅱ
Ⅲ
Ⅳ
第一组
0.25
0.35
0.45 0.65
第二组 0.30
0.40
0.55 0.75
第三组 0.35
0.45
0.65 0.90
第十二页,共二十二页。
例:试用振型分解反应谱法计算图示框架多遇地震时的层间剪力。 抗震设防烈度为8度,Ⅱ类场地,设计地震分组为第二组。
334.2kN 334.4kN
1 1.363 2 0.428 3 0.063
(4)计算各振型各楼层的水平(shuǐpíng)地
震作用
Fji j x ji jGi
167.4kN
第一振型
F11 0.139 1.363 0.334 270 9.8 167.4kN
F12 0.139 1.363 0.667 270 9.8 334.4kN
1.000
m3 180t K3 98MN/m m2 270t K2 195MN/m m1 270t K1 245MN/m
T1 0.467s T2 0.208s T3 0.134s (2)计算各振型的地震影响系数
1 0.139 2 0.16 3 0.16 (3)计算各振型的振型参与系数
F13 0.139 1.3631.000 180 9.8 334.2kN
计算水平地震作用的振型分解反应谱法课件

反应谱的确定需要考虑地震动的强度、持续时间、频 谱特性等因素。根据不同的地震动输入和结构特性, 可以采用不同的反应谱形式,如单自由度、多自由度 或弹性反应谱等。
计算步骤
步骤1
建立结构的振动方程。根据结构的质量、 刚度和阻尼矩阵,建立结构的振动方程。
步骤5
组合各个模态的反应值。将各个模态的最 大反应值进行组合,得到整个结构的地震 反应。
开展跨学科合作,引入人工智能、大数据等先进技术,提升振型分解反应谱法的计 算效率和精度,推动其在实际工程中的应用。
实际应用建议
在实际工程中,建议根据具体情况选 择适合的地震动输入和计算方法,综 合考虑结构的特点、地震环境等因素 。
加强抗震设计和抗震措施的培训和技 术交流,提高工程人员的专业水平和 安全意识,确保工程质量和安全。
方法原理
解耦是通过将复杂的振动方程简化为多个简单的振动 方程的过程。在解耦过程中,通常采用模态分解或特 征值分解等方法,将结构的振动方程表示为若干个独 立的模态方程。
单击此处添加正文,文字是您思想的提一一二三四五 六七八九一二三四五六七八九一二三四五六七八九文 ,单击此处添加正文,文字是您思想的提炼,为了最 终呈现发布的良好效果单击此4*25}
振型是结构在地震作用下产生的一种振动形态,每个振型具有特定的频 率和阻尼比。在计算过程中,通常将结构分解为若干个振型,以便更准
确地模拟结构的地震反应。
反应谱是一种描述地震动强度与结构反应之间的关系的方法。它通过将 地震动强度与结构在不同频率下的最大加速度、速度和位移反应联系起 来,为结构的地震反应分析提供了依据。
结果验证与评估
对比分析
将计算结果与实测数据进行对比,分析误差来源和改进方向。
评估结论
振型分解反应谱法

振型分解反应谱法振型分解反应谱法是用来计算多自由度体系地震作用的一种方法。
该法是利用单自由度体系的加速度设计反应谱和振型分解的原理,求解各阶振型对应的等效地震作用,然后按照一定的组合原则对各阶振型的地震作用效应进行组合,从而得到多自由度体系的地震作用效应。
振型分解反应谱法一般可考虑为计算两种类型的地震作用:不考虑扭转影响的水平地震作用和考虑平扭藕联效应的地震作用。
适用条件〔1〕高度不超过40米,以剪切变形为主且质量和刚度沿高度分布比较均匀的结构,以及近似于单质点体系的结构,可采用底部剪力法计算。
〔此为底部剪力法的适用范围〕〔2〕除上述结构以外的建筑结构,宜采用“振型分解反应谱法”。
〔3〕特别不规则的建筑、甲类建筑和标准规定的高层建筑,应采用时程分析法进行补充计算。
刚重比刚重比是指结构的侧向刚度和重力荷载设计值之比,是影响重力二阶效应的主要参数刚重比=Di*Hi/GiDi-第i楼层的弹性等效刚度,可取该层剪力与层间位移的比值Hi-第i楼层层高Gi-第i楼层重力荷载设计值刚重比与结构的侧移刚度成正比关系;周期比的调整将导致结构侧移刚度的变化,从而影响到刚重比。
因此调整周期比时应注意,当某主轴方向的刚重比小于或接近标准限值时,应采用加强刚度的方法;当某主轴方向刚重比大于标准限值较多时,可采用削弱刚度的方法。
同样,对刚重比的调整也可能影响周期比。
特别是当结构的周期比接近标准限值时,应采用加强结构外围刚度的方法标准上限主要用于确定重力荷载在水平作用位移效应引起的二阶效应是否可以忽略不计。
见高规5.4.1和5.4.2及相应的条文说明。
刚重比不满足标准上限要求,说明重力二阶效应的影响较大,应该予以考虑。
标准下限主要是控制重力荷载在水平作用位移效应引起的二阶效应不致过大,防止结构的失稳倒塌。
见高规5.4.4及相应的条文说明。
刚重比不满足标准下限要求,说明结构的刚度相对于重力荷载过小。
但刚重比过分大,则说明结构的经济技术指标较差,宜适当减少墙、柱等竖向构件的截面面积。
计算水平作用的振型分解反应谱法

计算水平作用的振型分解反应谱法水平作用的振型分解反应谱法是一种用于结构地震响应分析的方法。
它通过将结构的地震响应分解为多个模态响应,并结合每个模态的频率、阻尼和模态形态,计算出结构在不同地震波作用下的反应谱。
水平作用的振型分解反应谱法的基本原理是基于结构的振型分解理论。
振型分解理论认为,结构的地震响应可以看作是一系列模态振型的叠加效应。
每个模态都代表了结构在不同频率下的振动行为。
根据模态分解的原理,可以将结构的振动方程简化为模态响应方程。
在计算水平作用的振型分解反应谱时,首先需要确定结构的振型特性,包括结构的固有周期、振型形态和阻尼比。
通常可以通过有限元分析或振动试验等方法来确定这些特性。
然后,需要确定地震波的加速度谱。
地震波的加速度谱描述了地震波在不同频率下的强度。
可以通过查阅地震动数据库或根据地震动参数进行计算来获取。
接下来,可以根据结构的振型特性和地震波的加速度谱,计算每个模态下的反应谱。
对于每个模态,可以首先计算出结构的频率响应函数。
频率响应函数描述了结构在单一频率下的响应特性,包括振幅和相位。
然后,将频率响应函数和地震波的加速度谱进行卷积积分,得到模态响应谱。
模态响应谱描述了结构在单个模态下的振动响应特性,包括最大位移、最大加速度和最大应变等。
最后,将每个模态的响应谱按照其中一种组合规则进行叠加,得到整个结构的反应谱。
常见的组合规则包括将每个模态响应谱按照线性叠加或主应力法进行组合。
线性叠加方法适用于结构的线性响应范围,主应力法适用于结构的非线性响应范围。
通过计算水平作用的振型分解反应谱,可以获得结构在地震作用下的振动响应特性。
这些特性可以用于评估结构的抗震性能,指导结构的设计和加固,以增强结构的地震抗力。
振型分解反应谱法

结构设计系列之振型分解反应谱法苏义前言我国规范对于常规结构设计有两个方法:底部剪力法和振型分解反应谱法。
其中,底部剪力法视多质点体系为等效单质点体系,且其地震作用沿高度呈倒三角形分布,当结构层数较高或体系较复杂时,其计算假再用,因部剪时,其计算假定不再适用,因此规范规定底部剪力法仅适用于高度不超过40m、以剪切变形为主且质量和刚度沿高度分布比较均匀的结构。
因此,一般结构均采用振型分解反应谱法。
振型分解反应谱法的基本步骤:通过体系的模态分析,求出多自由度体系的振型通过体系的模态分析求出多自由度体系的振型向量、参与系数等等;然后把每个振型看作单自由度体系,求出其在规定反应谱的地震加速度作用下产生的地震效应;最后把所有振型的地震效应式进行叠,得到体系震应应按一定方式进行叠加,就会得到体系地震效应的解。
注意注意:振型分解反应谱法只适用于弹性分析,对于弹塑性体系,由于力与位移不再具有对应关系,性体系,由于力与位移不再具有一一对应关系,该法不再适用。
目录一模态分析二反应谱分析三振型组合方法四方向组合方法一、模态分析模态分析也被称作振型叠加法动力分析,是线性体系地震分析中最常用且最有效的方法。
它最主要的优势在于其计算一组正交向量之后,可以将大型整体平衡方程组缩减为相对数量较少的解耦二阶平解阶微分方程,这样就明显减少了用于数值求解这些方程的计算时间。
模态分析为结构相关静力分析提供相关结构性能,包括结构静力地震作用分析和静力风荷载分析。
模态分析是其它动力分析的基础,包括反应谱分析和时程分析。
一、模态分析特征向量分析用于确定体系的无阻尼自由振动的模态和频率,分析这些自振模态是理解结构性能很好的工具。
下面我们以不考虑阻尼的高层建筑为例,了解一下关下面我们以不考虑阻尼的高层建筑为例,了解下关于无阻尼自由振动的一些基本概念。
一、模态分析对于一般的高层建筑,我们可以将其看作多自由度体系。
根据每个质点的力学平衡条件,建立每个质点的振动平衡方程式,联立这些方程式,即为多自由度体系的振动平衡方程组。
振型分解反应谱法具体解释

精选ppt课件
11
The End
Thanks!
精选ppt课件
12
精选ppt课件
9
补充
振型分解反应谱法常用于计算水平地震 作用,且前面所讲的是未考虑扭转振动 的影响,同志们可以参考相关资料得到 相应考虑扭转振动影响的计算过程。
精选ppt课件
10
参考文献
东南大学,建筑结构抗震设计 胡聿贤,地震工程学 卢存恕等,建筑抗震设计实例 王焕定,结构力学 朱伯龙等,建筑结构抗震设计原理
结构物最不利的地震反应为最大的地震 反应,而与其他的动力反应参数无关。
精选ppt课件
4
振型分解反应谱法的理论依据
达朗贝尔原理(列动力平衡方程) 振型正交性 叠加原理 哈米顿原理
精选ppt课件
5
计算过程
将结构简化,建立n自由度结构的频率方程,求出 n个频率及周期
M • x • ( t) C x • ( t) K x ( t) M I x g ( t)
求各频率对应的振型,形成主振型向量。
计算振型参与系数 rn n来自r nXTj MI XTj MXj
mi Xji
i1
n
mi X2ji
i1
精选ppt课件
6
计算过程
根据场地类别确定场地的特征周期Tg,综合该地 区抗震设防烈度及地震分组和反应谱确定每个
振型地震影响系数
计算第j振型第i个质点的水平作用
振型分解反应谱法
制作人 路建波
精选ppt课件
1
振型分解反应谱法
什么是振型分解反应谱法 振型分解反应谱法的基本假设 振型分解反应谱法的理论依据 计算过程 振型分解反应谱法的不足
精选ppt课件
振型分解反应谱法
如何解j振型对应的广义坐标方程
Dj (t)
2
j
j
Dj
2 j
D
j
(t)
j
xg (t)
已知:对于单自由度体系
x 2x 2x xg (t)
x(t) 1
d
t 0
xg (
)e
(t
)
sin
d
(t
)d
对于j振型折算体系(右图)
j
(t
)
1
j
t 0
xg (
)e
j
j
(t
)
sin
j
(t
)d
D
j
(t
)
j j
其中: Fji (t) mi[x ji jj (t) x ji j xg (t)]
---t时刻第j振型i质点的水平地震作用
Fji (t) mi[x ji jj (t) x ji j xg (t)]
---t时刻第j振型i质点的水平地震作用
体系j振型i质点水平地震作用标准值为:
Fji Fji (t) max mi x ji j j (t) xg (t) max
0.55 0.75
第三组 0.35
0.45
0.65 0.90
例:试用振型分解反应谱法计算图示框架多遇地震时的层间剪力。 抗震设防烈度为8度,Ⅱ类场地,设计地震分组为第二组。
解:(1)求体系的自振周期和振型
0.334
0.667
4.019
X 1 0.667 X 2 0.666 X 3 3.035
F1n
F2n
F jn
Fnn
mi
F1i
F2i
F ji
Fni
盈建科采用振型分解反应谱法
盈建科采用振型分解反应谱法振型分解反应谱法是盈建科在结构动力学领域应用的一种方法,该方法可用于分析建筑物在地震作用下的反应,以及评估结构的抗震性能。
本文将详细介绍盈建科采用振型分解反应谱法的原理、步骤和应用案例,以便更好地理解和应用该方法。
首先,我们来了解振型分解反应谱法的原理。
该方法基于振型分解原理,通过将结构动力学问题转化为模态坐标下的一系列单自由度系统,进而求解得到结构的振动模态及其对地震激励的响应。
通过振型分解,我们可以更清晰地了解结构的各个振动模态对地震荷载的响应程度,从而为结构的设计和抗震评估提供依据。
接下来,我们将介绍盈建科采用振型分解反应谱法的具体步骤。
首先,需要确定结构的振型和振型参数。
这可以通过有限元分析、实测数据或者经验公式等方法来获取。
然后,我们可以得到结构的振型矩阵和振型频率。
接下来,需要求解各个模态下的约化质量、模态合成系数和模态质量参与系数。
最后,将得到的各个模态的反应谱与相关地震谱进行叠加计算,得到结构在地震作用下的反应谱。
除了上述步骤,盈建科还将振型分解反应谱法应用于多个工程案例中。
以某高层建筑为例,盈建科使用该方法对其进行抗震性能评估。
通过振型分解反应谱法的分析,我们得到了该建筑在不同振动模态下的反应值,进而评估了其在地震作用下的结构安全性。
通过该方法,我们发现了一些振动模态下结构的薄弱部位,并进行了相应的结构加固设计,确保了建筑在地震中的稳定性和安全性。
总结起来,盈建科采用振型分解反应谱法是一种有效的结构动力学分析方法。
通过该方法,我们可以更清晰地了解结构的振动模态及其对地震荷载的响应,为结构的设计和抗震评估提供依据。
通过应用实例的案例分析,我们证明了该方法在工程实践中的可行性和有效性。
盈建科将继续致力于研究和应用结构动力学领域的先进方法,为建筑行业的发展做出贡献。
振型分解反应谱法具体解释.ppt
制作人 路建波
振型分解反应谱法
什么是振型分解反应谱法 振型分解反应谱法的基本假设 振型分解反应谱法的理论依据 计算过程 振型分解反应谱法的不足
什么是振型分解反应谱法
假定建筑结构是线弹性的多自由度体系, 利用振型分解和振型正交性的原理,将 求解n个自由度弹性体系的地震反应分解 为求解n个独立的等效单自由度弹性体系 的最大地震反应,进而求得对应于每一 个振型的作用效应(弯矩、剪力、 轴向 力),再按一定法则将每个振型的作用效 应组合成总的地震作用效应进行截面抗 震验算。
达朗贝尔原理(列动力平衡方程) 振型正交性 叠加原理 哈米顿原理
计算过程
将结构简化,建立n自由度结构的频率方程,求出 n个频率及周期
x(t ) M I xg (t ) M x(t ) C x(t ) K
Fji i i X jiGi
然后将各个质点处的作用力叠加
计算过程
计算各振型层间剪力,因为各个振型求出的是 最大的反应,需将其组合 n
Fi
2 F i j 1
最后求出结构的反应
振型分解反应谱法的不足
该方法只能是在结构弹性范围内计算, 未考虑结构的塑性状态,并且该方法也 没有考虑时间因素,只是计算了过程中 最大的加速度作为控制因素。
求各频率对应的振型,形成主振型向量。 计算振型参与系数 rn n
X Tj M I r n X T M X j j
m X
i 1 n i 1 i
ji
2 m X i ji
计算过程
根据场地类别确定场地的特征周期Tg,综合该 地区抗震设防烈度及地震分组和反应谱确定每 个振型地震影响系数 计算第j振型第i个质点的水平作用
振型分解反应谱法
振型分解反应谱法振型分解反应谱法就是用来计算多自由度体系地震作用得一种方法、该法就是利用单自由度体系得加速度设计反应谱与振型分解得原理,求解各阶振型对应得等效地震作用,然后按照一定得组合原则对各阶振型得地震作用效应进行组合,从而得到多自由度体系得地震作用效应。
振型分解反应谱法一般可考虑为计算两种类型得地震作用:不考虑扭转影响得水平地震作用与考虑平扭藕联效应得地震作用。
适用条件(1)高度不超过40米,以剪切变形为主且质量与刚度沿高度分布比较均匀得结构,以及近似于单质点体系得结构,可采用底部剪力法计算、(此为底部剪力法得适用范围)(2) 除上述结构以外得建筑结构,宜采用“振型分解反应谱法”。
(3) 特别不规则得建筑、甲类建筑与规范规定得高层建筑,应采用时程分析法进行补充计算。
刚重比刚重比就是指结构得侧向刚度与重力荷载设计值之比,就是影响重力二阶效应得主要参数刚重比=Di*Hi/GiDi—第i楼层得弹性等效刚度,可取该层剪力与层间位移得比值Hi-第i楼层层高Gi-第i楼层重力荷载设计值刚重比与结构得侧移刚度成正比关系;周期比得调整将导致结构侧移刚度得变化,从而影响到刚重比。
因此调整周期比时应注意,当某主轴方向得刚重比小于或接近规范限值时,应采用加强刚度得方法;当某主轴方向刚重比大于规范限值较多时,可采用削弱刚度得方法、同样,对刚重比得调整也可能影响周期比。
特别就是当结构得周期比接近规范限值时,应采用加强结构外围刚度得方法规范上限主要用于确定重力荷载在水平作用位移效应引起得二阶效应就是否可以忽略不计。
见高规5.4。
1与5、4.2及相应得条文说明。
刚重比不满足规范上限要求,说明重力二阶效应得影响较大,应该予以考虑。
规范下限主要就是控制重力荷载在水平作用位移效应引起得二阶效应不致过大,避免结构得失稳倒塌。
见高规5、4.4及相应得条文说明。
刚重比不满足规范下限要求,说明结构得刚度相对于重力荷载过小。
但刚重比过分大,则说明结构得经济技术指标较差,宜适当减少墙、柱等竖向构件得截面面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
振型分解反应谱法振型分解反应谱法就是用来计算多自由度体系地震作用得一种方法。
该法就是利用单自由度体系得加速度设计反应谱与振型分解得原理,求解各阶振型对应得等效地震作用,然后按照一定得组合原则对各阶振型得地震作用效应进行组合,从而得到多自由度体系得地震作用效应。
振型分解反应谱法一般可考虑为计算两种类型得地震作用:不考虑扭转影响得水平地震作用与考虑平扭藕联效应得地震作用。
适用条件(1) 高度不超过40米,以剪切变形为主且质量与刚度沿高度分布比较均匀得结构,以及近似于单质点体系得结构,可采用底部剪力法计算。
(此为底部剪力法得适用范围)(2) 除上述结构以外得建筑结构,宜采用“振型分解反应谱法”。
(3) 特别不规则得建筑、甲类建筑与规范规定得高层建筑,应采用时程分析法进行补充计算。
刚重比刚重比就是指结构得侧向刚度与重力荷载设计值之比,就是影响重力二阶效应得主要参数刚重比=Di*Hi/GiDi-第i楼层得弹性等效刚度,可取该层剪力与层间位移得比值Hi-第i楼层层高Gi-第i楼层重力荷载设计值刚重比与结构得侧移刚度成正比关系;周期比得调整将导致结构侧移刚度得变化,从而影响到刚重比。
因此调整周期比时应注意,当某主轴方向得刚重比小于或接近规范限值时,应采用加强刚度得方法;当某主轴方向刚重比大于规范限值较多时,可采用削弱刚度得方法。
同样,对刚重比得调整也可能影响周期比。
特别就是当结构得周期比接近规范限值时,应采用加强结构外围刚度得方法规范上限主要用于确定重力荷载在水平作用位移效应引起得二阶效应就是否可以忽略不计。
见高规5、4、1与5、4、2及相应得条文说明。
刚重比不满足规范上限要求,说明重力二阶效应得影响较大,应该予以考虑。
规范下限主要就是控制重力荷载在水平作用位移效应引起得二阶效应不致过大,避免结构得失稳倒塌。
见高规5、4、4及相应得条文说明。
刚重比不满足规范下限要求,说明结构得刚度相对于重力荷载过小。
但刚重比过分大,则说明结构得经济技术指标较差,宜适当减少墙、柱等竖向构件得截面面积。
长细比长细比=计算长度/回转半径。
所以很显然,减小计算长度或者加大回转半径即可。
这里需要注意得就是,计算长度并非实际长度,而就是实际长度乘以长度系数,长度系数则与柱子两端得约束刚度有关。
说白了就就是要瞧与柱相连得梁或者基础就是否给力,如果这些构件得刚度越高,那么长度系数就越小,柱子得计算长度也就越短。
具体公式您可以去瞧钢结构规范,我记得长度系数得具体算法就是附录D。
至于回转半径,那就是个几何概念,您去瞧瞧基本得几何手册(当然要高中以上得)就明白如何加大回转半径了,大学课本上有。
高层设计得难点在于竖向承重构件(柱、剪力墙等)得合理布置,设计过程中控制得目标参数主要有如下七个:一、轴压比:主要为限制结构得轴压比,保证结构得延性要求,规范对墙肢与柱均有相应限值要求,见抗规6、3、7与6、4、6,高规6、4、2与7、2、14及相应得条文说明。
轴压比不满足要求,结构得延性要求无法保证;轴压比过小,则说明结构得经济技术指标较差,宜适当减少相应墙、柱得截面面积。
轴压比不满足时得调整方法:1、程序调整:SATWE程序不能实现。
2、人工调整:增大该墙、柱截面或提高该楼层墙、柱混凝土强度。
二、剪重比:主要为限制各楼层得最小水平地震剪力,确保周期较长得结构得安全,见抗规5、2、5,高规3、3、13及相应得条文说明。
这个要求如同最小配筋率得要求,算出来得水平地震剪力如果达不到规范得最低要求,就要人为提高,并按这个最低要求完成后续得计算。
剪重比不满足时得调整方法:1、程序调整:在SATWE得“调整信息”中勾选“按抗震规范5、2、5调整各楼层地震内力”后,SATWE按抗规5、2、5自动将楼层最小地震剪力系数直接乘以该层及以上重力荷载代表值之与,用以调整该楼层地震剪力,以满足剪重比要求。
2、人工调整:如果还需人工干预,可按下列三种情况进行调整:1)当地震剪力偏小而层间侧移角又偏大时,说明结构过柔,宜适当加大墙、柱截面,提高刚度。
2)当地震剪力偏大而层间侧移角又偏小时,说明结构过刚,宜适当减小墙、柱截面,降低刚度以取得合适得经济技术指标。
3)当地震剪力偏小而层间侧移角又恰当时,可在SATWE得“调整信息”中得“全楼地震作用放大系数”中输入大于1得系数增大地震作用,以满足剪重比要求。
三、刚度比:主要为限制结构竖向布置得不规则性,避免结构刚度沿竖向突变,形成薄弱层,见抗规3、4、2,高规4、4、2及相应得条文说明;对于形成得薄弱层则按高规5、1、14予以加强。
刚度比不满足时得调整方法:1、程序调整:如果某楼层刚度比得计算结果不满足要求,SATWE自动将该楼层定义为薄弱层,并按高规5、1、14将该楼层地震剪力放大1、15倍。
2、人工调整:如果还需人工干预,可按以下方法调整:1)适当降低本层层高,或适当提高上部相关楼层得层高。
2)适当加强本层墙、柱与梁得刚度,或适当削弱上部相关楼层墙、柱与梁得刚度。
四、位移比:主要为限制结构平面布置得不规则性,以避免产生过大得偏心而导致结构产生较大得扭转效应。
见抗规3、4、2,高规4、3、5及相应得条文说明。
位移比不满足时得调整方法:1、程序调整:SATWE程序不能实现。
2、人工调整:只能通过人工调整改变结构平面布置,减小结构刚心与形心得偏心距;调整方法如下:1)由于位移比就是在刚性楼板假定下计算得,最大位移比往往出现在结构得四角部位;因此应注意调整结构外围对应位置抗侧力构件得刚度;同时在设计中,应在构造措施上对楼板得刚度予以保证。
2)利用程序得节点搜索功能在SATWE得“分析结果图形与文本显示”中得“各层配筋构件编号简图”中快速找到位移最大得节点,加强该节点对应得墙、柱等构件得刚度;也可找出位移最小得节点削弱其刚度;直到位移比满足要求。
五、周期比:主要为限制结构得抗扭刚度不能太弱,使结构具有必要得抗扭刚度,减小扭转对结构产生得不利影响,见高规4、3、5及相应得条文说明。
周期比不满足要求,说明结构得抗扭刚度相对于侧移刚度较小,扭转效应过大,结构抗侧力构件布置不合理。
周期比不满足时得调整方法:1、程序调整:SATWE程序不能实现。
2、人工调整:只能通过人工调整改变结构布置,提高结构得抗扭刚度;总得调整原则就是加强结构外围墙、柱或梁得刚度,适当削弱结构中间墙、柱得刚度;利用结构刚度与周期得反比关系,合理布置抗侧力构件,加强需要减小周期方向(包括平动方向与扭转方向)得刚度,或削弱需要增大周期方向得刚度。
当结构得第一或第二振型为扭转时可按以下方法调整:1)SATWE程序中得振型就是以其周期得长短排序得。
2)结构得第一、第二振型宜为平动,扭转周期宜出现在第三振型及以后。
见抗规3、5、3条3款及条文说明“结构在两个主轴方向得动力特性(周期与振型)宜相近”。
3)当第一振型为扭转时,说明结构得抗扭刚度相对于其两个主轴(第二振型转角方向与第三振型转角方向,一般都靠近X轴与Y轴)得抗侧移刚度过小,此时宜沿两主轴适当加强结构外围得刚度,并适当削弱结构内部得刚度。
4)当第二振型为扭转时,说明结构沿两个主轴方向得抗侧移刚度相差较大,结构得抗扭刚度相对其中一主轴(第一振型转角方向)得抗侧移刚度就是合理得;但相对于另一主轴(第三振型转角方向)得抗侧移刚度则过小,此时宜适当削弱结构内部沿“第三振型转角方向”得刚度,并适当加强结构外围(主要就是沿第一振型转角方向)得刚度。
5)在进行上述调整得同时,应注意使周期比满足规范得要求。
6)当第一振型为扭转时,周期比肯定不满足规范得要求;当第二振型为扭转时,周期比较难满足规范得要求。
六、刚重比:主要就是控制在风荷载或水平地震作用下,重力荷载产生得二阶效应不致过大,避免结构得失稳倒塌,见高规5、4、1与5、4、4及相应得条文说明。
刚重比不满足要求,说明结构得刚度相对于重力荷载过小;但刚重比过分大,则说明结构得经济技术指标较差,宜适当减少墙、柱等竖向构件得截面面积。
刚重比不满足时得调整方法:1、程序调整:SATWE程序不能实现。
2、人工调整:只能通过人工调整增强竖向构件,加强墙、柱等竖向构件得刚度。
七、层间受剪承载力比:主要为限制结构竖向布置得不规则性,避免楼层抗侧力结构得受剪承载能力沿竖向突变,形成薄弱层,见抗规3、4、2,高规4、4、3及相应得条文说明;对于形成得薄弱层应按高规5、1、14予以加强。
层间受剪承载力比不满足时得调整方法:1、程序调整:在SATWE得“调整信息”中得“指定薄弱层个数”中填入该楼层层号,将该楼层强制定义为薄弱层,SATWE按高规5、1、14将该楼层地震剪力放大1、15倍。
2、人工调整:如果还需人工干预,可适当提高本层构件强度(如增大柱箍筋与墙水平分布筋、提高混凝土强度或加大截面)以提高本层墙、柱等抗侧力构件得抗剪承载力,或适当降低上部相关楼层墙、柱等抗侧力构件得抗剪承载力。
上述几个参数得调整涉及构件截面、刚度及平面位置得改变,在调整过程中可能相互关联,应注意不要顾此失彼。
如果结构竖向较规则,第一次试算时可只建一个结构标准层,待结构得周期比、位移比、剪重比、刚重比等满足之后再添加其它标准层;这样可以减少建模过程中得重复修改,加快建模速度。
自振周期特征周期1、自振周期:就是结构本身得动力特性。
与结构得高度H,宽度B有关。
当自振周期与地震作用得周期接近时,共振发生,对建筑造成很大影响,加大震害。
2、特征周期:就是建筑场地自身得周期,抗震规范中就是通过地震分组与地震烈度查表确定得。
结构得自振周期顾名思义就是反映结构得动力特性,与结构得质量及刚度有关,具体对单自由度就只有一个周期,而对于多自由度就有同模型中采用得自由度相同得周期个数,周期最大得为基本周期,设计用得主要参考数据!而特征周期就是,在地震影响系数曲线中,水平段与下降段交点得横坐标,反映了地震震级,震源机制(包括震源深度)、震中距等地震本身方面得影响,同时也反映了场地得特性;如软弱土层得厚度,类型等场地类别,所以我认为特征周期同时反映了地震动及场地得特性!它在确定地震影响曲线时用到!1.特征周期:就是建筑物场地得地震动参数由场地得地质条件决定;2、自振周期有结构子身得结构特点决定用结构力学方法求解;主要指第一振型得主振周期3.结构得自振周期主要就是避免与场地得卓越周期重合产生共振;4、卓越周期与特征周期有关;卓越周期由场地得覆盖土层厚度与土层剪切波速计算求解(见工程地质手册)。
设计特征周期:抗震设计用得地震影响系数曲线中,反映地震等级,震中距与场地类别等因素得下降段起始点对应得周期值、-----根据其所在地得设计地震分组与场地类别确定、详见抗震规范、自振周期:就是结构本身得动力特性、与结构得H,B有关、当自振周期与地震作用得1/f接近时,共振发生,对建筑造成很大影响、另外: 目前就场地得有关周期,经常出现场地脉动(卓越)周期,地震动卓越周期与反应谱特征周期等名词。
