evalgraph函数
Creo常用函数.doc

Creo(PROE)中关系式的理解一)关系式中可以用下列数学函数式表达:1)、正弦sin( )2)、余弦cos( )3)、正切tan( )4)、反正弦asin( )5)、反余弦acos( )6)、反正切atan( )7)、双曲线正弦sinh( )8)、双曲线余弦cosh( )9)、双曲线正切tanh( )以上九种三角函数式所使用的单位均为“度”。
10)、平方根sqrt( )11)、以10为底的对数log( )12)、自然对数ln( )13)、e的幂exp( )14)、绝对值abs( )15)、不小于其值的最小整数(上限值)ceil( )16)、不超过其值的最大整数(下限值)floor( )可以给函数ceil和floor加一个可选的自变量,用它指定要圆整的小数位数。
带有圆整参数的这些函数的语法是:ceil(parameter_name或number, number_of_dec_places)floor (parameter_name 或number, number_of_dec_places)其中的parameter_name或number意为参数名称或者一个带小数位的精确数值后面跟随着的number_of_dec_places意为十进位的小数位数,是可选值:A)可以被表示为一个数或一个使用者自定义参数。
如果该参数值是一个实数,则被截尾成为一个整数。
B)它的最大值是8。
如果超过8,则不会舍入要舍入的数(第一个自变量),并使用其初值。
C)如果不指定它,则功能同前期版本一样。
使用不指定小数部分位数的ceil和floor函数,其举例如下:ceil (10.2) 值为11floor (10.2) 值为10使用指定小数部分位数的ceil和floor函数,其举例如下:ceil (10.255, 2) 等于10.26ceil (10.255, 0) 等于11 [ 与ceil (10.255)相同]ceil(10.25531415926,7)等于10.2553142ceil(10.25531415926,8)等于10.25531416floor (10.255, 2) 等于10.25floor (10.255, 0) 等于10.Floor(10.2531415926,7)等于10.2553141Floor(10.2531415926,8)等于10.25531415举例一:以上函数式通常用的四种表达式如下图:以上两种曲线是在proe中的曲线—从方程—指定坐标系(选系统中固有的坐标系)—选笛卡儿坐标,就会出现公式界面,再输入如上公式。
#CREO关系式函数说明教程

CREO关系式函数说明1)absabs() 为绝对值函数例如:x=20*(t-0.5)+5*cos(t*540)y=10*sin(t*540)z=abs(t-0.5)总是没办法输出曲线,有谁清楚为什么?后来发现一个方法也可以实现绝对值即z=sqrt((t-0.5)^2)2)acosacos () 为反余弦3)asinasin () 为反正弦4)atanatan () 为反正切5)atan2atan2 () 为反正切弧度制6)bound函数bound(x,first,last)返回的是大于等于last而小于等于last并且等于或接近x的值。
例:a=bound(3,1,8) 则a=3 因为3在1和8之间,所以a=3a=bound(8,1,4) 则a=4 因为8>4,所以a=4为最接近结果a=bound(1,5,12) 则a=5 因为1<5,所以a=5为最接近结果7)cable_len函数???8)ceilceil() 为不小于其值的最小整数9)comparegraphs函数???10)coscos() 为余弦11)coshcosh() 为双曲线余弦12)dbl_in_tol???13)dead???14)eang???15)ecoordx???16)ecoordy???17)edist???18)elen???19)evalgraph("图形名称", x) 为图形取值函数曲线表计算使使用者能用曲线表特征,通过关系来驱动尺寸。
尺寸可以是草绘器、零件或组件尺寸。
格式如下:evalgraph("图形名称", x) ,其中graph_name是曲线表的名称,x是沿曲线表x-轴的值,返回y值。
对于混合特征,可以指定轨线参数trajpar作为该函数的第二个自变量。
注释:曲线表特征通常是用于计算x-轴上所定义范围内x值对应的y值。
当超出范围时,y值是通过外推的方法来计算的。
#CREO关系式函数说明报告

CREO关系式函数说明1)absabs() 为绝对值函数例如:x=20*(t-0.5)+5*cos(t*540)y=10*sin(t*540)z=abs(t-0.5)总是没办法输出曲线,有谁清楚为什么?后来发现一个方法也可以实现绝对值即z=sqrt((t-0.5)^2)2)acosacos () 为反余弦3)asinasin () 为反正弦4)atanatan () 为反正切5)atan2atan2 () 为反正切弧度制6)bound函数bound(x,first,last)返回的是大于等于last而小于等于last并且等于或接近x的值。
例:a=bound(3,1,8) 则a=3 因为3在1和8之间,所以a=3a=bound(8,1,4) 则a=4 因为8>4,所以a=4为最接近结果a=bound(1,5,12) 则a=5 因为1<5,所以a=5为最接近结果7)cable_len函数???8)ceilceil() 为不小于其值的最小整数9)comparegraphs函数???10)coscos() 为余弦11)coshcosh() 为双曲线余弦12)dbl_in_tol???13)dead???14)eang???15)ecoordx???16)ecoordy???17)edist???18)elen???19)evalgraph("图形名称", x) 为图形取值函数曲线表计算使使用者能用曲线表特征,通过关系来驱动尺寸。
尺寸可以是草绘器、零件或组件尺寸。
格式如下:evalgraph("图形名称", x) ,其中graph_name是曲线表的名称,x是沿曲线表x-轴的值,返回y值。
对于混合特征,可以指定轨线参数trajpar作为该函数的第二个自变量。
注释:曲线表特征通常是用于计算x-轴上所定义范围内x值对应的y值。
当超出范围时,y值是通过外推的方法来计算的。
proe各种函数说明

关系类型
有两种类型的关系: ·等式 - 使等式左边的一个参数等于右边的表达式。这种关系用于给尺寸和参数赋值。例如:
简单的赋值:d1 = 4.75
复杂的赋值:d5 = d2*(SQRT(d7/3.0+d4))
·比较 - 比较左边的表达式和右边的表达式。这种关系通常用于作为一个约束或用于逻辑分支的条件语句中。例如:
—使用者参数名不能包含非字母数字字符,诸如!、@、#、$。
飞碟 球坐标 rho=20*t^2 theta=60*log(30)*t phi=7200*t "rho=200*t" "theta=900*t" "phi=t*90*10"
篮子 圆柱坐标 r=5+0.3*sin(t*180)+t theta=t*360*30 z=t*5
正弦曲线 笛卡尔坐标系 eyf4 x=50*t y=10*sin(t*360) z=0
螺旋线(Helical curve) 圆柱坐标 r=t theta=10+t*(20*360) z=t*3
蝴蝶曲线 球坐标 rho = 8 * t theta = 360 * t * 4 phi = -360 * t * 8
·数组关系 - 使用数组所特有的关系。
注释:
—如果试图将截面之外的关系指派给已经由截面关系驱动的参数,则系统再生模型时给出错误信息。试图将关系指派给已经由截面之外关系驱动的参数时也同样。删除关系之一并重新生成。
—如果组件试图给已经由零件或子组件关系驱动的尺寸变量指派值时,出现两个错误信息。删除关系之一并重新生成。
关于关系
关系(也被称为参数关系)是使用者自定义的符号尺寸和参数之间的等式。关系捕获特征之间、参数之间或组件组件之间的设计关系,因此,允许使用者来控制对模型修改的影响作用。 关系是捕获设计知识和意图的一种方式。和参数一样,它们用于驱动模型 - 改变关系也就改变了模型。关系可用于控制模型修改的影响作用、定义零件和组件中的尺寸值、为设计条件担当约束(例如,指定与零件的边相关的孔的位置)。 它们用在设计过程中来描述模型或组件的不同部分之间的关系。关系可以是简单值(例如,d1=4)或复杂的条件分支语句。
CREO2.0可变截面扫描与关系函数的高级应用
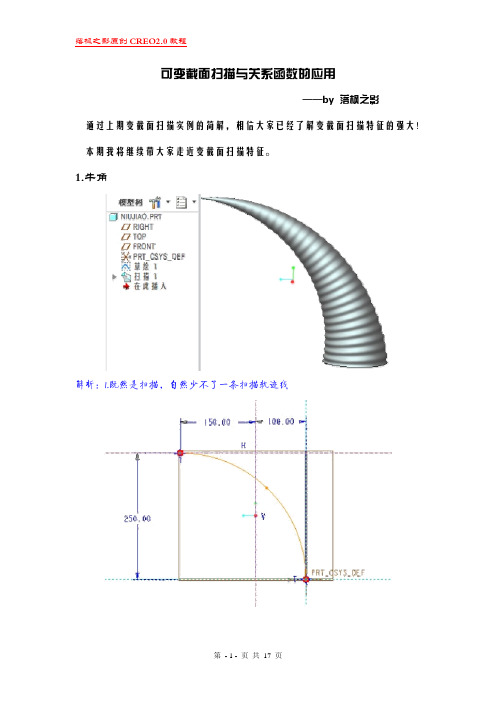
可变截面扫描与关系函数的应用——by落枫之影通过上期变截面扫描实例的简解,相信大家已经了解变截面扫描特征的强大!本期我将继续带大家走近变截面扫描特征。
1.牛角解析:1.既然是扫描,自然少不了一条扫描轨迹线2.退出草绘,选择变截面扫描工具选择草绘曲线作为扫描轨迹线,绘制如下图截面.3.分析此牛角,以圆作为扫描截面,那么圆截面大小将有两种变化A.直径越来越小【可以使用关系((1-trajpar)*直径))来完成】B.直径作正弦(或余弦)变化【可以使用关系(直径+Asin(trajpar*360*n))来完成】综上所述,截面关系可写成:sd3=(1-trajpar)*100-2*(1-trajpar)*sin(trajpar*360*30)+0.005像这种复杂的关系式并不是一次就能写出来的,大都是先写个大概,然后再慢慢调整关系中的数值来完成。
这条关系式虽复杂,但并不难懂。
在截面圆直径逐步减小的同时,让其正弦变化的振幅从2到0线性递减,从而形成牛角表面凹凸逐步平缓的效果。
2.扭纹灯罩解析:初拿此图确实让人不知如何下手。
倘若你有看过上期的果盘教程,相信你已经有了解题的思路。
1.草绘变截面扫描轨迹2.绘制如下图所示截面。
在变截面扫描中,有关系驱动的截面中,约束十分重要。
同样的截面,同样的画法,不一样约束,可能会导致不一样的结果。
所以我一般都会按住【shift键+鼠标左键】拖动图形来验证截面约束是否是我想要的结果。
截面绘制要灵活,不可生搬硬套。
所绘制的截面必须包含以下信息A控制扭纹角度【180度扭转可使用关系:A+trajpat*1(80-A)(A为初始角度),】B.控制灯罩轮廓(类似锥形,也就是扫描截面逐渐变小)【可使用图形控制】C.控制灯罩凸纹逐渐变浅。
【可使用图形控制】3.先不写关系,退出草绘和变截面扫描特征,并将【在此插入】拖到变截面扫描特征的上方,使用图形工具,命名为“tu“,绘制如下图所示图形再次使用图形工具,命名为“tu2”,绘制如下图所示图形4.编辑可变截面扫描特征,进入草绘截面,加入如下图所示的关系式。
ProeCreoUG曲线方程大全及关系式、函数的说明资料

Proe Creo UG 曲线方程大全及关系式、函数的说明资料Pro/E 各种曲线方程集合 1.碟形弹簧 圓柱坐标 方程:r = 5 theta = t*3600z =(sin(3.5*theta-90))+24*t图1圆柱坐标(cylindrical ) 方程: r=ttheta=10+t*(20*360) z=t*3图34.蝴蝶曲线 球坐标方程:rho = 8 * t theta = 360 * t * 4 phi = -360 * t * 8图4图5笛卡儿坐标方程:x = 4 * cos ( t *(5*360))y = 4 * sin ( t *(5*360))z = 10*t图611.心脏线圓柱坐标方程:a=10r=a*(1+cos(theta))theta=t*360Pro/E 各种曲线方程集合(二)Array22.外摆线迪卡尔坐标方程:theta=t*720*5b=8a=5x=(a+b)*cos(theta)-b*cos((a/b+1)*theta)y=(a+b)*sin(theta)-b*sin((a/b+1)*theta)z=0图22 23. Lissajous 曲线theta=t*360a=1b=1c=100n=3x=a*sin(n*theta+c)y=b*sin(theta) Array图23 24.长短幅圆内旋轮线卡笛尔坐标方程:a=5b=7c=2.2theta=360*t*10x=(a-b)*cos(theta)+c*cos((a/b-1)*theta)y=(a-b)*sin(theta)-c*sin((a/b-1)*theta)图2425.长短幅圆外旋轮线卡笛尔坐标方程:theta=t*360*10a=5b=3c=5x=(a+b)*cos(theta)-c*cos((a/b+1)*theta)y=(a+b)*sin(theta)-c*sin((a/b+1)*theta)图2526. 三尖瓣线a=10x = a*(2*cos(t*360)+cos(2*t*360))y = a*(2*sin(t*360)-sin(2*t*360))图2627.概率曲线!方程:笛卡儿坐标x = t*10-5y = exp(0-x^2)图2728.箕舌线笛卡儿坐标系a = 1x = -5 + t*10y = 8*a^3/(x^2+4*a^2)图2829.阿基米德螺线柱坐标a=100theta = t*400r = a*theta图2930.对数螺线柱坐标theta = t*360*2.2a = 0.005r = exp(a*theta)图3031.蔓叶线笛卡儿坐标系a=10y=t*100-50solvex^3 = y^2*(2*a-x)for x图3132.tan曲线笛卡儿坐标系x = t*8.5 -4.25y = tan(x*20)图3233.双曲余弦x = 6*t-3y = (exp(x)+exp(0-x))/2图3334.双曲正弦x = 6*t-3y = (exp(x)-exp(0-x))/2图34 35.双曲正切y = (exp(x)-exp(0-x))/(exp(x)+exp(0-x))图3536.一峰三驻点曲线x = 3*t-1.5y=(x^2-1)^3+1图3637.八字曲线x = 2 * cos ( t *(2*180))y = 2 * sin ( t *(5*360))z = 0图37r=t*(10*180)+1theta=10+t*(20*180)z=t图3839.圆x = cos ( t *(5*180))y = sin ( t *(5*180))z = 0图39 40.封闭球形环绕曲线rho=2theta=360*tphi=t*360*10图4041.柱坐标螺旋曲线x = 100*t * cos ( t *(5*180))y = 100*t * sin ( t *(5*180))z = 0Pro/E 各种曲线方程集合(三)42.蛇形曲线x = 2 * cos ( (t+1) *(2*180))y = 2 * sin ( t *(5*360))z = t*(t+1)图4243.8字形曲线柱坐标theta = t*360r=10+(8*sin(theta))^2图4344.椭圆曲线笛卡尔坐标系a = 10b = 20theta = t*360x = a*cos(theta)y = b*sin(theta)图4445.梅花曲线柱坐标theta = t*360r=10+(3*sin(theta*2.5))^2图4546.另一个花曲线theta = t*360r=10-(3*sin(theta*3))^2z=4*sin(theta*3)^2图4647.改一下就成为空间感更强的花曲线了;)theta = t*360r=10-(3*sin(theta*3))^2z=(r*sin(theta*3))^2图4748.螺旋上升的椭圆线a = 10b = 20theta = t*360*3x = a*cos(theta)y = b*sin(theta)z=t*12图4849.甚至这种螺旋花曲线theta = t*360*4r=10+(3*sin(theta*2.5))^2z = t*16图4950 鼓形线笛卡尔方程r=5+3.3*sin(t*180)+ttheta=t*360*10z=t*10图50 51 长命锁曲线笛卡尔方程:a=1*t*359.5b=q2*t*360c=q3*t*360rr1=w1rr2=w2rr3=w3x=rr1*cos(a)+rr2*cos(b)+rr3*cos(c)y=rr1*sin(a)+rr2*sin(b)+rr3*sin(c)图5152 簪形线球坐标方程:rho=200*ttheta=900*tphi=t*90*10图52 53.螺旋上升曲线r=t^10theta=t^3*360*6*3+t^3*360*3*3z=t^3*(t+1)图5354.蘑菇曲线rho=t^3+t*(t+1)theta=t*360phi=t^2*360*20*20图5455. 8字曲线a=1b=1x=3*b*cos(t*360)+a*cos(3*t*360)Y=b*sin(t*360)+a*sin(3*t*360)图5556.梅花曲线theta=t*360r=100+50*cos(5*theta)z=2*cos(5*theta)图5657.桃形曲线rho=t^3+t*(t+1)theta=t*360phi=t^2*360*10*10图5758.名稱:碟形弹簧建立環境:pro/e圓柱坐r = 5theta = t*3600z =(sin(3.5*theta-90))+24图5859.环形二次曲线笛卡儿方程:x=50*cos(t*360)y=50*sin(t*360)z=10*cos(t*360*8)图5960 蝶线球坐标:rho=4*sin(t*360)+6*cos(t*360^2)theta=t*360phi=log(1+t*360)*t*360图6061.正弦周弹簧笛卡尔:ang1=t*360ang2=t*360*20x=ang1*2*pi/360y=sin(ang1)*5+cos(ang2)z=sin(ang2)Pro/E 各种曲线方程集合(四)62.环形螺旋线x=(50+10*sin(t*360*15))*cos(t*360)y=(50+10*sin(t*360*15))*sin(t*360)z=10*cos(t*360*5)图6263.内接弹簧x=2*cos(t*360*10)+cos(t*180*10)y=2*sin(t*360*10)+sin(t*180*10)z=t*6图6364.多变内接式弹簧x=3*cos(t*360*8)-1.5*cos(t*480*8)y=3*sin(t*360*8)-1.5*sin(t*480*8)z=t*8图6465.柱面正弦波线柱坐标:方程r=30theta=t*360z=5*sin(5*theta-90)图65 66. ufo (漩涡线). 球坐标:rho=t*20^2theta=t*log(30)*60phi=t*7200图6667. 手把曲线thta0=t*360thta1=t*360*6r0=400r1=40r=r0+r1*cos(thta1)x=r*cos(thta0)y=r1*sin(thta1)z=0图6768.篮子圆柱坐标r=5+0.3*sin(t*180)+ttheta=t*360*30z=t*5图6869. 圆柱齿轮齿廓的渐开线方程:afa=60*tx=10*cos(afa)+pi*10*afa/180*sin(afa)x=10*sin(afa)-pi*10*afa/180*cos(afa)z=0注:afa为压力角,取值范围是0到60,10为基圆半径。
ProeCreoUG曲线方程大全及关系式、函数的说明资料
Proe Creo UG 曲线方程大全及关系式、函数的说明资料Pro/E 各种曲线方程集合 1.碟形弹簧 圓柱坐标 方程:r = 5theta = t*3600z =(sin(3.5*theta-90))+24*t图12.葉形线.圆柱坐标(cylindrical ) 方程: r=ttheta=10+t*(20*360) z=t*3图3图5笛卡儿坐标方程:x = 4 * cos ( t *(5*360))y = 4 * sin ( t *(5*360))z = 10*t图611.心脏线圓柱坐标方程:a=10r=a*(1+cos(theta))theta=t*360Pro/E 各种曲线方程集合(二)Array22.外摆线迪卡尔坐标方程:theta=t*720*5b=8a=5x=(a+b)*cos(theta)-b*cos((a/b+1)*theta)y=(a+b)*sin(theta)-b*sin((a/b+1)*theta)z=0图22 23. Lissajous 曲线theta=t*360a=1b=1c=100n=3x=a*sin(n*theta+c)y=b*sin(theta)图23 24.长短幅圆内旋轮线卡笛尔坐标b=7c=2.2theta=360*t*10x=(a-b)*cos(theta)+c*cos((a/b-1)*theta)y=(a-b)*sin(theta)-c*sin((a/b-1)*theta)图24 25.长短幅圆外旋轮线卡笛尔坐标方程:theta=t*360*10a=5b=3c=5x=(a+b)*cos(theta)-c*cos((a/b+1)*theta)y=(a+b)*sin(theta)-c*sin((a/b+1)*theta)图2526. 三尖瓣线a=10x = a*(2*cos(t*360)+cos(2*t*360))y = a*(2*sin(t*360)-sin(2*t*360))图26 27.概率曲线!方程:笛卡儿坐标x = t*10-5y = exp(0-x^2)图27 28.箕舌线笛卡儿坐标系a = 1x = -5 + t*10y = 8*a^3/(x^2+4*a^2)图28 29.阿基米德螺线柱坐标a=100theta = t*400r = a*theta图29 30.对数螺线柱坐标theta = t*360*2.2a = 0.005r = exp(a*theta)图30 31.蔓叶线笛卡儿坐标系a=10y=t*100-50solvex^3 = y^2*(2*a-x)for x图31 32.tan曲线笛卡儿坐标系x = t*8.5 -4.25y = tan(x*20)图32 33.双曲余弦x = 6*t-3y = (exp(x)+exp(0-x))/2图33 34.双曲正弦x = 6*t-3y = (exp(x)-exp(0-x))/2图34 35.双曲正切y = (exp(x)-exp(0-x))/(exp(x)+exp(0-x))图35 36.一峰三驻点曲线x = 3*t-1.5y=(x^2-1)^3+1图36 37.八字曲线x = 2 * cos ( t *(2*180))y = 2 * sin ( t *(5*360))z = 0图37r=t*(10*180)+1theta=10+t*(20*180)z=t图38 39.圆x = cos ( t *(5*180))y = sin ( t *(5*180))z = 0图39 40.封闭球形环绕曲线rho=2phi=t*360*10图40 41.柱坐标螺旋曲线x = 100*t * cos ( t *(5*180))y = 100*t * sin ( t *(5*180))z = 0Pro/E 各种曲线方程集合(三)42.蛇形曲线x = 2 * cos ( (t+1) *(2*180))y = 2 * sin ( t *(5*360))z = t*(t+1)图42 43.8字形曲线柱坐标theta = t*360r=10+(8*sin(theta))^2图43 44.椭圆曲线笛卡尔坐标系a = 10b = 20theta = t*360x = a*cos(theta)y = b*sin(theta)图44 45.梅花曲线柱坐标theta = t*360r=10+(3*sin(theta*2.5))^2图45 46.另一个花曲线theta = t*360r=10-(3*sin(theta*3))^2z=4*sin(theta*3)^2图46 47.改一下就成为空间感更强的花曲线了;)theta = t*360r=10-(3*sin(theta*3))^2z=(r*sin(theta*3))^2图4748.螺旋上升的椭圆线a = 10b = 20theta = t*360*3x = a*cos(theta)y = b*sin(theta)z=t*12图48 49.甚至这种螺旋花曲线theta = t*360*4r=10+(3*sin(theta*2.5))^2z = t*16图49 50 鼓形线笛卡尔方程r=5+3.3*sin(t*180)+ttheta=t*360*10z=t*10图50 51 长命锁曲线笛卡尔方程:a=1*t*359.5b=q2*t*360c=q3*t*360rr1=w1rr2=w2rr3=w3x=rr1*cos(a)+rr2*cos(b)+rr3*cos(c)y=rr1*sin(a)+rr2*sin(b)+rr3*sin(c)图51 52 簪形线球坐标方程:rho=200*ttheta=900*tphi=t*90*10图52 53.螺旋上升曲线r=t^10theta=t^3*360*6*3+t^3*360*3*3z=t^3*(t+1)图53 54.蘑菇曲线rho=t^3+t*(t+1)theta=t*360phi=t^2*360*20*20图54 55. 8字曲线a=1b=1x=3*b*cos(t*360)+a*cos(3*t*360)Y=b*sin(t*360)+a*sin(3*t*360)图55 56.梅花曲线theta=t*360r=100+50*cos(5*theta)z=2*cos(5*theta)图5657.桃形曲线rho=t^3+t*(t+1)theta=t*360phi=t^2*360*10*10图57 58.名稱:碟形弹簧建立環境:pro/e圓柱坐r = 5theta = t*3600z =(sin(3.5*theta-90))+24图58 59.环形二次曲线笛卡儿方程:x=50*cos(t*360)y=50*sin(t*360)z=10*cos(t*360*8)图59 60 蝶线球坐标:rho=4*sin(t*360)+6*cos(t*360^2)theta=t*360phi=log(1+t*360)*t*360图60 61.正弦周弹簧笛卡尔:ang1=t*360ang2=t*360*20x=ang1*2*pi/360y=sin(ang1)*5+cos(ang2)z=sin(ang2)Pro/E 各种曲线方程集合(四)62.环形螺旋线x=(50+10*sin(t*360*15))*cos(t*360)y=(50+10*sin(t*360*15))*sin(t*360)z=10*cos(t*360*5)图62 63.内接弹簧x=2*cos(t*360*10)+cos(t*180*10)y=2*sin(t*360*10)+sin(t*180*10)z=t*6图63 64.多变内接式弹簧x=3*cos(t*360*8)-1.5*cos(t*480*8)y=3*sin(t*360*8)-1.5*sin(t*480*8)z=t*8图64 65.柱面正弦波线柱坐标:方程r=30theta=t*360z=5*sin(5*theta-90)图65 66. ufo (漩涡线)球坐标:rho=t*20^2theta=t*log(30)*60phi=t*7200图66 67. 手把曲线thta0=t*360thta1=t*360*6r0=400r1=40r=r0+r1*cos(thta1)x=r*cos(thta0)y=r1*sin(thta1)z=0图67 68.篮子圆柱坐标r=5+0.3*sin(t*180)+ttheta=t*360*30z=t*5图68 69. 圆柱齿轮齿廓的渐开线方程:afa=60*tx=10*cos(afa)+pi*10*afa/180*sin(afa)x=10*sin(afa)-pi*10*afa/180*cos(afa)z=0注:afa为压力角,取值范围是0到60,10为基圆半径。
creo evalgraph 用法
CREO中的Evalgraph功能主要用于对散点数据进行曲线拟合,帮助用户方便快捷地进行数据分析和曲线设计。
具体使用方法如下:
1. 打开CREO软件,并导入需要进行曲线拟合的散点数据。
2. 在软件界面中,选择“工具”菜单下的“关系”选项。
3. 在弹出的“关系”对话框中,输入对应的数学关系式。
在CREO 中,可以使用系统默认的基准控制曲线计算函数Evalgraph,其格式如下:sd#=evalgraph(“graph_name”, x_value),其中sd#代表欲变化的参数(sd表示草绘尺寸),graph_name表示的是基准图形的名称,x_value代表扫描的“行程”。
4. 输入完成后,点击“确定”按钮,CREO将会自动进行曲线拟合,并生成对应的曲线。
5. 在生成的曲线上,用户可以根据实际需要进行调整和修改,以达到更好的拟合效果。
需要注意的是,在使用Evalgraph功能时,用户需要对数学关系式进行正确的编写,以确保生成的曲线能够准确地拟合散点数据。
同时,在拟合过程中,用户还可以根据需要对曲线的平滑度、逼近程度等参数进行调整,以达到更好的拟合效果。
creo关系式函数说明
creo关系式函数说明CREO关系式函数说明1) absabs() 为绝对值函数例如:x=20*(t-0.5)+5*cos(t*540)y=10*sin(t*540) z=abs(t-0.5)总是没办法输出曲线,有谁清楚为什么, 后来发现一个方法也可以实现绝对值即 z=sqrt((t-0.5)^2)2) acosacos () 为反余弦3) asinasin () 为反正弦4) atanatan () 为反正切5) atan2atan2 () 为反正切弧度制6) bound函数bound(x,first,last) 返回的是大于等于last而小于等于last并且等于或接近x的值。
例:a=bound(3,1,8) 则a=3 因为3在1和8之间,所以a=3 a=bound(8,1,4) 则a=4 因为8>4,所以a=4为最接近结果 a=bound(1,5,12) 则a=5 因为1<5,所以a=5为最接近结果7) cable_len函数,,,8) ceilceil() 为不小于其值的最小整数9) comparegraphs函数,,,10) coscos() 为余弦11) coshcosh() 为双曲线余弦12) dbl_in_tol,,,13) dead,,,14) eang,,,15) ecoordx,,,16) ecoordy,,,17) edist,,,18) elen,,,19)evalgraph("图形名称", x) 为图形取值函数曲线表计算使使用者能用曲线表特征,通过关系来驱动尺寸。
尺寸可以是草绘器、零件或组件尺寸。
格式如下:evalgraph("图形名称", x) ,其中graph_name是曲线表的名称,x是沿曲线表x-轴的值,返回y值。
对于混合特征,可以指定轨线参数trajpar作为该函数的第二个自变量。
注释:曲线表特征通常是用于计算x-轴上所定义范围内x值对应的y值。
CREO关系式函数说明资料
CREO关系式函数说明1)absabs() 为绝对值函数例如:x=20*(t-0.5)+5*cos(t*540)y=10*sin(t*540)z=abs(t-0.5)总是没办法输出曲线,有谁清楚为什么?后来发现一个方法也可以实现绝对值即z=sqrt((t-0.5)^2)2)acosacos () 为反余弦3)asinasin () 为反正弦4)atanatan () 为反正切5)atan2atan2 () 为反正切弧度制6)bound函数bound(x,first,last)返回的是大于等于last而小于等于last并且等于或接近x的值。
例:a=bound(3,1,8) 则a=3 因为3在1和8之间,所以a=3a=bound(8,1,4) 则a=4 因为8>4,所以a=4为最接近结果a=bound(1,5,12) 则a=5 因为1<5,所以a=5为最接近结果7)cable_len函数???8)ceilceil() 为不小于其值的最小整数9)comparegraphs函数???10)coscos() 为余弦11)coshcosh() 为双曲线余弦12)dbl_in_tol???13)dead???14)eang???15)ecoordx???16)ecoordy???17)edist???18)elen???19)evalgraph("图形名称", x) 为图形取值函数曲线表计算使使用者能用曲线表特征,通过关系来驱动尺寸。
尺寸可以是草绘器、零件或组件尺寸。
格式如下:evalgraph("图形名称", x) ,其中graph_name是曲线表的名称,x是沿曲线表x-轴的值,返回y值。
对于混合特征,可以指定轨线参数trajpar作为该函数的第二个自变量。
注释:曲线表特征通常是用于计算x-轴上所定义范围内x值对应的y值。
当超出范围时,y值是通过外推的方法来计算的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
如果你很了解这个公式sd1=evalgraph("g1",trajpar*100)
那就没有必要再看下去了.本节只是对此用法的最简单介绍.
sd1=evalgraph("g1",trajpar*100)
简单说这句的意思就是将基准图形G1特定范围内的每一个横坐标
对应的纵坐标的值赋给SD1.SD1是一个尺寸名称.
Trajpar*100的意思是在G1图形中取X=0与X=100之间的只一段所对应的
纵坐标作为取值范围. Trajpar是[0,1]的一个范围.开始取0,结束取1.
这类公式多见于可变截面扫描中对可变尺寸的控制.
以下简单分析一下.
可变截面扫描的元素为:(截面和轨迹都是直线,且相互垂直)
上面这个变截面扫描相信谁都会创建,其中扫描截面的尺寸受函数影响.
sd1=evalgraph("g1",trajpar*100)
当扫描轨迹长度为100的时候.扫描出来的曲面(显示线框模式)
和基准图形G1从某种角度来看是一样的:Y从开始25变化到结束75.
当扫描轨迹长度为50的时候.扫描出来的曲面的斜边部分变得异常陡峭.
Y依然从开始的25变化到75,但是中间距离因为缩减成50,
因此变化的趋势更明显了.
当扫描轨迹长度为200的时候.扫描出来的曲面的斜边部
分变得非常平缓.Y依然从开始的25变化到75,但是中间距
离因为增加了一倍,因此变化的斜度就少了很多.
上面几个图的斜度没有标出来,单靠眼睛已经可以明显辨别出其变化的趋势了.
从上面几个图到底带来了什么启示呢?对于同一个公式
sd1=evalgraph("g1",trajpar*100)
所扫描出来的曲面的Y坐标总是要从25开始75结束.
而中间扫描轨迹的长度只会影响
其变化的剧烈程度.就好像在爬山.
归纳上面几个图,我想这个函数你应该明白了至少一半.
接着看一下trajpar的影响.
看下图.将原来sd1=evalgraph("g1",trajpar*100)
修改为:sd1=evalgraph("g1",trajpar*200)
扫描轨迹长度为100
这个图的Y坐标从25开始从125结束.
但是我基准图形最高只画到75,125是怎么出来的呢?
试着将基准图形延长一下,测量X为200对应的Y值,恰恰就是125.
在基准图形测量X为50时候基准图形对应的Y坐标之后发现,恰好是50.
上面修改了两次Trajpar的乘数之后发现Y的结束坐标有了变化.这说明了什么呢?Trajpar*100就说明允许取Y最大值为基准图形上X为100所对应的Y值
Trajpar*200就说明允许取Y最大值为基准图形上X为200所对应的Y值,
不够长的话自动寻找延长线上的点(考虑一下如果基准图形是曲线而不是直线的情况)Trajpar*50就说明允许取Y最大值为基准图形上X为50所对应的Y值
因此可以知道evalgraph()
函数的第二个参数实际上控制SD1可取值的范围.
第一个参数当然是基准图形.
如果再修改一下:
<span style="display:none" ; style="$ _" a5 l$ u9 D& r. `6 p1 |1 t sd1=evalgraph("g1",20+trajpar*100)
那就变成是取基准图形上最小X=20对应的Y值
最大X=20+100 对应的Y值.。
