同弧所对的圆周角均相等(几何证明)
《圆周角》 讲义

《圆周角》讲义一、引入在我们探索圆的世界时,圆周角是一个非常重要的概念。
想象一下,你在操场上跑步,绕着圆形跑道,从不同的位置观察圆心,角度会有所不同。
这些角度与圆的关系,就是我们今天要研究的圆周角。
二、圆周角的定义圆周角指的是顶点在圆上,并且两边都和圆相交的角。
比如,在圆O 中,点 A 在圆上,角 AOB 就是一个圆周角。
需要注意的是,圆周角的两个边必须与圆相交,仅仅顶点在圆上是不够的。
三、圆周角定理圆周角定理是圆周角这一知识体系中的核心内容。
它指出:一条弧所对的圆周角等于它所对圆心角的一半。
让我们通过一个例子来理解。
在圆 O 中,弧 AB 所对的圆心角是∠AOB,所对的圆周角有∠ACB。
根据圆周角定理,∠ACB =1/2∠AOB。
这个定理的证明可以通过多种方法来完成,这里我们先不展开讨论。
四、圆周角定理的推论1、同弧或等弧所对的圆周角相等在同一个圆或等圆中,如果两条弧相等,那么它们所对的圆周角也相等。
比如,在圆 O 中,弧 AB =弧 CD,那么∠AEB =∠CFD。
2、半圆(或直径)所对的圆周角是直角半圆所对的圆心角是 180°,所以它所对的圆周角就是 90°。
如果圆中有一条直径,那么它所对的圆周角一定是直角。
例如,在圆 O 中,AB 是直径,那么∠ACB = 90°。
这个推论在解决很多与圆相关的几何问题时非常有用。
3、 90°的圆周角所对的弦是直径如果一个圆周角是 90°,那么它所对的弦一定是圆的直径。
这是上述推论的逆定理。
五、圆周角的应用圆周角的知识在实际生活和数学问题中有着广泛的应用。
在建筑设计中,设计师常常需要利用圆周角的知识来确保圆形结构的稳定性和对称性。
在数学问题中,比如求圆内接三角形的边长、角度等,圆周角定理及其推论可以帮助我们找到解题的关键。
例如,已知一个圆的半径为 r,圆内接三角形的一个圆周角为 60°,求三角形的边长。
1-2.5.与圆有关的比例线段(切割线定理)

割线定理:从圆外一点引圆的两条割线,这一点到每一条 割线与圆的交点的两条线段长的乘积相等.
应用格式(几何语言描述):
∵PAB,PCD是⊙O 的割线,∴ PA∙PB=PC∙PD.
C
C
B
点P从圆内移动到圆外
D
P
O
D
图5 O
P
A 图3
B A
PA∙PB=PC∙PD
PA∙PB=PC∙PD
使割线PA绕P点
证明:连接AC、AD,同样可以证明
又∵∠ACF=∠AEC. ∴∠CFG=∠ACF. 故FG//AC. ……(6)
你还能推出其他结论吗?
问题3 在图2中,使线段AC继续绕A旋转,使割线CFD 变成切线CD,得到图3. 此时又能推出哪些结论?
B
B
E
D
E
A
D
O 图2
A Q
O 图3
F
G
CG
PC
探究3:可以推出探究1、2中得到的(1)——(6)的所有结论. 此外,
同理可证BD•AE=AC•CE. …………………… (3) ∵AC=AB,∴由(2)(3)可得BE•CD=BD•CE. ………(4)
问题2 在图1中,使线段AC绕A旋转,得到图2.其中EC 交圆于G,DC交圆于F.此时又能推出哪些结论?
问题2 在图1中,使线段AC绕A旋转,得到图2.其中 EC交圆于G,DC交圆于F.此时又能推出哪些结论?
例3 如图,两圆相交于A、B两点,P P 为两圆公共弦AB上任意一点,从P引
D B
两圆的切线PC、PD,求证:PC=PD.
证明:由切割线定理可得:
A
PC2=PA∙PB, PD2=PA∙PB.
C
∴PC2=PD2. 即PC=PD.
圆周角定理

A
C O
B
解: 作OC⊥AB于C, 则 BC 3,
OC 1 在 Rt BOC 中, OC OB BC 1 OB 2
2 2
B 30
BOC 60
AOB 120
故选(C)
例2 如图, AB与CD相交于圆内一点P. 求证: AD 的度数与 BC
证明: 分三种情况讨论.
A O
⑴圆心O在 BAC 的一边上.
OA OC, C BAC. 等边对等角. 1 BAC BOC BOC BAC C 三角形的外角等于不相邻两内角的和 . B 2 A ⑵圆心O在 BAC 的内部. 作直径AD, 利用⑴的结果,有 1 1 BAD BOD, DAC DOC. O 2 2 C 1 BAD DAC (BOD DODC ). 2 B 1 即 BAC BOC 2 ⑶圆心O在 BAC 的外部. 作直径AD, 利用⑴的结果,有 A 1 1 BAD BOD, DAC DOC. 2 2 O 1 C BAD DAC (BOD DODC ). 2 1 B BAC BOC 即 2
70
解: 因为O为 ABC 的外心, 故以O为圆心做ABC 的外接圆O, 连结OC,
B
O
140
C
所对的圆周角,圆心角 ∵ BAC , BOC 分别是弧 BC
∴ 由圆周角定理得 BOC 2BAC 140
又∵ OB OC
1 (180 140 ) 20 OBC OCB ∴ 2
例1 如图, AD是 ABC 的高, AE是 ABC 的外接圆直径.
求证: AB AC AE AD
分析:
AC AD AB AC AE AD 写成比例式 AE AB 故只需证明 Rt ADC ∽RtABE
中考数学临考题号押广东卷21题(几何证明与计算)(解析版)
【小问2详解】
根据(1)的结论,平行四边形AFCE是菱形,
∴EF、AC相互垂直平分,且AE=EC=CF=FA,
∴EF=2OE,AC=2OA,
∵BC=8,AB=4,
∴BE=BC-EC=8-EC=8-AE, ,
∴OA= ,
在Rt△ABE中,利用勾股定理,有 ,
即: ,解得:AE=5,
(1)求证:四边形 是菱形.
(2)当AB 4,BC 8时,求线段EF的长.
【分析】(1)利用EF是AC的垂直平分线,可得∠EAC=∠ECA,∠CAF=∠FCA,在矩形中有 ,即有∠ECA=∠CAF,∠ECF=∠CFD,即可证得∠CFD=∠EAF,则有 ,再结合 ,AE=EC,可证四边形AFCE是菱形;
∴∠ACF=∠EDC.
∴ED=EC.
【小问2详解】
解:如(1)中图所示,过点C作CG⊥OB于点G,设线段OE与 交于点H.
∵ 的直径 ,OC,OB是 的半径,
∴ .
∵∠A和∠BOC分别是 所对的圆周角和圆心角,∠A=30°,
∴∠BOC=2∠A=60°.
∴ ,S扇OBC .
∴ .
∴点C右侧的阴影面积S右=S扇OBC- .
(2)连接 ,根据同弧所对的圆周角相等,可得 ,进而根据正切值以及已知条件可得 的长,勾股定理即可求得 ,进而即可求得圆的半径.
【详解】
(1)连接 ,如图,
是 的切线,
,
,
,
,
,
,
.
(2)连接
是 的直径,
,
,
,
,
,
,
,
,
.
即 的半径为 .
6.(2021·山东青岛·中考真题)如图,在 中, 为 边的中点,连接 并延长,交 的延长线于点 ,延长 至点 ,使 ,分别连接 , , .
几何证明选讲定理大全

与圆周角定理有什么关系?
若∠ADB+∠ABC=180°,则ABCD四点共圆; 若∠PAD=∠DCB,则ABCD四点共圆; 若∠ADB=∠ACB,则ABCD四点共圆;
P
A C D O B
练习
情况唯一吗?
1.⊙O1和⊙O2都经过A、B两点,经过A点的直线CD与 ⊙O1交于点C,与⊙O2交于点D,经过B点的直线EF与 ⊙O1交于点E,与⊙O2交于点F,求证:CE∥DF.
BC EF AC DF
合比
?
AB BC AC DE EF DF
BC AC EF DF
AB DE AC DF
C 1、如图:EF∥AB,BF:FC= 5 :4, AC=3厘米,则CE=( )
4 cm 3
E
F B
2、已知在△ABC中,DE∥BC,EF∥DC,那么下列结论不成立的 A 是( ) B
解析 ∵E 是 AB 的中点, ∴AB=2EB. ∵AB=2CD,∴CD=EB. 又 AB∥CD,∴四边形 CBED 是平行四边形. ∴CB∥DE, ∠DEM=∠BFM, ∴ ∴△EDM∽△FBM. ∠EDM=∠FBM, DM DE ∴ = .∵F 是 BC 的中点, BM BF 1 ∴DE=2BF.∴DM=2BM,∴BM= DB=3. 3
E
B
选修4-1相关定理
弦切角的性质
弦切角
弦切角:顶点在圆上,一边和圆相交、
E
另一边和圆相切的角叫做弦切角. 要点: 顶点在圆上 一边和圆相交 A 一边和圆相切
E A O B C D E 极限状态
O D
C
B
A(D)
O
B
C
∠EAB=∠BCD
∠EAB=∠BCA
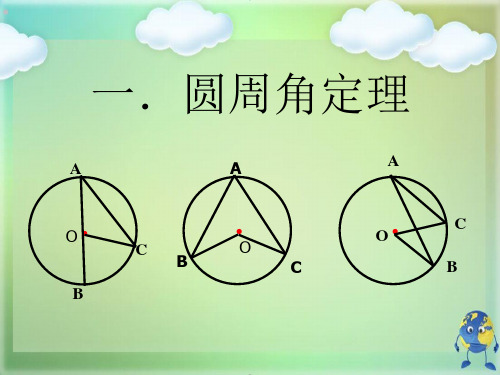
圆周角定理
判断AB与AC的大小有什么关系?为什么?
例4. 如图,AB与CD相交于圆内一点P.求证:
∠BAC= ∠BOC
∠BAC= ∠BOC
B D C 例1:如图:AB,AC是⊙O的两条弦,延长CA到D,
3.方法上主要学习了圆周角定理的证明渗透了“特殊到一般”的思想方法和分类讨论的思想方法. (2)等弦所对的圆周角相等或互补;
一.圆周角定理
A
A
O●
●
C
O
B
C
B
A
C O●
B
一. 圆周角定理
圆周角定理:圆上一条弧所对的圆周角等于它所对 的圆心角的一半.
已知:如图,在⊙O中,B C
A
A
所对的圆周角和圆心角分别
是∠BAC, ∠BOC .
O ●
●
求证:∠ BAC=
1
∠
BOC
B
O
C
C
2
B
分析2: 以直径为分界线,可以得到另外两类圆周角及 相应的圆心角,如下图(2),(3)所示.只要能将它们 化归为(1)的特殊情形,问题就能解决.
延长BD到点C,使CD=BD,连接AC. 的度数与 的度数和的一半等于∠APD的度数.
判断AB与AC的大小有什么关系?为什么? 已知:如图,在⊙O中, 所对的圆周角和圆心角分别是∠BAC, ∠BOC .
判断AB与AC的大小有什么关系?为什么? 的度数与 的度数和的一半等于∠APD的度数.
(2)半圆(直径)所对的圆心角是多少度?圆周角是多少度?
小结: 圆周角/圆心角定理
• 1.圆心角(central angle):顶点在圆心上的角叫做圆 心角.(1)在同圆或等圆中,两圆心角相等⇔其所对的弦 (或弧)也相等;(2)圆心角的度数等于它所对的弧的度 数.
圆周角定理及推论

用于判断某 用于判断某个 条线是否过 圆周角是否是 圆心 直角
例1
已知:如图,在△ABC中,AB=AC, 以AB为直径的圆交BC于D,交AC于E, 求证:⌒ ⌒ BD=DE
A
证明:连结AD.
删去“同圆或等圆”的条件,结论都不
∵AB是圆的直径 E ∴∠ADB=90°, C D ∴AD⊥BC B ∵AB=AC, ∴AD平分∠BAC,即∠BAD=∠CAD, ∴⌒ ⌒ BD= DE (同圆或等圆中,相等的圆周角所对 弧相等)。
1.同弧或等弧所对的圆周角相等; 在同圆或等圆中,相等的圆周角所对的 弧相等. 2.半圆(或直径)所对的圆周角是直角; 90°的圆周角所对的弦是直径. 条件“同弧或等弧”改为“同弦或等 弦”,或
圆周角和圆心角的关系
过点B作直径BD.由1可得: ∠ABD =
1 1 ∠AOD,∠CBD = 2 ∠COD, 2 1 = (∠AOD2
A
∠ABD -∠CBD 1 ∠COD), ∴ ∠ABC = ∠AOC.
C
B
●
O
2
一条弧所对的圆周角等于它所 对的圆心角的一半.
练习
求圆中角X的度数
120° O A
圆周角 定理及推论
圆周角定义
定义:顶点在圆上,并且两边都与圆相
交的角叫做圆周角。
如图所示:∠ACB 为圆周角
圆周角定理
同弧或等弧所对的圆周角的度 数是圆心角度数的一半。也可 以说成:一条弧所对的圆周角 等于圆心角的一半。
圆周角定理:在同圆或等圆中,
几何语言:
圆的性质与圆周角定理.知识精讲(2014-2015)-学生版

圆的性质与圆周角定理中考内容中考要求ABC圆的性质知道圆的对称性,了解弧、弦、圆心角的关系能用弧、弦、圆心角的关系解决简单问题;能用垂径定理解决相关问题 能运用圆的性质解决有关问题 圆周角 了解圆周角与圆心角的关系;知道直径所对的圆周角是直角 会求圆周角的度数,能用圆周角的知识解决与角有关的简单问题能综合运用几何知识解决与圆周角有关的问题⎧⎧⎪⎪⎨⎪⎪⎪⎪⎩⎨⎪⎪⎪⎪⎩弦圆的性质弧圆心角圆的性质与圆周角定理圆周角定理一、弧、弦、圆心角的关系1. 弧、弦、圆心角之间的关系:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.2. 推论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量分别相等.【注意】因为一条弦对的弧有两条,所以由弦等得出弧等时,这里的弧等指的是弦对的劣弧与劣弧相等,优弧与优弧相等。
【补充】“圆心角、弧、弦和弦的弦心距”四组量中,有一组量对应相等,其他的三组量也对应相等,换言之为“四有一推三”,但当用到“弦心距”时,需要用全等先证明再用。
二 、圆周角定理1. 圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半.中考考纲知识精讲知识网络图【注意】在应用定理时,一定要保证“同弧或等弧”的前提。
【定理的证明】在⊙O 中,同一弧所对的圆周角和圆心角的位置关系有三种情况,如图1。
应分三种情况进行讨论。
(3)(2)(1)图1AB CDOABCOOD CBA如图1,已知:在⊙O 中,BC 所对的圆周角是BAC ∠,圆心角是BOC ∠。
求证:12BAC BOC ∠=∠ 证明:由圆周角在圆内的位置关系,分三种情况讨论。
(1) 圆心O 在BAC ∠的一条边上(如图1-(1))12OA OC C BAC BAC BOC BOC BAC C =⇒∠=∠⎫⇒∠=∠⎬∠=∠+∠⎭(2) 圆心O 在BAC ∠的内部,(如图1-(2)),作直径AD ,由(1)得出结论得:1112()1222BAD BOD BAD DAC BOD DOC BAC BOC DAC DOC ⎫∠=∠⎪⎪⇒∠+∠=∠+∠=∠=∠⎬⎪∠=∠⎪⎭ (3) 圆心O 在BAC ∠的外部,(如图1-(3)),作直径AD ,由(1)得出结论得:1112()1222DAB DOB DAC DAB DOC DOB BAC BOC DAC DOC⎧∠=∠⎪⎪⇒∠-∠=-∠-∠⇒∠=∠⎨⎪∠=∠⎪⎩ 2. 圆周角定理的推论(1)推论1:同弧或等弧所对的圆周角相等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
同弧所对的圆周角均相等
证明:构造定点A和定点O,以O为圆心,以AO为半径作圆:⊙O 在⊙O上构造定点B,在优弧BA
̂上构造一动点P.
连接AP,BP,OP,AO,BO,AB.则∠APB为AB
̂所对的圆周角. (1)当点O在△ABP之外时
1.当点O在△ABP的PB一侧时
∠APB=∠APO-∠BPO
∠APB=(π-∠PAO-∠AOP)-π−∠BOP
2
∠APB=(π-∠PAO-∠AOP)-π−∠AOP−∠AOB
2
∠APB=π
2-∠PAO-1
2
∠AOP+1
2
∠AOB
过O作DO⊥AP,D为AP上的垂足. ∵点A,点P在⊙O上;
∴PO=AO;
∴∠AOD=1
2
∠AOP;
∴∠APB=π
2-(∠PAO+∠AOD)+1
2
∠AOB=1
2
∠AOB.
2.同理可证点O在△ABP的PA一侧时: ∠APB=1
2
∠AOB
(2)当点O在△ABP之内时
∠APB=∠APO+∠BPO
∠APB=π−∠AOP
2+π−∠BOP
2
∠APB=π-1
2
(∠BOP+∠AOP)
∠APB=π-1
2
(2π-∠AOB)
∠APB=1
2
∠AOB
(3)当点O 在AP 上时: ∠APB=
π−∠BOP 2 ∠APB=π−π+∠AOB
2 ∠APB=1
2∠AOB
同理可证点O 在BP 上时:
∠APB=1
2∠AOB
综上所述:点P 在优弧BA ̂上任意一点都有:∠APB=12
∠AOB ∵A,B,O 为定点;
∴∠AOB 的大小固定;
∴∠APB 的大小固定且为∠AOB 的一半. 即:同弧所对的圆周角均相等.。
