八年级数学证明课件2
合集下载
北师版数学八年级上册精品课件2 一定是直角三角形吗

A
即AB2+BC2=AC2∴△ABC是Rt△
答:船转弯后,是沿正西方向航行的。
2.如图,哪些是直角三角形,哪些不是,说说你的理由?
①②
③
④ ⑥
⑤
答案: ④⑤是直角三角形 ①②③⑥不是直角三角形
小结: 1、如果三角形的三边长a,b,c满足 a2 +b2=c2,那么这个三角形是直角三角形。 2. 勾股数:满足a2 +b2=c2的三个正整数,
几个直角三角形,你是如何判断的?与你的同伴交流。 易知:△ABE,△DEF,△FCB
A 2 E 2 D 均为直角三角形
1
F
由勾股定理知
4
BE2=22+42=20,EF2=22+12=5,
3 BF2=32+42=25
B
4
C ∴BE2+EF2=BF2 ∴ △BEF是直角三角形
2.一艘在海上朝正北方向航行的轮船,在航行240海里时方位
称为勾股数.
实验结果: ① 5,12,13满足a2+b2=c2,可以构成直角三角形; ② 7,24,25满足a2+b2=c2,可以构成直角三角形; ③ 8,15,17满足a2+b2=c2 ,可以构成直角三角形.
90
120
60
150
12 13
30
180
0
5
90 120
150
24
60
25
30
提问1 同学们还能找出哪些勾股数呢? 提问2 今天的结论与前面学习的勾股定理
有哪些异同呢? 提问3 到今天为止,你能用哪些方法判断一个
三角形是直角三角形呢?
例.一个零件的形状如图(a)所示,按规定这个零件中∠A和
人教版数学八年级数学下册 勾股定理的证明 课件

2023-2024学年人教版数学八年级下册第17章勾股定理
勾股定理的证明
勾股定理
如果直角三角形的两条直角边分别为a,b, 斜边长为c, 那么a²+b²=c².
勾股定理是平面几何中一个极为重 要的定理,历史上不同时代、不同国别 的不同人士曾先后给出数百种证明.
其中,我国古代对这个定理的证明 尤其出色.
赵爽 刘徽
欧几里得 达芬奇
勾股定理的众多证明方法 倾注着历史上不同民族顶级数
学家的智慧,折射着不同文化 背景下创造性数学思维的光芒, 并且东西易趣,交相辉映.
华蘅芳 加菲尔德
对于数学来说,整个文明世界就是 一个国家!
——希尔伯特
参考文献:
数学文化小丛书 李大潜主编 高等教育出版社
再见!
总统证法(J.A.Garfield
a
a²+b²=c²
达芬奇证法中国改良版
b
c
a
达芬奇证法中国改良版
cb
/a
a b
C
达芬奇证法中国改良版
b
L
a
ba
C
“弦图”这一简洁优美的 证明显示了中国古代数学家的 智慧与成就,经过艺术处理的 弦图作为北京2002年国际数学 家大会的会徽,经各国代表传 扬全球四方.
勾股定理的证明
勾股定理
如果直角三角形的两条直角边分别为a,b, 斜边长为c, 那么a²+b²=c².
勾股定理是平面几何中一个极为重 要的定理,历史上不同时代、不同国别 的不同人士曾先后给出数百种证明.
其中,我国古代对这个定理的证明 尤其出色.
赵爽 刘徽
欧几里得 达芬奇
勾股定理的众多证明方法 倾注着历史上不同民族顶级数
学家的智慧,折射着不同文化 背景下创造性数学思维的光芒, 并且东西易趣,交相辉映.
华蘅芳 加菲尔德
对于数学来说,整个文明世界就是 一个国家!
——希尔伯特
参考文献:
数学文化小丛书 李大潜主编 高等教育出版社
再见!
总统证法(J.A.Garfield
a
a²+b²=c²
达芬奇证法中国改良版
b
c
a
达芬奇证法中国改良版
cb
/a
a b
C
达芬奇证法中国改良版
b
L
a
ba
C
“弦图”这一简洁优美的 证明显示了中国古代数学家的 智慧与成就,经过艺术处理的 弦图作为北京2002年国际数学 家大会的会徽,经各国代表传 扬全球四方.
八年级数学上册讲解命题、定理与证明命题课件
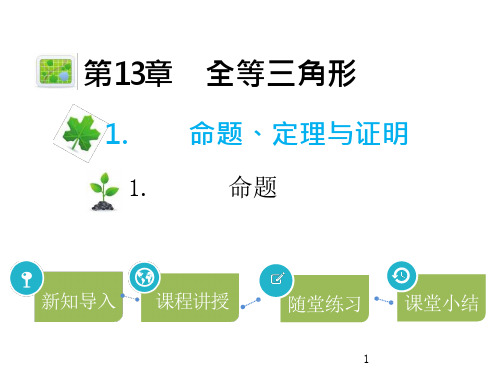
⑴同位角相等,两直线平行; 条件: 同位角相等 结论: 两直线平行 如果同位角相等,那么两直线平行.
7
课程讲授
1 命题
例2 指出下列命题的条件和结论,并改写成“如果……, 那么……”的形式:
⑵三个角都相等的三角形是等边三角形. 条件: 一个三角形的三个角相等 结论: 这个三角形是等边三角形 如果一个三角形的三边相等,那么这个三角 形是等边三角形.
3
课程讲授
1 命题
如果两个角是对顶角,那么这两个角相等; 正确 两直线平行,同旁内角相等; 错误
定义:它们都是判断某一件事情的语句,像这样表
示判断的语句叫做命题.
4
课程讲授
1 命题
例1 判断下列语句是否为命题. (1)长度相等的两条线段是相等的线段吗? 不是
(2)两条直线相交,有且只有一个交点; 是 3 不相等的两个角不是对顶角; 是 4 欢迎前来参加北京冬奥会!不是 5 两个锐角的和是钝角; 是
(1)全等三角形的对应边相等; 条件: 两个三角形全等 结论:这两个三角形的对应边相等
如果两个三角形全等,那么它们的对应边相等
13
随堂练习
2.把下列命题改写成“如果……,那么……”的形式,并分 别指出它们的条件和结论: (2)在同一平面内,垂直于同一条直线的两条 直线互相平行.
条件: 在同一平面内,有两条直线分别垂直于第三条直线 结论:这两条直线互相平行
15
课堂小结
命题
定义 表示判断的语句叫做命题.
真命题与假 命题
如果条件成立,那么结论一定成立. 像这样的命题,称为真命题.
当条件成立时,不能保证结论总是正 确,或者说结论不成立,像这样的命 题,称为假命题.
16
第13章 全等三角形
7
课程讲授
1 命题
例2 指出下列命题的条件和结论,并改写成“如果……, 那么……”的形式:
⑵三个角都相等的三角形是等边三角形. 条件: 一个三角形的三个角相等 结论: 这个三角形是等边三角形 如果一个三角形的三边相等,那么这个三角 形是等边三角形.
3
课程讲授
1 命题
如果两个角是对顶角,那么这两个角相等; 正确 两直线平行,同旁内角相等; 错误
定义:它们都是判断某一件事情的语句,像这样表
示判断的语句叫做命题.
4
课程讲授
1 命题
例1 判断下列语句是否为命题. (1)长度相等的两条线段是相等的线段吗? 不是
(2)两条直线相交,有且只有一个交点; 是 3 不相等的两个角不是对顶角; 是 4 欢迎前来参加北京冬奥会!不是 5 两个锐角的和是钝角; 是
(1)全等三角形的对应边相等; 条件: 两个三角形全等 结论:这两个三角形的对应边相等
如果两个三角形全等,那么它们的对应边相等
13
随堂练习
2.把下列命题改写成“如果……,那么……”的形式,并分 别指出它们的条件和结论: (2)在同一平面内,垂直于同一条直线的两条 直线互相平行.
条件: 在同一平面内,有两条直线分别垂直于第三条直线 结论:这两条直线互相平行
15
课堂小结
命题
定义 表示判断的语句叫做命题.
真命题与假 命题
如果条件成立,那么结论一定成立. 像这样的命题,称为真命题.
当条件成立时,不能保证结论总是正 确,或者说结论不成立,像这样的命 题,称为假命题.
16
第13章 全等三角形
人教版八年级数学下册17.1勾股定理的证明(比较全的证明方法)ppt课件
b
a
∵ S梯 形 AB CD = = 1
1 2
B
a+b 2
2 又 ∵S梯 形 AB CD =S AED +S EBC+S 1 1 1 1 = ab+ ba+ c2= (2ab+c2) 2 2 2 2 比 较上 面 二 式得 c2=a2+b2
(a2+2ab+b2)
CED
向常春的证明方法
S梯形ABCD 1 1 2 1 ( a b b )( a b ) a ab 2 2 2
那么:
朱实 中 黄实 b a
返回
( b- a) 2
ab c 4 ( b a )2 2
2
得: c2 =a2+ b2.
证明1:
该图2002年8月在北京召开的国际数学家大会的会标示意图,取材于我国古代数学著作《勾股圆方图》。
a c b
a
2 c 大正方形的面积可以表示为 ; 1 2 (b a ) 4 ab 也可以表示为 2 c 1 2 ∵ c2= (b a ) 4 ab 2 2 2 =b -2ab+a + 2ab b =a2+b2
G
已知:如图,以在Rt△ABC中, ∠ACB=90°,分别以a、b、c为边向外作 正方形.
K
H C b A c a B
F
求证:a2 +b2=c2.
D E
传说中毕达哥拉斯的证法
证明:从Rt△ABC的三边向外各作一个正方形(如图),作CN⊥DE交AB于M,那么正方形 ABED被分成两个矩形.连结CD和KB. ∵由于矩形ADNM和△ADC同底(AD),等高(即平行线AD和CN间的距离),
北师大版八年级下册数学第一章 三角形的证明第3节《线段的垂直平分线(2)》参考课件

结论:三角形三条边的垂直平分线相交 于一点.
你想证明这个命题吗? 你能证明这个命题吗?
老师期望: 你能写出规范的证明过程.
如何证三条直线交于一点?
命题:三角形三条边的垂直平分线相 交于一点.
基本想法是这样的:我们知道,两条直 线相交只有一个交点。要想证明三条直线 相交于一点只要能证明两条直线的交点在 第三条直线上即可.这时可以考虑前面刚 刚学到的逆定理.
如图,在△ABC中,设AB,BC的垂直平分线相交
于点P,连接AP,BP,CP.
A
∵点P在线段AB的垂直平分线上,
∴PA=PB .
同理,PB=PC.
∴PA=PC.
B
∴点P在线段AC的垂直平分线上,
P C
∴AB,B线相交于 一点,并且这一点到三个顶点的距离相等.
1、书籍是朋友,虽然没有热情,但是非常忠实。2022年2月28日星期一2022/2/282022/2/282022/2/28 2、科学的灵感,决不是坐等可以等来的。如果说,科学上的发现有什么偶然的机遇的话,那么这种‘偶然的机遇’只能给那些学有素养的人,给那些善于 独立思考的人,给那些具有锲而不舍的人。2022年2月2022/2/282022/2/282022/2/282/28/2022 3、书籍—通过心灵观察世界的窗口.住宅里没有书,犹如房间里没有窗户。2022/2/282022/2/28February 28, 2022 4、享受阅读快乐,提高生活质量。2022/2/282022/2/282022/2/282022/2/28
点的距离相等).
aA
c
b
P
B
C
老师提示:这是证明三条直线交于一点的根据.
三 挑战自我
(1)已知三角形的一条边及这条边上的高, 你能作出三角形吗?
北师大版八年级数学上册《平行线的判定》平行线的证明PPT课件

学习目标 • 单击此处编辑母版文本样式
三 级
级
此 处
四 级
编
五
辑
• 二级
级
母
击 此 处 编
1.了•解三•级并四级掌握平行线的判定公理和定版文 理.(重点辑)
2.了解证•明五级的一般步骤.(难点)本样
式
母 版
标
题
样
式
2200232/53//55/5
2
2
•
•
•
• •
观单•察单击与击请此思此找处考处编出辑图编母中版辑文的母本平导样版行式入标线新!题它课样五们四 级式三级为二级什单击此处编辑么平行?
• 二级
级
母
单 击 此 处 编
• 三级
• 四级 • 五级
版 文
辑
本
母
样 式
版
标
题
样
式
2200232/53//55/5
3
3
•
•
•
• •
讲授新课 单
单
知单识击点1此平处行编线辑的母判版定标题样式三 级
二 级
击 此 处
击 此
• 单公相•击二等理此级,处编那两辑么条母这直版文两线本条被样直第式线三平条行直五 级.线四 级 所截编辑母,如果同位处编角
练单一练击:此根处据编条辑件完母成版填标空题. 样式三C二级 级
击
此1
处
F 3
① ∵• 单∠击此1处=_编_辑∠_母_2_版(文已本样知式)
四 级
编
五
辑
∴•A二B•级∥三级CE(内错角相等,两直级线平行母版)
②
∵ ∴
∠CD1∥• +四_B•级∠_五F_级(3_同_=旁18内0o(角已互知补),两直A线文本样式平行
18.2.1第2课时矩形的判定课件(共34张PPT) 2025年春人教版数学八年级下册
即PD=CQ,
所以24-x=3x,
解得x=6.
即经过6s,四边形PQCD是平行四边形.
随堂练习
(2)经过多长时间,四边形PQBA是矩形?
解:设经过ys,四边形PQBA为矩形,
即AP=BQ,
∴y=26-3y,解得y=6.5,
即经过6.5s,四边形PQBA是矩形.
课后小结
定义
矩形的
判定
有一个角是直角的平行四边
四边形窗框是否成矩形,一种方法是量一量这个四边形的两条对角
线长度,如果对角线长相等,则窗框一定是矩形,你现在知道为什
么了吗?
对角线相等的平行四边形是矩形.
知识讲解
例1 已知:如图,在□ABCD中,AC , DB是它的两条对角线,
AC=DB.求证:□ABCD是矩形.
证明:∵AB = DC,BC = CB,AC = DB,
形是矩形
对角线相等的平行四边形是矩形
判定
定理
有三个角是直角的四边形是矩形
谢谢观看
∴∠B=∠ACB=∠FAE=∠EAC,
随堂练习
∴AE∥CD.
又∵DE∥AB,
∴四边形AEDB是平行四边形,
∴AE平行且等于BD.
又∵BD=DC,
∴AE平行且等于DC,
故四边形ADCE是平行四边形.
又∵∠ADC=90°,
∴平行四边形ADCE是矩形.
随堂练习
6.如图,在梯形ABCD中,AD∥BC,∠B=90°,AD
边:对边平行且相等
矩形
角:四个角都是直角
对角线:对角线互相平分且相等
情境导入
思考
工人师傅在做门窗或矩形零件时,如何确保图形是矩形呢?
现在师傅带了两种工具(卷尺和量角器),他说用这两种工具的
所以24-x=3x,
解得x=6.
即经过6s,四边形PQCD是平行四边形.
随堂练习
(2)经过多长时间,四边形PQBA是矩形?
解:设经过ys,四边形PQBA为矩形,
即AP=BQ,
∴y=26-3y,解得y=6.5,
即经过6.5s,四边形PQBA是矩形.
课后小结
定义
矩形的
判定
有一个角是直角的平行四边
四边形窗框是否成矩形,一种方法是量一量这个四边形的两条对角
线长度,如果对角线长相等,则窗框一定是矩形,你现在知道为什
么了吗?
对角线相等的平行四边形是矩形.
知识讲解
例1 已知:如图,在□ABCD中,AC , DB是它的两条对角线,
AC=DB.求证:□ABCD是矩形.
证明:∵AB = DC,BC = CB,AC = DB,
形是矩形
对角线相等的平行四边形是矩形
判定
定理
有三个角是直角的四边形是矩形
谢谢观看
∴∠B=∠ACB=∠FAE=∠EAC,
随堂练习
∴AE∥CD.
又∵DE∥AB,
∴四边形AEDB是平行四边形,
∴AE平行且等于BD.
又∵BD=DC,
∴AE平行且等于DC,
故四边形ADCE是平行四边形.
又∵∠ADC=90°,
∴平行四边形ADCE是矩形.
随堂练习
6.如图,在梯形ABCD中,AD∥BC,∠B=90°,AD
边:对边平行且相等
矩形
角:四个角都是直角
对角线:对角线互相平分且相等
情境导入
思考
工人师傅在做门窗或矩形零件时,如何确保图形是矩形呢?
现在师傅带了两种工具(卷尺和量角器),他说用这两种工具的
八年级数学下册4-3反例与证明课件浙教版
练习6
已知一个集合A包含三个元素a、b、 c,且a、b、c互不相等。请使用反 例证明A的子集不可能是三个两两不 等的元素。
思考题:如何更好地理解和运用反例
思考1
通过观察和分析反例,我们可以 更好地理解一个命题的局限性。 请举例说明如何运用反例来探究 一个数学命题的正确性和适用范
围。
思考2
在数学证明中,反例常常被用来 否定一个普遍性的结论。请思考 在什么情况下使用反例进行证明
在使用反例进行证明时,需要注意逻辑的严密性和正确性,确保结论的 可靠性和准确性。
反例的使用应该适度,不能过度依赖反例,否则可能会导致证明的片面 性和偏颇性。
06 练习与思考
练习题一:构造反例
01
02
03
练习1
请举出一个反例,说明“ 所有偶数都可以被2整除 ”这一命题是错误的。
练习2
请举出一个反例,说明“ 所有三角形都是等边三角 形”这一命题是错误的。
理方法。
证明的目的是为了确认某个命题 或结论的正确性,并使其成为公
认的知识。
证明的步骤与要点
明确前提条件
在开始证明之前,需要明确已 知的前提条件,这是推理的基
础。
构建逻辑结构
根据已知条件和命题,构建逻 辑结构,确定需要证明的目标 。
使用合适的推理规则
选择合适的推理规则,如演绎 推理、归纳推理、反证法等, 进行逻辑推理。
通过构造反例,可以证明某个命题或概念在某些情况下不成立,从而完善数学理论 体系。
反例在证明中具有举足轻重的地位,它可以提供一种有效的反驳手段,帮助人们更 好地理解和掌握数学证明的方法和技巧。
02 反例的构造方法
基于已知事实的反例构造
已知事实
已知一个集合A包含三个元素a、b、 c,且a、b、c互不相等。请使用反 例证明A的子集不可能是三个两两不 等的元素。
思考题:如何更好地理解和运用反例
思考1
通过观察和分析反例,我们可以 更好地理解一个命题的局限性。 请举例说明如何运用反例来探究 一个数学命题的正确性和适用范
围。
思考2
在数学证明中,反例常常被用来 否定一个普遍性的结论。请思考 在什么情况下使用反例进行证明
在使用反例进行证明时,需要注意逻辑的严密性和正确性,确保结论的 可靠性和准确性。
反例的使用应该适度,不能过度依赖反例,否则可能会导致证明的片面 性和偏颇性。
06 练习与思考
练习题一:构造反例
01
02
03
练习1
请举出一个反例,说明“ 所有偶数都可以被2整除 ”这一命题是错误的。
练习2
请举出一个反例,说明“ 所有三角形都是等边三角 形”这一命题是错误的。
理方法。
证明的目的是为了确认某个命题 或结论的正确性,并使其成为公
认的知识。
证明的步骤与要点
明确前提条件
在开始证明之前,需要明确已 知的前提条件,这是推理的基
础。
构建逻辑结构
根据已知条件和命题,构建逻 辑结构,确定需要证明的目标 。
使用合适的推理规则
选择合适的推理规则,如演绎 推理、归纳推理、反证法等, 进行逻辑推理。
通过构造反例,可以证明某个命题或概念在某些情况下不成立,从而完善数学理论 体系。
反例在证明中具有举足轻重的地位,它可以提供一种有效的反驳手段,帮助人们更 好地理解和掌握数学证明的方法和技巧。
02 反例的构造方法
基于已知事实的反例构造
已知事实
新浙教版八年级上册初中数学全册教学课件 (2)可修改全文
新浙教版初中数学全册课件
八年级上册
第1章 三角形的初步认识
1.1 认识三角形
第1课时 三角形及其三角、三边的关系
目 录
CONTENTS
1 学习目标 3 新课讲解 5 当堂小练 7 布置作业
2 新课导入 4 课堂小结 6 拓展与延伸
学习目标
1.三角形的定义. 2.三角形的表示方法及有关概念.(重点) 3.三角形的分类. (重点、难点)
新课讲解
练一练
所有的命题都是基本事实。 X 所有的真命题都是定理 。 X 所有的定理是真命题 。 √ 所有的基本事实是真命题 。 √
课堂小结
1.知识方面: 真命题与假命题的概念
当堂小练
1. “两点之间,线段最短”这个语句是( B ) A、定理 B、基本事实 C、定义 D、只是命题
当堂小练
2. “同一平面内,不相交的两条直线叫做平行线”这 个语句是( C ) A、定理 B、基本事实 C、定义 D、只是命题
当堂小练
3.下列各阴影部分的面积有何关系?
S乙>S甲=S丙
拓展与延伸
在△ABC中,AE,AD分别是BC边上的中线和高。说明△ABE的面积
与△AEC的面积相等。
解: ∵ AE是BC边上的中线
A
∴ BE = EC
1 ∵S △ABE= 2 BE · AD
1 S △AEC= 2 EC · AD
B
C ED
新课导入
一对父子的谈话
爸爸,什 么叫法律?
法律就是法 国的律师
那么什么 是法盲?
法盲就是法 国的盲人
新课讲解 知识点1 定义的定义 可见,在交流时对名称和术语要有共同的认识才行。
一般地,能清楚地规定某一名称或术语的意义的句子叫做该名称或 术语的定义.
八年级上册
第1章 三角形的初步认识
1.1 认识三角形
第1课时 三角形及其三角、三边的关系
目 录
CONTENTS
1 学习目标 3 新课讲解 5 当堂小练 7 布置作业
2 新课导入 4 课堂小结 6 拓展与延伸
学习目标
1.三角形的定义. 2.三角形的表示方法及有关概念.(重点) 3.三角形的分类. (重点、难点)
新课讲解
练一练
所有的命题都是基本事实。 X 所有的真命题都是定理 。 X 所有的定理是真命题 。 √ 所有的基本事实是真命题 。 √
课堂小结
1.知识方面: 真命题与假命题的概念
当堂小练
1. “两点之间,线段最短”这个语句是( B ) A、定理 B、基本事实 C、定义 D、只是命题
当堂小练
2. “同一平面内,不相交的两条直线叫做平行线”这 个语句是( C ) A、定理 B、基本事实 C、定义 D、只是命题
当堂小练
3.下列各阴影部分的面积有何关系?
S乙>S甲=S丙
拓展与延伸
在△ABC中,AE,AD分别是BC边上的中线和高。说明△ABE的面积
与△AEC的面积相等。
解: ∵ AE是BC边上的中线
A
∴ BE = EC
1 ∵S △ABE= 2 BE · AD
1 S △AEC= 2 EC · AD
B
C ED
新课导入
一对父子的谈话
爸爸,什 么叫法律?
法律就是法 国的律师
那么什么 是法盲?
法盲就是法 国的盲人
新课讲解 知识点1 定义的定义 可见,在交流时对名称和术语要有共同的认识才行。
一般地,能清楚地规定某一名称或术语的意义的句子叫做该名称或 术语的定义.
鲁教版(五四制)八年级数学下册菱形的性质与判定(第2课时)课件
B
O2
F
C
EF⊥AC
OA=OC
证明:∵EF是AC的垂直平分线
∴OA=OC,AC⊥EF
∵AD∥BC
∴∠1=∠2
在△AOE和△COF中 B
1 2 OA OC
AOE COF
A
E
1
D
O2
F
C
∴△AOE≌△COF
∴AE=CF ∵AE∥CF ∴四边形AFCE是平行四边形 ∵AC⊥EF
∴□ AFCE是菱形
验证活动2 在桌面上用你手中四根等长的小棒首尾顺次相接,搭出的四边
形真的是菱形吗?
证明猜想2
已知:四边形ABCD中, AB=BC=CD=DA
D
C
求证:四边形ABCD是菱形。 A
B
证明:∵AB=CD,AD=BC
∴四边形ABCD是平行四边形。
又∵AD=AB
∴□ABCD是菱形。
定理 四边相等的四边形是菱形。
定理 对角线互相垂直的平行四边形是菱形。
菱形的判定定理:(对角线)
对角线互相垂直的平行四边形是菱形。B
几何语言表示:
A
O
C
∵AC⊥BD
D
∴□ABCD是菱形
练一练 判断对错
1.对角线相等且互相平分的四边形是菱形 2.对角线互相平分且垂直的四边形是菱形 3.对角线相等的四边形是菱形 4.对角线垂直的平行四边形是菱形 5.对角线互相平分的平行四边形是菱形。
6.1菱形的性质与判定(2)
菱形的判定
学习目标
1.理解并掌握菱形的两个判定定理。(重点)
2.会用菱形的判定方法进行有关的证明和计算。 (难点)
3.通过菱形与平行四边形判定方法的类比,进一 步体会类比的思想方法。
