2020届高考理科数学全优二轮复习训练：专题12 解答题解题技巧

合集下载

2020版新高考二轮复习理科数学专项小测1 12选择4填空 Word版含解析

题型增分特训选填题专项小测第一部分“12选择＋4填空”专项小测(一) 45分钟满分：80分时间：分．在每小题一、选择题：本题共12小题，每小题5分，共60 给出的四个选项中，只有一项是符合题目要求的．2) B＝(＋x －2＜0}，则A∩|01．已知集合A＝{x＜x＜2}，B＝{x|x1} ＜－2＜＜x＜2} xB．{x|xA．{|12}＜－2C．{x|0＜x＜1}＜xD．{x|2，1}＜x＜＝{x|－2，B＝{x|x＋x－2＜0}2}A解析：∵＝{x|0＜x＜C.x{A∴∩B＝x|0＜＜1}，故选C答案：) |＝(2ii)＋．若复数2z满足(1z)(1＋＝1＋，i是虚数单位，则|z12 B.A. 223D.C.2＋2i，z)(1＋i)＝1解析：因为(1＋i1＋i－i?3＋1＋2i?1＋2i??1＝z|－1＝，所以|所以z＝－1＝－1＝22?－i＋i??11＋i?1112????22＋＝，故选A.????222????答案：A0.92019，则(0.9，c＝) ，3．已知a＝log2019b＝20190.9A．a＜c＜b B．a ＜b＜cD．b＜c＜a＜．Cb＜ac0.90＝1,0<c>2019＝＝＝2019<log因为解析：a＝log10，b20190.90.920190＝1，所以a<c<b0.9<0.9，故选A.答案：A年春运期间十二个城市售出的往返机票的平均价2019．如图是4．格以及相比去年同期变化幅度的数据统计图，给出下列4个结论：①深圳的变化幅度最小，北京的平均价格最高；②深圳和厦门往返机票的平均价格同去年相比有所下降；③平均价格从高到低位于前三位的城市为北京，深圳，广州；④平均价格的涨幅从高到低位于前三位的城市为天津，西安，上海．其中正确结论的个数是()A．1 B．2D．3．4C解析：变化幅度看折线图，越接近零轴者变化幅度越小，位于零轴下方者表明价格下跌；平均价格看条形图，条形图越高平均价格越高，所以结论①②③都正确，结论④错误，故选C.答案：C4cos2x5．函数y＝的部分图象大致是()2π＋x?x－24cos?x4cos2，)(x)＝f(x＝，所以f(－x解析：由题意，因为f22πx?－?x＋＋πx4cos2；轴对称，排除选项D)＝是偶函数，其图象关于y所以函数f(x2π＋x4cos24，＜0，则yx＝1，则y＝y又因为当x＝0时，＝，排除选项A；令π1＋πC.故选C答案：542的值为a的系数为－)56的展开式中x，则实数－6．若(1ax ＋x)(2 ．．－2 BA4．C．3D54422项为＋x，故展开式中＋x])x＝[(1－ax)解法一：解析：(1－ax33352122332＝－aa－12，所以－－12a)x4－(ax－)x＋CC－ax)(x)＝(4aCC(24432.＝56，解得a5；A的系数不可能为负数，2＝－，则x所以排除选项解法二：若a54825－(的系数为C(1－x)x，则＋，则中，若选项Ba＝2(1－axx×)＝85B.，符合题意，故选＝－1)56B答案：a，则)b2－a(3⊥)b＋a(，且2＝|b|，1＝|a|满足b，a．已知向量7．)b的夹角为(与23 B.ππA.34ππD.C. 4322ba·，则3a3＋a·b－2b＋＝0(解析：由题意，得a＋b)·(3a－2b)＝21ba·b，所以a与＝1，则cos〈a，b〉＝＝＝－4＝0，∴a·b2|b|a|·|21×πD.，故选的夹角为4D答案：A.已知3b，C所对的边分别为asin，b，c中，8．在△ABC内角A，B)＝(cosB＝2b－c，则A－aππB.A. 462ππD.C.33Asin及正弦定理可得，3sinBB·＝2b－ca解析：由3bsinA－cos－BsinAcosB)＝2sinB－＋cosB＝2sinB－sinC＝2sinB－sin(Asin－AsinB≠0，B.因为所以3sinA所以3sinBsinA＝2sinB－cosAsinBcosAsin，ππ??A＋＋cosA＝2，即sin＝1，又A∈(0，π)，所以A＝. ??63??答案：C9．已知等差数列{a}的前n项和为S，a＝4，S＝15，则数列5nn41??的前2 019项和为() ??a·a??1nn＋2 0182 018B. A.2 0202 0192 0172 019D. C. 2 0192 020解析：设等差数列{a}的公差为d，∵a＝4，S＝15，∴a＋3d＝145n5×414,5a＋d ＝15，联立解得a＝d＝1，∴a＝1＋n－1＝n，∴＝n112aa nn1＋1111111??…－＋的前，则数列2019项和S＝1－＋＝－??aa32n21?n＋?n＋1n??1nn＋2019111C.＝，故选＋－＝1－2020202020202019C答案：22yxB，0)的焦点分别为F，F，点A＋10．已知椭圆＝1(a＞b ＞2221ba)23，则椭圆方程为(|于F，AB|＝4，|FF|＝在椭圆上，AB⊥FF21122222yxx21 ＝1 B.＋A.＋y＝2332222yxxy1＝D.＋C.＋＝19962222yx在，，F，点AB椭圆＋＝1(a＞b＞0)的焦点分别为F解析：2221ba2b2，＝4＝3，|FF|＝23，可得c，椭圆上，AB⊥FF于F|AB|＝4，22112a22yx222C.，故选＝1＝3，b，则所求椭圆方程为＝6＋c＝a－b，解得a69C 答案：π??＋x)，则下列说法中错误的是((x)＝4cosxcos11．已知f??3??的最小正周期为π(x)A．函数fππ??，－)在上单调递减B．函数f(x?? 126??π??＋x2图象上各点的横坐标cos(x)的图象可以由函数y＝C．函数f??3??倍得到不变，纵坐标伸长为原来的27π??1，图象的一个对称中心x)是函数f(D.??12??ππ????22x＋x＋＋2cos1，＝2cosx－3sin2x解析：f(x)＝4coscosx＝????33????πππ2ππ????－，0，，因为t2x＋正确；当T＝＝π，Ax∈∈时，所以????212632????ππππ????－，0，上为减函数，故f(x)1t＝为增函数，y在x＝2＋2cos＋在????21263????ππ??，－＝上为减函数，B正确；函数f(x)的图象可以由函数在y??126??π??＋2x倍再向上图象上各点的横坐标不变，纵坐标伸长为原来的cos2??3??ππx1时，Z，当k＝，平移1个单位得到，C 错误；令2x＋＝kπ＋k∈237π7π??1，C.正确，故选x)＝，故图象的一个对称中心，D为f(??1212??C 答案：πACBAC＝，ABC12．已知三棱锥P－ABC中，PA⊥平面，且∠3)BCAB，PA＝1，＝3，则该三棱锥的外接球的体积等于(2＝ππ331313 A. B.26π53513πD.C. 26BC＝，r则2解析：如图，设△ABC 外接圆的圆心为O，半径为r1πsin33.＝23，＝r上，ABC垂直的直线HO由题意知球心O在过O且与平面11.－d＝＝d，则OH11令HO＝PA＝，OO11222＋r，①RtR，则在△OOB 中有R＝d设球半径为1222 r(1＝－d)，②中有在Rt△OHPR＋1 ＝，由①②两式得d211313??222＝，R3)(＋＝R所以＝，??224??．4413??33Rπ×＝＝所以该三棱锥的外接球的体积为V＝×π?? 332??π1313A.，故选6A答案：分．5分，共20二、填空题：本题共4小题，每小题x处的切线方程为(0))(0，fb∈R)x)＝ae在点＋b(a，13．已知函数f(________. ＝－bx＋1，则ay＝2xx(0))f(0，(x)e′(x)＝a在点，因为函数x解析：由f()＝aef＋b，得f ba＋?＝1＝f?0??，12，b＝－解得＝2x＋1，所以a＝处的切线方程是y?a＝0?＝2f′???3.b＝得a－3答案：，＝164，aS.若a－a＝{14．已知a}是等比数列，前n项和为4nn23 ________．则S的值为3得意，由题，公比为qa设等比数列{a}的首项为解析：1n2，＝4aq－aq－aa＝??1231 2，2，q＝解得a＝?13，16aa ＝q＝??1433?2?1－a?1－q?2114.＝＝所以S＝32－－q1114答案：两人争夺冠军，若比赛采用“五局三B．在一场对抗赛中，A，152在第一A每局获胜的概率均为，且各局比赛相互独立，则胜制”，A 3 ．局失利的情况下，经过五局比赛最终获得冠军的概率是________2A胜A获胜，第2,3,4局失利为事实，经过解析：第1局A5局2218??12.＝×5胜局，B1局，局比赛最终获得冠军的概率是×C×??332733??8 答案：27两B，A交于C与中心在原点的双曲线0＝y3－x．已知直线16．→→FBA·是C的右焦点，若F点，＝0，则C的离心率为________．F、3y所以直线与双曲线的交点A＝0解析：因为直线x经过原点，－→→FBA·的中点，由FOB＝0，得B关于原点对称，所以OA＝，即O是AB3，，所以∠BOF＝＝c，直线x30°－3y＝0的斜率为，FA⊥FBOF＝OB313c3c??代入双曲线＝c，将点B·cos30°sin30°＝c，y ＝c·x则＝c，??BB2222??c3c????22????2222c3c????2244222ca－8，得＝－1＝－，即1因为c＝ab＋4，得a3＋c2222b4aa4b22222222因为＝a－3c0.20a整理得0caa即0＝，(2－c)(2－3)＝，2－c＝或＞1，所以e＝e2.答案：2。

2020届二轮(理科数学) 小题专练12 专题卷(全国通用)

小题专练·作业 (十二)一、选择题1．(2019·衡水中学第七次调研·4)在△ABC 中，点D 在线段BC 上，且BD ＝3DC ，若AD →＝λAB →＋μAC →，则λμ＝( )A.12 B.13 C ．2 D.23答案 B解析本题考查平面向量基本定理．因为AD →＝AB →＋BD →＝AB →＋34BC →＝AB →＋34(AC →－AB →)＝14AB →＋34AC →，所以λ＝14，μ＝34，所以λμ＝13.故选B.2．(2019·广东四校期末联考·9)已知P 是边长为2的等边三角形ABC 边BC 上的动点，则AP →·(AB →＋AC →)的值( ) A ．有最大值8 B ．是定值6C ．有最小值2D ．与P 点的位置有关答案 B解析本题可利用平面向量的坐标运算求解．以BC 的中点D 为坐标原点，BC 所在的直线为x 轴建立平面直角坐标系xDy ，则A(0，3)，B(－1，0)，C(1，0)，设P 点的坐标为(x ，0)，其中－1≤x ≤1，则有AB →＝(－1，－3)，AC →＝(1，－3)，AP →＝(x ，－3)，AB →＋AC →＝(0，－23)，则AP →·(AB →＋AC →)＝6.故选B.3．(2019·山东青岛调研)已知向量a ＝(－1，1)，b ＝(3，m)．若a ∥(a ＋b )，则m ＝( ) A ．－2 B ．2 C ．－3 D ．3 答案 C解析 ∵a ＝(－1，1)，b ＝(3，m)，∴a ＋b ＝(2，m ＋1)． ∵a ∥(a ＋b )，∴－(m ＋1)－2＝0，解得m ＝－3.故选C.4．(2019·长春质量监测)已知平面向量a ，b 满足|a |＝|b |＝1，若(2a －b )·b ＝0，则向量a ，b 的夹角为( ) A ．30°B ．45°C ．60°D ．120°答案 C解析由题意知2a ·b －b 2＝0，即2|a |·|b |cos 〈a ，b 〉－|b |2＝0，得cos 〈a ，b 〉＝12，所以向量a 与b 的夹角为60°.故选C.5．(2019·吉林调研测试)已知等边三角形ABC 的边长为2，则|AB →＋2BC →|＝( ) A ．2 3 B ．27 C ．3 2 D ．3 3答案 A解析由题意得|AB →＋2BC →|＝（|AB →|＋2|BC →|）2＝22＋4×22＋4AB →·BC→＝4＋16＋4×2×2cos120°＝2 3.故选A.6．(2019·江西抚州调研测试)在小正方形边长为1的正方形网格中，向量a ，b 的大小与方向如图，则向量a ，b 所成角的余弦值是( )A.22 B.68585C.155D.61313答案 B解析建立如图所示的平面直角坐标系，易得a ＝(1，2)，b ＝(4，1)，则cos 〈a ，b 〉＝a ·b|a ||b |＝65×17＝68585.故选B.7．(2019·湖北部分重点中学联考)△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，且A ＝π3，c ＝4，a ＝26，则C ＝( ) A.3π5B.π4C.π4或3π5D.π3或2π5答案 B解析由正弦定理a sinA ＝c sinC ，得sinC ＝22.又a>c ，所以A>C ，所以C ＝π4.故选B.8．(2019·广东珠海二模)在△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，且2c －2acosB ＝b ，则角A 的大小为( ) A.π6 B.π4 C.π3 D.π2答案 C解析在△ABC 中，∵2c －2acosB ＝b ，∴由正弦定理可得2sinC －2sinAcosB ＝sinB.即2sin(A ＋B)－2sinAcosB ＝sinB ，∴2sinAcosB ＋2cosAsinB －2sinAcosB ＝sinB ，可得2cosAsinB ＝sinB.∵B 为△ABC 的内角，∴sinB≠0，∴cosA ＝12.又∵A ∈(0，π)，∴A ＝π3.故选C.9．在△ABC 中，∠B ＝60°，AD 是∠BAC 的平分线，交BC 于点D ，AD ＝2BD ，则cos ∠BAC ＝( ) A.14 B.24 C.34D.64 答案 A解析在△ABD 中，AD sinB ＝BD sin ∠BAD ，∴sin ∠BAD ＝BD AD ·sinB ＝22×32＝64，∴cos ∠BAC＝1－2sin 2∠BAD ＝1－2×(64)2＝14.故选A. 10．(2019·广西南宁、玉林、贵港等市摸底)在△ABC 中， A ，B ，C 的对边分别为a ，b ，c ，已知c ＝3，C ＝π3，sinB ＝2sinA ，则△ABC 的周长是( )A ．3 3B ．2＋ 3C ．3＋ 3D ．4＋ 3答案 C解析在△ABC 中，sinB ＝2sinA ，∴由正弦定理得b ＝2a ，由余弦定理得c 2＝a 2＋b 2－2abcosC ＝a 2＋4a 2－2a 2＝3a 2.又c ＝3，∴a ＝1，b ＝2，∴△ABC 的周长是a ＋b ＋c ＝1＋2＋3＝3＋ 3.故选C.11．在△ABC 中，三边上的高的大小依次为113，15，111，则△ABC 为( )A ．锐角三角形B ．直角三角形C ．钝角三角形D ．不存在这样的三角形答案 C解析设△ABC 的三边分别为a ，b ，c ，S △ABC ＝12a·113＝12b·111＝12c·15，所以a 13＝b 11＝c5.设a＝13k ，b ＝11k ，c ＝5k(k>0)．因为11k ＋5k>13k ，所以能构成三角形，取大角A ，则cosA ＝b 2＋c 2－a 22bc ＝（11k ）2＋（5k ）2－（13k ）22×11k×5k <0，所以A 为钝角，所以△ABC 为钝角三角形．故选C.12．(2019·保定摸底)已知在河岸A 处看到河对岸两个帐篷C ，D 分别在北偏东45°和北偏东30°方向，若向东走30米到达B 处再次观察帐篷C ，D ，此时C ，D 分别在北偏西15°和北偏西60°方向，则帐篷C ，D 之间的距离为( ) A ．1015米 B ．106米 C ．515米 D ．56米答案 C解析由题意可得∠DAB ＝60°，∠CAB ＝45°，∠CBA ＝75°，∠DBA ＝30°，在△ABD 中，∠DAB ＝60°，∠DBA ＝30°，AB ＝30，所以∠ADB ＝90°，sin ∠DAB ＝sin60°＝BDBA，解得BD ＝15 3.在△ABC 中，∠CAB ＝45°，∠CBA ＝75°，所以∠ACB ＝60°，AB sin60°＝BCsin45°，解得BC ＝10 6.在△BCD 中，∠CBD ＝∠CBA －∠DBA ＝45°，则由余弦定理得cos ∠CBD ＝cos45°＝BC 2＋BD 2－CD 22BC·BD ，即22＝（106）2＋（153）2－CD 22×106×153，得CD ＝515.故选C.二、填空题13．(2019·湖北调研考试)《数学九章》中对已知三角形三边长求三角形的面积的求法填补了我国传统数学的一个空白，与著名的海伦公式等价，由此可以看出我国古代已具有很高的数学水平，其求法是：“以小斜幂并大斜幂减中斜幂，余半之，自乘于上，以小斜幂乘大斜幂减上，余四约之，为实，一为从隅，开平方得积．”若把以上这段文字写成公式，即S ＝14[c 2a 2－（c 2＋a 2－b 22）2].已知△ABC 满足(sinA －sinB)(sinA ＋sinB)＝sinAsinC －sin 2C ，且AB ＝2BC ＝22，则用以上给出的公式可求得△ABC 的面积为________．答案3解析方法一：设△ABC 的内角A ，B ，C 的对边分别为a ，b ，c.由(sinA －sinB)(sinA ＋sinB)＝sinAsinC －sin 2C ，根据正弦定理得(a －b)(a ＋b)＝ac －c 2，整理可得c 2＋a 2－b 2＝ac ，解得b＝ 6 .则由提供的公式可得△ABC 的面积S ＝14[a 2c 2－（ac 2）2]＝34ac ＝34×2×22＝3.方法二：虽然本题条件中给出了公式，但由于是填空题，因此也可利用课本上的公式来求．设△ABC 的内角A ，B ，C 的对边分别为a ，b ，c.由已知等式结合正弦定理，得c 2＋a 2－b 2＝ac ，则cosB ＝c 2＋a 2－b 22ca ＝12，所以B ＝π3，于是S △ABC ＝12acsinB ＝12×2×22sin π3＝ 3.14．(2019·山西五地市联考)已知向量a ＝(x ，2)，b ＝(－2，1)，若a 与2a －b 共线，则|b ||a |＝________．答案 12解析本题考查平面向量的运算、平面向量共线的条件．由题意得2a －b ＝(2x ＋2，3)，则由a 与2a －b 共线得2(2x ＋2)－3x ＝0，解得x ＝－4，则|a |＝（－4）2＋22＝25，|b |＝（－2）2＋12＝5，则|b ||a |＝12.15．(2019·江南三省十校联考)已知向量a ，b 满足|a |＝1，b ＝2，|a ＋b |＝5，则|2a －b |＝________．答案 2 2解析本题考查向量的模的计算、平面向量的数量积．由题意，向量a ，b 满足|a |＝1，|b |＝2，|a ＋b |＝5，所以|a ＋b |2＝1＋2a ·b ＋4＝5，所以a ·b ＝0，所以|2a －b |＝4－4a ·b ＋4＝2 2.16．已知向量a ＝(1，3)，b ＝(3，m)，且b 在a 上的投影为3，则向量a 与b 的夹角为 ________．答案 π6解析设向量a 与b 的夹角为θ.∵b 在a 上的投影为3，且|a |＝12＋（3）2＝2，a ·b ＝3＋3m ，∴|b |cosθ＝|b |×a ·b ||a ||b |＝3＋3m 2＝3，解得m ＝ 2.∴|b |＝2 3.∴cosθ＝a ·b |a ||b |＝3＋3×32×23＝32.∵θ∈[0，π]，∴向量a 与b 的夹角为π6. 17.如图，在一个坡度一定的山坡AC 的顶上有一高度为25 m 的建筑物CD ，为了测量该山坡相对于水平地面的坡度θ，在山坡的A 处测得∠DAC ＝15°，沿山坡前进50 m 到达B 处，又测得∠DBC ＝45°，根据以上数据可得cosθ＝________．答案3－1解析 ∵∠DAC ＝15°，∠DBC ＝45°，∴∠ADB ＝30°.在△ABD 中，由正弦定理，得ABsin ∠ADB＝BD sin ∠BAD ，即5012＝BD 6－24，∴BD ＝25(6－2) m ．在△BCD 中，由正弦定理，得CDsin ∠DBC ＝BD sin ∠BCD ，即2522＝25（6－2）sin ∠BCD ，∴sin ∠BCD ＝3－1，∴cosθ＝sin(180°－∠BCD)＝sin ∠BCD ＝3－1.18．在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c.给出下列四个命题： ①若sin2A ＝sin2B ，则△ABC 为等腰三角形； ②若sinA ＝cosB ，则△ABC 为直角三角形；③若cosA a ＝sinB b ＝cosC c，则△ABC 为等腰直角三角形；④若cos(A －B)cos(B －C)cos(C －A)＝1，则△ABC 为正三角形．其中，正确命题的序号为________. 答案 ③④解析 ①若sin2A ＝sin2B ，则2A ＝2B 或2A ＋2B ＝π，所以A ＝B 或A ＋B ＝π2，所以△ABC是等腰三角形或直角三角形，所以该命题错误；②若sinA ＝cosB ，则sinA ＝sin(π2－B)，所以A ＝π2－B 或A ＋π2－B ＝π，所以A ＋B ＝π2或A －B ＝π2，则△ABC 不一定为直角三角形，所以该命题错误；③若cosA a ＝sinB b ＝cosA c ，则cosA sinA ＝sinB sinB ＝cosC sinC ，所以A ＝C ＝π4，所以△ABC为等腰直角三角形，所以该命题正确；④若cos(A －B)·cos(B －C)cos(C －A)＝1，则cos(A －B)＝cos(B －C)＝cos(C －A)＝1，所以A ＝B ＝C ，所以△ABC 是正三角形，所以该命题正确． 19．(2019·石家庄模拟考试)在△ABC 中，a ，b ，c 分别是角A ，B ，C 的对边，若ccosB ＋bcosC ＝2acosA ，AM →＝23AB →＋13AC →，且AM ＝1，则b ＋2c 的最大值是________．答案 2 3解析本题考查正弦定理、两角和与差的正弦公式、基本不等式．由题意，利用正弦定理将ccosB ＋bcosC ＝2acosA 化简，得sinCcosB ＋sinBcosC ＝2sinAcosA ，∴sin(B ＋C)＝sinA ＝2sinAcosA.∵sinA≠0，∴cosA ＝12.∵A 为三角形的内角，∴A ＝π3.∵AM →＝23AB →＋13AC →，∴AM→2＝(23AB →＋13AC →)2，即1＝19(b ＋2c)2－29bc ≥19(b ＋2c)2－19(b ＋2c 2)2，即(b ＋2c)2≤12，∴b ＋2c ≤23，当且仅当b ＝2c 时，取等号，即b ＋2c 的最大值为2 3.20．已知a ，b ，c 分别是△ABC 的内角A ，B ，C 的对边，且2cosAcosC(tanAtanC －1)＝1.若D 为AC 的中点，且BD ＝1，则△ABC 的面积的最大值是________．答案33解析本题考查正弦定理与余弦定理、三角恒等变换、三角形的面积公式、基本不等式．由2cosAcosC·(tanAtanC －1)＝1，得2cosAcosC(sinAsinCcosAcosC－1)＝1，∴2(sinAsinC －cosAcosC)＝1，∴cos(A ＋C)＝－12，∴cosB ＝12.又0<B<π，∴B ＝π3.在△ABD 中，由余弦定理得c 2＝1＋(b 2)2－2×1×b 2×cos ∠ADB ， ①在△CBD 中，由余弦定理得a 2＝1＋(b 2)2－2×1×b2×cos ∠CDB ， ② ①②相加得a 2＋c 2＝2＋b 22＝2＋a 2＋c 2－2accosB 2，整理得a 2＋c 2＝4－ac ，∵a 2＋c 2≥2ac ，∴ac ≤43，∴△ABC 的面积S ＝12acsinB ≤12×43×32＝33，当且仅当a ＝c ＝233时取等号，∴△ABC的面积的最大值为33.1.(2018·河南中原名校3月联考题)如图，在直角梯形ABCD 中，AB ＝2AD ＝2CD ，E 为BC 边上一点，BC →＝3EC →，F 为AE 的中点，则BF →＝( ) A.23AB →－13AD → B.13AB →－23AD →C ．－23AB →＋13AD →D ．－13AB →＋23AD →答案 C解析方法一：如图，取AB 的中点G ，连接DG ，CG ，则易知四边形DCBG 为平行四边形，所以BC →＝GD →＝AD →－AG →＝AD →－12AB →，所以AE →＝AB→＋BE →＝AB →＋23BC →＝AB →＋23(AD →－12AB →)＝23AB →＋23AD →，于是BF →＝AF →－AB →＝12AE →－AB →＝12(23AB →＋23AD →)－AB →＝－23AB →＋13AD →.故选C.方法二：BF →＝BA →＋AF →＝BA →＋12AE →＝－AB →＋12(AD →＋12AB →＋CE →)＝－AB →＋12(AD →＋12AB →＋13CB →)＝－AB →＋12AD →＋14AB →＋16(CD →＋DA →＋AB →)＝－23AB →＋13AD →.故选C.2．(2018·武汉调研)已知平面向量a ，b ，e 满足|e |＝1，a ·e ＝1，b ·e ＝－2，|a ＋b |＝2，则a ·b 的最大值为( ) A ．－1B ．－2C ．－52D ．－54答案 D解析不妨设e ＝(1，0)，则a ＝(1，m)，b ＝(－2，n)(m ，n ∈R )，则a ＋b ＝(－1，m ＋n)，所以|a ＋b |＝1＋（m ＋n ）2＝2，所以(m ＋n)2＝3，即3＝m 2＋n 2＋2mn ≥2mn ＋2mn ＝4mn ，当且仅当m ＝n 时等号成立，所以mn ≤34，所以a ·b ＝－2＋mn ≤－54，综上可知，a ·b 的最大值为－54.故选D.3．(2018·福州四校联考)已知向量a ，b 为单位向量，且a ·b ＝－12，向量c 与a ＋b 共线，则|a ＋c |的最小值为( ) A ．1 B.12 C.34 D.32答案 D解析方法一：∵向量c 与a ＋b 共线，∴可设c ＝t(a ＋b )(t ∈R )，∴a ＋c ＝(t ＋1)a ＋t b ，∴(a ＋c )2＝(t ＋1)2a 2＋2t(t ＋1)a ·b ＋t 2b 2.∵向量a ，b 为单位向量，且a ·b ＝－12，∴(a ＋c )2＝(t ＋1)2－t(t ＋1)＋t 2＝t 2＋t ＋1≥34，∴|a ＋c |≥32，∴|a ＋c |的最小值为32.故选D.方法二：∵向量a ，b 为单位向量，且a ·b ＝－12，∴向量a ，b 的夹角为120°，在平面直角坐标系中，不妨设向量a ＝(1，0)，b ＝(－12，32)，则a ＋b ＝(12，32)．∵向量c 与a ＋b 共线，∴可设c ＝(12t ，32t)(t ∈R )，∴a ＋c ＝(1＋t 2，32t)，∴|a ＋c |＝（1＋t 2）2＋3t 24＝t 2＋t ＋1≥32，∴|a ＋c |的最小值为32.故选D. 4．(2018·郑州质量预测二)已知平面向量a ，b ，c 满足|a |＝|b |＝|c |＝1，若a ·b ＝12，则(a ＋c )·(2b－c )的最小值为( ) A ．－2 B ．－ 3 C ．－1 D ．0答案 B解析设a 与b 的夹角为θ，则|a |·|b |cosθ＝12，即cosθ＝12，因为0≤θ≤π，所以θ＝π3，令OA →＝a ，OB →＝b ，以OA →的方向为x 轴的正方向建立如图所示的平面直角坐标系，则a ＝OA →＝(1，0)，b ＝OB →＝(12，32)，设c ＝OC →＝(cosα，sinα)(0≤α≤2π)，则(a ＋c )·(2b－c )＝(1＋cosα，sinα)·(1－cosα，3－sinα)＝(1＋cosα)(1－cosα)＋sinα·(3－sinα)＝1－cos 2α＋3sinα－sin 2α＝3sinα≥－3(当且仅当α＝3π2时取等号)．故选B.5．(2018·福建莆田联考)在△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，若asinBcosC ＋csinBcosA ＝12b ，且a>b ，则B ＝( )A.π6B.π3 C.2π3 D.5π6答案 A解析 ∵asinBcosC ＋csinBcosA ＝12b ，∴根据正弦定理可得sinAsinBcosC ＋sinCsinBcosA ＝12sinB ，即sinB(sinAcosC ＋sinCcosA)＝12sinB.∵sinB≠0，∴sin(A ＋C)＝12，即sinB ＝12.∵a>b ，∴A>B ，即B 为锐角， ∴B ＝π6.故选A.6．在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，若a ＝4，sinA ＝45，tanC ＝7，则△ABC的面积为( ) A ．7 2 B ．7 C ．14 2 D ．14 答案 B解析由sinA ＝45，得cosA ＝±35.由tanC ＝7，得sinC ＝7210，cosC ＝210.若cosA ＝－35，则sinB ＝sin(A ＋C)＝－17250<0，与sinB>0矛盾，故cosA ＝35，则sin(A ＋C)＝22.由sinA ＝45，tanC ＝7，得A>π4，C>π4，所以A ＋C>π2，所以A ＋C ＝3π4，故B ＝π4.由正弦定理a sinA ＝bsinB ，得b ＝522，所以△ABC 的面积为12×4×522×7210＝7.7．(2019·河南普通高中适应性考试)已知△ABC 的三边长分别为a ，b ，c ，面积为S ，且a 2＋b 2－c 2＝43S ，c ＝1，则3b －a 的最大值为( ) A. 3B ．2C ．3 D. 2答案 B解析本题考查三角形与三角恒等变换的综合．a 2＋b 2－c 2＝2abcosC ＝43×12absinC ⇒tanC＝33，C ∈(0，π)⇒C ＝π6，又c ＝1，易知△ABC 外接圆直径为1sin π6＝2，则3b －a ＝23sinB －2sinA ＝23sinB －2sin(B ＋π6)＝2sin(B －π6)，当B ＝2π3时，3b －a 取得最大值2.故选B.8．(2019·衡水中学第七次调研)如图，要测量底部不能到达的某铁塔AB 的高度，在塔的同一侧选择C ，D 两观测点，且在C ，D 两点测得塔顶的仰角分别为45°，30°.在水平面上测得∠BCD ＝120°，C ，D 两地相距600 m ，则铁塔AB 的高度是( ) A ．120 2 m B ．480 m C ．240 2 m D ．600 m答案 D解析本题考查余弦定理的实际应用．设AB ＝x m ，则BC ＝x m ，BD ＝3x m ，在△BCD 中，由余弦定理知cos ∠BCD ＝BC 2＋CD 2－BD 22BC·CD ，即x 2＋6002－3x 22·x·600＝－12，解得x ＝600，即铁塔的高度为600 m ．故选D.9．(2019·湖南四校调研联考，10)△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，且sinAsinB ＋sinC ＋ba ＋c＝1，则C ＝( ) A.π6 B.π3 C.2π3 .5π6 答案 B解析由正弦定理可得sinA sinB ＋sinC ＋b a ＋c ＝a b ＋c ＋ba ＋c ＝1，整理可得a 2＋b 2－c 2＝ab.∴由余弦定理的推论可得cosC ＝a 2＋b 2－c 22ab ＝ab 2ab ＝12.又由C ∈(0，π)，可得C ＝π3.故选B.10．(2019·山西运城康杰中学模拟)已知a 与b 为单位向量，且a ⊥b ，向量c 满足|c －a －b |＝2，则|c |的取值范围为( ) A ．[1，1＋2] B ．[2－22，2＋2] C ．[2，22] D ．[3－22，3＋22]答案 B解析 ∵a ，b 是单位向量且a ·b ＝0，∴可设a ＝(1，0)，b ＝(0，1)，设c ＝(x ，y)，则c －a －b ＝(x －1，y －1)．∵向量c 满足|c －a －b |＝2，∴（x －1）2＋（y －1）2＝2，∴(x －1)2＋(y －1)2＝4.∴点(x ，y)在圆心为C(1，1)，半径为r ＝2的圆C 上，∴|OC|＝ 2.∵|c |＝x 2＋y 2表示点(x ，y)与原点的距离，∴2－2≤|c |＝x 2＋y 2≤2＋ 2.故选B.11．(2019·黑龙江大庆实验中学月考)△ABC 的外接圆的圆心为O ，半径为1.若AB →＋AC →＝2AO →，且|OA →|＝|AC →|，则向量BA →在向量BC →方向上的投影为( ) A.32 B.32C ．3D ．－32答案 A解析如图，取BC 边的中点D ，连接AD ，则AB →＋AC →＝2AD →＝2AO →，∴点O 和点D 重合．∵点O 是△ABC 外接圆的圆心，|OA →|＝|AC →|，∴∠BAC＝90°，∠BOA ＝∠120°，∠ABO ＝30°.在△AOB 中，由|OA →|＝|OB →|＝1及余弦定理，得|AB →|2＝1＋1－2×(－12)＝3，|AB →|＝ 3.∵∠ABO ＝30°，∴向量BA →在向量BC →方向上的投影为|BA→|cos ∠ABO ＝32.12．在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，且2ccosB ＝2a ＋b ，若△ABC 的面积S ＝3c ，则ab 的最小值为( ) A ．28 B ．36 C ．48 D ．56 答案 C解析在△ABC 中，2ccosB ＝2a ＋b ，由正弦定理，得2sinCcosB ＝2sinA ＋sinB.又A ＝π－(B ＋C)，所以sinA ＝sin[π－(B ＋C)]＝sin(B ＋C)，所以2sinCcosB ＝2sin(B ＋C)＋sinB ＝2sinBcosC ＋2cosBsinC ＋sinB ，得2sinBcosC ＋sinB ＝0.因为sinB≠0，所以cosC ＝－12.又0<C<π，所以C ＝2π3.由S ＝3c ＝12absinC ＝12ab×32，得c ＝ab4.由余弦定理，得c 2＝a 2＋b 2－2abcosC ＝a 2＋b 2＋ab ≥2ab ＋ab ＝3ab(当且仅当a ＝b 时取等号)，所以(ab4)2≥3ab ，得ab ≥48，所以ab 的最小值为48.故选C.13．(2018·陕西质检一)已知△ABC 的内角A ，B ，C 的对边分别是a ，b ，c ，且(a 2＋b 2－c 2)(acosB＋bcosA)＝abc ，若a ＋b ＝2，则c 的取值范围为________．答案 [1，2)解析由sinAcosB ＋sinBcosA ＝sin(A ＋B)＝sinC 及正弦定理，可知acosB ＋bcosA ＝c ，则由(a 2＋b 2－c 2)·(acosB ＋bcosA)＝abc ，得a 2＋b 2－c 2＝ab ，由余弦定理可得cosC ＝12，则C ＝π3，B ＝2π3－A ，由正弦定理a sinA ＝b sinB ＝c sinC ，得asinA＝b sin （2π3－A ）＝csinπ3.又a ＋b ＝2，所以csinA 32＋csin （2π3－A ）32＝2，即c ＝3sinA ＋sin （2π3－A ）＝1sin （A ＋π6）.因为A ∈(0，2π3)，所以A ＋π6∈(π6，5π6)，sin(A ＋π6)∈(12，1]，则c ∈[1，2)．14．一艘海轮从A 出发，沿南偏东75°的方向航行100 n mile 后到达海岛B ，然后从B 出发，沿南偏东15 °的方向航行50 n mile 后到达海岛C.如果下次航行直接从A 沿南偏东θ方向出发到达C ，则sinθ＝________．答案342＋1428解析根据题意，画出大致图形，如图所示．由题意得∠ABC ＝180°－75°＋15°＝120°，在△ABC 中，根据余弦定理可得，AC ＝AB 2＋BC 2－2AB×BC×cos ∠ABC ＝1002＋502－2×100×50×cos120°＝507.根据正弦定理可得，BC sin ∠CAB ＝AC sin ∠ABC ，所以sin ∠CAB ＝BC×sin ∠ABC AC ＝50×32507＝2114.又∠CAB 为锐角，所以cos ∠CAB ＝5714，sinθ＝sin(75°－∠CAB)＝sin75°cos ∠CAB －sin ∠CABcos75°＝342＋1428.15．(2018·贵阳监测)在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，且满足a ＝4，asinB ＝3bcosA ，则△ABC 面积的最大值是________．答案 4 3解析由正弦定理可得sinAsinB ＝3sinBcosA ，得sinA ＝3cosA ，则tanA ＝3，所以在△ABC 中，A ＝π3.又a 2＝b 2＋c 2－2bccosA ＝b 2＋c 2－bc ≥2bc －bc ＝bc ，所以bc ≤16(当且仅当b ＝c 时取等号)．所以S △ABC ＝12bcsinA ≤12×16×32＝43，所以△ABC 面积的最大值是4 3.16．(2018·福建八校联考)如图所示，在圆内接四边形ABCD 中，AB ＝6，BC ＝3，CD ＝4，AD ＝5，则四边形ABCD 的面积为________．答案 610解析如图所示，连接BD ，因为四边形ABCD 为圆内接四边形，所以A ＋C ＝180°，则cosA ＝－cosC ，利用余弦定理得cosA ＝62＋52－BD 22×6×5，cosC ＝32＋42－BD 22×3×4，解得BD 2＝2477，所以cosC ＝－37.由sin 2C ＋cos 2C ＝1，得sinC ＝2107，因为A ＋C ＝180°，所以sinA ＝sinC ＝2107，S 四边形ABCD ＝S △ABD ＋S △BCD ＝12×5×6×2107＋12×3×4×2107＝610. 17．(2019·江苏苏州调研测试)如图，△ABC 为等腰三角形，∠BAC ＝120°，AB ＝AC ＝4，以A 为圆心，1为半径的圆分别交AB ，AC 于点E ，F ，点P 是劣弧EF 上的一点，则PB →·PC →的取值范围是________．答案 [－11，－9]解析以A 为原点，以BC 的垂直平分线为y 轴，建立平面直角坐标系．由∠BAC ＝120°，AB ＝AC ＝4，可得B(－23，－2)，C(23，－2)．∵|AP →|＝1，∴可设P(cosα，sinα)，76π≤α≤116π，则－1≤sinα≤－12，PB →＝(－23－cosα，－2－sinα)，PC →＝(23－cosα，－2－sinα)，∴PB →·PC→＝cos 2α－12＋(2＋sinα)2＝－7＋4sinα∈[－11，－9]．。

2020版高考理科数学二轮专题提分教程全国通用版仿真模拟卷二+Word版含解析

仿真模拟卷二本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．共150分，考试时间120分钟．第Ⅰ卷一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合P ＝{0,1,2}，Q ＝{x |x <2}，则P ∩Q ＝( ) A ．{0} B ．{0,1} C ．{1,2} D ．{0,2}答案 B解析因为集合P ＝{0,1,2}，Q ＝{x |x <2}，所以P ∩Q ＝{0,1}．2．已知复数z 满足|z |＝2，z ＋z －＝2(z －为z 的共轭复数)(i 为虚数单位)，则z ＝( )A ．1＋iB ．1－iC ．1＋i 或1－iD ．－1＋i 或－1－i 答案 C解析设z ＝a ＋b i(a ，b ∈R )，则z －＝a －b i ，z ＋z －＝2a ，所以⎩⎨⎧ a 2＋b 2＝2，2a ＝2，得⎩⎨⎧a ＝1，b ＝±1，所以z ＝1＋i 或z ＝1－i.3．若a >1，则“a x >a y ”是“log a x >log a y ”的( ) A ．必要不充分条件 B ．充分不必要条件 C ．充要条件D ．既不充分也不必要条件答案 A解析由a >1，得a x >a y 等价为x >y ， log a x >log a y 等价为x >y >0，故“a x >a y ”是“log a x >log a y ”的必要不充分条件．4．已知a ＝log 52，b ＝log 0.50.2，c ＝0.50.2，则a ，b ，c 的大小关系为( ) A ．a <c <b B ．a <b <c C ．b <c <a D ．c <a <b 答案 A解析因为a ＝log 52<log 55＝12， b ＝log 0.50.2>log 0.50.25＝2，0．51<c ＝0.50.2<0.50，即12<c <1，所以a <c <b .5．执行如图所示的程序框图，则输出的i 的值为( )A ．4B ．5C ．6D ．7答案 C解析由题可得S ＝3，i ＝2→S ＝7，i ＝3→S ＝15，i ＝4→S ＝31，i ＝5→S ＝63，i ＝6，此时结束循环，输出i ＝6.6．已知{a n }，{b n }均为等差数列，且a 2＝4，a 4＝6，b 3＝9，b 7＝21，则由{a n }，{b n }公共项组成新数列{c n }，则c 10＝( )A ．18B ．24C ．30D ．36 答案 C解析 (直接法)由题意，根据等差数列的通项公式得，数列{a n }的首项为3，公差为1，a n ＝n ＋2，数列{b n }的首项为3，公差为3，b n ＝3n ，则易知两个数列的公共项组成的新数列{c n }即为数列{b n }，由此c 10＝b 10＝30，故选C.7．已知直线y ＝x ＋m 和圆x 2＋y 2＝1交于A ，B 两点，O 为坐标原点，若AO →·AB →＝32，则实数m ＝( )A ．±1B ．±32C ．±22D ．±12 答案 C解析联立⎩⎨⎧y ＝x ＋m ，x 2＋y 2＝1，得2x 2＋2mx ＋m 2－1＝0，∵直线y ＝x ＋m 和圆x 2＋y 2＝1交于A ，B 两点，O 为坐标原点，∴Δ＝－4m 2＋8＞0，解得－2<m <2，设A (x 1，y 1)，B (x 2，y 2)，则x 1＋x 2＝－m ，x 1x 2＝m 2－12，y 1y 2＝(x 1＋m )(x 2＋m )＝x 1x 2＋m (x 1＋x 2)＋m 2，AO →＝(－x 1，－y 1)，AB →＝(x 2－x 1，y 2－y 1)，∵AO →·AB →＝32，∴AO →·AB →＝x 21－x 1x 2＋y 21－y 1y 2＝1－m 2－12－m 2－12＋m 2－m 2＝2－m 2＝32，解得m ＝±22.8．在△ABC 中，a ，b ，c 分别为角A ，B ，C 的对边，若△ABC 的面积为S ，且43S ＝(a ＋b )2－c 2，则sin ⎝ ⎛⎭⎪⎫C ＋π4＝( ) A ．1 B ．22C ．6－24D ．6＋24答案 D解析由43S ＝(a ＋b )2－c 2，得43×12ab sin C ＝a 2＋b 2－c 2＋2ab ，∵a 2＋b 2－c 2＝2ab cos C ，∴23ab sin C ＝2ab cos C ＋2ab ，即3sin C －cos C ＝1，即2sin ⎝ ⎛⎭⎪⎫C －π6＝1，则sin ⎝ ⎛⎭⎪⎫C －π6＝12，∵0<C <π， ∴－π6<C －π6<5π6，∴C －π6＝π6，即C ＝π3，则sin ⎝ ⎛⎭⎪⎫C ＋π4＝sin ⎝ ⎛⎭⎪⎫π3＋π4＝sin π3cos π4＋cos π3sin π4＝32×22＋12×22＝6＋24. 9．关于函数f (x )＝x －sin x ，下列说法错误的是( ) A ．f (x )是奇函数B ．f (x )在(－∞，＋∞)上单调递增C ．x ＝0是f (x )的唯一零点D ．f (x )是周期函数答案 D解析 f (－x )＝－x －sin(－x )＝－x ＋sin x ＝－f (x )，则f (x )为奇函数，故A 正确；由于f ′(x )＝1－cos x ≥0，故f (x )在(－∞，＋∞)上单调递增，故B 正确；根据f (x )在(－∞，＋∞)上单调递增，f (0)＝0，可得x ＝0是f (x )的唯一零点，故C 正确；根据f (x )在(－∞，＋∞)上单调递增，可知它一定不是周期函数，故D 错误．10．已知log 2(a －2)＋log 2(b －1)≥1，则2a ＋b 取到最小值时，ab ＝( ) A ．3 B ．4 C ．6 D ．9答案 D解析由log 2(a －2)＋log 2(b －1)≥1，可得a －2>0，b －1>0且(a －2)(b －1)≥2.所以2a ＋b ＝2(a －2)＋(b －1)＋5≥22(a －2)(b －1)＋5≥22×2＋5＝9，当2(a －2)＝b －1且(a －2)(b －1)＝2时等号成立，解得a ＝b ＝3.所以2a ＋b 取到最小值时，ab ＝3×3＝9.11．已知实数a >0，函数f (x )＝⎩⎪⎨⎪⎧e x－1＋a2，x <0，ex －1＋a 2x 2－(a ＋1)x ＋a2，x ≥0，若关于x 的方程f [－f (x )]＝e －a ＋a2有三个不等的实根，则实数a 的取值范围是( )A.⎝ ⎛⎭⎪⎫1，2＋2e B ．⎝ ⎛⎭⎪⎫2，2＋2eC.⎝ ⎛⎭⎪⎫1，1＋1e D ．⎝ ⎛⎭⎪⎫2，2＋1e答案 B解析当x ＜0时，f (x )为增函数，当x ≥0时，f ′(x )＝e x －1＋ax －a －1， f ′(x )为增函数，令f ′(x )＝0，解得x ＝1，故函数f (x )在(0,1)上单调递减，在(1，＋∞)上单调递增，最小值为f (1)＝0. 由此画出函数f (x )的大致图象如图所示．令t ＝－f (x )，因为f (x )≥0，所以t ≤0，则有⎩⎪⎨⎪⎧f (t )＝e －a＋a 2，f (t )＝e t －1＋a 2，解得－a ＝t －1，所以t ＝－a ＋1，所以f (x )＝a －1. 所以方程要有三个不同的实数根，则需a 2＜a －1＜1e ＋a 2，解得2＜a ＜2e ＋2.12．已知△ABC 的顶点A ∈平面α，点B ，C 在平面α同侧，且AB ＝2，AC ＝3，若AB ，AC 与α所成的角分别为π3，π6，则线段BC 长度的取值范围为( )A ．[2－3，1]B ．[1，7]C ．[7， 7＋23]D ．[1,7＋23]答案 B解析如图，过点B ，C 作平面的垂线，垂足分别为M ，N ，则四边形BMNC 为直角梯形．在平面BMNC 内，过C 作CE ⊥BM 交BM 于点E .又BM＝AB·sin∠BAM＝2sin π3＝3，AM＝2cosπ3＝1，CN＝AC·sin∠CAN＝3sin π6＝32，AN＝3cosπ6＝32，所以BE＝BM－CN＝32，故BC2＝MN2＋34.又AN－AM≤MN≤AM＋AN，即12＝AN－AM≤MN≤AM＋AN＝52，所以1≤BC2≤7，即1≤BC≤7，故选B.第Ⅱ卷本卷包括必考题和选考题两部分．第13～21题为必考题，每个试题考生都必须作答．第22、23题为选考题，考生根据要求作答．二、填空题：本大题共4小题，每小题5分，共20分．13．已知向量a＝(1，λ)，b＝(3,1)，c＝(1,2)，若向量2a－b与c共线，则向量a在向量c方向上的投影为________．答案0解析向量2a－b＝(－1,2λ－1)，由2λ－1＝－2，得λ＝－12.∴向量a＝⎝⎛⎭⎪⎫1，－12，∴向量a在向量c方向上的投影为|a|cos〈a，c〉＝a·c|c|＝1－2×125＝0.14．在△ABC中，a，b，c分别为内角A，B，C的对边，且2ab sin C＝3(b2＋c2－a2)，若a＝13，c＝3，则△ABC的面积为________．答案3 3解析由题意得2ab sin C2bc＝3·b2＋c2－a22bc，即a sin Cc＝3cos A，由正弦定理得sin A＝3cos A,所以tan A＝3，A＝π3.由余弦定理得13＝32＋b2－2×3b cos π3，解得b＝4，故面积为12bc sin A＝12×4×3×32＝3 3.15．已知点M 为单位圆x 2＋y 2＝1上的动点，点O 为坐标原点，点A 在直线x ＝2上，则AM →·AO→的最小值为________．答案 2解析设A (2，t )，M (cos θ，sin θ)，则AM→＝(cos θ－2，sin θ－t )，AO →＝(－2，－t )，所以AM →·AO →＝4＋t 2－2cos θ－t sin θ. 又(2cos θ＋t sin θ)max ＝4＋t 2，故AM →·AO→≥4＋t 2－4＋t 2. 令s ＝4＋t 2，则s ≥2，又4＋t 2－4＋t 2＝s 2－s ≥2，当s ＝2，即t ＝0时等号成立，故(AM →·AO →)min＝2. 16．已知函数f (x )＝x 2－2mx ＋m ＋2，g (x )＝mx －m ，若存在实数x 0∈R ，使得f (x 0)<0且g (x 0)<0同时成立，则实数m 的取值范围是________．答案 (3，＋∞)解析当m >0，x <1时，g (x )<0，所以f (x )<0在(－∞，1)上有解，则⎩⎨⎧f (1)<0，m >0或⎩⎨⎧m >0，Δ>0，f (1)≥0，m <1，即m >3或⎩⎨⎧m >0，m 2－m －2>0，3－m ≥0，m <1，故m >3.当m <0，x >1时，g (x )<0，所以f (x )<0在(1，＋∞)上有解，所以⎩⎨⎧f (1)<0，m <0，此不等式组无解．综上，m 的取值范围为(3，＋∞)．三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤．17．(本小题满分12分)已知函数f (x )＝cos x (3sin x －cos x )＋12.(1)求f ⎝ ⎛⎭⎪⎫π3的值；(2)当x ∈⎣⎢⎡⎦⎥⎤0，π2时，不等式c <f (x )<c ＋2恒成立，求实数c 的取值范围．解 (1)f (x )＝3sin x cos x －cos 2x ＋12＝32sin2x －12cos2x＝sin ⎝ ⎛⎭⎪⎫2x －π6，所以f ⎝ ⎛⎭⎪⎫π3＝1.(2)因为0≤x ≤π2，所以－π6≤2x －π6≤5π6，所以－12≤sin ⎝ ⎛⎭⎪⎫2x －π6≤1. 由不等式c <f (x )<c ＋2恒成立，得⎩⎪⎨⎪⎧c <－12，c ＋2>1，解得－1<c <－12.所以实数c 的取值范围为⎝ ⎛⎭⎪⎫－1，－12. 18．(本小题满分12分)如图，在△BCD 中，∠BCD ＝90°，BC ＝CD ＝1，AB⊥平面BCD ，∠ADB ＝60°，E ，F 分别是AC ，AD 上的动点，且AE AC ＝AFAD ＝λ(0<λ<1)．(1)求证：无论λ为何值，总有平面BEF ⊥平面ABC ； (2)是否存在实数λ，使得平面BEF ⊥平面ACD . 解 (1)证明：∵AB ⊥平面BCD ，CD ⊂平面BCD ，∴AB⊥CD.∵CD⊥BC，AB∩BC＝B，AB，BC⊂平面ABC，∴CD⊥平面ABC.又∵AEAC＝AFAD＝λ(0<λ<1)，∴无论λ为何值，恒有EF∥CD，∴EF⊥平面ABC.又∵EF⊂平面BEF，∴无论λ为何值，总有平面BEF⊥平面ABC.(2)假设存在λ，使得平面BEF⊥平面ACD.由(1)知BE⊥EF，∵平面BEF⊥平面ACD，平面BEF∩平面ACD＝EF，BE⊂平面BEF，∴BE⊥平面ACD.又∵AC⊂平面ACD，∴BE⊥AC.∵BC＝CD＝1，∠BCD＝∠ABD＝90°，∠ADB＝60°，∴BD＝2，∴AB＝2tan60°＝6，∴AC＝AB2＋BC2＝7.由Rt△AEB∽Rt△ABC，得AB2＝AE·AC，∴AE＝67，∴λ＝AEAC＝67.故当λ＝67时，平面BEF⊥平面ACD.19．(本小题满分12分)某行业主管部门为了解本行业中小企业的生产情况，随机调查了100个企业，得到这些企业第一季度相对于前一年第一季度产值增长率y的频数分布表．(1)分别估计这类企业中产值增长率不低于40%的企业比例、产值负增长的企业比例；(2)求这类企业产值增长率的平均数与标准差的估计值(同一组中的数据用该组区间的中点值为代表)．(精确到0.01)附：74≈8.602.解(1)根据产值增长率频数分布表得，所调查的100个企业中产值增长率不低于40%的企业频率为14＋7100＝0.21.产值负增长的企业频率为2100＝0.02.用样本频率分布估计总体分布得这类企业中产值增长率不低于40%的企业比例为21%，产值负增长的企业比例为2%.(2)y－＝1100×(－0.10×2＋0.10×24＋0.30×53＋0.50×14＋0.70×7)＝0.30，s2＝1100i＝15n i(y i－y－)2＝1100×[(－0.40)2×2＋(－0.20)2×24＋02×53＋0.202×14＋0.402×7]＝0.0296，s＝0.0296＝0.02×74≈0.17.所以，这类企业产值增长率的平均数与标准差的估计值分别为0.30,0.17.20．(本小题满分12分)如图，在平面直角坐标系xOy中，椭圆C：x2a2＋y2b2＝1(a>b>0)的焦点为F1(－1,0)，F2(1,0)．过F2作x轴的垂线l，在x轴的上方，l与圆F2：(x－1)2＋y2＝4a2交于点A，与椭圆C交于点D.连接AF1并延长交圆F2于点B，连接BF2交椭圆C于点E，连接DF1.已知|DF1|＝5 2.(1)求椭圆C的标准方程；(2)求点E的坐标．解(1)设椭圆C的焦距为2c.因为F1(－1,0)，F2(1,0)，所以|F1F2|＝2，c＝1.又因为|DF 1|＝52，AF 2⊥x 轴，所以|DF 2|＝|DF 1|2－|F 1F 2|2＝⎝ ⎛⎭⎪⎫522－22＝32，因此2a ＝|DF 1|＋|DF 2|＝4，从而a ＝2. 由b 2＝a 2－c 2，得b 2＝3.因此，椭圆C 的标准方程为x 24＋y 23＝1. (2)解法一：由(1)知，椭圆C ：x 24＋y 23＝1，a ＝2，因为AF 2⊥x 轴，所以点A 的横坐标为1.将x ＝1代入圆F 2的方程(x －1)2＋y 2＝16，解得y ＝±4.因为点A 在x 轴上方，所以A (1,4)．又F 1(－1,0)，所以直线AF 1：y ＝2x ＋2.由⎩⎨⎧ y ＝2x ＋2，(x －1)2＋y 2＝16，得5x 2＋6x －11＝0，解得x ＝1或x ＝－115.将x ＝－115代入y ＝2x ＋2，得y ＝－125，因此B 点坐标为⎝ ⎛⎭⎪⎫－115，－125. 又F 2(1,0)，所以直线BF 2：y ＝34(x －1)．由⎩⎪⎨⎪⎧ y ＝34(x －1)，x 24＋y 23＝1，得7x 2－6x －13＝0，解得x ＝－1或x ＝137.又因为E 是线段BF 2与椭圆的交点，所以x ＝－1. 将x ＝－1代入y ＝34(x －1)，得y ＝－32.因此E 点坐标为⎝ ⎛⎭⎪⎫－1，－32. 解法二：由(1)知，椭圆C ：x 24＋y 23＝1.如图，连接EF 1.因为|BF 2|＝2a ，|EF 1|＋|EF 2|＝2a ，所以|EF 1|＝|EB |，从而∠BF 1E ＝∠B .因为|F 2A |＝|F 2B |，所以∠A ＝∠B ，所以∠A ＝∠BF 1E ，从而EF 1∥F 2A .因为AF 2⊥x 轴，所以EF 1⊥x 轴．因为F 1(－1,0)，由⎩⎪⎨⎪⎧ x ＝－1，x 24＋y 23＝1，得y ＝±32.又因为E 是线段BF 2与椭圆的交点，所以y ＝－32.因此E 点坐标为⎝ ⎛⎭⎪⎫－1，－32. 21．(本小题满分12分)已知函数f (x )＝ln x －x e x ＋ax (a ∈R )．(1)若函数f (x )在[1，＋∞)上单调递减，求实数a 的取值范围；(2)若a ＝1，求f (x )的最大值．解 (1)由题意知，f ′(x )＝1x －(e x ＋x e x )＋a ＝1x －(x ＋1)e x ＋a ≤0在[1，＋∞)上恒成立，所以a ≤(x ＋1)e x －1x在[1，＋∞)上恒成立．令g (x )＝(x ＋1)e x －1x ，则g ′(x )＝(x ＋2)e x ＋1x 2>0，所以g (x )在[1，＋∞)上单调递增，所以g (x )min ＝g (1)＝2e －1，所以a ≤2e －1.(2)当a ＝1时，f (x )＝ln x －x e x ＋x (x >0)．则f ′(x )＝1x －(x ＋1)e x ＋1＝(x ＋1)⎝ ⎛⎭⎪⎫1x －e x ，令m (x )＝1x －e x ，则m ′(x )＝－1x 2－e x <0，所以m (x )在(0，＋∞)上单调递减．由于m ⎝ ⎛⎭⎪⎫12>0，m (1)<0，所以存在x 0>0满足m (x 0)＝0，即e x 0＝1x 0. 当x ∈(0，x 0)时，m (x )>0，f ′(x )>0；当x ∈(x 0，＋∞)时，m (x )<0，f ′(x )<0. 所以f (x )在(0，x 0)上单调递增，在(x 0，＋∞)上单调递减．所以f (x )max ＝f (x 0)＝ln x 0－x 0e x 0＋x 0，因为e x 0＝1x 0，所以x 0＝－ln x 0，所以f (x 0)＝－x 0－1＋x 0＝－1，所以f (x )max ＝－1.请考生在第22、23题中任选一题作答．如果多做，则按所做的第一题计分，作答时请写清题号．22．(本小题满分10分)选修4－4：坐标系与参数方程在平面直角坐标系xOy 中，以坐标原点O 为极点，x 轴正半轴为极轴，建立极坐标系，已知直线l 的参数方程为⎩⎨⎧ x ＝2t ，y ＝2＋t(t 为参数)，曲线C 的极坐标方程为ρcos 2θ＝8sin θ.(1)求曲线C 的直角坐标方程，并指出该曲线是什么曲线；(2)若直线l 与曲线C 的交点分别为M ，N ，求|MN |.解 (1)因为ρcos 2θ＝8sin θ，所以ρ2cos 2θ＝8ρsin θ，即x 2＝8y ，所以曲线C 表示焦点坐标为(0,2)，对称轴为y 轴的抛物线．(2)设点M (x 1，y 1)，点N (x 2，y 2)，直线l 过抛物线的焦点(0,2)，则直线的参数方程⎩⎨⎧x ＝2t ，y ＝2＋t 化为一般方程为y ＝12x ＋2，代入曲线C 的直角坐标方程，得x 2－4x －16＝0，所以x 1＋x 2＝4，x 1x 2＝－16，所以|MN |＝(x 1－x 2)2＋(y 1－y 2)2 ＝1＋⎝ ⎛⎭⎪⎫122·(x 1－x 2)2＝1＋⎝ ⎛⎭⎪⎫122·(x 1＋x 2)2－4x 1x 2 ＝1＋⎝ ⎛⎭⎪⎫122·42－4×(－16)＝10. 23．(本小题满分10分)选修4－5：不等式选讲已知函数f (x )＝|x ＋4|，不等式f (x )>8－|2x －2|的解集为M .(1)求M ；(2)设a ，b ∈M ，证明：f (ab )>f (2a )－f (－2b )．解 (1)将f (x )＝|x ＋4|代入不等式，整理得|x ＋4|＋|2x －2|>8.①当x ≤－4时，不等式转化为－x －4－2x ＋2>8，解得x <－103，所以x ≤－4；②当－4<x <1时，不等式转化为x ＋4＋2－2x >8，解得x <－2，所以－4<x <－2；③当x ≥1时，不等式转化为x ＋4＋2x －2>8，解得x >2，所以x >2.综上，M ＝{x |x <－2或x >2}．(2)证明：因为f (2a )－f (－2b )＝|2a ＋4|－|－2b ＋4|≤|2a ＋4＋2b －4|＝|2a ＋2b |，所以要证f (ab )>f (2a )－f (－2b )，只需证|ab ＋4|>|2a ＋2b |，即证(ab ＋4)2>(2a ＋2b )2，即证a 2b 2＋8ab ＋16>4a 2＋8ab ＋4b 2，即证a 2b 2－4a 2－4b 2＋16>0，即证(a 2－4)(b 2－4)>0，因为a ，b ∈M ，所以a 2>4，b 2>4，所以(a 2－4)(b 2－4)>0成立，所以原不等式成立．。

专题12 利用导数解决函数的单调性-学会解题之高三数学万能解题模板【2022版】(原卷版)

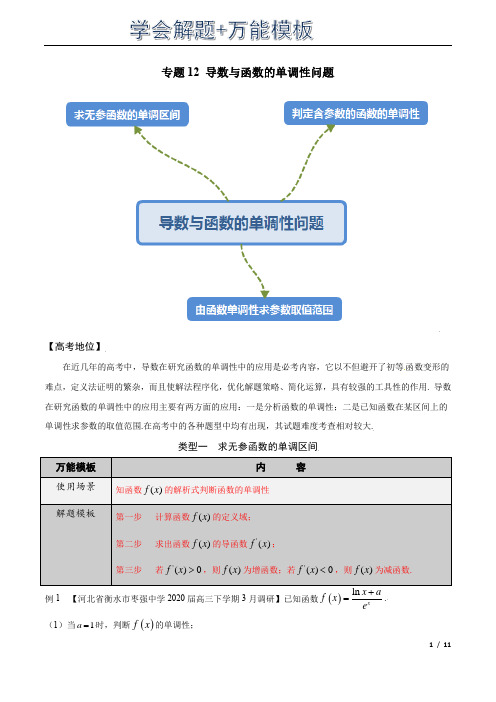
专题12 导数与函数的单调性问题【高考地位】在近几年的高考中，导数在研究函数的单调性中的应用是必考内容，它以不但避开了初等函数变形的难点，定义法证明的繁杂，而且使解法程序化，优化解题策略、简化运算，具有较强的工具性的作用. 导数在研究函数的单调性中的应用主要有两方面的应用：一是分析函数的单调性；二是已知函数在某区间上的单调性求参数的取值范围.在高考中的各种题型中均有出现，其试题难度考查相对较大.类型一求无参函数的单调区间万能模板内容使用场景知函数()f x 的解析式判断函数的单调性解题模板第一步计算函数()f x 的定义域；第二步求出函数()f x 的导函数'()f x ；第三步若'()0f x >，则()f x 为增函数；若'()0f x <，则()f x 为减函数.例1 【河北省衡水市枣强中学2020届高三下学期3月调研】已知函数()ln xx af x e+=. （1）当1a =时，判断()f x 的单调性；【变式演练1】函数，的单调递增区间为__________．【来源】福建省三明第一中学2021届高三5月校模拟考数学试题【变式演练2】已知函数，则不等式的解集为___________.【来源】全国卷地区“超级全能生”2021届高三5月联考数学（文）试题（丙卷）【变式演练3】【黑龙江省哈尔滨六中2020届高三高考数学（文科）二模】已知函数()2sin f x x x =-+，若3(3)a f =，(2)b f =--，2(log 7)c f =，则,,a b c 的大小关系为（） A ．a b c <<B ．b c a <<C ．c a b <<D ．a c b <<【变式演练4】【湖南省湘潭市2020届高三下学期第四次模拟考试】定义在R 上的连续函数()f x ，导函数为()f x '．若对任意不等于1-的实数x ，均有()()()10x f x f x '+->⎡⎤⎣⎦成立，且()()211x f x f x e -+=--，则下列命题中一定成立的是（）A ．()()10f f ->B ．()()21ef f -<-C ．()()220e f f -<D ．()()220e f f ->类型二判定含参数的函数的单调性万能模板内容使用场景函数()f x 的解析式中含有参数解题模板第一步计算函数()f x 的定义域并求出函数()f x 的导函数'()f x ；第二步讨论参数的取值范围，何时使得导函数'()f x 按照给定的区间大于0或小于0；第三步根据导函数的符号变换判断其单调区间.例2 【黑龙江省大庆市第四中学2020届高三下学期第四次检测】已知函数()()2ln 21f x x x ax a R =+-+∈.（1）讨论()f x 的单调性；【变式演练5】（主导函数是一次型函数）【福建省三明市2020届高三（6月份）高考数学（文科）模拟】已知函数()=1,f x nx ax a R -∈.（1）讨论函数f x （）的单调性；()2sin sin 2f x x x =⋅0,2x π⎡⎤∈⎢⎥⎣⎦()()2ln 1x xf x x e e -=+++()()2210f x f x --+≤【变式演练6】（主导函数为类一次型）【山东省威海荣成市2020届高三上学期期中考试】已知函数()x f x e ax -=+.（I ）讨论()f x 的单调性；【变式演练7】（主导函数为二次型）【2020届山西省高三高考考前适应性测试（二）】已知函数()2ln af x x a x x=--，0a ≥. （1）讨论()f x 的单调性；【变式演练8】（主导函数是类二次型）【山西省太原五中2020届高三高考数学（理科）二模】已知函数2()(1)x f x k x e x =--，其中k ∈R.（1）当k 2≤时，求函数()f x 的单调区间；【变式演练9】已知函数，若在区间上单调递增，则的取值范围是（）A ．B ．C ．D ．【来源】江西省南昌市新建区第一中学2020-2021学年高三上学期期末考试数学（文）试题类型三由函数单调性求参数取值范围万能模板内容使用场景由函数单调性求参数取值范围解题模板第一步计算函数()f x 的定义域并求出函数()f x 的导函数'()f x ；第二步根据题意转化为相应的恒成立问题；第三步得出结论.例3．【江苏省南通市2019-2020学年高三下学期期末】若()()21ln 242f x x b x =-++在()2,-+∞上是减函数，则实数b 的范围是（） A ．(],1-∞-B ．(],0-∞C ．(]1,0-D ．[)1,-+∞【变式演练11】（转化为任意型恒成立）【四川省绵阳市2020高三高考数学（文科）三诊】函数2()(2)x f x e x ax b =-++在(1,1)-上单调递增，则2816a b ++的最小值为（）A ．4B ．16C ．20D ．18()22ln f x x x =-()f x ()2,1m m +m 1,14⎡⎫⎪⎢⎣⎭1,4⎡⎫+∞⎪⎢⎣⎭1,12⎡⎫⎪⎢⎣⎭[)0,1【变式演练12】（转化为变号零点）【山西省运城市2019-2020学年高三期末】已知函数2()ln 1f x x a x =-+在(1,2)内不是单调函数，则实数a 的取值范围是（） A ．[)2,8B ．[]2,8C ．(][),28,-∞+∞ D ．()2,8【变式演练13】（直接给给定单调区间）【辽宁省六校协作体2019-2020学年高三下学期期中考试】已知函数()32113f x x mx nx =+++的单调递减区间是()3,1-，则m n +的值为（） A ．-4B ．-2C ．2D ．4【变式演练14】（转化为存在型恒成立）【四川省仁寿第一中学北校区2019-2020学年高三月考】若f （x ）321132x x =-++2ax 在（1，+∞）上存在单调递增区间，则a 的取值范围是( )A ．（﹣∞，0]B ．（﹣∞，0）C ．[0，+∞）D ．（0，+∞）【高考再现】1．（2021·全国高考真题（理））设2ln1.01a =，ln1.02b =， 1.041c =-．则（） A ．a b c <<B ．b c a <<C ．b a c <<D ．c a b <<2．（2021·全国高考真题（理））已知且，函数．（1）当时，求的单调区间；（2）若曲线与直线有且仅有两个交点，求a 的取值范围． 3．已知函数. （1）讨论的单调性；（2）设，为两个不相等的正数，且，证明：. 【来源】2021年全国新高考Ⅰ卷数学试题 4.【2017山东文，10】若函数()e xf x (e=2.71828,是自然对数的底数)在()f x 的定义域上单调递增,则称函数()f x 具有M 性质,下列函数中具有M 性质的是A . ()2xf x -= B. ()2f x x = C. ()3xf x -= D. ()cos f x x =5.【2017江苏，11】已知函数31()2e ex x f x x x =-+-, 其中e 是自然对数的底数. 若2(1)(2)0f a f a -+≤,0a >1a ≠()(0)a x x f x x a=>2a =()f x ()y f x =1y =()()1ln f x x x =-()f x a b ln ln b a a b a b -=-112e a b<+<则实数a 的取值范围是 ▲ .6．【2020年高考全国Ⅰ卷文数20】已知函数()()e 2xf x a x =-+．（1）当1a =时，讨论()f x 的单调性；（2）若()f x 有两个零点，求a 的取值范围．7．【2020年高考全国Ⅰ卷理数21】已知函数()2e xf x ax x =+-．（1）当1a =时，讨论()f x 的单调性；（2）当0x ≥时，()3112f x x ≥+，求a 的取值范围． 8．【2020年高考全国Ⅱ卷文数21】已知函数()2ln 1f x x =+．（1）若()2f x x c ≤+，求c 的取值范围；（2）设0a >，讨论函数()()()f x f a g x x a-=-的单调性．9.（2018年新课标I 卷文）已知函数f (x )=ae x −lnx −1∈ （1）设x =2是f (x )的极值点．求a ，并求f (x )的单调区间；（2）证明：当a ≥1e 时，f (x )≥0∈10.【2018年全国普通高等学校招生统一考试理科数学（新课标I 卷）】已知函数f(x)=1x −x +alnx ∈ （1）讨论f(x)的单调性；（2）若f(x)存在两个极值点x 1,x 2，证明：f (x 1)−f (x 2)x 1−x 2<a −2．【反馈练习】1．【2020届广东省梅州市高三总复习质检（5月）】已知0x >，a x =，22xb x =-，()ln 1c x =+，则（）A ．c b a <<B ．b a c <<C ．c a b <<D ．b c a <<2.【2020届山东省威海市高三下学期质量检测】若函数()()()1cos 23sin cos 212f x x a x x a x =+++-在0,2π⎡⎤⎢⎥⎣⎦上单调递减，则实数a 的取值范围为( )A ．11,5⎡⎤-⎢⎥⎣⎦B ．1,15⎡⎤-⎢⎥⎣⎦C ．[)1,1,5⎛⎤-∞-⋃+∞ ⎥⎝⎦D ．(]1,1,5⎡⎫-∞-⋃+∞⎪⎢⎣⎭3.【河南省十所名校2019—2020学年高三毕业班阶段性测试】若函数()sin24sin f x x x m x =--在[0,2π]上单调递减，则实数m 的取值范围为（） A ．(2,2)-B ．[2,2]-C ．(1,1)-D ．[1,1]-4.【黑龙江哈尔滨市第九中学2019-2020学年高三阶段验收】函数()3f x x ax =+，若对任意两个不等的实数()1212,x x x x >，都有()()121233f x f x x x ->-恒成立，则实数a 的取值范围是（） A ．()2,-+∞B ．[)3,+∞C ．(],2-∞-D ．(),3-∞5.【湖北省武汉市新高考五校联合体2019-2020学年高三期中检测】若函数3211()232f x x x ax =-++ 在2,3⎡⎫+∞⎪⎢⎣⎭上存在单调增区间，则实数a 的取值范围是_______. 6.【四川省宜宾市2020届高三调研】若对(]0,1t ∀∈，函数2()(4)2ln g x x a x a x =-++在(,2)t 内总不是单调函数，则实数a 的取值范围是______7.【河南省南阳市第一中学校2019-2020学年高三月考】若函数()22ln f x x x =-在定义域内的一个子区间()1,1k k -+上不是单调函数，则实数k 的取值范围______.8．若函数在区间是增函数，则的取值范围是_________．【来源】陕西省宝鸡市眉县2021届高三下学期高考模拟文科数学试题 9．已知函数，若对任意两个不同的，，都有成立，则实数的取值范围是________________【来源】江西省景德镇市2021届高三上学期期末数学（理）试题10．【黑龙江省哈尔滨师范大学附属中学2020-2021学年高三上学期开学考试】（1）求函数()sin cos (02)f x x x x x π=+<<的单调递增区间；()cos 2sin f x x a x =+,62ππ⎛⎫⎪⎝⎭a ()()1ln 1xf x x x+=>1x 2x ()()1212ln ln f x f x k x x -≤-k（2）已知函数2()ln 43f x a x x x =-++在1,22⎡⎤⎢⎥⎣⎦上单调递增，求实数a 的范围.11.【黑龙江省哈尔滨三中2020届高三高考数学（文科）三模】函数()()21ln 1x f x x x -=-+. （1）求证：函数()f x 在()0,∞+上单调递增；（2）若m ，n 为两个不等的正数，求证ln ln 2m n m n m n->-+. 12．【湖北省黄冈中学2020届高三下学期适应性考试】已知函数()()ln 1ln f x ax x a x =-+，()f x 的导数为()f x '.（1）当1a >-时，讨论()f x '的单调性；（2）设0a >，方程()3f x x e =-有两个不同的零点()1212,x x x x <，求证121x e x e+>+. 13.【湖南省永州市宁远、道县、东安、江华、蓝山、新田2020届高三下学期六月联考】已知函数()()()ln 12f x a x x a =+-∈R ．（1）讨论()f x 的单调性；（2）当0x ≥时，()1xf x e ≥-，求实数a 的取值范围．14．【2020届山西省高三高考考前适应性测试（二）】已知函数()xf x ae ex =-，()()ln 1xg x x b x e =--，其中,a b ∈R .（1）讨论()f x 在区间()0,∞+上的单调性；（2）当1a =时，()()0f x g x ≤，求b 的值.15．【河南省2020届高三（6月份）高考数学（文科）质检】已知函数2()22ln ()f x x ax x a R =-+∈.（1）讨论函数()f x 的单调性；（2）若()f x 存在两个极值点()1221,x x x x >，求证：()()()2121(2)f x f x a x x -<--. 16.【山东省2020年普通高等学校招生统一考试数学必刷卷】已知实数0a >，函数()22ln f x a x a x x=++，()0,10x ∈．（1）讨论函数()f x 的单调性；（2）若1x =是函数()f x 的极值点，曲线()y f x =在点()()11,P x f x ，()()22,Q x f x ()12xx <处的切线分别为12,l l ，且12,l l 在y 轴上的截距分别为12,b b ．若12//l l ，求12b b -的取值范围．17.【福建省2020届高三（6月份）高考数学（理科）模拟】已知函数()()()2ln 222f x x a x x =++++，0a >.（1）讨论函数()f x 的单调性；（2）求证：函数()f x 有唯一的零点.18．【山东省潍坊市五县2020届高三高考热身训练考前押题】已知函数()f x 满足222(1)()2(0)2x f f x x f x e -'=+-，21()(1)24x g x f x a x a ⎛⎫=-+-+ ⎪⎝⎭，x ∈R ．（1）求函数()f x 的解析式；（2）求函数()g x 的单调区间；（3）当2a ≥且1≥x 时，求证：1ln ln x e x e a x x--<+-．19．【陕西省商洛市商丹高新学校2020届高三下学期考前适应性训练】已知函数3()ln ()f x x a x a R =-∈.∈1）讨论函数()f x 的单调性∈∈2）若函数()y f x =在区间(1,]e 上存在两个不同零点∈求实数a 的取值范围.20．【2020年普通高等学校招生全国统一考试伯乐马模拟考试】已知函数()()22xxf x ax a e e =-++.（1）讨论函数()f x 的单调性；（2）若函数()()()2212x x g x f x ax x a e e =-++-存在3个零点，求实数a 的取值范围. 21．【金科大联考2020届高三5月质量检测】已知函数()()()()()22224ln 2144f x x ax x a x a a x a =--+++∈R ．（∈）讨论函数()f x 的单调性；（∈）若0a ≤，证明：函数()f x 在区间)1,a e -⎡+∞⎣有且仅有一个零点．22．已知函数.（1）若，求函数的单调区间；（2）求证：对任意的，只有一个零点.【来源】全国Ⅱ卷2021届高三高考数学（理）仿真模拟试题 23．已知函数. （1）当时，判断的单调性；（2）若有两个极值点，求实数的取值范围.【来源】安徽省合肥六中2021届高三6月份高考数学（文）模拟试题 24．已知函数. （1）求的单调性；（2）设函数，讨论的零点个数. 【来源】重庆市高考康德卷2021届高三模拟调研卷数学试题（三） 25．已知函数，（1）讨论的单调性；（2）若，，，用表示，的最小值，记函数，，讨论函数的零点个数．【来源】山东省泰安肥城市2021届高三高考适应性训练数学试题（二） 26．已知（）（1）讨论的单调性；（2）当时，若在上恒成立，证明：的最小值为. 【来源】贵州省瓮安中学高三2021届6月关门考试数学（理）试题27．已知函数.（1）讨论的单调性；()321()13f x x a x x =--+2a ＝-()f x a ∈R ()f x ()21ln 2f x x ax x ax =-+1a =()f x ()f x a ()()cos sin ,0,2f x x x x x π=-∈()f x ()()(01)g x f x ax a =-<<()g x ()ln()xf x x a x a=+-+a R ∈()f x 4a =()1cos (2sin )2g x x x mx x =++0m >}{min ,m n m n }{()min ()()h x f x g x =，[],x ππ∈-()h x ()ln f x x ax =+a R ∈()f x 1a =()()1f x k x b ≤++()0,∞+221k b k +--1e -+2()2ln ,()f x x ax x a R =+++∈()f x（2）若恒成立，求的最大值.【来源】广东省佛山市五校联盟2021届高三5月数学模拟考试试题 28．已知函数．（1）若，证明：在单调递增；（2）若恒成立，求实数的取值范围．【来源】黑龙江省哈尔滨市第三中学2021届高三五模数学（理）试题 29．已知函数．（1）若在上为增函数，求实数a 的取值范围；（2）设，若存在两条相互垂直的切线，求函数在区间上的最小值．【来源】四川省达州市2021 届高三二模数学（文）试题 30．已知函数. （1）如果函数在上单调递减，求的取值范围；（2）当时，讨论函数零点的个数.【来源】内蒙古赤峰市2021届高三模拟考试数学（文）试题 31．已知函数．（1）若在R 上是减函数，求m 的取值范围；（2）如果有一个极小值点和一个极大值点，求证有三个零点．【来源】安徽省淮南市2021届高三下学期一模理科数学试题32．已知函数．（1）若函数在上为增函数，求实数的取值范围；（2）当时，证明：函数有且仅有3个零点．【来源】重庆市第二十九中学校2021届高三下学期开学测试数学试题()xf x e ≤a ()ln x f x xe ax a x =--0a ≤()f x ()0,∞+()0f x ≥a 21()cos 2f x x ax x =++()f x [0,)+∞21()()2g x f x x =-()g x sin ()1()x g x F x x -+=,2ππ⎡⎤⎢⎥⎣⎦1()ln(1)1f x a x x =-+-()()22g x f x x =-+(1,)+∞a 0a >()y f x =21()e 1()2x f x x mx m =+-+∈R ()f x ()f x 1x 2x ()f x ()e sin 1xf x ax x =-+-()f x ()0,∞+a 12a ≤<()()()2g x x f x =-11/ 11。

2020高考数学(理科)二轮专题复习课标：考前增分策略第2部分第5关 Word版含答案

③
代入椭圆方程并整理，得(4k2＋3)x2－8k2x＋4(k2－3)
＝0.
设 A(x1，y1)，B(x2，y2)，则有 x1＋x2＝4k82k＋2 3，x1x2
＝44kk22－＋33.
④
高考二轮专题复习
返回目录
在方程③中令 x＝4，得 M 的坐标为(4,3k)．从而 k1 ＝yx11－－321，k2＝yx22－－321，k3＝34k－－132＝k－12.由于 A，F，B 三点共线，则有 k＝kAF＝kBF，即有x1y－1 1＝x2y－2 1＝k.
fn＋1(xn＋1)＝xnn＋＋11＋xn＋1－1＝0，xn＋1∈12，1，于是有 fn(xn)＝0＝fn＋1(xn＋1) ＝xnn＋＋11＋xn＋1－1<xnn＋1＋xn＋1－1＝fn(xn＋1)．
高考二轮专题复习
返回目录
又由(1)知 fn(x)在12，1上是单调递增的，故 xn<xn＋1(n≥2)，所以数列 x2，x3，…，xn，…是递增数列．
高考二轮专题复习
返回目录
方法二设 xn 是 fn(x)在12，1内的唯一零点， fn＋1(xn)fn＋1(1)＝(xnn＋1＋xn－1)(1n＋1＋1－1) ＝xnn＋1＋xn－1<xnn＋xn－1＝0，则 fn＋1(x)的零点 xn＋1 在(xn,1)内，故 xn<xn＋1(n≥2)，所以数列 x2，x3，…，xn，…是递增数列．
【例 2】设函数 fn(x)＝xn＋bx＋c(n∈N*，b，c∈R)． (1)设 n≥2，b＝1，c＝－1，证明：fn(x)在区间12，1 内存在唯一零点； (2)设 n＝2，若对任意 x1，x2∈[－1,1]，有|f2(x1)－ f2(x2)|≤4，求 b 的取值范围；

2020年高考数学(文)二轮专项复习专题12 不等式选讲

专题12 不等式选讲不等式选讲是高考的选考内容之一，考查的重点是不等式的证明、绝对值不等式的解法以及数学归纳法在不等式中的应用等，命题的热点是绝对值不等式的解法，以及绝对值不等式与函数的综合问题的求解．本部分命题形式单一、稳定，是三道选考题目中最易得分的，所以可重点突破.【知识要点】1．含有绝对值的不等式的解法 (1)|f (x )|＞a (a ＞0)⇔f (x )＞a 或f (x )＜－a ； (2)|f (x )|＜a (a ＞0)⇔－a ＜f (x )＜a ；(3)|x －a |＋|x －b |≥c (c ＞0)和|x －a |＋|x －b |≤c (c ＞0)型不等式的解法法一：利用绝对值不等式的几何意义求解，体现了数形结合的思想；法二：利用“零点分段法”求解，体现了分类讨论的思想； 2．绝对值三角不等式|a |－|b |≤|a ±b |≤|a |＋|b |.此性质可用来解不等式或证明不等式． 3．基本不等式定理1：设a ，b ∈R ，则a 2＋b 2≥2ab .当且仅当a ＝b 时，等号成立．定理2：如果a ，b 为正数，则a ＋b2≥ab ，当且仅当a ＝b 时，等号成立．定理3：如果a ，b ，c 为正数，则a ＋b ＋c 3≥3abc ，当且仅当a ＝b ＝c 时，等号成立．定理4：(一般形式的算术—几何平均不等式)如果a 1、a 2、…、a n 为n 个正数，则a 1＋a 2＋…＋a nn ≥na 1a 2…a n ，当且仅当a 1＝a 2＝…＝a n 时，等号成立． 4．柯西不等式(1)设a ，b ，c ，d 为实数，则(a 2＋b 2)(c 2＋d 2)≥(ac ＋bd )2，当且仅当ad ＝bc 时等号成立． (2)若a i ，b i (i ∈N *)为实数，则(∑ni ＝1a 2i )(∑ni ＝1b 2i )≥(∑ni ＝1a i b i )2，当且仅当b i ＝0(i ＝1,2，…，n )或存在一个数k ，使得a i ＝kb i (i ＝1,2，…，n )时，等号成立．(3)柯西不等式的向量形式：设α，β为平面上的两个向量，则|a |·|β|≥|α·β|，当且仅当这两个向量同向或反向时等号成立．【复习要求】（1）理解绝对值的几何意义，并能利用绝对值不等式的几何意义证明以下不等式：① ;b a b a +≤+② ;b c c a b a -+-≤-（2）会利用绝对值的几何意义求解以下类型的不等式：c b ax ≤+ c b ax ≥+ a b x c x ≥-+-（3）会用不等式①和②证明一些简单问题。

2020届高三二轮复习数学(全国卷)备考策略最全最新

转向
素养导向下高考数学命题走向
2.能力立意与素养导向比较（强调、特点、目标与要求）
能
能
力
力
立
立
意
意
与比较
素养导向
素养导向
强调特点目标
强调特点要求目的
知识、智力、能力和技能的全面考查
追求知识覆盖全面，题目结构完整
目标指向明确，要有一定的反应速度
不仅是知识和智力，更是知识迁移和后天习得
数据分析
收集数据，整理数据，提取信息，构建模型，进行推断，获得结论.
素养导向下高考数学命题走向
1.中国学生发展素养导向（总体框架、基本内涵确定考查目标）
中国学生发提展出核心素养
核心素养的总体框架
高考评价体系
核心素养的基本内涵
命题
考确查标定目志
标
能素力养立导意向
探索和表述论证过程，理解命题体系，有逻辑地表达与交流
数学学科核心素养
数学建模
发现和提出问题，建立和求解模型，检验和完善模型，分析和解决问题.
直观想象
建立数与形的联系，利用几何图形描述问题，借助几何直观理解问题，运用空间想象认识事物.
数学运算
理解运算对象，掌握运算法则，探索运算思路，选择运算方法，设计运算过程，求得运算结果.
与原理科相比
映射三视图算法系统抽样几何概型二元一次不等式组与简单线性规划推理与证明定积分与微积分基本定理统计案例
增加的内容
有限样本空间百分位数空间向量与立体几何数学建模活动与数学探究活动
弱化的内容
计数原理常用逻辑用语
有限样本空间百分位数数学建模活动与数学探究活动

2020高考理科数学二轮考前复习方略练习：专题一高考解答题的审题与答题示范(一)三角函数与解三角形类

2020高考理科数学二轮考前复习方略练习：专题一高考解答题的审题与答题示范(一)三角函数与解三角形类 1 / 2 高考解答题的审题与答题示范 (一) 三角函数与解三角形类解答题［解题助思·迅速切入］ [思想流程 ] —— 三角函数问题重在 “ 变 ” —— 变角、变式

[审题方法 ] —— 审条件条件是解题的主要资料，充分利用条件间的内在联系是解题的必经之路．审察条件要充分发掘每一个条件的内涵和隐含信息，发掘条件的内在联系．

［满分示例·规范答题］ a2 (此题满分 12 分 )△ ABC的内角 A，B，C的对边分别为 a，b，c.已知△ ABC的面积为 3sin A.

典例 (1) 求 sin Bsin C；

(2) 若 6cos Bcos C=1， a=3，求△ ABC的周长 .

审题路线

标准答案阅卷现场 1 a2 第(1)问第 (2)问 (1)由题设得 2acsin B＝

，①

① ② ③ ④ ⑤ ⑥ ⑦ ⑧ ⑨ ⑩ 3sin A得 1 csin B＝ a .② 分 2 1 2 1 1 1 1 1 1 1 即 3sin A 2 点 6 分 6 分 2020高考理科数学二轮考前复习方略练习：专题一高考解答题的审题与答题示范(一)三角函数与解三角形类 2 / 2 由正弦定理得 1

sin A 变

2sin Csin B＝ 3sin A 式． ③

2 故 sin Bsin C＝3.④

(2)由题设及 (1)

得 cos Bcos C－ sin Bsin C＝－ 12，⑤ 1 B＋ C＝ 2π

即 cos(B＋C)＝－，因此， 2 3

π 故 A＝ .⑥

由题设得 1

a2 ，⑦

2bcsin A＝3sin A 即 bc＝ 8.⑧

由余弦定理得 b2＋c2－bc＝ 9，即 (b＋ c)2－ 3bc＝9，得 b＋c＝ 33.⑨ 故△ ABC 的周长为 3＋ 33.⑩

第 (1)问踩点得分说明 ①写出 1acsin B＝ a

(新高考)2020版高考数学二轮复习专项小测3“12选择+4填空”理

专项小测(三) “12选择＋4填空”时间：45分钟满分：80分一、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知全集U ＝R ，集合A ＝{x |x 2－3x ＋2≥0}，则∁R A ＝( ) A ．(1,2) B ．[1,2]C ．(－∞，1]∪[2，＋∞)D ．(－∞，1)∪(2，＋∞)解析：由题意，得∁R A ＝{x |x 2－3x ＋2＜0}＝{x |1＜x ＜2}，故选A. 答案：A2．已知i 为虚数单位，复数z (2＋i)＝3＋2i ，则下列结论正确的是( ) A ．z 的共轭复数为85－15iB ．z 的虚部为－15C ．z 在复平面内对应的点在第二象限D ．|z |＝95解析：因为复数z (2＋i)＝3＋2i ，所以z ＝3＋2i 2＋i ＝(3＋2i )(2－i )(2＋i )(2－i )＝8＋i5，由此可得z＝8＋i 5，选项A 错误；因为z ＝8－i 5，所以z 的虚部为－15，选项B 正确；z 在复平面内对应的点为⎝ ⎛⎭⎪⎫85，－15，在第四象限，选项C 错误；|z |＝⎝ ⎛⎭⎪⎫852＋⎝ ⎛⎭⎪⎫－152＝6525＝655，选项D 错误，故选B.答案：B3．已知向量AB →＝(1,2)，AC →＝(－3,1)，则AB →·BC →＝( ) A ．6 B ．－6 C ．－1D ．1解析：∵AB →＝(1,2)，AC →＝(－3,1)，∴BC →＝AC →－AB →＝(－4，－1)，∴AB →·BC →＝1×(－4)＋2×(－1)＝－6，故选B.答案：B4．下列函数既是奇函数，又在[－1,1]上单调递增的是( )A ．f (x )＝|sin x |B ．f (x )＝ln e －xe ＋xC ．f (x )＝12(e x －e －x)D ．f (x )＝ln(x 2＋1－x )解析：对于选项A ，f (－x )＝|sin(－x )|＝|sin x |＝f (x )，f (x )为偶函数，排除 A.对于选项B ，f (－x )＝lne ＋x e －x ＝－ln e －x e ＋x ＝－f (x )，f (x )为奇函数，且f (x )＝ln e －xe ＋x＝ln ⎝⎛⎭⎪⎫－1＋2e e ＋x ，易知其在[－1,1]上为减函数，排除B.对于选项C ，f (－x )＝12(e －x －e x )＝－12(e x －e －x )＝－f (x )，f (x )为奇函数．又y ＝e x 与y ＝－e －x在[－1,1]上均为增函数，所以f (x )＝12(e x －e －x )在[－1,1]上为增函数，满足条件．对于选项D ，f (－x )＋f (x )＝ln(x 2＋1＋x )＋ln(x 2＋1－x )＝ln1＝0，即f (－x )＝－f (x )，f (x )为奇函数．又f (0)＝0，f (1)＝ln(2－1)＜0＝f (0)，不满足f (x )在[－1,1]上为增函数，排除D.综上可知，选C.答案：C5．已知(x ＋1)6(ax －1)2的展开式中，x 3系数为56，则实数a 的值为( ) A ．6或－1 B ．－1或4 C ．6或5D ．4或5解析：因为(x ＋1)6(ax －1)2＝(x ＋1)6(a 2x 2－2ax ＋1)，所以(x ＋1)6(ax －1)2的展开式中x 3系数是C 36－2a ·C 46＋C 56a 2＝6a 2－30a ＋20，∴6a 2－30a ＋20＝56，解得a ＝6或－1，故选A.答案：A6．已知双曲线C ：x 2a 2－y 2b2＝1(a ＞0，b ＞0)的两条渐近线均与圆x 2＋y 2－6y ＋5＝0相切，则双曲线C 的离心率为( )A.32B.23C.62D.94解析：双曲线的渐近线方程为y ＝±b ax ，即±bx －ay ＝0，圆x 2＋y 2－6y ＋5＝0化为标准方程是x 2＋(y －3)2＝4，若渐近线与此圆相切，则3aa 2＋b2＝3ac ＝2，则e ＝c a ＝32，故选A. 答案：A7．如图，圆柱的底面半径为1，平面ABCD 为圆柱的轴截面，从A 点开始，沿着圆柱的侧面拉一条绳子到C 点，若绳子的最短长度为3π，则该圆柱的侧面积为( )A ．42π2B ．22π2C ．52π2D ．4π2解析：沿AD 将圆柱的侧面展开，绳子的最短长度即侧面展开图中A ，C 两点间的距离，连接AC ，所以AC ＝3π，展开后AB 的长度为π.设圆柱的高为h ，则AC 2＝AB 2＋h 2，即9π2＝π2＋h 2，得h ＝22π，所以圆柱的侧面积为2×π×1×22π＝42π2，故选A.答案：A8．《中国好歌曲》的五位评委给一位歌手给出的评分分别是：x 1＝18，x 2＝19，x 3＝20，x 4＝21，x 5＝22，现将这五个数据依次输入如图程序框进行计算，则输出的S 值及其统计意义分别是( )A ．S ＝2，即5个数据的方差为2B ．S ＝2，即5个数据的标准差为2C ．S ＝10，即5个数据的方差为10D ．S ＝10，即5个数据的标准差为10解析：由程序框图知：算法的功能是求S ＝(x 1－20)2＋(x 2－20)2＋…＋(x i －20)2的值，∵跳出循环的i 值为5，∴输出S ＝15×[(18－20)2＋(19－20)2＋(20－20)2＋(21－20)2＋(22－20)2]＝15×(4＋1＋0＋1＋4)＝2，故选A.答案：A9．2013年华人数学家张益唐证明了孪生素数猜想的一个弱化形式．孪生素数猜想是希尔伯特在1900年提出的23个问题之一，可以这样描述：存在无穷多个素数p ，使得p ＋2是素数，素数对(p ，p ＋2)称孪生素数．在不超过30的素数中，随机选取两个不同的数，其中能够组成孪生素数的概率是( )A.115B.215C.245D.445解析：不超过30的素数有2,3,5,7,11,13,17,19,23,29，共10个，根据素数对(p ，p ＋2)称为孪生素数，则由不超过30的素数组成的孪生素数为(3,5)，(5,7)，(11,13)，(17,19)，共有4组，能够组成孪生素数的概率为P ＝4C 210＝445，故选D. 答案：D10．函数f (x )＝sin ⎝ ⎛⎭⎪⎫ωx ＋π6(ω＞0)的最小正周期为π，将函数y ＝f (x )的图象向左平移π4个单位后得到y ＝g (x )的图象，则下列命题中不正确的是( ) A ．函数y ＝g (x )图象的两条相邻对称轴之间距离为π2B ．函数y ＝g (x )图象关于x ＝11π12对称C ．函数y ＝g (x )图象关于⎝⎛⎭⎪⎫7π24，0对称D ．函数y ＝g (x )在⎝⎛⎭⎪⎫0，5π12内为减函数解析：由题可知，函数f (x )的最小正周期为π，其中ω>0，所以ω＝2ππ＝2，所以函数f (x )＝sin ⎝ ⎛⎭⎪⎫2x ＋π6，将函数f (x )＝sin ⎝ ⎛⎭⎪⎫2x ＋π6的图象向左平移π4个单位后得到g (x )＝cos ⎝⎛⎭⎪⎫2x ＋π6，对于A 项，函数g (x )的最小正周期为T ＝2πω＝2π2＝π，相邻两条对称轴之间的距离为T 2＝π2，故A 项正确．对于选项B ，令2x ＋π6＝k π(k ∈Z )，可得函数g (x )的对称轴为x ＝k π2－π12(k ∈Z )，当k ＝2，x ＝11π12，故B 项正确．对于C 项，令2x ＋π6＝π2＋k π(k ∈Z )，可得函数g (x )的对称中心为⎝⎛⎭⎪⎫π6＋k π2，0(k ∈Z )，此时7π24不满足π6＋k π2，故C 项错误．对于选项D 项，由k π≤2x ＋π6≤(k ＋1)π(k ∈Z )，解得k π2－π12≤x ≤5π12＋k π2(k ∈Z )，当k ≥0时，函数g (x )的单调递减区间为⎝ ⎛⎭⎪⎫－π12，5π12，故D 项正确．故选C.答案：C11．长方体ABCD －A 1B 1C 1D 1中，AB ＝AA 1＝2AD ，E 是DD 1的中点，BF ＝C 1K ＝14AB ，设过点E ，F ，K 的平面与平面ABCD 的交线为l ，则直线l 与直线A 1D 1所成角的正切值为()A ．1B ．2C ．3D ．4解析：延长KE ，交CD 延长线于点M ，延长KF ，交CB 延长线于点N ，连结MN ，则MN 是过点E 、F 、K 的平面与平面ABCD 的交线l ，∵A 1D 1∥CN ，∴∠MNC 是直线l 与直线A 1D 1所成角(或所成角的补角)，设AB ＝AA 1＝2AD ＝2，∵E 是DD 1的中点，BF ＝C 1K ＝14AB ，∴DE ＝1，BF ＝C 1K＝14AB ＝12，∵CK ＝32，∴MD MC ＝DE CK ，NB NC ＝BF CK ，即MD MD ＋2＝132，NBNB ＋1＝1232，解得MD ＝4，NB ＝12，∴MC ＝4＋2＝6，CN ＝32，∴tan ∠MNC ＝MC NC ＝632＝4，∴直线l 与直线A 1D 1所成角的正切值为4，故选D. 答案：D12．对任意m ∈⎣⎢⎡⎦⎥⎤1e ，e 2，都存在x 1，x 2(x 1，x 2∈R ，x 1≠x 2)，使得ax 1－＝ax 2－＝m ln m －m ，其中e 为自然对数的底数，则实数a 的取值范围是( )A ．(e 2，＋∞) B ．(1，＋∞) C ．(1，e 2)D ．(0,1)解析：由题意可知，对任意m ∈⎣⎢⎡⎦⎥⎤1e ，e 2关于x 的方程ax －e x＝m ln m －m 总有两个不相等的实数根．令f (m )＝m ln m －m ，m ∈⎣⎢⎡⎦⎥⎤1e ，e 2，则f ′(m )＝ln m ＋1－1＝ln m ，当m ∈⎣⎢⎡⎭⎪⎫1e ，1时，f ′(m )＜0，当m ∈(1，e 2]时，f ′(m )＞0，所以f (m )在⎣⎢⎡⎭⎪⎫1e ，1上单调递减，在(1，e 2]上单调递增，所以f (m )min ＝f (1)＝－1.又f ⎝ ⎛⎭⎪⎫1e ＝1e ln 1e －1e ＝－2e ，f (e 2)＝e 2ln e 2－e 2＝e 2，且f ⎝ ⎛⎭⎪⎫1e ＞－1，所以f (m )的值域为[－1，e 2]，则所求问题转化为ax －e x ＝k (k ∈[－1，e 2])至少有两个实数根，即e x＝ax －k (k ∈[－1，e 2])至少有两个实数根．考查临界情况：当k ＝e 2时，直线y ＝ax －e 2与指数函数y ＝e x相切．由y ＝e x得y ′＝e x ，设切点为(x 0，)，则切线斜率，y 的切线方程为y －＝(x －x 0)，切线过点(0，－e 2)，得－e 2－＝(0－x 0)，即e 2＋＝x 0，显然方程e 2＋＝x 0的根为x 0＝2，此时切线的斜率k ＝e 2，如图．由图可知，当切线的斜率a ＞e 2时，方程k ＝ax －e 2有两个不相等的实数根，所以a ＞e 2，故选A.答案：A二、填空题：本题共4小题，每小题5分，共20分． 13．若sin ⎝⎛⎭⎪⎫π2＋α＝13，则cos2α＋cos α＝________.解析：由sin ⎝ ⎛⎭⎪⎫π2＋α＝13，得cos α＝13，所以cos2α＋cos α＝2cos 2α－1＋cos α＝2×⎝ ⎛⎭⎪⎫132－1＋13＝－49.答案：－4914．已知函数f (x )＝⎩⎪⎨⎪⎧3x －2－5，x ＜3，－log 2(x ＋1)，x ≥3，若f (m )＝－6，则f (m －61)＝________.解析：∵函数f (x )＝⎩⎪⎨⎪⎧3x －2－5，x ＜3，－log 2(x ＋1)，x ≥3，f (m )＝－6，∴当m ＜3时，f (m )＝3m －2－5＝－6，无解；当m ≥3时，f (m )＝－log 2(m ＋1)＝－6，解得m ＝63， ∴f (m －61)＝f (2)＝32－2－5＝－4.答案：－415．已知两圆x 2＋y 2＋4ax ＋4a 2－4＝0和x 2＋y 2－2by ＋b 2－1＝0恰有三条公切线，若a ∈R ，b ∈R ，且ab ≠0，则1a 2＋1b2的最小值为________．解析：由题意得两圆相外切，两圆的标准方程分别为(x ＋2a )2＋y 2＝4，x 2＋(y －b )2＝1，圆心分别为(－2a,0)，(0，b )，半径分别为2和1，∴4a 2＋b 2＝3，∴4a 2＋b 2＝9，∴1a 2＋1b 2＝⎝ ⎛⎭⎪⎫1a 2＋1b 2×4a 2＋b 29＝59＋b 29a 2＋4a 29b 2≥59＋49＝1，当且仅当b 29a 2＝4a 29b2时，等号成立，∴1a 2＋1b2的最小值为1.答案：116．如图，抛物线E ：y 2＝4x 的焦点为F ，点M 与F 关于坐标原点O 对称，过F 的直线与抛物线交于A ，B 两点，使得AB ⊥BM ，又A 点在x 轴上的投影为C ，则|AF |＋|AC |－|BF |－|BC |＝________.解析：设A (x 1，y 1)，B (x 2，y 2)，对于一般的抛物线方程y 2＝2px 和过焦点的直线方程x＝my ＋p2，联立直线方程与抛物线方程得y 2－2pmy －p 2＝0，则y 1y 2＝－p 2，x 1x 2＝y 212p ·y 222p ＝p 24，则x 1x 2＝1，又AB ⊥BM ，得B 在以MF 为直径的圆上，故x 22＋y 22＝1，而y 22＝4x 2 ，得1－x 22＝y 22＝4x 2，又|AF |－|BF |＝1＋x 1－(1＋x 2)＝x 1－x 2＝1x 2－x 2＝1－x 22x 2＝4x 2x 2＝4.由1－x 22＝4x 2，可得x 2＝5－2(负值舍去)，则x 1＝1x 2＝5＋2，从而可得A (5＋2,25＋2)，B (5－2，－25－2)，注意到C (5＋2,0)，可得|AC |2－|BC |2＝4(5＋2)－[42＋4(5－2)]＝0，则|AC |－|BC |＝0，故|AF |＋|AC |－|BF |－|BC |＝4.答案：4。

2020高考理科数学二轮分层特训卷：方法技巧专练(一) Word版含解析

专练(一)技法1 直接法1．[2019·唐山市摸底考试]设z ＝i (1－2i )2－i ，则|z |＝( )A.5 B ．2 C.415D ．1答案：D解析：解法一 ∵z ＝i (1－2i )2－i ＝2＋i 2－i＝(2＋i )25＝35＋45i ，∴|z |＝⎝⎛⎭⎫352＋⎝⎛⎭⎫452＝1，故选D.解法二 |z |＝⎪⎪⎪⎪⎪⎪i (1－2i )2－i ＝|i (1－2i )||2－i|＝|i||1－2i|5＝55＝1，故选D. 2．[2019·湖南长沙雅礼中学月考]设集合A ＝{1，2，3，4}，B ＝{0，1，2，4，5}，全集U ＝A ∪B ，则集合∁U (A ∩B )中的元素共有( )A ．3个B ．4个C ．5个D ．6个答案：A解析：由题意得A ∪B ＝{0，1，2，3，4，5}，A ∩B ＝{1，2，4}，所以∁U (A ∩B )＝{0，3，5}，故选A.3．[2019·广东佛山一中期末]已知△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，其中b ＝3，c ＝2.O 为△ABC 的外心，则AO →·BC →＝( )A.34B.52C.54D.56 答案：B解析：∵BC →＝AC →－AB →，∴AO →·BC →＝AO →·AC →－AO →·AB →，又O 为△ABC 的外心，b ＝3，c＝2.∴AO →在AC →，AB →上的投影分别为32，1，∴AO →·BC →＝AO →·AC →－AO →·AB →＝92－2＝52.故选B.4．[2019·全国卷Ⅰ，8]如图是求12＋12＋12的程序框图，图中空白框中应填入( )A ．A ＝12＋AB ．A ＝2＋1AC ．A ＝11＋2AD ．A ＝1＋12A答案：A 解析：本题主要考查含有当型循环结构的程序框图，考查考生的推理论证能力，考查的核心素养是逻辑推理．A ＝12，k ＝1，1≤2成立，执行循环体；A ＝12＋12，k ＝2，2≤2成立，执行循环体；A ＝12＋12＋12，k ＝3，3≤2不成立，结束循环，输出A .故空白框中应填入A ＝12＋A .故选A. 技法2 排除法5．[2019·全国卷Ⅰ，1]已知集合M ＝{x |－4<x <2}，N ＝{x |x 2－x －6<0}，则M ∩N ＝( ) A ．{x |－4<x <3} B ．{x |－4<x <－2} C ．{x |－2<x <2} D ．{x |2<x <3} 答案：C解析：本题主要考查集合的交运算、解一元二次不等式等，考查考生的化归与转化能力、运算求解能力，考查的核心素养是数学运算．通解 ∵N ＝{x |－2<x <3}，M ＝{x |－4<x <2}，∴M ∩N ＝{x |－2<x <2}，故选C. 优解由题得N ＝{x |－2<x <3}．∵－3∉N ，∴－3∉M ∩N ，排除A ，B ；∵2.5∉M ，∴2.5∉M ∩N ，排除D.故选C.6．[2019·安徽五校第二次质检检测]函数y ＝x 2＋12x的图象大致为( )答案：C解析：因为函数y ＝x 2＋12x 为奇函数，所以其图象关于原点对称，当x >0时，y ＝12x 2＋1x 2＝121＋1x 2，所以函数y ＝x 2＋12x 在(0，＋∞)上单调递减，所以排除选项B ，D ；又当x ＝1时，y ＝22<1，所以排除选项A ，故选C.7．[2019·广东广州一测]如图，一高为H 且装满水的鱼缸，其底部装有一排水小孔，当小孔打开时，水从孔中匀速流出，水流完所用时间为T .若鱼缸水深为h 时，水流出所用时间为t ，则函数h ＝ f (t )的图象大致是( )答案：B解析：水位由高变低，排除C ，D.水流完半缸前下降速度先快后慢，水流完半缸后下降速度先慢后快，故选B.8．[2019·长春市质量检测(二)]定义在[0，π]上的函数y ＝sin ⎝⎛⎭⎫ωx －π6(ω>0)有零点，且值域M ⊆⎣⎡⎭⎫－12，＋∞，则ω的取值范围是( ) A.⎣⎡⎦⎤12，43 B.⎣⎡⎦⎤43，2 C.⎣⎡⎦⎤16，43 D.⎣⎡⎦⎤16，2 答案：C解析：法一由0≤x ≤π，得－π6≤ωx －π6≤ωπ－π6，当x ＝0时，y ＝－12.因为函数y ＝sin ⎝⎛⎭⎫ωx －π6在[0，π]上有零点，所以0≤ωπ－π6，ω≥16.因为值域M ⊆⎣⎡⎭⎫－12，＋∞，所以ωπ－π6≤π＋π6，ω≤43，从而16≤ω≤43.故选C. 法二当ω＝2时，因为x ∈[0，π]，所以2x －π6∈⎣⎡⎦⎤－π6，116π，则y ∈[－1，1]⃘⎣⎡⎭⎫－12，＋∞，排除B 、D.当ω＝14时，满足条件，排除A ，故选C.技法3 特值法9．已知a ，b 为实数，且a ≠b ，a <0，则( )A ．a >2b －b 2aB ．a <2b －b 2aC ．a ≥2b －b 2aD ．a ≤2b －b 2a答案：B解析：因为a ，b 为实数，且a ≠b ，a <0，所以a －⎝⎛⎭⎫2b －b 2a ＝(a －b )2a <0，所以a <2b －b 2a .10．方程ax 2＋2x ＋1＝0至少有一个负根的充要条件是( ) A ．0＜a ≤1 B ．a ＜1C ．a ≤1D ．0＜a ≤1或a ＜0 答案：C解析：当a ＝0时，x ＝－12，故排除A 、D.当a ＝1时，x ＝－1，排除B.11．计算tan ⎝⎛⎭⎫π4＋αcos 2α2cos 2⎝⎛⎭⎫π4－α＝( )A ．－2B ．2C ．－1D ．1 答案：D解析：取α＝π12，则原式＝tan ⎝⎛⎭⎫π4＋π12cos π62cos 2⎝⎛⎭⎫π4－π12＝3×322×34＝1.12．如图所示，在▱ABCD 中，AP ⊥BD ，垂足为点P ，且AP ＝3，则AP →·AC →＝________.答案：18解析：把▱ABCD 看成正方形，则点P 为对角线的交点，AC ＝6，则AP →·AC →＝18.技法4 图解法13．[2019·全国卷Ⅰ，7]已知非零向量a ，b 满足|a |＝2|b |，且(a －b )⊥b ，则a 与b 的夹角为( )A.π6B.π3C.2π3D.5π6 答案：B解析：本题主要考查平面向量的垂直、平面向量的夹角，考查考生的化归与转化能力、运算求解能力，考查的核心素养是逻辑推理、数学运算．设a 与b 的夹角为α，∵(a －b )⊥b ，∴(a －b )·b ＝0，∴a·b ＝b 2，∴|a |·|b |cos α＝|b |2，又|a |＝2|b |，∴cos α＝12，∵α∈(0，π)，∴α＝π3.故选B.14．[2018·全国卷Ⅰ，12]设函数f (x )＝⎩⎪⎨⎪⎧2－x ，x ≤01，x >0，则满足f (x ＋1)<f (2x )的x 的取值范围是( )A ．(－∞，－1]B ．(0，＋∞)C ．(－1，0)D ．(－∞，0) 答案：D解析：当x ≤0时，函数f (x )＝2－x 是减函数，则f (x )≥f (0)＝1.作出f (x )的大致图象如图所示，结合图象可知，要使f (x ＋1)<f (2x )，则需⎩⎪⎨⎪⎧x ＋1<0，2x <0，2x <x ＋1或⎩⎨⎧x ＋1≥0，2x <0所以x <0，故选D.15．[2019·河北保定摸底]已知实数x ，y 满足⎩⎪⎨⎪⎧x －2y ≤0，2x ＋y －10≤0，x ≥1，设向量a ＝(y －2x ，m )，b ＝(1，－1)，若a ∥b ，则m 的最大值为( )A ．－6B ．6C ．1D ．－1 答案：B解析：因为a ＝(y －2x ，m )，b ＝(1，－1)，a ∥b ，所以m ＝2x －y ，作出可行域如图中阴影部分所示，做出直线2x －y ＝0，并平移，结合图象易知，m ＝2x －y 取得最大值的最优解为(4，2)，所以m 的最大值为6.故选B.16．[2019·吉林二调]已知函数f (x )＝⎩⎪⎨⎪⎧e |x －1|，x >0，－x 2－2x ＋1，x ≤0，若关于x 的方程f 2(x )－3f (x )＋a ＝0(a ∈R )有8个不等的实数根，则a 的取值范围是( )A.⎝⎛⎭⎫0，14B.⎝⎛⎭⎫13，3C ．(1，2) D.⎝⎛⎭⎫2，94 答案：D解析：函数f (x )＝⎩⎪⎨⎪⎧e |x －1|，x >0，－x 2－2x ＋1，x ≤0的图象如图，关于x 的方程f 2(x )－3f (x )＋a ＝0有8个不等的实数根， f (x )必须有4个不相等的实数根，由函数f (x )图象可知f (x )∈(1，2)，令t ＝f (x )，方程f 2(x )－3f (x )＋a ＝0化为 a ＝－t 2＋3t ，t ∈(1，2)，a ＝－t 2＋3t ，开口向下，对称轴为t ＝32，可知a 的最大值为－⎝⎛⎭⎫322＋3×32＝94， a 的最小值为2(取不到)，所以a ∈⎝⎛⎦⎤2，94.故选D.。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

专题复习检测
A卷
1．(2018年天津模拟)在△ABC中，内角A，B，C所对的边分别为a，b，c，且8sin
2

－2cos 2C＝7.
A＋B
2

(1)求tan C的值；
(2)若c＝，sin B＝2sin A，求a，b的值．
3

【解析】(1)在△ABC中，∵A＋B＋C＝π，

∴＝－，则sin ＝cos .
A＋B2π2C2A＋B2C
2

由8sin2－2cos 2C＝7，得8cos2－2cos 2C＝7.
A＋B2C
2

∴4(1＋cos C)－2(2cos
2
C－1)＝7，

即(2cos C－1)2＝0，解得cos C＝.
1
2

∵0＜C＜π，∴C＝，∴tan C＝tan＝.
π3π
3
3

(2)由sin B＝2sin A，得b＝2a.①

又c＝，由余弦定理得c2＝a2＋b2－2abcos ，
3
π
3

即a2＋b2－ab＝3.②
联立①②，解得a＝1，b＝2.
2．(2019年陕西宝鸡检测)等差数列{an}的前n项和为Sn，数列{bn}是等比数列，满足
a1＝3，b1＝1，b2＋S2＝10，a5－2b2＝a3.
(1)求数列{an}和{bn}的通项公式；
(2)若cn＝Error!设数列{cn}的前n项和为Tn，求T2n.
【解析】(1)设等差数列{a
n}的公差为d，等比数列{bn
}的公比为q.

∵a1＝3，b1＝1，b2＋S2＝10，a5－2b2＝a3，
∴Error!解得d＝2，q＝2.
∴an＝2n＋1，bn＝2
n－1
.

(2)由(1)知S
n
＝＝n(n＋2)，

n3＋2n＋1


∴cn＝
Error!

∴T2n＝＋(21＋23＋25＋…＋2
2n－1
)＝＋.

(1－13＋13－15＋…＋12n－1－12n＋1)
2n
2n＋1
24n－1


3
3．某商场计划销售某种产品，现邀请生产该产品的甲、乙两个厂家进场试销10天．两
个厂家提供的返利方案如下：甲厂家每天固定返利70元，且每卖出一件产品厂家再返利2
元；乙厂家无固定返利，卖出40件以内(含40件)的产品，每件产品厂家返利4元，超出40
件的部分每件返利6元．经统计，两个厂家这10天的销售量如下茎叶图所示.

(1)现从甲厂家试销的10天中抽取两天，求这两天的销售量都大于40的概率；
(2)若将频率视作概率，回答以下问题：
①记乙厂家的日返利额为X(单位：元)，求X的分布列和数学期望；
②商场拟在甲、乙两个厂家中选择一家长期销售，如果仅从日返利额的角度考虑，请利
用所学的统计学知识为商场作出选择，并说明理由．

【解析】(1)记“抽取的两天销售量都大于40”为事件A，则P(A)＝＝.
C22C2101
45

(2)①设乙产品的日销售量为a，则
当a＝38时，X＝38×4＝152；
当a＝39时，X＝39×4＝156；
当a＝40时，X＝40×4＝160；
当a＝41时，X＝40×4＋1×6＝166；
当a＝42时，X＝40×4＋2×6＝172.
∴X的所有可能取值为：152,156,160,166,172.
∴X的分布列为
X152156160166172

p
1101515251
10

∴EX＝152×＋156×＋160×＋166×＋172×＝162.
1101515251
10

②依题意，甲厂家的日平均销售量为：
38×0.2＋39×0.4＋40×0.2＋41×0.1＋42×0.1＝39.5，
∴甲厂家的日平均返利额为：70＋39.5×2＝149元．
由①得乙厂家的日平均返利额为162元(＞149元)，
∴推荐该商场选择乙厂家长期销售．
4．(2019年山东淄博模拟)如图，六面体ABCDHEFG中，四边形ABCD为菱形，
AE，BF，CG，DH都垂直于平面ABCD.若DA＝DH＝DB＝4，AE＝CG＝3.
(1)求证：EG⊥DF；
(2)求BE与平面EFGH所成角的正弦值．
【解析】(1)证明：连接AC，由AECG可知四边形AEGC为平行四边形，∴EG∥AC.
又AC⊥BD，AC⊥BF，∴EG⊥BD，EG⊥BF.
∵BD∩BF＝B，∴EG⊥平面BDHF.
又DF⊂平面BDHF，∴EG⊥DF.
(2)设AC∩BD＝O，EG∩HF＝P，由已知得平面ADHE∥平面BCGF，∴EH∥FG.
同理可得EF∥HG.
∴四边形EFGH为平行四边形，∴P为EG的中点．又O为AC的中点，∴OPAE，
从而OP⊥平面ABCD.
又OA⊥OB，∴OA，OB，OP两两垂直，得BF＝2.
如图，建立空间直角坐标系O－xyz，则B(0,2,0)，E(2，0,3)，F(0，2,2)，P(0,0,3)，
3

∴＝(2，－2,3)，＝(2，0,0)，＝(0,2，－1)．
BE→ 3PE→ 3PF
→

设平面EFGH的法向量为n＝(x，y，z)，
由Error!得
Error!

令y＝1，则z＝2.∴n＝(0,1,2)．
设BE与平面EFGH所成角为θ，

则sin θ＝＝.
|BE→ ·n|
|BE→ |·|n|
45

B卷
5．(2019年广东广州综合测试)已知点C(1,0)，点A，B是⊙O：x
2＋y2
＝9上任意两个不

同的点，且满足·＝0，设P为弦AB的中点．
AC→ BC
→

(1)求点P的轨迹T的方程；
(2)试探究在轨迹T上是否存在这样的点：它到直线x＝－1的距离恰好等于到点C的距
离？若存在，求出这样的点的坐标；若不存在，说明理由．
【解析】(1)连接CP，OP.
由·＝0，知AC⊥BC，
AC→ BC
→

∴|CP|＝|AP|＝|BP|＝|AB|.
1
2

易知|OP|2＋|AP|2＝|OA|2，
即|OP|2＋|CP|2＝9.
设点P(x，y)，则(x2＋y2)＋[(x－1)2＋y2]＝9，化简得x2－x＋y2＝4.
(2)存在．根据抛物线的定义，到直线x＝－1的距离等于到点C(1,0)的距离的点都在抛物

线y2＝2px(p>0)上，其中＝1.
p
2

∴p＝2，故抛物线方程为y2＝4x，
联立Error!化简得x2＋3x－4＝0，
解得x1＝1，x2＝－4.
由x≥0，故取x＝1，此时y＝±2.
故满足条件的点存在，其坐标为(1，－2)和(1,2)．
6．(2018年北京顺义区二模)已知函数f(x)＝e
2x
＋mx，其中m≤0.

(1)当m＝－1时，求曲线y＝f(x)在点(0，f(0))处的切线方程；
(2)若不等式f(x)＞0在定义域内恒成立，求实数m的取值范围．
【解析】(1)当m＝－1时，f(x)＝e2x－x，则f′(x)＝2e2x－1，∴f′(0)＝1.
又f(0)＝1，∴曲线y＝f(x)在点(0，f(0))处的切线方程为y＝x＋1.
(2)f(x)的定义域为R，且f′(x)＝2e
2x
＋m，m≤0.

当m＝0时，f(x)＝e2x＞0恒成立，满足条件．

当m＜0时，由f′(x)＞0，解得x＞ln，
12(－m
2
)

∴f(x)在内单调递增，
(12ln(－m2)，＋∞)

在内单调递减．
(－∞，12ln(－m2))
∴f(x)在x＝ln处取得最小值
12(－m
2
)

.
m2[ln(－m
2
)－1]

∴＞0，解得－2e＜m＜0.
m2[ln(－m
2
)－1]

综上，当m∈(－2e,0]时，不等式f(x)＞0在定义域内恒成立．